2. 四川大学灾后重建与管理学院, 成都 610207;
3. 地下信息探测技术与仪器教育部重点实验室, 北京 100083;
4. 深地科学与工程教育部重点实验室, 四川大学, 成都 610065
2. Institute for Disaster Management and Reconstruction, Sichuan University, Chengdu 610207, China;
3. Key Laboratory of Geo-detection of Ministry of Education, Beijing 100083, China;
4. Key Laboratory of Deep Earth Science and Engineering(Sichuan University), Ministry of Education, Chengdu 610065, China
大地电磁测深法(Magnetotellurics, MT)是一种天然源频率域电磁法,其以自然产生的平面电磁波为场源,通过观测地表正交的电磁场分量获取地下的电阻率结构(陈乐寿和王光锷,1990).有限单元法由于可以利用非结构化不规则三角形或四面体网格对地下空间进行离散,在起伏地形及复杂异常体的构建中有天然的优势(Li and Dai, 2011; Mitsuhata and Uchida, 2004),成为大地电磁测深数值模拟方法的重要分支.相对有限差分法或积分方程法而言,有限单元法运算效率较低,因此对其运算效率的提高也成为学界研究的热点.除并行计算外,其改进的策略主要集中在插值形函数、网格剖分方式、二次场及边界条件控制,求解器的选择及其预条件化等方面(如,陈小斌等,2000;刘小军等,2007;汤井田等,2009;吴娟等,2012;汤井田等,2014;殷长春等,2017).其中,求解离散获得的大型线性稀疏矩阵的方法一直是这一领域研究的核心问题.
此类方法笼统而言可以分为三类,一类为直接法,即将离散系统矩阵利用LU或LDLT分解法分解为三角矩阵,之后通过消元法一次进行求解(Grayver and Kolev, 2015; Schwarzbach et al., 2011),其主要优点为计算方法成熟,稳定性较高,且有较多高效的通用开源及商业软件包可以使用,如MUMPS,PARDISO等.特别是在可控源类电磁法中,对于多个相同频率、不同位置的发射场源而言,由于离散获得的系统矩阵相同,而仅有右端项不同,因此进行一次矩阵分解就可以应用于多个场源的计算(Cai et al., 2017),从而可以大大提高正演模拟的效率.而直接法的主要不足在于矩阵分解时,存储额外元素需要占用大量内存,以及元素交换(pivoting)时大量时间的占用,特别是当求解网格自由度(DoF)较大时,所需的内存空间对于目前的普通计算机平台而言较难承受.
另一类为多重网格法,指在离散尺度不同的多级网格中,在较稀疏的网格下首先消除较低频率的误差,之后在较细网格中逐级消除高频误差,并进行迭代求解的方法(柳建新等,2011;杨振威等,2017).然而,对于传统的几何多重网格法而言,建立多级网格需要严格的从粗至细的等级细分(hierarchical refinement),这在非结构化有限单元网格中难以实现.此外,在大地电磁法中获得的系统矩阵往往并非对角占优矩阵,通用的代数多重网格算法往往效果欠佳(Beck, 1999).
最后一类为Krylov子空间法,通过猜测一个初始值,并在初始值的基础上多次迭代进行求解(Liu et al., 2008; Siripunvaraporn et al., 2002).对于大地电磁测深法而言,由于MT的每个“场源”为不同频率的平面波,其方程离散系统内包含角频率参数;因此,对应一个特定频率进行分解获得的L/U矩阵通常无法直接应用到另一个频率当中(Schwarzbach, 2009).由此可知,利用直接法进行大地电磁测深数值模拟并不存在明显的技术优势.Krylov子空间方法由于其算法简洁,所需额外存储量及运算量均较小的优点,已成为大地电磁测深数值模拟的主要求解方法.以往学者多利用通用求解器,如BiCGstab或GMRES等算法,以及相应的通用预条件算法,如不完全LU分解,不完全乔姆斯基分解等算法进行计算(徐志锋和吴小平,2010;王亮等,2013;苏晓波等,2015).
然而,由于三维电磁有限单元法的双旋度系统方程的特殊性和非结构化网格求解域离散方式的复杂性,变分问题离散成的线性系统往往具有很严重的病态性,常规预条件矩阵算法效率通常较低.Um等(2013)指出,如果将ILU矩阵进行元素置换计算的容差设置得很小(~10-8),即在ILU分解接近于LU分解(LU分解可以近似地看作容差为零的ILU分解)时,作为预条件矩阵使用Krylov子空间算法时将有较大提升.然而,容差设置接近于零时,ILU分解的时间与内存耗费已经接近于普通LU分解的量级(Saad, 2003),再利用Krylov子空间类算法,相对于直接法并无优势.因此,有必要针对双旋度系统方程的特点,研究一种高效的预条件方法,以提高电磁法有限元数值模拟计算的效率.
后文将依据有限差分法中LIN(Low induction numbers)预条件方法的思路(Druskin et al., 1999; Newman and Alumbaugh, 2002),首先从时谐麦克斯韦方程的变分形式出发,分析导致迭代方法求解效率下降的旋度算子零空间问题,并针对棱边有限元的特点,基于亥姆霍兹分解理论,利用节点辅助空间构建预条件算法,最后利用合成模型的算例验证这一算法的可靠性及有效性.
1 时谐麦克斯韦方程组的变分形式与散度规范问题假设求解域Ω中不存在自由电荷,一般形式的麦克斯韦方程组可以表示为
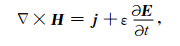
|
(1a) |
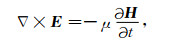
|
(1b) |
其中,H=H(r, t)、E=E(r, t)以及j=j(r, t)分别为随时间及空间变化的磁场、电场与电流密度场,μ与ε分别为磁导率和介电常数.若引入欧姆定律j=σE,并取时谐因子为e-iωt,对于某个固定的角频率ω,可得麦克斯韦方程组的时谐形式

|
(2a) |

|
(2b) |
电导率σ表征电性在模型中的分布,对(2b)式两侧取旋度,并将(2a)式代入(2b)式的右侧,即可消去磁场H,从而推导出电场双旋度方程(curl-curl equation)

|
(3) |
方程中,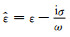
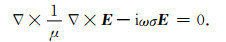
|
(4) |
对于地球物理电磁法问题,一般在求解域边界Γ的切向方向给出Dirichlet型的边界条件,即:
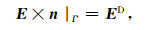
|
(5) |
n为边界法向方向,ED为边界场值.本文中,我们在求解域的上边界直接给出均匀电场边界条件,而在四周边界和底边界采用大地电磁测深一维正演计算出的电场作为边界条件.借助矢量恒等式,(4)式可转化为下述弱解问题,即寻找E∈H(curl; Ω)(H(curl)为希尔伯特向量空间中的旋度相容空间),对于所有v∈H(curl; Ω)满足变分弱形式:

|
(6) |
其中(·, ·)表示向量内积.
为了便于边界条件的确定和起伏地形的加入,频率域地球物理电磁方法的模型域除包含所研究的地下介质外,还须包含地表上方的空气域.然而,若假定空气为理想介质(σair=0),(4)式左边第二项将不复存在,又由于方程右端为零,在这一情况下,旋度算子的整个零空间(nullspace)都可能是方程的解,从而难以通过迭代求解法获得唯一解.另一方面,根据亥姆霍兹定律,要唯一确定某个矢量场,必须同时确定这一矢量场的散度和旋度.然而,若(4)式中左边第二项消失,方程将只能对矢量场旋度项进行约束,而无法对散度项进行约束.这将使得满足(4)式的E,对于任意标量场φ,有无穷多的E′=E+∇φ均可能是方程的解.
为避免上述情况,一般将空气电导率设置为一个很小而非零(如σair=10-10S·m-1)的数值(Chave and Jones, 2012),从而防止了系统的奇异化.然而,即使σ不为零,在系统近似稳态时,即当ω趋于零时,(4)式左边第二项仍将趋于零,在数值方法的截断误差下,方程的奇异问题仍可能出现(Avdeev, 2007),从而导致Krylov子空间迭代方法求解系统方程过慢,或根本无法达到所要求的精度,我们称这一问题为散度规范类问题.
要使边值问题(4)和(5)适定,消除旋度算子零空间的影响,必须加入散度规范,如库仑(Jiang et al., 1996)或洛仑兹规范(Weiss, 2013);但是,若直接在求解区域显式地规定矢量场的散度,如在空气中规定库仑规范:
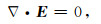
|
(7) |
而在地下介质中规定:

|
(8) |
并将上述方程与(4)式进行联立,由于未知量的个数(电场值)不变,而方程的数量增加了,这一问题将变为超定,仍无法获得唯一解.解决这一问题的自然思路是引入更多的未知量,如加入电场标量势(E-V)(Schwarzbach, 2009),或者放弃求解E,转而直接求解电场矢量势和磁场标量势(T-Ω)(Mitsuhata and Uchida, 2004),或磁矢势和电场标量势(A-φ)(陈辉等, 2016; Weiss, 2013).此外,散度校正类方法并不在求解系统方程时加入散度规范(Mackie et al., 1994; Smith, 1996),而是在迭代计算出电场E之后,利用散度规范求解出∇φ,并对电场进行修正(Farquharson and Miensopust, 2011).
类似地,Newman和Alumbaugh(2002)提出利用预条件计算的形式引入规范条件,从而达到回避旋度算子零空间,提高迭代方法收敛速度的效果.在此,我们沿着Newman等人的思路,并不将散度规范显式的加入系统方程中,也不将双旋度方程获得的电磁场矢量依次进行散度校正,而是基于亥姆霍兹分解理论,在棱边有限元离散系统中研究构建预条件方法,从而隐式的将预条件过程加入散度规范,具体步骤将在第3节中介绍.
2 非结构化四面体棱边有限元在三维棱边有限元问题中,未知量(电场)定义在网格单元(如四面体或六面体)的棱边上.对于某个四面体单元的六个棱边,有:

|
(9) |
其中, Ek为定义在第k条棱边上的切向电场值,而Nk为相应棱边的矢量形函数,为简单起见,使用最低阶形函数;若设第k个棱边由节点i→j连接而成,则:
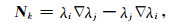
|
(10) |
式中,λ为节点的重心坐标.形函数的旋度可以相应地表示为:

|
(11) |
由此,构建(4)的离散形式,获得一个NDoF×NDoF阶,对称但非自伴(Hermitian)的复系统矩阵A,求解由这一矩阵构建的线性方程:
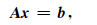
|
(12) |
从而可以得到电场在棱边上的分布;再由(2b)式(法拉第电磁感应定律),利用离散旋度算子即可求取离散磁场分布:
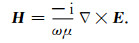
|
(13) |
若设大地电磁场的平面偏振波XY极化模式的电磁分量为Ex1, Ey1, Hx1, Hy1,YX极化模式的电磁分量为Hx2, Ex2, Hy2, Ey2,大地电磁测深阻抗张量即可通过(14)式进行计算:

|
(14) |
进而计算视电阻率与相位:
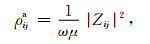
|
(15a) |

|
(15b) |
由于在采用棱边元的矢量形函数插值时,单元内部的散度场恒为零(Jin, 2014),而旋度场不为零;因此,一般认为棱边有限元中的散度规范问题是自然解决的(Liu et al., 2008).然而,在实际应用中,虽然在单元内部的电流密度的散度场为零,但不同单元之间的电流密度的法向分量并无显式的约束关系.在电导率不连续的单元边界仍可能出现不连续的电流密度,进而导致散度不为零(Farquharson and Miensopust, 2011).此外,旋度算子所具有的非平凡(non-trivial)零空间,仍可能引起Krylov子空间类算法迭代求解缓慢,尤其是在正演迭代的初期更为明显.因此,即使在棱边元形函数条件下,仍有必要考虑如何回避旋度算子的零空间问题.
3 基于亥姆霍兹分解的预条件矩阵对于线性代数系统(12),常见Krylov子空间算法多从某个初始值x0出发,采取某种线性迭代方式进行求解,可表示为:

|
(16) |
本文称C为迭代算子,其随具体采取算法的不同而各异.第j次迭代的残差为
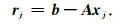
|
(17) |
一般而言,提高Krylov子空间方法效率的关键在于高效率地构建一个预条件矩阵P,转而求解线性系统

|
(18) |
从而获得x (Saad, 2003).理想的预条件矩阵一般需要满足两个条件,即:(1)P尽可能接近于A,即P-1A→I;(2)构建P的耗费远低于求解原始系统(Saad and van der Vorst, 2000).这样就可以使得原始系统的病态程度尽可能降低,同时实现系统的高效求解.为了避免直接构建预条件矩阵造成的计算及存储耗费,本研究通过求解预条件矩阵P的残差解的形式,进行隐式的预条件运算.对于预条件后的系统方程,残差的表达式(17)式将变为
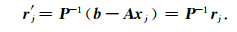
|
(19) |
简而言之,对第j次迭代进行预条件的过程也就相当于求解辅助线性系统:
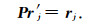
|
(20) |
为简洁起见,以下我们略去残差向量的下标j.若有理想的P→A,则(20)式转化为:

|
(21) |
显然,边界上的残差应为零,因此有边界条件为:

|
(22) |
当P=A时,P-1Ax=Ix=P-1b,也就是说第一次迭代就获得了准确解.然而,求解上述系统的难度与求解原始方程完全相同,这使得预条件失去了意义.但反过来,如果可以找到一种可以快速近似求解上述系统的方法,迭代算法就可以迅速收敛,获得满足误差要求的解.
根据亥姆霍兹定理,任何一个矢量场均可以被分解为一个无散场和无旋场的叠加(Newman and Alumbaugh, 2002),因此不妨设:
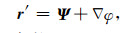
|
(23) |
并且,Ψ满足以下条件:
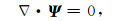
|
(24) |
此处,Ψ与φ即相当于矢量位和标量位.显然,Ψ存在于无散空间内,而∇φ存在于梯度(无旋)空间内.对于∇φ,由于梯度算子的值域空间属于旋度算子的零空间(range(grad)ker(curl)),旋度的散度恒为零,将(21)式的两侧取散度,并将(23)式代入,有:

|
(25) |
又根据(24)式,可得:

|
(26) |
由(22)式可以推出其边界条件:
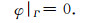
|
(27) |
这是一个拉普拉斯型方程,不难求解φ并得到残差的无旋项∇φ.而对于无散空间内的Ψ,首先将(23)式代入(21)式,并利用梯度的旋度恒为零的性质,可以得到:
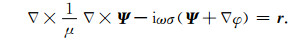
|
(28) |
在此,结合矢量恒等式:

|
(29) |
可以推得:
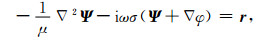
|
(30) |
其相应的边界条件为:
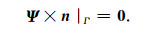
|
(31) |
将前述求解得到的∇φ代入(31)式,即可获得一个矢量泊松方程,进而求解出Ψ,从而可计算出r′=Ψ+∇φ,完成预条件过程.需要注意的是,这一预条件过程是将残差向量r′进行亥姆霍兹分解从而进行预条件运算,而非将电场或磁场场值进行亥姆霍兹分解,这一点与求解磁矢势和电场标量势的A-φ算法有着本质区别(陈辉等, 2016; Weiss, 2013).总体而言,这一预条件过程将残差分解映射到无散空间和无旋空间内,隐式地加入散度规范,从而回避了旋度算子的零空间问题,也有效地解决了散度规范问题(Weiss and Newman, 2002).此外,注意到(30)与(26)两式的联立与双旋度系统方程是完全等效的,而数值求解拉普拉斯方程与泊松方程的形式,相对于双旋度方程而言要容易得多,因此,上述流程同时满足预条件方法的两个要求,是一种较为理想的预条件手段.
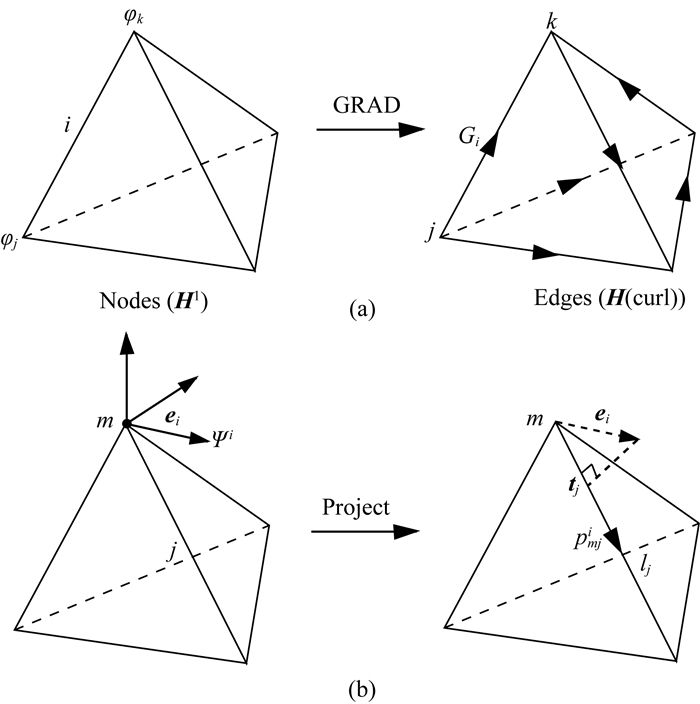
然而,在有限单元法的实际计算中,欲求解(26)式(标量拉普拉斯方程)的变分问题,必须首先在求解域内定义势场φ的分布,并定义相应的离散的散度算子和梯度算子.由于Nédélec棱边单元构成的子空间H(curl)是一个旋度相容空间,无法定义势场和此类算子.为规避这一问题,我们可以借助网格中节点单元构成的子空间H1定义势场,进而定义离散梯度算子∇(离散散度算子即为其转置),将节点空间中的势场转换到棱边空间中的矢量场(势场的梯度).若某棱边i上有坐标分别为xj和xk的节点,在利用最低阶形函数离散时,在棱边i上的局部梯度算子即可以直接利用节点j和k上的标量场定义:
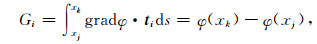
|
(32) |
其中ti为棱边i的单位方向矢量,如图 1a所示.
|
图 1 (a) 节点单元空间中的势场向棱边单元空间中的矢量场的梯度运算;(b)节点单元空间中的矢量场分量向棱边单元空间中的投影 Fig. 1 (a) Gradient operation from scalar potential field in nodal space to vector field in edge space; (b) Projection of an orthogonal vector component in nodal space to vector field in edge space |
类似地,欲求解(30)式(矢量泊松方程)的变分问题,也面临上述的散度算子和梯度算子的定义问题,同样可以借助节点单元进行辅助求解.但是,若将Ψ定义为在节点单元上的矢量场,将难以把这一矢量场利用节点元形函数直接投影至棱边上.为规避这一问题,我们可以首先将矢量场Ψ进行正交分解,即:

|
(33) |
其中ei为全局坐标系中的正交单位矢量.
由此,定义在某节点m上的第i个正交方向的矢量场,对于连接在m上的某个棱边j的投影分别为
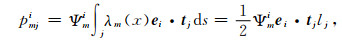
|
(34) |
其中lj是棱边j的长度,如图 1b所示,λm为节点m的形函数(Jin, 2014).这样,(30)式就转化成了三个标量泊松方程,结合(26)式对应的标量拉普拉斯方程,在预条件运算过程中,共需求解4个辅助方程.
4 算例 4.1 可靠性验证本文采用通用的COMMEMI 3D-2(Zhdanov et al., 1997)模型验证正演算法的正确性和有效性.如图 2所示,COMMEMI 3D-2是一个水平层状模型中赋存一个高阻-低阻组合三维异常体的复杂地电模型,其自提出以来已经逐渐成为大地电磁测深数值模拟领域的标准模型.我们取模型域范围为120 km×120 km×120 km,基于电磁场传播的耗散性,网格剖分程序将网格尺寸自动设置为随距中心异常体的距离的增大而增大,以减小离散后系统的网格个数,降低内存耗费;网格剖分算法基于距离函数表征几何形态,Delaunay三角剖分形成拓扑结构,并以力平衡方程约束网格质量(Du and Wang, 2006; Persson and Strang, 2004).为保证测站附近的计算精度,在所设剖面附近进行了网格自动细分,具体模型的离散化及电导率分布情况如图 3a所示,离散网格数为203853,自由度(棱边个数)为241262.一般用网格偏离度q表示网格的质量,如正四面体的q值为1,四面体的内角差越大,网格质量越差,q越小;而一般认为q值大于0.5的网格质量是可以接受的(Persson and Strang, 2004; Jin, 2014).图 3b显示了离散获得的模型网格的偏离度q(中值为0.82),说明其质量相对较高.

|
图 2 COMMEMI 3D-2模型(Zhdanov et al., 1997)的电导率分布,(a)中的黑色实线表示正演计算MT传递函数的测线位置 Fig. 2 Conductivity distribution of COMMEMI 3D-2 model (Zhdanov et al., 1997), the solid line in (a) denotes the profile where the MT transfer functions are calculated |
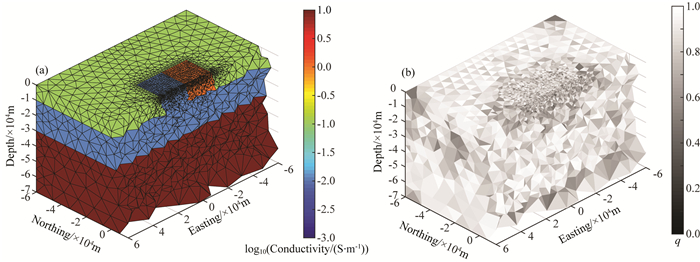
|
图 3 利用非结构化有限单元离散化的COMMEMI 3D-2模型 (a)网格剖分情况; (b)以q值表示的网格质量. Fig. 3 COMMEMI 3D-2 model discretized with unstructured finite element mesh (a) Scheme of generated mesh; (b) Mesh quality represented by q value. |
将求解域与偏微分方程离散获得系统矩阵,并根据边界条件定义右端项后,即可对离散的系统进行求解.对于双旋度系统方程,由于其系统矩阵不具备正定性,并考虑到求解预条件问题的计算量较大,为避免在一次迭代过程中同时计算P-1r′和(PT)-1r′,进行两次预条件运算,研究中选择无转置拟最小残差法(TFQMR)作为主系统的求解器.对于四个辅助系统,同样首先考虑利用Krylov子空间方法进行求解.由于泊松方程与拉普拉斯方程离散获得的系统矩阵均是对称正定的,可以利用预条件共轭梯度算法(PCG),借助不完全乔姆斯基分解(ICC)生成预条件矩阵,进行快速求解,以下简称为HD-PCG预条件方式.在此,主求解程序的停止相对残差设置为10-10,而辅助系统的停止相对残差设置为10-7.本节研究的数值模拟环境为Intel(R) core i7(R),主频为2.20 GHz的便携式计算机,装配8 GB内存,以下所有运算对比均仅用单线程进行.
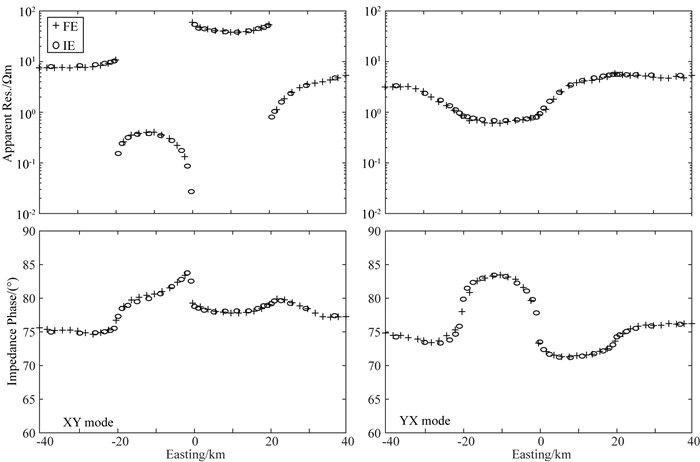
由于积分方程法被认为可以获得半解析解的求解精度,在此我们将本研究中算法计算的响应与前人利用积分方程法计算的视电阻率与相位响应(Farquharson and Miensopust, 2011)进行对比,以验证算法的可靠性.首先针对频率0.1 Hz与0.001 Hz,分别对XY模式与YX模式进行了试算.为对比计算响应,在模型地表中部设计了一条长度为80 km,点距为2 km的东西向测线,如图 2a所示.对于0.1 Hz,XY模式的情况,经过140次迭代计算,耗时310 s后,正演模拟自动停止.同样的问题在0.001 Hz,XY模式的情况下需进行152次迭代计算,耗时367 s.计算获得的测线站点位置的视电阻率与相位响应分别如图 4与图 5所示.显然,对于两个频率的视电阻率和相位响应均与前人获得的结果有较好吻合,特别是相对低频信号的0.001 Hz的响应与积分方程法结果对应较为理想,这说明研究获得的棱边元有限单元数值模拟方法及相应的预条件矩阵是可靠的.而相对高频信号0.1 Hz的响应在电阻率突变边界及测线两端位置均与积分方程结果有一定误差(在边界处最大可达到视电阻率值的20%),推测是由于网格离散不够精细造成,特别是对于测线两端的测点,由于靠近测线两端的位置更接近模型边界,网格尺度逐渐增大,不利于高频电磁场信号的模拟.此外,结构化网格(积分方程法)与非结构化网格(有限单元法)中不同的插值方法对求解也存在影响.
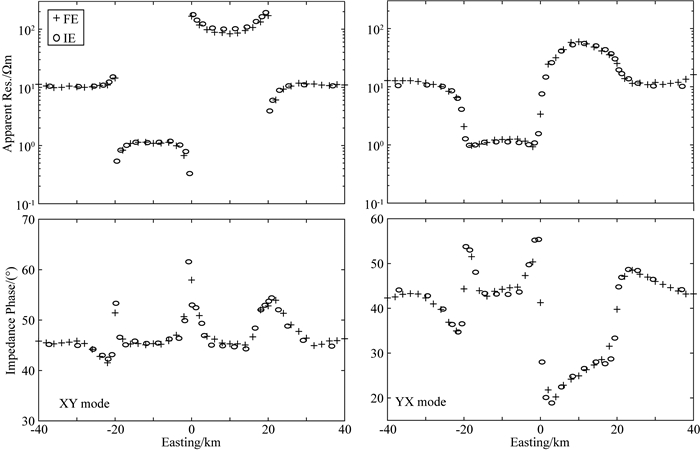
|
图 4 COMMEMI 3D-2模型0.1 Hz的视电阻率及相位响应对比;其中十字为本研究中算法获得的结果,圆圈响应来自积分方程法的结果(Farquharson and Miensopust, 2011) Fig. 4 Comparison of apparent resistivities and phases calculated for the COMMEMI 3D-2 model at a frequency of 0.1 Hz. The crosses are solution obtained using the presented method while the open circles are from Farquharson and Miensopust (2011) |
|
图 5 COMMEMI 3D-2模型0.001 Hz的视电阻率及相位响应对比;其中十字为本研究中算法获得的结果,圆圈响应来自积分方程法的结果(Farquharson and Miensopust, 2011) Fig. 5 Comparison of apparent resistivities and phases calculated for the COMMEMI 3D-2 model at a frequency of 0.001 Hz. The crosses are solution obtained using the presented method while the open circles are from Farquharson and Miensopust (2011 |
为对比基于亥姆霍兹分解的预条件方法的有效性,在此利用不完全LU分解预条件矩阵对COMMEMI 3D-2模型XY模式0.001 Hz的响应进行了对比求解,所用计算平台与参数与前述计算完全一致.然而,在计算耗时273 s,迭代3000次后,采用ILU预条件矩阵的正演迭代的残差仍达到3.19×10-7,未能收敛.可见,棱边有限元离散化获得的双旋度方程的病态程度较高,难以利用通用预条件矩阵进行求解.由于ILU预条件方法未达到自动收敛停止,为直接将HD-PCG法预条件算法与ILU方法进行对比,研究也计算了停止相对残差为3.0×10-7的情况,如图 6所示,此时HD-PCG方法迭代次数为43次,计算耗时102.1 s.显然,在同等计算精度下,HD-PCG方法的收敛效率(43次)远高于ILU方法(3000次),这说明基于亥姆霍兹分解的预条件运算大幅度的降低了双旋度系统方程的病态程度;然而,在另一方面,虽然基于亥姆霍兹分解的预条件方法的迭代次数有了大大降低,其耗时(102.1 s)相对于ILU算法(273 s)并未有相应程度的提高.究其原因,是由于在每次迭代过程中都需要调用四次Krylov子空间方法(PCG)求解辅助系统方程,导致全局计算效率偏低.

|
图 6 TFQMR算法预条件求解收敛情况对比 其中实线为利用Krylov子空间算法(PCG)求解的亥姆霍兹分解预条件算法,虚线为利用AMG算法求解的亥姆霍兹分解预条件算法,点线为ILU分解预条件算法,注意在此只截取了前1000次迭代的结果. Fig. 6 Convergence comparison of TFQMR method with different pre-conditioners The solid line denotes Helmholtz decomposition pre-conditioning with Krylov space solvers (PCG). Dashed line is the same pre-conditioning with AMG solver, while the dotted line shows result for incomplete LU pre-conditioning. Note that only the residual from first 1000 iterations are shown. |
解决上述问题的关键是如何快速求解预条件矩阵中的四个辅助系统方程.前人研究表明,求解预条件系统并不需很高的求解精度即可能有较好的预条件效果(Xu, 1996).鉴于辅助系统(拉普拉斯或泊松系统)的矩阵均为对角占优的,为求解效率起见,我们利用代数多重网格法AMG (Beck, 1999),将当前网格进行级联疏化,在较稀疏的网格下快速获得较低精度的解,利用V循环(V-cycle)近似目标网格的解,进行预条件运算(Grayver and Bürg, 2014; Hiptmair and Xu, 2007),以下简称HD-AMG预条件方式.对于上述的同一问题(XY模式,0.001 Hz),利用HD-AMG方法达到预期残差仅耗时32.7 s,大大提高了求解速度.另一方面,由于在此使用的多重网格方法的求解精度有限,预条件计算的收敛效果相对HD-PCG时的情况有所下降,导致双旋度系统方程的收敛速度下降,TFQMR算法共需迭代104次,如图 6所示;但系统方程的精度并未受预条件效果的影响.
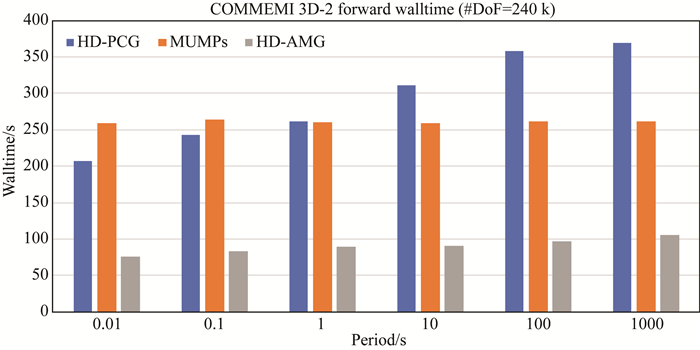
为进一步考察对比在不同频段各个方法的正演效率,研究统计了频率为100 Hz、10 Hz、1 Hz、0.1 Hz、0.01 Hz及0.001 Hz时,上述COMMEMI 3D-2模型采用TFQMR算法,并分别利用HD-PCG以及HD-AMG预条件方法的XY/YX模式平均正演计算时间.计算时间的统计利用有限元分析中常用的多波前直接求解法(MUMPs)的正演耗时作为参考,详细情况如图 7所示.图示结果显示,在较低网格自由度的情况下,采用本文提出的预条件方法的迭代解法中,HD-PCG算法的速度与直接解法基本相当,但直接法具有不受场源频率影响的优势;HD-AMG方法具有显著的效率优势,即使在低频段,耗时增加也不明显;而HD-PCG耗时随频率降低存在明显的递增趋势,这应该是由于在频率较低时,式(4)左侧第二项在系统方程中的相对权重减小,而双旋度算子的相对权重增大,其零空间影响了迭代方法的收敛效率.
|
图 7 不同频率时HD-PCG、HD-AMG与MUMPs的求解效率对比 Fig. 7 Walltime comparison of TFQMR method with different pre-conditioners (PCG, AMG) and MUMPs for different frequencies |
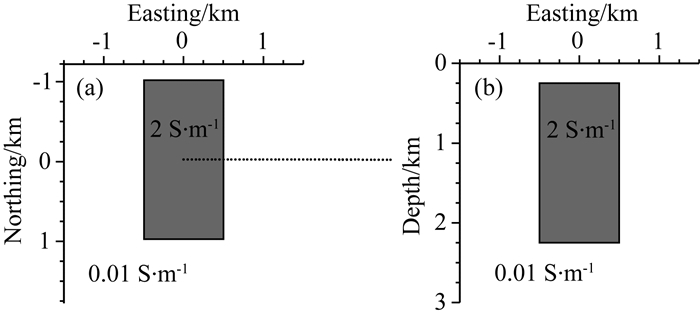
为验证本研究中实现的预条件算法对于较大自由度棱边有限单元问题的实用有效性,本文以COMMEMI 3D-1模型(图 8)为基准进行测试,模拟环境为Intel(R) Xeon(R) E5 2600,主频为2.40 GHz的服务器,装配128 GB内存,运算对比仍以单线程进行.首先,为保证严谨性,仍进行了算法计算的可靠性测试.根据模型的尺度,针对频率10 Hz与0.1 Hz,分别对XY模式与YX模式进行了试算,并与前人利用直接法计算获得的响应(Ren et al. 2013)进行了对比.由于模型本身的对称性,仅在模型地表中部的东侧布设了一条长为3 km,点距为0.1 km的测线,以对比计算获得的传递函数响应,结果如图 9和图 10所示.
|
图 8 COMMEMI 3D-1模型(Zhdanov et al., 1997)的电导率分布,(a)中的虚线表示正演计算MT传递函数的测线位置 Fig. 8 Conductivity distribution of COMMEMI 3D-1 model (Zhdanov et al., 1997), the dotted line in (a) denotes the profile where the MT transfer functions are calculated |
|
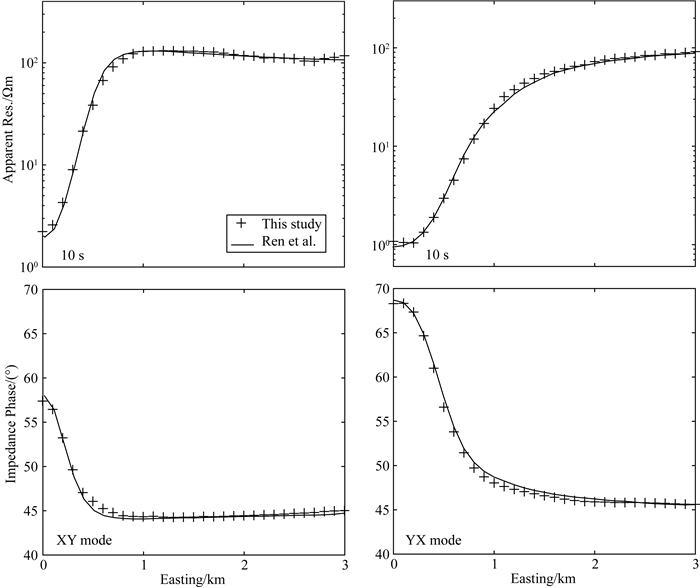
图 9 COMMEMI 3D-1模型0.1 Hz的视电阻率及相位响应对比;其中十字为本研究中算法获得的结果,实线响应来自Ren et al. (2013) Fig. 9 Comparison of apparent resistivities and phases calculated for the COMMEMI 3D-1 model at a frequency of 0.1 Hz. The crosses are solution obtained using the presented method while the solid lines are from Ren et al. (2013) |

|
图 10 COMMEMI 3D-1模型10 Hz的视电阻率及相位响应对比; 其中十字为本研究中算法获得的结果,实线响应来自Ren et al. (2013) Fig. 10 Comparison of apparent resistivities and phases calculated for the COMMEMI 3D-1 model at a frequency of 10 Hz. The crosses are solution obtained using the presented method while the solid lines are from Ren et al. (2013) |
从图中可知,本文方法的计算结果与前人结果具有很好的对比性,表明计算结果可靠.同一频点的剖面响应曲线的光滑程度及精度显然也会受网格剖分情况的影响,并且离模型界面越远,计算精度往往更高,不同解法间的误差也会更小.另外,对比图 9和图 10还可以发现,在网格剖分相同的情况下,根据电磁场的变化特性,低频响应较高频响应的计算误差相对较小,但受边界条件形式及网格具体剖分情况(尤其是测点附近的网格剖分)影响,这一现象并不一定具有普适性.
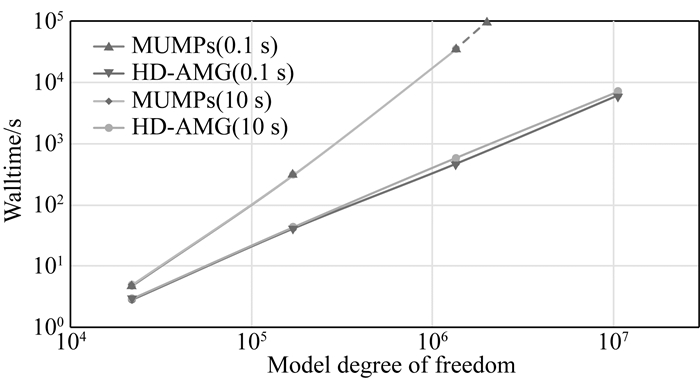
其次,在上述模型的基础上,利用网格细分方法,获得了多种不同尺度的网格(网格自由度数由约2万到约1000万不等),并以相同的场源参数进行试算,与上述算例类似,计算同样采用单线程进行,结果如表 1及图 11所示.经过对比不难发现,基于亥姆霍兹分解的预条件方法可以很好地克服旋度算子的零空间影响双旋度方程在迭代方法中的收敛效率这一问题,具有良好的收敛性,其迭代次数与求解自由度数量级关系不大,但由于矩阵运算的效率问题,正演时间仍与求解自由度数量级有关.而基于多波前算法的MUMPs直接算法正演计算所需时间与自由度成指数关系(O4/3),在较小自由度的问题中(2万左右)其效率还与HD-AMG方法相当,但在自由度为130万的中等大小问题中,其计算时间就超过HD-AMG方法接近两个数量级,这也充分说明了本文提出的算法的高效性.普遍认为,多波前算法的优势在于大规模、高精度的并行运算(利用数万至数十万CPU并行),但大规模并行计算的成本对于地球物理电磁法勘探工作而言一般过高,本文提出的HD-AMG方法可作为一种廉价的代替形式,提高电磁法数值模拟的效率.
|
|
表 1 COMMEMI 3D-1模型不同自由度模型正演效率对比 Table 1 Performance of forward modelling of COMMEMI 3D-1 model for different DoFs |
|
图 11 COMMEMI 3D-1模型不同自由度模型正演效率对比图示,MUMPs解法因在千万级别自由度时内存需求过大,无法计算,并且其对频率变化不敏感,因而两条曲线基本重合(以虚线表示耗时变化趋势) Fig. 11 Illustration of computing performance for COMMEMI 3D-1 model with different DoFs. For a DoF of 10 million, MUMPs needs so large memory that the result cannot be presented here, and it′s obvious that its efficiency is almost independent of frequency (the trend for walltime is indicated by the dashed line) |
直接解法由于方法本身的限制,其耗费内存也随自由度增加而急剧增长(按照O3速度递增),其耗费内存从较低DoF(2万)时的约0.2 GB,增长到中小自由度时(约17万)的约4.5 GB,再增长至较大自由度时(约130万)的104 GB.而在1000万自由度的情况下,其内存需求甚至超过了3000 GB,即使采用MUMPs算法中,将部分矩阵写入磁盘的所谓OOC模式下,所需内存也超过1000 GB,在本研究的计算平台上无法实现,这也让直接法在普通小型工作站或小型计算集群中难以用于大规模的实际正反演工作.相比之下,采用基于亥姆霍兹分解的预条件矩阵的迭代算法,由于需要额外的存储辅助拉普拉斯方程与泊松方程的稀疏矩阵,其内存耗费要高于通用的预条件方法,但即便如此,在自由度为一千万的大型网格的计算中,其耗费的内存也仅为21 GB左右,远低于直接法的耗费,这也使得在小型计算集群以至小型工作站上对较大自由度的问题进行正演求解,甚至利用中等自由度(数百万)的网格进行反演成为可能.
5 结论本研究针对棱边有限元大地电磁测深数值模拟中的迭代法效率问题,利用辅助节点单元实现了一种高效的基于亥姆霍兹分解的预条件算法,并通过多重网格法实现了这一算法的快速求解.为了避免直接构建预条件矩阵造成的计算及存储耗费,本研究通过求解预条件矩阵残差解的形式,进行隐式的预条件运算,并在预条件中引入散度规范,避免了旋度算子的非平凡零空间对Krylov子空间迭代算法的效率影响.本文方法的核心在于并不直接求解电磁场的矢量或标量位,而利用矢量及标量位构建预条件方法,而将电场双旋度方程的预条件问题转化为了求解残差向量的矢量和标量位的拉普拉斯方程和泊松方程问题.
通过三维理论模型的试算验证了亥姆霍兹分解预条件算法的可靠性;进行的不同自由度网格的正演数值实验证明了这一算法可以显著提高非结构化有限单元离散条件下的大地电磁测深数值模拟迭代计算的收敛性,具有效率较高而耗费内存较低的特点,基本可以在高性能工作站或小型计算集群上胜任中/大规模网格的地球物理电磁三维有限元正演模拟研究.未来研究拟整合MPI并行框架,探索有效的并行策略,进一步提高算法的效率,为以后进行高效的反演方法研究奠定基础.
致谢 作者感谢中南大学郭荣文教授关于多重网格方法的有益讨论以及两位匿名评审人对稿件提出的建设性意见.
Avdeev D B. 2007. EM Modeling, Forward. //Gubbins D, Herrero-Bervera E, ed. Encyclopedia of Geomagnetism and Paleomagnetism. Dordrecht: Springer, 215-218.
|
Beck R. 1999. Algebraic multigrid by component splitting for edge elements on simplicial triangulations. Tech. rep. (Vol. SC99-40). Berlin: Zuse Institute.
|
Cai H Z, Hu X Y, Li J H, et al. 2017. Parallelized 3D CSEM modeling using edge-based finite element with total field formulation and unstructured mesh. Computers & Geosciences, 99: 125-134. |
Chave A D, Jones A G. 2012. The Magnetotelluric Method: Theory and Practice. Cambridge: Cambridge University Press.
|
Chen H, Yin C C, Deng J Z. 2016. A finite-volume solution to 3D frequency-domain electromagnetic modelling using Lorenz-gauged magnetic vector and scalar potentials. Chinese Journal of Geophysics (in Chinese), 59(8): 3087-3097. DOI:10.6038/cjg20160831 |
Chen L S, Wang G E. 1990. The Magnetotelluric Sounding Method (in Chinese). Beijing: Geological Publishing House.
|
Chen X B, Zhang X, Hu W B. 2000. Application of finite-element direct iteration algorithm to MT 2-D forward computation. Oil Geophysical Prospecting (in Chinese), 35(4): 487-496. |
Druskin V L, Knizhnerman L A, Lee P. 1999. New spectral Lanczos decomposition method for induction modeling in arbitrary 3-D geometry. Geophysics, 64(3): 701-706. DOI:10.1190/1.1444579 |
Du Q, Wang D S. 2006. Recent progress in robust and quality Delaunay mesh generation. Journal of Computational and Applied Mathematics, 195(1-2): 8-23. DOI:10.1016/j.cam.2005.07.014 |
Farquharson C G, Miensopust M P. 2011. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction. Journal of Applied Geophysics, 75(4): 699-710. DOI:10.1016/j.jappgeo.2011.09.025 |
Grayver A V, Kolev T V. 2015. Large-scale 3D geoelectromagnetic modeling using parallel adaptive high-order finite element method. Geophysics, 80(6): E277-E291. DOI:10.1190/geo2015-0013.1 |
Grayver A V, Bürg M. 2014. Robust and scalable 3-D geo-electromagnetic modelling approach using the finite element method. Geophysical Journal International, 198(1): 110-125. DOI:10.1093/gji/ggu119 |
Hiptmair R, Xu J C. 2007. Nodal auxiliary space preconditioning in H (curl) and H (div) spaces. SIAM Journal on Numerical Analysis, 45(6): 2483-2509. DOI:10.1137/060660588 |
Jiang B N, Wu J, Povinelli L A. 1996. The origin of spurious solutions in computational electromagnetics. Journal of Computational Physics, 125(1): 104-123. |
Jin J M. 2014. The Finite Element Method in Electromagnetics. 3rd ed. New York: Wiley-IEEE Press.
|
Li Y G, Dai S K. 2011. Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures. Geophysical Journal International, 185(2): 622-636. DOI:10.1111/j.1365-246X.2011.04974.x |
Liu C S, Ren Z Y, Tang J T, et al. 2008. Three-dimensional magnetotellurics modeling using edgebased finite-element unstructured meshes. Applied Geophysics, 5(3): 170-180. DOI:10.1007/s11770-008-0024-4 |
Liu J X, Guo R W, Tong X Z, et al. 2011. Boundary truncation of magnetotelluric modeling based on multigrid method. Journal of Central South University (Science and Technology) (in Chinese), 42(11): 3429-3437. |
Liu X J, Wang J L, Yu P. 2007. Secondary field-based two-dimensional magnetotelluric numerical modeling by finite element method. Journal of Tongji University (Natural Science) (in Chinese), 35(8): 1113-1117. |
Mackie R L, Smith J T, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite difference equations: the magnetotelluric example. Radio Science, 29(4): 923-935. DOI:10.1029/94RS00326 |
Mitsuhata Y, Uchida T. 2004. 3D magnetotelluric modeling using the T-Ω finite-element method. Geophysics, 69(1): 108-119. DOI:10.1190/1.1649380 |
Newman G A, Alumbaugh D L. 2002. Three-dimensional induction logging problems, Part 2: A finite-difference solution. Geophysics, 67(2): 484. DOI:10.1190/1.1468608 |
Persson P O, Strang G. 2004. A simple mesh generator in matlab. SIAM Review, 46(2): 329-345. DOI:10.1137/S0036144503429121 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Saad Y, Van Der Vorst H A. 2000. Iterative solution of linear systems in the 20th century. Journal of Computational and Applied Mathematics, 123(1-2): 1-33. DOI:10.1016/S0377-0427(00)00412-X |
Saad Y. 2003. Iterative Methods for Sparse Linear Systems 2nd ed. Boston: Society for Industrial and Applied Mathematics.
|
Schwarzbach C. 2009. Stability of finite element solutions to Maxwell′s equations in frequency domain [Ph. D. thesis]. Frieberg: University of Frieberg, Germany.
|
Schwarzbach C, Brner R U, Spitzer K. 2011. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—A marine CSEM example. Geophysical Journal International, 187(1): 63-74. DOI:10.1111/j.1365-246X.2011.05127.x |
Siripunvaraporn W, Egbert G, Lenbury Y. 2002. Numerical accuracy of magnetotelluric modeling: a comparison of finite difference approximations. Earth, Planets and Space, 54(6): 721-725. DOI:10.1186/BF03351724 |
Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part Ⅱ: Biconjugate gradient solution and an accelerator. Geophysics, 61(5): 1319-1324. DOI:10.1190/1.1444055 |
Su X B, Li T L, Zhu C, et al. 2015. Study of three-dimensional MT forward modeling using vector finite element method. Progress in Geophysics (in Chinese), 30(4): 1772-1778. DOI:10.6038/pg20150433 |
Tang J T, Wang Y, Du H K, et al. 2009. A study of high frequency magnetotelluric numerical modeling by finite element method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 31(4): 297-302. |
Tang J T, Zhang L C, Gong J Z, et al. 2014. 3D frequency domain controlled source electromagnetic numerical modeling with coupled finite-infinite element method. Journal of Central South University (Science and Technology) (in Chinese), 45(4): 1251-1260. |
Um E S, Commer M, Newman G A. 2013. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the earth: Finite-element frequency-domain approach. Geophysical Journal International, 193(3): 1460-1473. DOI:10.1093/gji/ggt071 |
Wang L, Wang H, Xi Z Z, et al. 2013. Application of generalized minimal residual with preconditioning in the magnetotelluric forward modeling. Progress in Geophysics (in Chinese), 28(1): 165-170. DOI:10.6038/pg20130117 |
Weiss C J. 2013. Project APhiD: A Lorenz-gauged A-Φ decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous Earth. Computers & Geosciences, 58: 40-52. |
Weiss C J, Newman G A. 2002. Electromagnetic induction in a fully 3-D anisotropic earth. Geophysics, 67(4): 1104-1114. DOI:10.1190/1.1500371 |
Wu J, Xi Z Z, Wang H. 2012. Effects of grid size and boundary on MT forward modeling using finite element method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 34(1): 27-32. |
Xu J. 1996. The auxiliary space method and optimal multigrid preconditioning techniques for unstructured grids. Computing, 56(3): 215-235. |
Xu Z Z, Wu X P. 2010. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method. Chinese Journal of Geophysics (in Chinese), 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 |
Yang Z W, Feng L, Zhao N, et al. 2017. Calculating 2D Helmholtz equation based on multigrid method and application in magnetotelluric modeling. Oil Geophysical Prospecting (in Chinese), 52(1): 167-172. |
Yin C C, Zhang B, Liu Y H, et al. 2017. A goal-oriented adaptive algorithm for 3D magnetotelluric forward modeling. Chinese Journal of Geophysics (in Chinese), 60(1): 327-336. DOI:10.6038/cjg20170127 |
Zhdanov M S, Varentsov I M, Weaver J T, et al. 1997. Methods for modelling electromagnetic fields Results from COMMEMI—the international project on the comparison of modelling methods for electromagnetic induction. Journal of Applied Geophysics, 37(3-4): 133-271. DOI:10.1016/S0926-9851(97)00013-X |
陈辉, 殷长春, 邓居智. 2016. 基于Lorenz规范条件下磁矢势和标势耦合方程的频率域电磁法三维正演. 地球物理学报, 59(8): 3087-3097. DOI:10.6038/cjg20160831 |
陈乐寿, 王光锷. 1990. 大地电磁测深法. 北京: 地质出版社.
|
陈小斌, 张翔, 胡文宝. 2000. 有限元直接迭代算法在MT二维正演计算中的应用. 石油地球物理勘探, 35(4): 487-496. DOI:10.3321/j.issn:1000-7210.2000.04.011 |
柳建新, 郭荣文, 童孝忠, 等. 2011. 基于多重网格法的MT正演模型边界截取. 中南大学学报(自然科学版), 42(11): 3429-3437. |
刘小军, 王家林, 于鹏. 2007. 基于二次场的二维大地电磁有限元法数值模拟. 同济大学学报(自然科学版), 35(8): 1113-1117. DOI:10.3321/j.issn:0253-374X.2007.08.023 |
苏晓波, 李桐林, 朱成, 等. 2015. 大地电磁三维矢量有限元正演研究. 地球物理学进展, 30(4): 1772-1778. DOI:10.6038/pg20150433 |
汤井田, 王烨, 杜华坤, 等. 2009. 高频大地电磁法有限元数值模拟. 物探化探计算技术, 31(4): 297-302. DOI:10.3969/j.issn.1001-1749.2009.04.003 |
汤井田, 张林成, 公劲喆, 等. 2014. 三维频率域可控源电磁法有限元-无限元结合数值模拟. 中南大学学报(自然科学版), 45(4): 1251-1260. |
王亮, 王鹤, 席振铢, 等. 2013. 基于预处理广义极小残量法的大地电磁正演计算. 地球物理学进展, 28(1): 165-170. DOI:10.6038/pg20130117 |
吴娟, 席振铢, 王鹤. 2012. 网格尺寸及边界对大地电磁有限元正演精度的影响. 物探化探计算技术, 34(1): 27-32. DOI:10.3969/j.issn.1001-1749.2012.01.005 |
徐志锋, 吴晓平. 2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 |
杨振威, 冯磊, 赵宁, 等. 2017. 多重网格法二维Helmholtz方程解算及其在电磁法正演模拟中的应用. 石油地球物理勘探, 52(1): 167-172. |
殷长春, 张博, 刘云鹤, 等. 2017. 面向目标自适应三维大地电磁正演模拟. 地球物理学报, 60(1): 327-336. DOI:10.6038/cjg20170127 |
 2019, Vol. 62
2019, Vol. 62


