2. 四川省蜀通岩土工程公司, 成都 610084;
3. 西南科技大学环境与资源学院, 四川绵阳 621010
2. Sichuan Shutong Geotechnical Engineering Company, Chengdu 610084, China;
3. School of Environment and Resource, Southwest University of Science and Technology, Mianyang Sichuan 621010, China
大地电磁测深是探测地球深部电性结构的主要方法,通过在地表同步观测电场、磁场分量,定性或定量的分析获取地球一定深度范围内的电性结构模型,在油气勘探、固体矿产资源勘察、深部地质结构探测、地热和地下水资源调查、地震预测和地质灾害防治等领域应用广泛.在大陆动力学研究中,对岩石圈、软流圈和地幔结构以及它们之间相互作用和耦合关系的认识是非常必要的(赵国泽等,2001;魏文博等,2003).大地电磁研究主要关注岩石的电导率等电性参数变化,岩体的电导率与地球内部温度、流体、熔融和挥发物的体积、含量等有一定关联(Karato,1990;Bai and Kohlstedt, 1992).因此深部电性特征是揭示地球内部状态的重要物理参数,大地电磁特别是长周期大地电磁研究对于探索地球深部构造、物质组成、物理化学性质、热力学状态,及提升对地球构造、演化、地球动力学的认识具有重要的意义.最早Cagniard(1953)等提出大地电磁测深法时,将大地电磁场源和介质模型简化为理想的平面电磁波垂直入射水平层状介质.Srivastava(1965, 1966)研究了平面波场源入射层状球体介质的大地电磁正演理论,指出对于地壳尺度范围内的大地电磁测深,Cagniard的假设是可行的,但随着探测深度的加大,地球曲率的影响开始显现.因此,考虑地球曲率的大地电磁研究具有重要的意义.
随着仪器和计算机技术的全面发展,大地电磁测深已广泛开展二三维应用,在地球深部探测中发挥着重要的作用,如美国地球透镜计划(EarthScope)、欧洲地球探测计划(EuroProbe)、加拿大岩石圈探测计划(LithoProbe)以及我国的深部探测技术与实验研究专项(SinoProbe)等,都包含了大量研究地球深部电性结构的大地电磁测深工作(魏文博等,2010).根据电磁波趋肤效应,大地电磁探测深度与介质电阻率和电磁波频率有关,地幔尺度的大地电磁观测数据需要持续数天、数月甚至数年.但长周期的电场强度很弱,易受浅层电导率的影响,且长时间电场采集的漂移问题严重,长周期(数十天以上)电场测量的漂移问题较难实现校正(汤吉和赵国泽,2005),有效观测周期一般小于105s,这直接影响大地电磁测深法对地球更深部电性结构的探测.从目前深部探测项目发表的成果来看,大地电磁最大有效探测深度一般约300~400 km.尽管与地球平均半径6371 km相比,大地电磁探测深度还不算大,但上述深部探测项目中不乏数千公里的长剖面,与地球半径相比,曲率效应可能无法忽略,传统的在笛卡尔坐标系下将介质模型假设为水平拉伸投影后的直角边界模型可能无法适用.王绪本等(2013)研究了二维扇形边界的大地电磁模拟,在跨越龙门山的碌曲至合川长剖面做了考虑地球曲率的资料反演试验性探索研究,指出不考虑地球曲率的大地电磁模拟方法可能会导致大剖面反演结果可靠性降低.另外,李世文等(2017)研究地磁测深时指出,与需要同时观测电场和磁场分量的大地电磁测深法不同,地磁测深法(GDS)只观测低频磁场,研究范围105~107s,探测深度范围可达中下地幔,但地磁测深浅部需要用大地电磁数据进行约束.因此,针对大尺度的长周期大地电磁测深,考虑地球曲率的数值模拟具有重要的意义.
国内外学者近年对大地电磁三维正演进行了大量研究,但研究前提都做了场源为平面电磁波的假设.三维正演问题的本质是求复杂介质的三维电磁扩散方程数值解,主要计算方法有积分方程法、有限差分法和有限单元法等,其中有限差分法以实现简单、计算量较小的优点,在三维正演模拟中使用最为广泛.最早Jones和Pascoe(1972)、Lines和Jones(1973)提出三维有限差分法,利用高斯-塞德松弛技术求解简单模型网格化电场的双旋度扩散方程.随后Mackie等(1993)采用交错网格有限差分法实现了三维大地电磁正演,Smith(1996)详细研究了三维交错网格有限差分法的性质、误差分析和散度校正方法.Siripunvaraporn等(2002)比较了求解电场方程和求解磁场方程的精度,认为直接求解电场的方法精度较高.在国内,谭捍东等(2003)较系统的论述了从磁场出发的交错网格有限差分大地电磁三维正演过程.陈辉等(2011)比较了交错网格有限差分法中求解线性方程组时不同散度校正方法的精度和效率,指出磁场散度残差复校正较优.秦策等(2017)实现了基于二次场的交错网格有限差分三维大地电磁正演.薛帅等(2017)研究了耦合PML边界条件的三维大地电磁二次场有限差分,通过压缩模型求解空间提高了三维计算效率.
以上三维模拟研究都是基于笛卡尔坐标系,未考虑地球曲率影响.考虑地球曲率的三维模拟过去只在全球性的地磁测深研究中出现,Uyeshima和Schultz(2000)采用交错有限差分实现了基于二次场的全球性地磁测深三维正演,Yoshimura和Oshiman(2002)采用四面体剖分实现了边界有限元三维地磁测深正演,Ribaudo等(2012)采用FlexPDE软件实现了全球地磁测深模拟,Kelbert等(2009, 2014)在Uyeshima正演研究基础上实现了地磁测深三维反演.与这些全球性的地磁测深三维模拟不同,区域性的大地电磁需要考虑研究区侧边界条件,且需要求解电场和磁场,场源的形式也有所区别,因此地磁测深模拟难以直接适用于大地电磁模拟.
在大地电磁场源问题上,过去许多学者对平面电磁波产生了异议.Wait(1954)提出,如果电磁波场的横向均匀范围并不远大于其穿趋肤深度,那么Cagniard(1953)所提出的大地电磁理论公式将不能成立,须引入相应的校正项.Price(1962)引入了场源的影响项ν(2π/ν表示场源横向波长),并给出了ν的取值范围一般在1.57×10-4~1.57×10-2 km-1.Madden和Nelson(1964)研究认为平面波的假设普遍适用于中纬度地区、周期数千秒内的大地电磁测深.Hermance和Peltier(1970)采用线电流源研究了均匀和层状大地模型的场源效应,高文(1991)进一步对线电流源分析了电阻率、周期对场源效应的混合影响,提出了平均电阻率法,但需多测点同步观测.Peltier和(1971)又认为Hermance的线电流源模型过于简化,难以模拟实际中的场源分布,认为真实的大地电磁场源在横向上存在高斯分布,采用高斯电流源模拟了大地电磁响应.在地磁测深领域,由于其观测尺度较大,一般采用球谐函数的主要项P10来模拟赤道上空的等效环电流源(Uyeshima and Schultz, 2000;Kelbert et al., 2009, 2014;李建平等,2018; 李世文等, 2017),但这种全球性研究的场源在区域性探测的大地电磁中又存在差异.由此可以看出,当研究尺度变大时大地电磁场源变得较为复杂,本文仅从地球曲率影响角度做初步探索研究,主要开展球坐标系下三维大地电磁数值模拟算法研究,即是将麦克斯韦方程组在球坐标系下离散计算,场源简化看作垂直地面向地心传播的电磁波,这其实与地磁测深P10场源相似.
1 球坐标三维大地电磁正演算法 1.1 控制方程在大地电磁研究的频率范围内(约105~10-5Hz),由于频率相对较低,满足似稳电磁场,可以忽略位移电流.取地下介质的磁导率为真空磁导率,时谐因子为e-iωt,此时电磁强度矢量和磁场强度矢量满足的Maxwell方程积分形式为

|
(1) |

|
(2) |
式中E和H分别为电场强度和磁场强度矢量,J为电流密度, dl为封闭积分的围线, dS为围线包含的面积,真空磁导率μ0=4π×10-7H·m-1,σ为介质电导率,ω为圆频率.
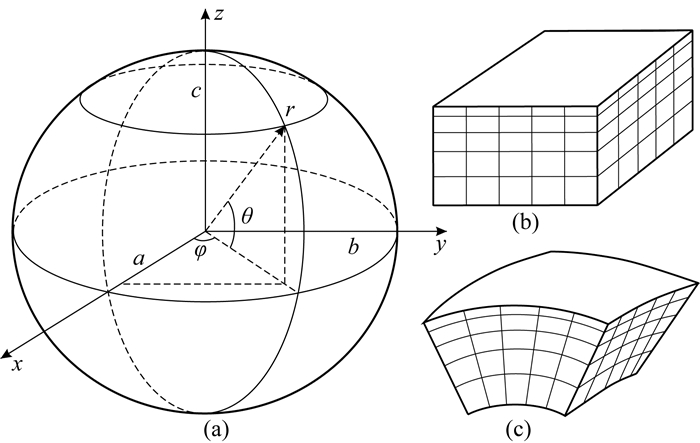
1.2 数值离散采用数值模拟方法计算电磁场场值的分布,需要将连续形式的积分或微分方程转化成离散的形式.由于球坐标系下Maxwell方程组的差分形式离散化较为复杂,这里对Maxwell方程组的积分形式离散化得出线性方程.与笛卡尔坐标模拟步骤一样,在离散化之前需要进行网格剖分,即沿r、θ、φ三个坐标轴方向,分别用若干平行的球面以不同的间距划分成若干个小的网格单元,图 1为坐标系统和网格剖分示意图.
|
图 1 坐标系统和网格剖分示意图 (a)坐标系统;(b)笛卡尔坐标网格剖分;(c)球坐标网格剖分. Fig. 1 Coordinates system and grid subdivision (a) Coordinates system; (b) Cartesian coordinate grid subdivision; (c) Spherical coordinates grid subdivision. |
在大地电磁二维数值模拟时,电磁场离散值的采样点往往取在同一网格节点上.而在三维模拟时,则采用交错网格剖分方式,交错采样网格的最大特点是能自动保证电磁场分布遵守能量守恒定律,在求得电场或磁场的分布后,可以方便的求得磁场或电场的分布.交错网格的采样方式有FDH和FDE两种,为了发挥大地电磁和地磁测深互补优势,这里采用FDH方案,以方便后期开展大地电磁和地磁测深联合解释研究.
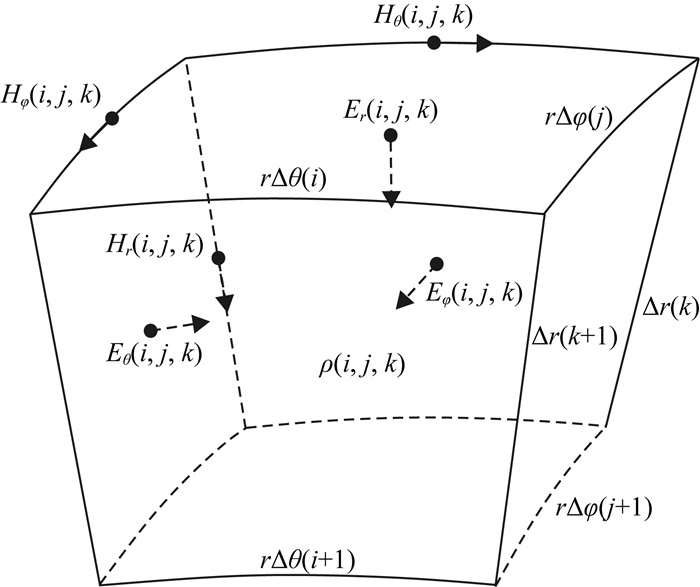
在球坐标系中,沿θ轴方向剖分成Nθ段,每段的编号i沿θ轴方向序号递增,i=1, 2, …, Nθ,网格弧度为Δθ(i)(1, …, Nθ);沿φ轴方向被剖分成Nφ段,网格弧度为Δφ(j)(1, …, Nφ);沿r轴方向被剖分成Nr段,网格间距为Δr(k)(1, …, Nr).对于某倒立四棱柱网格单元(i, j, k)(图 2),rΔθ(i)、rΔθ(i+1)、rΔφ(j)、rΔφ(j+1)、Δr(k)和Δr(k+1)分别为此单元的各边长,ρ(i, j, k)为此单元的电阻率值,此单元的六个电场或磁场分量的采样点位置如图 2示.Hθ(i, j, k)、Hφ(i, j, k)、Hr(i, j, k)分别为对应边缘磁场值.
|
图 2 球坐标交错网格 Fig. 2 Staggered grid in spherical coordinates |
在对模型空间按交错网格剖分形式离散化后,可对Maxwell积分方程式在球坐标系下离散化展开,以此求取交错网格有限差分方程(详见附录A).
1.3 方程组及求解求取离散FDH交错采样方案的三维MT有限差分格式后,对于每个方程,展开后的差分格式等价于电磁场的某个交错网格采样分量和它周围多个采样分量之间满足线性关系.如附录(A13)式可等价认为Hθ(i, j, k)可以根据周围的四个Hθ分量、四个Hφ分量及四个Hr分量求出,将这个模式扩展到网格的边缘,如果边界上的磁场已知,即可通过解线性方程组从而求取网格内部每个采样点上的Hθ、Hφ、Hr值.方程组形式为
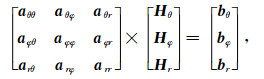
|
(3) |
其中,Hθ、Hφ和Hr为求解向量,分别是离散磁场编号存储的一维向量的子向量,bθ、bφ和br分别是各子向量对应的右端项子向量.aθθ、aφφ, …, arr等分别为附录A中式(13、14、15)中不同单元相关的a、b、c系数组成.根据边界条件类型,将其在线性方程组中的贡献加入方程组的左边或右端项即形成定解问题,其中球坐标系三维大地电磁正演边界条件的形式和笛卡尔坐标系完全相同,只是侧边界条件的计算仍需考虑地球曲率,侧边界场值可参考扇形边界条件下的大地电磁二维正演进行计算(王绪本等,2013).方程组的求解采用目前在三维大地电磁数值模拟中使用较广泛的预条件BICGSTAB迭代法(Smith,1996;Newman and Alumbaugh, 2000;谭捍东等,2003),并在迭代过程中开展静态散度校正,球坐标中的散度校正和方程求解与笛卡尔坐标中的形式相似,本文就不再细述.所不同的是,在笛卡尔坐标中存在Sx和Sy两个极化模式,在球坐标系中则表征为Sθ、Sφ两个极化模式,因此球坐标系大地电磁阻抗张量为:
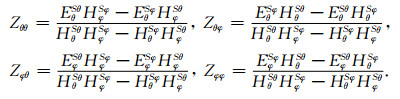
|
(4) |
为验证本文的球坐标系三维大地电磁有限差分正演算法的正确性,与一维理论模型和三维标准模型进行了对比测试.地球平均半径6371 km,因此在测区范围较小时,球坐标理论上应该与笛卡尔坐标正演结果一致,为了比较两种算法的计算精度,我们也实现了笛卡尔坐标有限差分三维大地电磁正演算法.选取一个3层地电模型进行对比,模型第一层电阻率100 Ωm,厚1000 m,第二层电阻率1 Ωm,厚1000 m,第三层电阻率100 Ωm.对于一维模型,利用理论公式计算出视电阻率和阻抗相位的解析解.计算过程中球坐标和笛卡尔坐标系正演算法使用相同的网格剖分,网格数为30×30×40,背景模型是100 Ωm均匀半空间.计算了从1000 Hz到0.0001 Hz共8个频率的视电阻率和相位响应.表 1是两种坐标系数值解与解析解的对比结果,球坐标解和笛卡尔坐标解完全一致,均与解析解吻合良好,视电阻率平均相对误差1.4%,相位平均误差0.23°.
|
|
表 1 三层模型解析解和笛卡尔坐标系及球坐标系数值解对比 Table 1 Comparison of cartesian coordinate solution and spherical coordinate solution and analytical solution of 3-layer model |
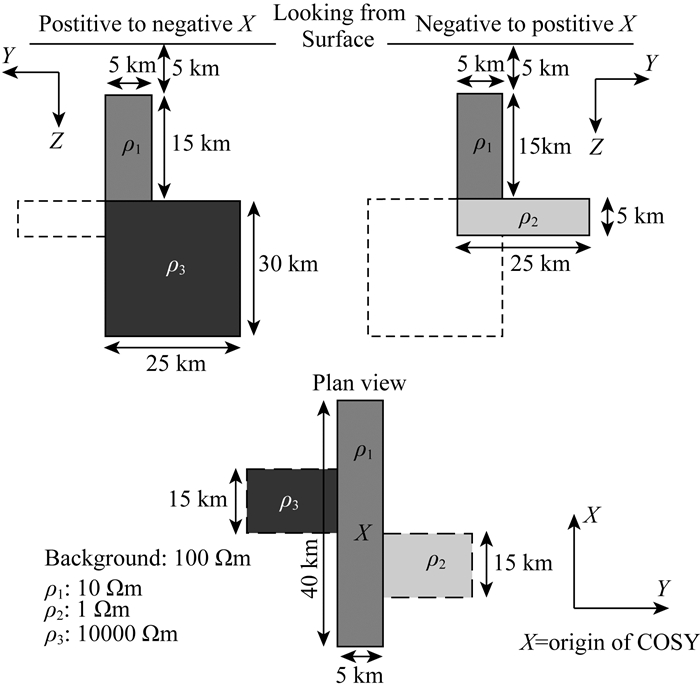
三维正演测试模型选用2008年国际三维大地电磁反演讨论会上提出的DTM1标准测试模型(http://www.complete-mt-solutions.com/mtnet/workshops/mt3dinv/2008_Dublin/dublin_forward.html),该模型在100 Ωm的均匀半空间中设置了三个电阻率异常块,电阻率分别为10 Ωm,1 Ωm,10000 Ωm,如图 3所示.
|
图 3 DTM1模型示意图 Fig. 3 Sketch of DTM1 model |
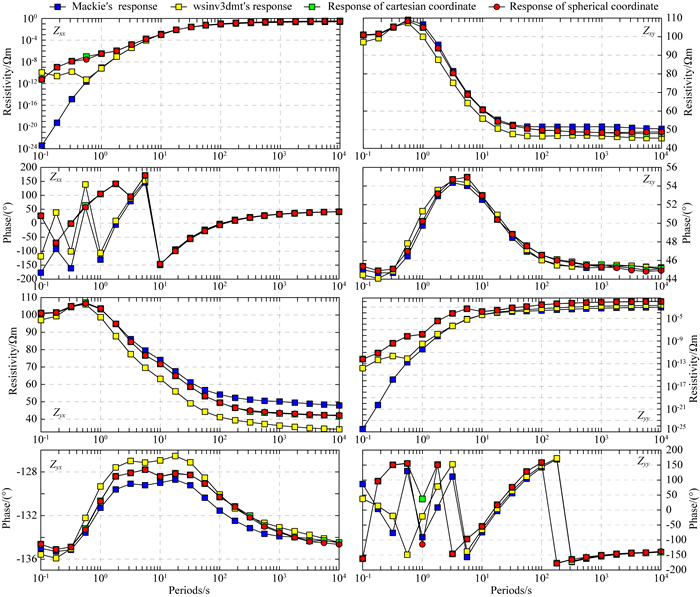
国内外诸多三维MT算法均对此模型做了计算,公开的数据结果表明,平面中心(0 km,0 km)测点由于刚好位于深部两个高低阻异常体相交的角点位置,在交错网格有限差分中需将单元电阻率做加权平均,因此(0 km,0 km)测点是该模型响应的最奇异点,一般均选取该位置测点进行算法比较.图 4是本文的结果与Mackie(1993)和Siripunvaraporn等(2002)有限差分正演结果Zxx、Zxy、Zyx、Zyy视电阻率和阻抗相位的对比曲线,计算频率从10~0.0001 Hz共21个频点.可以看出,本文计算结果与Makie计算结果较为接近,Makie和Siripunvaraporn的计算结果存在一定的差别,这可能主要是不同网格剖分所致,我们的计算网格采用40×40×60,对于最重要的主对角元xy和yx,球坐标系和笛卡尔坐标系正演曲线基本介于Makie和Siripunvaraporn之间,吻合较好.另外,将穿越构造最复杂的X=0测线正演断面进行成图,图 5给出了四种计算结果,计算结果基本一致.球坐标和笛卡尔坐标系正演结果重合度较高,(0 km,0 km)测点曲线图也显示误差非常小,均方误差小于0.1%,曲线基本重合.因此,结合一维和三维计算结果分析,本文的球坐标系大地电磁正演算法是可靠的,当模型尺度远小于地球半径时,球坐标系和笛卡尔坐标系正演结果基本一致.
|
图 4 DTM1模型(0, 0)点处的响应对比 Fig. 4 Comparison of the obtained DTM1 model responses at site (0, 0) |

|
图 5 DTM1模型测线x=0的响应对比 Fig. 5 Comparison of the obtained DTM1 model responses at Line x=0 |
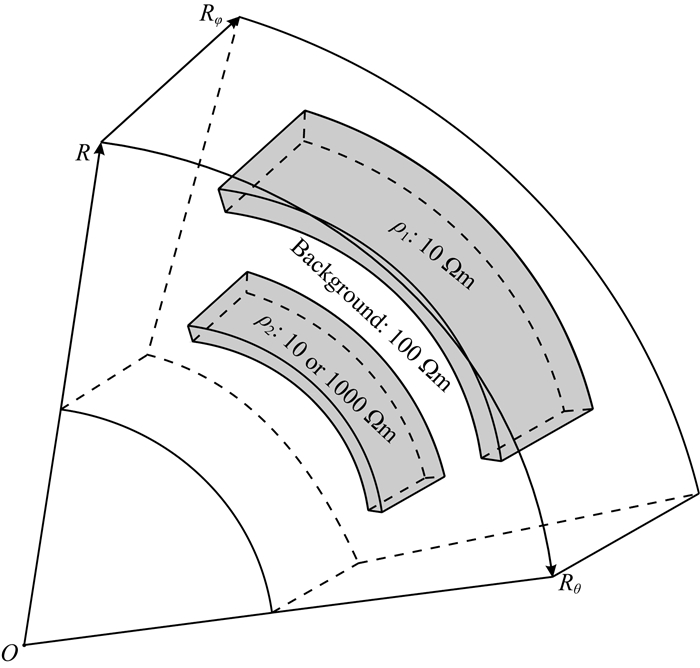
探测尺度较小时,球坐标响应结果与笛卡尔坐标系几乎一致,那么随着探测尺度的加大,地球曲率的影响程度如何,对响应特征有何改变,这需要对大尺度模型做进一步计算分析.为了分析异常体不同埋深、不同尺寸和不同电阻率的情况,设计模型如图 6所示,共计算S1-S3三种模型,模型尺寸和电阻率见表 2.球坐标θ方向与笛卡尔坐标的X轴对应,φ方向与Y轴对应.异常体深度分别为30~50 km和170~210 km,低阻和高阻异常体电阻率分别为10 Ωm和1000 Ωm,异常体在两个方向上的地表横向宽度分别为1600 km和800 km.计算过程中球坐标和笛卡尔坐标系正演算法使用相同的网格剖分,网格均为50×50×60,表层单元网格横向宽度均为40 km宽的等距网格,背景模型是100 Ωm均匀半空间,计算频率从10~0.0001 Hz共21个频点.
|
图 6 球坐标系模型示意图 Fig. 6 Sketch of spherical coordinates model |
|
|
表 2 球坐标系模型尺寸 Table 2 Model size of spherical coordinates |
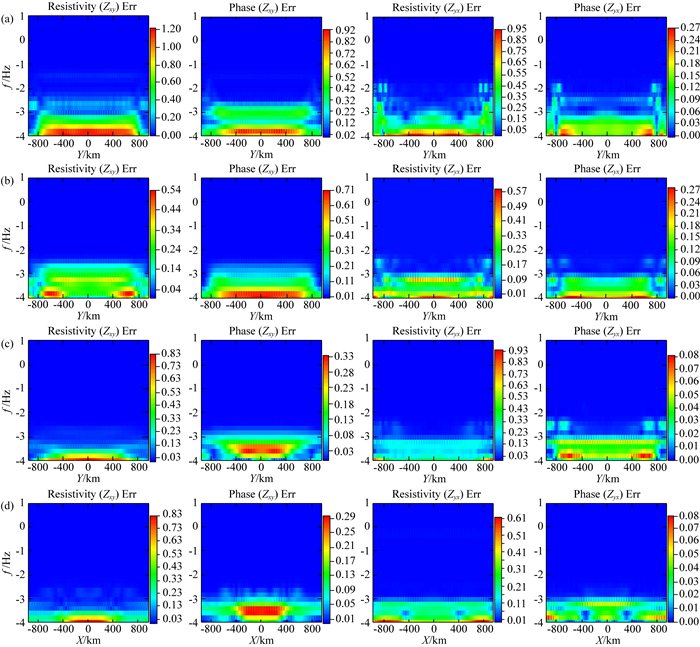
分别对S1—S3三个模型做了球坐标系和笛卡尔坐标系的正演计算,图 7为三个模型的基于两种坐标系的典型测线计算相对误差断面.图 7a为S1模型X=0测线误差断面,低阻异常埋深30~50 km,异常体宽度1600 km.假如以0.1%作为考虑误差的界线,主对角元Resistivity(Zxy)、Phase(Zxy)、Resistivity(Zyx)、Phase(Zyx)误差分别在在周期T=320 s、100 s、320 s、100 s后开始往低频逐渐变大,最大误差分别为1.20%、0.92%、0.95%、0.27%,Zxy误差较大值的平面位置主要集中在异常体附近,Zyx误差较大值的平面位置横跨模型区域.图 7b为S2模型X=0测线误差断面,低阻异常埋深170~210 km,异常体宽度1600 km.主对角元误差分别在周期T=560 s、560 s、320 s、1800 s后开始往低频逐渐变大,最大误差分别为0.54%、0.71%、0.57%、0.27%,Zxy误差较大值的平面位置主要集中在异常体附近,Zyx误差较大值的平面位置横跨模型区域.图 7c为S3模型X=0测线误差断面,高阻异常埋深170~210 km,异常体宽度1600 km.主对角元误差分别在周期T=3200 s、1800 s、560 s、10000 s后开始往低频逐渐变大,最大误差分别为0.83%、0.33%、0.93%、0.08%,Zxy误差较大值的平面位置主要集中在异常体附近,Zyx误差较大值的平面位置横跨模型区域.图 7d为S3模型Y=0测线误差断面,异常体宽度800 km,主对角元误差分别在周期T=1800 s、1800 s、1800 s、10000 s后开始往低频逐渐变大,最大误差分别为0.83%、0.29%、0.61%、0.08%,Zxy误差较大值的平面位置主要集中在异常体附近,Zyx误差较大值的平面位置横跨模型区域.
|
图 7 球坐标系和笛卡尔坐标系模型响应相对误差 (a) S1模型X=0测线; (b) S2模型X=0测线; (c) S3模型X=0测线; (d) S3模型Y=0测线. Fig. 7 Error between cartesian coordinate solution and spherical coordinate solution (a) Line X=0 of S1 model; (b) Line X=0 of S2 model; (c) Line X=0 of S3 model; (d) Line Y=0 of S3 model. |
对比分析异常体不同埋深的图 7(a, b),可以看出异常体埋深浅时,两种坐标系计算结果起始偏离的频率较高,且最大误差值较高,埋深较大则起始偏离频率变低,最大误差值相对较小.对比分析异常体电阻率不同的图 7(b, c),可以看出低阻异常比高阻异常起始偏离的频率较高,低阻异常比高阻异常视电阻率最大误差较小,相位最大误差相对较大.对比分析异常体横向尺度不同的图 7(c, d),可以看出异常体尺度大小对起始偏离的频率影响不大,但尺度较大异常模型的最大误差相对较大.
上述模型虽然能看出两种计算结果在低频段存在差异,但最大相对误差值还不算大,这可能跟模型复杂度以及计算频率等因素有关.为此,以较复杂的3D标准测试模型DTM1为基础,将DTM1模型进行放大扩展,模型相对位置示意图与图 3一致,但异常体尺寸变为表 3所示.两种坐标系仍然使用相同的网格剖分,网格均为40×40×60,表层单元网格x和y横向宽度均为100 km宽的等距网格,背景模型是100 Ωm均匀半空间,计算频率从10~0.00001 Hz共25个频点.
|
|
表 3 放大尺寸的DTM1模型 Table 3 Model size of extension DTM1 |
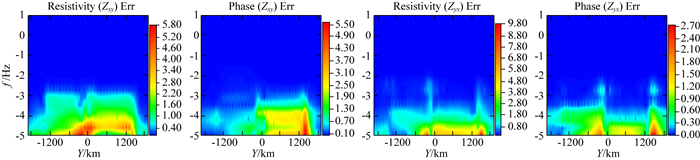
图 8为两种坐标系模型正演结果中测线X=0误差断面,主对角元Resistivity(Zxy)、Phase(Zxy)、Resistivity(Zyx)、Phase(Zyx)误差往低频逐渐变大,周期T>10000 s后差异基本都大于2%,最大误差分别为5.8%、5.5%、9.8%、2.7%.图 9为在模型中测线X=0上同频点、不同测点的曲线对比图,实线为球坐标三维大地电磁主对角元视电阻率和阻抗相位曲线,虚线为笛卡尔坐标系计算结果.由于两种坐标系计算结果在周期T < 1000 s内差异较小,因此仅选取周期分别为1000 s、10000 s、32000 s和100000 s频点进行对比.差异也表现为随频率变低而变大,差异较大位置集中在模型电阻率突变区域.
|
图 8 放大尺寸DTM1模型X=0测线响应误差 Fig. 8 Error between cartesian coordinate response and spherical coordinate response at line(X=0) of extension DTM1 model |

|
图 9 放大尺寸DTM1模型X=0测线响应曲线对比 Fig. 9 Responses comparison of extension DTM1 model at line(X=0) |
对于大区域乃至全球性大地电磁测深而言,地球曲率的影响开始显现,因而在球坐标系下开展三维大尺度的大地电磁研究具有重要意义.本文详细阐述了球坐标系下三维大地电磁正演基本理论和公式,通过与一维解析解和三维标准测试模型进行计算对比,验证了本文算法的正确性,并对比传统的笛卡尔坐标计算结果得出以下结论:
(1) 相较于传统的笛卡尔坐标系模拟方法,球坐标系模拟更直观合理,能避免传统笛卡尔坐标拉伸投影所引入的误差.球坐标系模拟方法完全可代替目前的笛卡尔坐标模拟方法.
(2) 基于球坐标和笛卡尔坐标的三维大地电磁正演响应值随着频率变低差异越明显.
(3) 球坐标和笛卡尔坐标计算结果差异度与频率、模型结构和电阻率有关.本文模型计算结果在数万秒周期处已出现最大接近10%的差异,表明对于较大尺度的长周期大地电磁,地球曲率影响不能忽略.
虽然在周期小于万秒情况时,两种坐标系正演结果差异还不算大,但正演模拟本身是分别基于笛卡尔坐标和球坐标系,两种模型实际形态就完全不同,且较小的正演误差可能会在反演中被放大,因此迫切需要开展考虑地球曲率的三维大地电磁反演研究.另外,正如地磁研究者指出,地磁测深浅部需要用大地电磁数据进行约束.随着仪器技术的发展,大地电磁探测尺度可能会逐渐变大,希望能基于本文的研究工作,陆续开展系统性的考虑地球曲率的大地电磁研究以及场源效应研究.将大地电磁计算方式从块到球,从地壳尺度一直延伸到地幔尺度,更准确的模拟和反演地球深部构造.
致谢各位评审专家在本文修改过程中提出了诸多宝贵意见,在此致以诚挚的谢意.
附录A首先对文中Maxwell积分方程式(1)进行离散化处理,按电流密度J的分量形式离散化.
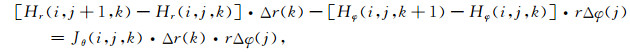
|
(A1) |
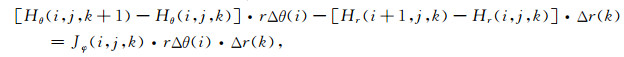
|
(A2) |
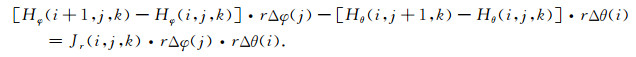
|
(A3) |
定义在各电场分量采样点处的电阻率值为相邻网格单元电阻率的网格间距加权平均值:
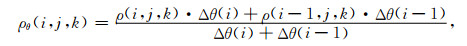
|
(A4) |
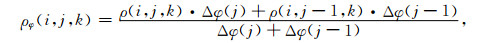
|
(A5) |
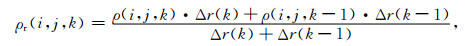
|
(A6) |
电场E和电流密度J的离散关系为
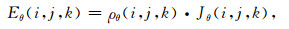
|
(A7) |
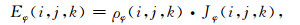
|
(A8) |
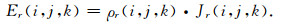
|
(A9) |
同理,对文中Maxwell积分方程式(2)按磁场H的各分量离散化:

|
(A10) |
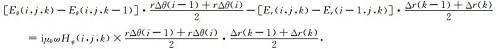
|
(A11) |
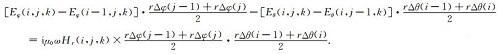
|
(A12) |
将上述方程联立消除电场分量后,对于研究区内部的每个Hθ(i, j, k)、Hφ(i, j, k)和Hr(i, j, k)分量,都可以分别与其周围的12个磁场分量建立线性关系,满足(A13)、(A14)、(A15)式的线性方程:

|
(A13) |
(A13) 式中各系数的表达式分别为

|
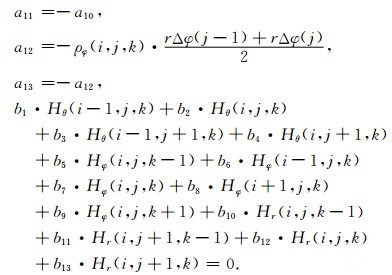
|
(A14) |
(A14) 式中各系数的表达式分别为
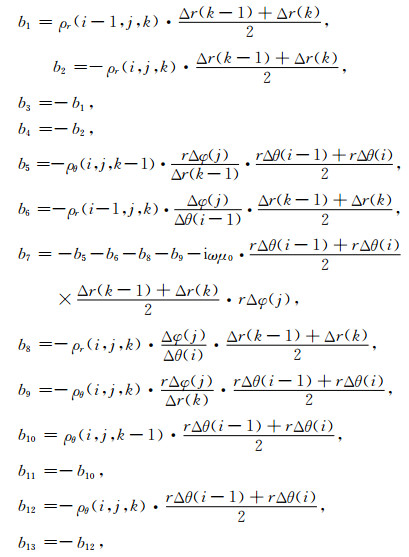
|

|
(A15) |
(A15) 式中各系数的表达式分别为

|
(A13) 式中的a0、(A14)式中的b0和(A15)式中的c0在模型内部单元离散时值为0,在边界单元由边界条件确立.
Bai Q, Kohlstedt D L. 1992. Substantial hydrogen solubility in olivine and implications for water storage in the mantle. Nature, 357(6380): 672-674. DOI:10.1038/357672a0 |
Cagniard L. 1953. Basic theory of the magnetotelluric method of geophysical prospecting. Geophysics, 18(3): 605-635. DOI:10.1190/1.1437915 |
Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method. Chinese Journal of Geophysics (in Chinese), 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
Hermance J F, Peltier W R. 1970. Magnetotelluric fields of a line current. Journal of Geophysical Research, 75(17): 3351-3356. DOI:10.1029/jb075i017p03351 |
Jones F W, Pascoe L J. 1972. The perturbation of alternating geomagnetic fields by three-dimensional conductivity inhomogeneities. Geophysical of Journal of the Royal Astronomical Society, 27(5): 479-485. DOI:10.1111/j.1365-246x.1972.tb06103.x |
Karato S. 1990. The role of hydrogen in the electrical conductivity of the upper mantle. Nature, 347(6290): 272-273. DOI:10.1038/347272a0 |
Kelbert A, Schultz A, Egbert G. 2009. Global electromagnetic induction constraints on transition-zone water content variations. Nature, 460(7258): 1003-1006. DOI:10.1038/nature08257 |
Kelbert A, Kuvshinov A, Velímsky J, et al. 2014. Global 3-D electromagnetic forward modelling: a benchmark study. Geophysical Journal International, 197(2): 785-814. DOI:10.1093/gji/ggu028 |
Li J P, Weng A H, Li S W, et al. 2018. 3-D forward method for geomagnetic depth sounding based on finite difference method in spherical coordinate. Journal of Jilin University (Earth Science Edition) (in Chinese), 48(2): 411-419. DOI:10.13278/j.cnki.jjuese.20170061 |
Li S W, Weng A H, Li J P, et al. 2017. 1-D inversion of C-response data from geomagnetic depth sounding with shallow resistivity constraint. Chinese Journal of Geophysics (in Chinese), 60(3): 1201-1210. DOI:10.6038/cjg20170330 |
Lines L R, Jones F W. 1973. The perturbation of alternating geomagnetic fields by an island near a coastline: reply. Canadian Journal of Earth Sciences, 10(11): 1703-1704. DOI:10.1139/e73-166 |
Mackie R L, Madden T R, Wannamaker P E. 1993. Three-dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions. Geophysics, 58(2): 215-226. DOI:10.1190/1.1443407 |
Madden T, Nelson P. 1964. A defence of Cagniard′s magnetotelluric method. Geophysics, 43(5): 89-95. |
Newman G A, Alumbaugh D L. 2002. Three-dimensional induction logging problems, Part 2: A finite-difference solution. Geophysics, 67(2): 484. DOI:10.1190/1.1468608 |
Peltier W R, Hermance J F. 1971. Magnetotelluric fields of a gaussian electrojet. Canadian Journal of Earth Sciences, 8(8): 338-346. DOI:10.1139/e71-034 |
Price A T. 1962. The theory of magnetotelluric methods when the source field is considered. Journal of Geophysical Research, 67(3): 1907-1918. DOI:10.1029/jz067i005p01907 |
Qin C, Wang X B, Zhao N. 2017. Parallel Three-dimensional forward modeling and inversion of magnetotelluric based on a secondary field approach. Chinese Journal of Geophysics (in Chinese), 60(6): 2456-2468. DOI:10.6038/cjg20170633 |
Ribaudo J T, Constable C G, Parker R L. 2012. Scripted finite element tools for global electromagnetic induction studies. Geophysical Journal International, 188(2): 435-446. DOI:10.1111/j.1365-246x.2011.05255.x |
Siripunvaraporn W, Egbert G, Lenbury Y. 2002. Numerical accuracy of magnetotelluric modeling: A comparison of finite difference approximations. Earth, Planets and Space, 54(6): 721-725. DOI:10.1186/bf03351724 |
Smith J T. 1996. Conservative Modeling of 3-D Electromagnetic fields, Part Ⅱ: Biconjugate gradient solution and an accelerator. Geophysics, 61(5): 1319-1324. DOI:10.1190/1.1444055 |
Srivastava S P. 1965. Method of interpretation of magnetotelluric data when source field is considered. Journal of Geophysical Research, 70(4): 945-954. DOI:10.1029/jz070i004p00945 |
Srivastava S P. 1966. Theory of the magnetotelluric method for a spherical conductor. Geophysical Journal International, 11(4): 373-387. DOI:10.1111/j.1365-246x.1966.tb03090.x |
Tan H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method. Chinese Journal of Geophysics (in Chinese), 46(5): 705-711. |
Tang J, Zhao G Z. 2005. A extension study of LMT by useing the equivalent relationship between GDS and MT response function. //The 21st Annual Meeting of Chinese Geophysical.
|
Uyeshima M, Schultz A. 2000. Geoelectromagnetic induction in a heterogeneous sphere: a new three-dimensional forward solver using a conservative staggered-grid finite difference method. Geophysical Journal International, 140(3): 636-650. DOI:10.1046/j.1365-246x.2000.00051.x |
Wait J R. 1954. On the relation between telluric currents and the Earth′s magnetic field. Geophysics, 19(9): 281-289. DOI:10.1190/1.1437994 |
Wang X B, Luo W, Zhang G, et al. 2013. Electrical resistivity structure of Longmenshan crust-mantle under sector boundary. Chinese Journal of Geophysics (in Chinese), 56(8): 2718-2727. DOI:10.6038/cjg20130820 |
Wei W B, Jin S, Ye G F, et al. 2003. Methods to study electrical conductivity of continental lithosphere. Earth Science Frontiers (in Chinese), 10(1): 15-23. DOI:10.3321/j.issn:1005-2321.2003.01.003 |
Wei W B, Jin S, Ye G F, et al. 2010. On the conductive structure of Chinese continental lithosphere-experiment on "Standard Monitoring Network" of Continental EM Parameters (SinoProbe-01). Acta Geologica Sinica (in Chinese), 84(6): 788-800. |
Wen K. 1991. Line source effects on Magnetotelluric responses. Acta Geophysica Sinica (in Chinese), 34(2): 210-215. |
Xue S, Bai D H, Tang J, et al. 2017. Three-dimensional finite difference method for the magnetotelluric secondary field with coupled PML boundary conditions. Chinese Journal of Geophysics (in Chinese), 60(1): 337-348. DOI:10.6038/cjg20170128 |
Yoshimura R, Oshiman N. 2002. Edge-based finite element approach to the simulation of geoelectromagnetic induction in a 3-D sphere. Geophysical Research Letters, 29(3): 9-1. DOI:10.1029/2001GL014121 |
Zhao G Z, Tang J, Liang J G, et al. 2001. Measuement of network-mt in two areas of ne china for study of upper mantle conductivity structure of the back-arc region. Seismology and Geology, 23(2): 143-152. DOI:10.3969/j.issn.0253-4967.2001.02.003 |
陈辉, 邓居智, 谭捍东, 等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究. 地球物理学报, 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
高文. 1991. 大地电磁感应的场源效应. 地球物理学报, 34(2): 210-215. DOI:10.3321/j.issn:0001-5733.1991.02.010 |
李建平, 翁爱华, 李世文, 等. 2018. 基于球坐标系下有限差分的地磁测深三维正演. 吉林大学学报(地球科学版), 48(2): 411-419. DOI:10.13278/j.cnki.jjuese.20170061 |
李世文, 翁爱华, 李建平, 等. 2017. 浅部约束的地磁测深C-响应一维反演. 地球物理学报, 60(3): 1201-1210. DOI:10.6038/cjg20170330 |
秦策, 王绪本, 赵宁. 2017. 基于二次场方法的并行三维大地电磁正反演研究. 地球物理学报, 60(6): 2456-2468. DOI:10.6038/cjg20170633 |
谭捍东, 余钦范, Booker J, 等. 2003. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 46(5): 705-711. DOI:10.3321/j.issn:0001-5733.2003.05.019 |
汤吉, 赵国泽. 2005.利用GDS的等效MT响应函数扩展长周期电磁测深研究. //中国地球物理学会第二十一届年会论文集.长春: 中国地球物理学会.
|
王绪本, 罗威, 张刚, 等. 2013. 扇形边界条件下的龙门山壳幔电性结构特征. 地球物理学报, 56(8): 2718-2727. DOI:10.6038/cjg20130820 |
魏文博, 金胜, 叶高峰, 等. 2003. 大陆岩石圈导电性的研究方法. 地学前缘, 10(1): 15-23. DOI:10.3321/j.issn:1005-2321.2003.01.003 |
魏文博, 金胜, 叶高峰, 等. 2010. 中国大陆岩石圈导电性结构研究—大陆电磁参数"标准网"实验(SinoProbe-01). 地质学报, 84(6): 788-800. |
薛帅, 白登海, 唐静, 等. 2017. 耦合PML边界条件的三维大地电磁二次场有限差分法. 地球物理学报, 60(1): 337-348. DOI:10.6038/cjg20170128 |
赵国泽, 汤吉, 梁竞阁, 等. 2001. 用大地电磁网法在长春等地探测上地幔电导率结构. 地震地质, 23(2): 143-152. DOI:10.3969/j.issn.0253-4967.2001.02.003 |
 2019, Vol. 62
2019, Vol. 62


