2. 湖南师范大学信息科学与工程学院, 长沙 410081
2. College of Information Science and Engineering, Hunan Normal University, Changsha 410081, China
勘探地球物理方法包括重力、磁法、电磁法和地震等多种勘探方法(傅承义等,1985;Nabighian,1987;Kalscheuer et al., 2008;Ren et al., 2013;Garcia et al., 2015;Tang et al., 2018;Hu et al., 2019).大地电磁测深法(Magnetotelluric,MT)是一种以天然交变电磁场为场源,通过测量地表相互正交的电场和磁场获得地下电性结构分布的电磁勘探方法(Tikhonov,1950).该方法具有探测深度大、工作频率宽等优点,已在探测地壳深部结构和矿产资源勘查等领域得到广泛应用.由于源自地球外部宇宙空间的大地电磁场信号极其微弱且频带范围极宽,野外采集的数据不可避免地会受到各种电磁噪声的干扰.尤其是在矿集区,人烟稠密、无线通讯基站等因素严重制约了大地电磁数据质量,导致视电阻率-相位曲线过度失真,极大地影响了地下电性结构的可解释性及采集数据本身的可靠性(吕庆田等,2015).为此,如何消除大地电磁信号中的强干扰、提升大地电磁数据质量成为该研究领域的重要课题.新兴的现代信号处理技术,如Hilbert-Huang变换(汤井田等,2008;Chen et al., 2012)、信息熵与有理函数滤波(雷达等,2010)、方差比维纳滤波(Kapple,2012)、S变换(陈海燕等,2012;景建恩等,2012)、数学形态滤波(汤井田等,2012;李晋等,2016a)、同步时间序列依赖(王辉等,2014)、信号子空间增强(李晋等,2014)、小波变换及综合算法(Trad and Travassos, 2000;范翠松等,2008;凌振宝等,2016)、信噪辨识与递归分析(李晋等, 2017a, 2017b)、压缩感知重构算法(Li G et al., 2017)、独立分量分析(曹小玲等,2018)、分形-熵与聚类(Li et al., 2018)等均被应用至该领域,试图从不同程度污染的大地电磁数据中获取真实的电性结构;其研究成果逐步加深了对大地电磁信号和噪声的认识,推动了强电磁干扰环境下大地电磁处理技术的蓬勃发展.
分析国内外相关文献可知,互功率谱和加权平均功率谱法虽对不相关噪声具有一定的抑制能力,但电磁噪声往往是同时作用在各道电磁信号上,属于相关噪声,导致该方法失效;远参考道法虽能消除同一测点各道之间不相关的电磁噪声,并对各道之间同源电磁噪声也有较好的效果,但经远参考处理后,单点数据的误差棒不同程度地变大了,特别是在受电磁干扰污染严重、校正量较大的数据段,该现象尤为明显,且参考道距离的选择是一个比较实际的问题;Robust处理法对于MT资料中的非高斯正态分布噪声的消除具有优越性,能有效减少视电阻率和相位的分散度,但Robust法无法消除输入端的噪声,且无法剔除噪声较多、能量较强时的近源电磁相关噪声对数据的干扰;小波变换虽能有效压制大地电磁局部相关噪声,但小波变换过分依赖于小波基函数的选取,有时随着尺度增大,相应正交基函数的频谱局部性变差,使其对大地电磁信号更精细分解受到限制;近年来,Hilbert-Huang变换应用到电法勘探,并能有效抑制大地电磁信号中的工频干扰,与小波变换相比不需要选择基函数,具有更强的时频刻画能力.经验模态分解(Empirical Mode Decomposition,EMD)能将待处理信号分解为一系列固有模态函数(Intrinsic Mode Function,IMF),这些IMF具有正交性、完备性和自适应性等特点,并能对待处理信号进行不同尺度的描述(Huang et al., 1998);然而,EMD存在边界效应及模态混叠现象,在分解过程中往往导致某一个模态或多个模态包含不同尺度的信号或相似信号.在EMD的基础上,学者们提出了固有时间尺度分解(Intrinsic Time-scale Decomposition,ITD),该方法能将待处理信号自适应地分解为一系列频率由高到低的旋转分量(Proper Rotation,PR)和一个单调趋势的残余量,克服了EMD的模态混叠现象,具有算法简单、运行速度快等特点(Frei and Osotio, 2007).由于ITD的基线信号是基于相邻极值点间每一段信号的线性变换,方法虽维持了极值点间的单调特性,但分解出的PR分量则有可能出现明显的波形失真,且仍存在端点效应.鉴于上述递归式模态分解的不足,针对大地电磁信号的非线性、非平稳特性,文中引入变分模态分解(Variational Mode Decomposition,VMD)对其进行信噪分离研究(Dragomiretskiy and Zosso, 2014).该方法将模态的估计转变为变分问题的求解,通过在频域中不断更新各模态的中心频率,较好地克服了EMD和ITD在信号分解中的不足;已成功应用于滚动轴承故障诊断(刘长良等,2015)、内燃机噪声源识别(姚家驰等,2016)、肌间耦合特性(杜义浩等,2017)和GNSS电离层闪烁(Sivavaraprasad et al., 2017)等领域.同时,为了进一步剔除VMD在提取大地电磁强干扰轮廓特征时残余的尖脉冲干扰,文中运用匹配追踪(Matching Pursuit,MP)做二次信噪分离处理.MP是一种贪婪算法,该算法通过对过完备原子库中的原子进行搜索,实现信号的最优匹配;已广泛应用于地震数据压缩重构(Tang et al., 2012)、信号去噪(朱会杰等,2015)和图像恢复(Li W et al., 2016)等领域.文中将VMD和MP相结合,应用于矿集区音频大地电磁(Audio magnetotelluric,AMT)噪声压制,其优势在于VMD能克服传统递归式筛选模态方法(EMD、ITD)中的模态混叠和端点效应;针对VMD残留的尖脉冲,MP能进一步精细分离出微弱的大地电磁有用信号.实验结果表明,时间域序列中的大尺度强干扰得到有效剔除,视电阻率-相位曲线更为光滑、连续,低频段的数据质量得到明显改善.
1 算法原理 1.1 变分模态分解VMD是一种完全非递归、自适应的信号分解方法,该方法通过迭代搜寻变分模型的最优解来确定每阶分量的中心频率和带宽,从而在频域内自适应地实现信号的有效分离.VMD的整体结构是变分问题,其约束条件是使每阶模态的估计带宽之和最小,且各模态之和等于输入信号,受约束的变分模型(Li F Y et al., 2017)表述如下:

|
(1) |
式中,f为待分析信号,μk为模态函数,ωk为每阶模态的中心频率.
在此基础上,引入二次惩罚因子α和拉格朗日乘子λ(t),将受约束的变分问题转换为非约束的变分问题,求取式(1)的最优解(唐贵基和王晓龙,2015),其表达式为:
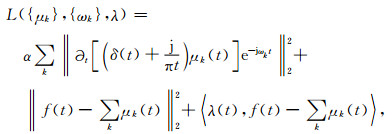
|
(2) |
式中,α用于确保信号的重构精度,λ(t)使约束条件更具严格性.
这样变分问题则可使用交替方向乘子法(Alternate Direction Method of Multipliers,ADMM)来求解,通过交替更新μkn+1、ωkn+1和λn+1来寻求拉格朗日表达式的鞍点.
其中,μkn+1可表述为:
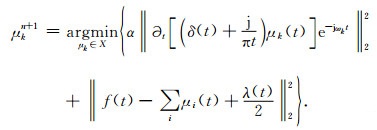
|
(3) |
利用Parseval傅里叶等距变换,将μkn+1转换至频域,得到各模态的频域更新(Zhao and Li, 2017).同时,将中心频率的取值也转换至频域,得到中心频率的更新方法.频域内模态函数、中心频率和λ的更新表达式为:

|
(4) |

|
(5) |
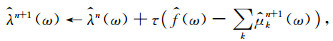
|
(6) |
对于判别精度e>0,若上述更新满足判定表达式(An and Pan, 2017),则终止迭代.判定表达式为:

|
(7) |
最终,VMD将待分析信号f自适应地分解为K个窄带的模态分量μk(k∈1, 2, …, K).
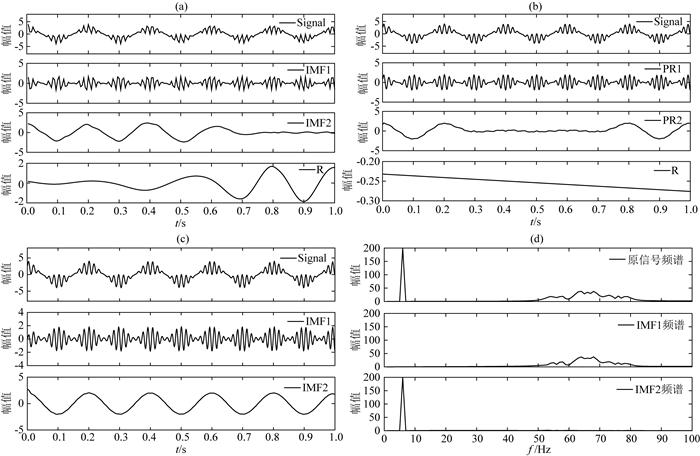
图 1所示为模拟的仿真信号f(t)=(1+cos(20πt))sin(120πt+30t2)+2cos(10πt)经EMD、ITD和VMD的分解效果图.
|
图 1 仿真信号分解效果图 (a) EMD;(b) ITD;(c) VMD;(d) VMD频谱. Fig. 1 Decomposition effect of simulated signal (a) EMD; (b) ITD; (c) VMD; (d) Spectrum of VMD. |
从图 1a和图 1b可知,EMD得到的IMF2分量存在明显的模态混叠和端点效应,其结果已不能表征待分析信号的固有特性;ITD将待分析信号f从频率高低自适应分解,当分解至PR2时,出现了严重的波形失真,该阶分量已不能表征f的时频分布特性.分析图 1c和图 1d可知,经VMD分解得到的模态分量能很好地表征f中60 Hz的调幅-调频成分及5 Hz的单频成分,其幅值和频谱也严格对应f中的各分量.相比于上述循环递归筛选模态方式的不同,VMD具有严格的数学模型和坚实的理论基础,其实质是多个自适应维纳滤波器组,表现出更好的噪声鲁棒性.由于VMD在受约束的变分框架进行频域的模态更新,从而避免了时域中模态分解的不足,同时提高了信号的分解精度.为此,VMD得到的各阶模态分量能更加准确地反映待分析信号中不同成分的振荡特征信息;若模态个数选取恰当,则能有效避免模态混叠、抑制端点效应等问题(Liu et al., 2016;武英杰等,2018).
1.2 匹配追踪匹配追踪可追溯至1993年由Mallat和Zhang提出的过完备字典,即在一组非正交基上将信号分解得到稀疏表示系数,其基本思想是在每次迭代过程中选取最佳的原子进行匹配,并不断更新残差直至迭代终止(Mallat and Zhang, 1993).算法最初是用来解决稀疏分解问题,后来学者们相继提出了一些改进算法,不断完善信号的最优匹配.该算法主要分为冗余字典的构造、原子匹配及残差分解,具体过程如下:
(1) 冗余字典的构造
构造冗余字典的目的在于根据信号自身特点灵活选取最优匹配原子,为此冗余字典一般需根据待处理信号的结构和先验知识来设计,如果字典中原子的结构与待处理信号越相似,则目标信号在字典中自适应稀疏分解的效果越好(朱会杰等,2015).
对于任意给定信号f可用冗余字典D={gγ}γ∈Γ中最佳匹配原子的线性组合表示,其中Γ为参数组γ的集合.常用的字典原子有正余弦原子、小波原子、Ricker原子、Heaviside原子和Gabor原子等(Wang et al., 2013;李晋等,2018).
(2) 原子匹配与残差分解
由于字典中的原子是冗余的,要选取与信号f最为匹配的原子gγ0,需满足以下条件(Cui et al., 2016):
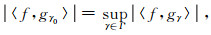
|
(8) |
式中,|〈f, gγ0〉|表示f与gγ0的内积,sup|〈f, gγ〉|表示上限值,则f可分解为:
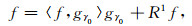
|
(9) |
式中,〈f, gγ0〉gγ0表示f在gγ0上的投影,R1f表示gγ0对f进行匹配后的残差(Cui et al., 2017).同时,R1f与gγ0是正交的.
为了使残差信号R1f尽可能的小,选择最佳原子使信号f与gγ0的内积最大化,并对残差信号进行逼近(杨午阳等,2017).当迭代至n+1次时,经n个原子逼近后的残差Rnf可表示为:

|
(10) |
经M次迭代后,f可表示为:

|
(11) |
式中,RMf表示f分解为M个原子逼近后的残差.
由于残差呈指数衰减,f可近似表示为:
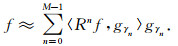
|
(12) |
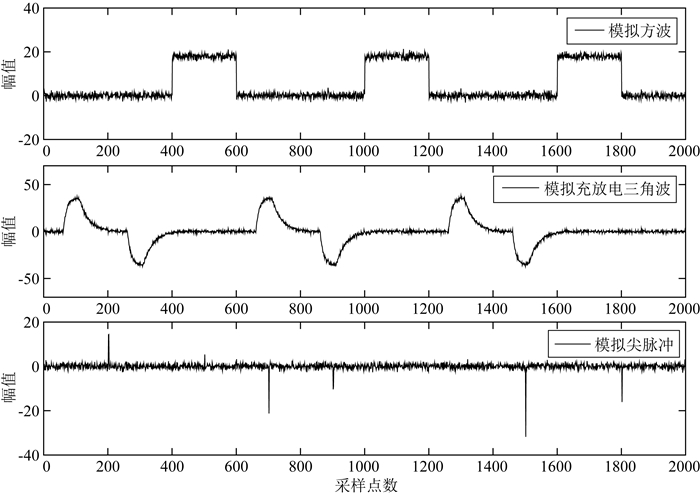
观测矿集区实测大地电磁数据可知,时间域序列中充斥大量类方波、类充放电三角波和类尖脉冲干扰(Li et al., 2019).为了分析VMD方法对大尺度强干扰的去噪性能,模拟上述典型强干扰进行仿真实验,三类大尺度强干扰时域波形如图 2所示.
|
图 2 模拟大尺度强干扰时域波形图 Fig. 2 Time domain waveform of simulated large-scale strong interference |
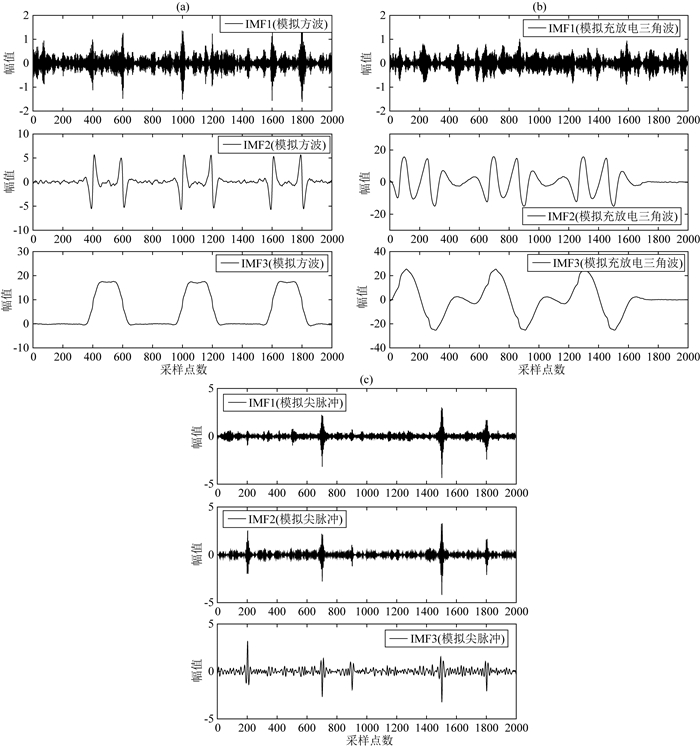
图 3所示为上述三类模拟信号经VMD分解后得到的各阶IMF分量.
|
图 3 模拟大尺度强干扰VMD效果图 Fig. 3 VMD effect of simulated large-scale strong interference |
从图 3可知,VMD将三类大尺度强干扰自适应地分解为3个模态分量,每个模态均具有一定的物理含义(谢平等,2016).分析仿真实验中的IMF1分量可知,该分量通常由大量类似于大地电磁微弱信号的随机信息组成.为此,文中后续利用VMD提取的大尺度轮廓特征则是通过将IMF1以外的其余IMF分量进行叠加得到.
2.2 模态的选取上述分析可知,VMD方法中模态个数(K)的选取尤为关键,将直接影响大尺度强干扰轮廓特征的光滑度及最终的重构效果(Xue et al., 2016).接下来,文中通过分析中心频率、相似度和信噪比等参数指标,综合评判不同K值情况下典型大尺度强干扰的去噪性能,相关参数定义如下:
(1) 相似度
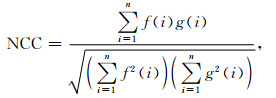
|
(13) |
式中,f(i)和g(i)分别表示原始信号和重构信号.其中,NCC∈[-1, 1],-1表示两曲线相位相反,0表示正交,1表示完全相同;NCC越趋近于1,则表示两曲线的相似度越高.
(2)信噪比

|
(14) |
SNR越大,表示去噪效果越好.
表 1—表 3分别所示为这三类典型强干扰在不同K值情况下的去噪性能.其中,中心频率对应每个模态分量的固有频率,NCC和SNR是经VMD分解得到的大尺度轮廓特征与仿真实验中模拟的大尺度干扰进行的分析对比.
|
|
表 1 不同K值的去噪性能对比(模拟方波) Table 1 De-noising performance comparison of different K-value (Simulated square wave) |
|
|
表 2 不同K值的去噪性能对比(模拟充放电三角波) Table 2 De-noising performance comparison of different K-value (Simulated charge and discharge triangular wave) |
|
|
表 3 不同K值的去噪性能对比(模拟尖脉冲) Table 3 De-noising performance comparison of different K-value (Simulated sharp pulse) |
分析表 1—表 3可知,对于三类模拟的大尺度强干扰,从K为4开始出现了中心频率相近的模态,相似度和信噪比急剧下降.当K为3时,三类大尺度强干扰的相似度和信噪比均达到最大值,同时观测相应的中心频率可知,此时各模态之间较好地避免了混叠现象(Wang and Markert, 2016).
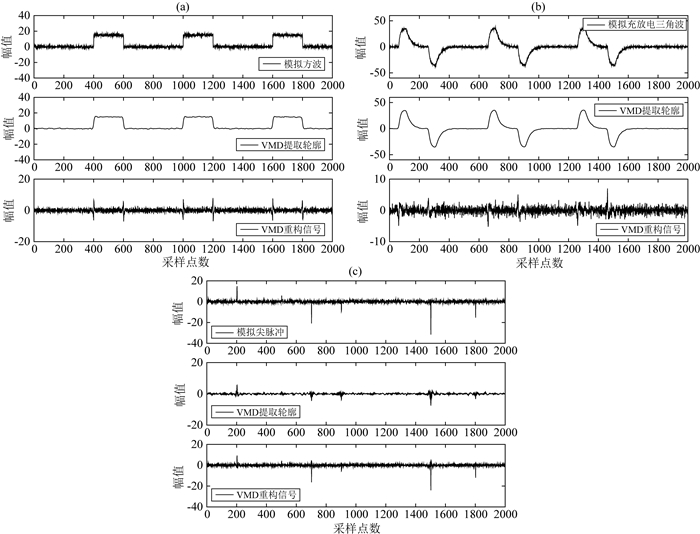
图 4所示为这三类模拟的强干扰经VMD(K=3)获取的大尺度轮廓特征及重构信号.
|
图 4 模拟大尺度强干扰经VMD获取的轮廓特征及重构信号 Fig. 4 Contour characteristic and reconstructed signal through VMD for simulated large-scale strong interference |
从图 4可知,VMD方法虽能较好地提取大尺度方波和充放电三角波的轮廓特征,但在重构信号的突变边缘出现了尖(窄)脉冲干扰.同时,结合表 3分析模拟尖脉冲的仿真实验可知,VMD方法提取尖脉冲时效果不佳,获得的轮廓特征中毛刺现象较为严重.由于匹配追踪(MP)能自适应地从冗余字典中选取与待处理信号相匹配的原子进行线性组合,该方法能较好地表征信号中的突变成分.为此,文中接下来采用MP对VMD重构信号进行二次信噪分离处理,以剔除残余的尖脉冲干扰.
2.3 二次信噪分离图 5所示为上述模拟的大尺度强干扰经MP二次信噪分离的仿真效果图.其中,冗余字典由正余弦原子和小波原子组成;正余弦原子用于匹配平稳成分,小波原子则用来匹配具有一定突变的非平稳成分.

|
图 5 模拟大尺度强干扰二次信噪分离效果图 Fig. 5 Signal-noise further separation effect of simulated large-scale strong interference |
分析图 5可知,MP方法能较好地提取VMD重构信号中残余的尖脉冲,补偿了VMD在尖(窄)脉冲提取过程中的不足,二次重构信号中保留了更多丰富、可靠的低频细节成分.
2.4 EMTF仿真分析为进一步考察方法的有效性,通过对EMTF开源包提供的原始时间序列添加典型的大尺度强干扰,对比分析重构信号与原始信号的相似度,以及远参考和本文所提方法去噪前后的视电阻率曲线来综合评判方法的去噪性能.
EMTF是由Egbert G D和Eisel M编写的大地电磁单点Robust估计与远参考分析的开源代码.该代码提供了两个100 Ωm均匀半空间的时间域数据,每个数据由5列长度为40000 s的数据构成,采样率为1 Hz(刘祥,2014).
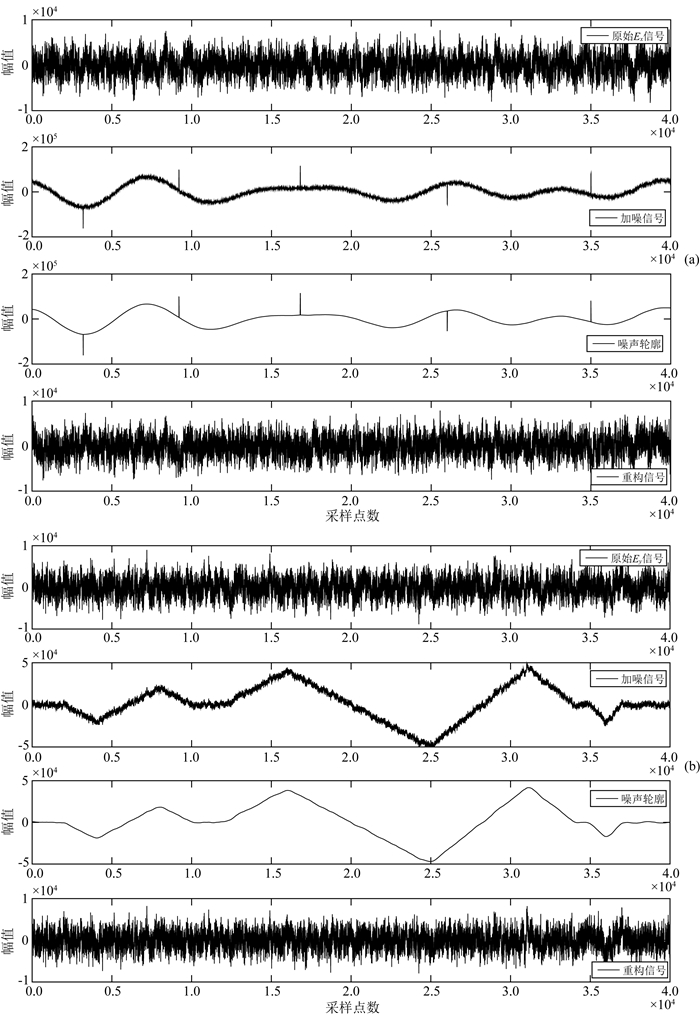
图 6所示为在EMTF提供的Ex和Ey原始数据(test1.asc文件)中分别添加大尺度正余弦尖脉冲和三角波干扰的时间域去噪效果.
|
图 6 EMTF中Ex和Ey的信噪分离效果图 Fig. 6 Signal-noise separation effect of Ex and Ey for EMTF (a) Ex; (b) Ey. |
分析图 6可知,本文所提方法能较好地提取大尺度强干扰的轮廓特征,通过计算重构信号(Ex和Ey)与原始信号(Ex和Ey)的相似度发现,其相似度分别达到0.9626和0.9664,有用信号得到了较好的恢复.
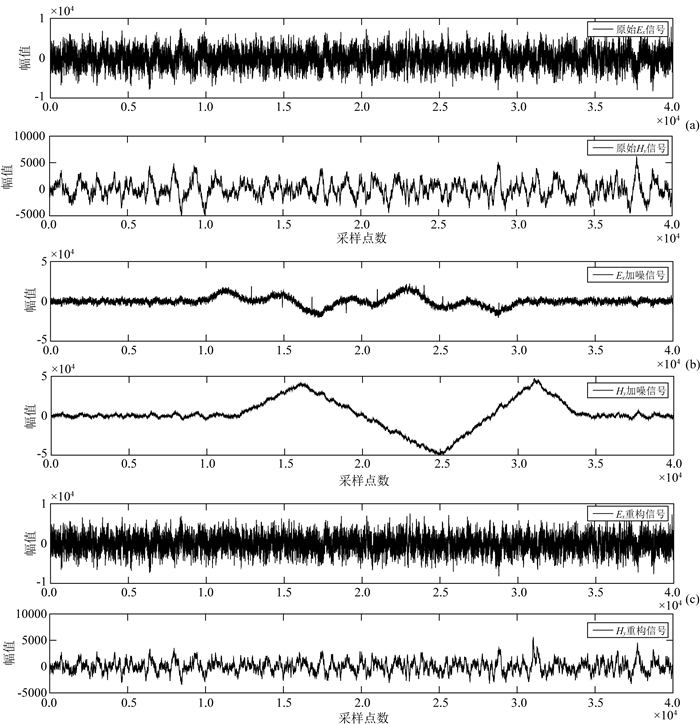
接下来,文中探讨加噪前后及远参考处理的视电阻率曲线对比情况.考虑到异常数据占总数据一半以上时,阻抗回归关系已被完全淹没(汤井田等,2013).为此,文中仅对Ex和Hy两道的原始数据添加一半长度(20000 s)的噪声进行去噪性能分析,如图 7所示.
|
图 7 EMTF信噪分离效果图 (a)原始数据;(b)加噪数据;(c)重构数据. Fig. 7 Signal-noise separation effect of EMTF (a) Original data; (b) Noisy data; (c) Reconstructed data. |
分析图 7可知,重构数据(Ex和Hy)与原始数据(Ex和Hy)的相似度分别达到0.9764和0.9218,大尺度噪声干扰得到了较好的压制.
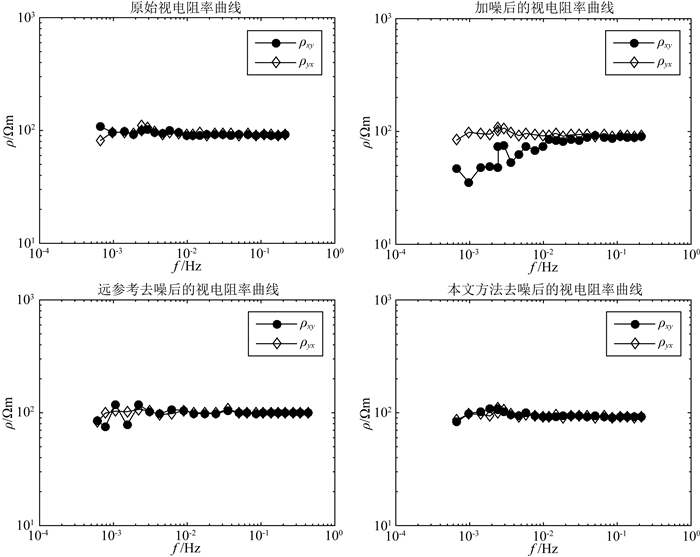
图 8所示为图 7中的数据经EMTF计算得到的视电阻率曲线对比图.其中,远参考去噪后的视电阻率曲线是由EMTF源代码中的test2.asc文件对图 7b中的加噪数据进行远参考的处理效果.
|
图 8 EMTF视电阻率曲线对比图 Fig. 8 Comparison of apparent resistivity curve for EMTF |
分析图 8可知,由于Ex和Hy受到强噪声干扰,导致 ρxy方向的视电阻率曲线低频段向下偏倚,突跳严重.远参考虽能有效消除一些噪声干扰,但低频段的个别频点仍有跳变现象、曲线不够光滑.对比本文所提方法,低频段频点的突变现象明显降低,曲线光滑、连续,其形态已接近于未受噪声干扰原始数据的视电阻率曲线形态特征.
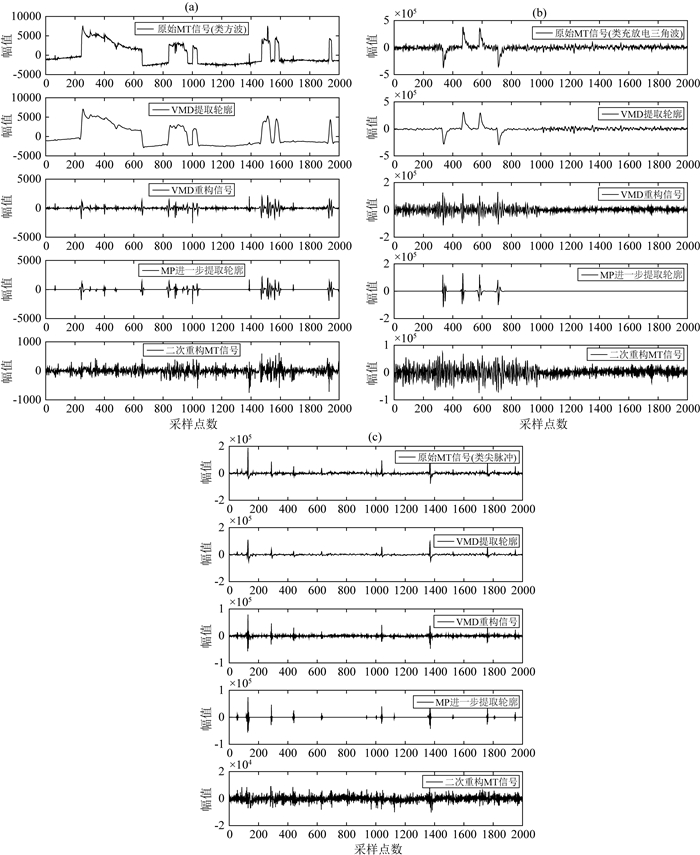
3 实测资料处理 3.1 时间域去噪效果为了验证本文所提方法的实用性,对矿集区含大尺度类方波、类充放电三角波和类尖脉冲干扰的实测MT数据(24 Hz采样)进行噪声压制,如图 9所示.
|
图 9 实测MT数据时间域滤波效果图 Fig. 9 Time domain filtering effect of measured MT data |
从图 9可知,原始MT信号受到类周期性突跳及波动的大尺度类方波、类充放电三角波和类尖脉冲干扰,这些干扰能量强、幅度大,微弱的MT有用信号几乎被完全湮没.VMD方法虽能初步获取大尺度强干扰的轮廓特征,但重构信号往往出现尖脉冲干扰.经MP二次信噪分离后,VMD重构信号中的突变尖脉冲得到了更有效的提取,二次重构信号则基本剔除了大尺度强干扰;低频缓变化信息得到了较好的保留,微弱的MT信号其本质特征得到了更好的还原.
3.2 实测点分析本文选用加拿大凤凰公司V5-2000采集的实测AMT数据进行分析处理.测点数据的采集时长约为1 h,采样频率分为高频(24000 Hz)、中频(2400 Hz)和低频(150 Hz)三种类型.其中,高频和中频在全时段交替采集,分别以TS2和TS3格式进行存储;低频在全时段采集,以TS4格式进行存储.由于反映测点深部的信息集中在低频段,因此本文仅针对低频段的实测数据进行噪声压制.
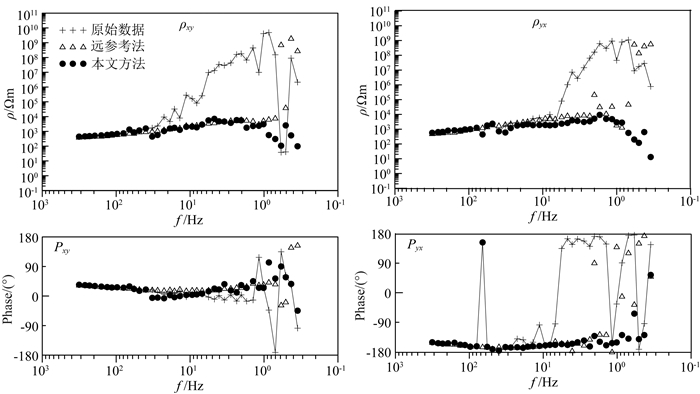
图 10—图 12分别给出了庐枞矿集区3个AMT实测点(D012520、D012535、D012550)的原始数据、远参考法及本文所提方法处理后的视电阻率-相位曲线对比图.
|
图 10 测点D012520视电阻率-相位曲线对比图 Fig. 10 Comparison of apparent resistivity-phase curve for site D012520 |

|
图 11 测点D012535视电阻率-相位曲线对比图 Fig. 11 Comparison of apparent resistivity-phase curve for site D012535 |

|
图 12 测点D012550视电阻率-相位曲线对比图 Fig. 12 Comparison of apparent resistivity-phase curve for site D012550 |
分析图 10—图 12中3个AMT测点原始数据的视电阻率-相位曲线可知,3组曲线的整体形态均不光滑且连续性差,尤其是低频段的视电阻率和相位突变剧烈.在30~0.5 Hz频段,视电阻率都呈45°左右渐近线快速上升,3个测点的视电阻率值分别从103/103/102 Ωm急剧上升至1010/1011/108 Ωm,最高提升了近8个数量级;相应的相位接近于0°或±180°,且跳变紊乱,该频段内近20个频点的数据可信度急剧下降;在0.5~0.3 Hz频段,D012520测点的视电阻率值突然下降至100 Ωm左右,相位跳变紊乱.同时,观测图 10—图 12的时域波形发现这3个实测点的原始数据均受到大尺度强干扰的影响,正常有用信号完全失真.由此可知,这些测点均受到了典型的近源干扰,若仍由原始数据来表征时频特性俨然已不能真实反映地下电性分布.经远参考法处理后,在30~5 Hz频段,视电阻率曲线变得较为光滑、连续;然而在3~0.3 Hz频段,视电阻率曲线仍呈45°左右上升趋势,对应的相位曲线突跳剧烈.由于远参考法对输入端引起的相关噪声无能为力,而矿集区实测点又受到了持续的强人文电磁干扰;为此,对于该类持续的强干扰,远参考法很难达到预期的实际效果.分析对比本文所提方法,3个测点的视电阻率-相位曲线的整体形态均变得光滑、连续,视电阻率值相对稳定.在30~0.5 Hz频段,近源效应已完全消失,视电阻率-相位曲线紊乱、剧烈跳变的现象不复存在;在3~0.3 Hz频段,视电阻率-相位曲线的平稳度大为提升.
图 13给出了上述测点D012550同一时段电道Ex和磁道Hy处理前后的时间域波形片段.从图 13可知,原始数据的电道和磁道均不同程度地出现了类周期性充放电三角波、类脉冲等大尺度强干扰,其能量幅值远高于正常有用信号几个数量级.经本文方法处理后,叠加在大尺度强干扰上的微弱信号得到了有效提取,真实的大地电磁有用信息得到了更好的还原.

|
图 13 测点D012550时域波形片段 Fig. 13 Time domain waveform sections of site D012550 |
为进一步评判所提方法的效果,接下来利用天然场源和人文场源在电磁场极化方向上的差异,对所研结果进行定性分析.由于天然场源没有固定的形式,其极化方向是随机变化的,表现在时间上为无序性,对应的电磁场极化方向也是随机的(Weckmann et al., 2005).人文场源一般具有固定的形式,极化方向相对稳定,因此电磁场极化方向可能会集中在某个或某部分方向上(周聪,2016).
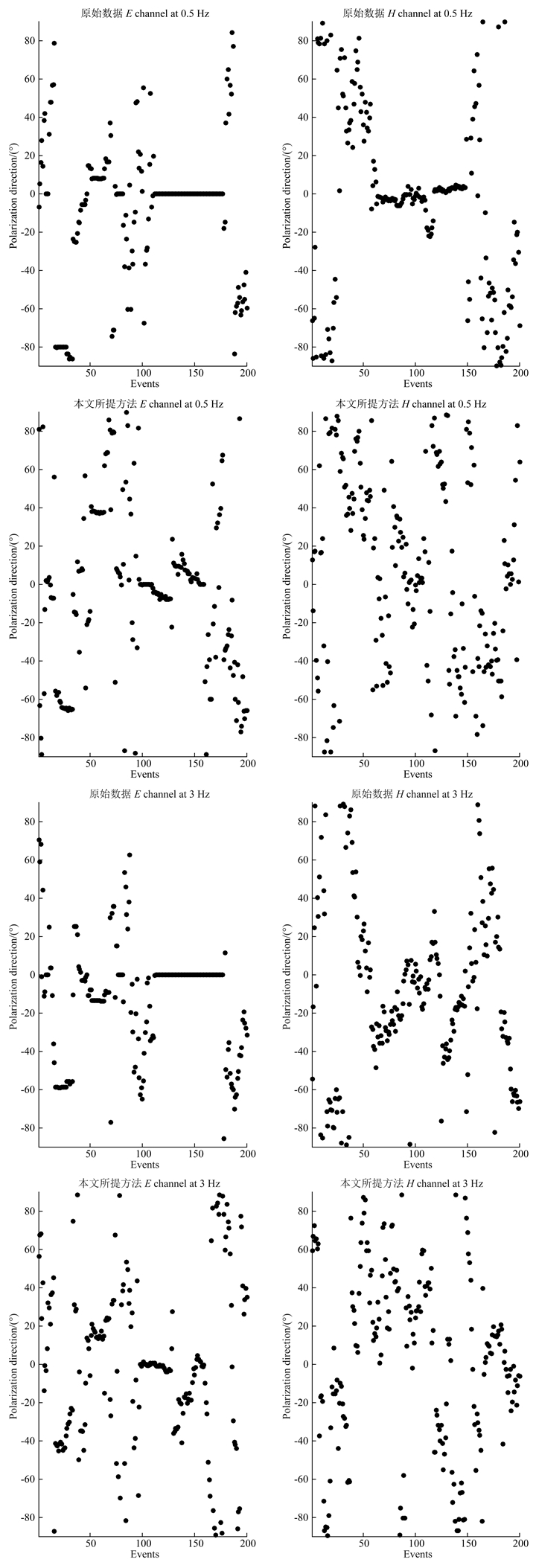
图 14给出了上述D012550测点经本文所提方法处理前后0.5 Hz和3 Hz的电磁场极化方向对比图.
|
图 14 测点D012550电磁场极化方向对比图 Fig. 14 Comparison of polarization direction of electromagnetic field for site D012550 |
分析图 14可知,D012550测点原始数据的电磁场极化方向呈高度集中趋势,尤其是电场极化方向在-20°~20°表现出明显的聚集性和规律性.结合电磁场极化方向的定义和时间域波形可知,该测点受到了强烈的电磁噪声干扰(张弛,2013).经本文所提方法处理后,0.5 Hz和3 Hz的电磁场极化方向都较原始数据有显著改善,极化点随机变化的趋势增大,极化方向的分布逐渐呈离散、无序状态.这些特征均符合天然大地电磁场的极化特征,一定程度上可以说明测点所包含的电磁场有用信息逐渐占主导地位、强人文电磁干扰得到了有效压制.
综上所述,本文所提方法能有效压制矿集区中大尺度强干扰,低频段的数据质量得到明显改善,其结果更为真实地反映了测点本身所固有的电性结构信息.
4 总结针对矿集区AMT数据的时间域序列中通常出现类周期性的大尺度强干扰,导致视电阻率-相位曲线呈近源趋势、低频段的数据质量急剧下降等问题,本文将VMD和MP相结合,研究了基于VMD和MP的AMT噪声压制方法.通过探讨中心频率、相似度和信噪比等参数指标,综合评价了有效模态对典型强干扰的去噪性能,初步获取了大尺度强干扰的轮廓特征;由于VMD重构信号中易残余尖脉冲干扰,结合AMT信号特征,将具有平稳成分的正余弦原子和非平稳成分的小波原子构造冗余字典,采用匹配追踪对VMD重构信号做二次信噪分离处理.实验结果表明:本文所提方法能有效剔除时间域序列中的大尺度强干扰,重构信号中保留了更多的低频缓变化信息及细节成分,近源干扰得到了有效压制;视电阻率-相位曲线更为光滑、连续,低频段的数据质量得到明显改善.
目前,本文仅是讨论了矿集区典型强干扰中VMD有效模态个数的选取,以及构造预定原子类型的冗余字典匹配残余的尖脉冲干扰.VMD和MP作为新兴的信号处理方法,如何根据矿集区复杂的电磁干扰环境,结合人工智能等手段自适应选取VMD中最优模态的个数及MP中冗余字典的原子类型,进一步改善矿集区AMT低频段的数据质量、提高信噪分离精度,将是今后的研究重点.
An X L, Pan L P. 2017. Bearing fault diagnosis of a wind turbine based on variational mode decomposition and permutation entropy. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk & Reliability, 231(2): 200-206. |
Cao X L, Liu K Y, Yan L J. 2018. Magnetotelluric data de-noising based on wavelet transform and independent component analysis. Oil Geophysical Prospecting (in Chinese), 53(1): 206-213. |
Chen H Y, Wei W B, Jing J E, et al. 2012. The generalized S-transform and its application in the processing of magnetotelluric sounding data. Progress in Geophys (in Chinese), 27(3): 988-996. DOI:10.6038/j.issn.1004-2903.2012.03.020 |
Chen J, Heincke B, Jegen M, et al. 2012. Using empirical mode decomposition to process marine magnetotelluric data. Geophysical Journal International, 190(1): 293-309. DOI:10.1111/j.1365-246X.2012.05470.x |
Cui L L, Wu N, Ma C Q, et al. 2016. Quantitative fault analysis of roller bearings based on a novel matching pursuit method with a new step-impulse dictionary. Mechanical Systems & Signal Processing, 68-69: 34-43. |
Cui L L, Yao T C, Zhang Y, et al. 2017. Application of pattern recognition in gear faults based on the matching pursuit of a characteristic waveform. Measurement, 104: 212-222. DOI:10.1016/j.measurement.2017.03.021 |
Dragomiretskiy K, Zosso D. 2014. Variational mode decomposition. IEEE Transactions on Signal Processing, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
Du Y H, Qi W J, Zou C, et al. 2017. Intermuscular coupling characteristics based on variational mode decomposition-coherence. Acta Physica Sinica (in Chinese), 66(6): 068701. |
Fan C S, Li T L, Wang D Y. 2008. Treatment of wavelet transform for square wave noise in MT data. Journal of Jilin University (Earth Science Edition) (in Chinese), 38(S1): 61-63. |
Frei M G, Osorio I. 2007. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 463(2078): 321-342. DOI:10.1098/rspa.2006.1761 |
Fu C Y, Chen Y T, Qi G Z. 1985. The Introduction to Geophysics (in Chinese). Beijing: Science Press.
|
Garcia X, Seillé H, Elsenbeck J, et al. 2015. Structure of the mantle beneath the Alboran Basin from magnetotelluric soundings. Geochemistry, Geophysics, Geosystems, 16(12): 4261-4274. DOI:10.1002/2015GC006100 |
Hu S G, Tang J T, Ren Z Y, et al. 2019. Multiple underwater objects localization with magnetic gradiometry. IEEE Geoscience and Remote Sensing Letters, 16(2): 296-300. DOI:10.1109/LGRS.2018.2870839 |
Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
Jing J E, Wei W B, Chen H Y, et al. 2012. Magnetotelluric sounding data processing based on generalized S transformation. Chinese J. Geophys (in Chinese), 55(12): 4015-4022. DOI:10.6038/j.issn.0001-5733.2012.12.013 |
Kalscheuer T, Pedersen L B, Siripunvaraporn W. 2008. Radiomagnetotelluric two-dimensional forward and inverse modelling accounting for displacement currents. Geophysical Journal International, 175(2): 486-514. DOI:10.1111/j.1365-246X.2008.03902.x |
Kapple K N. 2012. A data variance technique for automated despiking of magnetotelluric data with a remote reference. Geophysical Prospecting, 60(1): 179-191. DOI:10.1111/j.1365-2478.2011.00965.x |
Lei D, Zhao G Z, Zhang Z J, et al. 2010. A processing method of CSAMT data with strong electromagnetic interferences by using information entropy and rational function filtering. Progress in Geophys (in Chinese), 25(6): 2015-2023. |
Lü Q T, Dong S W, Tang J T, et al. 2015. Multi-scale and integrated geophysical data revealing mineral systems and exploring for mineral deposits at depth: A synthesis from SinoProbe-03. Chinese J. Geophys (in Chinese), 58(12): 4319-4343. DOI:10.6038/cjg20151201 |
Li F Y, Zhang B, Zhai R, et al. 2017. Depositional sequence characterization based on seismic variational mode decomposition. Interpretation, 5(2): E97-E106. DOI:10.1190/INT-2016-0069.1 |
Li G, Xiao X, Tang J T, et al. 2017. Near-source noise suppression of AMT by compressive sensing and mathematical morphology filtering. Applied Geophysics, 14(4): 581-589. DOI:10.1007/s11770-017-0645-6 |
Li J, Tang J T, Wang L, et al. 2014. Noise suppression for magnetotelluric sounding data based on signal subspace enhancement and endpoint detection. Acta Physica Sinica (in Chinese), 63(1): 019101. |
Li J, Tang J T, Cai J H, et al. 2016. Separation and identification of magnetotelluric weak data using multi-scale morphology and recurrence plot. Journal of Central South University (Science and Technology) (in Chinese), 47(11): 3890-3898. |
Li J, Tang J T, Xu Z M, et al. 2017a. Magnetotelluric noise suppression base on signal-to-noise identification in ore concentration area. Chinese J. Geophys (in Chinese), 60(2): 722-737. DOI:10.6038/cjg20170224 |
Li J, Tang J T, Yan H, et al. 2017b. Identification and separation of magnetotelluric signal and noise based on recurrence analysis and clustering. Chinese J. Geophys (in Chinese), 60(5): 1918-1936. DOI:10.6038/cjg20170525 |
Li J, Yan H, Tang J T, et al. 2018. Magnetotelluric noise suppression based on matching pursuit and genetic algorithm. Chinese J. Geophys (in Chinese), 61(7): 3086-3101. DOI:10.6038/cjg2018L0229 |
Li J, Zhang X, Gong J Z, et al. 2018. Signal-noise identification of magnetotelluric signals using fractal-entropy and clustering algorithm for targeted de-noising. Fractals, 26(2): 1840011. DOI:10.1142/S0218348X1840011X |
Li J, Zhang X, Tang J T, et al. 2019. Audio magnetotelluric signal-noise identification and separation based on multifractal spectrum and matching pursuit. Fractals, 27(1): 1940007. DOI:10.1142/S0218348X19400073 |
Li W, Liu F, Jiao L C, et al. 2016. A group matching pursuit for image reconstruction. Signal Processing: Image Communication, 49: 47-62. DOI:10.1016/j.image.2016.10.002 |
Ling Z B, Wang P Y, Wan Y X, et al. 2016. A combined wavelet transform algorithm used for de-noising magnetotellurics data in the strong human noise. Chinese J. Geophys (in Chinese), 59(9): 3436-3447. DOI:10.6038/cjg20160926 |
Liu C L, Wu Y J, Zhen C G. 2015. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering. Proceedings of the CSEE (in Chinese), 35(13): 3358-3365. |
Liu X. 2014. Research on the influence of square wave noises on magnetotelluric remote reference method [Master′s thesis] (in Chinese). Changsha: Central South University.
|
Liu Y Y, Yang G L, Li M, et al. 2016. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Processing, 125: 349-364. DOI:10.1016/j.sigpro.2016.02.011 |
Mallat S G, Zhang Z F. 1993. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41(12): 3397-3415. DOI:10.1109/78.258082 |
Nabighian M N. 1987. Electromagnetic Methods in Applied Geophysics: Volume 1, Theory. Society of Exploration Geophysicists.
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Sivavaraprasad G, SreePadmaja R, VenkataRatnam D. 2017. Mitigation of ionospheric scintillation effects on GNSS signals using variational mode decomposition. IEEE Geoscience and Remote Sensing Letters, 14(3): 389-393. DOI:10.1109/LGRS.2016.2644723 |
Tang G, Ma J W, Yang H Z. 2012. Seismic data denoising based on learning-type overcomplete dictionaries. Applied Geophysics, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
Tang G J, Wang X L. 2015. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing. Journal of Xi′an Jiaotong University (in Chinese), 49(5): 73-81. |
Tang J T, Hua X R, Cao Z M, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data. Chinese J. Geophys (in Chinese), 51(2): 603-610. |
Tang J T, Li J, Xiao X, et al. 2012. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data. Chinese J. Geophys (in Chinese), 55(5): 1784-1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
Tang J T, Zhang C, Xiao X, et al. 2013. Comparison of methods for magnetotelluric impedance estimation. The Chinese Journal of Nonferrous Metals (in Chinese), 23(9): 2351-2358. |
Tang J T, Hu S G, Ren Z Y, et al. 2018. Localization of multiple underwater objects with gravity field and gravity gradient tensor. IEEE Geoscience and Remote Sensing Letters, 15(2): 247-251. DOI:10.1109/LGRS.2017.2784837 |
Tikhonov A N. 1950. On determining electrical characteristics of the deep layers of the Earth′s crust. Dokl. Acad. Nauk. SSSR, 73(2): 295-297. |
Trad D O, Travassos J M. 2000. Wavelet filtering of magnetotelluric data. Geophysics, 65(2): 482-491. DOI:10.1190/1.1444742 |
Wang H, Wei W B, Jin S, et al. 2014. Removal of magnetotelluric noise based on synchronous time series relationship. Chinese J. Geophys (in Chinese), 57(2): 531-545. DOI:10.6038/cjg20140218 |
Wang X Q, Zhu H J, Wang D, et al. 2013. The diagnosis of rolling bearing based on the parameters of pulse atoms and degree of cyclostationarity. Journal of Vibroengineering, 15(3): 1560-1575. |
Wang Y X, Markert R. 2016. Filter bank property of variational mode decomposition and its applications. Signal Processing, 120: 509-521. DOI:10.1016/j.sigpro.2015.09.041 |
Weckmann U, Magunia A, Ritter O. 2005. Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme. Geophysical Journal International, 161(3): 635-652. DOI:10.1111/j.1365-246X.2005.02621.x |
Wu Y J, Xin H W, Wang J G, et al. 2018. Rolling bearing fault diagnosis based on the variational mode decomposition filtering and extreme point envelope order. Journal of Vibration and Shock (in Chinese), 37(14): 102-107. |
Xie P, Yang F M, Li X X, et al. 2016. Functional coupling analyses of electroencephalogram and electromyogram based on variational mode decomposition-transfer entropy. Acta Physica Sinica (in Chinese), 65(11): 118701. |
Xue Y J, Cao J X, Wang D X, et al. 2016. Application of the variational-mode decomposition for seismic time-frequency analysis. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 9(8): 3821-3831. DOI:10.1109/JSTARS.2016.2529702 |
Yang W Y, Yang Q, He X, et al. 2017. Research and application of improved high precision matching pursuit method. Chinese J. Geophys (in Chinese), 60(7): 2825-2832. DOI:10.6038/cjg20170727 |
Yao J C, Xiang Y, Li S Y, et al. 2016. Noise sources identification method of internal combustion engine based on VMD-ICA-CWT. Journal of Huazhong University of Science and Technology (Natural Science Edition) (in Chinese), 44(7): 20-24. |
Zhang C. 2010. Magnetotelluric data quality assessment and impedance estimation [Master′s thesis] (in Chinese). Changsha: Central South University.
|
Zhao H S, Li L. 2017. Fault diagnosis of wind turbine bearing based on variational mode decomposition and Teager energy operator. IET Renewable Power Generation, 11(4): 453-460. DOI:10.1049/iet-rpg.2016.0070 |
Zhou C. 2016. Theoretical and experimental study of space-time array electromagnetic method and three-dimensional electrical structure of Lu-Zong ore district [Ph. D. thesis] (in Chinese). Changsha: Central South University.
|
Zhu H J, Wang X Q, Rui T, et al. 2015. Implication of improved matching pursuit in de-noising for square wave. Journal of PLA University of Science and Technology (Natural Science Edition) (in Chinese), 16(4): 305-309. |
曹小玲, 刘开元, 严良俊. 2018. 大地电磁的小波变换——独立分量分析去噪. 石油地球物理勘探, 53(1): 206-213. |
陈海燕, 魏文博, 景建恩, 等. 2012. 广义S变换及其在大地电磁测深数据处理中的应用. 地球物理学进展, 27(3): 988-996. DOI:10.6038/j.issn.1004-2903.2012.03.020 |
杜义浩, 齐文靖, 邹策, 等. 2017. 基于变分模态分解-相干分析的肌间耦合特性. 物理学报, 66(6): 068701. |
范翠松, 李桐林, 王大勇. 2008. 小波变换对MT数据中方波噪声的处理. 吉林大学学报(地球科学版), 38(S1): 61-63. |
傅承义, 陈运泰, 祁贵仲. 1985. 地球物理学基础. 北京: 科学出版社.
|
景建恩, 魏文博, 陈海燕, 等. 2012. 基于广义S变换的大地电磁测深数据处理. 地球物理学报, 55(12): 4015-4022. DOI:10.6038/j.issn.0001-5733.2012.12.013 |
雷达, 赵国泽, 张忠杰, 等. 2010. 强干扰地区CSAMT数据信息熵与有理函数滤波的处理方法. 地球物理学进展, 25(6): 2015-2023. DOI:10.3969/j.issn.1004-2903.2010.06.017 |
吕庆田, 董树文, 汤井田, 等. 2015. 多尺度综合地球物理探测:揭示成矿系统、助力深部找矿——长江中下游深部探测(SinoProbe-03)进展. 地球物理学报, 58(12): 4319-4343. DOI:10.6038/cjg20151201 |
李晋, 汤井田, 王玲, 等. 2014. 基于信号子空间增强和端点检测的大地电磁噪声压制. 物理学报, 63(1): 019101. |
李晋, 汤井田, 蔡剑华, 等. 2016. 利用多尺度形态学和递归图分离辨识大地电磁微弱信号. 中南大学学报(自然科学版), 47(11): 3890-3898. |
李晋, 汤井田, 徐志敏, 等. 2017a. 基于信噪辨识的矿集区大地电磁噪声压制. 地球物理学报, 60(2): 722-737. DOI:10.6038/cjg20170224 |
李晋, 汤井田, 燕欢, 等. 2017b. 基于递归分析和聚类的大地电磁信噪辨识及分离. 地球物理学报, 60(5): 1918-1936. DOI:10.6038/cjg20170525 |
李晋, 燕欢, 汤井田, 等. 2018. 基于匹配追踪和遗传算法的大地电磁噪声压制. 地球物理学报, 61(7): 3086-3101. DOI:10.6038/cjg2018L0229 |
凌振宝, 王沛元, 万云霞, 等. 2016. 强人文干扰环境的电磁数据小波去噪方法研究. 地球物理学报, 59(9): 3436-3447. DOI:10.6038/cjg20160926 |
刘长良, 武英杰, 甄成刚. 2015. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断. 中国电机工程学报, 35(13): 3358-3365. |
刘祥. 2014.方波噪声对大地电磁远参考效果影响研究[硕士论文].长沙: 中南大学.
|
唐贵基, 王晓龙. 2015. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用. 西安交通大学学报, 49(5): 73-81. |
汤井田, 化希瑞, 曹哲民, 等. 2008. Hilbert-Huang变换与大地电磁噪声压制. 地球物理学报, 51(2): 603-610. DOI:10.3321/j.issn:0001-5733.2008.02.034 |
汤井田, 李晋, 肖晓, 等. 2012. 数学形态滤波与大地电磁噪声压制. 地球物理学报, 55(5): 1784-1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
汤井田, 张弛, 肖晓, 等. 2013. 大地电磁阻抗估计方法对比. 中国有色金属学报, 23(9): 2351-2358. |
王辉, 魏文博, 金胜, 等. 2014. 基于同步大地电磁时间序列依赖关系的噪声处理. 地球物理学报, 57(2): 531-545. DOI:10.6038/cjg20140218 |
武英杰, 辛红伟, 王建国, 等. 2018. 基于VMD滤波和极值点包络阶次的滚动轴承故障诊断. 振动与冲击, 37(14): 102-107. |
谢平, 杨芳梅, 李欣欣, 等. 2016. 基于变分模态分解-传递熵的脑肌电信号耦合分析. 物理学报, 65(11): 118701. DOI:10.7498/aps.65.118701 |
杨午阳, 杨庆, 何欣, 等. 2017. 改进的高精度匹配追踪方法研究及应用. 地球物理学报, 60(7): 2825-2832. DOI:10.6038/cjg20170727 |
姚家驰, 向阳, 李胜杨, 等. 2016. 基于VMD-ICA-CWT的内燃机噪声源识别方法. 华中科技大学学报(自然科学版), 44(7): 20-24. |
张弛. 2013.大地电磁数据质量评价与阻抗估计[硕士论文].长沙: 中南大学.
|
周聪. 2016.时空阵列电磁法及试验研究兼论庐枞矿集区三维电性结构[博士论文].长沙: 中南大学.
|
朱会杰, 王新晴, 芮挺, 等. 2015. 改进的匹配追踪在方波信号滤波中的应用. 解放军理工大学学报(自然科学版), 16(4): 305-309. |
 2019, Vol. 62
2019, Vol. 62

