2. 有色金属成矿预测与地质环境监测教育部重点实验室(中南大学), 长沙 410083;
3. 核资源与环境国家重点实验室, 东华理工大学, 南昌 330013
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring(Central South University), Changsha 410083, China;
3. State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang 330013, China
电磁法是一种重要的勘探地球物理方法,主要有被动源电磁法和人工源电磁法(Nabighian, 1987; Chen et al., 2011; Ren et al., 2013; Grayver et al., 2014; 任政勇等, 2017; Chave et al., 2017).相对于被动源电磁法,人工源电磁法具有信号强、分辨率高的特点,场源主要有方波信号和伪随机信号两种,其中以伪随机信号为场源的电磁法可通过一次发送和接收获得多个频率的地电信息,提高了野外工作效率和抗干扰能力(何继善, 2010a, 2010b; Ziolkowski et al., 2011).由于大地是一个开放的环境,在数据采集过程中不可避免地会受到各种噪声的干扰,尤其是人文干扰,幅度大且频率范围宽,常使观测信号畸变,为电磁法工作的开展和推广带来了极大的困扰(Szarka, 1988; 汤井田等, 2017, 2018; 杨洋等, 2018; Yang et al., 2018; Chave, 2017; Li et al., 2019).因此,如何有效压制强电磁干扰,为后续处理解释提供可靠数据仍然是当前电磁勘探中极为重要的研究课题.
伪随机多频电磁信号通过编码一次发送可以同时接收到多个频率信号,同时在人工源电磁法勘探中,通常进行冗余测量,获得各频点的多个频谱数据,具有一定的抗干扰性.然而,测量的信号包含了有效信号和干扰信号.在人工源数据处理中,常将剔除异常值后的频谱数据的均值作为测量结果,从而获取可靠的有效信号.为压制噪声影响,国内外学者提出了多种数据处理方法.稳健阻抗估计是一种主流的提高阻抗估计质量的方法(Egbert and Livelybrooks, 1996; Chave and Thomson, 2003; 周聪等, 2015; Liu et al., 2016).但由于场源不同,人工源电磁法场源极化方向固定,不同方向上的信号能量差异大,在近区平面波假设不再成立,稳健阻抗估计在人工源电磁数据处理中可能导致错误的结果(Streich et al., 2013);小波变换过分依赖于小波函数的选择,且随着尺度的增大,相应正交基函数的频谱局部性变差,使信号的精细分解受限(Trad and Travassos, 2000; 凌振宝等, 2016);数字滤波技术需综合考虑电磁测深方法、仪器、有效信号时频特征甚至是工作环境等多种因素,在噪声和有用信号在大范围相互重叠的情况下,去噪效果不佳(Olsen and Hohmann, 1992; 邓靖武等, 2004);采用人机联作去噪虽能较好改善数据质量,但操作不可避免地引入了主观因素,编辑结果因人而异,且工作量巨大.
张必明等(2015)采用自适应双向均方差阈值法,采用单一阈值控制异常剔除,该方法在少量频点被污染时能有效压制噪声影响.然而,实测的各频点数据受噪声影响程度不一致,采用单一阈值控制可能会出现有效数据被剔除或者噪声数据未被处理的情况,且该方法未考虑曲线整体的圆滑连续性.Mo等(2017)提出了一种基于灰色建模和稳健M估计的人工源电磁数据处理方法,并结合阈值法大幅提高了对异常值占比的容忍度及处理结果的效果,处理后频谱数据曲线趋于光滑.但由于需要多次试验来寻找合适的阈值,数据处理比较耗时.总的来说,现有的各种单一的去噪技术均具有一定的优势,同时也存在一定局限性.
作为平滑滤波的一种,有理函数滤波克服传统滤波算法在保护信号细节时,耗时长、平滑能力低等缺点,在函数近似、插值和图像处理等方面得到广泛应用,并可用于恢复干扰少的频率域电磁场数据曲线的基本形态(Ramponi, 2001; 严家斌和刘贵忠, 2006; 雷达等, 2010).但因其过度依赖于原始曲线的趋势分析,当干扰严重出现连续飞点或某一频段形态失真时,会造成资料的二次污染,且滤波参数的选择不当会使滤波结果脱离真实情况(黄皓平, 1991).
针对上述问题,本文提出了一种基于灰色判别准则和有理函数滤波的伪随机电磁信号数据处理方法.在滤波前,引入灰色判别准则对原始数据进行初步处理,剔除明显的异常值,还原曲线的基本走势.然后对经灰色判别准则处理后得到的曲线进行有理函数滤波,用充分接近真实值的滤波结果约束数据的二次优化处理,从而达到剔除残余噪声的目的,并克服了滤波参数选择不当可能导致的滤波结果脱离真实值的问题.且由于经灰色判别准则处理后大部分噪声干扰消除殆尽,故选择相同滤波参数处理干扰程度不一的数据同样可以有效剔除干扰,且在一定范围内选择任意参数都可大幅改善数据质量.
1 方法原理 1.1 灰色判别准则灰色判别准则实际是利用灰色系统理论中的累加生成法,通过累加后得到累加曲线,从曲线变化规律获取信息并用于离群值判别,原理如下(施冬等, 1998; 朱坚民等, 2010; Kayacan et al., 2010; Ayvaz et al., 2014):
对于某测点的某一频点的伪随机电磁频谱数据,可以表示为序列x=(x(k)|k=1, 2, …, L),其中,xk表示第k个频谱数据,L表示该频点频谱数据的个数.当实测数据受到噪声干扰时,电磁频谱数据序列存在无规律的、随机的或有明显的跳动.将序列从小到大排列成序列x(0),有:
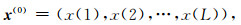
|
(1) |
其中,x(k)≤x(k+1)(k=1, 2, …, L-1).
将排序后的电磁频谱数据序列x(0)经一次累加生成后,可以获得新序列x(1):
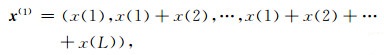
|
(2) |
如图 1中实线2所示.其平均累加序列(如图 1中虚线1所示)可以表示为:
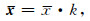
|
(3) |
|
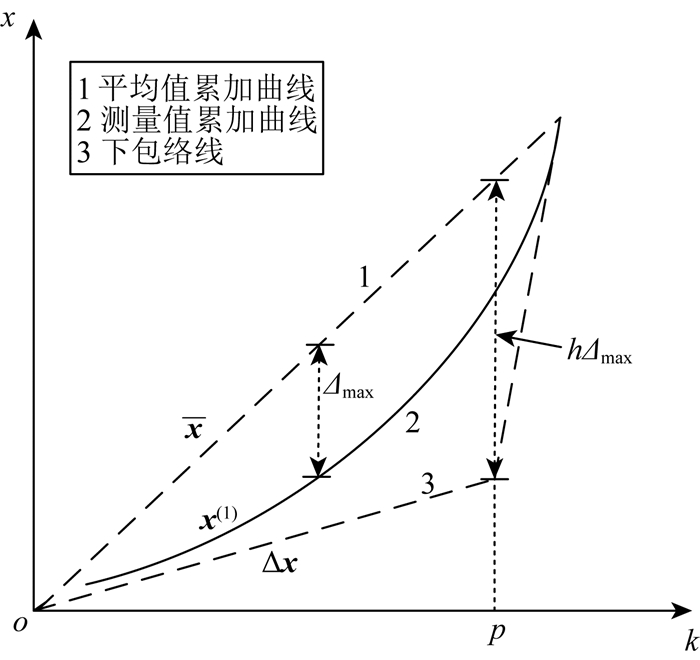
图 1 灰色区域图 Fig. 1 Gray area |
其中,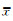


|
(4) |
其中:

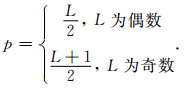
|
(5) |
根据测量值不确定度的灰分析,Δx系列随着测量次数k的增大,由0开始逐渐增加至最大值,随后由于随机误差的叠加相消效应,又逐渐减小到0.若测量中不出现异常值,在随机误差的作用下,测量累加曲线变化并约束在一个三角区域内,如图 1所示.
如果,x(1)(1)≤Δx(1),那么认为相应的最小测量值x(1)为受到噪声干扰的异常值;如果,x(1)(k-1)≤Δx(k-1),那么认为相应的最大测量值x(k)为受到噪声干扰的异常值,然后相应的剔除对应位置上的异常值,从而达到剔除明显异常值的目的.将处理后得到的序列命名为y=(yj|j=1, 2, …, M),M为保留频谱数据的个数.
1.2 有理函数滤波将经过灰色判别准则剔除明显异常值后的伪随机电磁频谱数据进行有理函数滤波,进一步消除残余噪声的影响.有理函数通常定义为两个多项式的比值,只需较少参数就能表示信号的变换关系(Ramponi, 2001; 雷达等, 2010).对于序列y中的连续三个伪随机电磁频谱数据(yj-1, yj, yj+1),其中,1≤j-1<j<j+1≤M,其对称的线性低通滤波系统可以表示为:
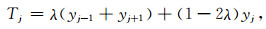
|
(6) |
式中,0 < λ < 1/3.上述滤波器的响应函数随着频率的增加而单调减小,具有低通滤波的特性,其截止频率为λ的反函数.因此,在使用该方法进行滤波时,具有压制高频信号的特点,从而使滤波后的信号模糊化.为了方便数据处理,将公式(6)写成如下形式:
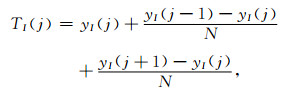
|
(7) |
式中,截止频率N=1/λ,I表示迭代的次数.
为了避免这类线性滤波器在进行数据处理时导致信号模糊化的问题,需要控制改正项的变化,并对信息的重要性进行估计,使其对重要的高频信息的影响变小.本文通过估计梯度值的大小来判定信息的重要性,采用中心差分代替微分,改进公式(7)中的有理函数滤波模型,改进后的有理函数滤波模型如下:
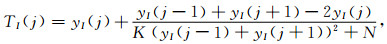
|
(8) |
式中,K称为正参数,为一正数,即K>0.从而使得改进后的利用中心差分进行估计的滤波模型具有带通滤波响应特征.从式(8)可知,当K=0时,滤波模型退化为线性滤波方程,K→∞时滤波器将不被激活.
1.3 处理流程综上所述,基于灰色判别准则和有理数函数滤波的数据处理算法步骤如下:
(1) 基于灰色判别准则剔除各个频点频谱数据中的明显异常值,取各个频点存留频谱数据的均值,得到序列X1(i), i=1, 2, …, n,n为频点个数;
(2) 对X1(i)进行有理函数滤波,得到滤波曲线X2(i);
(3) 计算X1(i), X1(i+1), X1(i+2)构成三条折线段的斜率k1, k2, k3.若存在k1 < k3 < k2或k2 < k3 < k1,则X1(i+1)为局部极值点,并对相应频点的频谱数据进行处理;
(4) 采用公式(9),将从小到大排序后的频谱数据分为两段[1, m1]、[m2, M],基于灰色建模计算标准差σ1、σ2.若σ1>σ2,剔除第一个数据,反之剔除最后一个数据.更新数据,M=M-1,重新分段,直到数据个数小于设定的值.取每次处理后的稳健均值,计算与前一个频点的斜率k1,保留与滤波曲线对应斜率最为接近的值;

|
(9) |
式中,M为单个频点频谱数据个数;INT()为取整函数,k为奇偶因子.N为偶数时,k=0,N为奇数时,k=1.
(5) 处理完所有频点后,为消除残余异常对处理结果的影响,转步骤(3),再处理一次转步骤(6);
(6) 结束算法.
算法在处理过程中只剔除端点的数据点,删除后更新数据,在接下来的每次迭代中,算法不断趋向样本数据中分布最集中的一部分,使得算法具有自适应优化的特点;通过不依赖数据分布规律和数量的灰色建模方法计算标准差,通过稳健估计算法分配权重的方式来削弱离群值对估计结果的影响,减小甚至避免后续处理出现异常误判或有效值误删的情况,故算法适用离群值比例大的小样本数据;经灰色判别准则处理,大致还原真实信号的形态走势,大大降低异常对滤波的影响,以保证滤波曲线能高度逼近真实信号;用滤波曲线约束数据自动处理,避免人为控制,极大提高了处理效率和数据的可靠性.另外算法实现简单,设备配置要求低,适用于各种计算环境.
2 数据仿真实验 2.1 仿真结果评价标准野外噪声干扰错综复杂.分析大量伪随机多频电磁信号,比较常见的强噪声干扰有方波噪声、工频噪声、充放电噪声、脉冲噪声等,这些噪声都是由于复杂的外界因素和人文因素引起的,其能量强、频带广(汤井田等, 2018; 张必明等, 2015; 李晋等, 2017; Liu et al., 2017, 2019).为测试算法效果并分析噪声的影响规律,在以下仿真实验中,向实测无明显干扰的伪随机多频电磁时域数据的各个频组中逐点添加同种噪声.各种类型噪声强度为原始数据的30~60倍,数据长度约为原始数据的1/5.将加噪前的时域数据分别分成若干段,每段时域数据长度为最低频率周期的整数倍,利用数字相干检测技术提取每段数据主频点的振幅.对每个频点的振幅求均值,可得到加噪前频谱数据曲线z(i), i=1, 2, …, n.用本文方法对加噪后的数据进行处理,得到处理后的频谱数据曲线s(i), i=1, 2, …, n.通过计算z(i)与s(i)的曲线相似度NCC、信噪比SNR和误差ERR来评价处理效果(Cai et al., 2009; 汤井田等, 2017; Li et al., 2017),具体表达式如下所示:
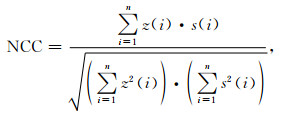
|
(10) |
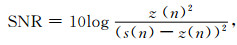
|
(11) |

|
(12) |
NCC为1时表示两个信号完全一样,为0表示正交,为-1表示两个信号的绝对值相同而符号相反.曲线相似度NCC越接近1,信噪比SNR越大,误差ERR越接近0,表示处理效果越好.
2.2 不同滤波参数的仿真结果频谱曲线滤波是算法的重要一步,选择合适的滤波参数可高精度还原理想曲线,提高数据质量.为分析滤波参数对数据处理的影响,对图 2所示受不同干扰影响的加噪数据进行处理.图 2a和图 2c分别为仿真所添加的工频干扰和脉冲干扰的频谱曲线,加入工频干扰后的曲线在中频段出现不同程度的凸起,其中48 Hz处的频谱约增大一个数量级,脉冲干扰影响范围在100 Hz以下,能量在10~0.1 Hz频段达到最大值,电位差频谱曲线的100 Hz以后频段受到不同程度的影响,0~1 Hz频段最为严重.采用本文方法进行去噪处理,处理结果如图 2b和图 2d所示,频谱曲线变得光滑,逼近原始数据.

|
图 2 两类噪声干扰的频谱及处理前后对比 (a)工频噪声频谱;(b)工频噪声处理前后电位差频谱曲线;(c)脉冲噪声频谱;(d)脉冲噪声处理前后电位差频谱曲线. Fig. 2 Spectrum of two kinds of noise and results comparison (a) Spectrum of power frequency noise; (b) Potential difference spectrum curve before and after processing power frequency noise; (c) Spectrum of impulse noise; (d) Potential difference spectrum curve before and after processing impulse noise. |
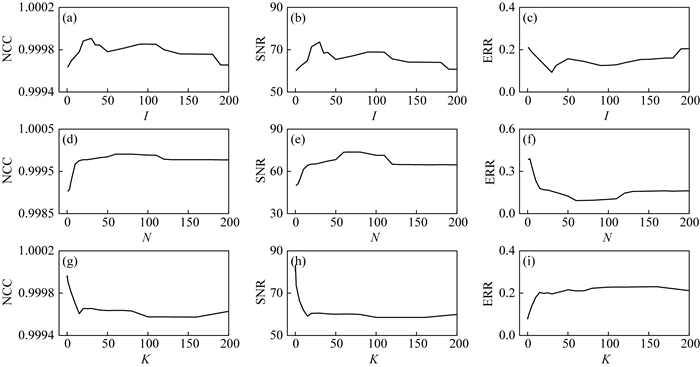
从图 3和图 4中可以看出,被噪声污染的频谱曲线比原始曲线的相似度NCC低,信噪比SNR为负数,误差大.保持其他两个参数不变,依次改变式(8)中迭代次数I、正参数K和截止频率N.两图曲线变化趋势一致:(1)固定K=0.1,N=100,随着I值的增加,曲线相似度NCC和信噪比SNR值变大,误差ERR下降,当I达到某一数值时,各项评价指标均达到最优.I值的持续增大导致仿真效果缓慢变差,最后趋于稳定;(2) N值的选取对仿真效果的影响与I值类似,固定K=0.1,I=70,当N等于某一个值时,处理效果最好;(3)固定I=70,N=100,K值取较小时,结果最佳,随着K的增大,NCC和SNR迅速下降,ERR急速上升,随后缓慢变化.其中,对于干扰程度较大的信号,选择更大的迭代次数可以更接近原始信号.
|
图 3 工频干扰下不同滤波参数的影响 (a—c)不同I的处理效果;(d—f)不同N的处理效果;(e—i)不同K的处理效果. Fig. 3 Influence of different filter parameters under power noise (a—c) Results of different I; (d—f) Results of different N; (e—i) Results of different K. |

|
图 4 脉冲干扰下不同滤波参数的影响 (a—c)不同I的处理效果;(d—f)不同N的处理效果;(e—i)不同K的处理效果. Fig. 4 Influence of different filter parameters under impulse noise (a—c) Results of different I; (d—f) Results of different N; (e—i) Results of different K. |
综上分析,过大的I、K和过小的N会导致滤波曲线与待处理数据曲线相差甚远,虽然曲线平滑但会丢失大量特征信息;反之,滤波曲线虽足够接近待处理数据,但因保留过多原始信息不能有效剔除离群值.故需选择在滤波曲线充分逼近原始信号同时能保持圆滑、连续走势的滤波参数.此外,由于经灰色判别准则处理后大部分噪声干扰消除殆尽,故选择相同滤波参数处理干扰程度不一的数据同样可以有效剔除干扰,且在一定范围内选择任意参数都可大幅改善数据质量,说明本文算法具有较强的适应性,为数据的批量处理提供一种可能的途径.
采用灰色判别准则剔除明显异常后,根据滤波参数的作用规律,选择滤波参数I=30,N=70,K=0.1和I=100,N=70,K=0.1分别对受工频、脉冲干扰影响的电位差频谱曲线滤波,得到参考曲线.图 4b、d中,经本文方法处理后,噪声干扰被有效消除,能量高达原始信号几个数量级的异常得以剔除,高精度还原出加噪前的曲线.表 1列出处理前后的定量评价标准.本文方法处理后的伪随机多频电磁频谱数据曲线与原始曲线相似度NCC分别提高到0.9999、0.9995,信噪比SNR上升约100 dB,误差显著下降.
|
|
表 1 处理效果的定量评价 Table 1 Quantitative evaluation of results |
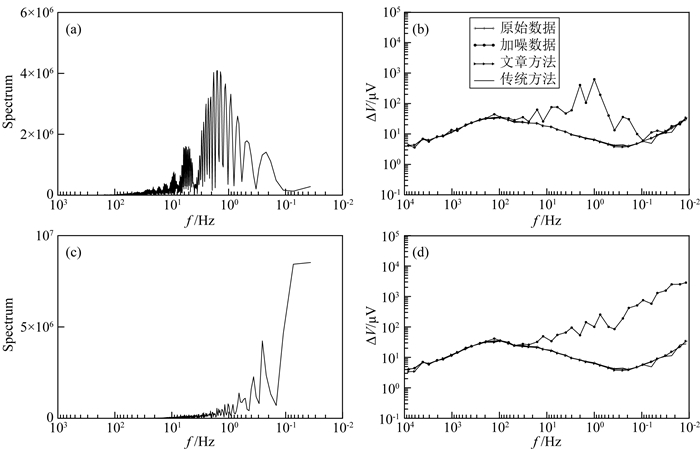
在上述高质量伪随机电磁数据中分别加入充放电噪声和方波噪声,两类噪声的频谱曲线如图 5a、c所示.两种噪声干扰范围主要集中在中低频段.其中,充放电噪声的主要频率范围在100 Hz以下频段,能量主要集中在10~0.1 Hz,相应频段的电位差频谱曲线有明显的突变,上升近3个数量级;方波噪声的频谱能量影响范围主要在10 Hz以后的频段,在电位差频谱曲线中表现为10 Hz以后的曲线迅速抬升,最大可达原始数据的3个数量级.上述噪声都造成伪随机多频电磁数据质量严重下降,中低频段出现不同程度的飞点,曲线形态不明确;噪声幅度大于原始信号的若干倍甚至几个数量级,信噪比SNR降至负数,曲线相似度NCC低,误差极大.
|
图 5 两类噪声干扰的频谱及处理前后对比 (a)充放电噪声频谱;(b)充放电噪声处理前后电位差频谱曲线;(c)方波噪声频谱;(d)方波噪声处理前后电位差频谱曲线. Fig. 5 Spectrum of two kinds of noise and results comparison (a) Spectrum of charge and discharge noise; (b) Potential difference spectrum curve before and after processing charge and discharge noise; (c) Spectrum of square wave noise; (d) Potential difference spectrum curve before and after processing square wave noise. |
采用本文方法进行去噪处理,并将之与传统的采用自适应双向均方差阈值法(张必明等, 2015)进行去噪处理的结果进行对比,如图 5b、d所示.两类方法均能基本消除噪声造成的异常,处理数据的NCC、SNR以及ERR三项定量评价标准都明显改善,如表 2所示.经自适应双向均方差法处理的频谱曲线存在部分频点数据被过度剔除导致曲线凹陷,或异常未剔除干净的现象.由于该方法采用单个阈值控制处理全部频点频谱数据,而各频点受干扰程度不一,导致有效数据的误删或异常得不到有效剔除,且控制阈值的选择在一定程度上引入了人为控制的因素.采用本文方法处理后的频谱曲线的中低频段突跳频点得到有效恢复,电位差频谱曲线干净圆滑,连续性提高,与原始频谱曲线基本重合.处理后的频谱曲线与原始曲线的相似度高达0.9997,信噪比分别提升至62.573 dB和59.759 dB,误差值显著下降.
|
|
表 2 与传统方法处理效果定量评价 Table 2 Quantitative evaluation of results with traditional method |
为验证本文方法对伪随机电磁实测数据的处理效果,选择重庆某地区的伪随机多频电磁法勘探数据进行去噪处理.该工区内测量环境复杂,干扰众多.部分测点受附近矿山、高压电线、公路等的干扰,噪声源能量大,甚至完全淹没有效信号.现选择存在明显强干扰影响的3线进行处理,并从两个方面对数据质量综合评价:一是基于统计学方法,利用公式(13)计算各个频点数据的相对均方误差大小,一般而言相对均方误差在10%及以下表明数据可靠,相对均方误差在5%及以下表明数据质量良好(张必明等, 2015);二是在对数坐标系中观测频谱曲线的形态.由于伪随机信号各主频点之间的相关性高,未受或受干扰程度小的曲线形态平滑,表明数据质量好.δr的计算公式如下:
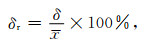
|
(13) |
式中,δ为均方误差.
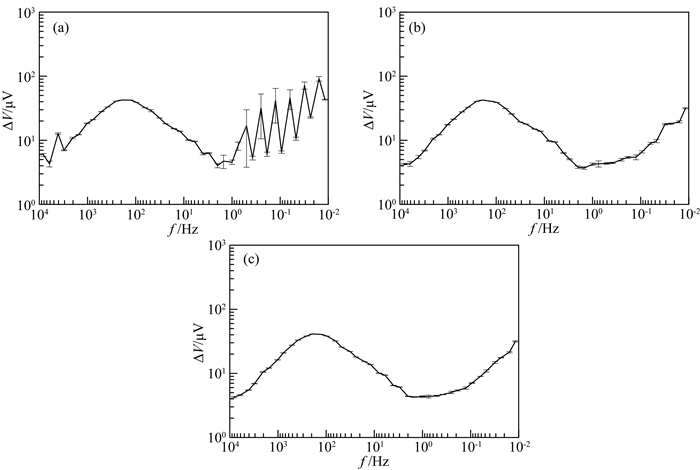
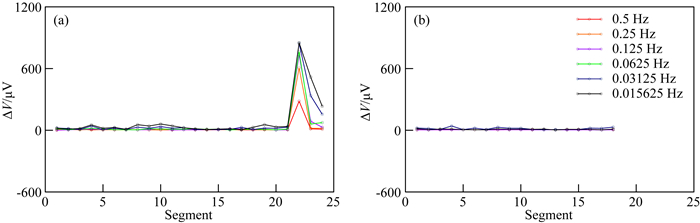
以3线的3115号测点为例讨论处理效果,原始数据和采用本文方法进行处理的结果如图 6所示.该测点在0.75~3072 Hz较为平滑,相对均方误差小,此频段数据质量较好;4096 Hz、0.5 Hz及以下频段曲线跳变剧烈,电位差频谱曲线连续性差.对0.5 Hz及以下各频点原始数据分布进行对比分析,如图 7a,数据中存在明显的、能量强的飞点,且随着频率的降低,异常幅度及受干扰范围都有所增加.基于灰色判别准则处理后,各尖峰形态基本消除,误差棒显著减小,曲线走势恢复正常.图 7b中,噪声造成的异常均有效剔除,各频点数据分布集中.但由于灰色判别准则仅对单个频点的数据处理,未考虑整个频谱曲线.故在灰色判别准则处理的基础上,选择合适的滤波参数进行有理函数滤波,将能正确反映曲线形态的滤波曲线作为参考曲线,约束频谱数据的二次优化处理,经优化处理后的曲线相对误差变小,曲线光滑度以及连续性有所提高,数值回归正常,如图 6c所示.
|
图 6 No.3115测点处理前后对比 (a)原始曲线;(b)灰色判别处理曲线;(c)优化曲线. Fig. 6 Results comparison of survey station No.3115 (a) Raw curve; (b) Curve after grey judgement; (c) Curve with optimization. |
|
图 7 No.3115部分频点频谱数据分布 (a)原始数据;(b)处理数据. Fig. 7 Data distribution of several frequencies of survey station No.3115 (a) Raw data; (b) Processed data. |
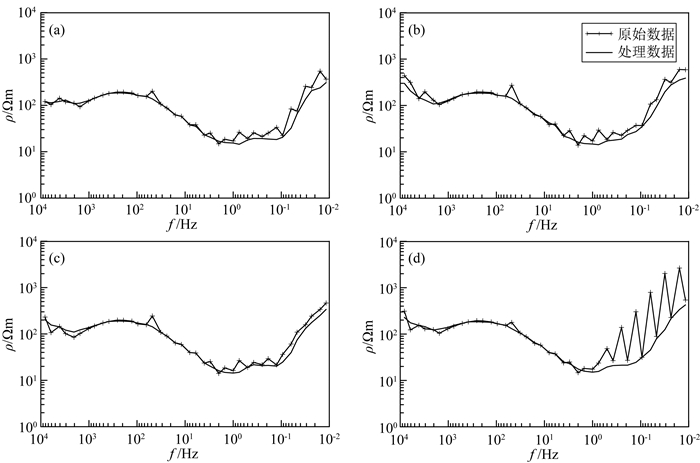
图 8为该测线中四个测点处理前后的电位差频谱曲线图.每个测点都受到不同程度的干扰,主要体现在4096~2048 Hz、48 Hz以及1 Hz以后频段曲线发生畸变,连续性较差.尤其是3170号测点,整个低频段跳变剧烈,呈现“锯齿”状,其能量较周围频点高达一个数量级.选择滤波参数I=60, K=0.1, N=50,经本文方法处理后,曲线形态明显改善,噪声导致的严重跳变、锯齿得到有效剔除,有用信号得以保留.原本偏倚的数据、脱节的“飞点”得以校正,整个频段曲线光滑,无毛刺.
|
图 8 实测数据处理前后的电位差频谱曲线 Fig. 8 Potential difference spectrum of measured data before and after processing (a) 3155; (b) 3160; (c) 3165; (d) 3170. |
图 9给出了该工区3线连续22个测点的原始视电阻率和采用本文方法处理后的视电阻率曲线图.从图中可以看出,经过本文方法处理后,各测点处的视电阻率曲线变得平稳,相邻测点的视电阻率曲线走势比较一致:1024~8192 Hz频段,视电阻率呈平缓的下降趋势;随着频率的降低,视电阻率升高并在128 Hz附近到达极值点,随后逐渐下降;1~0.1 Hz频段的曲线变化平稳,小于1 Hz频段视电阻率递增.为了对比处理前后的数据质量,计算3线各测点处各频点电位差频谱数据的相对均方差,并取平均值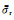
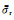
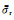
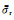

|
图 9 3线测点视电阻率曲线图 (a)原始视电阻率; (b)处理后视电阻率. Fig. 9 Apparent resistivity results of survey stations on line 3 (a) Raw data; (b) Processed data. |
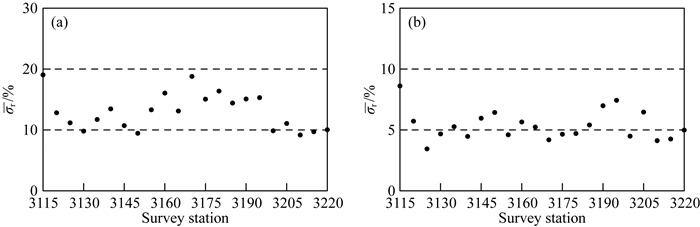
|
图 10 3线测点的平均相对均方误差 (a)处理前;(b)处理后. Fig. 10 Average relative mean square error of survey stations on line 3 (a) Raw data; (b) Processed data. |
针对伪随机电磁法存在的强干扰噪声,本文提出了一种基于灰色判别准则与有理函数滤波的数据处理方法,通过系统仿真实验及实测数据处理得出以下结论:
(1) 本文方法通过灰色判别准则剔除显著异常值,结合有理函数滤波进行二次优化处理,处理过程中引入稳健估计、灰色建模等方法,在保留高质量频点数据的同时,可实现对频谱数据中异常的有效识别和剔除.
(2) 在仿真实验中,选取合适的滤波参数可高度还原加噪前数据曲线.噪声强度对滤波参数选择的影响较小,且在合适范围内选任意滤波参数均可明显提升数据质量,表明本文方法具有可行性和较强的适应性,为数据批量预处理提供一种可能.
(3) 经实测数据预处理对比分析,本文方法可显著改善强干扰背景下的电磁数据质量,采用本文方法处理后,视电阻率曲线变得光滑平稳,相对误差减小,整体连续性提高.
此外,本文提出的方法能在高效处理数据的同时,保证数据的质量和曲线整体的光滑度,为提高海量伪随机电磁数据的质量和处理效率提供了一种可能性.
Ayvaz B, Bolturk E, Kaçtıoĝlu S. 2014. A grey system for the forecasting of return product quantity in recycling network. International Journal of Supply Chain Management, 3(3): 105-112. |
Cai J H, Tang J T, Hua X R, et al. 2009. An analysis method for magnetotelluric data based on the Hilbert-Huang Transform. Exploration Geophysics, 40(2): 197-205. |
Chave A D, Thomson D J. 2003. A bounded influence regression estimator based on the statistics of the hat matrix. Journal of the Royal Statistical Society: Series C (Applied Statistics), 52(3): 307-322. DOI:10.1111/1467-9876.00406 |
Chave A D. 2017. Estimation of the magnetotelluric response function: The path from robust estimation to a stable maximum likelihood estimator. Surveys in Geophysics, 38(5): 837-867. DOI:10.1007/s10712-017-9422-6 |
Chave A D, Mattsson J, Everett M E. 2017. On the physics of frequency domain controlled source electromagnetics in shallow water. 2: transverse anisotropy. Geophysical Journal International, 211(2): 1046-1061. DOI:10.1093/gji/ggx360 |
Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method. Chinese J. Geophys (in Chinese), 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
Deng J W, Deng M, Wei W B, et al. 2004. The application of decimation filter in marine bottom magnetotelluric exploration. Journal of Jilin University: Earth Science Edition (in Chinese), 34(2): 271-276. |
Egbert G D, Livelybrooks D W. 1996. Single station magnetotelluric impedance estimation: Coherence weighting and the regression M-estimate. Geophysics, 61(4): 964-970. DOI:10.1190/1.1444045 |
Grayver A V, Streich R, Ritter O. 2014. 3D inversion and resolution analysis of land-based CSEM data from the Ketzin CO2 storage formation. Geophysics, 79(2): E101-E114. DOI:10.1190/geo2013-0184.1 |
He J S. 2010a. Wild Field Electromagnetics and Pseudo-Random Signal Method (in Chinese). Beijing: Higher Education Press.
|
He J S. 2010b. Closed addition in a three-element set and 2n sequence pseudo-random signal coding. Journal of Central South University (Science and Technology) (in Chinese), 41(2): 632-637. |
Huang H P. 1991. Electromagnetic data processing using the singular value decomposition method. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese), 34(5): 644-650. |
Kayacan E, Ulutas B, Kaynak O. 2010. Grey system theory-based models in time series prediction. Expert Systems with Applications, 37(2): 1784-1789. DOI:10.1016/j.eswa.2009.07.064 |
Lei D, Zhao G Z, Zhang Z J, et al. 2010. A processing method of CSAMT data with strong electromagnetic interferences by using information entropy and rational function filtering. Progress in Geophysics (in Chinese), 25(6): 2015-2023. |
Li G, Xiao X, Tang J T, et al. 2017. Near-source noise suppression of AMT by compressive sensing and mathematical morphology filtering. Applied Geophysics, 14(4): 581-589. DOI:10.1007/s11770-017-0645-6 |
Li J, Tang J T, Yan H, et al. 2017. Identification and spearation of magnetotelluric signal and noise based on recurrence analysis and clustering. Chinese J. Geophys (in Chinese), 60(5): 1918-1936. DOI:10.6038/cjg20170525 |
Li J, Zhang X, Tang J T, et al. 2019. Audio magnetotelluric signal-noise identification and separation based on multifractal spectrum and matching pursuit. Fractals, 27(1): 1940007. DOI:10.1142/S0218348X19400073 |
Lin Z B, Wang P Y, Wan Y X, et al. 2016. A combined wavelet transform algorithm used for de-noising magnetotellurics data in the strong human noise. Chinese J. Geophys (in Chinese), 59(9): 3436-3447. DOI:10.6038/cjg20160926 |
Liu W Q, Chen R J, Cai H Z, et al. 2016. Robust statistical methods for impulse noise suppressing of spread spectrum induced polarization data, with application to a mine site, Gansu province, China. Journal of Applied Geophysics, 135: 397-407. DOI:10.1016/j.jappgeo.2016.04.020 |
Liu W Q, Chen R J, Cai H Z, et al. 2017. Correlation analysis for spread-spectrum induced-polarization signal processing in electromagnetically noisy environments. Geophysics, 82(5): E243-E256. DOI:10.1190/geo2016-0109.1 |
Liu W Q, Lü Q T, Chen R J, et al. 2019. A modified empirical mode decomposition method for multiperiod time-series detrending and the application in full-waveform induced polarization data. Geophysical Journal International, 217(2): 1058-1079. DOI:10.1093/gji/ggz067 |
Mo D, Jiang Q Y, Li D Q, et al. 2017. Controlled-source electromagnetic data processing based on gray system theory and robust estimation. Applied Geophysics, 14(4): 570-580. DOI:10.1007/s11770-017-0646-5 |
Nabighian M N. 1987. Electromagnetic Methods in Applied Geophysics: Volume 1, Theory. SEG Books.
|
Olsen K B, Hohmann G W. 1992. Adaptive noise cancellation for time-domain EM data. Geophysics, 57(3): 466-469. DOI:10.1190/1.1443260 |
Ramponi G. 2001. Image processing with rational operators: Noise smoothing and anisotropic diffusion.// Proceedings of the 2nd International Symposium on Image and Signal Processing and Analysis. Pula, Croatia, Croatia: IEEE, 96-101.
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Ren Z Y, Chen C J, Tang J T, et al. 2017. A new integral equation approach for 3D magnetotelluric modeling. Chinese J. Geophys (in Chinese), 60(11): 4505-4515. DOI:10.6038/cjg20171134 |
Shi D, Zhang C S, Guo J S. 1998. The application of grey comprehensive evaluation in some low-resistivity oil-gas bearing intervals. Progress in Geophysics (in Chinese), 13(1): 73-78. |
Streich R, Becken M, Ritter O. 2013. Robust processing of noisy land-based controlled-source electromagnetic data. Geophysics, 78(5): E237-E247. DOI:10.1190/geo2013-0026.1 |
Szarka L. 1988. Geophysical aspects of man-made electromagnetic noise in the earth-A review. Surveys in Geophysics, 9(3-4): 287-318. DOI:10.1007/BF01901627 |
Tang J T, Li G, Xiao X, et al. 2017. Strong noise separation for magnetotelluric data based on a signal reconstruction algorithm of compressive sensing. Chinese J. Geophys (in Chinese), 60(9): 3642-3654. DOI:10.6038/cjg20170928 |
Tang J T, Li G, Zhou C, et al. 2018. Denoising AMT data based on dictionary learning. Chinese J. Geophys (in Chinese), 61(9): 3835-3850. DOI:10.6038/cjg2018L0376 |
Trad D O, Travassos J M. 2000. Wavelet filtering of magnetotelluric data. Geophysics, 65(2): 482-491. DOI:10.1190/1.1444742 |
Wang Z Y, Gao Y, Qin P. 2002. Detection of gross measurement errors using the grey system method. The International Journal of Advanced Manufacturing Technology, 19(11): 801-804. DOI:10.1007/s001700200091 |
Yan J B, Liu G Z. 2006. Smoothing scale of magnetotelluric sounding curve. Coal Geology & Exploration (in Chinese), 34(5): 60-62. |
Yang Y, He J S, Li D Q. 2018. A noise evaluation method for CSEM in the frequency domain based on wavelet transform and analytic envelope. Chinese J. Geophys (in Chinese), 61(1): 344-357. DOI:10.6038/cjg2018L0298 |
Yang Y, Li D Q, Tong T G, et al. 2018. Denoising controlled-source electromagnetic data using least-squares inversion. Geophysics, 83(4): E229-E244. DOI:10.1190/geo2016-0659.1 |
Zhang B M, Jiang Q Y, Mo D, et al. 2015. A novel method for handling gross errors in electromagnetic prospecting data. Chinese J. Geophys (in Chinese), 58(6): 2087-2102. DOI:10.6038/cjg20150623 |
Zhou C, Tang J T, Ren Z Y, et al. 2015. Application of the Rhoplus method to audio magnetotelluric dead band distortion data. Chinese J. Geophys (in Chinese), 58(12): 4648-4660. DOI:10.6038/cjg20151226 |
Zhu J M, Bin H Z, Wang Z Y, et al. 2000. A grey evaluation method of measurement result with standard uncertainty. Journal of Huazhong University of Science and Technology (in Chinese), 28(9): 84-86. |
Ziolkowski A, Wright D, Mattsson J. 2011. Comparison of pseudo-random binary sequence and square-wave transient controlled-source electromagnetic data over the Peon gas discovery, Norway. Geophysical Prospecting, 59(6): 1114-1131. DOI:10.1111/j.1365-2478.2011.01006.x |
陈辉, 邓居智, 谭捍东, 等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究. 地球物理学报, 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
邓靖武, 邓明, 魏文博, 等. 2004. 抽取滤波在海底大地电磁探测中的应用. 吉林大学学报:地球科学版, 34(2): 271-276. |
何继善. 2010a. 广域电磁法和伪随机信号电法. 北京: 高等教育出版社.
|
何继善. 2010b. 三元素集合中的自封闭加法与2n系列伪随机信号编码. 中南大学学报(自然科学版), 41(2): 632-637. |
黄皓平. 1991. 电磁法数据处理的奇异值分解法. 地球物理学报, 34(5): 644-650. DOI:10.3321/j.issn:0001-5733.1991.05.013 |
雷达, 赵国泽, 张忠杰, 等. 2010. 强干扰地区CSAMT数据信息熵与有理函数滤波的处理方法. 地球物理学进展, 25(6): 2015-2023. DOI:10.3969/j.issn.1004-2903.2010.06.017 |
李晋, 汤井田, 燕欢, 等. 2017. 基于递归分析和聚类的大地电磁信噪辨识及分离. 地球物理学报, 60(5): 1918-1936. DOI:10.6038/cjg20170525 |
凌振宝, 王沛元, 万云霞, 等. 2016. 强人文干扰环境的电磁数据小波去噪方法研究. 地球物理学报, 59(9): 3436-3447. DOI:10.6038/cjg20160926 |
任政勇, 陈超健, 汤井田, 等. 2017. 一种新的三维大地电磁积分方程正演方法. 地球物理学报, 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
施冬, 张春生, 郭甲世. 1998. 灰色综合评判法在低阻油气层中的应用. 地球物理学进展, 13(1): 73-78. |
汤井田, 李广, 肖晓, 等. 2017. 基于压缩感知重构算法的大地电磁强干扰分离. 地球物理学报, 60(9): 3642-3654. DOI:10.6038/cjg20170928 |
汤井田, 李广, 周聪, 等. 2018. 基于字典学习的音频大地电磁数据处理. 地球物理学报, 61(9): 3835-3850. DOI:10.6038/cjg2018L0376 |
严家斌, 刘贵忠. 2006. 大地电磁测深曲线平滑尺度. 煤田地质与勘探, 34(5): 60-62. DOI:10.3969/j.issn.1001-1986.2006.05.017 |
杨洋, 何继善, 李帝铨. 2018. 在频率域基于小波变换和Hilbert解析包络的CSEM噪声评价. 地球物理学报, 61(1): 344-357. DOI:10.6038/cjg2018L0298 |
张必明, 蒋奇云, 莫丹, 等. 2015. 电磁勘探数据粗大误差处理的一种新方法. 地球物理学报, 58(6): 2087-2102. DOI:10.6038/cjg20150623 |
周聪, 汤井田, 任政勇, 等. 2015. 音频大地电磁法"死频带"畸变数据的Rhoplus校正. 地球物理学报, 58(12): 4648-4660. DOI:10.6038/cjg20151226 |
朱坚民, 宾鸿赞, 王中宇, 等. 2000. 测量结果标准不确定度的灰色评定方法. 华中理工大学学报, 28(9): 84-86. DOI:10.3321/j.issn:1671-4512.2000.09.029 |
 2019, Vol. 62
2019, Vol. 62


