2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;
3. 江苏华东八一四地球物理勘查有限公司, 南京 210014
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring(Central South University), Ministry of Education, Changsha 410083, China;
3. East China 814 Geophysical Prospecting Co., Ltd, Nanjing 210014, China
天然场源电磁法具有理论简单,探测深度大等诸多优点,是一类重要的地球物理探测方法(Chave and Jones, 2012).按观测频段包括大地电磁法(MagnetoTellurics, MT),音频大地电磁法(Audio-frequency MagnetoTellurics, AMT)等.由于天然电磁场信号强度低、极化方向随机,因此观测数据通常信噪比低,抗噪能力弱.特别的,在AMT“死频带”(1~5 kHz)及MT“死频带”(1 Hz附近)信号强度极低(周聪等,2015),阻抗数据易畸变.为提高观测数据信噪比,人工场源被引入进行信号发送,以增强场源信号强度,改善数据质量.典型的人工源电磁法如可控源音频大地电磁法(Controlled Source Audio-frequency Magnetotelluric,CSAMT)(Goldstein and Strangway, 1975),广域电磁法(Wide Field Electromagnetic sounding methods, WFEM)(何继善, 2010)等.由于人工场源的引入,场源的影响随之出现,如非平面波效应、场源附加效应、场源阴影效应等(汤井田和何继善, 2005; 陈明生和闫述, 2005).
在天然场源及人工场源电磁法的理论中,均假设只存在单一类型的场源,而将其他场源信号作为噪声处理.如MT中将人工场源或人文场源视为相关噪声(Oettinger et al., 2001;汤井田等, 2012, 2018; Li G et al., 2017; Li J et al., 2018, 2019),而CSAMT中则将天然场视作相关噪声(汤井田和何继善, 2005;Streich, 2016).并试图仅从输出端观测数据出发,开发相应的数学算法压制此类相关噪声的影响.这种处理不仅可能引起错误的解释,还造成了数据的浪费.
为综合利用天然场源电磁法和人工源电磁法的优点,同时压制其不足,一种思路是将两者相结合,分别观测以获得两套数据,并综合进行解释(刘春明等,2013;姚文等, 2015;邓居智等, 2016).如加拿大凤凰公司的V8系统、美国Zonge公司的GDP-32系统等,可实现一套设备采集多种电磁勘探方法数据,或称为“多功能”电磁法.另一种策略是进行分频带观测的“混场源”电磁法,在不同的频段分别观测天然场和人工场,并进行组合分析.如美国劳雷公司研制的EH4电磁成像系统,在低频部分(10~1000 Hz)将天然电磁场视作场源,进行AMT勘探,而在高频部分(1~75 kHz)可通过增加可控人工发射源,进行CSAMT勘探.国内吉林大学、中国地质科学院地球物理地球化学勘查研究所等团队对这两种策略也进行了大量研究,并研制了相关仪器(程德福等,2004;王言章,2010;林品荣等,2010).可以看出,无论是“多功能”还是“混场源”,其立足点仍然是单一类型场源的理论,不仅效率相对较低,也无法解决“相关噪声”的影响及数据利用不足等问题.
事实上,如果将地球电磁勘探模型视作统一的系统,则不同类型的场源信号都应是系统的有效输入,其输出信号中均包含有系统响应信息.问题是如何通过合理的观测设计及数据处理,从输出数据中提取出分别对应于不同输入的系统响应.另外,随着分布式设计、阵列测量及面积性勘探的日渐普及,研究针对阵列数据的处理技术也尤显必要.基于上述理念与需求,本文提出了时空阵列混场源电磁法(Space-Time Array Hybird Sources ElectroMagnetic method, STAHSEM).首先,阐述了时空阵列混场源电磁法的基本原理,给出了时空阵列方程组及其求解方法,讨论了相应的解释参数提取方案;其次,讨论了时空阵列混场源电磁法发送及接收端的实施方案设计;第三,利用数值模拟方法,对本方法进行了论证;最后,对方法的特点进行了讨论.
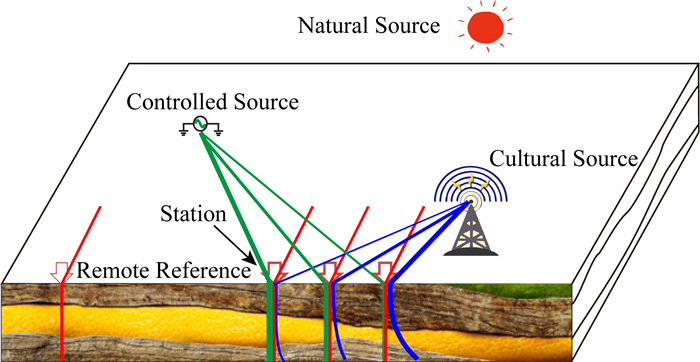
1 时空阵列混场源电磁法 1.1 数学物理模型实际电磁勘探环境中,输入端的场源类型可分为三大类,天然场源(Natural Source)、可控人工场源(Controlled Source)以及不可控的人文场源(Culture Source).天然场源主要来自宇宙或大距离尺度的外部空间,在全球都可以观测到,它的数量实际是无穷多个;可控人工场源是电磁勘探活动中人们对大地施加的主动激励,它的场源数量、激励强度及激励时刻可以为勘探人员所控制;未知人文场源主要指人类各种电磁活动造成的人文电磁场,如矿山开采所用的直流电机车、通讯电台等等,其数量众多,几乎与人类文明同步分布在地球的各个角落,对勘探人员而言其场源数量、激励信息等通常是未知的.输出端随着空间位置的不同,不同测站可观测到的电磁场信号组合具有不同特点.对某一场源,一般的,随发-收距离的增大,电磁场逐渐呈现出不均匀非平面波-不均匀平面波-均匀平面波的变化趋势,且信号强度逐渐减弱.因此,在远离测区的远参考站处,合理的位置选择能保证仅有天然场信号.而对测区内测站,不仅包含天然电磁场,还包含不同强度的可控人工场和不可控人文场.不同测站间信号组成的异同为实现响应分离提供了物理基础.多输入-多输出的电磁勘探简化物理模型如图 1所示.
|
图 1 多输入-多输出电磁勘探模型示意 Fig. 1 A simplified model of multi-input multi-output electromagnetic prospecting |
为对图 1所示的模型进行简化与数学描述,需引入几个说明、假设及相应的术语.
(1) 本文研究的是频域电磁法,因此以下术语及符号均为频域符号.在本文研究的频域范围(10 k~0.01 Hz)内,不考虑位移电流,对任一频点,电磁场方程相同.因此,为方便,除特别说明,下文中省去频率符号.
(2) 假设系统中存在一定长度的同步观测(可不连续)时段,这些时段共可划分为I个时窗,每个时窗内的时域观测数据通过时频转换提取出单个频谱数据.
(3) 假设在I个激励时窗内,系统中共包含L个场源.第l(l=1, 2, …, L)个场源在第i(i=1, 2, …, I)个时窗内的极化参数可记为Sli,构建阵列输入矩阵S,
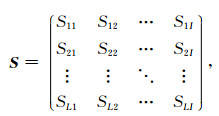
|
(1) |
S也可称为极化参数矩阵.
(4) 假设在I个观测时窗内,系统中共包含K个测道.各测道观测不同分量的电场、磁场或电磁场梯度信息,如Ex, Ey, Hx, Hy, Hz等.第k(k=1, 2, …, K)个测道在第i(i=1, 2, …, I)个时窗的观测数据可记为Xki,将所有观测数据写入同一个矩阵中,构成阵列输出矩阵X,

|
(2) |
(5) 假设系统满足线性时不变条件,即系统频率特性响应矩阵Ψ不随时窗变化,并且输出与输入间满足线性关系(Egbert, 1997, 2002; 周聪, 2016),
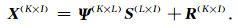
|
(3) |
(3) 式即为图 1所示阵列电磁勘探模型的频率域输出-输入关系表达式,其中,R为频域输出端噪声矩阵;各矩阵的上角标给出了它的维数.Ψ反映了地球电磁系统本身的特性,以及激励源和测道的空间信息,与激励延时(观测时窗)无关,也称为空间模数矩阵,其中的元素Ψkl称为空间模数.
进一步的,输入端的场源可分为L1个天然场源、L2个不可控人文场源以及L3个可控人工场源,L=L1+L2+L3;它们的输入极化参数矩阵分别设为A,B,C; 各测道对应于这三类场源的空间模数矩阵分别设为U,V,W,则(3)式可写为

|
(4) |
(4) 式即为一般条件下的电磁场阵列输入-输出关系的数学描述.在不同的场源环境中,方程式(4)可以进行不同形式的简化.例如,当环境中a)天然场信号占主导;b)可控人工场信号占主导时,(4)式可分别写为
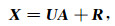
|
(5) |
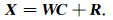
|
(6) |
(5), (6)式分别为MT及CSEM阵列形式的数据集方程.求解该方程,可以获得MT及CSEM阵列响应.
混场源条件下,电磁响应与MT及CSEM不同.当环境中同时存在不可忽略的天然场和可控人工场信号,而不可控人文场信号可以忽略或视做输出端噪声时,方程(4)式可写为
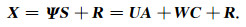
|
(7) |
上述模型中,观测数据矩阵X的两个维度分别为时窗和测道,即时间和空间;极化参数矩阵与空间模数矩阵则分别相对空间和时间独立.为方便,不妨将(3)—(7)式称为时空阵列方程组.通过合理的施工设计,获取时空阵列观测数据X以及可控人工场源的场源极化参数C,求解时空阵列方程组以估计空间模数U,V,W的值,进而提取出各测道相应的地电解释参数.我们将基于这一模型及求解思路的方法称为时空阵列电磁法.特别的,将与(4)式及(7)式所描述的混场源环境相对应的情形,称为时空阵列混场源电磁法.本文中,我们重点讨论(7)式的求解与模拟.
1.2 时空阵列方程组的求解方程组(4)式属于多元二次方程组,共有K×I个线性无关的方程,未知数不超过L(K+I)个.一般地,当K×I>L(K+I)时,方程组在理论上是可解的,可以采用非线性的求解方法,如主成分分析(Principal Component Analysis, PCA)等求解.特别的,由于天然场源发收距远大于观测尺度,各方向的天然场信号可以等效至两个不同的极化方向.当系统中天然场信号占主导时,可以采用PCA等方法提取对应的等效极化信息,直接求解(5)式(如Egbert, 1997).但当系统中存在其他不可忽略的场源信号时(如(7)式),直接求解法存在较大的误差.因为此时小发收距场源的空间信息不可忽略,PCA所获得的主成分已不能与不同场源成分相对应.因此在混场源条件下需研究更优的求解算法.
本文提出一种分步策略,对(7)式进行求解.
1.2.1 构建数据矩阵Egbert (1997)指出,L1个天然场源的作用可等效视作两个正交水平方向(标记为x, y方向)的极化信号.基于前文所做假设,输入端不考虑未知人文场源的条件下,第i(i=1, 2, …, I)个时窗第k(k=1, 2, …, K)个测道的观测电磁场数据可展开为

|
(8) |
其中,Xli,Rli分别为观测数据与输出端噪声,Ali,Cli分别为天然场及可控人工场的极化参数,Ukl,Wkl等分别为与测道及场源相应的空间模数.
具体的,假设测站j(j=1, 2, …, J)处包含常规5分量电磁场测道,(7)式可分解为
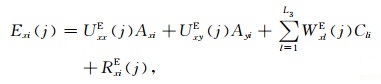
|
(9a) |

|
(9b) |
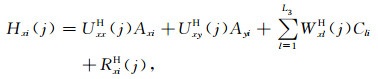
|
(9c) |
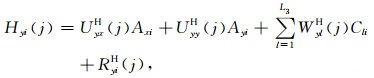
|
(9d) |

|
(9e) |
其中,UxxE,WxlE等分别为与测道及场源相应的空间模数,上角标为测道类型标识.
实际中,不同测站的测道数可根据需要进行不同的选择,灵活布设(9)式中所述的测道,还可布设电磁场梯度分量等测道,进而得到不同的观测数据组合.
对测区内的观测数据,利用各待求测站的阵列数据,根据(2)式构建目标数据矩阵X.由前文可知X满足(7)式.
在距离人工源足够远的地区布置一定数量的同步远参考道(Gamble et al., 1979),通过合理的位置选择,可保证远参考测站中以天然场信号为主.进而可根据(2)式以远参考测站数据构建主要包含天然场信号的参考数据矩阵Xr.由前文可知Xr满足
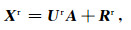
|
(10) |
其中,Ur为与Xr各测道对应的空间模数,Rr为对应的输出端噪声.
需说明,远参考站的数量不受限制,可在测区外挑选多个远参考站,择优构建参考数据矩阵.当条件受限时,至少应包含一个远参考测站,观测两道相交的电场或两道相交的磁场,并尽可能进行张量布设,以获得更丰富的数据信息.
此外,可控人工场源的极化参数均可记录,利用L3个场源在I个时窗内的记录数据,根据(1)式构建人工场源极化参数矩阵C.
1.2.2 估计场源极化参数利用数据降维方法(如主成分分析方法,以符号PCA表示)求解(10)式可提取天然场极化参数A.Egbert(1997)及Smirnov和Egbert(2012)提出了具体的算法.为方便,此处简单进行说明.对矩阵Xr进行奇异值分解,
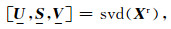
|
(11) |
其中,svd表示矩阵的奇异值分解,U, S, V分别为奇异值分解所得的参数矩阵.
奇异值分解后,特征值矩阵S中的特征值元素按从大到小的顺序排列.对包含L个输入的系统,观测响应的主要信息可由前1~L个主导特征值及其特征向量的乘积表征,而剩余较小的特征值及其特征向量则表征了输出端的噪声.于是可取
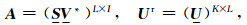
|
(12) |
其中,上角标*表示矩阵转置;(U)K×L表示U的1~L列组成的K×L阶矩阵,(SV*)L×I表示SV*的1~L行组成的L×I阶矩阵.如前所述,(10)式条件下可等效视L=L1≈2.
必须指出,上述分解过程并不唯一,因为,
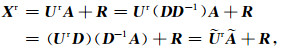
|
(13) |
其中,D为任意L×L维可逆矩阵,
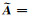
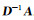
因此,在没有更多先验信息的情况下,并不能从时空阵列数据矩阵中获得系统空间模数或场源极化参数的精确解.但注意到此处我们并不需要场源极化参数的精确解,仅仅需获得其变化特征即可.即(12)式中获得的任意A均可进行下一步计算,不影响天然场张量转换函数的求解,1.3节中将进行详述.
利用(11)—(12)式获取的天然场源极化参数A的估计值、观测记录的人工场源极化参数C,组合成场源极化参数矩阵S,
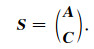
|
(14) |
利用最小二乘,对测站信号时空数据矩阵X以及极化参数矩阵S进行回归分析,求解空间模数矩阵U,
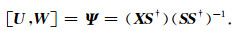
|
(15) |
(15) 式中用到了一个隐含条件,矩阵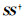
实际中,输出端噪声的影响不可避免,并且噪声的概率密度通常是非高斯分布的,此时仅通过数据叠加难以获得高质量空间模数估计结果.为获得最优估计结果,必须采用稳健估计方法.
在上述的处理策略中,主要涉及两类问题的稳健估计,一是极化参数矩阵未知时,利用时空阵列方程组估计场源极化参数矩阵的过程,即(11)—(12)式;可采用稳健的主成分分析算法(如Egbert,2002;Smirnov and Egbert, 2012)等方法进行求解.二是已获得极化参数矩阵的估计值时,利用时空阵列方程组求解空间模数矩阵的过程,即(15)式;可采用稳健最小二乘估计(如Chave and Thomson, 1989)进行求解.
1.3 解释参数的提取获得空间模数矩阵U,W的估计值后,即可提取解释参数,如阻抗视电阻率、倾子矢量及场分量视电阻率等.
如前所述,空间模数矩阵仅与地电参数、测道位置信息相关,而不随时窗变化,反映了地球电磁系统本身的特征.地电结构信息的获取则需要对空间模数矩阵进行进一步的挖掘,消除测道方位信息的影响.
1.3.1 天然场源阻抗当场源参数未知时,无法直接利用单测道获得解释参数,此时必须考虑利用不同类型场分量间的转换函数来消除空间位置信息的影响,并通过求解张量关系压制场源方向参数的影响,才可获得仅与地下介质相关的有效解释参数.
如(13)式所示,对于空间中的任意两种类型的张量观测数据,如电场和磁场,将其置于统一的时空阵列数据矩阵中进行求解,获得张量空间模数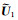
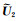

|
(16) |
不难发现,(16)式中转换函数T具有唯一性,可用于提取解释参数.
此处以常规张量电磁场测量条件为例,说明天然场阻抗张量ZMT的提取.如(9)式所示,假设测站j(j=1, 2, …, J)处包含水平4分量电磁场测道,则有

|
(17) |
其中,UE(j)、UH(j)分别表示j测站处张量电场、磁场测道与天然电磁场所对应的空间模数矩阵,ZMT(j)为相应的阻抗张量,可展开为

|
(18a) |

|
(18b) |
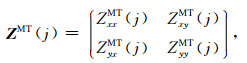
|
(18c) |
(18a) 及(18b)式中各张量元素的意义如(9)式所示.
根据(17)式获得的阻抗即可计算相应的视电阻率及相位.同理,在不同的张量测道条件下,可以获得不同的大地电磁转换函数,如倾子矢量、大地磁场张量等(Chave and Jones, 2012).
1.3.2 人工场源阻抗当系统中的人工场源也为张量形式时,同样可利用不同类型场分量间的张量转换函数获得解释参数.仿照(17)式所述方案,假设系统中包含L3(L3≥2)个可控人工场源,若在测站j处进行水平4分量张量测量,则相对应的阻抗张量为
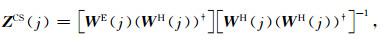
|
(19) |
其中,WE和WH为2×L3维张量.
注意(19)式给出的是L3个场源统一的阻抗张量.实际上,对任意两个不同方位的场源,均可采用类似(19)式的方式获得相应的阻抗张量.
当系统中的人工场源为标量形式时,无法获得张量转换函数.但与常规CSAMT方法类似,在部分特殊观测区域内,可以获得相应的标量阻抗及其视电阻率.例如,在单个水平电偶极子场源(L3=1)条件下,假设测站j处包含水平2分量的旁侧排列Ex/Hy测量(汤井田和何继善,2005),则可近似获得阻抗
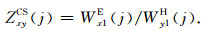
|
(20) |
类似的,可根据不同的观测方案求解其他形式的阻抗及其视电阻率,不作赘述.
1.3.3 场分量视电阻率可控人工场源条件下,由于测站的发收距与极化方向等位置信息可进行测量记录,通过推导各测道空间模数函数的显式表达式,可直接从该表达式中提取解释参数,如场分量视电阻率等.此处以广域视电阻率(何继善,2010; 汤井田等,2011)的求解进行说明.
假设可控人工场源l为水平电偶极子源,测道k为水平电场y方向(Ey)测道,与场源l的距离为rkl,方位角为φkl,则测道k对应于场源l的观测数据Xki(l)表达式为(汤井田和何继善,2005),
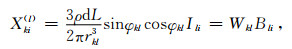
|
(21) |
其中Bli=IlidL/2π为场源的极化参数,Wkl=3ρsinφklcosφkl/rkl3为相应的空间模数.
则Ey视电阻率的求解方式为
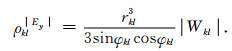
|
(22) |
类似的,可求取其他形式的广域视电阻率或波区场分量视电阻率.
需说明,与(19)—(22)式的求解不同,常规CSAMT/WFEM是直接以观测到的人工场和天然场的总场来进行阻抗张量或视电阻率计算.例如常规Ey视电阻率的求解(汤井田等,2011),

|
(23a) |
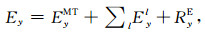
|
(23b) |
其中;EyMT,Eyl及RyE分别为天然场信号,不同源的人工场信号及输出端噪声.
不难看出,采用(23)式进行计算会造成视电阻率的偏倚.特别的,野外实际工作中,CSAMT/WFEM场源在高频端发送信号往往较弱,造成高频观测信号中的天然场成分无法忽略(真齐辉和底青云, 2017; 杨洋,2017).另外,当发收距偏大时,人工场信号显著衰减,天然场成分的影响增大,这些因素都将影响传统方法的数据处理质量.而本文方案中,通过1.2节的求解已压制了天然场的影响,空间模数W仅与人工场信号相关,可望提高人工场相关解释参数的处理质量.
2 时空阵列混场源电磁法的实施方案电磁法实施方案的内容包括:发送端设计、接收端设计、噪声分析、工作参数设计、数据采集与评价等.此处简单讨论时空阵列混场源的发送端与接收端设计,其他方面可参看常规方法.
2.1 发送端方案(a) 发送场源的选择:可采用单一场源和复合型场源,形式灵活.复合型场源可采用近年见诸应用的L型电偶极子源与三角型电偶极子源等(Streich et al., 2010; 王显祥等, 2014).
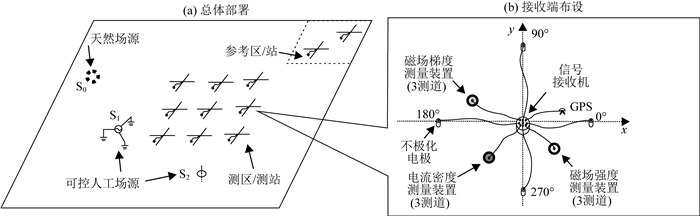
(b) 发送阵列的选择:阵列采用面阵的形式在地表随机布设,可控场源的类型、数量、布设形式、布设位置不受限制,可根据地形、障碍物的分布灵活布设.如图 2所示的多场源阵列激励示意,在测区周围选择合适的地点布设多个场源,即可利用多场源同时激励、相互补充,达到测区内人工源信号测量空间的全覆盖(汤井田和何继善, 2005; 汤井田等, 2013;刘志新等,2017).
|
图 2 时空阵列混场源电磁法野外实施方案示意 (a)总体部署;可控人工场源的个数可以为1个或多个,测区内及参考区可布设1个或多个测站. (b)接收端单测站布设;可根据需要选取图中所示不同测道进行组合; 其中磁场梯度与电流密度测量装置为预设测道,其观测数据同样可以包含在本文所述的勘探模型中. Fig. 2 A sketch of the field implementation scheme for space-time array hybrid source electromagnetic method (a) Overall deployment; the number of controlled sources can be one or more, and one or more stations can be installed in the survey area and the remote reference area. (b) The layout of a single station; the installment of channels shown in the diagram can be selected according to practical requirements. The magnetic field gradient and current density measurement devices are preset channels, and their recording data can also be included in the array model. |
(c) 激励形式:发送信号可采用方波、双频信号、伪随机信号等(何继善,2010; 罗维斌等,2012; 真齐辉和底青云, 2017),可通过改变发送方波的幅值及电流方向进行时间阵列激励(王显祥等, 2014).所有场源的激励可同时进行,无需分步,以保障施工效率;也可根据需要分步进行,灵活施工.
(d) 参数记录:在发送端,需记录场源装置系数、场源位置及发送电流等参数.
2.2 接收端方案(a) 在测区内布设J(J≥1)个测站,测站的空间分布形式不限;在每个测站处,可进行多测道观测,也可进行单测道测量.
(b) 在测区外噪声环境相对平静的地区布设J′(J′≥1)个远参考站;在每个参考站处,进行多测道的张量布设,最少需布设两道水平磁场.
实际中,根据环境噪声水平以及现场地质地形条件进行针对性的施工设计.图 2给出了实施方案的一个示例.其中电流密度和磁场梯度测道数据的利用可参考周聪(2016).
3 数值模拟利用数值模拟,可以对本文所提方法的有效性进行评估.一维条件下,可利用快速Hankel变换完成相应的数值计算(汤井田和何继善,2005),高维模型则可使用有限体积、有限元、积分方程等方法进行计算(Weiss, 2013; Ren et al., 2013, 2014; 任政勇等,2017).
3.1 数值模拟流程(1) 设计算例,包括地电模型、观测频段及输入输出方式等;基于多场源-多测道的简化模型,设置场源数量、时窗数量、测站及测道数量,发送端利用接地电偶极子或不接地磁偶极子作为场源,接收端进行多类型场分量的张量观测;
(2) 计算空间模数;在每一个场源l(l=1, 2, …, L)均为单位激励的条件下,计算每个测道k(k=1, 2, …, K)的空间模数Ψkl,组成空间模数矩阵Ψ;
(3) 设置场源极化参数;通过计算L×I维的均匀分布随机数,设置每个场源各时窗的极化参数Sli,组成极化参数矩阵S;通过调整极化参数,可以调节输入端信号强度比;
(4) 计算响应数据;将Ψ与S相乘,获得各个测道对所有场源的叠加响应数据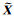
(5) 设置输出端噪声;设置不同干扰类型的输出端噪声,通过与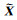
(6) 数据合成;计算观测数据矩阵
(7) 数据处理;使用本文方法进行求解,获得各测道对每一个场源的响应,以及1.3节所述的解释参数.对不同的频点,重复(2)—(7)步,可以获得整个观测频带的数据,注意各个频点是相互独立的.
需说明,如前所述,天然场源的作用可等效视作两个正交水平方向的极化信号(Egbert, 1997).因此模拟中,通过设置两个不同方向、发收距足够大的偶极子,模拟天然场源;通过设置不同方位、发收距尺度较小的偶极子,模拟可控人工场源.
通过改变参数设置,可以模拟实际信噪环境;通过不同条件下的处理结果与实际模型的对比,可验证方法的正确性及稳定性,以及不同解法的优劣.
3.2 测站数据的处理质量由于天然场时刻存在,因此在人工源电磁法中难以避免会有天然场的影响.本节我们选取广域电磁法为例,假设输入端同时存在人工场与天然场,比较常规WFEM方法与本文所述方法所求得的广域视电阻率的差异.
根据图 2所示方式布设输入及输出;在测区中心建立直角坐标系,x、y轴方向与各测站的电极布设方向一致.以下各例中,天然场源均以2个垂直磁偶极子模拟,分别位于x、y两个不同的极化轴上.
算例1中,设计模型为均匀半空间,电阻率为100 Ωm,发送及观测频带为104~10-1Hz,在该频带内对数均匀分布30个频点.输入端包含2个天然场源以及1个位于x轴的水平电偶极子场源l,距离测区中心6 km;输出端包含2个测站的阵列数据,其中1个为远参考站,距离测区中心300 km.测区内测站j处,观测Ex,Ey两分量电场;测区外远参考站rr处,观测4分量水平电磁场.共观测50个时窗,输出端噪声为信噪比等于2 dB的高斯随机噪声.测站j与场源l轴向间的角度为60°,以方便同时计算Ex,Ey广域视电阻率.根据3.1节所述模拟流程,图 3给出了阵列数据合成示意.注意在远参考站rr处,忽略可控人工场信号的影响.
|
图 3 阵列数据合成示意,f=0.1 Hz (a)天然场信号成分XA;(b)可控人工场信号成分XC;(c)输出端噪声R;(d)合成观测信号X.各测道类型如图下方图例所示,j表示测区内某测站,rr表示远参考站;电场强度的量纲为V·m-1,磁场强度的量纲为A·m-1. Fig. 3 A sketch of array data composition (a) Natural source component XA; (b) Controlled source component XC; (c) Output noise R; (d) Composite signal X. The types of the channels are shown in the legend, jdenotes the target station, rr denotes remote reference. |
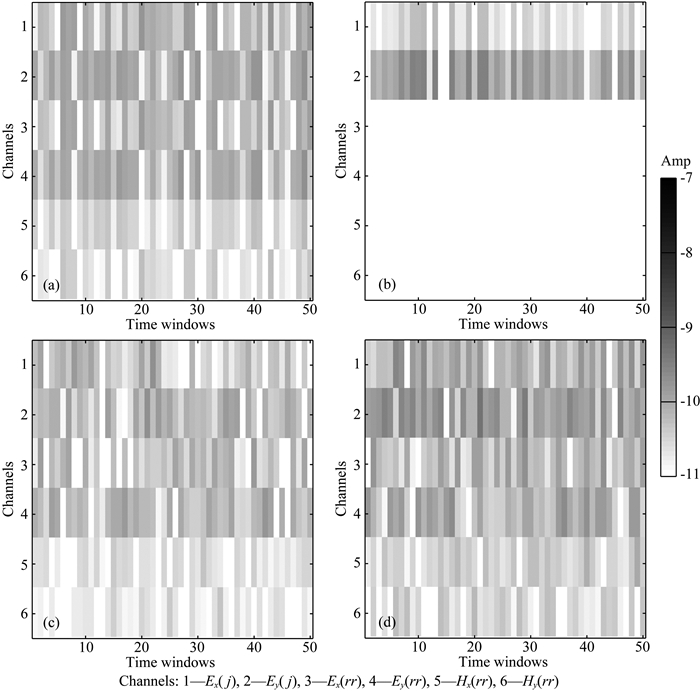
实际中,人工场高频信号较弱,而中低频信号较强(真齐辉和底青云, 2017; 杨洋,2017).为模拟这一环境,对不同频段的信号成分强度进行了不同的权重设置,使得高频段人工场与天然场在一个量级,而中低频段人工场信号占主导.图 4(a, b)给出了测站j处Ex, Ey中不同信号成分的比较,其数值为各时窗信号幅值绝对值的均值.图 4(c, d)给出了不同方法所得广域视电阻率的对比.从图中可以看出,在天然场成分不可忽略的高频段,采用传统单站计算方法(如(23)式)所获得的广域视电阻率出现了明显的偏倚;在100~10 Hz频段,x方向的单站广域视电阻率在部分频点也出现了偏倚,这是因为该频点内某些时窗的天然场成分仍然较强.只在天然场成分可以忽略的低频段,传统单站计算方法所获得的广域视电阻率才与真值相符.而采用本文所述的阵列处理方法(如(22)式),无论天然场信号是否可忽略,所得的广域视电阻率均与模型真值误差较小.
|
图 4 测站j处观测信号及不同方法所得广域视电阻率的对比 (a, b)各频点Ex, Ey中不同信号成分幅值(各时窗幅值绝对值的均值)的比较;其中Ex, Ex(A), Ex(C)及Ex(R)分别表示x方向合成信号、天然场成分、人工场成分及输出端噪声,y方向类似;其中,高频人工场信号较弱,中低频人工场信号占主导;(c, d)不同方法所获得的广域视电阻率ρ(Ex), ρ(Ey)对比,ρ(single)表示传统方法(如(23)式)所得视电阻率,ρ(array)表示本文方法(如(22)式)所得的视电阻率. Fig. 4 Comparison of the observed signals and the WFEM apparent resistivities estimated by different methods at the station j (a, b) The comparison of different signal components (mean of absolute values of all segments) in Ex, Ey; Ex, Ex(A), Ex(C) and Ex(R) denote the composite signal, natural field components, controlled field components and output noise of x direction respectively, and those of y direction are similar. In this example, the controlled field signal is weak in the high frequency band while is dominant in the middle and low frequency bands. (c, d) The comparison of WFEM apparent resistivities estimated by different methods, ρ(single) and ρ(array) denote the results of ordinary method (calculated by Eq.(23)) and our method (calculated by Eq.(22)) respectively. |
如1.3节所述,混场源条件下,当测站处以张量方式观测时,利用本文方法可以同时获得天然场与人工场阻抗数据.本节中,设计了部分模型及算例,比较常规CSAMT方法与本文所述方法所求得的阻抗视电阻率的差异.
算例2中,设计模型为均匀半空间,模型电阻率、发送及观测频点等其他参数与前例相同.输入端包含2个不同极化方向的天然场源以及2个不同极化方向的磁偶极子可控人工场源,输出端含有高斯随机噪声.共布设2个同步测站,其中1个为远参考站,另一个为测区内的待求测站j.各测站处进行水平张量观测,测量2道水平电场、2道水平磁场,共8个测道;另有测量时窗60个.为便于对比,x方向的人工场源与测站间的发收距更小.
采用(17)式和(19)式分别估计天然场和人工场阻抗张量,并计算视电阻率和相位.同时,采用最小二乘法及远参考法(Gamble et al., 1979)等常规方法估计阻抗数据,并计算视电阻率和相位,以作为对比;远参考法采用远参考站的磁道作为参考道.
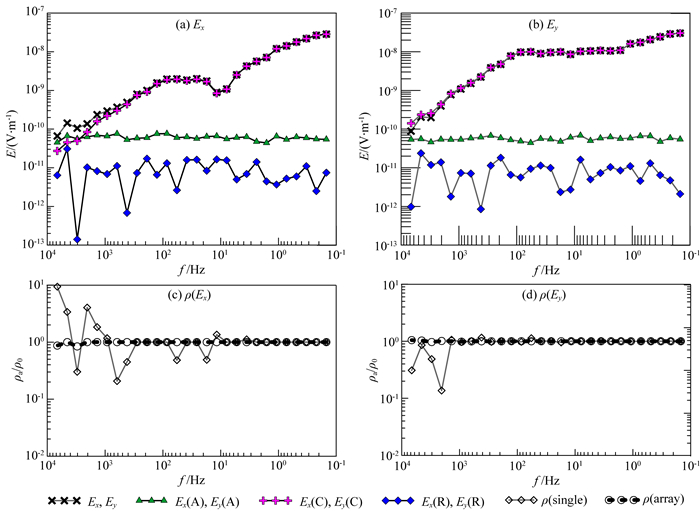
图 5给出了测站j处不同方法阻抗视电阻率、相位估计结果示意.不难发现,在人工源条件下,直接利用最小二乘(LS)、远参考法(RRLS)等阻抗估计手段,获得的阻抗视电阻率、相位数据存在明显的非平面波畸变.而利用本文所提供的数据处理方法,同时获得了对应于天然场张量阻抗的视电阻率、相位(图中A-MT对应的数据)以及对应于人工场的张量阻抗的视电阻率、相位(图中A-CS对应的数据).随着频率的降低,天然场张量阻抗视电阻率ρa与地下真实电阻率ρ0一致(ρa/ρ0=1),相位稳定为45°,表明所求得的天然场张量阻抗不受人工场源的影响,可以获得不受畸变的地下电性信息;另外,人工场张量阻抗在人工场源的“远区”,也即数据的高频段,同样可以获得不受畸变的频率测深数据;而在“近区”,也即低频段,表现与理论的“近源”特征(Oettinger et al., 2001; 汤井田等,2012)一致.
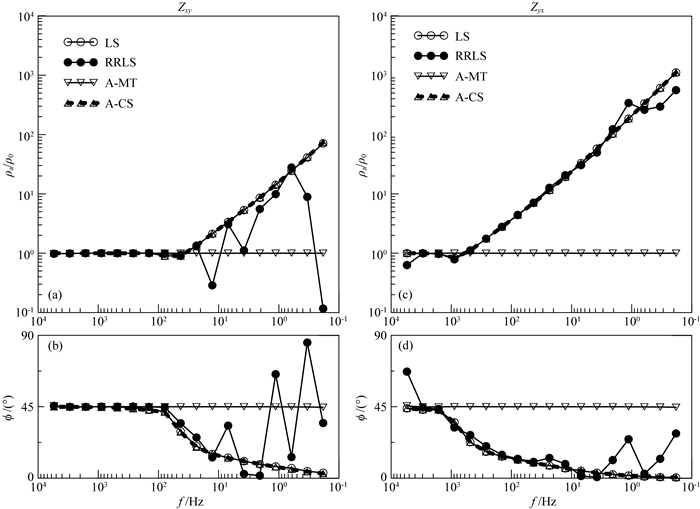
|
图 5 均匀半空间条件下不同方法阻抗视电阻率、相位估计结果对比 (a, b) xy方向的阻抗视电阻率、相位;(c, d) yx方向的阻抗视电阻率、相位.图例中“LS”和“RRLS”分别表示最小二乘、远参考法估计结果,“A-MT”和“A-CS”分别表示本文方法所得的天然场及可控人工场阻抗估计结果;ρa为计算视电阻率,ρ0为模型真实电阻率. Fig. 5 Comparison of the apparent resistivity and phase results estimated by different methods on an uniform half space model (a, b) Apparent resistivity and phase of xy direction; (c, d) Apparent resistivity and phase of yx direction. "LS" and "RRLS" denote the results estimated by least squares and remote reference method respectively, "A-MT" and "A-CS" denote the results of natural and controlled source impedances estimated by our method respectively. ρa denotes the estimated apparent resistivity while ρ0 is the true resistivity of the model. |
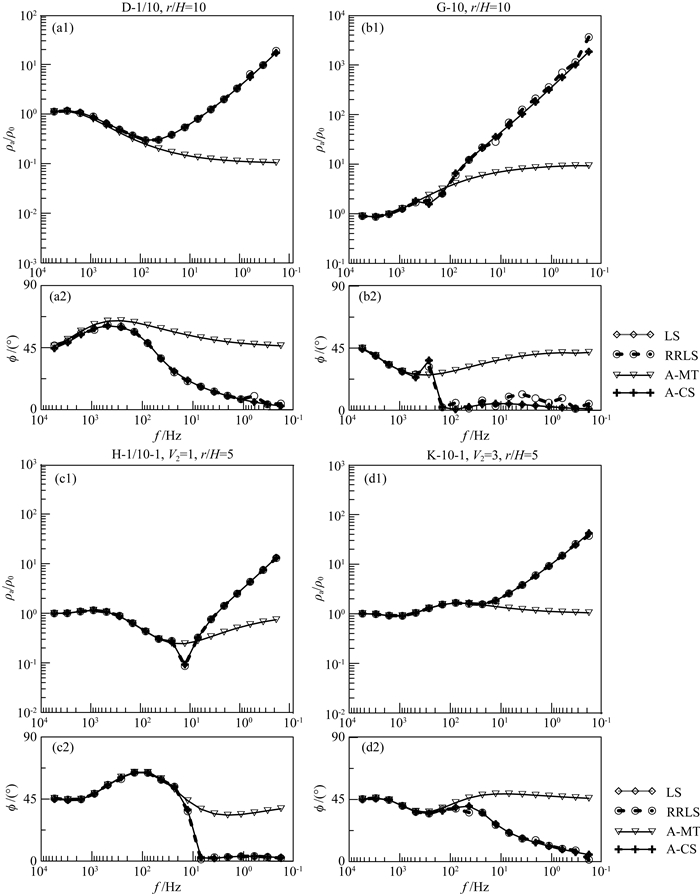
改变前述模型中的地电条件,测试多层介质模型.算例3中,设计了两层D型、G型、三层H型及K型等几类典型介质,其他参数与前例相同.图 6分别给出了不同方法阻抗视电阻率、相位估计结果的对比.可以看出,在多层条件下,可以获得与前述均匀半空间条件下类似的结论.在高频端,天然场阻抗张量和人工场阻抗张量均能反映地电介质的真实变化;但在低频段,人工场阻抗张量出现显著的非平面波畸变,不再反映地下电性信息,而天然场阻抗张量则不受非平面波畸变影响,仍能得到不受畸变的地电参数响应结果.利用本文方法,实现了天然场阻抗张量和人工场阻抗张量的分离.
|
图 6 多层介质表面不同方法阻抗视电阻率、相位估计结果对比 (a1, a2) D型介质; (b1, b2) G型介质; (c1, c2) H型介质; (d1, d2) K型介质.各子图中上图为视电阻率,下图为相位.模型说明中,大写字母代表地电断面类型,后面的数字依次表示ρ2/ρ1、ρ3/ρ1、V2=h2/h1等;r表示垂直偶极矩方向的发收距;H为各层总厚度;其他符号意义与图 5相同. Fig. 6 Comparison of the apparent resistivity and phase results estimated by different methods on multilayered earth (a1, a2) D-type model; (b1, b2) G-type model; (c1, c2) H-type model; (d1, d2) K-type model. In each subgraph, the above shows apparent resistivity while the bottom shows phase. For the model descriptions show as titles, the capitals represent the model type, the numbers in the following order denote ρ2/ρ1, ρ3/ρ1, V2=h2/h1 and so on, r denotes the distance of receiver-transmitter in the perpendicular direction of the dipole source, H denotes the total thickness of each layer, and the other symbols have the same meaning as Fig. 5. |
当系统的输入、输出及地电条件等情况更复杂时,观测电磁场也更为复杂,常规方法的数据质量保障更为困难,而本文方法提供了可能的处理途径.
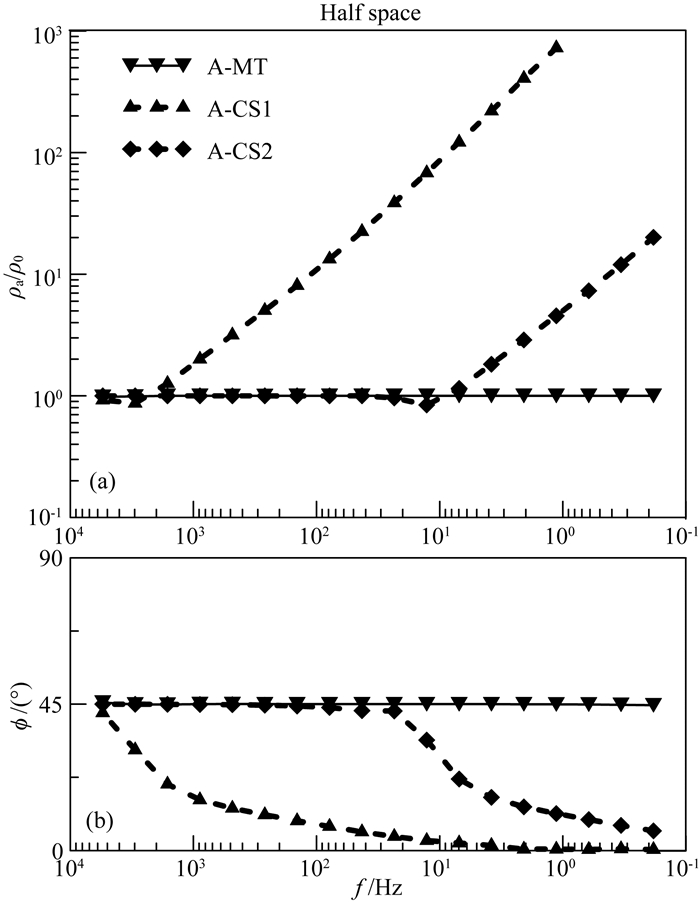
例如,当系统中存在更复杂的人工场源(L3>2)时,利用本文方法,如(17)、(19)及(20)式,可获得对应于不同场源的空间模数及解释参数.算例4中,给出了多场源条件下地电参数的获取示意.在两坐标方向各增加一个可控人工场源,地电介质选为均匀半空间,其他模拟条件与前述相同.结果如图 7所示,因两方向结果类似,此处仅给出了xy方向的阻抗视电阻率及相位.不难看出,利用本文方法,可分别提取对应于L3个人工场源的阻抗张量以及天然场源阻抗张量,随着场源发收距的不断增大,其对应的阻抗张量有效频率也逐渐降低.实际中,发收距的大小与信号的强弱也紧密相关,结合各场源对应的解释参数,进行综合分析,可获得对地电介质更为全面的认识.
|
图 7 多场源条件下地电参数的估计结果 (a, b) xy方向的视电阻率、相位.模型为均匀半空间,采用本文方法进行计算;“A-MT”为天然场源对应的阻抗视电阻率及相位,“A-CS1”、“A-CS2”分别为第1个、2个可控人工场源对应的阻抗视电阻率及相位. Fig. 7 The estimation result of geoelectric parameters under the condition of multi-source (a, b) Apparent resistivity and phase of xy direction calculated by our method; the model is uniform half space; "A-MT", "A-CS1" and "A-CS2" denote the results of natural source, one and another controlled source impedances estimated by our method respectively. |
当目标地质体处的地电条件为3D时,为获得更可靠的观测结果,需进行3D测量.此时,应用阵列采集方法(图 2),结合本文提供的阵列处理手段,有望提高处理效率与质量.算例5中,提供一个3D计算实例.空间模数的计算采用Weiss(2013)提供的APhiD三维有限体积电磁数值模拟程序,其他步骤与前例相同.模型条件如图 8所示,背景为1000 Ωm均匀半空间,3D异常体为10 Ωm低阻长方体.为保证计算精度,3D网格大小为114(x)×114(y)×83(z),测区范围及目标深度内网格间距为100 m×100 m×50 m,测区外网格间距逐渐增大以满足边界条件.关于数值模拟精度及异常体的响应特征等,可以参考Weiss(2013)和张林成等(2017)文献,本文不作分析;仅关注该程序所获得的电磁场观测数据,采用不同的数据处理方法所获得的视电阻率结果.

|
图 8 3D算例模型 背景为1000 Ωm均匀半空间,异常体为10 Ωm低阻长方体,测区外地表布置同时激励的两个水平电偶极子场源,测站在测区内地表呈阵列分布(如图 2),异常体埋深、尺寸、测区范围和人工源的空间位置如图中标识所示. Fig. 8 A 3D model example A 10 Ωm anomalous low resistance cuboid body is buried in the 1000 Ωm homogeneous earth. Two simultaneous horizontal electric dipole sources are arranged outside the survey area while array observation stations are deployed inside the survey area on the earth′s surface (as shown in Fig. 2). The marks indicate the buried depth and size of the anomalous body, the range of the survey area and the location of the controlled sources. |
本例中,测区外地表布置同时激励的两个水平电偶极子场源,对图 8所示异常体,假设目标深度为δ=500 m,场源距测区中心的发收距选择为r=12δ=6 km.测站在测区内地表呈阵列分布,每站进行张量布设,观测水平4道电磁场分量(如图 2),为便于显示,此处将测站直接布设于地表网格的交点处.测试频率为100 Hz,观测时窗数为100个,输出端噪声信噪比为10 dB.图 9给出了地表测区内不同数据处理算法估计的阻抗视电阻率ρxy响应结果对比,因为模型是对称的,ρyx响应不再列出.

|
图 9 不同数据处理算法对图 8模型测区内ρxy响应估计结果对比,频率f=100 Hz 其中,输入端含三种条件,仅天然场(a),仅人工场(b),天然场和人工场同时存在(c—f);(a—c)为最小二乘估计结果,(d)为远参考估计结果,(e, f)分别为本文方法所得到的天然场响应及人工场响应. Fig. 9 Comparison of ρxy response estimated by different data processing algorithm for the model shown in Fig. 8 at frequency 100 Hz inside the survey area Three input conditions are considered here, only natural sources (a), only controlled sources (b) and natural sources combined with controlled sources (c—f). Responses are estimated by least square method (a—c) and remote reference method (d), while (e, f) show the natural and controlled source responses obtained by our method respectively. |
从图 9中可以看出,纯天然场ρxy响应(a)可以较为清晰的勾勒出三维异常体x方向的两侧边界;而纯人工场响应(b)反映出,在所选测试频率(100 Hz)上测区范围基本位于人工源的近区及过渡区,数据受到了非平面波场的影响,出现了高阻型畸变.当输入端同时存在天然场和人工场时,直接采用常规最小二乘或远参考方法对叠加信号进行处理,所得结果(c, d)为纯天然场(a)与纯人工场响应(b)的中间值;相对而言,相比最小二乘所得结果(c),远参考方法的估计结果(d)与纯天然场响应(a)更为接近,但这两类常规方法均无法剔除非平面波效应的影响.而采用本文方法,获得的天然场响应结果(e)与纯天然场响应(a)相当,人工场响应结果(f)与纯人工场响应(b)相当.本例说明,本文方法适用于三维地电条件及三维数据处理等复杂情形,可实现天然场与人工场响应的分离,压制非平面波效应及场源效应的影响.
4 讨论与结论基于时空阵列输入-输出模型,本文提出了时空阵列混场源电磁法.其主要特点包括:①理论方面,将天然场信号与人工场信号均作为有用信号,而非视其中之一为相关噪声.②输入端人工场源的类型、数量、布设形式、激励方式及布设位置等不受限制,实际中可根据野外条件灵活布设场源;所有场源的激励可同时进行,无需分步.③输出端进行多站同步观测,测区内测站的布设方式灵活,可根据所需求取的目标参数,布设单个场分量测道,或进行多分量张量测量;同时在测区外布设张量远参考站.④采用阵列数据处理方法,所有待求数据可在统一的方程中进行处理,可在一次观测条件下,同时提取天然场信息及人工场信息.
本方法可实现天然场、人工场系统响应的分离,相对于常规天然场或人工场方法,它具有如下优势:①相较于天然场源电磁法,它可利用高强度的人工源信号,提高数据的观测质量;特别的,在AMT的“死频带”(1~5 kHz)(周聪等,2015)内,利用人工场信号计算其空间模数及解释参数,可望提高数据处理质量.②相较于常规的人工源电磁法,一方面,它可以压制天然场的影响,提高人工场相关解释参数的处理质量(算例1);另一方面,它可利用近似平面波的天然场信号,获得天然场解释参数,进而压制人工源造成的非平面波效应、场源阴影及附加作用等问题的影响(算例2~算例5).③相对于常规的“混然源”电磁法,本方法一次观测、一次处理,无需分时段采集、分别处理,可以同时获得天然场与人工场解释参数,不仅可望提高数据采集、处理效率,还可利用复杂混场源条件(算例4~5),提高数据分析质量.
本文研究的假设前提是不同的输入-输出作用于同一地下系统,实际中对于不同的测区,或在同一测区内不同测站的距离过远,导致不同测站间的人工场相关信息过小,则需要将观测数据根据实际分做两个或多阵列子集进行处理.此外,与常规远参考方法类似,当远参考站与测站距离相距过大时,高频信号间的相关性降低;此时利用远参考站获得的天然场极化参数估计目标测站的空间模数将存在误差;实际中,可参照常规远参考法的参考站选择标准,根据目标深度及观测频率选择合适的参考距.
本文的重点在于提出一种适用于多输入-多输出环境的时空阵列混场源电磁法理论模型,以提供进一步研究的基础.基于本文所述方法,深入分析多站阵列间的相互关系,可以研究未知人文场源信息的提取技术;利用不同测道间的转换函数,可进一步研究缺失数据的恢复、强不相关噪声的压制等技术;对比提取出的天然场和人工场解释参数(1.3节),可以分析人工场源响应中“场源效应”所携带的地质信息,推断场源与测区间可能的结构;在后续处理中既可以进行不同参数的单独反演,以得到多种模型进行联合解释;也可直接进行多种参数的联合反演,获得统一的电性模型加以解释.由于目前天然场与人工场数据的采集方式、采样率及数据格式仍存在差异,因此缺乏合适的实测数据,应用案例的研究也亟待补充.这些内容超出了本文的研究范围,将在下一步工作中深入.
综上,本文提出的时空阵列混场源电磁法具有多输入-多输出的特点,在时间和空间上均作阵列观测,并进行阵列处理,提取对应于不同场源的响应信息;本方法集合了天然场源电磁法和人工场源电磁法的优点,为实现多类型频率域电磁测深方法的统一处理提供了思路,是一种值得深入研究的电磁勘探新方法.
Chave A D, Thomson D J. 1989. Some comments on magnetotelluric response function estimation. Journal of Geophysical Research: Solid Earth, 94(B10): 14215-14225. DOI:10.1029/JB094iB10p14215 |
Chave A D, Jones A G. 2012. The Magnetotelluric Method: Theory and Practice. Cambridge: Cambridge University Press.
|
Chen D F, Wang J, Li X P, et al. 2004. Development in the research of HSSMT instrument. Progress in Geophysics (in Chinese), 19(4): 778-781. DOI:10.3969/j.issn.1004-2903.2004.04.012 |
Chen M S, Yan S. 2005. Analytical study on field zones, record rules, shadow and source overprint effects in CSAMT exploration. Chinese J. Geophys (in Chinese), 48(4): 951-958. |
Deng J Z, Zheng Y Q, Chen H, et al. 2016. Comparison of various frequency-domain electromagnetic methods for mineral exploration in Lengshuikeng ore-concentration area. Progress in Geophysics (in Chinese), 31(6): 2510-2520. DOI:10.6038/pg20160621 |
Egbert G D. 1997. Robust multiple-station magnetotelluric data processing. Geophysical Journal International, 130(2): 475-496. DOI:10.1111/j.1365-246X.1997.tb05663.x |
Egbert G D. 2002. Processing and interpretation of electromagnetic induction array data. Surveys in Geophysics, 23(2-3): 207-249. |
Gamble T D, Goubau W M, Clarke J. 1979. Magnetotellurics with a remote magnetic reference. Geophysics, 44(1): 53-68. DOI:10.1190/1.1440923 |
Goldstein M A, Strangway D W. 1975. Audio-frequency magnetotellurics with a grounded electric dipole source. Geophysics, 40(4): 669-683. DOI:10.1190/1.1440558 |
He J S. 2010. Wide Field Electromagnetic Method and Pseudo Random Signal Method (in Chinese). Beijing: Higher Education Press.
|
Li G, Xiao X, Tang J T, et al. 2017. Near-source noise suppression of AMT by compressive sensing and mathematical morphology filtering. Applied Geophysics, 14(4): 581-589. DOI:10.1007/s11770-017-0645-6 |
Li J, Zhang X, Gong J Z, et al. 2018. Signal-noise identification of magnetotelluric signals using fractal-entropy and clustering algorithm for targeted de-noising. Fractals, 26(2): 1840011. DOI:10.1142/S0218348X1840011X |
Li J, Zhang X, Tang J T, et al. 2019. Audio magnetotelluric signal-noise identification and separation based on multifractal spectrum and matching pursuit. Fractals, 27(1): 1940007. DOI:10.1142/S0218348X19400073 |
Lin P R, Guo P, Shi F S, et al. 2010. A study of the techniques for large-depth and multi-functional electromagnetic survey. Acta Geoscientica Sinica (in Chinese), 31(2): 149-154. |
Liu C M, Tong T G, He J S. 2013. Exploration of various electromagnetic method in some gold mine. The Chinese Journal of Nonferrous Metals (in Chinese), 23(9): 2422-2429. |
Liu Z X, Xue G Q, Zhang L B. 2017. Comparison and analysis on effective observation area of tensor CSAMT by numerical simulation method. Chinese J. Geophys (in Chinese), 60(8): 3278-3287. DOI:10.6038/cjg20170832 |
Luo W B, Li Q C, Tang J T. 2012. Coded source electromagnetic sounding method. Chinese J. Geophys (in Chinese), 55(1): 341-349. DOI:10.6038/j.issn.0001-5733.2012.01.035 |
Oettinger G, Haak V, Larsen J C. 2001. Noise reduction in magnetotelluric time-series with a new signal-noise separation method and its application to a field experiment in the Saxonian Granulite Massif. Geophysical Journal International, 146(3): 659-669. DOI:10.1046/j.1365-246X.2001.00473.x |
Ren Z Y, Chen C J, Tang J T, et al. 2017. A new integral equation approach for 3D magnetotelluric modeling. Chinese J. Geophys (in Chinese), 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2014. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling. Geophysics, 79(6): E255-E268. DOI:10.1190/geo2013-0376.1 |
Smirnov M Y, Egbert G D. 2012. Robust principal component analysis of electromagnetic arrays with missing data. Geophysical Journal International, 190(3): 1423-1438. DOI:10.1111/j.1365-246X.2012.05569.x |
Streich R, Becken M, Ritter O. 2010. Imaging of CO2 storage sites, geothermal reservoirs, and gas shales using controlled-source magnetotellurics: modeling studies. Geochemistry, 70(S3): 63-75. |
Streich R. 2016. Controlled-source electromagnetic approaches for hydrocarbon exploration and monitoring on land. Surveys in Geophysics, 37(1): 47-80. |
Tang J T, He J S. 2005. Methods and Applications of CSAMT (in Chinese). Changsha: Central South University Press.
|
Tang J T, Zhou C, Zhang L C. 2011. A new apparent resistivity of CSAMT defined by electric field y-direction. Journal of Jilin University (Earth Science Edition) (in Chinese), 41(2): 552-558. |
Tang J T, Xu Z M, Xiao X, et al. 2012. Effect rules of strong noise on magnetotelluric (MT) sounding in the Luzong ore cluster area. Chinese J. Geophys (in Chinese), 55(12): 4147-4159. DOI:10.6038/j.issn.0001-5733.2012.12.027 |
Tang J T, Zhou C, Xiao X. 2013. Selection of minimum transmit-receive distance of CSAMT on complicated media. The Chinese Journal of Nonferrous Metals (in Chinese), 23(6): 1681-1693. DOI:10.1016/S1003-6326(13)62648-5 |
Tang J T, Li G, Zhou C, et al. 2018. Denoising AMT data based on dictionary learning. Chinese J. Geophys (in Chinese), 61(9): 3835-3850. DOI:10.6038/cjg2018L0376 |
Wang X X, Di Q Y, Xu C. 2014. Characteristics of multiple sources and tensor measurement in CSAMT. Chinese J. Geophys (in Chinese), 57(2): 651-661. DOI:10.6038/cjg20140228 |
Wang Y Z. 2010. Research on key techniques for the hybrid-source magnetotelluric exploration [Ph. D. thesis] (in Chinese). Changchun: Jilin University.
|
Weiss C J. 2013. Project APhiD: A Lorenz-gauged A-Φ decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous Earth. Computers & Geosciences, 58: 40-52. DOI:10.1016/j.cageo.2013.05.002 |
Yang Y. 2017. Research on extraction for useful signal and denoising method based on periodic feature [Ph. D. thesis] (in Chinese). Changsha: Central South University.
|
Yao W, Li Q, Yang J, et al. 2015. The application and comparison of CSAMT and AMT: an example about Fe-Au mine in Beiya of Yunnan. Progress in Geophysics (in Chinese), 30(4): 1825-1832. DOI:10.6038/pg20150441 |
Zhang L C, Tang J T, Ren Z Y, et al. 2017. Forward modeling of 3D CSEM with the coupled finite-infinite element method based on the second field. Chinese J. Geophys (in Chinese), 60(9): 3655-3666. DOI:10.6038/cjg20170929 |
Zhen Q H, Di Q Y. 2017. High-frequency high-power CSAMT transmitting technology research. Chinese J. Geophys (in Chinese), 60(11): 4160-4164. DOI:10.6038/cjg20171103 |
Zhou C, Tang J T, Ren Z Y, et al. 2015. Application of the Rhoplus method to audio magnetotelluric dead band distortion data. Chinese J. Geophys (in Chinese), 58(12): 4648-4660. DOI:10.6038/cjg20151226 |
Zhou C. 2016. Theoretical and experimental study of space-time array electromagnetic method and three-dimensional electrical structure of Lu-Zong Ore District [Ph. D. thesis] (in Chinese). Changsha: Central South University.
|
陈明生, 闫述. 2005. CSAMT勘探中场区、记录规则、阴影及场源复印效应的解析研究. 地球物理学报, 48(4): 951-958. DOI:10.3321/j.issn:0001-5733.2005.04.031 |
程德福, 王君, 李秀平, 等. 2004. 混场源电磁法仪器研制进展. 地球物理学进展, 19(4): 778-781. DOI:10.3969/j.issn.1004-2903.2004.04.012 |
邓居智, 郑燕青, 陈辉, 等. 2016. 多种频率域电磁法在冷水坑矿集区的应用效果对比. 地球物理学进展, 31(6): 2510-2520. DOI:10.6038/pg20160621 |
何继善. 2010. 广域电磁法和伪随机信号电法. 北京: 高等教育出版社.
|
林品荣, 郭鹏, 石福升, 等. 2010. 大深度多功能电磁探测技术研究. 地球学报, 31(2): 149-154. |
刘春明, 佟铁钢, 何继善. 2013. 多种电磁法在某金矿的野外勘探应用. 中国有色金属学报, 23(9): 2422-2429. |
刘志新, 薛国强, 张林波. 2017. 张量CSAMT有效观测区域模拟对比分析. 地球物理学报, 60(8): 3278-3287. DOI:10.6038/cjg20170832 |
罗维斌, 李庆春, 汤井田. 2012. 编码电磁测深. 地球物理学报, 55(1): 341-349. DOI:10.6038/j.issn.0001-5733.2012.01.035 |
任政勇, 陈超健, 汤井田, 等. 2017. 一种新的三维大地电磁积分方程正演方法. 地球物理学报, 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
汤井田, 何继善. 2005. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社.
|
汤井田, 周聪, 张林成. 2011. CSAMT电场y方向视电阻率的定义及研究. 吉林大学学报(地球科学版), 41(2): 552-558. |
汤井田, 徐志敏, 肖晓, 等. 2012. 庐枞矿集区大地电磁测深强噪声的影响规律. 地球物理学报, 55(12): 4147-4159. DOI:10.6038/j.issn.0001-5733.2012.12.027 |
汤井田, 周聪, 肖晓. 2013. 复杂介质条件下CSAMT最小发收距的选择. 中国有色金属学报, 23(6): 1681-1693. |
汤井田, 李广, 周聪, 等. 2018. 基于字典学习的音频大地电磁数据处理. 地球物理学报, 61(9): 3835-3850. DOI:10.6038/cjg2018L0376 |
王显祥, 底青云, 许诚. 2014. CSAMT的多偶极子源特征与张量测量. 地球物理学报, 57(2): 651-661. DOI:10.6038/cjg20140228 |
王言章. 2010.混场源电磁探测关键技术研究[博士论文].长春: 吉林大学.
|
杨洋. 2017.基于周期性特征提取有效信号的去噪方法研究[博士论文].长沙: 中南大学.
|
姚文, 李琼, 杨剑, 等. 2015. 可控源与天然源音频大地电磁法对比应用研究:以云南北衙铁金矿为例. 地球物理学进展, 30(4): 1825-1832. DOI:10.6038/pg20150441 |
张林成, 汤井田, 任政勇, 等. 2017. 基于二次场的可控源电磁法三维有限元-无限元数值模拟. 地球物理学报, 60(9): 3655-3666. DOI:10.6038/cjg20170929 |
真齐辉, 底青云. 2017. 高频大功率CSAMT发射技术研究. 地球物理学报, 60(11): 4160-4164. DOI:10.6038/cjg20171103 |
周聪, 汤井田, 任政勇, 等. 2015. 音频大地电磁法"死频带"畸变数据的Rhoplus校正. 地球物理学报, 58(12): 4648-4660. DOI:10.6038/cjg20151226 |
周聪. 2016.时空阵列电磁法及试验研究——兼论庐纵矿集区三维电性结构[博士论文].长沙: 中南大学.
|
 2019, Vol. 62
2019, Vol. 62


