重力方法是了解地下数据密度分布的重要手段,在矿产、石油以及环境勘探等领域有着广泛应用.近年来,三维反演已经成为重磁数据定量解释的常规方法(Li and Oldenburg, 1996,1998;管志宁等,1998;Portniaguine and Zhdanov, 1999,2002;Boulanger and Chouteau, 2001;姚长利等, 2003, 2007;Farquharson,2008;孟小红等,2012;刘银萍等,2013;Liu et al., 2013, 2015).前人的研究表明,当反演的目标函数设计合理时,仅利用重力数据即可恢复出构造复杂度适中的场源(Li and Oldenburg, 1998;Farquharson,2008).但是,根据高斯定理,重力数据本身没有深度分辨率,即重力反演问题具有严重的多解性(Blakely,1996;Li and Oldenburg, 1998).为了进一步减少重力反演的非唯一性,最直接的办法就是引入额外的地质或地球物理先验信息.
已知的物性信息可以作为参考模型或者等式约束(Aster et al., 2005;Menke,2012)加入到反演的目标函数中.已知的物性信息还可用于获得具有尖锐边界的解,其中的代表性算法主要有两类.
第一类算法将已知的物性信息作为离散值约束改善反演结果,常用的方法是二值或者三值反演,即假设地下密度分布仅包含两种物性(已知正值或零)或者三种物性(已知正值、已知负值、零).由于此时的模型参数空间不再连续,因此多数算法无法利用目标函数的导数信息,往往采用随机搜索或系统搜索的策略来寻找次优解.Camacho等(2000)利用场源生长算法求解重力三值反演问题.Krahenbuhl和Li(2006, 2009)利用遗传算法和模拟退火算法求解重力二值反演问题.Uieda和Barbosa(2012)利用种种子算法求解重力梯度二值反演问题.Lu和Qian(2015)以及Li等(2017)利用水平集算法求解重磁二值反演问题,与基于搜索的算法不同,基于水平集的算法可以利用目标函数的导数信息.
第二类算法将已知的物性信息作为边界(上下界)约束,并结合稀疏模型范数来改善反演结果.此时的模型参数空间依然连续,因而反演的目标函数可以利用基于导数的算法求解.Last和Kubik(1983)在重力数据反演中极小化模型的总体积,其构建的模型范数被Portniaguine和Zhdanov(1999)称为最小支撑泛函,并进一步应用到磁数据反演(Portniaguine and Zhdanov, 2002).Portniaguine和Zhdanov(1999)将Last和Kubik(1983)构建的模型范数扩展为适用于模型梯度的情况,并定义为最小梯度支撑泛函,其反演算法称为聚焦反演.Van Zon和Roy-Chowdhury(2006)在重力数据反演中极小化模型的L1范数.Li等(2018)在磁数据反演中极小化模型的Lp范数(0 ≤p≤1).
Li等(2018)经过分析后认为,在磁数据反演中,当模型范数中仅包含模型长度项(即不包含模型导数相关项)时,第二类算法和第一类算法中的二值反演是等价的.Li等(2018)通过磁数据模型试验和实际数据试验验证了两类算法的等价性.在本文中,我们将Li等(2018)提出的Lp范数稀疏优化算法扩展到重力数据反演中,分析了稀疏反演算法与二值、三值反演的等价性,指出了其在实际应用时需要注意的问题,最后通过模型试验和矿区数据反演验证了稀疏反演算法的有效性.
1 重力Lp范数稀疏反演方法 1.1 正演问题如果假设观测的重力数据向量为d,其长度为N,地下密度模型向量为m,其长度为M,正演问题可以表述如下:
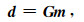
|
(1) |
其中G为重力数据d关于地下密度模型向量m的线性正演矩阵,其大小为N×M.
1.2 反演问题首先考虑无约束重力Lp范数反演问题,其目标函数具有如下形式:

|
(2) |
其中μ为正则化参数.φd为数据拟合差,其矩阵形式如下:
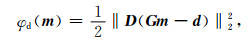
|
(3) |
其中,D为对角数据加权矩阵,其第i个对角元素为第i个观测数据的噪声标准差的倒数.φum为无约束模型Lp范数项,其形式如下:
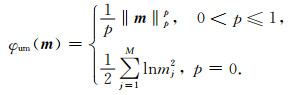
|
(4) |
式中,p=0的情况可以参考Rao和Kreutz-Delgado(1999).(2)式属于非线性反演问题,通常可以将其转化为迭代重加权最小二乘问题(Holland and Welsch, 1977;Daubechies et al., 2010),第n次迭代时的目标函数为

|
(5) |
其中W(n)为对角重加权矩阵,其元素由第n-1次迭代时的结果组成,具有如下形式:
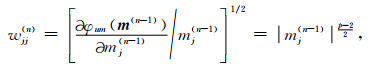
|
(6) |
当mj=0时,(6)式无定义,为了防止(6)式奇异,将(6)式修改为
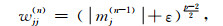
|
(7) |
其中ε为非常小的正数,我们通常设置为10-10.
本文重点关注物性上下界约束时的重力Lp范数(0 ≤p≤1)反演问题.与无约束反演类似,利用迭代重加权最小二乘技术,约束反演问题被表述为一系列约束最小二乘问题,其第n次迭代时的目标函数如下:
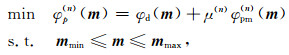
|
(8) |
其中φd由(3)式给出,μ(n)为第n次迭代时的正则化参数,mmin和mmax分别为每个单元物性下界和上界组成的向量.φpm(n)为第n次迭代时的模型目标函数,其形式如下:
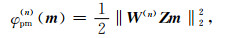
|
(9) |
其中,Z为对角深度加权矩阵,其形式见Li和Oldenburg(1998).W(n)由(7)式给出,W(0)设置为单位矩阵I.
(8) 式属于不等式约束线性反演问题,对于该问题的求解,当前已有多种算法成功应用到了重磁领域,如非线性投影法(Li and Oldenburg, 1996;Lelièvre and Oldenburg, 2006),内点法(Li and Oldenburg, 2003),以及梯度投影法(Lelièvre et al., 2009).本文选择内点法求解该问题,详细的算法见附录A.
假设每次迭代时的正则化参数已知,物性上下界约束重力Lp范数反演算法总结如下:
初始化:μ(0),W(0)=I,n=0.
重复:
(1) 利用附录A的算法求解(8)式得到m(n).
(2) n←n+1,更新μ(n),按照(7)式由m(n-1)生成W(n).
直到收敛.
1.3 稀疏反演方法与二值和三值反演的等价性分析Li等(2018)经过分析后认为,在磁测数据反演中,当模型范数中仅包含模型长度项(即不包含模型导数相关项)时,稀疏反演和二值反演是等价的.我们认为,该等价性也可以扩展到重力反演中.
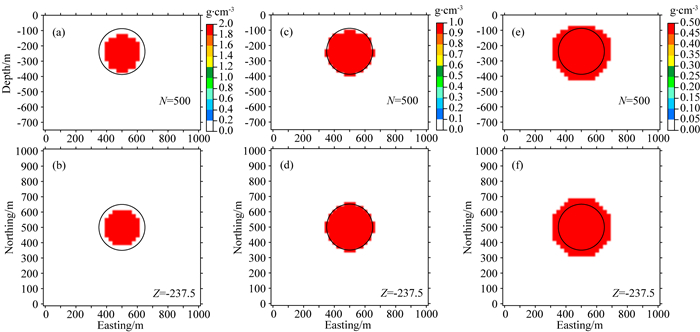
为了验证上述分析,我们采用与Li等(2018)类似的球体模型进行测试.球体的中心深度为237.5 m,半径为150 m,密度为1 g·cm-3.观测数据为21×21的网格数据,网格间距为50 m.模型区域则剖分为41×41×30的立方体单元,立方体的边长为25 m.针对该重力数据数据,利用本文算法,我们采用相同的下界约束(0 g·cm-3)和不同的上界约束(2、1、0.5 g·cm-3)进行三次反演.三次反演的p值均设置为0.反演结果中心切片如图 1所示,可以看出,在不同上界约束的条件下,反演结果均表现出二值特性,符合前述分析.图 1a和1b为上界约束设置为2 g·cm-3时的反演结果,此时反演结果的体积比真实模型要小.图 1c和1d为上界约束设置为1 g·cm-3时的反演结果,此时反演结果的体积与真实模型非常接近.图 1e和1f为上界约束设置为0.5 g·cm-3时的反演结果,此时反演结果的体积比真实模型要大.
|
图 1 不同物性上界约束条件下球体模型的反演结果中心切片图 (a—b)、(c—d)以及(e—f)分别为物性上界设置为2、1以及0.5 g·cm-3时的反演结果.物性下界均设置为0 g·cm-3.黑框代表了真实模型的位置. Fig. 1 Inversion results of the anomaly produced by the sphere model by using different upper bounds (a—b) The inversion result with an upper bound of 2 g·cm-3. (c—d) The inversion result with an upper bound of 1 g·cm-3. (e—f) The inversion result with an upper bound of 0.5 g·cm-3. The lower bounds of all inversions are set to 0 g·cm-3. The position of the true model is indicated by the black lines. |
尽管此处的分析是以球体为例,但上述等价性适用于任何形态的场源产生的重力数据,原因是任意复杂形态的场源所产生的重力数据均可被球体组合的线性叠加所近似.此外,当正、负数据同时存在时,将物性上、下界分别设置为已知正、负密度值时,稀疏反演方法将等价于三值反演.上述等价性将在后续章节中的模型试验和实际资料试验中进行验证.
2 模型试验为了验证本文重力数据Lp范数稀疏反演算法的有效性,我们进行了针对性的模型试验.此外,为了说明不同模型范数对反演结果的影响,我们也将稀疏反演方法的反演结果与常规的L2范数方法反演结果进行了对比.
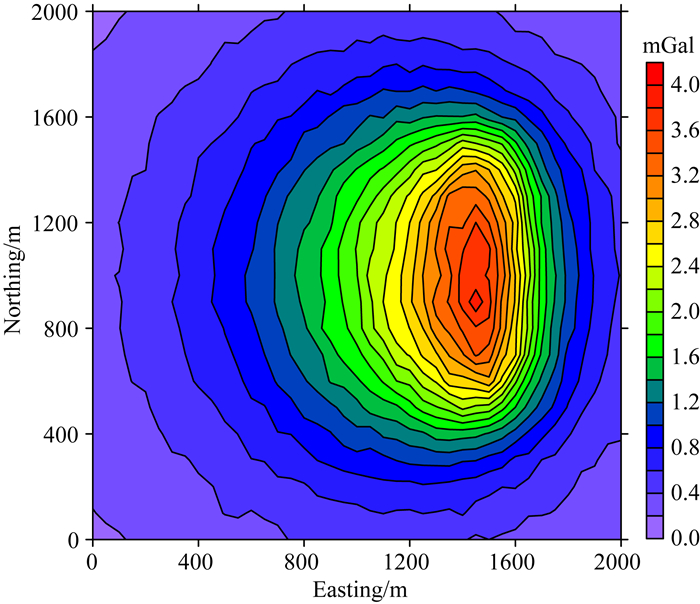
2.1 倾斜薄板模型第一个模型为倾斜薄板模型,该模型的空间位置和几何形态与Li和Oldenburg(1998)所使用的组合板状体模型中的右侧板状体相同.其南北向的延伸距离为500~1500 m,垂向延伸则从-100~-1000 m.板状体的倾角为45°,密度为1 g·cm-3.地表观测数据为21×41的网格数据,南北方向数据间隔为100 m,东西方向数据间隔为50 m.地面重力数据见图 2,其中包含标准差为2%数据绝对值加上0.01 mGal的高斯噪声.
|
图 2 薄板模型所产生的重力数据 Fig. 2 The gravity anomaly produced by the thin dipping slab model |
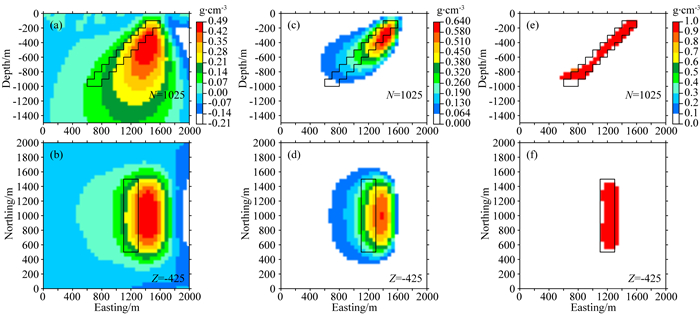
对于该模型,本文利用三种方法进行反演,将地下剖分为40×40×30的立方体,反演结果的中心切片如图 3所示.图 3a和3b为无约束L2范数反演的结果,重构场源的倾向接近垂直,且存在大量负密度虚假构造,反演结果较差.图 3c和3d为物性上下界约束L2范数的反演结果,其中上、下界分别设置为1和0 g·cm-3.由反演结果的物性分布(0~0.64 g·cm-3)可知,反演结果中的最小密度为0 g·cm-3,此时下界约束为有效约束,而反演结果中的最大密度仍然小于1 g·cm-3,上界约束实际上并不起作用.此时非负约束使得L2范数反演结果得到明显改善,但随着深度增加,反演结果的分辨率不断下降.图 3e和3f为物性上下界约束Lp范数的反演结果,其中上、下界分别设置为1和0 g·cm-3,p值设置为0.此时已知密度信息得到较好利用,反演结果表现出二值特性,深部分辨率得到明显改善.
|
图 3 倾斜薄板模型不同方法的反演结果中心切片图 (a—b)无约束L2范数反演结果;(c—d)物性上下界约束L2范数反演结果;(e—f)物性上下界约束Lp范数反演结果,其中p设置为0.在物性约束反演中,物性上、下界分别设置为1和0 g·cm-3.黑框代表了真实模型的位置. Fig. 3 Inversion results of the gravity anomaly produced by the thin dipping slab model by using different methods (a—b) The result of unconstrained L2-norm inversion. (c—d) The result of bound-constrained L2-norm inversion. (e—f) The result of bound-constrained Lp-norm inversion with p=0. The upper and lower bounds of bound-constrained inversions are set to 1 and 0 g·cm-3, respectively. The position of the true model is indicated by the black lines. |
第二个模型采用的是两个相距200 m的块体模型,其大小、埋深、密度参数各不相同.左侧块体为边长200 m的立方体,其顶部埋深为50 m,密度为1 g·cm-3.右侧块体为长方体,其水平方向边长均为200 m,垂向边长为250 m,顶部埋深150 m,密度为-1 g·cm-3.地表观测数据为21×21的网格数据,网格间距为50 m.地面重力数据数据见图 4,其中包含了标准差为2%数据绝对值的高斯噪声.

|
图 4 组合长方体模型所产生的重力数据 Fig. 4 The gravity anomaly produced by the model composed of two rectangular prisms |
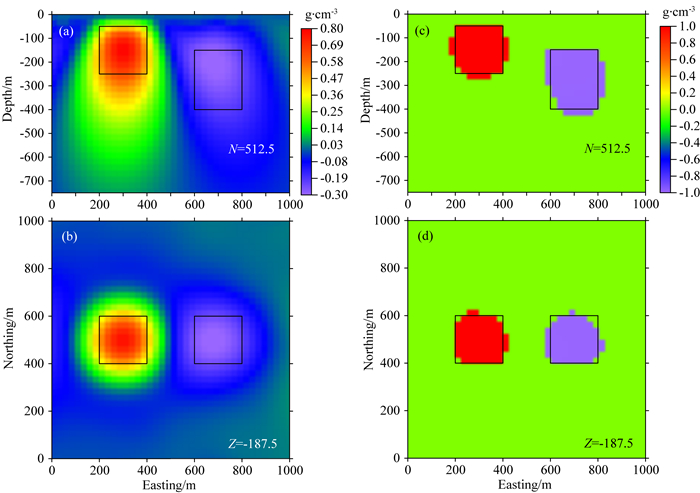
对于该模型,本文利用两种物性上下界约束方法进行反演,其中上、下界分别设置为1和-1 g·cm-3,将地下剖分为40×40×30的立方体,反演结果的中心切片如图 5所示.图 5a和5b为物性上下界约束L2范数的反演结果,反演结果中存在大量冗余构造.由反演结果的物性分布(-0.3~0.8 g·cm-3)可知,反演结果中的极大值和极小值均未达到物性上、下界,此时的物性上、下界约束实际上均为无效约束.图 5c和5d为物性上下界约束Lp范数的反演结果,其中p值设置为0.此时已知密度信息得到较好利用,反演结果表现出三值特性,无明显的冗余构造.
|
图 5 组合长方体模型重力数据不同方法的反演结果切片图 (a—b)物性上下界约束L2范数反演结果;(c—d)物性上下界约束Lp范数反演结果,其中p设置为0.物性上、下界分别设置为1和-1 g·cm-3.黑框代表了模型的真实位置. Fig. 5 Inversion results of the gravity anomaly produced by the model composed of two rectangular prisms by using different methods (a—b) The result of bound-constrained L2-norm inversion. (c—d) The result of bound-constrained Lp-norm inversion with p=0. The upper and lower bounds of both inversions are set to 1 and-1 g·cm3, respectively. The position of the true model is indicated by the black lines. |
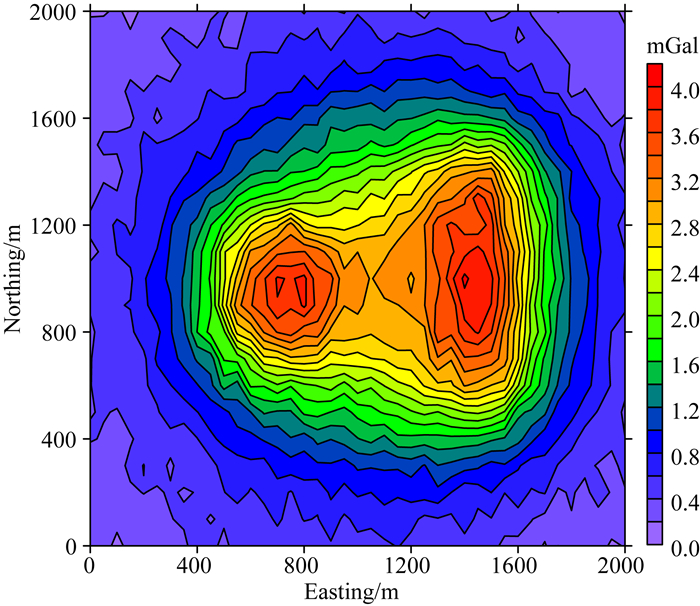
第三个模型采用的倾向相反的组合板状体,该模型的空间位置和几何形态见Li和Oldenburg(1998).左侧板状体的密度为0.8 g·cm-3.右侧板状体的密度为1 g·cm-3.地表观测数据为21×41的网格数据,南北方向数据间隔为100 m,东西方向数据间隔为50 m.地面重力数据见图 6,其中包含标准差为2%数据绝对值加上0.05 mGal的高斯噪声.
|
图 6 组合倾斜板状体模型所产生的重力数据 Fig. 6 The gravity anomaly produced by the model composed of two dipping slabs |
对于该模型,本文利用三种方法进行反演,将地下剖分为40×40×30的立方体,反演结果的中心切片如图 7所示.图 7a和7b为无约束L2范数反演的结果,重构场源较为发散,且存在大量负密度虚假构造,反演结果较差.图 7c和7d为物性上下界约束L2范数的反演结果,其中上、下界分别设置为1和0 g·cm-3.由反演结果的物性分布(0~0.7 g·cm-3)可知,反演结果中的最小密度为0 g·cm-3,此时下界约束为有效约束,而反演结果中的最大密度仍然小于1 g·cm-3,上界约束实际上并不起作用.此时非负约束使得L2范数反演结果得到明显改善.图 7e和7f为物性上下界约束Lp范数的反演结果,其中上、下界分别设置为1和0 g·cm-3,p值设置为0.此时已知密度信息得到较好利用,反演结果表现出二值特性.

|
图 7 组合倾斜板状体模型不同方法的反演结果中心切片图 (a—b)无约束L2范数反演结果;(c—d)物性上下界约束L2范数反演结果;(e—f)物性上下界约束Lp范数反演结果,其中p设置为0.在物性约束反演中,物性上、下界分别设置为1和0 g·cm-3.黑框代表了真实模型的位置. Fig. 7 Inversion results of the gravity anomaly produced by the model composed of two dipping slabs by using different methods (a—b) The result of unconstrained L2-norm inversion; (c—d) The result of bound-constrained L2-norm inversion; (e—f) The result of bound-constrained Lp-norm inversion with p=0. The upper and lower bounds of bound-constrained inversions are set to 1 and 0 g·cm-3, respectively. The position of the true model is indicated by the black lines. |
为了进一步说明本文重力数据Lp范数反演算法在实际应用中需要注意的事项,我们进行了两个附加的模型试验.第一个试验主要用于说明不准确的物性信息对反演结果的影响.第二个试验则主要用于说明不同类型的干扰场源对反演结果的影响.
2.4 不准确的物性信息对反演结果的影响前述模型试验均假设物性信息准确,我们测试不准确的物性信息对反演结果的影响.采用稀疏反演方法,对图 2所示薄板模型产生的重力数据进行两次反演.
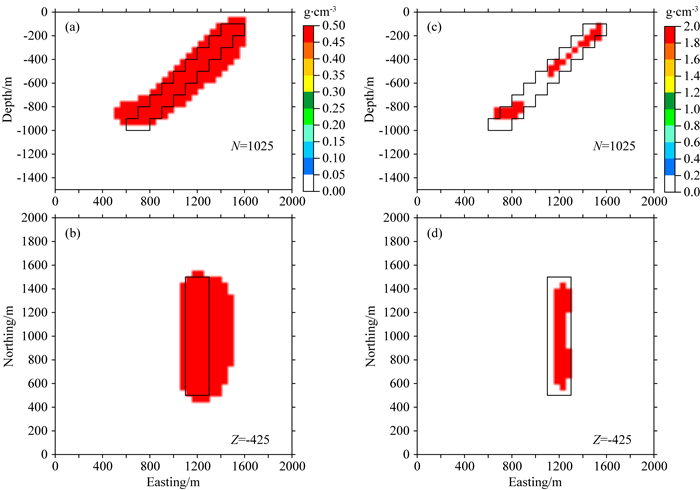
两次反演的物性下界均设置为0 g·cm-3,上界分别设为0.5和2 g·cm-3,将地下剖分为40×40×30的立方体,反演结果的中心切片如图 8所示.图 8a和8b为物性上界设置为0.5 g·cm-3时的反演结果,图 8c和8d为物性上界设置为2 g·cm-3时的反演结果.可以看出,当物性上界比真实值小时,反演结果的体积就比真实场源的体积要大;反之,当物性上界比真实值大时,反演结果的体积就比真实场源的体积要小.上述观察说明可靠的物性信息对于反演结果的体积估计是比较重要的.因此,在基于重力数据反演的矿产储量估计中,精确的物性信息将会提高储量估计的准确性.此外,在物性信息不准确的情况下,反演结果依然保持了较高的深部分辨率.相比于L2范数反演,场源的一些关键构造信息,如中心位置、构造方向等,依然得到了良好的恢复.
|
图 8 倾斜薄板模型不同物性上界的反演结果中心切片图 (a—b)物性上界设置为0.5 g·cm-3时的反演结果;(c—d)物性上界设置为2 g·cm-3时的反演结果.黑框代表了真实模型的位置. Fig. 8 Inversion results of the gravity anomaly produced by the thin dipping slab model by using different upper bounds (a—b) The inversion result with an upper bound of 0.5 g·cm-3; (c—d) The inversion result with an upper bound of 2 g·cm-3. The position of the true model is indicated by the black lines. |
前述组合块体模型中的两个块体水平距离较远(200 m),场源之间的相互干扰较小.我们将两个块体的水平距离拉近(0 m),且考虑两个块体的密度均为正和一正一负两种不同的情况,来试验不同类型的干扰场源对反演结果的影响.
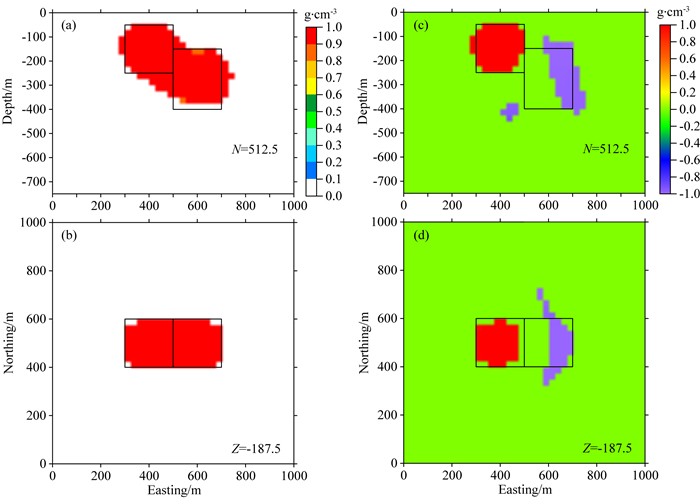
为了简单起见,两种情况的重力数据不再展示.这里,假设物性上、下界均已知.图 9a和9b为两个块体密度均为正时的反演结果,可以看出,尽管存在部分冗余构造,但浅部和深部两个块体都得到了较好的成像.图 9c和9d为两个块体密度为一正一负时的反演结果,可以看出,此时浅部块体的成像效果依然较好,而深部块体的成像效果较差.产生上述现象的原因可能是密度符号相同的场源产生的数据相互叠加,两者的信息均得到的保留,而密度符号不同的场源产生的数据相互抵消,两者的信息存在部分损失,且深部块体的信息损失更大.上述试验表明,当场源的规模相近时,若叠加数据由纯正密度场源产生时,埋藏较深和较浅的场源的成像效果可能相当;若叠加数据由正、负密度场源产生时,埋藏深的场源的成像效果可能相对较差.
|
图 9 不同组合块体模型重力数据的反演结果切片图 (a—b)两个块体密度均为正值时的反演结果; (c—d)两个块体密度一正一负时的反演结果.黑框代表了真实模型的位置. Fig. 9 Inversion results of gravity anomalies produced by different models composed of two rectangular prisms (a—b) The inversion result of the gravity anomaly produced by the model composed of two positive prisms; (c—d) The inversion result of the gravity anomaly produced by the model composed of a positive prism and a negative prism. The position of the true model is indicated by the black lines. |
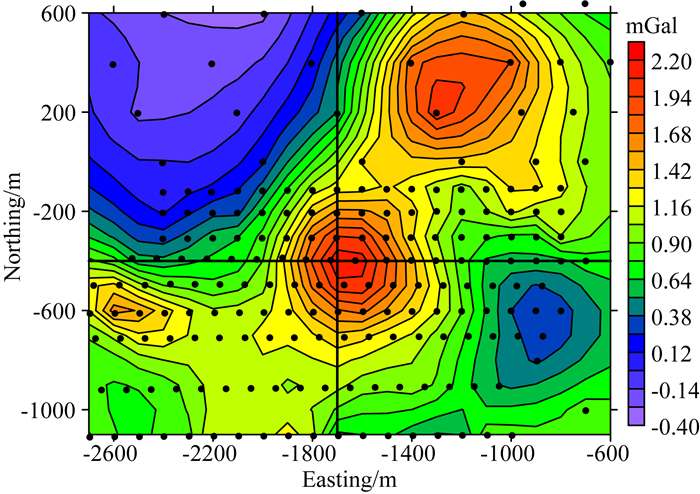
将本文方法应用到墨西哥萨卡特卡斯州圣尼古拉斯硫化物铜锌矿区重力数据反演.该矿床所在区域的主岩为铁镁质和长英质的火山岩,与围岩(2.8 g·cm-3)相比,块状硫化物表现为高密度(4.2 g·cm-3).对于该区域的重力数据反演,前人已经做了很多工作(Phillips,2001;Lelièvre and Oldenburg, 2009),因此,本例主要用于验证方法在实际数据反演中的有效性.测点数据共计198个,分布不均匀.我们将其网格化为22×18的网格数据,网格间距为100 m,网格化以后的剩余重力异常见图 10.
|
图 10 圣尼古拉斯硫化物铜锌矿区剩余重力数据(两条互相垂直的黑线代表了已知地质剖面的位置) Fig. 10 The gravity anomaly of San Nicolas massive sulfide copper-zinc deposit (The two orthogonal lines indicate the positions of known geological sections) |
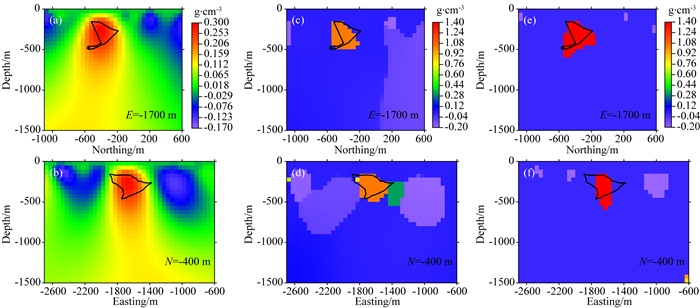
为了说明不同方法在实际数据反演中的效果与特点,我们利用三种方法对图 10所示剩余重力数据进行反演,物性上、下界分别设置为1.4和-0.2 g·cm-3,模型区域剖分为42×34×30的立方体单元,与已知地质剖面位置相同的反演结果切片图如图 11所示.图 11a和11b为物性上下界约束L2范数的反演结果,反演结果中存在大量冗余构造,难以反映场源的复杂形状.由反演结果的物性分布(-0.17~0.3 g·cm-3)可知,反演结果中的极大值和极小值均未达到物性上、下界,此时的物性上、下界约束实际上均为无效约束.图 11c和11d为物性上下界约束全变分(即极小化模型梯度的L1范数)反演结果,反演结果表现出分段常值的特性,边界明显且冗余构造较少.图 11e和11f为物性上下界约束Lp范数的反演结果,其中p值设置为0.此时已知密度信息得到较好利用,反演结果表现出三值特性.
|
图 11 圣尼古拉斯硫化物铜锌矿区重力数据不同方法的反演结果切片图 (a—b)物性上下界约束L2范数反演结果;(c—d)物性上下界约束全变分反演结果;(e—f)物性上下界约束Lp范数反演结果,其中p设置为0.物性上、下界分别设置为1.4和-0.2 g·cm-3.黑框代表了已知矿体的位置. Fig. 11 Inversion results of the gravity anomaly of San Nicolas massive sulfide copper-zinc deposit by using different methods (a—b) The result of bound-constrained L2-norm inversion; (c—d) The result of bound-constrained total varation inversion; (e—f) The result of bound-constrained Lp-norm inversion with p=0. The upper and lower bounds of both inversions are set to 1.4 and-0.2 g·cm-3, respectively. The position of the ore body is indicated by the black lines. |
重力数据反演具有固有的非唯一性,引入先验信息是减少反演非唯一性的常用手段.本文提出了一种重力数据稀疏反演方法.该方法通过求解物性上下界约束时的Lp范数优化问题来获得深度分辨率高、具有尖锐边界的反演结果.利用迭代重加权最小二乘技术,Lp范数优化问题被转化为了一系列的L2范数优化问题,每次物性上下界约束的L2范数优化问题可以利用内点法进行求解.为了更好的理解本文方法,我们揭示了本文方法与二值、三值反演算法的等价性,并分析了实际应用中需要注意的问题.最后,通过模型试验以及实际矿区数据反演验证了本文方法的有效性.此外,本文方法也可以扩展到井中重力或重力梯度数据的反演,具有良好的应用前景.
附录A 物性上下界约束重力数据最小二乘反演的内点法内点法是近年来求解大规模不等式约束优化问题中最流行的方法之一,其基本思想是将不等式约束优化问题转化为一系列等式约束优化问题进行求解.简单起见,首先将(8)式的符号进行简化,去掉代表第n次迭代的所有上标:

|
(A1) |
对于(A1)式,我们直接给出采用内点法优化的目标函数

|
(A2) |
其中,λ为障碍参数,φλ为障碍函数,其形式如下:
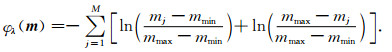
|
(A3) |
通过添加对数障碍项,不等式约束就隐含到了目标函数中,障碍项的作用是沿着模型可行域的边界形成一个障碍并防止模型在目标函数优化的过程中越界.对于固定的μ而言,该方法求解一系列非线性优化问题,在迭代过程中,λ不断减小,随着λ趋近于0,障碍项占总目标函数的比重不断减小,最终解也就趋近了(A1)式的解.将(3)、(9)、(A3)式代入(A2)式中,得到(A2)式的矩阵形式如下:

|
(A4) |
该式的优化包含两重迭代:其中外部迭代过程是根据不同的正则化参数μ和对应数据拟合差之间的关系确定与已知数据噪声水平相一致的μ,合适的μ值可以通过一维线性搜索确定,此处不再赘述;而内部迭代则是对于固定的μ值,求解对应的m,这里假设已知合适的μ值,而重点阐述内部迭代过程.采用牛顿法对(A4)式进行极小化,可以得到第k次迭代时目标函数下降方向的求解公式:
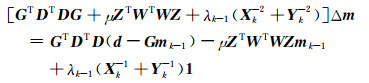
|
(A5) |
式中,Δm为目标函数的下降方向,Xk为对角矩阵,其主对角线上的元素为mk-1-mmin,Yk为对角矩阵,其主对角线上的元素为mk-1-mmax.1表示所有元素均为1的列向量.利用(A5)式,结合合适的迭代步长选择以及障碍参数更新策略,即可迭代求解最终结果.这里,我们依旧采用Li和Oldenburg(2003)的方法.对于固定的μ值,详细的迭代算法如下:
初始化:m0=0.001,λ0=φp(m0)/φλ(m0),k=1.
重复:
(1) 由mk-1生成Xk和Yk.
(2) 采用预处理共轭梯度法求解(A5)式得到Δm.
(3) mk←mk-1+γβΔm,其中γ=0.925,
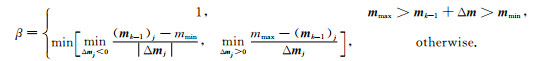
|
(4) λk←[1-min(β, γ)]λk-1.
(5) k←k+1.
直到收敛.
上述算法的解释及方法的原理可以参考Li和Oldenburg(2003)以及Nocedal和Wright(2006).当障碍函数充分小,障碍项对总目标函数的贡献很小的时候,迭代停止.我们在实际编程中通常设置三个附加准则来保证迭代成功,一是目标函数的改变量小于1%,二是障碍项与总目标函数的比值小于1%,三是达到预先设置的最大迭代次数.
Aster R C, Borchers B, Thurber C H. 2005. Parameter Estimation and Inverse Problems. Boston, MA: Academic Press.
|
Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press.
|
Boulanger O, Chouteau M. 2001. Constraints in 3D gravity inversion. Geophysical Prospecting, 49(2): 265-280. DOI:10.1046/j.1365-2478.2001.00254.x |
Camacho A G, Montesinos F G, Vieira R. 2000. Gravity inversion by means of growing bodies. Geophysics, 65(1): 95-101. DOI:10.1190/1.1444729 |
Daubechies I, DeVore R, Fornasier M, et al. 2010. Iteratively reweighted least squares minimization for sparse recovery. Communications on Pure and Applied Mathematics, 63(1): 1-38. |
Farquharson C G. 2008. Constructing piecewise-constant models in multidimensional minimum-structure inversions. Geophysics, 73(1): K1-K9. DOI:10.1190/1.2816650 |
Guan Z N, Hou J S, Huang L P, et al. 1998. Inversion of gravity and magnetic anomalies using pseduo-BP neural network method and its application. Acta Geophysica Sinica (in Chinese), 41(2): 242-251. |
Holland P W, Welsch R E. 1977. Robust regression using iteratively reweighted least-squares. Communications in Statistics-Theory and Methods, 6(9): 813-827. DOI:10.1080/03610927708827533 |
Krahenbuhl R A, Li Y G. 2006. Inversion of gravity data using a binary formulation. Geophysical Journal International, 167(2): 543-556. DOI:10.1111/j.1365-246X.2006.03179.x |
Krahenbuhl R A, Li Y G. 2009. Hybrid optimization for lithologic inversion and time-lapse monitoring using a binary formulation. Geophysics, 74(6): I55-I65. DOI:10.1190/1.3242271 |
Last B J, Kubik K. 1983. Compact gravity inversion. Geophysics, 48(6): 713-721. DOI:10.1190/1.1441501 |
Lelièvre P G, Oldenburg D W. 2006. Magnetic forward modelling and inversion for high susceptibility. Geophysical Journal International, 166(1): 76-90. DOI:10.1111/j.1365-246X.2006.02964.x |
Lelièvre P G, Oldenburg D W. 2009. A comprehensive study of including structural orientation information in geophysical inversions. Geophysical Journal International, 178(2): 623-637. DOI:10.1111/j.1365-246X.2009.04188.x |
Lelièvre P G, Oldenburg D W, Williams N C. 2009. Integrating geological and geophysical data through advanced constrained inversions. Exploration Geophysics, 40(4): 334-341. DOI:10.1071/EG09012 |
Li W B, Lu W T, Qian J L, et al. 2017. A multiple level-set method for 3D inversion of magnetic data. Geophysics, 82(5): J61-J81. DOI:10.1190/geo2016-0530.1 |
Li Y G, Oldenburg D W. 1996. 3-D inversion of magnetic data. Geophysics, 61(2): 394-408. DOI:10.1190/1.1443968 |
Li Y G, Oldenburg D W. 1998. 3-D inversion of gravity data. Geophysics, 63(1): 109-119. DOI:10.1190/1.1444302 |
Li Y G, Oldenburg D W. 2003. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophysical Journal International, 152(2): 251-265. DOI:10.1046/j.1365-246X.2003.01766.x |
Li Z L, Yao C L, Zheng Y M, et al. 2018. 3D magnetic sparse inversion using an interior-point method. Geophysics, 83(3): 1-56. |
Liu S, Hu X Y, Liu T Y, et al. 2013. Magnetization vector imaging for borehole magnetic data based on magnitude magnetic anomaly. Geophysics, 78(6): D429-D444. DOI:10.1190/geo2012-0454.1 |
Liu S, Hu X Y, Xi Y F, et al. 2015. 2D sequential inversion of total magnitude and total magnetic anomaly data affected by remanent magnetization. Geophysics, 80(3): K1-K12. DOI:10.1190/geo2014-0019.1 |
Liu Y P, Wang Z W, Du X J, et al. 2013. 3D constrained inversion of gravity data based on the Extrapolation Tikhonov regularization algorithm. Chinese Journal of Geophysics (in Chinese), 56(5): 1650-1659. DOI:10.6038/cjg20130522 |
Lu W T, Qian J L. 2015. A local level-set method for 3D inversion of gravity-gradient data. Geophysics, 80(1): G35-G51. DOI:10.1190/geo2014-0188.1 |
Meng X H, Liu G F, Chen Z X, et al. 2012. 3-D gravity and magnetic inversion for physical properties based on residual anomaly correlation. Chinese Journal of Geophysics (in Chinese), 55(1): 304-309. DOI:10.6038/j.issn.0001-5733.2012.01.030 |
Menke W. 2012. Geophysical Data Analysis: Discrete Inverse Theory: MATLAB Edition. New York: Academic Press.
|
Nocedal J, Wright S. 2006. Numerical Optimization. New York: Springer.
|
Phillips N D. 2001. Geophysical inversion in an integrated exploration program: Examples from the San Nicolas deposit [Master's thesis]. Vancouver: University of British Columbia.
|
Portniaguine O, Zhdanov M S. 1999. Focusing geophysical inversion images. Geophysics, 64(3): 874-887. DOI:10.1190/1.1444596 |
Portniaguine O, Zhdanov M S. 2002. 3D magnetic inversion with data compression and image focusing. Geophysics, 67(5): 1532-1541. DOI:10.1190/1.1512749 |
Rao B D, Kreutz-Delgado K. 1999. An affine scaling methodology for best basis selection. IEEE Transactions on signal processing, 47(1): 187-200. DOI:10.1109/78.738251 |
Uieda L, Barbosa V C F. 2012. Robust 3D gravity gradient inversion by planting anomalous densities. Geophysics, 77(4): G55-G66. DOI:10.1190/geo2011-0388.1 |
Van Zon T, Roy-Chowdhury K. 2006. Structural inversion of gravity data using linear programming. Geophysics, 71(3): J41-J50. DOI:10.1190/1.2197491 |
Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese Journal of Geophysics (in Chinese), 46(2): 252-258. |
Yao C L, Zheng Y M, Zhang Y W. 2007. 3-D gravity and magnetic inversion for physical properties using stochastic subspaces. Chinese Journal of Geophysics (in Chinese), 50(5): 1576-1583. |
管志宁, 侯俊胜, 黄临平, 等. 1998. 重磁异常反演的拟BP神经网络方法及其应用. 地球物理学报, 41(2): 242-251. DOI:10.3321/j.issn:0001-5733.1998.02.013 |
刘银萍, 王祝文, 杜晓娟, 等. 2013. 基于Extrapolation Tikhonov正则化算法的重力数据三维约束反演. 地球物理学报, 56(5): 1650-1659. DOI:10.6038/cjg20130522 |
孟小红, 刘国峰, 陈召曦, 等. 2012. 基于剩余异常相关成像的重磁物性反演方法. 地球物理学报, 55(1): 304-309. DOI:10.6038/j.issn.0001-5733.2012.01.030 |
姚长利, 郝天珧, 管志宁, 等. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
姚长利, 郑元满, 张聿文. 2007. 重磁异常三维物性反演随机子域法方法技术. 地球物理学报, 50(5): 1576-1583. DOI:10.3321/j.issn:0001-5733.2007.05.035 |
 2019, Vol. 62
2019, Vol. 62


