2. 智能技术与系统国家重点实验室, 北京 100084;
3. 北京信息科学与技术国家研究中心, 北京 100084;
4. 清华大学自动化系, 北京 100084;
5. 中国石化胜利油田物探研究院, 山东东营 257022
2. State Key Laboratory of Intelligent Technology and Systems, Tsinghua University, Beijing 100084, China;
3. Tsinghua University Beijing National Research Center for Information Science and Technology, Beijing 100084, China;
4. Department of Automation, Tsinghua University, Beijing 100084, China;
5. Shengli Oilfield Geophysical Research Institute of Sinopec, Dongying Shandong 257022, China
在地震勘探过程中, 受环境噪声影响, 地震数据通常含有很多随机噪声.随机噪声的存在影响地震数据的后续处理精度, 为此, 研究者们针对随机噪声压制提出了很多有效的算法, 主要包括空域去噪算法、变换域去噪算法、综合性去噪算法.对于空域去噪算法, Rudin等(1992)从最小化图像全变分(Total Variation, TV)角度提出一种基于偏微分方程的去噪算法.Gilboa等(2003)在此基础上又提出对纹理自适应的最小化全变分方法, 在噪声去除和纹理保持两者之间进行权衡.Bonar和Sacchi(2012)基于地震数据通常存在冗余结构的假设, 提出非局部均值去噪算法.该方法在地震数据中寻找结构相似的区域, 基于相似区块分组进行去噪, 达到良好的保边效果.对于变换域去噪算法, Canales(1984)根据同相轴的可预测性提出F-X反褶积去噪算法, 经过改进(Gulunay, 1986; Hornbostel, 1991), 该算法已成为地震信号去噪领域的常用算法.空域的结构相似性在变换域通常表现为低秩性.结合低秩性假设, 研究者们提出了基于奇异值分解的去噪算法, 根据噪声方差确定收缩阈值进行主成分提取(Freire and Ulrych, 1988;Lu, 2006).其他的变换域去噪算法也采用类似的阈值收缩算法, 包括curvelets变换(Hennenfent and Herrmann, 2006; 彭才等, 2008)、seislet变换(Fomel and Liu, 2010)、wavelet变换(Zhang and Ulrych, 2003; 刘鑫等, 2006; 汪金菊等, 2016).此外, 变换域去噪算法还包括基于词典学习的自适应基变换算法(Tang et al., 2012; Zhu et al., 2015; 邵婕等, 2016; Zhu et al., 2017; 程时俊等, 2018).作为一种数据驱动算法, 词典学习算法充分利用数据自身的特点进行去噪.综合性去噪算法采用空域、变换域相结合的方式, 在空域利用结构相似性进行聚类, 基于聚类结果进行变换以达到更好的低秩化效果(Dabov et al., 2007; Dong et al., 2013).
自2012年AlexNet(Krizhevsky et al., 2012)赢得ILSVRC(ImageNet Large-Scale Visual Recognition Challenge)以来, 神经网络逐渐成为诸多计算机科学行业的主流研究方向.各种高效的网络结构被陆续提出, 比如VGGNet(Simonyan and Zisserman, 2014)、U-Net(Ronneberger et al., 2015)、FCN(Shelhamer et al., 2014)、ResNet(He et al., 2016)、ShuffleNet(Zhang et al., 2017b)、SENet(Hu et al., 2017)、DenseNet(Huang et al., 2017)等.神经网络也被广泛应用到地震反演(Das et al., 2018)、断层检测(Xiong et al., 2018)、插值(Wang et al., 2018)等地震信号研究领域.在去噪领域, 较为常用的网络结构是DnCNN(Zhang et al., 2017a)和U-Net.Ma(2018)将DnCNN(Zhang et al., 2017a)用于地震数据去噪, 在无需对数据进行建模、无需人工选择参数的情况下达到了高质量的去噪效果.然而, 作为一种数据驱动的学习算法, DnCNN的推广性受到数据集结构特点、噪声分布的限制, 因此难以在实际数据中加以推广.Liu等(2018)提出了一种基于数据增广和U-Net的地震随机噪声压制方法, 使用人工合成数据集Pluto中的少量数据进行增广, 生成有标签数据集来训练网络, 在Sigsbee数据集上测试并取得了优异的去噪效果.该方法是对CNN推广性的有效探索, 但用人工合成数据训练的网络, 推广应用于实际数据时, 难以得到令人满意的结果.针对Liu等(2018)的方法应用于实际数据时所面临的问题, 本文提出一种有效的数据生成和增广方法, 实现一种基于CNN的去噪框架.我们利用目前已有的去噪方法先从实际地震数据中分别获得与实际干净数据具有相似纹理特征的估计干净数据, 以及与实际噪声概率分布相似的估计噪声, 然后进行数据增广生成训练样本集.人工合成数据和实际数据的实验表明:相较于F-X反褶积, BM3D和自适应频域滤波, 所提出的方法在人工合成数据和实际数据上都取得了更好的去噪性能.
此外, 本文采用神经网络可视化方法(Erhan et al., 2009; Mordvintsev et al., 2015)对CNN的去噪机理进行了探索.实验结果表明, 本文所采用的可视化算法能在一定程度上揭示网络每一层的学习内容.
1 方法原理本文提出一种基于数据增广的CNN训练框架.该框架主要包括数据增广过程和CNN训练过程.
1.1 CNN结构含随机噪声的地震数据可以表示为
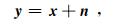
|
(1) |
其中, y表示含噪数据, x表示干净数据, n表示随机噪声.去噪算法的目标是尽可能精确地从含噪数据y中恢复出干净数据x.
神经网络处理过程可看作一个变换函数fW(·), 将数据从输入空间映射到输出空间(Zhang et al., 2018).其中, W表示所有网络参数.训练过程采用残差学习方法, 通过网络学习输入数据对应的噪声n, 使得网络收敛过程更加平滑(Zhang et al., 2017a).同时采用L1范数, 使得回归过程对离群值更具鲁棒性.此外, 为进一步提高去噪效果, 在目标函数中对去噪结果加入TV约束项, 使用λ调控两个优化项之间的权重.网络训练过程的目标函数如下:
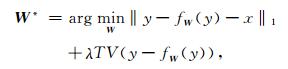
|
(2) |
其中, TV(·)表示TV约束项.
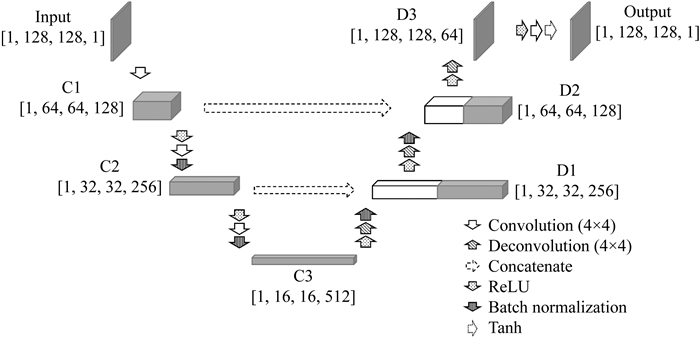
U-Net是一种广泛应用的端到端学习网络, 能够融合不同尺度的特征达到更好的学习效果.DnCNN结合残差学习和批归一化(Batch Normalization, BN), 构建了适用于去噪的神经网络.本文结合两者的优势构建网络结构.如图 1所示, 本文采用的网络结构包含一个编码过程和一个解码过程.编码过程采用三层堆叠的卷积结构, 卷积核大小设置为4×4, 卷积步长设置为2.其中, 步长取2的卷积层与步长为2的池化层效果类似(Springenberg et al., 2014), 两者均实现了降采样, 使网络在层数较浅的情况下能获得更大的感知域.每经过一个卷积操作, 网络中特征图(Feature Map)的长和宽减小为原来的1/2, 为充分保留有效特征, 设置通道数变为原来的两倍.与DnCNN相似, 我们在第2、3层卷积之后加入BN层.此外, 图 1中的“Input”层相当于公式(1)中的y, “Output”层相当于公式(1)中的n, 即通过神经网络学习输入信号中所含的噪声, 应用DnCNN中批归一化与残差学习相结合的方式, 获得更快的收敛过程和更好的去噪效果.从图 1可见, 编码过程包含C1、C2、C3层, 计算可得其感知域大小分别为4×4、10×10、22×22.对应地, 解码过程采用三层堆叠的反卷积结构, 分别表示为D1、D2、D3.每经过一个反卷积, 特征图的长和宽变为原来的两倍, 通道数变为原来的1/2, 实现编码、解码过程的结构对称.与U-Net相似, 我们在编码和解码对应层之间加入了两根跨接线, 使得网络能够有效地融合不同尺度的特征.此外, 反卷积过程容易产生棋盘效应(Odena et al., 2016), 因此本算法在D3层之后又加入一个卷积层以减弱棋盘效应.
|
图 1 去噪网络结构 Fig. 1 The structure of Denoising neural network |
对于合成数据, 我们能够得到干净数据, 并采用计算机模拟生成随机噪声.为使网络对噪声方差具有较好的容忍度, 我们对训练集添加不同方差水平的噪声.考虑同一数据上不同区域的信号强度是变化的, 在相同全局方差的情况下会有不同的局部信噪比(Signal-to-Noise Ratio, SNR), 我们根据局部区域的信号强度添加相应方差水平的加性高斯噪声, 取均值为0, 标准差计算方法如下:

|
(3) |
其中, σ表示噪声的标准差, abs(·)表示对区域xpart逐点求取绝对值, mean(·)表示求取均值.该式使用绝对值平均估计所选区域内的平均信号强度, 得到信号强弱的大致估计, γ取值范围根据经验得到.
其次, 我们对训练数据进行空间降采样、时间降采样、旋转变换、镜像变换、强度变换和裁剪, 以增加训练数据集的多样性.其中, 强度变换经验性地采用T1:x↦x3/4和T2:x↦x5/4.
1.3 实际数据增广策略对于实际数据, 由于缺乏真实的干净数据和噪声, 我们利用已有去噪方法来生成有标签的训练样本集.本文中, 我们采用了自适应频域滤波算法(Zhou et al., 2015)对实际数据体进行去噪, 将获得的去噪结果作为干净数据的近似, 并对去除的噪声进行进一步的有效信号消除来作为真实噪声的近似.图 2a为原始数据, 图 2c为自适应频域滤波算法的滤波结果, 可以看出, 滤波结果和真实的干净数据应该具有纹理相似性.考虑到实际噪声类型未知, 我们不再采用加性高斯噪声.我们首先提取自适应频域滤波算法去除的噪声, 如图 2b所示, 可以看到, 去除的噪声中存在残余的有效信号.因此, 我们使用高斯滤波、双边滤波(Chaudhury et al., 2011)来进一步消除噪声中的有效信号, 获得的提纯噪声数据如图 2d所示.通过上述步骤, 我们从实际地震数据中分别生成了与干净数据纹理相似的估计干净数据, 以及与实际噪声数据概率分布相近的估计噪声, 结合估计干净数据和估计噪声可得到有噪地震数据作为网络输入.最后, 我们采用与人工合成数据相同的数据增广方法来增加标签数据集的多样性.

|
图 2 实际数据预处理 (a)实际数据; (b)已有算法去除的噪声; (c)已有算法去噪结果; (d)对(b)的滤波结果. Fig. 2 Preprocess of real data (a) Real data; (b) and (c) The denoising result of traditional method; (d) The filtering result of (b). |
本文采用两种神经网络可视化方法, 分别为选择算法和基于梯度上升的迭代算法(Erhan et al., 2009).网络中每一个特征图对应一种结构, 随着网络深度的加深, 感知域的增大, 特征图对应的结构逐渐变得复杂.能够最大化特征图上激活值的输入结构代表了该特征图实际学习到的结构.选择算法从训练集中挑选使指定特征图激活值最大化的前N个样本, 对N个样本按照激活值加权, 得到该特征图学习到的纹理结构.基于梯度上升的迭代算法将输入图像当作变量, 最大化指定特征图的激活值, 迭代得到特征图实际学习到的内容, 对应的学习目标如下:

|
(4) |
其中, W*表示训练得到网络参数, hW*(·)表示指定特征层单元的激活值, y表示输入图像.我们所采用的梯度上升算法如下:
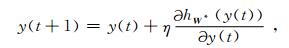
|
(5) |
其中, η表示学习率, t表示迭代次数.
我们通过以上两种方法可视化层C1、C2、C3、D1、D2、D3以及输出层的每个特征图.随着层数的加深, 可视化结果受棋盘格现象(Odena et al., 2016)和局部最优值的影响变大.为减弱层数深度导致的不良影响, 我们进一步将选择算法与基于梯度上升的迭代算法相结合, 以选择算法得到的加权图作为迭代算法的初始值.
2 数值算例本节我们在合成数据和实际数据上对算法的有效性进行测试.对于合成数据, 我们使用Pluto数据集的3个共偏移距道集来构造训练数据集, 增广后进行CNN训练, 使用Sigsbee数据集的共偏移距道集进行测试.训练过程所使用的参数值通过实验结果挑选得到, 能达到较好的收敛效果.设置训练初始学习率为2×10-4, 使用Adam算法(Kingma and Ba, 2014)优化学习目标.网络的输入输出大小均设置为128×128, 设置epoch为2000次, 每个epoch的迭代次数为1000次, 批大小(batch size)为1.网络大约在500次epoch时几乎收敛, 但实验结果发现进一步训练能使测试集去噪结果更优.对于实际数据, 我们采用F3(Netherlands Offshore F3 Block)数据集进行实验, 采用了自适应频域滤波算法(Zhou et al., 2015)对前20个纵测线进行滤波, 生成有标签数据进行增广, 形成训练集对网络进行训练, 剩余的纵测线作为测试集, 在60次epoch时即可取得较好的去噪效果.
对于可视化过程, 由于一个特征图上所有点经过相同的卷积过程得到, 因此其学习的结构相同, 我们选择每个特征图的中心点进行激活值最大化, 取该中心点对应的感知域作为该点表征的结构.选择算法设置N为6.基于梯度上升的迭代算法设置批大小为50, 迭代次数为2000, 从中选择使指定层激活值最大的前6张输入图像, 根据激活值加权得到初始化值.梯度上升阶段取迭代次数为400次.
2.1 合成数据测试我们对Sigsbee数据添加不同方差水平的噪声, 对每个方差水平进行20次去噪实验, 以输出去噪结果的平均SNR值作为评价指标.对比F-X反褶积算法和BM3D去噪算法, 我们得到表 1所示结果.相较于F-X反褶积算法, 我们的方法取得平均3.4 dB的提高, 相较于BM3D, 取得平均1.1 dB的提高.
|
|
表 1 不同噪声水平下的去噪图片SNR值对比(单位:dB) Table 1 SNR of denoising images with different input noise levels (Unit:dB) |
此外, 我们的算法采用了噪声学习和数据增广的方式训练网络以提升去噪效果.为证明本算法的有效性, 我们对比了信号学习和不进行数据增广的噪声学习方法的去噪结果, 如表 1所示, 本算法在不同噪声水平下均取得了更好的去噪效果.
F-X反褶积、BM3D、本文算法的去噪结果以及差剖面如图 3所示, 此处差剖面指无噪数据与去噪结果差值的绝对值.观察差剖面结果, 我们发现F-X反褶积在去噪时对有效信号的保持效果较差且去噪程度不够, 如图 3c和3d所示, 滤波结果中残留了较多噪声且差剖面有较明显的有效信号残留.从图 3f和图 3h可见, BM3D和本文算法的去噪残差中的有效信号相较于F-X反褶积算法有明显降低.此外, 观察图中黑框区域, F-X反褶积和BM3D对弱绕射信号的保护能力较差, 而本文算法以噪声作为学习目标, 对有效信号的损伤少, 能更好地保护弱信号.

|
图 3 Sigsbee数据去噪结果 (a)加噪数据; (b)干净数据; (c) F-X反褶积去噪结果; (d) F-X反褶积去噪差剖面; (e) BM3D去噪结果; (f) BM3D去噪差剖面; (g)本算法去噪结果; (h)本文算法去噪差剖面. Fig. 3 The denoising results of Sigsbee (a) Noisy data; (b) Clean data; (c) The denoising result of F-X deconvolution; (d) The noise data obtained by F-X deconvolution; (e) The denoising result of BM3D; (f) The noise data obtained by BM3D; (g) The denoising result of our method; (h) The noise data obtained by our method. |
从另一个角度, 我们绘制了去噪结果的SNR分布图, 根据像素点周围的3×3区域计算SNR值作为该像素点对应的SNR值, 结果如图 4所示.从中可见, F-X反褶积算法对原始有噪数据各个区域的SNR值提升都相对较小, BM3D对部分高信噪比同相轴的SNR值提升不足, 而本文算法无论对高信噪比区域还是低信噪比区域都有较明显的提升效果.

|
图 4 Sigsbee去噪结果的SNR分布图 (a)有噪数据; (b) F-X反褶积去噪; (c) BM3D去噪; (d)本算法去噪. Fig. 4 The SNR map of Sigsbee (a) Noisy input; (b) F-X deconvolution; (c) BM3D; (d) Our method. |
我们将本文算法应用到F3实际数据中进行去噪, 并和自适应频域滤波算法(Zhou et al., 2015)进行对比.图 5和图 6给出了(a)原始数据、(b)自适应频域滤波、(c)自适应频域滤波消除的噪声、(d)本文方法滤波结果和(e)本文方法滤波消除的噪声.从图 5和图 6可以看出, 相比于自适应频域滤波算法, 本文算法去噪效果更优.如图 5(c、e)方框和图 6(c、e)箭头所示, 自适应频域滤波算法去除的噪声中含有较多的有效信号残余, 而本文算法在去除噪声的同时几乎不损失有效信号.对比图 5(b、d), 本文算法对信号的保幅效果更好.另一方面, 如图 6方框所示, 原始数据中含有网状弱噪声, 自适应频域滤波算法能在一定程度上去除该噪声, 但仍有少量残余, 而本文算法在几乎完全去除了网状弱噪声且保留了轴的连续性, 得到了更好的去噪结果.需要指出的是, 本文的训练数据是通过自适应滤波算法生成的, 而实验结果表明由本文算法能获得优于自适应频域滤波算法的去噪效果, 这主要得益于本文算法中的数据增广方法.

|
图 5 F3数据去噪结果部分Ⅰ (a)原始数据; (b)自适应频域滤波算法去噪结果; (c)自适应频域滤波算法去除的噪声; (d)本文算法去噪结果; (e)本文算法去除的噪声. Fig. 5 The denoising results of F3, Part Ⅰ (a) Original data; (b) The denoising result of adaptive frequency domain filtering algorithm; (c) The noise obtained by adaptive frequency domain filtering algorithm; (d) The denoising result of our method; (e) The noise obtained by our method. |

|
图 6 F3数据去噪结果部分Ⅱ (a)原始数据; (b)自适应频域滤波算法去噪结果; (c)自适应频域滤波算法去除的噪声; (d)本文算法去噪结果; (e)本文算法去除的噪声. Fig. 6 The denoising results of F3, Part Ⅱ (a) Original data; (b) The denoising result of adaptive frequency domain filtering algorithm; (c) The noise obtained by adaptive frequency domain filtering algorithm; (d) The denoising result of our method; (e) The noise obtained by our method. |
本文采用选择算法和基于梯度上升的迭代算法最大化特征图的激活值.图 7显示了C2层256个特征图的可视化结果, C2层感知域大小为10×10.图 7a基于梯度上升算法得到.图 7c表示从训练集中挑选出使激活值最大化的前6个样本, 按激活值加权得到图 7b, 即为选择算法得到的结果.两种可视化方法的结果在大多数特征图上较为一致, 且由图 7可知, C2层学习到的特征是较为简单、底层的纹理特征.

|
图 7 C2层可视化结果 (a)梯度上升算法可视化; (b)选择算法可视化; (c)选择算法Top 6结果. Fig. 7 The visualization results of C2 (a) Gradient ascent algorithm; (b) Selection algorithm; (c) Top 6 of selection algorithm. |
随着网络深度的增大, 梯度上升算法引入更多棋盘格噪声.为减弱噪声和局部最优值的影响, 我们使用选择算法得到的特征结构初始化梯度上升算法, 得到C3层512个特征图的可视化结果如图 8所示.其中, 图 8中的黑色图片表示初始化图片无法有效地激活对应特征点, 使得梯度值为零, 无法进行梯度上升.C3层的感知域大小为22×22, 从图 8有效可视化图片可见, 网络在C3层学习到弧线、交叉线等更为复杂的结构.实验结果表明, 网络的学习目标虽然是噪声, 但网络内部的学习内容本质上是对信号和噪声的表达, 并通过不同的表达特征实现信号与噪声的分离.

|
图 8 C3层可视化结果 Fig. 8 The visualization result of C3 |
此外, 我们对比了学习噪声和学习信号的可视化结果, 如图 9所示.由于网络深层的可视化受噪声影响很大, 因此采用选择算法进行可视化.图 9a为学习噪声的输出层可视化结果, 16张图片分别表示16次重复实验的可视化结果, 从中可见, 输出层往往会对类似噪声的结构比较敏感.图 9b表示学习信号的可视化结果, 在学习信号的情况下, 输出层的敏感对象是多种信号结构的叠加.本文采用的方法在一定程度上能对网络的学习内容加以解释.

|
图 9 不同学习目标下输出层可视化结果 (a)学习噪声; (b)学习信号. Fig. 9 The visualization results of output layer with different learning target (a) Noise as target; (b) Signal as target. |
本文提出的基于数据增广和CNN的去噪算法能够有效应用于合成数据、实际数据去噪.相较于F-X反褶积、BM3D和自适应滤波算法, 本文算法既能有效去除噪声, 又能更好地保护有效信号.这一方面得益于CNN强大的特征表达能力, 本文使用的U-Net网络采用非线性编码、解码结构, 通过跨线融合不同尺度的特征, 使得网络能有效回归训练目标.另一方面, 本文所提出的数据集增广方法为CNN提供了丰富、可靠的训练数据.结合对神经网络可视化结果的分析, 本文的主要结论与相关讨论如下:
(1) 基于神经网络的端到端去噪算法能有效地从数据中学习地震数据的纹理特征, 根据神经网络可视化结果可知, 网络浅层表达较为简单、底层次的纹理特征, 深层表达更为复杂、全局的特征.
(2) 数据增广方法能够增强网络的推广性.作为一种基于数据驱动的学习算法, 增强网络推广性的一种直接方法是增加训练数据集的多样性.
(3) 对于实际地震数据去噪问题, 利用目前已有的去噪方法先从实际地震数据中分别获得和未知干净数据具有相似纹理特征的估计干净数据, 以及与实际噪声概率分布相似的估计噪声, 通过数据增广形成训练样本集, 可以有效解决基于神经网络去噪方法应用于实际地震数据中所面临的训练样本集缺少问题.
(4) 神经网络可视化的研究结果一定程度上显示了网络各层学习到的内容, 但实验发现网络深层可视化结果受噪声影响较大, 使得本文的可视化方法就完全解释网络学习内容而言还有一定距离, 需要进一步研究.
Bonar D, Sacchi M. 2012. Denoising seismic data using the nonlocal means algorithm. Geophysics, 77(1): A5-A8. DOI:10.1190/geo2011-0235.1 |
Canales L L. 1984. Random noise reduction.//54th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, doi: 10.1190/1.1894168.
|
Chaudhury K N, Sage D, Unser M. 2011. Fast O(1) bilateral filtering using trigonometric range kernels. IEEE Transactions on Image Processing, 20(12): 3376-3382. DOI:10.1109/TIP.2011.2159234 |
Cheng S J, Han L G, Yu J L, et al. 2018. Seismic data denoising based on improved K-SVD dictionary learning method. Global Geology (in Chinese), 37(2): 627-635. |
Dabov K, Foi A, Katkovnik V, et al. 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 16(8): 2080-2095. DOI:10.1109/TIP.2007.901238 |
Das V, Pollack A, Wollner U, et al. 2018. Convolutional neural network for seismic impedance inversion.//88th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 2071-2075.
|
Dong W S, Shi G M, Li X. 2013. Nonlocal image restoration with bilateral variance estimation:A low-rank approach. IEEE Transactions on Image Processing, 22(2): 700-711. DOI:10.1109/TIP.2012.2221729 |
Erhan D, Bengio Y, Courville A, et al. 2009. Visualizing higher-layer features of a deep network. Technical report 1341, University of Montreal, 1341(3): 1. |
Fomel S, Liu Y. 2010. Seislet transform and seislet frame. Geophysics, 75(3). |
Freire S L, Ulrych T J. 1988. Application of singular value decomposition to vertical seismic profiling. Geophysics, 53(6): 778-785. DOI:10.1190/1.1442513 |
Gilboa G, Zeevi Y Y, Sochen N. 2003. Texture preserving variational denoising using an adaptive fidelity term.//Proceedings of the VLSM. Nice, France.
|
Gulunay N. 1986. FXDECON and complex Wiener prediction filter.//56th Ann. Internat Mtg., Soc. Expi. Geophys., Expanded Abstracts, doi: 10.1190/1.1893128.
|
He K M, Zhang X Y, Ren S Q, et al. 2016. Deep residual learning for image recognition.//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA: IEEE770-778, doi: 10.1109/CVPR.2016.90.
|
Hennenfent G, Herrmann F J. 2006. Seismic denoising with nonuniformly sampled curvelets. Computing in Science & Engineering, 8(3): 16-25. DOI:10.1109/MCSE.2006.49 |
Hornbostel S C. 1991. Spatial prediction filtering in the t-x and f-x domains. Geophysics, 56(12): 2019-2026. DOI:10.1190/1.1443014 |
Hu J, Shen L, Albanie S, et al. 2017. Squeeze-and-excitation networks. arXiv preprint arXiv: 1709.01507.
|
Huang G, Liu Z, Van Der Maaten L, et al. 2017. Densely connected convolutional networks.//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA: IEEE, doi: 10.1109/CVPR.2017.243.
|
Kingma D P, Ba J. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv: 1412.6980.
|
Krizhevsky A, Sutskever I, Hinton G E. 2012. Imagenet classification with deep convolutional neural networks.//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., doi: 10.1145/3065386.
|
Liu J, Lu W, Zhang P. 2018. Random noise attenuation using convolutional neural networks.//88th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts.
|
Liu X, He Z H, Huang D J. 2006. Seismic data denoising research based on wavelet transform. Petroleum Geophysics (in Chinese), 4(4): 15-18. |
Lu W K. 2006. Adaptive noise attenuation of seismic images based on singular value decomposition and texture direction detection. Journal of Geophysics and Engineering, 3(1): 28-34. DOI:10.1088/1742-2132/3/1/004 |
Ma J. 2018. Deep learning for attenuating random and coherence noise simultaneously.//88th Ann. Internat Mtg., Soc. Expi. Geophys., Expanded Abstracts.
|
Mordvintsev A, Olah C, Tyka M. 2015. Inceptionism:Going deeper into neural networks. Google Research Blog. |
Odena A, Dumoulin V, Olah C. 2016. Deconvolution and checkerboard artifacts. Distill. DOI:10.23915/distill |
Peng C, Chang Z, Zhu S J. 2008. Noise elimination method based on curvelet transform. Geophysical Prospecting for Petroleum (in Chinese), 47(5): 461-464. DOI:10.3969/j.issn.1000-1441.2008.05.006 |
Ronneberger O, Fischer P, Brox T. 2015. U-net: Convolutional networks for biomedical image segmentation.//International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany: Springer.
|
Rudin L I, Osher S, Fatemi E. 1992. Nonlinear total variation based noise removal algorithms. Physica D:Nonlinear Phenomena, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
Shao J, Sun C Y, Tang J, et al. 2016. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain. Oil Geophysical Prospecting (in Chinese), 51(2): 254-260. DOI:10.13810/j.cnki.issn.1000-7210.2016.02.007 |
Shelhamer E, Long J, Darrell T. 2014. Fully convolutional networks for semantic segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39(4): 640-651. DOI:10.1109/TPAMI.2016.2572683 |
Simonyan K, Zisserman A. 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv: 1409.1556.
|
Springenberg J T, Dosovitskiy A, Brox T, et al. 2014. Striving for simplicity: The all convolutional net. arXiv preprint arXiv: 1412.6806.
|
Tang G, Ma J W, Yang H Z. 2012. Seismic data denoising based on learning-type overcomplete dictionaries. Applied Geophysics, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
Wang B, Zhang N, Lu W, et al. 2018. Deep learning based seismic data interpolation:A preliminary result. Geophysics, 84(1): 11-20. |
Wang J J, Yuan L, Liu W R, et al. 2016. Dual-tree complex wavelet domain bivariate method for seismic signal random noise attenuation. Chinese Journal of Geophysics (in Chinese), 59(8): 3046-3055. DOI:10.6038/cjg20160827 |
Xiong W, Ji X, Ma Y, et al. 2018. Seismic fault detection with convolutional neural network. Geophysics, 83(5): O97-O103. DOI:10.1190/geo2017-0666.1 |
Zhang K, Zuo W M, Chen Y J, et al. 2017a. Beyond a gaussian denoiser:Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
Zhang K, Zuo W M, Zhang L. 2018. FFDnet:Toward a fast and flexible solution for CNN-based image denoising. IEEE Transactions on Image Processing, 27(9): 4608-4622. DOI:10.1109/TIP.2018.2839891 |
Zhang R F, Ulrych T J. 2003. Physical wavelet frame denoising. Geophysics, 68(1): 225-231. DOI:10.1190/1.1543209 |
Zhang X Y, Zhou X Y, Lin M X, et al. 2017b. Shufflenet: An extremely efficient convolutional neural network for mobile devices. arXiv preprint arXiv: 1707.01083.
|
Zhou J X, Lu W K, He J W, et al. 2015. A data-dependent fourier filter based on image segmentation for random seismic noise attenuation. Journal of Applied Geophysics, 114: 224-231. DOI:10.1016/j.jappgeo.2015.01.020 |
Zhu L C, Liu E T, McClellan J H. 2015. Seismic data denoising through multiscale and sparsity-promoting dictionary learning. Geophysics, 80(6): WD45-WD57. DOI:10.1190/geo2015-0047.1 |
Zhu L C, Liu E T, McClellan J H. 2017. Joint seismic data denoising and interpolation with double-sparsity dictionary learning. Journal of Geophysics and Engineering, 14(4): 802-810. DOI:10.1088/1742-2140/aa6491 |
程时俊, 韩立国, 于江龙, 等. 2018. 基于改进K-SVD字典学习方法的地震数据去噪. 世界地质, 37(2): 627-635. DOI:10.3969/j.issn.1004-5589.2018.02.030 |
刘鑫, 贺振华, 黄德济. 2006. 基于小波变换的地震资料去噪处理研究. 油气地球物理, 4(4): 15-18. |
彭才, 常智, 朱仕军. 2008. 基于曲波变换的地震数据去噪方法. 石油物探, 47(5): 461-464. DOI:10.3969/j.issn.1000-1441.2008.05.006 |
邵婕, 孙成禹, 唐杰, 等. 2016. 基于字典训练的小波域稀疏表示微地震去噪方法. 石油地球物理勘探, 51(2): 254-260. DOI:10.13810/j.cnki.issn.1000-7210.2016.02.007 |
汪金菊, 袁力, 刘婉如, 等. 2016. 地震信号随机噪声压制的双树复小波域双变量方法. 地球物理学报, 59(8): 3046-3055. DOI:10.6038/cjg20160827 |
 2019, Vol. 62
2019, Vol. 62


