2. 成都理工大学地球物理学院, 成都 610059;
3. 中海油研究总院有限责任公司, 北京 100027
2. School of Geophysics, Chengdu University of Technology, Chengdu 610059, China;
3. CNOOC Research Institute Co. Ltd., Beijing 100027, China
地震勘探中通常采集到的地震记录往往伴随有随机噪声的干扰, 这大大降低了地震数据的质量, 增加了后续的数据处理与解释的难度.在实际研究中, 提出了许多压制随机噪声干扰的算法(王典等, 2006), 而当前被大量应用的都是基于模型驱动方式的传统去噪方法, 如频率域滤波法、F-K滤波法(李立超, 2014)、小波变换(Jacques et al., 2011; Kaplan et al., 2009)、曲波变换法(Hennenfent and Herrmann, 2006; Ma and Plonka, 2011), 这些方法都是仅仅针对单一轴进行去噪, 呈现断层、拐角处的连续性较差.
目前基于数据驱动的字典学习去噪方式可以有效解决传统去噪的这一问题, 字典学习假设信号数据可以由一个过度完备字典的几个元素表示, 通过概率优化的方式求解这几个元素的最小值来进行信号的去噪.较多学者率先从单一固定字典如DCT字典(Deka and Baishnab, 2012)、Gabor字典(苏金善和栾雪琴, 2008)出发用于固定特性的信号去噪, 随后提出了自适应学习型完备字典(Olshausen and Millman, 2000)与K-SVD算法, 并在基于分解补丁、反复学习的思想下提出了目前最新的在线字典学习算法(Mairal et al., 2009).由于在线字典学习是数据驱动方式下的去噪, 它没有传统去噪方法针对某一特定轴或某些特定信号才能进行去噪的烦恼, 但在线字典学习去噪算法也有着自己的不足, 2012年唐刚将学习型完备字典应用到了地震信号去噪当中去(Tang et al., 2012), 2014年, Beckouche与Ma将在线字典的思想运用到地震信号去噪当中(Beckouche and Ma, 2014), 他们在面对实际较为复杂的地震数据时, 去噪结果虽然不错但都还有着难以去除的一些噪声, 这些噪声往往是分布较为集中且能量较强, 基于稀疏表示的在线字典学习算法在理论上对这种噪声无能为力.
为了解决在线字典学习去噪在面对实际数据时遇到这一类噪声的问题, 本文提出了基于模型驱动约束方式下的在线字典学习去噪算法, 即先通过传统去噪算法得到一个较为优良的学习样本, 在构建字典的时候将该样本进行学习后再进行求解稀疏解的去噪过程, 这样既可以得到传统去噪方式去除大能量噪声的优点又能避开传统去噪面对实际地质构造会产生不连续性的缺点, 充分利用模型约束再对数据本身的稀疏性进行挑选, 进而得到一个较为完美的去噪结果.本文先通过在理论模型上对模型约束下的在线字典学习去噪和单独使用在线字典学习去噪、传统小波变换去噪进行了对比, 表明在线字典学习去噪远优于传统时频域去噪, 模型约束可以得到更好的结果, 并且以理论模型的样本差异实验作为基础, 接着再针对实际数据的去噪过程中, 运用本文提出的基于模型驱动约束方式下的在线字典学习去噪算法完美克服了单独使用在线字典学习去噪会产生无法去除噪声的困难.
1 在线字典学习方法原理人工智能下的在线字典学习方法以数据驱动方式, 反复进行学习构建字典方式, 求得信号的稀疏性解以实现对信号的去噪.
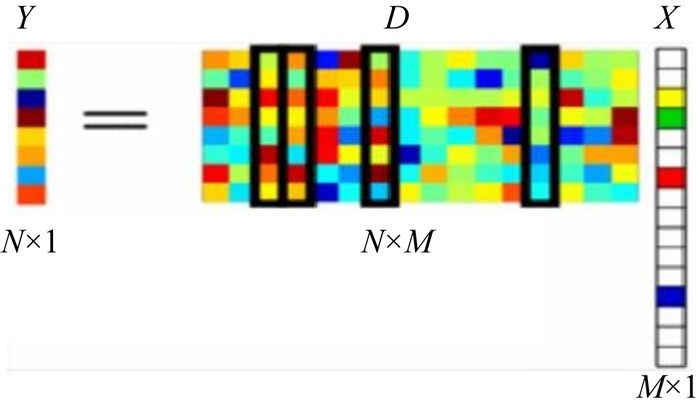
1.1 在线字典学习方法字典学习又称稀疏编码, 或者叫求解稀疏表示, 指的是信号数据可以由一个过度完备字典的几个元素表示.即将信号Y用字典D和稀疏编码X来表示, 示意图如图 1.
|
图 1 字典学习问题图解 Fig. 1 Dictionary learning problem illustration |
图 1中Y表示信号, D表示字典, X为稀疏编码, 当M=N时, 该字典是完备的; 当M>N时, 则该字典中的原子线性相关, 属于超完备字典(许德鑫, 2016).超完备冗余字典一般可以写为下面的数学形式:
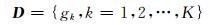
|
(1) |
字典中的元素是张成整个希尔伯特向量空间H的单位矢量, 且K»N, D为字典, 集合中的所有元素表示字典中的原子.
经典字典学习问题中有这样的表述(Olshausen, 1997; Aharon et al., 2006), 对于一个有限的信号训练集X=[x1, …, xn], 其中X∈Rm×n并且优化这样一个经验成本函数:

|
(2) |
其中, D表示字典并且D∈Rm×n, 每列表示基向量, 如果要使D表示合适的信号x, 则损失函数l(x, D)应该足够小.通常样本数量n较大, 而信号维数m较小.但是也存在k«n, 并且每个信号在其表示中仅使用字典D中的几个元素的情况.
将l(x, D)定义为l1范数的求解稀疏编码最优解问题:
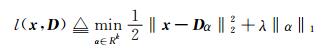
|
(3) |
其中, λ是正则化参数.可以知道l1范数能使α获得更好的稀疏性, 并且λ的值和‖α‖0的稀疏性之间没有任何联系.
为了防止D被任意地扩大(这将导致α的任意小值), 通常将其列(dj)kj=1限制为具有小于或等于1的l2范数.调用矩阵C的凸集来验证这个约束:

|
(4) |
注意到最小化经验成本fn(D)的问题对于D而言并不是凸的, 它可以被重新写成一个关于字典D和稀疏分解系数α=[α1, …, αn]联合优化问题:
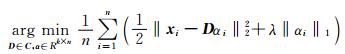
|
(5) |
虽然这样联合起来并不是凸的, 但当一个变量固定的时候, 相对于两个变量D和α中的每一个都是凸的了.
然而, 学习全尺寸数据字典原子在计算上不易处理, 因为它需要大量的训练样本, 并且每个维度的原子都要被学习.受过训练的字典也会太大, 以至于不能在实践中使用, 因为过度完备字典包含的原子比其维数都多.基于补丁的方法可以克服这个限制(Aharon et al., 2006).数据被分成小块, 分别去噪.因此, 学习问题变成了下面一个最优化问题:
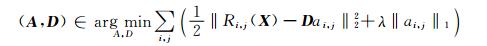
|
(6) |
其中A和D是被计算的稀疏系数矩阵和字典, X是训练数据, Ri, j是位置(i, j)处提取的补丁.A=(ai, j)i, j是稀疏编码矩阵, 此中ai, j是字典中Ri, j(X)的稀疏分解, λ是在所学字典中数据表示形式的数据保真度和稀疏性之间平衡的参数, 即稀疏控制参数.值得注意的是, (6)式中的最小化优化函数前一项
图 2为在线字典学习算法.假设训练集的样本都是独立同分布并且服从p(x)分布, 在内部循环中一次抽取一个样本xt, 就像随机梯度下降算法一样, 并交替使用经典的计算稀疏编码系数的方法来计算xt, 同时分解上一次迭代获得的字典Dt-1来求得αt, 通过字典的逐步更新, 新字典Dt将会由一个最小化的函数C计算得到
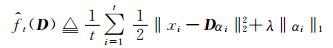
|
(7) |

|
图 2 在线字典学习算法 Fig. 2 Online dictionary learning algorithm |
在算法的前几个步骤中计算稀疏系数αi.这样做有两点好处:
(1) 二次函数f聚合了在算法的前几个步骤中计算出的信息, 即向量a, 并且很容易知道其从上面的公式经验成本f上限.
(2) 知道其f的前后迭代很相近, 因此字典D的迭代也很相近.
1.2.2 字典更新更新字典的算法使用块坐标下降和热重启技术, 其主要优点之一是它没有参数, 并且不需要任何学习速率的调整, 但这在约束优化设置中可能十分困难.具体地说, 图 3为字典更新算法, 算法使用一些简单的代数方式按顺序更新字典D的每列.在实践中, 由于向量αi是稀疏的, 矩阵A的系数通常集中在对角线上, 这使得块坐标下降效率更高, 迭代很快收敛.

|
图 3 字典更新算法 Fig. 3 Dictionary update algorithm |
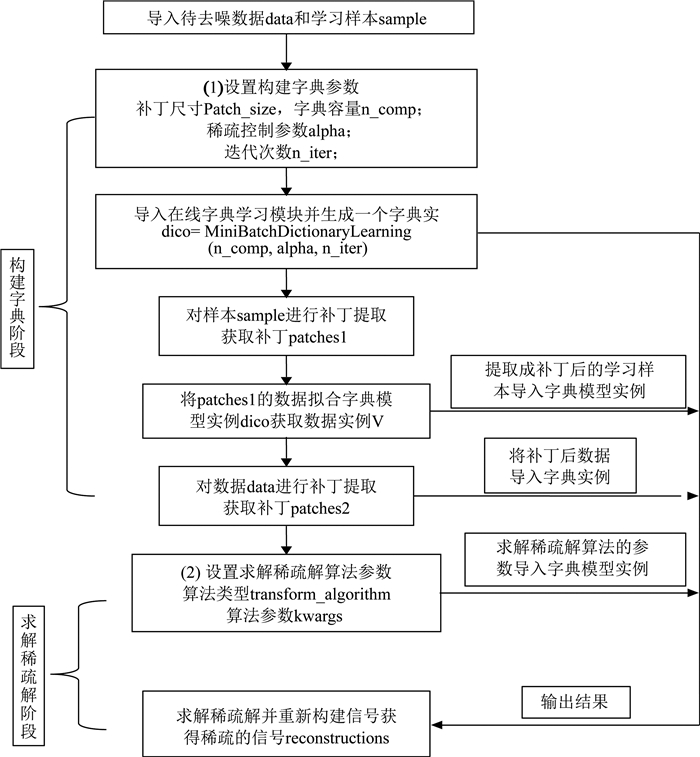
去噪或压制噪声的目的是为了突出有效信号, 提高信噪比, 在线字典学习可压制或消除强、弱随机噪声, 并在模型约束下, 可压制或消除相干噪声.图 4是在线字典学习法去噪处理流程图.由图 4可看出, 在线字典学习去噪处理分为两个阶段, 即构建字典阶段和求解稀疏解阶段.
|
图 4 在线字典学习法去噪处理流程 Fig. 4 Online dictionary learning method denoising process |
在线字典学习中参数包括字典构建参数设置和求解稀疏解参数设置.表 1给出了构建字典参数方案.
|
|
表 1 构建字典参数 Table 1 The parameters of dictionary construction |
由表 1可看出, 在构建字典时, 值得注意的是补丁尺寸m和稀疏控制参数λ的选择, 补丁尺寸大小的选择决定了构建字典和求解稀疏解的时间和原子特征的多少, 补丁大小一般由数据的大小决定, 数据越大, 特征越复杂, 则补丁尺寸越大.对应的稀疏控制参数λ这里给出一个经验性的值.
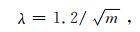
|
(8) |
式中
表 2给出了求解稀疏解算法的参数设置.由表 2可看出, 在求解稀疏解时, 其使用的算法(表 2中LARS算法和OMP算法)可对遍历的原子数(表 2中为1、2和5)进行调试和调整, 以获得最佳的算法和参数.在这里, 根据LARS算法和OMP算法的特性得到了A方案(表 1)的最佳搭配遍历时原子数分别为5和1.
|
|
表 2 求解稀疏解算法 Table 2 Solving the sparse solution algorithm |
为了让式(6)中整个目标优化函数f= 

|
图 5 数据驱动模式与模型驱动模式的结合图 Fig. 5 Combination of data driven mode and model driven mode |
在线字典学习去噪应用中, 分别对理论模型所形成的含噪声的合成纪录和实际地震数据进行了去噪处理, 以证明在线字典学习的可行性和有效性, 以及去噪效果.模型包含了楔形模型和多层模型(两层以上), 实际地震数据为海洋地震剖面.为提高实际地震数据去噪效果, 还采用了数据驱动与模型驱动相结合技术进行了去噪处理, 获得了高信噪比的地震剖面.
在线字典学习去噪实验采用信噪比来作为参考(程时俊等, 2018):
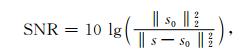
|
(9) |
其中, s0为去除随机噪声后的数据, s为原始数据.
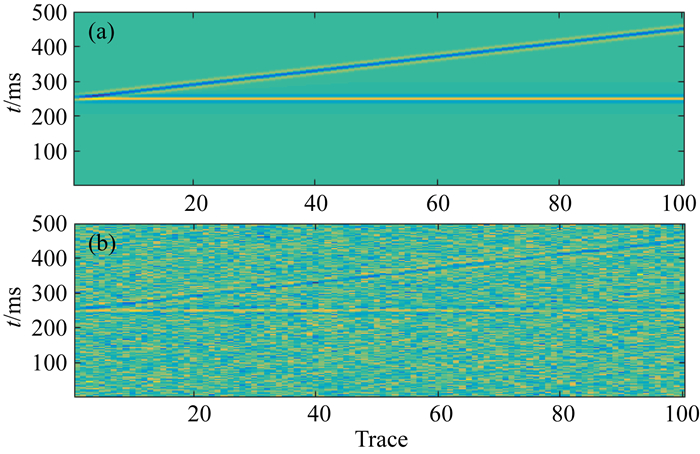
3.1 二维楔形模型弱信号时的去噪效果分析图 6为楔形模型合成纪录和含噪声剖面.楔形模型的参数为100道, 每道长500 ms, 采样间隔为1 ms, 采样点数为500个.添加3倍的随机噪声后SNR=-9.7143.
|
图 6 楔形模型合成地震记录(a)和含噪后合成地震记录(b) Fig. 6 Wedge model synthetic seismic recording (a) and post-noise recording (b) |
在去噪处理时, 模型约束即使用原始不带噪声模型数据进行学习构建字典后再求解稀疏解, 而单纯的在线字典学习则使用加噪后的原始数据进行.应用表 1中的A方案构建字典进行处理, 获得如图 7所示的剖面.为了凸显剖面效果, 图 7中的6幅图均是图 6模型中的部分截取, 第一行的(a)(c)(e)是小波变换、单独使用在线字典学习和模型约束下的在线字典学习三种算法的去噪效果, 而第二行的(b)(d)(f)则是其对应的去噪残差.在添加了3倍噪声的弱信号情况下, 从第二行的去噪残差中可以看得出小波变换和单独使用在线字典学习的去噪效果都不是特别理想, 但基于模型约束下的在线字典学习去噪残差则十分完美, 仅仅只有一点随机噪声的残差存在.不同去噪方法对信噪比SNR=-9.7143的楔形模型形成的合成纪录去噪后的剖面的信噪比如表 3所示.由表 3可知, 模型约束在线字典方法对信噪比的提升最大, 远远领先其他两种算法, 能够获得高品质的剖面.

|
图 7 楔形模型弱信号情况下不同算法去噪结果与去噪残差剖面图对比 (a)小波变换去噪结果; (b)小波变换去噪残差; (c)单独使用在线字典学习去噪结果; (d)单独使用在线字典学习去噪残差; (e)模型约束下的在线字典学习去噪结果; (f)模型约束下的在线字典学习去噪残差. Fig. 7 Comparison of denoising results of different algorithms and denoising residue profiles for weak signals in wedge models (a) Wavelet transform denoising results; (b) Wavelet transform denoising residuals; (c) Using online dictionary to learn denoising results; (d) Using online dictionary to learn denoising residuals; (e) Model constraint Online dictionary learning denoising results; (f) Online dictionary learning denoising residuals under model constraints. |
|
|
表 3 楔形模型的弱信号情况不同算法去噪信噪比对比 Table 3 Weak signal condition of wedge model comparison of different signal denoising SNR |
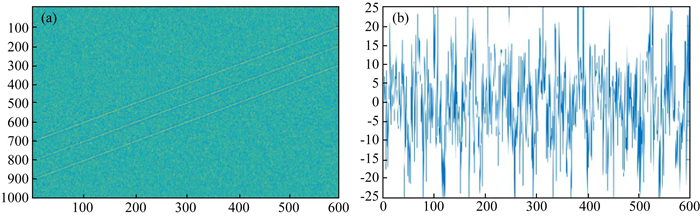
图 8是倾斜三层模型的含噪音剖面及其30 Hz切片振幅图, 模型参数为600道, 每道长1000 ms, 子波主频为30 Hz采样间隔为0.002 s.添加3倍的随机噪声后SNR=-12.2472.从图 8中可看到, 由于噪音的增加, 图中的信号已经被严重干扰, 只剩下大致轮廓可以识别, 其振幅谱几乎不可看.
|
图 8 含噪音三层模型(a)及其30 Hz切片振幅图(b) Fig. 8 Three-layer model with noise (a) and its 30 Hz slice amplitude map (b) |
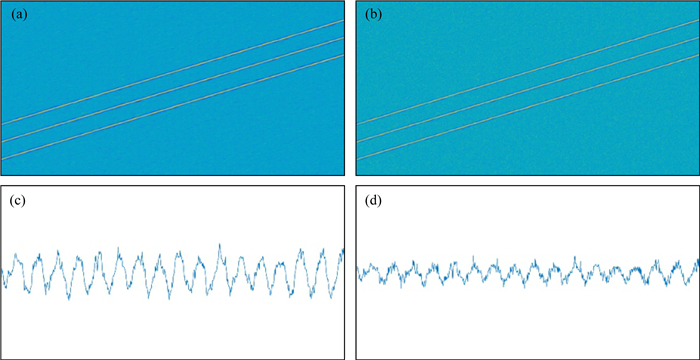
图 9为三层倾斜多层模型采用不同样本去噪处理后的地震剖面及其30 Hz切片振幅图.图 9左侧(a)、(c)图是由不含噪音的理论样本即好的样本经过学习得到的, 而右侧(b)、(d)两图的学习样本是由含噪音的模型数据(图 8)即坏的样本得到的, 通过振幅图的对比可以明显的看到将不含任何噪声的数据即好样本进行学习能够得到十分良好的效果.
|
图 9 去噪结果样本差异对比 Fig. 9 Denoising result sample difference comparison |
实际地震数据所含的噪声变得很复杂, 噪声的成分复杂, 结构也复杂, 常规的各种去噪方法显得无能为力, 得不到较佳的效果, 而在线字典学习方法在处理成分复杂和结构复杂的噪声具有一定的优势.
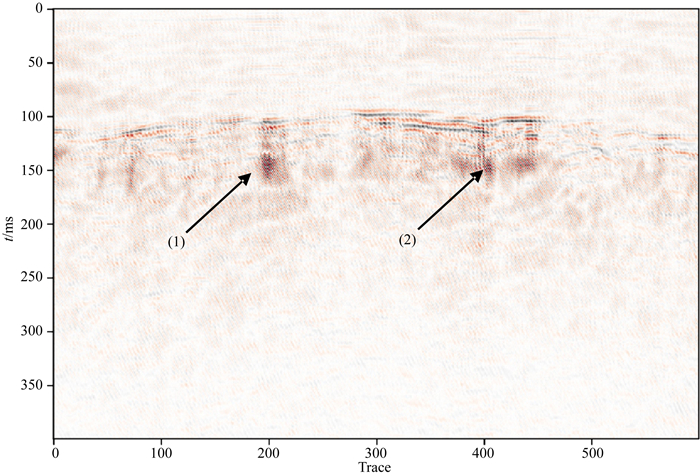
图 10为南海某处地震剖面段.由图 10可看出, 地震剖面中噪声十分复杂, 有随机噪声和相干噪声, 其能量比例远远超出了有效信号.图 11是经在线字典学习去噪处理后得到的地震剖面, 去噪后的地震剖面中的随机噪声基本去除, 使整个剖面更加清晰, 构造凸显和地层层位连续性增强, 地震剖面的品质大幅度提高.在图 11上相干噪声虽有一定的削弱, 但仍残存有相干噪声(图中(1)和(2)).原因是这两部分噪声能量比例大, 有效的地震信号能量比例小成为弱信号, 通过稀疏性的选择后还是无法去除.

|
图 10 南海某实际数据截取剖面 Fig. 10 A practical data interception profile in the South China Sea |
|
图 11 单独使用在线字典学习去噪后无法去除的相干噪声(1)(2) Fig. 11 Coherent noises that can't be removed (1) and (2) after denoising only using online dictionary learning alone |
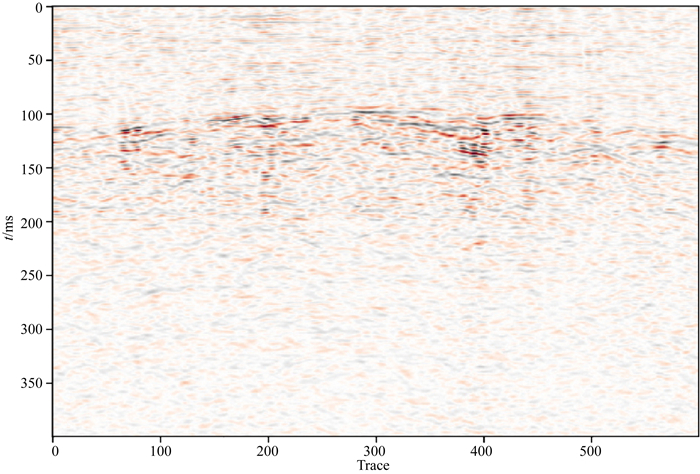
模型约束下的在线字典学习去噪方法是数据驱动和模型驱动联合, 两者结合充分发挥各自优势, 模型约束为在线字典学习提供一个良好的学习样本, 即先通过传统方法(贾瑞生, 2015)获取一个良好的学习样本(图 12), 再进行去噪的优化处理就可以得到一个较优质的地震剖面, 如图 13所示, 图 13中已见不到图 11中的相干噪声, 地震剖面中的噪声去除的十分干净, 并且保留在线字典学习稀疏性的特征, 获得的去噪后的数据非常完美.实现了噪声压制和有效信号突出的双赢.
|
图 12 经EMD方法去噪后的样本数据 Fig. 12 Sample data denoising by EMD |

|
图 13 数据驱动和模型驱动联合去噪处理 Fig. 13 Denoising effect after learning using good samples(without coherent noises (1) and (2)) |
在线字典学习方法以数据驱动方式, 反复进行学习构建字典方式, 求得信号的稀疏性解以实现对信号的去噪, 在线字典学习方法的去噪对弱信号有着非常好的效果, 即使在高噪声水平下在线字典学习方法也能得到优良的地震剖面, 通过不同去噪方法对理论数据和实际数据的去噪处理对比分析, 在线字典学习方法的去噪效果优于常规去噪方法.
在噪声成分复杂和噪声结构复杂的情况下, 模型约束下的在线字典学习去噪方法可将复杂噪声消除得十分干净, 对理论数据与实际数据的去噪处理效果表明, 所得到的地震剖面清晰, 构造凸显和地层连续性得到明显改善和增强.因此模型约束下的在线字典学习去噪方法具有优良的去噪特性, 去噪能力强, 是检测弱信号的一种有效的方法技术, 也是AI大数据时代的研究发展方向, 具有广阔的推广应用价值.
Aharon M, Elad M, Bruckstein A. 2006. rmK-SVD:an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
Beckouche S, Ma J M. 2014. Simultaneous dictionary learning and denoising for seismic data. Geophysics, 79(3): A27-A31. DOI:10.1190/geo2013-0382.1 |
Cheng S J, Han L G, Yu J L, et al. 2018. Seismic data denoising based on improved K-SVD dictionary learning method. Global Geology (in Chinese), 37(2): 627-635. |
Deka B, Baishnab D. 2012. Removal of random-valued impulse noise using overcomplete DCT dictionary.//Proceedings of the Cube International Information Technology Conference. New York, NY, USA: ACM: 42-46.
|
Hennenfent G, Herrmann F J. 2006. Seismic denoising with nonuniformly sampled curvelets. Computing in Science & Engineering, 8(3): 16-25. |
Jacques L, Duval L, Chaux C, et al. 2011. A panorama on multiscale geometric representations, intertwining spatial, directional and frequency selectivity. Signal Processing, 91(12): 2699-2730. DOI:10.1016/j.sigpro.2011.04.025 |
Jia R S, Zhao T B, Sun H M, et al. 2015. Microseismic signal denoising method based on empirical mode decomposition and independent component analysis. Chinese J.Geophys (in Chinese), 58(3): 1013-1023. |
Kaplan S T, Sacchi M D, Ulrych T J. 2009. Sparse coding for data-driven coherent and incoherent noise attenuation.//79th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Li L C. 2014. Research of seismic signal denoising based on sparse decomposition algorithm[Master's thesis] (in Chinese). Daqing: Northeast Petroleum University.
|
Ma J W, Plonka G. 2011. The curvelet transform. IEEE Signal Processing Magazine, 27(2): 118-133. |
Mairal J, Bach F, Ponce J, et al. 2009. Online dictionary learning for sparse coding.//Proceedings of the 26th Annual International Conference on Machine Learning. New York, NY, USA: ACM, 689-696.
|
Olshausen B A, Millman K J. 1997. Learning sparse overcomplete image representations. Proceedings of the SPIE, 4119: 445-452. |
Su J S, Luan X Q. 2008. Research of image denoising based on Gabor filter. Journal of Yili Normal University (Natural Science Edition) (in Chinese), (4): 15-19. |
Tang G, Ma J W, Yang H Z. 2012. Seismic data denoising based onlearning-type overcomplete dictionaries. Applied Geophysics, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
Wang D, Liu C, Liu Y, et al. 2006. Study of the noise elimination methods in the reflection seismic exploration. Progress in Geophysics (in Chinese), 21(3): 957-970. |
Xu D X. 2016. Research on Seismic Denoising Based on The Sparse Representation and Dictionary Learning[Master's thesis] (in Chinese). Changchun: Jilin University.
|
程时俊, 韩立国, 于江龙, 等. 2018. 基于改进K-SVD字典学习方法的地震数据去噪. 世界地质, 37(2): 627-635. DOI:10.3969/j.issn.1004-5589.2018.02.030 |
李立超. 2014.基于稀疏分解算法的地震信号去噪研究[硕士论文].大庆: 东北石油大学.
|
苏金善, 栾雪琴. 2008. 基于Gabor滤波器的图像去噪研究. 伊犁师范学院学报(自然科学版), (4): 15-19. DOI:10.3969/j.issn.1673-999X.2008.04.004 |
王典, 刘财, 刘洋, 等. 2006. 反射法地震勘探噪声消除技术研究. 地球物理学进展, 21(3): 957-970. DOI:10.3969/j.issn.1004-2903.2006.03.040 |
许德鑫. 2016.基于稀疏表示和字典学习的地震数据去噪研究[硕士论文].长春: 吉林大学.
|
贾瑞生, 赵同彬, 孙红梅, 等. 2015. 基于经验模态分解及独立成分分析的微震信号降噪方法. 地球物理学报, 58(3): 1013-1023. |
 2019, Vol. 62
2019, Vol. 62


