2. 有色金属成矿预测教育部重点实验室, 长沙 410083
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Changsha 410083, China
探地雷达的正演模拟能够有助于更好地理解雷达波的传播规律与物理过程,了解典型地质体的雷达图像回波特征,丰富雷达模型数据库,有助于提高雷达资料解译水平.目前常用的探地雷达数值模拟方法有许多,包括有限单元法(底青云和王妙月,1999;冯德山和王珣,2017)、有限差分法(刘四新和曾昭发,2007;冯德山等,2010)及其衍生算法等,这些算法为了取得计算结果的高精度,大多需要配制精细的网格,从而使波场变化平缓处存在过采样,易导致计算资源的浪费.为了以最优的网格使计算达到较高精度,本文将自适应小波配点法引入到探地雷达数值模拟中,它能根据小波系数的大小自适应地配制多层小波配点,达到配点分布随波场变化动态地调节.
随着小波理论的应用日益推广,许多学者致力于将小波和经典的数值算法相结合,并用于微分方程数值求解中,构成了一个非常新颖的研究领域.主要包括小波有限元法(何正嘉等,2006;张新明等,2005)(wavelet-Galerkin)、小波配置(点)法(Cai and Wang, 1996;Vasilyev et al., 2001;Kevlahan and Vasilyev, 2005)(wavelet-collocation method,简称为WCM).其中WCM将网格自适应建立在小波系数分析之上,通过构建动态自适应网格,称为自适应小波配点法(AWCM),在求解大梯度、奇异性问题方面具有诱人应用前景.
Vasilyev等(1995)将二分点作为多层配置点,率先提出并构建了动态自适应多尺度WCM,并用于有限域(Vasilyev and Paolucci, 1996)及多维(Vasilyev and Paolucci, 1997)偏微分方程求解中;此后,Vasilyev根据小波分解进行自适应网格的筛选和插值,构建了多尺度第二代WCM,并将它用于湍流流动(Vasilyev and Bowman, 2000)、局部结构的多维发展方程(Vasilyev,2003)与椭圆微分方程(Vasilyev and Kevlahan, 2005)的动态自适应求解中;Cruz等(2002)、Karami等(2007)将自适应WCM用于化学工程突变结构问题的非线性、偏微分方程高效、高精度求解中;Fujii和Hoefer(2003)使用插值WCM求解Maxwell方程,模拟非均匀介质中的波传播现象并进行了二维介质波导的不连续性分析,模拟过程中结合亚网格技术,保证计算精度的同时提高了计算效率;Mehra和Kevlahan(2008)将第二代WCM用于球形域曲面上偏微分方程的自适应求解,建立了球面上嵌套的三角形网格,丰富了自适应WCM的应用领域;Yousefi等(2010)提出了一种改进的自适应WCM模拟弹性固体介质中二阶双曲型偏微分方程波传播问题;Li(2011)采用自适应插值WCM开展了波导光学设备、微环谐振器的数值模拟,计算效率高,具有较高的压缩比;Qin等(2014)对WCM解的存在性与惟一性进行了讨论.国内,傅晓玲(2000)借助小波多尺度理论,构造了二分点为基础的插值小波基函数,通过阈值运算控制小波系数及网格点的分布,实现了双曲型微分方程的自适应WCM求解;Wang和Yang(2006)利用第二代小波构造动态自适应计算网格求解一维声波波动方程,并给出声波传播的数值算例;汪丽艳(2007)应用第二代WCM结合自适应网格开展了具有突变结构的化学工程领域PDEs(Partial Differential Equations,偏微分方程)求解数值实验,结果表明该方法能够灵活地跟踪解的“不规则”特性,在大梯度区域分配稠密网格;宓铁良等(2009)构造了层层嵌套的自适应计算网格,结合小波系数阈值的网格细化技术,实现了二维声波波传问题的多尺度自适应第二代小波WCM数值模拟;王静(2009)采用第二代WCM求解了一维Maxwell方程,通过将小波系数和设定阈值进行比较来调节配点,达到跟踪函数奇异性变化,提高方程求解效率的目的;高欢乐等(2011)采用Lagrange插值细分方法构造了紧支撑双正交小波的尺度函数,以此函数作为第二代小波配点法的基函数,求解了第一边值条件控制的对流占优方程;胡俊华和田锦会(2013)将微分方程的数值解映射到小波系数空间,参考小波系数选择合适的阈值,构造了自适应网格,并将小波逆变换引入到Burgers方程的数值求解中,避免了直接在小波基上的运算,提高了计算效率.
由此可见,国内外利用WCM求解偏微分方程已成为研究热点,但大多局限于求解一维偏微分方程.从作者掌握的文献来看,仍未见将第二代WCM应用于二维GPR波动方程的正演求解的报道.鉴于小波配点法在求解奇异性问题方面的诱人应用前景,本文开展自适应第二代WCM的研究,不仅有助于丰富GPR数值模拟手段,而且可促进复杂地震波场、电磁法前沿计算问题的快速发展.
1 第二代插值小波及二维张量积构造 1.1 第二代插值小波函数构造Sweldens(Sweldens, 1996, 1998; Sweldens and Schröder,2000)提出了一种新小波构造方案,称为提升方案(Lifting Scheme),而将提升方案构造的小波称为第二代小波.第二代小波完全在真实物理空间中构造,继承了第一代小波变换的多尺度分解的性质,且运算更加快速,近年来被应用于偏微分方程的多尺度自适应求解中.
插值尺度函数是通过提升一套双正交小波滤波器lazy小波获得的,它又称为Deslauriers-Dubuc插值函数,也是Daubechies尺度函数的自相关函数(Satio and Beylkin, 1993).它的构建方法有多种:Deslauriers和Dubuc(1989)通过迭代插值过程构造了插值尺度函数;本文以图 1所示的提升算法构建该插值小波,图中S为分解算子,P为预测算子,U为更新算子,M为合并算子.重构过程是提升变换的逆变换,它们是结构对称的,可以实现精确重构.故仅重点介绍提升过程.
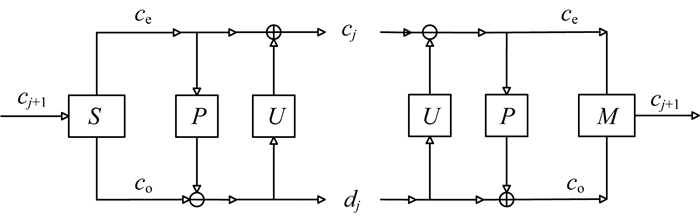
|
图 1 第二代小波提升算法的分解和重构过程 Fig. 1 Decomposition and reconstruction of second generation wavelet lifting algorithm |
(1) 分解:假设j+1尺度时,取xj+1, k处输入信号的样本值为cj+1={cj+1, k},可将其分解为奇数序列co和偶数序列ce.其中co={cj, 2k+1},ce={cj, 2k}(k为整数,取值范围与尺度值相关,当下标尺度为j时,其取值范围为[0, 2j]).
(2) 预测:通常情况下,输入信号具有局部相关性,即某点的信号值与它相邻点的值相关.在构造插值尺度小波时,用偶数序列的值ce预测奇数序列co,预测误差为细节信号dj, k
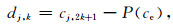
|
(1) |
式(1)中P(·)为预测算子.假设构造的提升插值小波为N阶,则
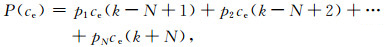
|
(2) |
式(2)中,p1, p2, …, pN为预测系数,它可以通过Lagrange插值定理确定(何正嘉等,2006)
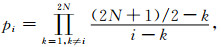
|
(3) |
当2N=2时,可以得到2点预测器P={1/2, 1/2};当2N=4时,可以得到4点预测器P={-1/16, 9/16, 9/16, -1/16}.
(3) 更新:不能仅仅让分解得到的偶数序列ce来表示逼近信号cj, k,因为它没有反映co的信息.因此需要使用细节信号dj, k对偶数序列ce进行更新

|
(4) |
更新器可参照文献(Sweldens and Schröder, 2000;何正嘉等,2006),结合公式(5)(6)进行求取.
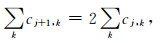
|
(5) |
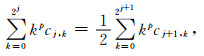
|
(6) |
式中p为消失矩,如果更新器的个数为N,则0≤p<N.公式给出了设计更新器的条件.当2N=2时的2点更新器U={1/4, 1/4};当2N=4时,得到的4点更新器U={-1/32, 9/32, 9/32, -1/32}.
得到预测系数与更新系数后,就可以应用插值细分方法(Sweldens and Schröder, 2000)迭代得到图 2所示的尺度函数ϕ(x)和小波函数ψ(x).为了与Deslauriers-Dubuc插值函数的表示方式一致,本文将N阶插值基函数简称DDN(x),它具有下列性质:

|
图 2 插值尺度函数与小波函数(1阶至4阶) Fig. 2 Interpolating scale function and wavelet function of one order to four order |
(1) DDN(N∈N)为偶对称函数且具有紧支撑性.
紧支集为[-2N+1, 2N+1],且DDN(x)=DDN(-x),x∈R.
(2) 满足插值性.DDN(k)=δk, ∀k∈Z.
(3) DDN(x)是2N阶Daubechies自相关尺度函数.
由于后面的计算中需要求DDN二分点处的导数值,由数值微分的理论可知,求离散点的导数可通过三次样条函数S(x)的导数值来替代.表 1为应用该样条求导法计算出的阶次为N=2,3,4时的插值导数系数.
|
|
表 1 空间偏导数系数DD′N(-j-1/2) Table 1 Space partial derivative coefficient DD′N(-j-1/2) |
求解二维GPR偏微分方程时,电场E及磁场H是关于时间变量t和空间变量x, y的函数,需要采用二维多分辨分析.现设一元插值尺度函数为Vj=DDN(x),插值小波函数为Wj=DlN(y),根据可分离小波理论,二维小波基可以用一维小波基的张量积来表示(Restrepo and Leaf, 1997),很容易推广到高维空间.令Wj为Vj在Vj+1中的正交补空间,即
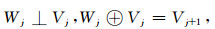
|
(6) |
式(6)中,⊕为直和符号.

|
(8) |
式中⊗是张量积的Kronecker符号.
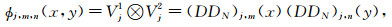
|
(9) |
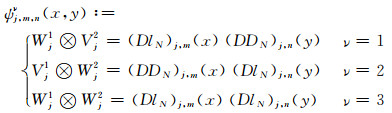
|
(10) |
而


|
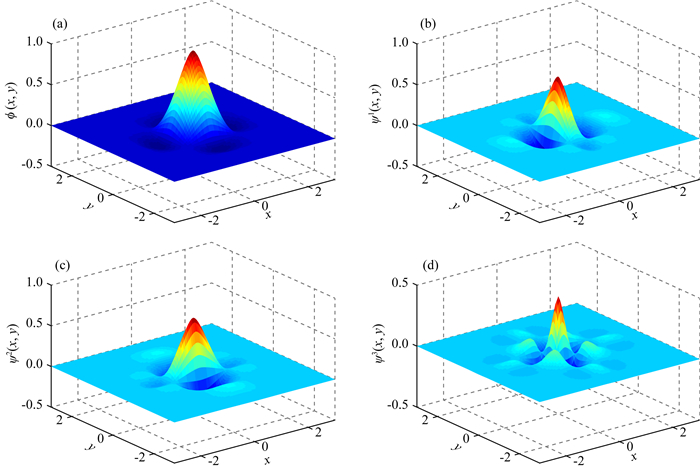
图 3 二维张量积插值尺度函数与小波函数(2阶) (a)尺度函数ϕ(x, y); (b)小波函数ψ1(x, y); (c)小波函数ψ2(x, y); (d)小波函数ψ3(x, y). Fig. 3 The map of two-dimensional tensor product scaling function of DB3 wavelet |
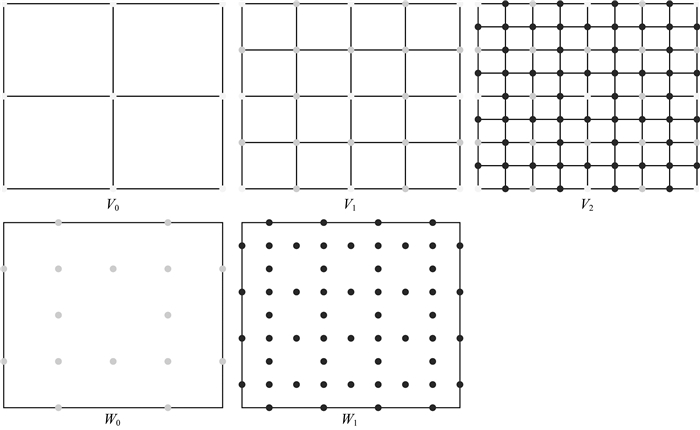
为了构建多尺度自适应网格,由小波尺度的层层嵌套特性可知,j尺度下的网格被j+1尺度下的网格所包含,其网格如图 4所示.在J尺度下,将某一时刻的雷达波场函数f(x, y)进行二维第二代小波变换.得到所有尺度上与计算网格相联系的小波系数和尺度系数,保留尺度系数对应的网格点.
|
图 4 第二代小波二维多尺度分解 Fig. 4 Two-dimensional multi-scale decomposition of second-generation wavelet |
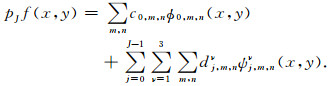
|
(11) |
式(11)为雷达波场完全小波变换表达式.由第二代小波变换的自适应特性,函数的多尺度分析从粗到细,网格细化则集中于雷达波场变化剧烈区域.在符合求解精度的前提下,通过引入阈值控制简化表达式(11),舍弃小于阈值ε对应的小波系数和网格点.为此,将函数f(x, y)的小波变换系数表示为大于阈值部分pJf≥(x)和小于阈值pJf<(x)两个部分的和,在求解过程中只保留pJf≥(x)的部分,将pJf<(x)部分小波系数dj, m对应的网格点删除:
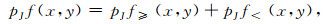
|
(12) |
其中:
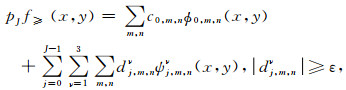
|
(13) |
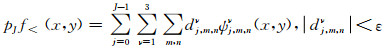
|
(14) |
式(13)为式(11)略去小于设定阈值配点的简化函数逼近第二代小波稀疏表达式.从而在雷达波场变化平缓区域,删除了小于阈值的系数所对应的配点,减少了计算过程中的网格数,对于大于阈值的小波系数所在的波场变化剧烈区域,进行网格局部加密,增加配点,以捕捉函数的突变结构.阈值的选取对于自适应网格的构造尤为重要,当阈值较小无法达到自适应网格的效果,阈值较大无法保证算法的精度,需要根据源的大小,模拟区域的大小,天线的主频、介质的分布以及选择的小波函数等因素通过实验选取一个合适的阈值.
为了自适应小波配点法求解雷达波场的顺利开展,需要建立系数cj, m, n、dj, m, n与自适应网格点之间的联系.设模拟区域的大小为L×L,j为位于jmin和jmax之间的整数.将模拟区域离散为2jmax×2jmax的小网格.网格点在分辨率j下的坐标定义为:xj, m=mL/2j,yj, n=nL/2j,其中jmin≤j≤jmax,m, n=0, 1, 2, …, 2j.定义网格
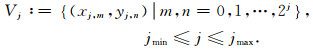
|
(15) |
明显的,Vj存在如下嵌套关系Vj∈Vj+1(j∈[jmin, jmax-1]),且xj, m=xj+1, 2m,yj, n=yj+1, 2n,同时定义
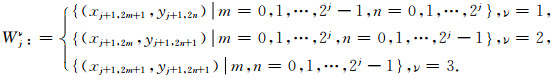
|
(16) |
其中Wj:=Wj1∪Wj2∪Wj3,对应于图 3中的3个二维小波函数.
在jmax下,有
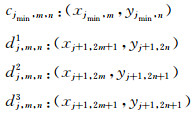
|
(17) |
其中尺度系数cjmin, m, n与小波系数dj, m, nν可由最高分辨尺度(细网格)条件下的cjmax, m, n通过归一化的2D小波变换推导出.
上面构造的自适应多尺度网格,对网格点进行了压缩,明确了当前时刻是否对某些点进行删除.自适应网格中的一些网格点在当前时刻不重要并不意味着它在下一个时刻不重要.因此,需要人为添加一些细网格,以保证网格能正确地捕获到波的传播过程,使自适应网格不仅具有压缩性,也具有扩展性.为此,引入邻域(Vasilyev and Bowan, 2000; Vasilyev, 2003;Li,2011)的概念.对于当前网格中任一点P=(xj, m, yj, n),其邻域的点表示为(xj′, m′, yj′, n′),其定义如下:
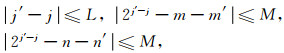
|
(18) |
其中,L决定包含在邻域中的尺度分辨率范围,M是物理空间邻域的宽度.通常取L=M=1,使邻域只包含同尺度或相邻尺度上与当前网格点相关的点.也就是说,如果P位于自适应网格中,不仅需要添加相同尺度的八个点,还需添加更细尺度的八个点,P点的邻域如图 5所示.
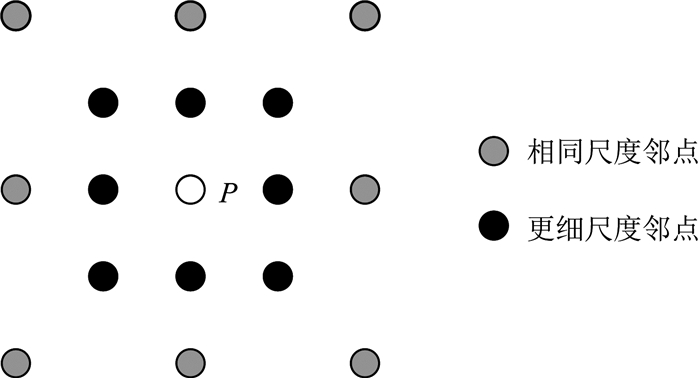
|
图 5 点P的邻域 Fig. 5 The adjacent zone of P point |
自适应网格构建及网格管理过程中,需要建立一个二维的布尔型掩码矩阵用来存储网格信息,该矩阵的取值为0或1,矩阵的维数对应某一方向最细网格点(最高分辨率)的数目,如果掩码取值为1,则对应的网格点将被包括在自适应网格中,否则,小于阈值ε对应的小波系数其掩码取值置0,舍弃这些网格点,得到一个被压缩的网格,能有效提高计算效率.但是,实际的GPR正演不是单个时间步的计算,每一个时间步进都需要执行快速小波变换.自适应网格体系中,当前时间步网格被删除,可能下个波前传播时间步,网格却变为重要网格,导致快速小波变换无法顺利进行,为了确保每一步小波变换的顺利进行,需要进行重构检验.假设小波系数dj, m, nν位于第n个时间步的自适应网格中,在下一个时间步中,为了对其进行小波变换,需要一些相邻点,以2阶提升插值小波为例,计算小波系数dj, m, nν所需的相邻点如图 6所示.
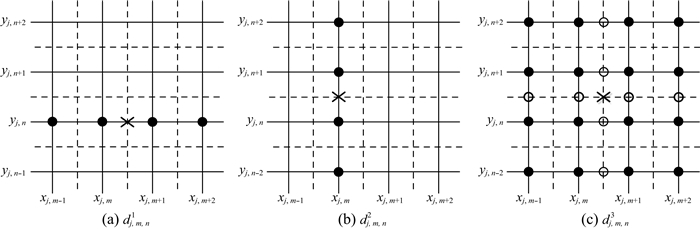
|
图 6 2阶提升插值小波计算dj, m, nν所需的相邻点 Fig. 6 The second-order lifting interpolated wavelet is used to calculate the dj, m, nν required neighbor points |
在邻域添加与重建检验之后,需要对自适应网格点的导数值进行求取及递推格式的建立.下面着重阐述这两方面的内容.
3.1 自适应网格的导数值求取目前,自适应网格点的导数值求取方法可归纳为三种:(a)全空间均匀差分法;(b)非均匀网格差分;(c)插值尺度法.本文采用效率最高的插值尺度法(Li,2011).如需计算t时刻自适应网格中的一点Q=(x0, y0)的导数,需先判定该点在x方向及y方向的分辨率等级,并在自适应网格中加入计算所需的邻近点,达到插值尺度法导数求取网格点导数的目的.
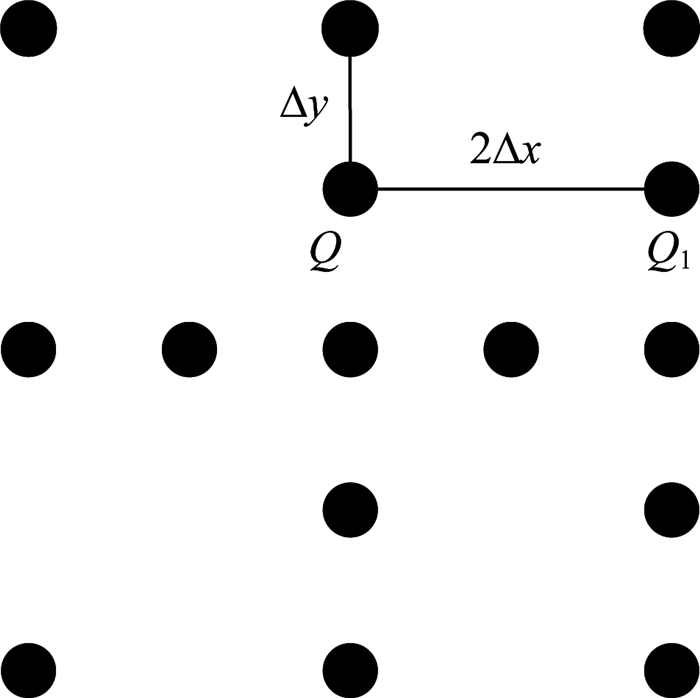
以x方向为例,若自适应网格中x方向距Q最近的一点为Q1=(x1, y0),则自适应网格中Q点x方向的分辨率等级为:
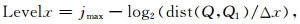
|
(19) |
式中Δx是计算网格中x方向的最小间距,dist(Q, Q1)=|x1-x0|.自适应网格点Q的分辨率等级示意图如图 7所示,x方向为jmax-1,y方向为jmax.
|
图 7 自适应网格点Q的分辨率等级 Fig. 7 Resolution level of the adaptive mesh point Q |
假设根据式(19)求出的Q的分辨率等级为j0,可将Q点的场值函数f通过Q点附近几个点的有限和Pj0f表示,这样,就可以通过Pj0f来近似场函数位于Q点的导数值.

|
(20) |
因此,由(ϕN)j0, m, n的插值性质可知:

|
(21) |
将式(21)代入式(20)可以得到
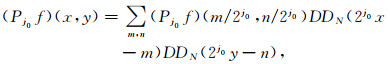
|
(22) |
将等式(22)两边求x方向偏导
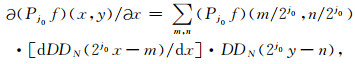
|
(23) |
DD′N值的计算已在表 1求得.因此,若Q=(m′/2j0, n′/2j0),可以很容易地得到
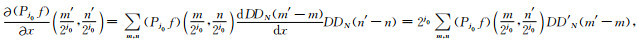
|
(24) |
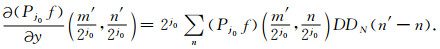
|
(25) |
在具体的程序实现过程中,以DD2为例,首先判断Q点x,y方向的分辨率等级,然后在相同尺度下,通过附近4N-2(N为插值尺度函数的阶次)个点值计算Q点的导数值.由于电场与磁场错半个网格,此时DD′N也要采用半个步长的值.
3.2 GPR方程递推格式由电磁场与电磁波的理论可知,二维TM模式GPR波满足的Maxwell方程可表示为:

|
(26) |
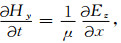
|
(27) |
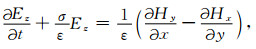
|
(28) |
其中E为电场强度(V·m-1),H为磁场强度(A·m-1),ε为介电常数(F·m-1),μ为磁导率(H·m-1),σ为电导率(S·m-1).
假定自适应网格中存在点Q,用Hx|Qk+1/2,Hy|Qk+1/2和Ez|Qk分别表示Hx、Hy、Ez在点Q的离散值(磁场与电场位置错半个网格),注意电场分量在整数步时间采样,而磁场值在半整数时间步采样,假设自适应网格中一点Q的分辨率等级为j0,我们可以将点Q表示为(xj0, m′, yj0, n′).采用插值尺度函数的导数对Maxwell方程离散,对于式(26)—(28)时间上采用中心差分离散,空间偏导数采用式(24)—(25)求取,其离散格式表示如下:
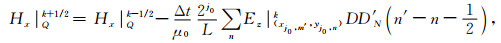
|
(29) |

|
(30) |
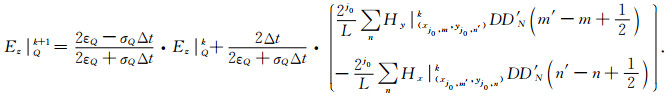
|
(31) |
由于式(29)—(31)中时间导数的离散采用了中心差分方案,故与显式FDTD算法类似.小波配点法也需要考虑Courant-Friedrichs-Lewy (CFL)稳定性条件,假设方程中两个方向的空间网格采用同样的步长Δs,则时间步长与空间步长满足的CFL条件可以写为:
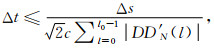
|
(32) |
式(32)中c为波速,DD′N(l)是前面表 1中给出的插值尺度滤波器系数的导数.应用自适应小波配点法开展GPR正演时,为了保证模拟精度不受数值不稳定的影响,常将步长Δs选为最精细尺度的步长.因为0时刻的电磁场值均为0,根据公式(29)—(31)再结合PML(Perfect Matched Layer,完全匹配层)边界条件,就可以进行显式递推.自适应小波配点法采用局部自适应的网格配制来求解的,与FDTD方法不同,它不需要固定的结构化网格,计算资源能更充分地被利用.
自适应小波配点法在求解时域GPR正演模拟的实现过程为:
(1) 模拟初始化.模拟区域大小,介质参数,天线参数,网格构造参数等;
(2) 场值,场值偏导数,掩码矩阵初始化;
(3) 对场值进行第二代小波变换,得到小波系数,根据阈值,构造自适应网格;
(4) 邻域添加(图 5),重构检验(图 6),改变对应掩码矩阵中的数值;
(5) 添加导数计算所需网格点,通过式(19)进行分辨率等级计算,并添加计算导数所需要的点,进行重构检验,改变对应掩码矩阵中的数值;
(6) 小波逆变换,得到当前时刻的场值,根据n+1时刻的自适应网格,对n时刻网格的场值进行插值;
(7) 根据n+1时刻的自适应网格,通过式(29)—(31)进行场值更新以及激励源的加载;
(8) 是否完成时间步进,若未完成则返回(3);
(9) 是否完成所有道数,若未完成则返回(2);
(10)正演结束,并输出数据绘制剖面.
4 自适应小波配点法探地雷达模拟实例 4.1 二维均匀模型为了验证自适应小波配点法GPR正演算法的正确性,建立图 8所示的均匀模型.模拟区域为2.0 m×2.0 m,模型介电常数9.0,电导率0.002 S·m-1.最大尺度V4网格为400×400,网格间距为0.005 m,CPML(Convolution Perfect Matched Layer,卷积完全匹配层)吸收层为80层.将主频为900 MHz布莱克曼-哈里斯脉冲置于模型的正中心,采样时间间隔为0.02 ns,模拟时窗为20 ns.自适应小波配点法中,插值小波阶次为2,阈值取ζ=5.0×10-5,多尺度分解层数为4.
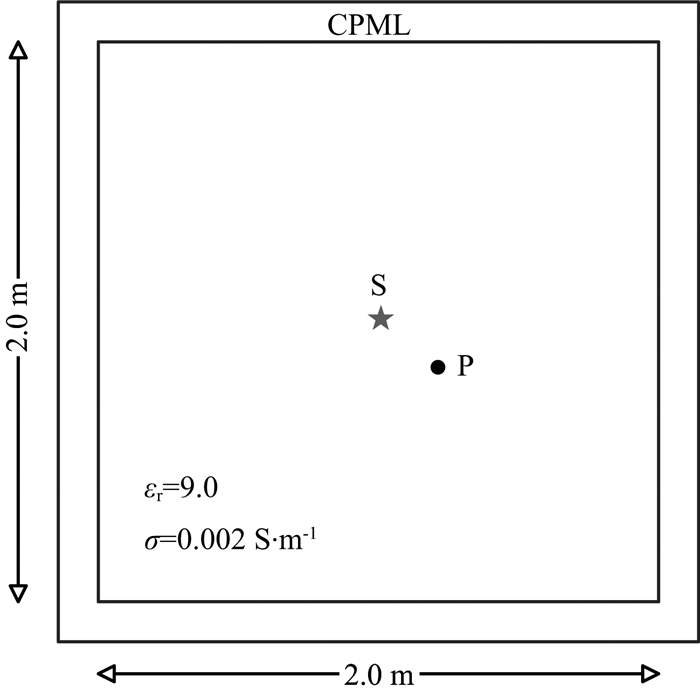
|
图 8 正演模型图 Fig. 8 The model map of forward simulation |
为了分析自适应小波配点法的计算精度、计算存储量、计算速度,对上述模型采用基于V4网格2阶有限差分算法进行模拟,源、采样间隔及时窗长度不变,并将其得到结果与自适应小波配点法进行对比.图 9为观测P(2.32 m,1.68 m)用两种不同方法计算得到波形对比图,图中FDTD(2阶)表示全网格下时域有限差分法得到的结果,AWCM表示自适应小波配点法得到的结果.从图中可以发现,AWCM得到的波形与FDTD算法波形基本一致.

|
图 9 观测点P波形对比图 Fig. 9 Comparison of waveforms at observation points P |
图 10为不同时间步下波场快照的二维散点图.从图中可以看出,自适应小波配点法的配点网格会随着电磁波的传播自适应地追随解的峰值进行加密,在解趋近于零的位置保持稀疏,计算结果符合电磁波的传播规律.在不同时间步中自适应网格点相对于原始网格均进行了较大压缩,这可以较为显著地减少计算量与存储量.

|
图 10 波场快照二维散点图 Fig. 10 The two-dimensional scatter plot of wavefield snapshot |
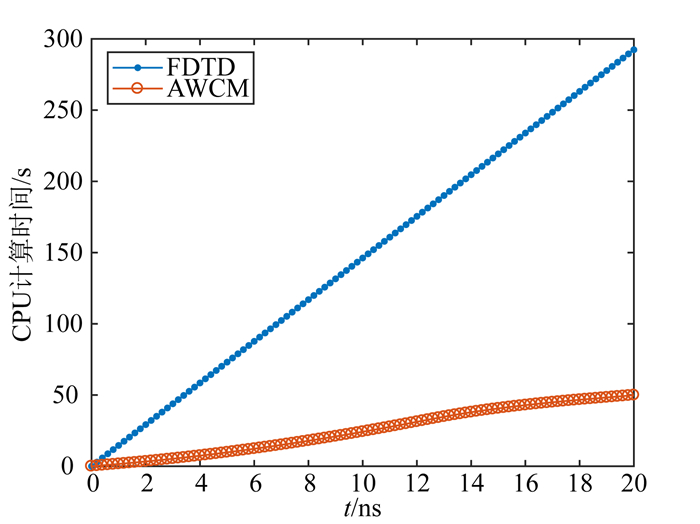
图 11为AWCM算法不同时间步的节点压缩比(当前时刻的节点总数与最大尺度节点总数的比值),由图可知,从0 ns至12 ns网格压缩比逐步上升,在12 ns处达到最大.对比图 10从0 ns至12 ns波从中心点向外传播,传播距离不断变大,自适应网格点逐渐增多,12 ns时波刚好传播至吸收边界处,之后由于完全匹配层的吸收衰减效果,节点逐渐减少,压缩比不断降低.图 12为AWCM算法计算时间与FDTD算法计算时间的对比图,由图可知,FDTD算法的计算时间曲线具有固定的斜率,AWCM计算时间曲线的斜率是不断变化的,计算时间曲线的斜率和网格点的数量是相关的.使用FDTD算法和AWCM算法模拟电磁波传播,在0 ns至20 ns时间段内,CPU运行时间分别为292.40 s、49.92 s,说明AWCM算法更高效.
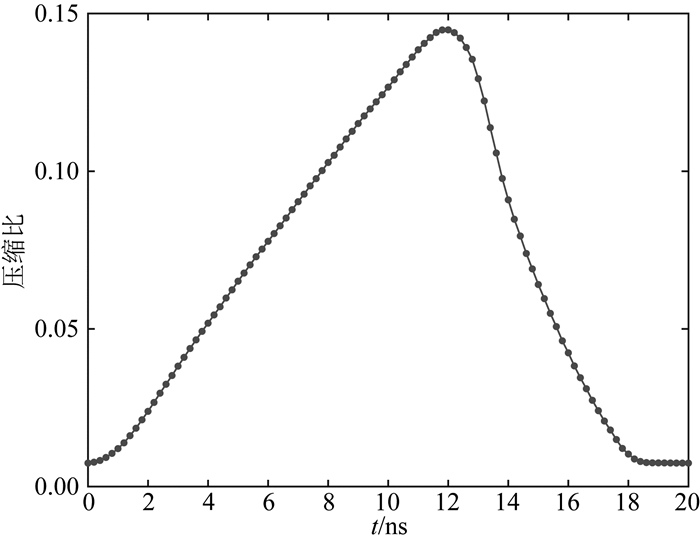
|
图 11 自适应网格压缩比时间变化图 Fig. 11 Adaptive grid compression ratio time variation graph |
|
图 12 计算时间对比 Fig. 12 Calculate time comparison |
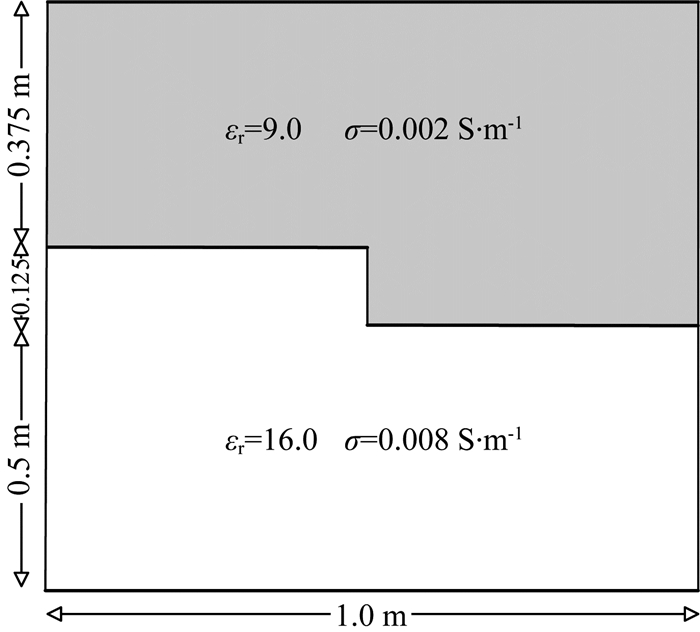
阶梯模型如图 13所示,长与宽为1.0 m×1.0 m,模型介电常数9.0,电导率0.002 S·m-1.最高分辨尺度V3网格为400×400,网格间距为0.0025 m.采用主频为900 MHz布莱克曼-哈里斯脉冲,自左向右同步移动,自激自收方式,每隔0.02 m采集一道数据,记录51道波形.时间步长为0.15 ns,时窗长度为150 ns,插值小波阶次为2,阈值取ζ=5.0×10-5,多尺度分解层数为3.
|
图 13 阶梯模型图 Fig. 13 The sketch map of ladder model |
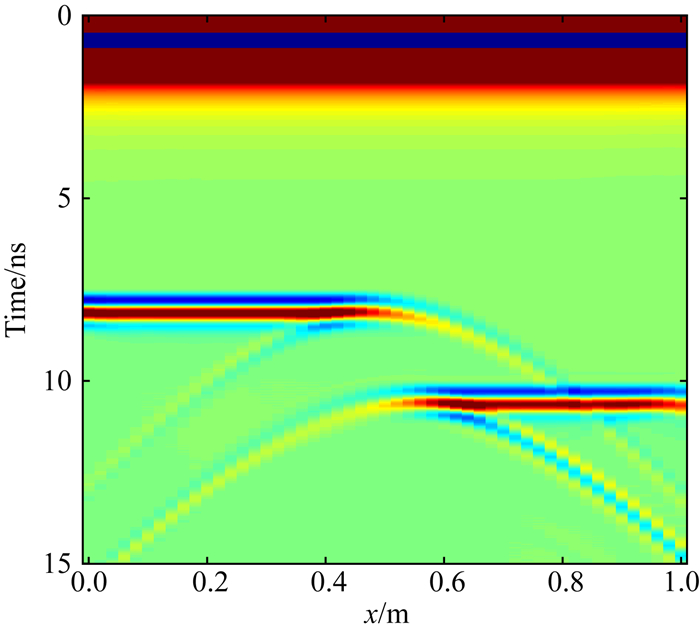
图 14为自适应小波配点法得到正演剖面,阶梯模型的左右两侧台面理论上信号到达时间与图中记录十分吻合.台阶模型中间的上下角点的双曲线绕射清晰可见.
|
图 14 阶梯模型雷达正演剖面 Fig. 14 The GPR simulation section of ladder model |
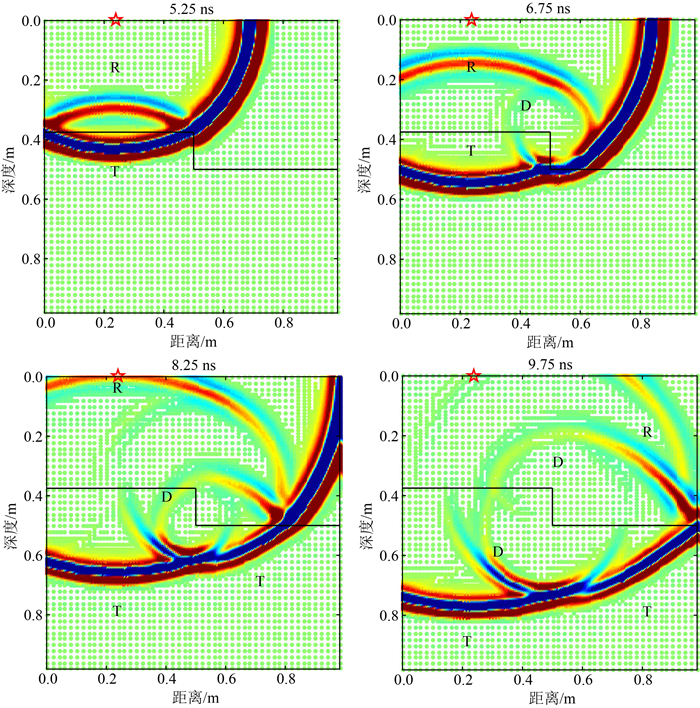
为了更清楚地反映AWCM算法的配点方式,对阶梯模型的波场快照进行分析.图 15为发射天线位于地表 0.24 m处不同时刻波场快照的二维散点图.图中可见,因界面引起的反射波(R)、透射波(T)以及角点产生的绕射波(D)均可识别,自适应网格随着波的传播与分裂不断地变化,在波场能量变化剧烈的地方稠密,在场值变化缓慢处稀疏.显然,波场快照直观地显示了AWCM算法能随波场变化动态地调整配点分布,计算中能以最优的网格得到较高精度的解,从而,在精度与效率之间取得满意的平衡.
|
图 15 发射天线位于0.24 m处的不同时刻波场快照 Fig. 15 The wavefield snapshot of different time with the transmitting antenna located at 0.24 m |
为了进一步验证算法对复杂模型的模拟效果,设计图 16所示的复杂模型,长与宽为1.0 m×1.0 m,模型为三层起伏介质,第二层介质中存在一空洞异常体,其圆心埋深为0.5 m,半径为0.1 m;第一层介质的相对介电常数5.0,电导率0.002 S·m-1,第二层介质的相对介电常数3.0,电导率0.002 S·m-1,第三层介质的相对介电常数9.0,电导率0.002 S·m-1.模型的最高分辨尺度V3网格为400×400,网格间距为0.0025 m.采用主频为900 MHz布莱克曼-哈里斯脉冲,自左向右同步移动,自激自收方式,每隔0.005 m采集一道数据,记录201道波形.时间步长为0.05 ns,时窗长度为150 ns,插值小波阶次为2,阈值取ζ=5.0×10-5,多尺度分解层数为3.
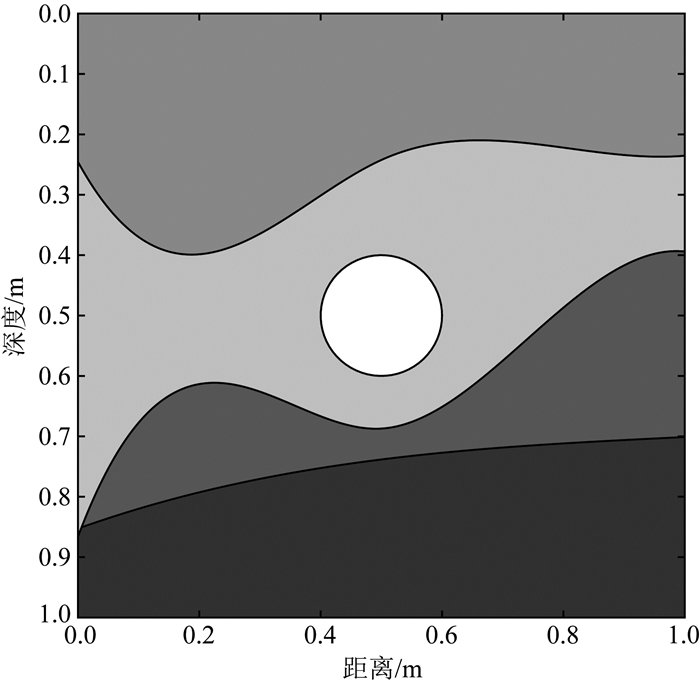
|
图 16 复杂模型图 Fig. 16 The sketch map of complex model |
图 17为自适应小波配点法得到正演剖面,从剖面图中可以发现,第一层介质与第二层介质分界面的反射波以及空洞上下界面的双曲反射波能容易的识别,第二层介质与第三层介质的反射界面仍能大概的识别,而最下一层界面基本无法识别.
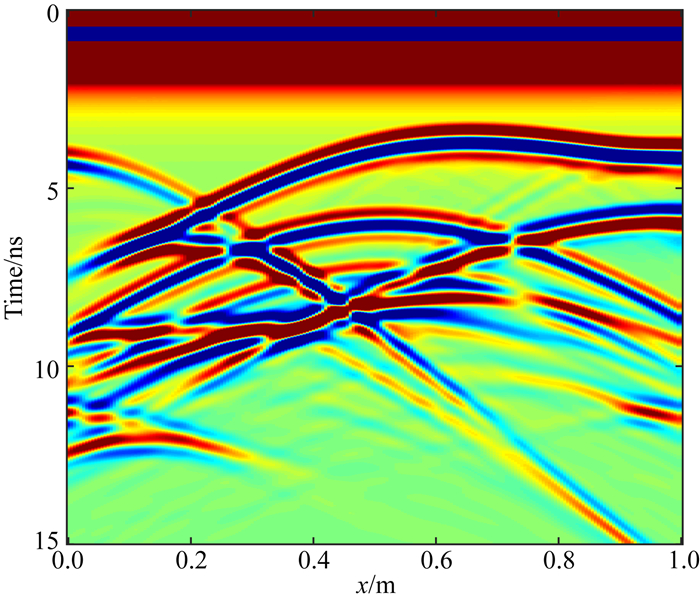
|
图 17 复杂模型雷达正演剖面 Fig. 17 The GPR simulation section of complex model |
为了更清楚地反映AWCM算法对于复杂模型的配点效果,对复杂模型的波场快照进行分析.图 18为发射天线位于地表 0.5 m处不同时刻波场快照的二维散点图.图中可见,在2.5 ns以及5 ns时,当波未传达至下方界面时,下方场值为0,此时配点为最小尺度,最为稀疏;在5 ns与7.5 ns时自适应网格会随着波的传播与分裂不断地变化,在波场能量变化剧烈的地方稠密,在场值变化缓慢处稀疏;10 ns时,由于波场的传播与衰减,在场值能量较小处,配点稀疏.
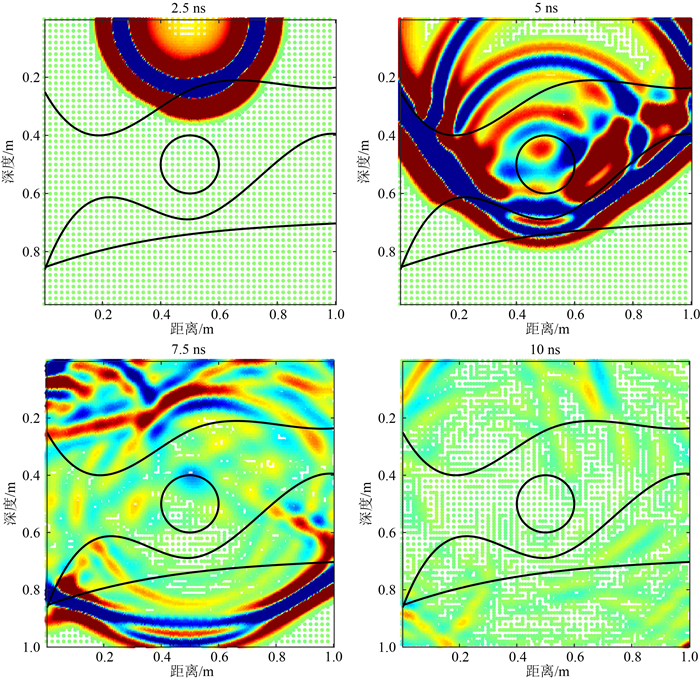
|
图 18 发射天线位于0.5 m处的不同时刻波场快照 Fig. 18 The wavefield snapshot of different time with the transmitting antenna located at 0.5 m |
显然,AWCM算法能很好地保持波场的传播特性,并能根据波场变化动态地调整配点分布,计算中能以最优的网格得到较高精度的解,在精度与效率之间取得满意的平衡.
5 结论(1) 第二代小波变换具有计算效率高、易于实现自适应的特性,本文构造了二维插值尺度函数与小波函数,并将它作为自适应计算网格的工具,将Maxwell方程的数值解映射到小波系数空间,每一小波系数和尺度系数均对应于真实物理空间的离散网格点,通过对小波系数的阈值判断实现自适应计算网格的构造.
(2) 三个模型算例证明了自适应小波配点法的正确性,它是一种高精度、高效率的数值模拟方法,能跟踪波场变化而动态调整配点分布,在场值较大、变化剧烈的地方具有较多的网格点,在场值较小、变化缓慢的地方具有较少的网格点.以最优的网格来开展正演计算.并且该算法具有较高的数据压缩率,可以大幅度的降低计算成本,在精度不变的情况下,提高GPR正演计算效率.
Cai W, Wang J Z. 1996. Adaptive multiresolution collocation methods for initial-boundary value Problems of Nonlinear PDEs. SIAM Journal on Numerical Analysis, 33(3): 937-970. DOI:10.1137/0733047 |
Cruz P, Mendes A, Magalhães F D. 2002. Wavelet-based adaptive grid method for the resolution of nonlinear PDEs. AIChE Journal, 48(4): 774-785. DOI:10.1002/(ISSN)1547-5905 |
Deslauriers G, Dubuc S. 1989. Symmetric iterative interpolation processes. Constructive Approximation, 5(1): 49-68. DOI:10.1007/BF01889598 |
Di Q Y, Wang M Y. 1999. 2D finite element modeling for radar wave. Chinese Journal of Geophysics (in Chinese), 42(6): 818-825. |
Feng D S, Chen C S, Dai Q W. 2010. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese Journal of Geophysics (in Chinese), 53(10): 2484-2496. DOI:10.3969/j.issn.0001-5733.2010.10.022 |
Feng D S, Wang X. 2017. Convolution perfectly matched layer for the Finite-Element Time-Domain method modeling of Ground Penetrating Radar. Chinese Journal of Geophysics (in Chinese), 60(1): 413-423. DOI:10.6038/cjg20170134 |
Fu X L. 2000. Adaptivity in solving hyperbolic PDEs using interpolating wavelets. Journal of North China University of Technology (in Chinese), 12(3): 31-35. |
Fujii M, Hoefer W J R. 2003. Interpolating wavelet collocation method of time dependent Maxwell's equations:Characterization of electrically large optical waveguide discontinuities. Journal of Computational Physics, 186(2): 666-689. DOI:10.1016/S0021-9991(03)00091-3 |
Gao H L, Zhao F Q, Li J. 2011. Second-generation wavelet collocation method for solving differential equation. Basic Sciences Journal of Textile Universities (in Chinese), 24(3): 317-321. |
He Z J, Chen X F, Li B, et al. 2006. Theory of the Wavelet Based Finite Element Methods and the Application in Engineering. Beijing: Science Press.
|
Hu J H, Tian J H. 2013. Numerical new algorithm of PDEs based on the second generation wavelet. Information Technology (in Chinese), 95(9): 88-90, 95. |
Karami A, Karimi H R, Moshiri B, et al. 2007. Wavelet-based adaptive collocation method for the resolution of nonlinear PDEs. International Journal of Wavelets, Multiresolution and Information Processing, 5(6): 957-973. DOI:10.1142/S0219691307002154 |
Kevlahan N K R, Vasilyev O V. 2005. An adaptive wavelet collocation method for fluid-structure interaction at high Reynolds numbers. SIAM Journal on Scientific Computing, 26(6): 1894-1915. DOI:10.1137/S1064827503428503 |
Li H J. 2011. Numerical simulation of a micro-ring resonator with adaptive wavelet collocation method[Ph. D. thesis]. Germany: Karlsruhe Institute of Technology. https://www.researchgate.net/publication/311589287_Numerical_simulation_of_a_micro-ring_resonator_with_adaptive_wavelet_collocation_method
|
Liu S X, Zeng Z F. 2007. Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium. Chinese Journal of Geophysics (in Chinese), 50(1): 320-326. |
Mehra M, Kevlahan N K R. 2008. An adaptive wavelet collocation method for the solution of partial differential equations on the sphere. Journal of Computational Physics, 227(11): 5610-5632. DOI:10.1016/j.jcp.2008.02.004 |
Mi T L, Sun B B, Yang H Z. 2009. Adaptive mesh based on second generation wavelet simulation wave propagation for 2D acoustic wave equation. Chinese Journal of Geophysics (in Chinese), 52(11): 2862-2869. DOI:10.3969/j.issn.0001-5733.2009.11.021 |
Qin X Q, Fang B Y, Tian S L, et al. 2014. The existence and uniqueness of solution to wavelet collocation. Applied Mathematics and Computation, 231: 63-72. DOI:10.1016/j.amc.2013.12.106 |
Restrepo J M, Leaf G K. 1997. Inner product computations using periodized Daubechies wavelets. International Journal for Numerical Methods in Engineering, 40(19): 3557-3578. DOI:10.1002/(ISSN)1097-0207 |
Satio N, Beylkin G. 1993. Multiresolution representations using the autocorrelation functions of compactly supported wavelets. IEEE Transactions on Signal Processing, 41(12): 3584-3590. DOI:10.1109/78.258102 |
Sweldens W. 1996. The lifting scheme:A custom-design construction of biorthogonal wavelets. Applied and Computational Harmonic Analysis, 3(2): 186-200. DOI:10.1006/acha.1996.0015 |
Sweldens W. 1998. The lifting scheme:A construction of second generation wavelets. SIAM Journal on Mathematical Analysis, 29(2): 511-546. DOI:10.1137/S0036141095289051 |
Sweldens W, Schröder P. 2000. Building your own wavelets at home. //Klees R, Haagmans R eds. Wavelets in the Geosciences. Berlin: Springer, 72-107.
|
Vasilyev O V, Paolucci S, Sen M. 1995. A multilevel wavelet collocation method for solving partial differential equations in a finite domain. Journal of Computational Physics, 120(1): 33-47. DOI:10.1006/jcph.1995.1147 |
Vasilyev O V, Paolucci S. 1996. A dynamically adaptive multilevel wavelet collocation method for solving partial differential equations in a finite domain. Journal of Computational Physics, 125(2): 498-512. DOI:10.1006/jcph.1996.0111 |
Vasilyev O V, Paolucci S. 1997. A fast adaptive wavelet collocation algorithm for multidimensional PDEs. Journal of Computational Physics, 138(1): 16-56. DOI:10.1006/jcph.1997.5814 |
Vasilyev O V, Bowman C. 2000. Second-generation wavelet collocation method for the solution of partial differential equations. Journal of Computational Physics, 165(2): 660-693. DOI:10.1006/jcph.2000.6638 |
Vasilyev O V, Yu V, Podladchikov Y Y, et al. 2001. Modelling of viscoelastic plume-lithosphere interaction using the adaptive multilevel wavelet collocation method. Geophysical Journal International, 147(3): 579-589. DOI:10.1046/j.1365-246x.2001.01540.x |
Vasilyev O V. 2003. Solving multi-dimensional evolution problems with localized structures using second generation wavelets. International Journal of Computational Fluid Dynamics, 17(2): 151-168. DOI:10.1080/1061856021000011152 |
Vasilyev O V, Kevlahan N K R. 2005. An adaptive multilevel wavelet collocation method for elliptic problems. Journal of Computational Physics, 206(2): 412-431. DOI:10.1016/j.jcp.2004.12.013 |
Wang J. 2009. Adaptive wavelets collocation method for solution of Maxwell's equations[Master's thesis] (in Chinese). Harbin: Harbin Institute of Technology.
|
Wang L Y. 2007. The construction and application of the second generation wavelet based on lifting scheme[Master's thesis] (in Chinese). Harbin: Harbin Institute of Technology.
|
Wang Y B, Yang H Z. 2006. Second generation wavelet based on adaptive solution of wave equation. International Journal of Nonlinear Sciences and Numerical Simulation, 7(4): 435-438. |
Yousefi H, Noorzad A, Farjoodi J. 2010. Simulating 2D waves propagation in elastic solid media using wavelet based adaptive method. Journal of Scientific Computing, 42(3): 404-425. DOI:10.1007/s10915-009-9328-7 |
Zhang X M, Liu K A, Liu J Q. 2005. A wavelet finite element method for the 2-D wave equation in fluid-saturated porous media. Chinese Journal of Geophysics (in Chinese), 48(5): 1156-1166. DOI:10.1002/cjg2.759 |
底青云, 王妙月. 1999. 雷达波有限元仿真模拟. 地球物理学报, 42(6): 818-825. DOI:10.3321/j.issn:0001-5733.1999.06.012 |
冯德山, 陈承申, 戴前伟. 2010. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报, 53(10): 2484-2496. DOI:10.3969/j.issn.0001-5733.2010.10.022 |
冯德山, 王珣. 2017. 基于卷积完全匹配层的非规则网格时域有限元探地雷达数值模拟. 地球物理学报, 60(1): 413-423. DOI:10.6038/cjg20170134 |
傅晓玲. 2000. 插值小波自适应求解双曲型偏微分方程. 北方工业大学学报, 12(3): 31-35. |
高欢乐, 赵凤群, 李静. 2011. 求解微分方程的二代小波配点法. 纺织高校基础科学学报, 24(3): 317-321. DOI:10.3969/j.issn.1006-8341.2011.03.001 |
何正嘉, 陈雪峰, 李兵, 等. 2006. 小波有限元理论及其工程应用. 北京: 科学出版社.
|
胡俊华, 田锦会. 2013. 基于第二代小波的PDEs数值新算法. 信息技术, (9): 88-90, 95. |
刘四新, 曾昭发. 2007. 频散介质中地质雷达波传播的数值模拟. 地球物理学报, 50(1): 320-326. DOI:10.3321/j.issn:0001-5733.2007.01.040 |
宓铁良, 孙兵兵, 杨慧珠. 2009. 基于第二代小波自适应网格的二维声波方程波传模拟. 地球物理学报, 52(11): 2862-2869. DOI:10.3969/j.issn.0001-5733.2009.11.021 |
王静. 2009. 自适应小波配点法求解Maxwell方程[硕士论文]. 哈尔滨: 哈尔滨工业大学. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D271007
|
汪丽艳. 2007. 基于提升格式的二代小波构造与应用[硕士论文]. 哈尔滨: 哈尔滨工业大学. http://cdmd.cnki.com.cn/Article/CDMD-10213-2008194182.htm
|
张新明, 刘克安, 刘家琦. 2005. 流体饱和多孔隙介质二维弹性波方程正演模拟的小波有限元法. 地球物理学报, 48(5): 1156-1166. DOI:10.3321/j.issn:0001-5733.2005.05.025 |
 2018, Vol. 61
2018, Vol. 61


