2. 有色金属成矿预测与地质环境监测教育部重点实验室(中南大学), 长沙 410083;
3. 东华理工大学省部共建核资源与环境国家重点实验室培育基地, 南昌 330013;
4. 核工业二三O研究所, 长沙 410011
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University), Ministry of Education, Changsha 410083, China;
3. State Key Laboratory Breeding Base of Nuclear Resources and Environment, East China University of Technology, Nanchang 330013, China;
4. Research Institute No.230, CNNC, Changsha 410011, China
在众多的地球物理方法中, 大地电磁法(Magnetotelluric, MT)与音频大地电磁法(Audio magnetotelluric, AMT)是重要的电磁勘探方法(范翠松等, 2008; 景建恩等, 2012; Ren et al., 2013, 2017, 2018),在矿产资源勘察和区域地质构造研究等领域得到广泛应用(陈辉等, 2011; 吕庆田等, 2015; Garcia et al., 2015; 任政勇等, 2017). MT信号(含AMT信号)是一种微弱的非平稳信号(Cai et al., 2009; Neukirch and Garcia, 2014),自提出开始,MT信号易受人文噪声影响的问题长期困扰着地球物理工作者(王书明和王家映, 2004; 肖晓等, 2011).进行MT或AMT勘探时,需要避开各类干扰源.中国地质矿产行业标准(DZ/T 0173-1997),《大地电磁测深法技术规程》明确规定,大地电磁法施工作业时,所选测点应该距离大型工厂、矿山、电站等设施2000 m以上,距离高压线500 m以上.这给大地电磁施工带来了极大的挑战,特别是干扰密布的矿集区,很多测点不具备施工条件,严重限制了方法的使用.音频大地电磁法以大地电磁法为基础,其场源特征、工作条件、观测参数与MT法基本相同,但频率更高.
数十年来,国内外学者提出了许多方法用于压制或者分离大地电磁信号中的噪声.其中具有里程碑意义的为远参考法(Goubau et al., 1978; Gamble et al., 1979)和Robust估计法(Egbert, 1997; Garcia and Jones, 2008), 这两种方法的处理结果获得广泛认可,已成为MT或者AMT数据处理的通用方法(Neukirch and Garcia, 2014).然而随着工业文明覆盖范围的增大,远参考点的选取变得愈发困难,实践经验表明,受人文干扰影响时,远参考法具有明显效果的测点所占的比例非常有限(汤井田等, 2012a; 王辉等, 2014; 李晋等, 2014; Li et al., 2018); Robust估计法要求观测到的数据大部分属于高质量的数据,这恰恰是实际情况中难以满足的条件(汤井田等,2013);数据段挑选法也可以获得可靠的结果,包括基于小波变换的数据段挑选(Weckmann et al., 2005)以及基于希尔伯特黄变换的数据段挑选(汤井田等, 2008; Cai et al., 2009; Neukirch and Garcia, 2014)等,然而实际环境中,很多干扰源都是持续存在的,因此数据段挑选常常无法奏效;周聪等(2015)针对AMT“死频带”提出了基于一维反演的Rhoplus校正法,但其应用前提是视电阻率或相位曲线中只有少数离群值,而持续性人文噪声可导致大量频点畸变.其他可用于AMT数据处理的手段还有小波滤波(Trad and Travassos, 2000; 范翠松等,2008;凌振宝等, 2016)、形态滤波(汤井田等, 2012a; 李晋等, 2014)、经验模态分解(汤井田等, 2008; Cai, 2016, 2017)、形态滤波与小波结合(汤井田等, 2015)等方法,这些方法有其自身的优势,但对于持续性人文噪声其效果也不甚理想.
综上,对于仅仅影响部分数据段的非持续性人文干扰,常规方法通常可以解决,但是对于持续性存在于整个采集过程的人文干扰,常规方法通常难以奏效,这类强干扰是本文重点关注的对象.
Mallat和Zhang(1993)首次提出了匹配追踪的概念,将信号分解为与冗余字典中的原子(或称为基)相匹配的部分以及与之不匹配的另一部分(残差),但是匹配追踪算法运算过于耗时,无法胜任海量AMT数据的处理.随着压缩感知理论的发展(Donoho, 2006; Candès and Wakin, 2008; Tang and Ma, 2011),在匹配追踪的基础上改进而来的信号重构算法受到广泛关注(Cai and Wang, 2011),这些改进的算法在重构精度和效率上得到显著改善,并被应用于大地电磁信噪分离(汤井田等,2017; Li et al., 2017),其通过设计与噪声匹配而对有用信号不敏感的冗余字典,分离出大地电磁信号中的强干扰成分.然而实测数据中的噪声形态复杂多样,预先设定的冗余字典无法与各类噪声完全匹配,从而不可避免的割裂噪声的完整结构,并损失部分有用信号.
Olshausen和Field (1996)利用自学习的方式,从大量图像样本中学习到了自然图像的特征原子,实现了少量的原子对自然图像的稀疏表示, 其成果发表在Nature杂志上,自学习型冗余字典开始受到关注.2004年一种叫做移不变稀疏编码(Shift invariant sparse coding, SISC)的字典学习方法被提出(Blumensath and Davies, 2004),并成功应用于孕妇与胎儿心跳的分离(Blumensath and Davies, 2005)以及音乐信号的分离(Blumensath and Davies, 2006; Plumbley et al., 2006).由于可以获得比传统方法更好的效果,SISC被多次改进并广泛应用于语音信号分离(Smith and Lewicki, 2006)和机械故障特征提取(Liu et al., 2011; 苗中华等,2014;Zhu et al., 2015; 朱会杰等, 2015b, 2016;余路等,2017)等领域.
学习型字典通过对信号样本进行训练,从给定样本中自主学习到信号或者噪声的规律(如干扰源的个数)与特征,最大限度的保留了信号或者噪声的完整信息,从而实现在不损失有用信号或者仅损失极少的有用信号的前提下,分离出信号中的噪声(Aharon et al., 2006).
AMT信号中的持续性干扰来源很多,例如电力系统产生的工频干扰,以及采矿、打桩等机械设备长时间工作时产生的干扰(汤井田等,2012b).与胎心监测信号以及机械故障信号类似,这类干扰的波形通常属于相关噪声,具有很强的规律性,相同或者相似的波形结构反复出现于数据采集的整个时间段,因此具有更大的挑战,当远参考法和数据段筛选等常规方法效果不佳时,本文基于移不变稀疏编码字典学习原理,提出一种有效的替代方法,用于分离出AMT信号中的持续性反复出现的强人文干扰.
1 方法原理 1.1 稀疏编码根据稀疏编码原理(Blumensath and Davies, 2005; Plumbley et al., 2006; 苗中华等,2014; 朱会杰等, 2015b, 2016),离散信号y=[y1, y2, …, yM]T可以表示成K个基与其系数的加权和:

|
(1) |
式中矩阵D∈RM×K称为字典,其列向量dk称为基函数或者原子,s=[s1, s2, …, sK]T是系数向量,ε为残差,服从方差为σ2的高斯分布.
字典D通常是冗余的,即M<K,多数情况下M≪K,如果D为满秩矩阵,s将有无穷多个解,但是稀疏表示所追求的是以最少的非零系数实现对信号的最佳逼近.因此,该问题可以表示为:
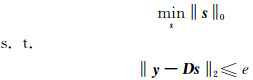
|
(2) |
式中‖·‖0表示l0范数,即向量中非零值的个数,‖·‖2表示l2范数,用于表征逼近误差,e为逼近误差的上限值,类似的,‖·‖1表示l1范数.
为了求得信号的最佳稀疏表示,需要解决两个问题,一是字典学习,即寻找能够与目标信号特征相符合的原子;当字典确定以后,即可以根据式(2)求得系数向量.
基于给定字典求解稀疏表示系数可以基于最大后验概率估计(Smith and Lewicki, 2006):
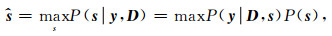
|
(3) |
式中P(y|D, s)表示基于式(1)模型相对给定系数的似然,P(s)表示系数的先验概率估计,并且s被假定统计独立于D,即:P(s|D)=P(s).基于式(1)中的高斯分布假设,该似然函数可变换为:
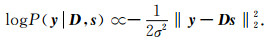
|
(4) |
为了促进系数的稀疏性,P(sk)通常选择为拉普拉斯分布,P(sk)∝exp(-θ|sk|); 同时,假设系数之间是统计独立的,即P(s)=∏kP(sk),则稀疏表示s的最大后验概率估计为:

|
(5) |
对于给定独立同分布的信号集Y={yi}i=1N,字典D可以根据最大似然估计推导:

|
(6) |
式中〈·〉y表示y的均值.基于独立同分布假设,似然函数P(Y|D)变为:

|
(7) |
同时,每一个样本的似然估计可以表示成:
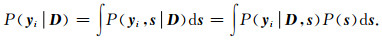
|
(8) |
根据式(4),并假设系数的先验概率分布为拉普拉斯分布,则似然式(8)可推导为:
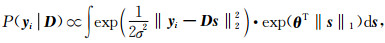
|
(9) |
式中s为隐含变量,使得P(yi|D)无法积分求得, 因此发展了多种逼近算法(Liu et al., 2011).对式(9)通过最大值近似求解积分(Olshausen and Field, 1996)得:
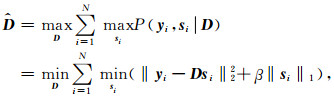
|
(10) |
式中第一项为逼近误差,第二项为具有惩罚参数β=2σ2θ的稀疏约束,从而将字典的最大似然估计转换成求解最优化问题.
1.2 移不变稀疏编码移不变稀疏编码是一种基于数据驱动的机器学习算法(Plumbley et al., 2006; Wang et al., 2015; 练秋生等,2015).与传统的稀疏表示不同,移不变稀疏编码将信号表示成基与系数的卷积,使得特征原子可以在信号的任意位置平移或翻转,给定有限数据集Y={y1, y2, …, yN},并假设基函数服从均匀分布,基函数与其对应系数的最大后验概率估计为:
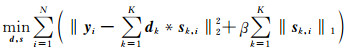
|
(11) |
s.t.
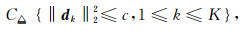
|
(12) |
式中“*”表示卷积算子,sk, i∈RM-K+1是基函数dk在信号yi中的稀疏激活,C定义了一个约束,防止求解dk太大而sk, i太小.当固定d不变时,可以基于凸优化方法求解s;当固定s不变时,可以基于凸优化方法求解d,字典学习可以通过反复的交替求解这两个问题来实现,当目标函数收敛后,基于学习到的基函数可以求得稀疏系数.基于最大后验概率的求解方式步骤简单,性能稳定,因此得到广泛应用(Liu et al., 2011).
1.3 AMT数据处理流程在进行数据处理时,将观测信号看成是天然AMT信号与人文噪声的线性叠加,由于天然AMT信号场源激发随机(肖晓等,2011),而持续性人文噪声通常都是有规律性的,因此,式(1)中的不同的基函数被用于表示不同类型的持续性人文噪声,将分离出人文干扰后的残差看成有用的AMT信号.
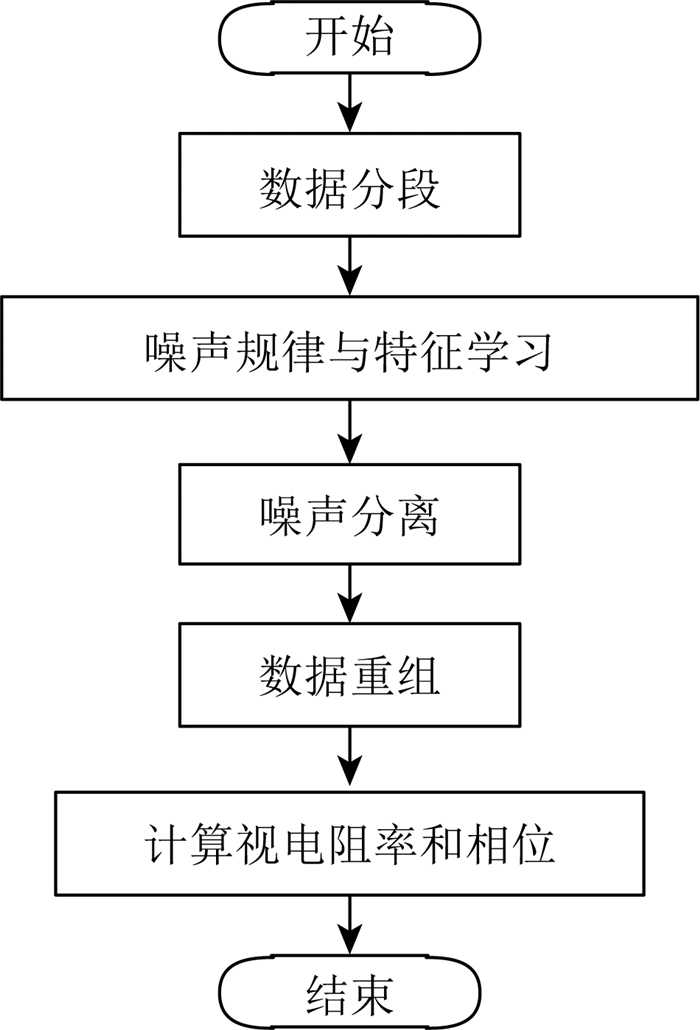
如图 1所示为本文所述AMT数据处理的基本流程,首先根据观测数据的长度和规律进行分段,由于观测数据的规模较大,如果将百万级别的数据分成数段分别处理,能够显著加快处理效率,此外,如果不同数据段之间所受人文干扰有明显差别,根据强干扰的类型分开处理也有利于获得更好的效果;第二步是利用移不变稀疏编码字典学习原理,从观测数据中学习到噪声的规律和特征结构(学习到的冗余字典);第三步是利用学习到的噪声特征结构对观测数据进行分解,分离出人文干扰,留下有用的天然大地电磁信号;第四步是数据重组,即用去噪后的数据替换原始数据;最后通过常规流程计算视电阻率和相位曲线.
|
图 1 AMT数据处理流程 Fig. 1 Flow chart of AMT data processing |
天然场源电磁法勘探时,受方波类噪声和似充放电噪声的影响非常普遍,这两类噪声通常幅度很大,且在傅里叶变换下具有无穷多个分量,因此影响的频率范围很广,是两类难以处理的噪声.伪随机方波信号中含有多种不同宽度的方波,似充放电波形中既有类似于尖脉冲的突变成分,也有类似于谐波的平稳成分,更能体现实际环境中复杂多样的噪声,因此试验中通过方波噪声和似充放电噪声来测试不同方法的优缺点.
为使得仿真结果更加接近实际情况,通过在无明显干扰的实测大地电磁数据中添加仿真产生的噪声,得到含噪信号,然后使用不同的方法对含噪信号进行信噪分离试验,最后通过信噪比SNR、重构误差E、曲线相似度(归一化互相关度)NCC、同一台计算机上处理耗时T四个指标(Li et al., 2017)对实验结果进行定量评价.试验中对比方法为形态滤波法(方波噪声采用3点直线型结构元素,似充放电噪声采用5点抛物线型结构元素,均为试验中最佳参数)和基于预设方波原子的IOMP法(朱会杰等,2015a).实测数据采集于青海人烟稀少的地方,通过时间域、频率域、极化方向(Weckmann et al., 2005; Escalas et al., 2013)以及视电阻率和相位曲线分析,可知该测点数据没有受明显人文干扰的迹象.
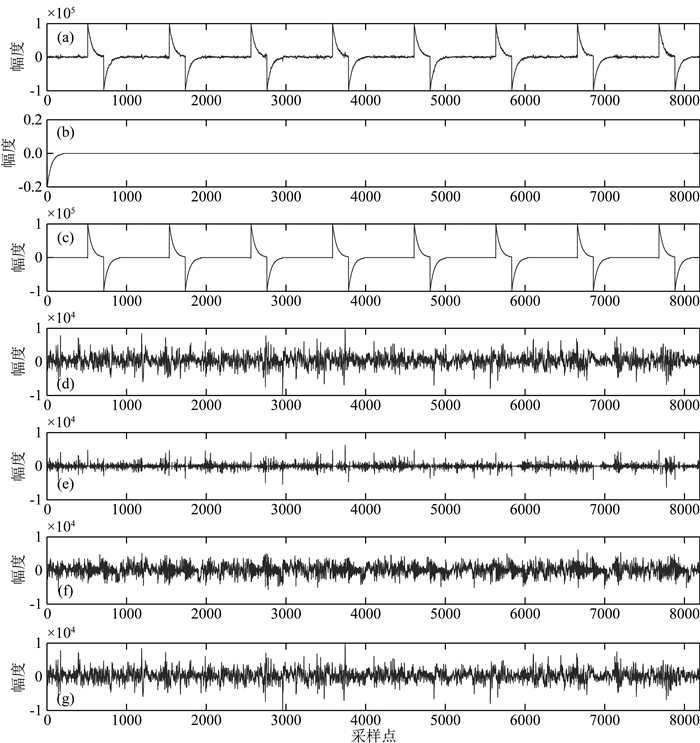
2.1 方波噪声分离测试时间域数据处理方法常常损失较多的低频信号,为此,首先从采样率为15 Hz的电场分量中截取一段长度为8192点的时间序列作为原始信号,加入伪随机七频方波,进行信噪分离试验,图 2所示为信噪分离实验结果.

|
图 2 伪随机方波噪声处理结果 (a)合成的含噪信号; (b) SISC学习到的特征原子; (c) SISC提取到的噪声; (d)原始信号; (e)形态滤波重构信号; (f) IOMP法重构信号; (g)本文方法重构信号. Fig. 2 Results of pseudo random square wave noise processing (a) Synthetic noisy data; (b) Learned atoms by SISC; (c) Extracted noise by the proposed method; (d) Original signal; (e) Signal from mathematical morphology filtering; (f) Filtered data by IOMP method; (g) Filtered data by the proposed method. |
如图 2a所示为加入伪随机七频波后得到的含噪信号,有用信号完全淹没在强噪声中,失去了天然大地电磁信号微弱、随机的特征,呈现出强规律性.含噪信号中包括8个相同的干扰结构,因此基函数的种类(对应干扰源的个数)设置为1,稀疏度(即原子个数)设置为8.另外,基函数的长度根据干扰信号的实际长度设置为512,迭代次数选择一个较大的值20.图 2b为依据上述参数,使用SISC字典学习方法从含噪信号中学习到的噪声结构(即特征原子),图 2c为本文方法分离出的噪声, 由图 2b和2c可知,提取到的特征原子和噪声轮廓非常的光滑,与理想的伪随机七频波非常接近,为后续优良的信噪分离效果奠定了基础.
图 2e为形态滤波法重构信号,图 2f为IOMP法重构信号,图 2g为本文方法重构信号.显然,与原始信号相比,形态滤波法损失了最多的有用信号,尤其是低频部分.IOMP法能取得不错的效果,仅在加入噪声的位置损失了少量低频信号,而本文方法很好地保留了原始信号.
由表 1可知,形态滤波法具有处理速度快的突出优点,处理时间几乎可以忽略不计,但是损失的有用信号也最多.本文方法的重构误差最小,信噪比最高,曲线相似度达到0.9694,能够最好的保留有用信号.此外,本文方法的处理时间相对基于预设冗余字典的IOMP法也显著减少,且可以通过减小迭代次数进一步缩短,因此更加有利于在海量AMT数据处理中的实际应用推广.
|
|
表 1 伪随机方波噪声处理结果定量评价 Table 1 Quantitative evaluation of pseudo random square wave noise processing results by different methods |
针对AMT信号受似充放电噪声影响严重的情况,从采样率为150 Hz的磁场分量中截取一段长度为8192点的时间序列作为原始信号,加入似充放电噪声,根据前述不同方法及参数设置规律进行信噪分离,得到图 3所示处理结果.
由图 3和表 2可知,对于似充放电噪声,本文方法也能够快速、准确地将其分离出来,且重构误差小、曲线相似度和信噪比显著提高.与原始信号相比可知,形态滤波法的缺点依然是损失较多的有用信号.由于方波原子与似充放电噪声匹配度不高,IOMP法也没有取得理想的效果,且耗时明显增加.本文方法由于能够自主学习噪声的特征结构,不受噪声的形态所限制,因此取得了令人满意的效果.
|
|
表 2 似充放电噪声处理结果定量评价 Table 2 Quantitative evaluation of quasi charge and discharge wave noise processing results by different methods |
应当说明的是,增大结构元素的长度时,形态滤波法损失的有用信号将显著减少,但是采样点数小于结构元素长度的噪声则无法滤除(汤井田等,2015).当设计与噪声更为匹配的原子时,IOMP法的处理效率可以显著提高,并且可以取得很好甚至比字典学习方法更好的效果,然而干扰信号的形态越复杂,设计与之匹配的原子库也越难.字典学习方法则不需要事先设计原子库,具有很强的通用性.
3 案例分析 3.1 四川省凉山州试验点分析为验证数据处理方法的有效性及便于对数据处理结果进行合理的评价,课题组于四川省凉山州使用加拿大凤凰公司V5-2000数据采集系统以及V8可控源信号发送系统进行了音频大地电磁信号观测试验,试验点编号记为S1.
观测时间包括当天7:15时到8:53时,其中7:15时到8:15时一共60 min内按照标准流程正常观测,将该时间段观测到的数据记为D1;8:16时到8:53时一共38 min,距离试验点1200 m处有加拿大凤凰公司V8发送系统在持续不断地发送不同频率的人工源信号,将该时间段观测到的数据记为D2.由于试验点人烟稀少,没有受到强人文干扰影响,因此可以认为通过D1数据集计算得到的视电阻率和相位曲线接近于该测点真实的大地电磁响应,可作为数据处理结果的评价标准.
3.1.1 时间域分析从8:16时到8:53时发送机按顺序一共发送了7种不同频率的方波信号,具体如表 3所示.由于充当负载的大地系统并非纯电阻电路,因此接收端观测到的信号并非理想的方波信号,而是畸变成似充放电波形.发送的人工源信号频率范围为0.125~1 Hz,但方波或似充放电信号均具有奇次谐波,因此实际受影响的频点并不局限于1 Hz以下.
在进行信噪分离时,为提高处理效率,根据人工源信号的主频率将数据分为7段.下面以第7频段人工源信号的处理为例进行说明.通过观察可知干扰信号可由一宽度为75个采样点的结构经过平移、翻转组成,因此将特征原子的宽度设置为75,基函数的种类设置为1;受第7频段人工源影响的AMT观测信号总采样点数约为38250,因此稀疏度等于信号长度除以特征原子宽度,即510;迭代次数根据经验设置为10.
|
|
表 3 人工源信号主频率及持续时间 Table 3 Principal frequencies and durations of the controlled source signal |
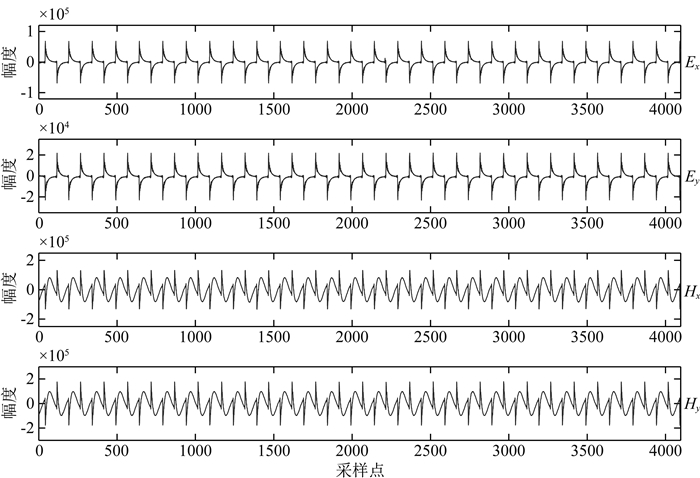
如图 4所示为受人工源影响的时间序列片段,采样频率为150 Hz,与图 4所示片段类似,D2数据集整个时间段都有很强的人工源信号,只是不同时间段信号的频率有所不同,完全没有天然大地电磁信号的特征.对于这种持续性存在的强噪声,现有的AMT数据处理手段很难获得良好的效果.
|
图 4 实验点S1去噪前时间序列片段,采样频率150 Hz Fig. 4 Raw time-series segments of the test site S1 with sampling rate of 150 Hz |
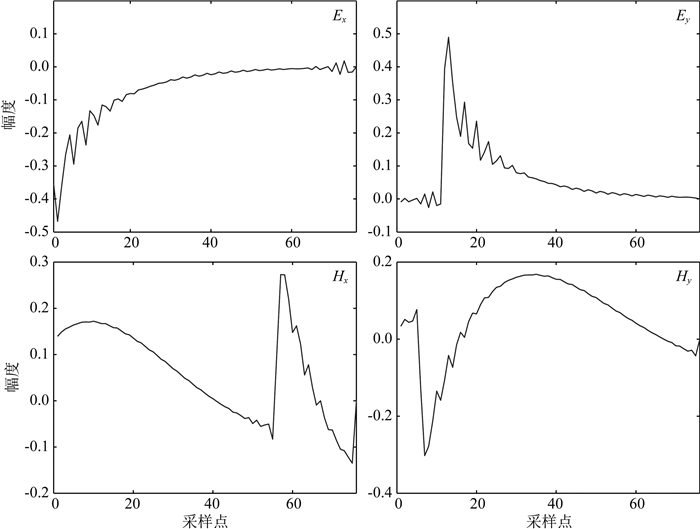
如图 5为学习到的特征原子.通过分析学习到的噪声结构可知,由于受到仪器硬件水平的限制,V8发射系统产生的人工源信号在上升沿和下降沿会产生有规律的锯齿状波形.实际情况中也是如此,由于设备开关的抖动等原因,AMT观测信号中的类充放电或者其他类型的干扰信号并非总是光滑的,如果使用预设的冗余字典方法来构建类似的原子,不仅难以精确匹配,还会因为自由参数过多而导致冗余字典库过于庞大,从而增大时间消耗.
|
图 5 SISC从图 4所示片段中学习到的特征原子 其中上半部分为电场分量中的特征原子,左半部分为东西方向电场或磁场分量中的特征原子. Fig. 5 Basic atoms learned by SISC from time series shown in Fig. 4 The upper part is basic atoms learned from electric components, and the left is basic atoms learned from east west directed components. |
如图 6为图 4所示时间序列经过本文方法去除人工源干扰后得到的AMT信号,从图中我们已经观察不到周期性的人工源信号,呈现出天然大地电磁信号微弱、随机的特征,从时间域效果来看,本文方法已经实现良好的信噪分离.
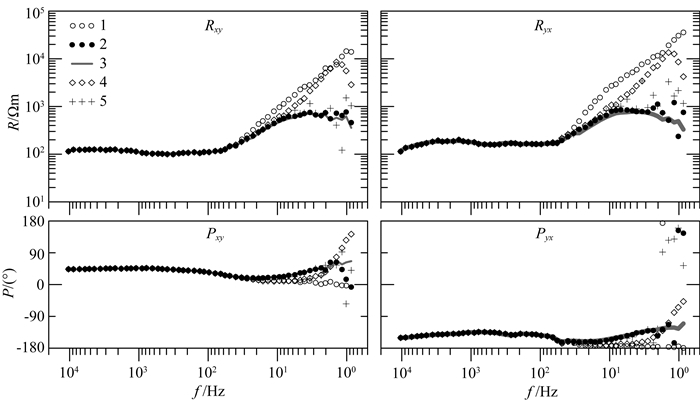
3.1.2 视电阻率与相位分析由图 7可知,处理前,受干扰段数据计算得到的视电阻率和相位曲线整体连续性很差,跳变剧烈,离群值多,相位曲线的数值分布在不合理的区间,与高质量的数据集计算得到的视电阻率和相位曲线有明显差异.经过本文方法将人工源信号分离之后,计算得到的视电阻率和相位曲线连续性和光滑度有显著改善,相位的数值回归到合理的区间,整体形态与无明显干扰时一致性好.单一的形态滤波法和基于预设方波原子的IOMP法则没有取得明显效果,其原因为形态滤波法和IOMP法去噪时对噪声的形态有一定的要求,而字典学习方法则无此限制.

|
图 7 试验点S1的视电阻率-相位曲线 其中上部为视电阻率曲线, 下部为对应的相位曲线, 曲线1由受干扰段数据集D2计算得到, 曲线2由受干扰段数据集D2经本文方法去噪后计算得到,曲线3由高质量数据集D1计算得到,曲线4由受干扰段数据集D2经3点直线型形态滤波法去噪后计算得到,曲线5由受干扰段数据集D2经基于预设方波原子的IOMP法去噪后计算得到. Fig. 7 Apparent resistivity and phase curves of site S1 The upper part is resistivity curves and bottom is phase curves. Curve 1 is obtained by noisy raw data set D2, curve 2 calculated from data set D2 but filtered by the proposed method, curve 3 obtained by noise-free data set D1, curve 4 calculated from data set D2 but filtered by the mathematical morphology filtering, curve 5 calculated from data set D2 but filtered by the IOMP method. |
值得注意的是,图 7中曲线2、4和5所示视电阻率和相位曲线使用的数据仅仅包括处理后的D2数据集,不包括质量好的D1数据集,这是本文与之前类似研究(李晋等,2014;汤井田等,2015)的重要区别之一,从而有力地证明本文所述方法能够从受人文干扰强烈的原始数据中,有效地分离出有用的AMT信号与人文干扰.
3.2 庐枞矿集区案例分析音频大地电磁法以高空中的天然交变电磁场为场源,距离观测点远,在地表观测到的信号幅值非常微弱; 由于场源的来源多样化并且随机化,因此观测到的大地电磁信号属于非平稳信号, 没有明显的规律性, 甚至类似于随机噪声(Manoj and Nagarajan, 2003; Neukirch and Garcia, 2014).
庐枞矿集区经济发达,电网交织,工矿企业密布,人文干扰严重.在该矿集区采集的大地电磁数据,有许多测点表现出明显的近源干扰,且有相当一部分经过远参考法处理和数据段筛选后依然没有明显改善.经过对远参考法处理效果不佳的测点数据观察发现,这些测点的时间序列中存在许多相同或者相似的结构,且持续、反复地出现于整个观测过程,这些结构在电场分量中通常表现为类充放电波形,在磁场分量中通常类似于欠阻尼振动波形,根据天然大地电磁信号的来源及特征可知,这种波形规则、周期性强的结构不属于天然大地电磁信号,需要将其滤除.
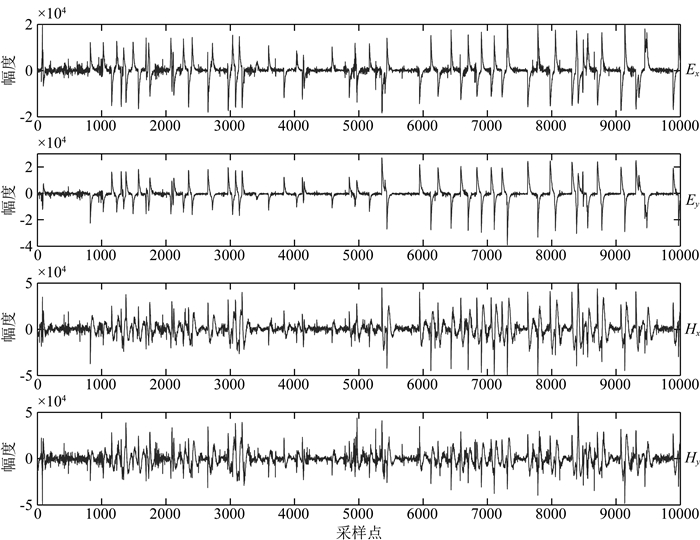
3.2.1 时间域分析图 8所示为庐枞矿集区实测点S2的时间序列片段,采样频率为150 Hz,采集设备为V5-2000.该测点观测时间约为70 min,其中前16 min无明显干扰(高质量数据段),第17 min开始受持续性人文干扰非常严重,采样率为150 Hz的时间序列中,从第17 min之后,始终分布着如图 8所示的强干扰信号,相似的噪声结构重复出现.
|
图 8 实测点S2去噪前时间序列片段,采样频率150 Hz Fig. 8 Raw time-series segments of the real site S2 with sampling rate of 150 Hz |
为验证本文方法的有效性,用本文方法对17~32 min内受干扰严重的数据(受干扰数据段)进行信噪分离,用分离出强干扰以后的数据计算视电阻率-相位曲线,与高质量数据段计算得到的视电阻率-相位曲线对比.
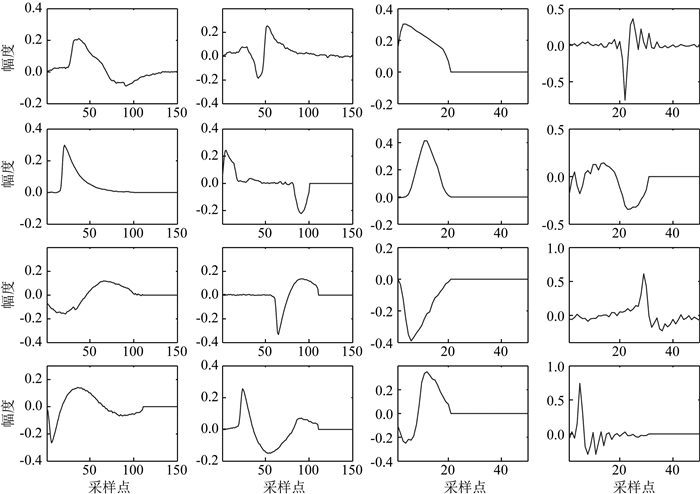
通过观察时间域信号的特征,将特征原子的类型(对应干扰源的个数)估计为5,原子宽度分别设置为150、150、50、50和50,稀疏度根据信号长度估计得到,迭代次数设置为10次,经过多次反复学习,移不变稀疏编码最终将特征原子的类型确定为4个,学习到的特征原子如图 9所示.
|
图 9 SISC从TS4中学习到的特征原子 其中第一至第四行分别对应Ex、Ey、Hx以及Hy分量中的原子. Fig. 9 Basic atoms learned by SISC from data set TS4 first row to the fourth row correspond to Ex, Ey, Hx and Hy components, respectively. |
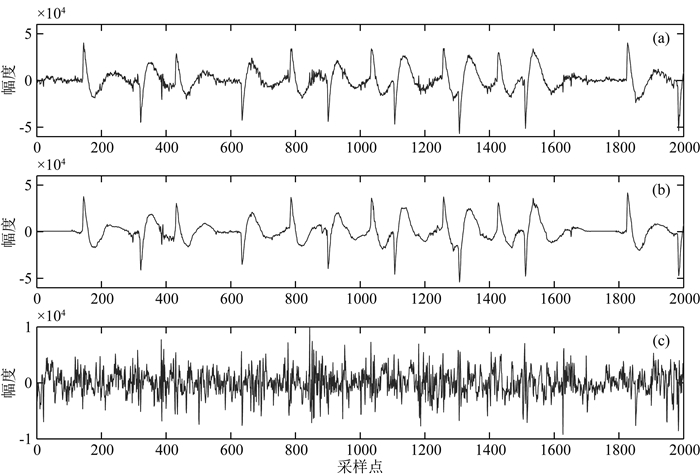
如图 10所示, 为便于更加清楚地分析信噪分离效果,从Hx分量上取出一段长度为2048个采样点的时域片段, 观察其去噪前后的变化.去噪前,Hx分量的波形具有明显的规律性,相似的结构重复的出现,并且出现的间隔大体相等、幅值相近,与天然大地电磁信号的随机特征不符; 此外,这些相似的结构其幅值量级明显大于其他数据段,因此也不具有天然大地电磁信号微弱的特征.本文方法分离出来的噪声轮廓较为光滑, 没有夹杂明显的有用信号, 去噪后的信号中周期性的结构完全消失, 恢复天然大地电磁信号的随机特征.
|
图 10 Hx分量信号片段信噪分离结果 (a)原始信号; (b) SISC分离出来的噪声; (c)残差, 即重构的AMT信号. Fig. 10 Signal-noise separation results of Hx segments (a) Raw data; (b) Noise; (c) Residual, i.e. recontructed AMT signal. |
图 11为使用学习到的特征原子对图 8所示时间序列进行稀疏分解的结果.由图 11可知,信号残差中周期性的结构完全消失,恢复天然场信号的微弱、随机状态.
3.2.2 视电阻率与相位分析如图 12所示,视电阻率-相位曲线3由高质量数据段计算得到(且与远参考法处理结果一致),该曲线连续、光滑,没有明显的离群值,所有视电阻率-相位曲线的数值分布于合理的区间.曲线1由原始的强干扰段数据计算所得,尽管该曲线连续性也较好,但是自低于40 Hz开始,视电阻率的数值呈近似于45°直线上升,对应相位的数值大多数接近于0°或者±180°,与CSAMT近区视电阻率-相位曲线规律类似,显然受到了明显的近源干扰(肖晓等, 2011)影响,不是地下电性结构的真实反映.曲线2为强干扰段数据经过本文方法分离出强干扰之后,计算得到的视电阻率-相位曲线,该曲线除低频部分有少数频点有所偏离以外,整体曲线与无强干扰情况下的曲线基本重合.由于该测点所受到的干扰信号宽度很窄,形态滤波法无法奏效.方波原子与窄脉冲有较好的匹配度,因此IOMP法对处理结果也有明显的改善,2 Hz以上的频点与无强干扰情况下的曲线基本一致.
同样值得注意的是,计算曲线2、4和5时,使用的数据仅包括进行强干扰分离后的17~32 min的数据,不包括1~16 min的高质量数据,从而再次证明本文方法能够对强干扰信号和有用的AMT信号进行准确分离.
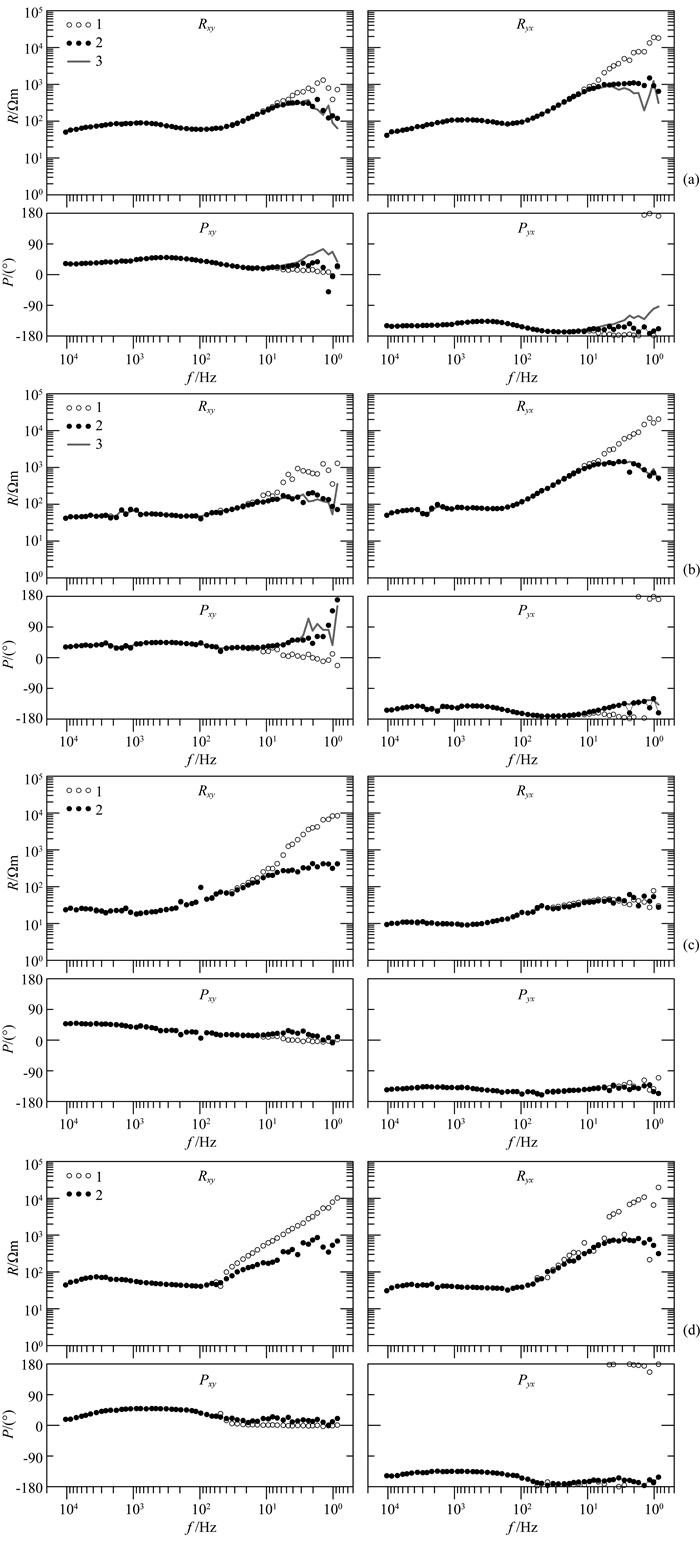
3.2.3 其他典型案例分析如图 13所示为庐枞矿集区其他典型AMT测点数据处理结果.这些测点均不同程度的受到了人文噪声的干扰,干扰信号的波形各不相同.测点S3和S4有部分时段没有受到强人文噪声影响,使用远参考法处理后视电阻率和相位曲线可以获得明显改善,且与未受强噪声影响时所得曲线基本一致;测点S5和S6全时段均有强人文噪声干扰,且视电阻率和相位曲线经过远参考处理后无明显改善.
对测点中受强干扰影响的数据段进行处理后,得到图 13所示视电阻率-相位曲线,结果表明,本文方法数据处理结果与远参考处理结果基本一致,当远参考法无法奏效时,本文方法依然取得了不错的效果.本文处理的AMT数据均不包含质量好的数据段,部分测点视电阻率-相位曲线中个别频点使用了SSMT2000软件进行简单的功率谱挑选.
4 结论音频大地电磁信号常常受到人文噪声的影响,远参考法、Robust阻抗估计以及数据段筛选等现有方法对于噪声压制有显著效果,然而这些方法并非所有的噪声问题都能够解决,特别是观测时间段内持续存在强人文噪声时,现有的方法通常效果不佳.针对这一问题,本文提出了基于移不变稀疏编码字典学习的音频大地电磁数据处理方法.经过仿真试验以及实测数据案例分析,获得了如下认识:
第一,对于AMT信号中有规律的噪声,不论波形简单或复杂,本文方法均能够准确将其分离,显著改善数据质量,当远参考法等常规方法无法奏效时,可作为一种有效的替代手段.
第二,本文方法根据噪声的规律自动学习得到干扰信号完整的特征结构,分离出人文干扰的同时能够最大限度的保留有用信号,处理结果可靠.
第三,本文方法相对于基于预先设定的冗余字典方法,在处理速度方面有明显的提高,更加适合海量AMT数据的处理.
本文方法适用于处理AMT信号中有一定规律的噪声,实际情况中,持续性存在的人文噪声以有规律者居多,对于少数长时间持续性存在且没有规律的人文噪声,使用本文方法处理时,由于学习到的特征原子与实际噪声的匹配度有所下降,因而在少数情况下,导致处理效果可能不太理想,这类人文噪声的有效处理需要进一步深入分析.
对于同一个测区甚至不同的测区,人文干扰的来源及特征是有规律可循的,通过字典学习等机器学习手段,从海量实测数据中获取人文干扰的规律与特征值得进一步深入研究.
致谢 作者感谢总装工程兵科研一所朱会杰博士在移不变稀疏编码理论与字典学习算法等方面给予的讨论与建议.
Aharon M, Elad M, Bruckstein A. 2006. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
Blumensath T, Davies M. 2004. On shift-invariant sparse coding. //Independent Component Analysis and Blind Signal Separation, Lecture Notes in Computer Science, Vol. 3195. Berlin, Heidelberg: Springer, 1205-1212.
|
Blumensath T, Davies M. 2005. Shift-invariant sparse coding for single channel blind source separation. //Workshop on Signal Processing with Adaptive Sparse Structured Representations (SPARS'05). France, 75-78. https://wenku.baidu.com/view/41ced0d076eeaeaad1f33033.html
|
Blumensath T, Davies M. 2006. Sparse and shift-Invariant representations of music. IEEE Transactions on Audio, Speech & Language Processing, 14(1): 50-57. |
Cai J H, Tang J T, Hua X R, et al. 2009. An analysis method for magnetotelluric data based on the Hilbert-Huang Transform. Exploration Geophysics, 40(2): 197-205. DOI:10.1071/EG08124 |
Cai J H. 2016. A combinatorial filtering method for magnetotelluric data series with strong interference. Arabian Journal of Geosciences, 9(13): 628. DOI:10.1007/s12517-016-2658-5 |
Cai J H. 2017. A time-frequency analysis method to obtain stable estimates of magnetotelluric response function based on Hilbert-Huang transform. Exploration Geophysics, 48(3): 192-200. DOI:10.1071/EG15014 |
Cai T T, Wang L. 2011. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Transactions on Information Theory,, 57(7): 4680-4688. DOI:10.1109/TIT.2011.2146090 |
Candès E J, Wakin M B. 2008. An introduction to compressive sampling. IEEE Signal Processing Magazine,, 25(2): 21-30. DOI:10.1109/MSP.2007.914731 |
Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluricmodeling with staggered-grid finite difference method. Chinese J. Geophys. (in Chinese), 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
Donoho D L. 2006. Compressed sensing. IEEE Transactions on Information Theory,, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
Egbert G D. 1997. Robust multiple-station magnetotelluric data processing. Geophysical Journal International,, 130(2): 475-496. DOI:10.1111/gji.1997.130.issue-2 |
Escalas M, Queralt P, Ledo J, et al. 2013. Polarisation analysis of magnetotelluric time series using a wavelet-based scheme:A method for detection and characterisation of cultural noise sources. Physics of the Earth & Planetary Interiors,, 218: 31-50. |
Fan C S, Li T L, Wang D Y. 2008. Treatment of wavelet transform for square wave noise in MT data. Journal of Jilin University (Earth Science Edition) (in Chinese), 38(S1): 61-63. |
Gamble T D, Goubau W M, Clarke J. 1979. Magnetotellurics with a remote magnetic reference. Geophysics, 44(1): 53-68. DOI:10.1190/1.1440923 |
Garcia X, Jones A G. 2008. Robust processing of magnetotelluric data in the AMT dead band using the continuous wavelet transform. Geophysics, 73(6): F223-F234. DOI:10.1190/1.2987375 |
Garcia X, Seillé H, Elsenbeck J, et al. 2015. Structure of the mantle beneath the Alboran Basin from magnetotelluric soundings. Geochemistry, Geophysics, Geosystems,, 16(12): 4261-4274. DOI:10.1002/2015GC006100 |
Goubau W M, Gamble T D, Clarke J. 1978. Magnetotelluric data analysis:removal of bias. Geophysics,, 43(6): 1157-1166. DOI:10.1190/1.1440885 |
Jing J E, Wei W B, Chen H Y, et al. 2012. Magnetotelluric sounding data processing based on generalized S transformation. Chinese J. Geophys. (in Chinese), 55(12): 4015-4022. DOI:10.6038/j.issn.0001-5733.2012.12.013 |
Li G, Xiao X, Tang J T, et al. 2017. Near-source noise suppression of AMT by compressive sensing and mathematical morphology filtering. Applied Geophysics, 14(4): 581-589. DOI:10.1007/s11770-017-0645-6 |
Li J, Tang J T, Xiao X, et al. 2014. Magnetotelluric data processing based on combined generalized morphological filter. Journal of Central South University (Science and Technology Edition) (in Chinese), 45(1): 173-185. |
Li J, Zhang X, Gong J Z, et al. 2018. Signal-noise identification of magnetotelluric signals using fractal-entropy and clustering algorithm for targeted de-noising. Fractals, 26(2): 1840011. DOI:10.1142/S0218348X1840011X |
Lian Q S, Shi B S, Chen S Z. 2015. Research advances on dictionary learning models, algorithms and applications. Acta Automatica Sinica (in Chinese), 41(2): 240-260. |
Ling Z B, Wang P Y, Wan Y X, et al. 2016. A combined wavelet transform algorithm used for de-noising magnetotellurics data in the strong human noise. Chinese J. Geophys. (in Chinese), 59(9): 3436-3447. DOI:10.6038/cjg20160926 |
Liu H N, Liu C L, Huang Y X. 2011. Adaptive feature extraction using sparse coding for machinery fault diagnosis. Mechanical Systems & Signal Processing,, 25(2): 558-574. |
Lv Q T, Dong S W, Tang J T, et al. 2015. Multi-scale and integrated geophysical data revealing mineral systems and exploring for mineral deposits at depth:A synthesis from SinoProbe-03. Chinese J. Geophys. (in Chinese), 58(12): 4319-4343. DOI:10.6038/cjg20151201 |
Mallat S G, Zhang Z F. 1993. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing,, 41(12): 3397-3415. DOI:10.1109/78.258082 |
Manoj C, Nagarajan N. 2003. The application of artificial neural networks to magnetotelluric time-series analysis. Geophysical Journal International,, 153(2): 409-423. DOI:10.1046/j.1365-246X.2003.01902.x |
Miao Z H, Zhou G X, Liu H N, et al. 2014. Tests and feature extraction algorithm of vibration signals based on sparse coding. Journal of Vibration and Shock (in Chinese), 33(15): 76-81, 118. |
Neukirch M, Garcia X. 2014. Nonstationary magnetotelluric data processing with instantaneous parameter. J. Geophys. Res.:Solid Earth,, 119(3): 1634-1654. DOI:10.1002/2013JB010494 |
Olshausen B A, Field D J. 1996. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 381(6583): 607-609. DOI:10.1038/381607a0 |
Plumbley M D, Abdallah S A, Blumensath T, et al. 2006. Sparse representations of polyphonic music. Signal Processing,, 86(3): 417-431. DOI:10.1016/j.sigpro.2005.06.007 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International,, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Ren Z Y, Chen C J, Tang J T, et al. 2017. A new integral equation approach for 3D magnetotelluric modeling. Chinese J. Geophys. (in Chinese), 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
Ren Z Y, Chen C J, Pan K J, et al. 2017. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surveys in Geophysics,, 38(2): 479-502. DOI:10.1007/s10712-016-9395-x |
Ren Z Y, Zhong Y Y, Chen C J, et al. 2018. Gravity Anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics,, 83(1): G1-G13. DOI:10.1190/geo2017-0219.1 |
Shi G M, Liu D H, Gao D H, et al. 2009. Advances in theory and application of compressed sensing. Acta Electronica Sinica (in Chinese), 37(5): 1070-1081. |
Smith E C, Lewicki M S. 2006. Efficient auditory coding. Nature,, 439(7079): 978-982. DOI:10.1038/nature04485 |
Tang G, Ma J W. 2011. Application of total-variation-based curvelet shrinkage for three-dimensional seismic data denoising. IEEE Geoscience and Remote Sensing Letters, 8(1): 103-107. DOI:10.1109/LGRS.2010.2052345 |
Tang J T, Hua X R, Cao Z M, et al. 2008. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data. Chinese J. Geophys. (in Chinese), 51(2): 603-610. |
Tang J T, Li J, Xiao X, et al. 2012a. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data. Chinese J. Geophys. (in Chinese), 55(5): 1784-1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
Tang J T, Xu Z M, Xiao X, et al. 2012b. Effect rules of strong noise on magnetotelluric (MT) sounding in the Luzong ore cluster area. Chinese J. Geophys. (in Chinese), 55(12): 4147-4159. DOI:10.6038/j.issn.0001-5733.2012.12.027 |
Tang J T, Zhang C, Xiao X, et al. 2013. Comparison of methods for magnetotelluric impedance estimation. The Chinese Journal of Nonferrous Metals (in Chinese), 23(9): 2351-2358. |
Tang J T, Liu Z J, Liu F Y, et al. 2015. The denoising of the audio magnetotelluric data set with strong interferences. Chinese J. Geophys. (in Chinese), 58(12): 4636-4647. DOI:10.6038/cjg20151225 |
Tang J T, Li G, Xiao X, et al. 2017. Strong noise separation for magnetotelluric data based on a signal reconstruction algorithm of compressive sensing. Chinese J. Geophys. (in Chinese), 60(9): 3642-3654. DOI:10.6038/cjg20170928 |
Trad D O, Travassos J M. 2000. Wavelet filtering of magnetotelluric data. Geophysics,, 65(2): 482-491. DOI:10.1190/1.1444742 |
Wang H, Wei W B, Jin S, et al. 2014. Removal of magnetotelluric noise based on synchronous time series relationship. Chinese J. Geophys. (in Chinese), 57(2): 531-545. DOI:10.6038/cjg20140218 |
Wang S M, Wang J Y. 2004. Application of higher-order statistics in magnetotelluric data processing. Chinese J. Geophys. (in Chinese), 47(5): 928-934. DOI:10.3321/j.issn:0001-5733.2004.05.027 |
Wang X Q, Zhu H J, Rui T, et al. 2015. Shift invariant sparse coding ensemble and its application in rolling bearing fault diagnosis. Journal of Vibroengineering,, 17(4): 1837-1748. |
Weckmann U, Magunia A, Ritter O. 2005. Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme. Geophysical Journal International,, 161(3): 635-652. DOI:10.1111/gji.2005.161.issue-3 |
Xiao X, Tang J T, Zhou C, et al. 2011. Magnetotelluric sounding in the Lujiang-Zongyang ore district and preliminary study of electrical structure. Acta Geologica Sinica (in Chinese), 85(5): 873-886. |
Yu L, Qu J L, Gao F, et al. 2017. Feature extraction of weak vibration signal based on improved sparse coding. Chinese Journal of Scientific Instrument (in Chinese), 38(3): 711-717. |
Zhou C, Tang J T, Ren Z Y, et al. 2015. Application of the Rhoplus method to audio magnetotelluric dead band distortion data. Chinese J. Geophys. (in Chinese), 58(12): 4648-4660. DOI:10.6038/cjg20151226 |
Zhu H J, Wang X Q, Zhao Y, et al. 2015. Sparse representation based on adaptive multiscale features for robust machinery fault diagnosis. Institution of Mechanical Engineers,, 229(12): 1303-2313. |
Zhu H J, Wang X Q, Rui T, et al. 2015a. Implication of improved matching pursuit in de-noising for square wave. Journal of PLA University of Science and Technology (Natural Science Edition) (in Chinese), 16(4): 305-309. |
Zhu H J, Wang X Q, Rui T, et al. 2015b. Shift invariant sparse coding for blind source separation of single channel mechanical signal. Journal of Vibration Engineering (in Chinese), 28(4): 625-632. |
Zhu H J, Wang X Q, Rui T, et al. 2016. Multi scale shift invariant sparse coding for robust machinery diagnosis. Transactions of Beijing Institute of Technology (in Chinese), 36(1): 19-24. |
陈辉, 邓居智, 谭捍东, 等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究. 地球物理学报, 54(06): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
范翠松, 李桐林, 王大勇. 2008. 小波变换对MT数据中方波噪声的处理. 吉林大学学报(地球科学版), 38(S1): 61-63. |
景建恩, 魏文博, 陈海燕, 等. 2012. 基于广义S变换的大地电磁测深数据处理. 地球物理学报, 55(12): 4015-4022. DOI:10.6038/j.issn.0001-5733.2012.12.013 |
李晋, 汤井田, 肖晓, 等. 2014. 基于组合广义形态滤波的大地电磁资料处理. 中南大学学报(自然科学版), 45(1): 173-185. |
练秋生, 石保顺, 陈书贞. 2015. 字典学习模型、算法及其应用研究进展. 自动化学报, 41(2): 240-260. |
凌振宝, 王沛元, 万云霞, 等. 2016. 强人文干扰环境的电磁数据小波去噪方法研究. 地球物理学报, 59(9): 3436-3447. DOI:10.6038/cjg20160926 |
吕庆田, 董树文, 汤井田, 等. 2015. 多尺度综合地球物理探测:揭示成矿系统、助力深部找矿——长江中下游深部探测(SinoProbe-03)进展. 地球物理学报, 58(12): 4319-4343. DOI:10.6038/cjg20151201 |
苗中华, 周广兴, 刘海宁, 等. 2014. 基于稀疏编码的振动信号特征提取算法与实验研究. 振动与冲击, 33(15): 76-81, 118. |
任政勇, 陈超健, 汤井田, 等. 2017. 一种新的三维大地电磁积分方程正演方法. 地球物理学报, 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
汤井田, 化希瑞, 曹哲民, 等. 2008. Hilbert-Huang变换与大地电磁噪声压制. 地球物理学报, 51(2): 603-610. DOI:10.3321/j.issn:0001-5733.2008.02.034 |
汤井田, 李晋, 肖晓, 等. 2012a. 数学形态滤波与大地电磁噪声压制. 地球物理学报, 55(5): 1784-1793. DOI:10.6038/j.issn.0001-5733.2012.05.036 |
汤井田, 徐志敏, 肖晓, 等. 2012b. 庐枞矿集区大地电磁测深强噪声的影响规律. 地球物理学报, 55(12): 4147-4159. DOI:10.6038/j.issn.0001-5733.2012.12.027 |
汤井田, 张弛, 肖晓, 等. 2013. 大地电磁阻抗估计方法对比. 中国有色金属学报, 23(9): 2351-2358. |
汤井田, 刘子杰, 刘峰屹, 等. 2015. 音频大地电磁法强干扰压制试验研究. 地球物理学报, 58(12): 4636-4647. DOI:10.6038/cjg20151225 |
汤井田, 李广, 肖晓, 等. 2017. 基于压缩感知重构算法的大地电磁强干扰分离. 地球物理学报, 60(9): 3642-3654. DOI:10.6038/cjg20170928 |
王辉, 魏文博, 金胜, 等. 2014. 基于同步大地电磁时间序列依赖关系的噪声处理. 地球物理学报, 57(2): 531-545. DOI:10.6038/cjg20140218 |
王书明, 王家映. 2004. 高阶统计量在大地电磁测深数据处理中的应用研究. 地球物理学报, 47(5): 928-934. DOI:10.3321/j.issn:0001-5733.2004.05.027 |
肖晓, 汤井田, 周聪, 等. 2011. 庐枞矿集区大地电磁探测及电性结构初探. 地质学报, 85(5): 873-886. |
余路, 曲建岭, 高峰, 等. 2017. 基于改进稀疏编码的微弱振动信号特征提取算法. 仪器仪表学报, 38(3): 711-717. DOI:10.3969/j.issn.0254-3087.2017.03.025 |
周聪, 汤井田, 任政勇, 等. 2015. 音频大地电磁法"死频带"畸变数据的Rhoplus校正. 地球物理学报, 58(12): 4648-4660. DOI:10.6038/cjg20151226 |
朱会杰, 王新晴, 芮挺, 等. 2015a. 改进的匹配追踪在方波信号滤波中的应用. 解放军理工大学学报(自然科学版), 16(4): 305-309. |
朱会杰, 王新晴, 芮挺, 等. 2015b. 基于移不变稀疏编码的单通道机械信号盲源分离. 振动工程学报, 28(4): 625-632. |
朱会杰, 王新晴, 芮挺, 等. 2016. 多尺度移不变稀疏编码及其在机械故障诊断中的应用. 北京理工大学学报, 36(1): 19-24. |
 2018, Vol. 61
2018, Vol. 61