2. 长安大学计算地球物理研究所, 西安 710054;
3. 阿联酋哈利法科技大学石油学院, 阿布扎比 2533
2. Institute of Computational Geophysics, Chang'an University, Xi'an 710054, China;
3. The Petroleum Institute, Khalifa University of Science and Technology, Po BOX 2533, Abu Dhabi, UAE
双相介质理论充分考虑了介质物性结构、流体性质以及固体骨架与孔隙流体间的相互作用对弹性波传播的影响,因此双相介质模型更能准确地描述实际地质结构和地层性质(杨顶辉等, 2000; 杨顶辉, 2002).起初对双相介质的研究主要是基于Biot理论(Biot, 1956a, 1956b),然而多数情况下Biot理论预测的波能量衰减和速度频散比实际观测值低,不能对实验结果和实际数据给出合理的解释(Winkler, 1985; Jones, 1986; Mavko and Jizba, 1991; Gist, 1994).研究发现,含流体孔隙介质中地震波的传播存在Biot流动和喷射流动这两种重要的波诱导流体流动形式,它们作为一个耦合过程共同对弹性波的传播产生影响,Dvorkin和Nur(1993)基于孔隙各向同性一维问题,将这两种流体流动机制有机地统一起来,提出了Biot-Squirt(BISQ)模型,该模型较之仅考虑宏观流动的Biot模型更能准确地预测地震波的衰减和频散.然而,BISQ模型在建立的过程中引入了一个描述喷射流动机制的微尺度参数,降低了BISQ模型准确预测实际岩石中波衰减和频散的能力(Gurevich and Lopatnikov, 1995).鉴于此,Diallo和Appel(2000)对孔隙流体压力公式进行重新推导,提出了一种不依赖于特征喷流长度参数的改进BISQ模型.改进后的BISQ模型在不引入特征喷流长度的情况下,将含流体孔隙介质中Biot流动和喷射流动两种重要的力学机制有机地结合起来,且各相关参数具有明确的物理意义和可实现性(Diallo et al., 2003).近年来,一些研究学者从波场数值模拟的角度研究了改进BISQ模型所揭示的含流体孔隙介质中弹性波的传播规律(韩翀等, 2007; 彭传正等, 2007; 周竹生和唐磊, 2012; 刘财等, 2013; 兰慧田等, 2014).
常用的地震波场数值模拟方法有伪谱法、有限差分法、谱元法和有限元法等,有限差分法因其具有编程易实现、计算效率高、对内存需求相对较小和并行计算程度高等优点而被广泛应用.但是当地形存在起伏时,应用传统笛卡尔坐标系的规则矩形网格,将不可避免地采用阶梯状网格近似来处理自由地表或介质分界面,从而造成数值散射.国内外许多学者针对这一情况对有限差分法做了改进,以便能够适用于含起伏地表条件下的地震波数值模拟(Jih et al., 1988; Tessmer et al., 1992; Opršal and Zahradník, 1999; Hestholm et al., 1999; Hestholm and Ruud, 1994, 2000; Hayashi et al., 2001; Tarrass et al., 2011).虽然取得了一定进展,但仍缺乏一种在曲线网格中较为准确地实施自由表面条件的方法.Zhang和Chen(2006)基于曲线网格提出了牵引力镜像法,较好地解决了自由地表问题,这种曲线网格有限差分法采用贴体网格来描述自由表面,地表的网格线紧贴地形,这样就避免了台阶近似造成的数值散射.Zhang等(2012)、Sun等(2016)将曲线网格有限差分法分别应用于各向同性和各向异性介质,证明了该方法可以精确的模拟含起伏地表情况下地震波的传播规律.
众所周知,起伏地形是普遍存在的,而浅地表介质通常都由富含孔隙的固体构成,孔隙中充填流体,这种介质的不均匀性会使波传播在地表处显示出更为复杂的特征(张煜等,2015),所以含起伏自由地表情况下双相介质中地震波传播规律的研究具有重要的实际意义.本文采用Zhang和Chen(2006)提出的曲线网格有限差分法,以基于改进BISQ模型的二维双相各向同性介质的一阶速度-应力方程为基础,推导出了曲线坐标系下对应的一阶速度-应力方程和自由地表边界条件,然后采用低频散、低耗散的同位网格MacCormack有限差分法来离散方程,并采用紧致的单边MacCormack差分格式结合牵引力镜像法来施加自由地表边界条件,实现了波场数值模拟,并且根据模拟结果具体分析了双相介质中地震波的传播特征,与此同时研究了地震波在自由地表和介质界面处的反射与透射现象,重点讨论了基于改进BISQ模型下含起伏地表各向同性双相介质中的地震波的传播特征.
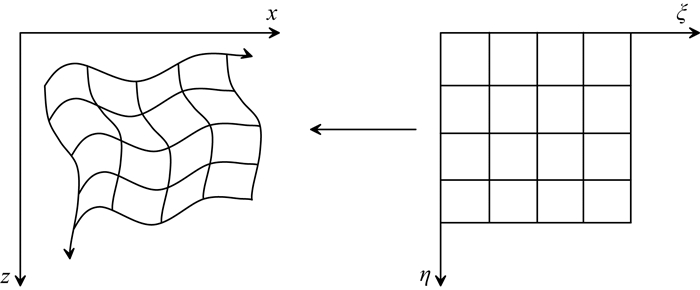
1 基于改进BISQ模型双相介质中曲线网格有限差分算法 1.1 曲线坐标系与直角坐标系的转换关系曲线网格方法实际上是将非规则物理空间变换到一个规则的计算空间,然后在这个规则的计算空间中进行均匀网格剖分(蒋丽丽和孙建国, 2008),因此,曲线网格可以通过计算空间到物理空间的坐标变换来获得(如图 1所示).
|
图 1 曲线网格和计算网格的网格变换关系 Fig. 1 Transform a boundary-conforming grid into a uniform grid |
本文采用Thompson等(1985)、蒋丽丽(2010)介绍的方法求取曲线坐标系与直角坐标系的转换关系.曲线网格生成之后,建立直角坐标系和曲线坐标系下网格点的一一对应关系:
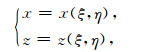
|
(1) |
对公式(1)分别关于x, z求偏导,为了公式表示方便简洁,引入记号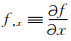

|
(2) |
由(2)式整理可以得到

|
(3) |
式中: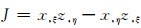
垂直于自由表面的单位向量:
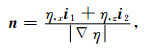
|
(4) |
式中:i1和i2分别是直角坐标系x-轴和z-轴的单位向量,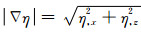
地震波在含流体孔隙介质中传播时存在Biot流动和喷射流动两种流体流动机制,Dvorkin和Nur(1993)基于孔隙各向同性一维问题将这两种流体流动机制有机地统一起来,提出了Biot-Squirt(BISQ)模型,该模型较之仅考虑宏观流动的Biot模型能更准确地预测地震波的衰减和频散.而Diallo和Appel(2000)针对BISQ模型提出了改进BISQ模型, 其优势在于在描述流体压力的表达式中不再含有不便于实际描述的微观参量, 更加方便了地震波波场模拟的实现.
在时空域内,基于改进BISQ模型的二维各向同性双相介质的一阶速度-应力方程可以表示为(Diallo and Appel, 2000; 周竹生和唐磊, 2012)

|
(5) |
式中: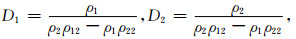
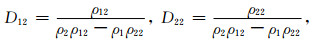
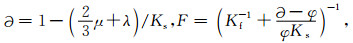
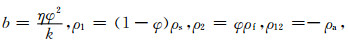
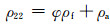
λ和μ为固体骨架的拉梅常数,φ表示孔隙度,ρs和ρf分别是固体和流体的密度,ρa表示固流耦合附加质量密度,∂为有效应力之孔隙弹性系数,Ks和Kf分别表示固体骨架和固体颗粒的体积模量,F表示Biot流动系数密度,η表示孔隙流体的黏滞系数,k表示孔隙介质的渗透率.
利用链锁法则和公式(5),本文推导出曲线坐标系下的一阶速度-应力方程:
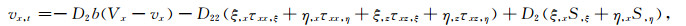
|
(6a) |
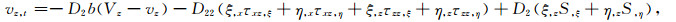
|
(6b) |

|
(6c) |
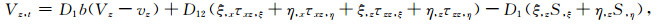
|
(6d) |
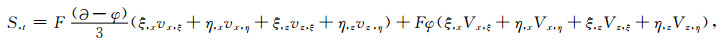
|
(6e) |
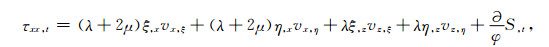
|
(6f) |
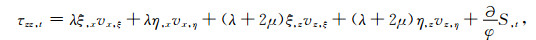
|
(6g) |

|
(6h) |
公式(6)可以用矩阵形式表示为

|
(7) |
其中:
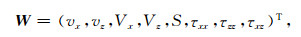
|
(8) |
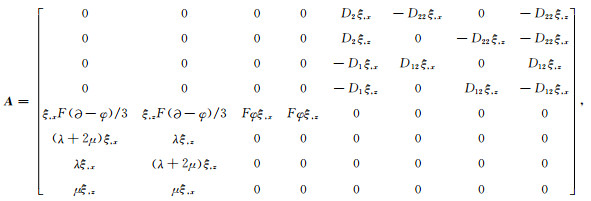
|
(9) |
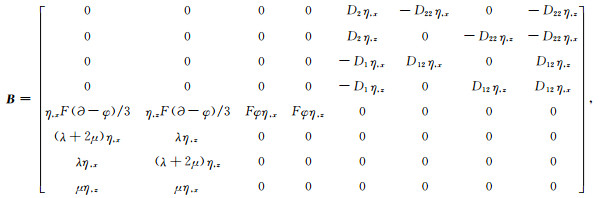
|
(10) |
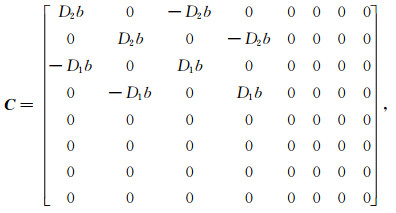
|
(11) |

|
(12) |
Hixon和Turkel(2000)采用Tam和Webb(1993)提出的DRP(Dispersion Relation Preserving)的方法对MacCormack格式的系数进行了优化,得到了低频散、低耗散的DRP/opt MacCormack格式.DRP/opt MacCormack是一种高阶优化的MacCormack类有限差分格式,相对于传统的2~4阶MacCormack格式,它能够更好地抑制数值频散, 祝贺君等(2009)将此方法应用于二维各向异性介质的地震波场数值模拟中,验证了DRP/opt MacCormack差分格式既保留了同位网格的优势又避免了它的缺点, 是一种有效地研究复杂各向异性介质中地震波传播规律的工具.本文采用DRP/opt MacCormack有限差分算子来离散方程.
同位网格MacCormack格式的两个偏心差分格式——向前差分和向后差分格式为(Hixon and Turkel, 2000)

|
(13) |
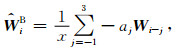
|
(14) |
其差分系数为

|
(15) |
二维情况下将上述单边差分格式进行组合构成DRP/opt MacCormack有限差分格式(Zhang and Chen, 2006),并对公式(7)进行离散:

|
(16) |
在时间方向上采用Hixon(1997),Hixon和Turkel(2000)提出的4~6阶低频散和低损耗的龙格库塔法(Runge-Kutta, 简写为RK),即采用四阶Runge-Kutta法和六阶Runge-Kutta法混合使用的高阶时间积分.结合DRP/opt MacCormack有限差分算子的时间积分具体实施步骤如下(Hixon, 1997; Hixon and Turkel, 2000):
在时间循环中,第一步采用四阶RK时间积分:
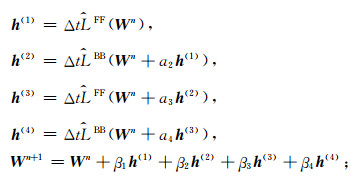
|
(17) |
第二步采用六阶RK时间积分:
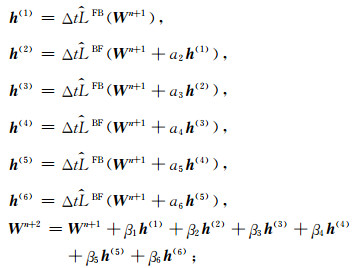
|
(18) |
第三步采用四阶RK时间积分:

|
(19) |
第四步采用六阶RK时间积分:
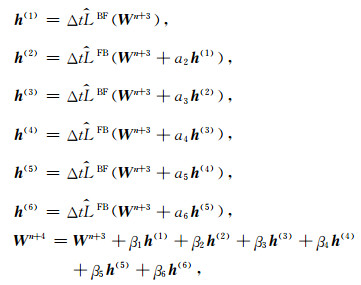
|
(20) |
其中四阶RK时间积分公式中:a1=0,a2=0.5,a3=0.5,a4=1;β1=1/6,β2=1/3,β3=1/3,β4=1/6.
六阶RK时间积分公式中:a1=0,a2=0.353323,a3=0.999597,a4=0.152188,a5=0.534216,a6=0.603907;β1=0.0467621,β2=0.137286,β3=0.170975,β4=0.197572,β5=0.282263,β6=0.165142.
1.4 自由地表边界条件在曲线坐标系中釆用Zhang和Chen(2006)提出的牵引力镜像法来处理弯曲地表的自由地表条件,在双相介质中,自由表面条件除了地表牵引力为零外,流体压力在地表的值也为零,即
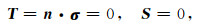
|
(21) |
其中T是牵引力,n是自由表面的单位法向量.设自由表面平行于ξ轴,通过把自由表面的单位法向量公式(4)代入到应力自由表面边界条件公式(21), 得到曲线坐标系下的应力自由表面边界条件:

|
(22) |
双相介质中应用牵引力镜像法,公式(6a)—(6d)的空间导数项需要展开成曲线坐标系中的保守形式:
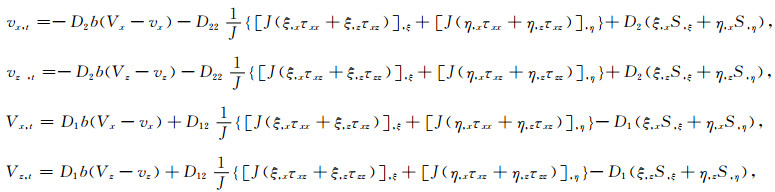
|
(23) |
对比公式(22)可以发现,公式(23)关于η求导项可以用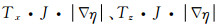

|
(24) |
自由表面格点上的牵引力分量为零的条件可以由速度自由表面条件保证,将(22)式左右两侧同时对时间求导,并将式(6e)—(6h)带入,得到

|
(25) |
式中:

|
(26) |

|
(27) |
在自由表面,先求出速度水平向导数,然后用(25)式求出速度垂向导数.
k=k0-1和k=k0-2网格层不满足DRP/opt MacCormack有限差分算子的使用条件,为使边界处的差分格式精度与内部高阶格式相匹配,k=k0-1和k=k0-2网格层的速度关于η轴的导数由单边4/4阶紧致MacCormack差分算子计算得到:
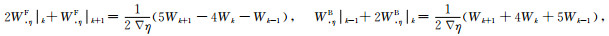
|
(28) |
公式(25)式中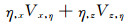
其他人工边界采用简单指数衰减层吸收边界的波场,波场衰减项为
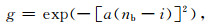
|
(29) |
其中a是衰减因子,nb是吸收层的宽度,i是吸收层内距离内边界的网格个数.
震源时间函数采用雷克子波:
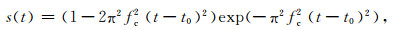
|
(30) |
其中fc为震源主频,t0为延迟时间.
2 数值模拟算例及分析 2.1 地表水平半空间模型和水平两层模型为了验证本文算法的正确性,我们设计了一个地表水平半空间模型和一个水平两层模型,模型大小和模型介质参数选择与兰慧田等(2014)设置的一致.两个模型均没有施加自由地表边界条件.
图 2为模型网格剖分示意图,模型大小均为2540 m×2540 m.其中图 2b模型界面位于-1680 m处;图 2c地表由高斯函数z=z0+b0exp[-(x-x0)2/a02]生成,z0=0 m,b0=-200 m,x0=1270 m,a0=600 m;图 2d地表由高斯函数z=z0+b0exp[-(x-x0)2/a02]+b1exp[-(x-x1)2/a12]生成,z0=0 m,b0=100 m,x0=840 m,a0=400 m,b1=-100 m,x1=1700 m,a1=400 m;图 2d介质分界面由高斯函数z=z0+b0exp[-(x-x0)2/a02]生成,z0=-1000 m,b0=200 m,x0=1270 m,a0=800 m.

|
图 2 模型网格剖分示意图 Fig. 2 Mesh generation of models |
地表水平半空间模型如图 2a所示,模型介质参数如表 1第a行所示,震源位于(1270 m,-1270 m)处;水平两层模型如图 2b所示,模型介质参数第一层如表 1第b行所示,第二层如表 1第c行所示,震源位于(1270 m,-1480 m)处.两个模型网格间距均为dx=dz=1 m,时间采样间隔均为0.1 ms,震源子波主频均为30 Hz,延迟时间均为0.04 s.
|
|
表 1 模型介质物性参数 Table 1 Simulation parameters for the models |
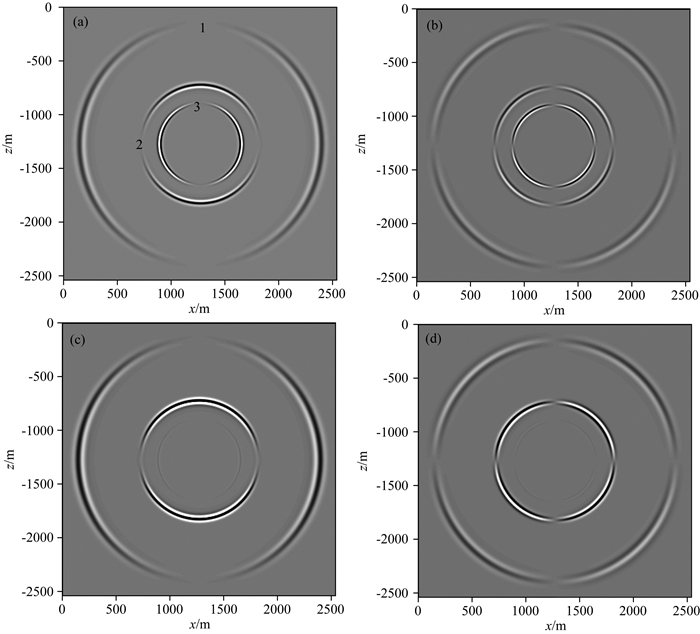
图 3为地表水平半空间模型模拟得到的0.35 s时刻的波场快照图,其中图a、b、c和d分别对应流相Vx分量、流相Vz分量、固相Vx分量和固相Vz分量.图 3a中所标震相1到3分别为快纵波、横波和慢纵波.波场数值模拟结果显示,当流体为非黏滞性时,快照中不仅出现了类似于单相各向同性介质中出现的纵波和横波,还出现了慢纵波,且慢纵波在固相中的振幅小于在流相中的振幅,即在流相中更容易观测到慢纵波;从图中可以看出各波前面都非常清晰,没有产生可见的网格频散现象.波场数值模拟结果与兰慧田等(2014)模拟得到的结果相符.
|
图 3 地表水平半空间模型0.35 s时刻的波场快照 (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz分量. Fig. 3 Wavefield snapshots at time of 0.35s for half-space model with horizontal surface (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz in solid phase. |
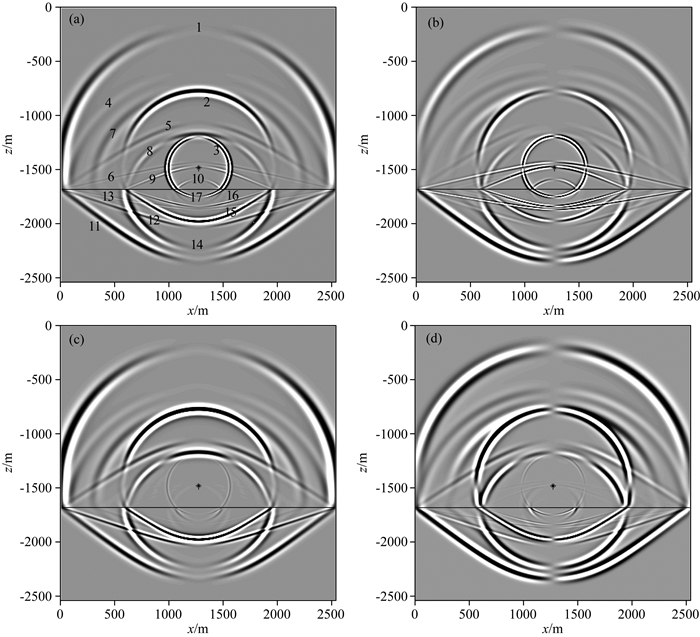
图 4为水平两层模型模拟得到的0.30 s时刻的波场快照图,其中图a、b、c和d分别对应流相Vx分量、流相Vz分量、固相Vx分量和固相Vz分量.波场数值模拟的结果显示,当两层介质中的流体均为非黏滞性时,快纵波、横波和慢纵波在介质分界面处均发生了反射和透射现象,并发生了波型转换;波场快照中可同时观测到多种波.图 4a所标的震相1到3分别为直达快纵波、直达横波和直达慢纵波,4到6分别是快纵波遇到界面反射形成的反射快纵波、转换横波和转换慢纵波,7到9分别为横波遇到界面反射形成的转换快纵波、反射横波和转换慢纵波,10为反射慢纵波,11到13分别为快纵波透过界面形成的透射快纵波、转换横波和转换慢纵波,14到16分别为横波透过界面后形成的透射转换快纵波、透射横波和透射转换慢纵波,17为透射慢纵波.波场数值模拟显示的各类波在介质分界面处的反射和透射规律与兰慧田等(2014)模拟得到的结果相符,验证了基于改进的BISQ模型双相各向同性介质中采用曲线网格有限差分法的正确性.
|
图 4 水平两层模型0.30s时刻的波场快照 (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz分量.图中黑色实线为界面位置, 黑星为震源位置. Fig. 4 Wavefield snapshots at time of 0.30s for horizontal two-layer model (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz component in solid phase. In figure the black lines and star represent the subsurface interface and the source location, respectively. |
虽然通过与前人研究工作的对比,我们验证了本文在基于改进BISQ模型双相各向同性介质中采用曲线网格有限差分法是正确可行的,但是并不能说明曲线网格方法相比于传统矩形网格方法在处理起伏地形时有更高的模拟精度.为了验证这个问题,对于含起伏地表半空间模型,我们分别采用了本文介绍的曲线网格和传统的矩形网格来剖分模型,其中矩形网格方法在地表处用阶梯状网格近似,两种方法均采用本文介绍的DRP/opt MacCormack差分格式进行数值模拟.模型如图 2c所示,震源位于(1270 m,-350 m)处,检波器排列深度为-250 m,模型介质参数如表 1第a行所示;两种方法时间采样间隔均为0.1 ms,震源子波主频均为60 Hz,延迟时间均为0.04 s;曲线网格平均网格间距为dx=dz=2 m,矩形网格间距为dx=dz=2 m.
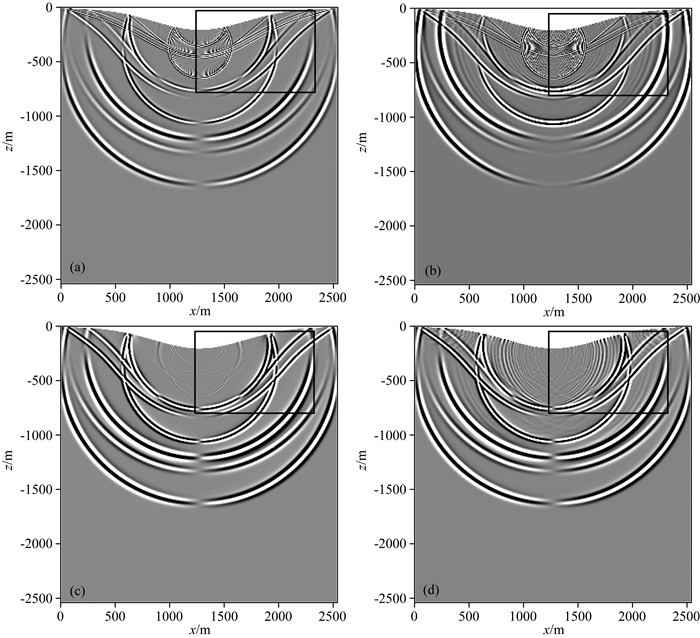
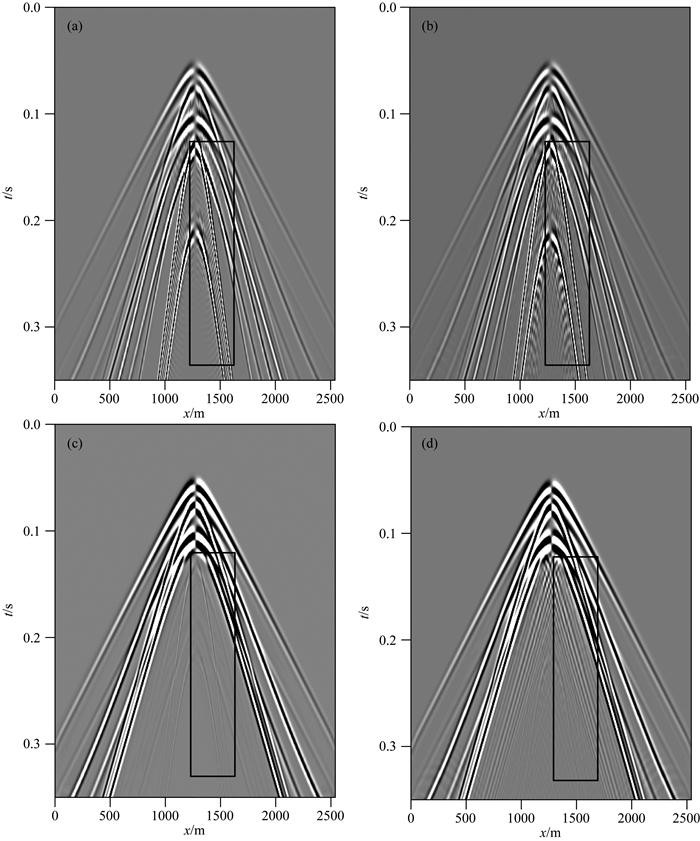
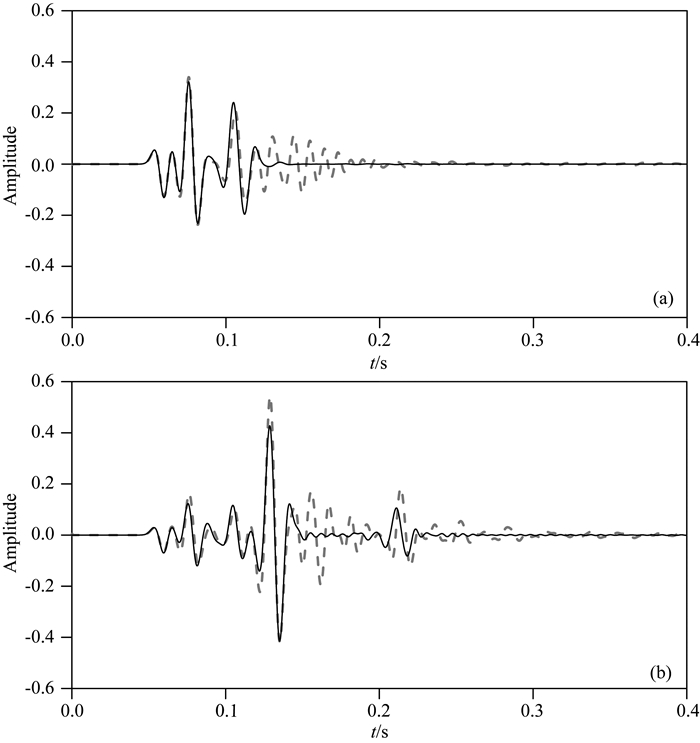
图 5为分别采用曲线网格和传统矩形网格方法对含起伏地表半空间模型模拟得到的0.30 s时刻的波场快照图.图 6为两种方法对含起伏地表半空间模型模拟得到的时间长度为0.35 s的单炮地震记录图,其中图a、b、c和d分别对应曲线网格方法流相Vz分量、矩形网格方法流相Vz分量、曲线网格方法固相Vz分量和矩形网格方法固相Vz分量.图 7为两种方法模拟得到的单道合成理论地震记录,其中检波器位于(1278 m,-250 m)处,图a表示固相Vz分量,图b表示液相Vz分量,实线表示曲线网格方法模拟结果,虚线表示矩形网格方法模拟结果.波场数值模拟的结果(图 5、图 6的黑色线框部分,图 7的0.15~0.25 s部分)显示,相比于曲线网格方法,传统矩形网格方法在地表处产生了明显可见的网格频散现象.对于起伏地质模型,曲线网格有限差分方法可以有效的提高模拟精度.
|
图 5 含起伏地表半空间模型0.30 s时刻的波场快照 (a)曲线网格流相Vz; (b)矩形网格流相Vz; (c)曲线网格固相Vz; (d)矩形网格固相Vz分量. Fig. 5 Wavefield snapshots at time of 0.30s for half-space model with undulating surface (a) Curvilinear grid Vz in fluid phase; (b) Rectangular grid Vz in fluid phase; (c) Curvilinear grid Vz in solid phase; (d) Rectangular grid Vz component in solid phase. |
|
图 6 含起伏地表半空间模型的单炮地震记录 (a)曲线网格流相Vz; (b)矩形网格流相Vz; (c)曲线网格固相Vz; (d)矩形网格固相Vz分量. Fig. 6 Common source point gather seismic sections for half-space model with undulating surface (a) Curvilinear grid Vz in fluid phase; (b) Rectangular grid Vz in fluid phase; (c) Curvilinear grid Vz in solid phase; (d) Rectangular grid Vz component in solid phase. |
|
图 7 含起伏地表半空间模型的单道合成理论地震图(检波器位置:1278 m,-250 m) (a)固相Vz分量; (b)液相Vz分量.图中实线、虚线分别为曲线、矩形网格方法模拟结果. Fig. 7 Synthetic seismogram for half-space model with undulating surface (receiver location:1278 m, -250 m) (a) Vz in solid phase; (b) Vz in fluid phase. In figure the solid and dotted lines indicate the results of curvilinear grid and rectangular grid, respectively. |
为了详细研究分析弹性波在基于改进BISQ模型含有起伏自由地表的双相各向同性介质中的传播规律,我们设计了一个含起伏地表半空间模型和一个起伏两层模型,作为对比我们还设计了一个地表水平的均匀半空间模型,模型均施加了自由地表边界条件.含自由地表水平半空间模型如图 2a所示,震源位于(1270 m,-100 m)处,检波器排列深度为-150 m,模型介质参数如表 1中第a行所示;含起伏地表半空间模型如图 2c所示,震源位于(1270 m,-350 m)处,检波器排列深度为-250 m,模型介质参数如表 1第a行所示;起伏两层模型如图 2d所示,震源位于(1270 m,-500 m)处,检波器排列深度为-400 m,模型介质参数第一层如表 1第b行所示,第二层如表 1第c行所示;三个模型其他参数设置一样:平均网格间距为dx=dz=1 m,时间采样间隔为0.1 ms,震源子波主频为60 Hz,延迟时间为0.04 s.
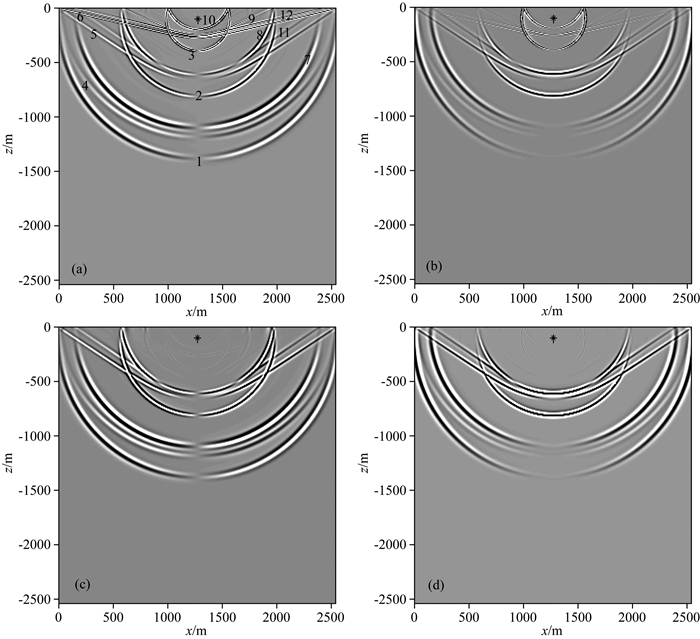
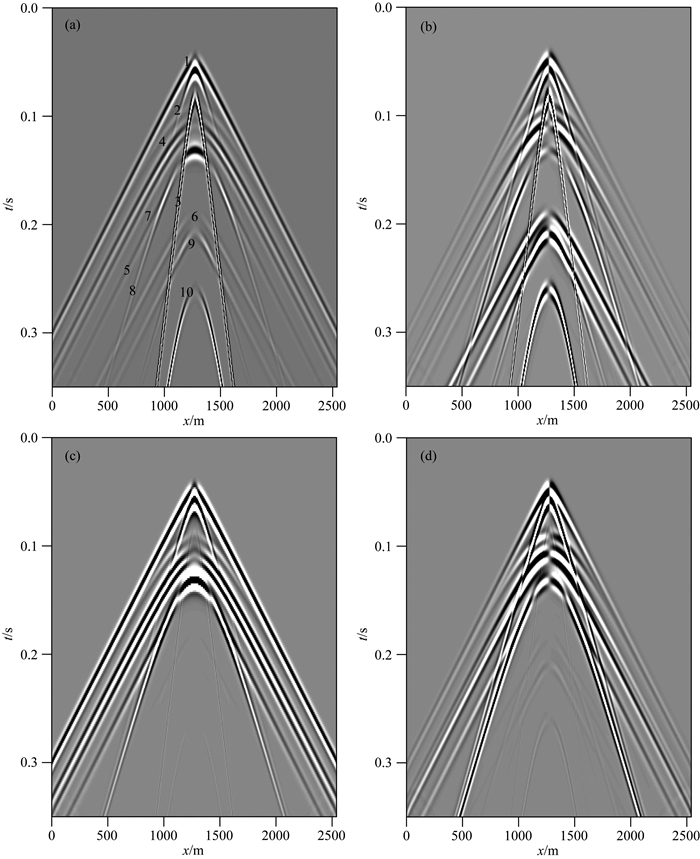
图 8为含自由地表水平半空间模型模拟得到的0.30 s时刻的波场快照图,图 9为含自由地表水平半空间模型模拟得到的时间长度为0.35 s的单炮地震记录图,其中图a、b、c和d分别对应流相Vx分量、流相Vz分量、固相Vx分量和固相Vz分量.波场数值模拟的结果显示,快纵波、横波和慢纵波传播到自由地表处发生了反射,并发生了波型转换;波场快照和单炮地震记录中可观测到多种波,图 8和图 9中a图所标的震相1到3分别为直达快纵波、直达横波和直达慢纵波,4到6分别是快纵波遇到自由地表反射形成的反射快纵波、转换横波和转换慢纵波,7到9分别为横波遇到自由地表形成的反射转换快纵波、反射横波和反射转换慢纵波,10为反射慢纵波;而11为连接横波折射形成的转换快纵波7和反射横波8的首波,12为连接横波折射形成的转换快纵波7和横波反射形成的转换慢纵波9的首波.
|
图 8 含自由地表水平半空间模型0.30 s时刻的波场快照(图中黑色星为震源位置) (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz. Fig. 8 Wavefield snapshots at time of 0.30 s for half-space model with horizontal free surface (In figure black star indicates source location) (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz component in solid phase. |
|
图 9 含自由地表水平半空间模型的单炮地震记录 (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz分量. Fig. 9 Common source point gather seismic sections for half-space model with horizontal surface (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz component in solid phase. |
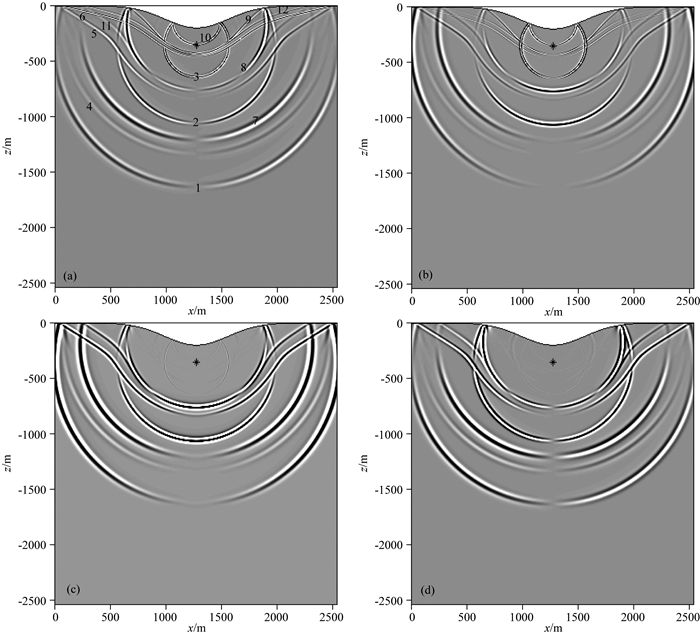
图 10为含起伏地表半空间模型模拟得到的0.30 s时刻的波场快照图,图 11为含起伏地表半空间模型模拟得到的时间长度为0.35 s的单炮地震记录图,其中图a、b、c和d分别对应流相Vx分量、流相Vz分量、固相Vx分量和固相Vz分量.波场数值模拟的结果显示,快纵波、横波和慢纵波传播到起伏自由地表处反射并发生了波型转换;图中所标震相与含自由地表水平半空间模型模拟结果一致,波场快照中各波前面清晰,没有产生可见的数值频散现象,说明曲线网格有限差分可以很好的解决地形起伏地质模型的波场模拟问题.
|
图 10 含起伏地表半空间模型0.30 s时刻的波场快照(图中黑色星为震源位置) (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz分量. Fig. 10 Wavefield snapshots at time of 0.30 s for half-space model with undulating surface (In figure the black star indicates the source location) (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz component in solid phase. |

|
图 11 含起伏地表半空间模型的单炮地震记录 (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz分量. Fig. 11 Common source point gather seismic sections for half-space model with undulating surface (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz component in solid phase. |
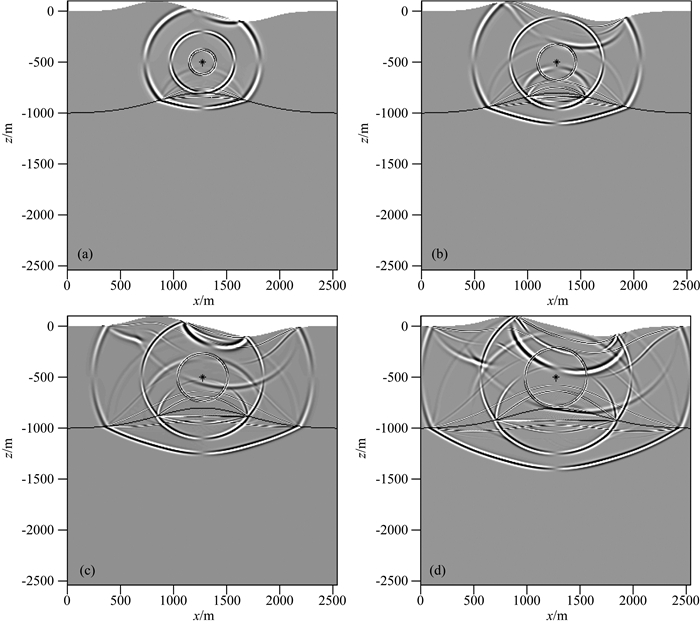
图 12为起伏两层模型流相Vz分量不同时刻的波场快照图,其中图a、b、c和d分别为0.15 s、0.20 s、0.25 s和0.30 s时刻的波场快照.图 13为起伏两层模型模拟得到的时间长度为0.35 s的单炮地震记录图,其中图a、b、c和d分别对应流相Vx分量、流相Vz分量、固相Vx分量和固相Vz分量.图 12的波场快照显示:0.15 s时刻快纵波向下传播遇到介质分界面,反射产生了反射快纵波和转换横波,透射产生了透射快纵波;0.20 s时刻快纵波向下传播遇到介质分界面发生了反射和透射,并产生了转换波,向上传播到达起伏地表产生了反射和转换波;0.25 s时刻横波相下传播遇到介质分界面发生了反射和透射,并产生了转换波;0.30 s时刻:由于界面的不规则性,介质分界面和自由地表产生的反射、透射和转换波形状不具有水平层状介质中的规则性;各时刻波场快照均可以观察到慢纵波.
|
图 12 起伏两层模型流相Vz分量不同时刻的波场快照(图中黑色星为震源位置) (a) 0.15 s; (b) 0.20 s; (c) 0.25 s; (d) 0.30 s. Fig. 12 Wavefield snapshots of Vz component in fluid phase at different time steps for undulated two-layered model (In figure black star indicates the source location) |
|
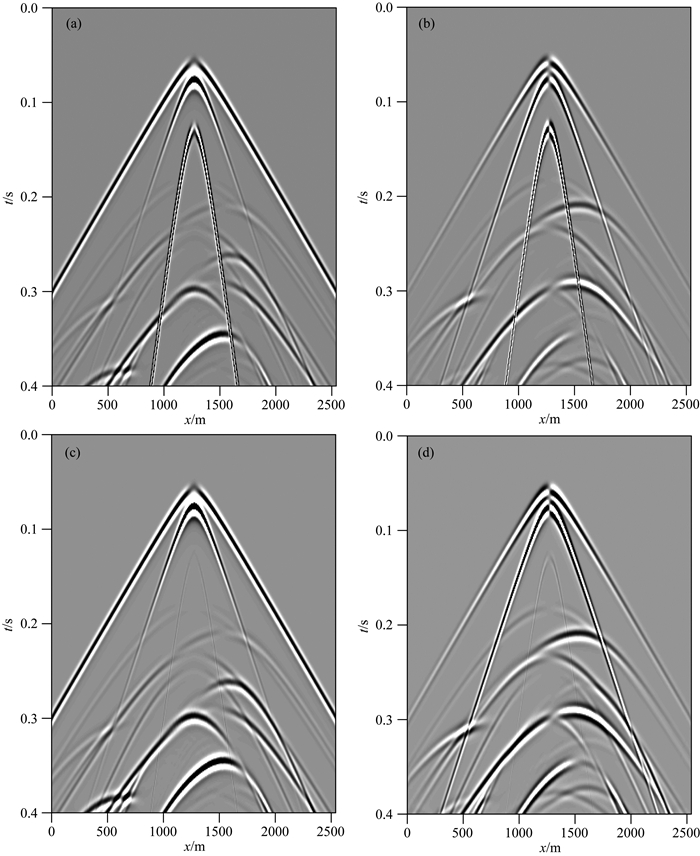
图 13 起伏两层模型中的单炮地震记录 (a)流相Vx; (b)流相Vz; (c)固相Vx; (d)固相Vz分量. Fig. 13 Common source point gather seismic sections for undulated two-layered model (a) Vx in fluid phase; (b) Vz in fluid phase; (c) Vx in solid phase; (d) Vz component in solid phase. |
以基于改进BISQ模型的二维双相各向同性介质一阶速度-应力方程为基础,推导出了曲线坐标系对应的一阶速度-应力方程和自由地表边界条件,用DRP/opt MacCormack有限差分法来离散方程,并采用牵引力镜像法来施加自由地表边界条件,实现了波场数值模拟;然后采用地表水平半空间模型、水平两层模型、含起伏自由地表的半空间模型和起伏两层模型进行了波场数值模拟,并与传统矩形网格方法做了对比,通过对模拟结果的总结和分析,得出了以下结论:
(1) 通过与前人结果的对比分析,验证了基于改进的BISQ模型双相各向同性介质中采用曲线网格有限差分法进行波场数值模拟的正确性;
(2) 当流体为非黏滞性时,固相和流相波场中均可以观察到快纵波、横波和慢纵波;在模型介质分界面和自由地表处,每种波都会发生反射(或反射转换)、或透射(或透射转换),从而产生多种波,使得波场信息非常丰富;通过分析各种波的传播特征,可以帮助我们加深对双相介质地震响应的认识;
(3) 当存在起伏地表或起伏介质分界面时,曲线网格有限差分法采用贴体网格来剖分模型,从而避免矩形网格阶梯状近似带来的数值频散;对于研究地震波在包含起伏地表或起伏界面的双相各向同性介质中的传播问题,曲线网格有限差法是一种有效且精确的方法.但是,当介质包含断层、地层尖灭等复杂地质构造时,曲线网格有限差法无法用贴体网格来精确的剖分模型,此方法不再适用.
(4) 曲线网格有限差法可以直接推广到三维各向同性双相介质,但是对于各向异性双相介质,由于波动方程的复杂性,本文施加自由地表的方法不再适用.
Biot M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range.. J. Acoust. Soc. Am., 28(2): 168-178. DOI:10.1121/1.1908239 |
Biot M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range. J. Acoust. Soc. Am., 28(2): 179-191. |
Diallo M S, Appel E. 2000. Acoustic wave propagation in saturated porous media:reformulation of the Biot/Squirt flow theory. J. Appl. Geophys., 44(4): 313-325. DOI:10.1016/S0926-9851(00)00009-4 |
Diallo MS, Prasad M, Appel E. 2003. Comparison between experimental results and theoretical predictions for P-wave velocity and attenuation at ultrasonic frequency. Wave Motion, 37(1): 1-16. DOI:10.1016/S0165-2125(02)00018-5 |
Dvorkin J, Nur A. 1993. Dynamic poroelasticity:a unified modelwith the squirt and the Biot mechanisms. Geophysics, 58(4): 524-533. DOI:10.1190/1.1443435 |
Gist G A. 1994. Interpreting laboratory velocity measurements in partially gas-saturated rocks. Geophysics, 59(7): 1100-1109. DOI:10.1190/1.1443666 |
Gurevich B, Lopatnikov S L. 1995. Velocity and attenuation of elastic waves in finely layered porous rocks. Geophys. J. Int., 121(3): 933-947. DOI:10.1111/gji.1995.121.issue-3 |
Han C, Chen X F, Jiang D, et al. 2007. Application of the improved BISQ model to seismic numerical simulation of two-phase media. Natural Gas Industry (in Chinese), 27(10): 49-52. |
Hayashi K, Bums D R, Toksöz M N. 2001. Discontinuous-grid finite-difference seismic modeling including surface topography. Bull. Seismol. Soc. Am., 91(6): 1750-1764. DOI:10.1785/0120000024 |
Hestholm S O, Ruud B O, Husebye E S. 1999. 3-D versus 2-D finite-difference seismic synthetics including real surface topography. Phys. Earth Planet. Int., 113(1-4): 339-354. DOI:10.1016/S0031-9201(99)00010-2 |
Hestholm S O, Ruud B O. 2000. 2D finite-difference viscoelastic wave modelling including surface topography. Geophys. Prosp., 48(2): 341-373. DOI:10.1046/j.1365-2478.2000.00185.x |
Hestholm S O, Ruud B O. 1994. 2D finite-difference elastic wave modelling including surface topography. Geophys. Prosp., 42(5): 371-390. DOI:10.1111/gpr.1994.42.issue-5 |
Hixon R. 1997. Evaluation of a high-accuracy MacCormack-type scheme using benchmark problems. J. Comput. Acous., 6(3): 291-305. |
Hixon R, Turkel E. 2000. Compact implicit MacCormack-type schemes with high accuracy. J. Comput. Phys., 158(1): 51-70. |
Jiang L L, Sun J G. 2008. Source terms of elliptic system in grid generation. Global Geology (in Chinese), 27(3): 298-305. |
Jiang L L. 2010. Body-fitted grid generation for the geological conditions[Ph. D. thesis]. Changchun: Jilin University.
|
Jih R, McLaughlin K L, Der Zoltan A. 1988. Free-boundary conditions of arbitrary polygonal topography in a two-dimensional explicit elastic finite-difference scheme. Geophysics, 53(8): 1045-1055. DOI:10.1190/1.1442541 |
Jones T D. 1986. Pore fluids and frequency-dependent wave propagation in rocks. Geophysics, 56(10): 1939-1953. |
Lan H T, Liu C, Guo Z Q. 2014. Modelling of seismic wave propagation in two-phase medium based on reformulated BISQ model using time-splitting staggered pseudospectral method. Global Geology (in Chinese), 33(1): 190-199. |
Li N. 2012. Finite difference seismoelectric wave modeling in 2D porous media with surface topography[Ph. D. thesis] (in Chinese). Hefei: University of Science and Technology of China.
|
Liu C, Lan H T, Guo Z Q, et al. 2003. Pseudo-spectral modeling and feature analysis of wave propagation in two-phase HTI medium based on reformulated BISQ mechanism. Chinese J. Geophys. (in Chinese), 56(10): 3461-3473. DOI:10.6038/cjg20131021 |
Mavko G M, Jizba D. 1991. Estimating grain-scale fluid effects on velocity dispersion in rocks. Geophysics, 56(12): 1940-1949. DOI:10.1190/1.1443005 |
Opršal I, Zahradník J. 1999. Elastic finite-difference method for irregular grids. Geophysics, 64(1): 240-250. DOI:10.1190/1.1444520 |
Peng C Z, Li C M, Wang M C. 2007. Seismic wave-field modeling based on the modefied BISQ model. Computing Techniques for Geophysical & Geochemical Exploration (in Chinese), 29(1): 15-18. |
Sun Y C, Zhang W, Chen X F. 2016. Seismic-wave modeling in the presence of surface topography in 2D general anisotropic media by a curvilinear grid finite-difference method. Bull. Seism. Soc. Am., 106(3): 1036-1054. DOI:10.1785/0120150285 |
Tam C K W, Webb J C. 1993. Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys., 107(2): 262-281. DOI:10.1006/jcph.1993.1142 |
Tarrass I, Giraud L, Thore P. 2011. New curvilinear scheme for elastic wave propagation in presence of curved topography. Geophys. Prosp., 59(5): 889-906. DOI:10.1111/gpr.2011.59.issue-5 |
Tessmer E, Kosloff D, Behle A. 1992. Elastic wave propagation simulation in the presence of surface topography. Geophys. J. Int., 108(2): 621-632. DOI:10.1111/gji.1992.108.issue-2 |
Thompson J F, Warsi Z U A, Mastin C W. 1985. Numerical Grid Generation: Foundations and Applications. New York: Elsevier North-Holland, Inc.
|
Winkler K W. 1985. Dispersion analysis of velocity and attenuation in Berea sandstone. Journal of Geophysical Research, 90(B8): 6793-6800. DOI:10.1029/JB090iB08p06793 |
Yang D H, Zhang Z J, Teng J W, et al. 2000. The study of two-phase anisotropy, questions and applied prospects. Progress in Geophysics (in Chinese), 15(2): 7-21. |
Yang D H. 2002. Finite Element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media. Chinese J. Geophys. (in Chinese), 45(4): 575-583. |
Zhang W, Chen X F. 2006. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation. Geophys. J. Int., 167(1): 337-353. DOI:10.1111/gji.2006.167.issue-1 |
Zhang W, Zhang Z G, Chen X F. 2012. Three-dimensional elastic wave numerical modelling in the presence of surface topography by a collocated-grid finite-difference method on curvilinear grids. Geophys. J. Int., 190(1): 358-378. DOI:10.1111/gji.2012.190.issue-1 |
Zhang Y, Xu Y X, Xia J H, et al. 2015. Characteristics and application of surface wave propagation in fluid-filled porous media. Chinese J. Geophys. (in Chinese), 58(8): 2759-2778. DOI:10.6038/cjg20150812 |
Zhou Z S, Tang L. 2012. Seismic modeling and numerical dispersion correcting in double-phase medium based on reformulated BISQ model. Journal of Central South University:Science and Technology (in Chinese), 43(4): 1411-1418. |
Zhu H J, Zhang W, Chen X F. 2009. Two-dimensional seismic wave simulation in anisotropic media by non-staggered finite difference method. Chinese Journal of Geophysics (in Chinese), 52(6): 1536-1546. DOI:10.3969/j.issn.0001-5733.2009.06.015 |
韩翀, 陈雪菲, 蒋东, 等. 2007. 改进BISQ模型在双相介质地震波数值模拟中的应用. 天然气工业, 27(10): 49-52. DOI:10.3321/j.issn:1000-0976.2007.10.013 |
蒋丽丽, 孙建国. 2008. 基于Poisson方程的曲网格生成技术. 世界地质, 27(3): 298-305. |
蒋丽丽. 2010. 面向地质条件的贴体网格生成技术[博士论文]. 长春: 吉林大学.
|
兰慧田, 刘财, 郭智奇. 2014. 利用时间分裂的错格伪谱法模拟地震波在基于改进BISQ模型的双相介质中的传播. 世界地质, 33(1): 190-199. |
李娜. 2012. 含起伏地表的二维双相介质中地震波及电磁波传播有限差分算法[博士论文]. 合肥: 中国科学技术大学.
|
刘财, 兰慧田, 郭智奇, 等. 2013. 基于改进BISQ机制的双相HTI介质波传播伪谱法模拟与特征分析. 地球物理学报, 56(10): 3461-3473. DOI:10.6038/cjg20131021 |
彭传正, 李才明, 王明春. 2007. 基于改进BISQ模型的地震波场数值模拟. 物探化探计算技术, 29(1): 15-18. |
杨顶辉, 张中杰, 滕吉文, 等. 2000. 双相各向异性研究、问题与应用前景. 地球物理学进展, 15(2): 7-21. |
杨顶辉. 2002. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报, 45(4): 575-583. |
张煜, 徐义贤, 夏江海, 等. 2015. 含流体孔隙介质中面波的传播特性及应用. 地球物理学报, 58(8): 2759-2778. DOI:10.6038/cjg20150812 |
周竹生, 唐磊. 2012. 改进BISQ模型的双相介质地震波场数值模拟及频散校正. 中南大学学报:自然科学版, 43(4): 1411-1418. |
祝贺君, 张伟, 陈晓非. 2009. 二维各向异性介质中地震波场的高阶同位网格有限差分模拟. 地球物理学报, 52(6): 1536-1546. DOI:10.3969/j.issn.0001-5733.2009.06.015 |
 2018, Vol. 61
2018, Vol. 61


