2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
叠前逆时偏移是一种基于双程波的偏移成像方法(Baysal et al., 1983),它利用正传波场与反传波场互相关得到反射界面的位置.逆时偏移可以利用回转波、菱柱波等复杂波场信息进行成像,相比于其他偏移方法具有精度高,没有近似处理,不受倾角限制和速度剧烈变化的优势,因此具有更好的成像效果(Baysal et al., 1993).但是逆时偏移存在计算效率低,存储量大(Phadke et al., 2012)和低频噪声等问题,并且严重依赖于初始速度模型.近年来随着研究的深入与计算能力的提升,叠前逆时偏移以及对应的全波形反演得到了长足的发展,其中新的波场重构方法与存储策略大大减小了计算机硬件的要求,使得三维地震资料的高分辨率成像具有可行性.
叠前逆时偏移与全波形反演等基于互相关原理的地球物理方法需要重构正传波场而存在巨大的计算量与存储量.近年来许多学者对此进行研究并取得了卓有成效的进展(Symes et al., 2008;Nguyen and Mcmechan, 2015),主要提出了五种波场重构思想(Wang, 2013):(1)直接保存法,将所有时间采样点的波场状态存储在内存或硬盘中,对某一时刻进行成像时提取存储的波场并与反传波场做互相关运算.直接保存法耗费极大的存储,且波场数据的反复读写操作造成巨大的I/O延迟,导致CPU等待时间过长,严重降低了计算效率.(2)基于有效边界存储的波场重构方法(王保利等,2012;Yang et al., 2014a),该方法存储每次正传波场的四周有效边界层,并利用最后两次时间采样的波场做逆时传播,将每个时间采样点对应的有效边界加入反传波场中从而重构出该时间点的波场值,有效边界法是一种非常高效的波场重构方法,对于2J阶精度交错网格有限差分只需要保存J-1层的波场值而非全部波场(Yang et al., 2014a),比直接保存法减少了大量存储,但是针对三维叠前逆时偏移,它仍然耗费存储,难以实用化.(3)基于随机边界条件波场重构方法(Clapp,2009;刘红伟等,2010;石颖等,2015;Shen and Clapp, 2015),在计算区域外设计随机分布的速度层,当波传入随机速度层后波场发生漫反射从而扰乱连续同相轴,减弱人工边界反射对成像结果的影响,当波场传播到最大时刻后逆时传播重构出正传波场.此方法不需要额外的存储量,只需经过两次的递推过程就能实现任意波场的重构,对于三维尺度的叠前逆时偏移是一种行之有效的方法(刘红伟等,2010).然而随机边界条的伪漫反射对成像产生随机噪声,降低成像结果的分辨率,特别是检波器附近的浅层位置尤为严重,通过多次叠加消除随机噪声对观测系统的布设提出了更高的要求(胡昊等,2013);同时伪漫反射效果取决于随机边界层的厚度与子波主频(Shen and Clapp, 2015),加入较厚的边界层将增大计算量与存储量.(4)基于检查点技术的重构方法(Griewank,1992;Griewank and Walther, 2000;Symes,2007;Stumm et al., 2009;Anderson et al., 2012),在正传过程中每隔一定时间间隔设置一个检查点并储存该点波场,从检查点出发通过反复递推重构任意时刻的波场.Griewank和Walther(2000)证明当检查点间隔为二项式分布时具有很好的计算效率.Symes(2007)提出优化检查点方法,每隔几个检查点保存一次波场状态,将它作为缓存点,需要重构某一时刻的波场时则寻找离该时刻最近的检查点,判断该点是否储存了波场,若没有则从最近的缓存点出发做正向传播得到该检查点的波场,将该波场保存并标记为缓存点,从该点出发再次做正演得到成像时刻的波场值.优化检查点技术比第一种方法极大的减少了存储量,它只需要保存少量的缓存点就能有效的重构波场值(Symes,2007).优化检查点采用计算换存储的策略,通过反复递推重构波场,递推次数随时间采样点数的增加呈指数增长,因此具有较高的重算率.(5)抽样插值法波场重构,Sun和Fu(2013, 2015)等提出在满足Nyquist采样定理的前提下对正传波场进行抽样,并通过数据压缩算法对抽样波场进行存储.Yang等(2016a, b)将有效边界层抽样存储,采用离散傅里叶插值(DFT),拉格朗日多项式插值等方法对信号进行重采样,插值重构任意时刻的有效边界层波场,通过最后两个时刻波场的反传并加入插值得到的有效边界层,重构出计算区域的波场值.基于插值思想的有效边界重构法比常规有效边界层重构法极大的减少了存储量,Yang证明对于三维模型甚至可以减少90%的存储量,从而使有效边界法实现三维逆时偏移变得可行(Yang et al., 2016a).
本文分析了常规波场重构方法的优缺点,得出在保证成像质量的前提下优化检查点技术内存消耗最少,是一种较为可行的三维波场重构方案.但是该方案具有较高的重算率,计算效率不高,针对这一问题,本文在优化检查点技术的基础上提出插值原理的波场重构方法,该方法从某时刻最近的检查点开始正向递推波场,满足Nyquist采样定理的前提下对波场进行抽样,通过插值算法重构相应时刻的波场值,从而避免了检查点与成像时刻的复返递推.考虑到波场重构的实时性与计算成本,本文运用牛顿多项式,三次样条与傅里叶变换三种多项式插值算法进行波场重构,并分析了三种算法的插值精度与计算效率.基于插值原理的优化检查点法只需从检查点出发做一次正演就能够插值重构出任意时刻波场,具有较高的计算效率,同时具有检查点法存储量少的优点.本文采用计算量最小的牛顿插值法进行波场重构与叠前逆时偏移,经Sigsbee速度模型测试与三维情况下的存储量分析,表明了插值波场重构的有效性与优越性,对于三维实际资料的逆时偏移与全波形反演具有实际意义.
1 叠前逆时偏移原理逆时偏移的基本原理是将采集的地震信号作为双程波动方程的边界条件,在时间上逆时传播得到反传波场值,同时从炮点出发求解波动方程得到正传波场,通过对应时刻的正传波场与反传波场做互相关运算从而输出成像剖面.
设各向同性一阶应力-速度声波方程(Yang et al., 2016a):
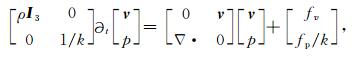
|
(1) |
令
逆时偏移的成像原理可以看作是炮点正向传播波场与检波器波场反向传播在对应时刻的零延迟互相关运算,定义零延迟互相关成像条件为

|
(2) |
式(2)为成像空间x处的成像值,ps(x, t)和pr(x, t)分别是正传波场与反传波场.从式(2)可以看出叠前逆时偏移需要同时求解任意时刻的正传波场与反传波场值.设任意tn时刻波场状态为un,可以得到如下认识:
(1) 重构n=N-1, …, 0时刻的波场,从t=0时刻开始正向传播总共需要进行O(N2)次递推计算,当N很大时存在巨大的计算量.
(2) 保存每一时刻{un, n=0, 1, …, N-1}的波场需要O(N)次递推计算,但存储量巨大,三维情况需要将数据存入硬盘从而造成较大的读写延迟,降低计算效率.
(3) 采用随机边界条件从最后两步波场开始反向递推到un,需要O(2N)次计算,并且不需要额外的存储量,但随机边界上产生的伪漫反射对Image (x)造成随机干扰(胡昊等,2013).
(4) 优化检查点设置少量缓存点,通过缓存点与优化检查点间的反复递推可以重构出任意时刻的波场(Symes,2007).缓存点设置过少,则存在较高的重算率,反之存储量增加.
通过以上分析得出计算量与存储量是一对矛盾体,计算量少意味着需要更多的存储,同理少量的存储需要更多的计算.优化检查点法通过反复递推能有效的降低存储量,但重算率较高,因此本文在此基础上对波场进行抽样存储,并对抽样波场插值重构出任意时刻波场,在不明显增加存储量的情况下避免了检查点到un的反复递推,提高检查点的计算效率,对于大规模的三维叠前逆时偏移与全波形反演是一种经济可行的方法.
2 基于优化检查点技术的波场插值重构Griewank(1992),Griewank和Walther(2000)提出检查点波场重构思想,Symes(2007)提出一种优化检查点技术:对N个时间采样设置Nc个检查点,没有保存所有的检查点波场,而是选取其中Nb个点作为缓存点保存波场,即Nb≤Nc≤N.互相关成像时对于某一时刻ti先找到离该时刻最近的缓存点(buffer),从缓存点递推到最近优化检查点Cj并保存该点的波场,再从该点递推到ti时刻的波场,具体过程如下:
(1) 选取检查点{Ci:i=0, 1,…, Nc}分布于0到N,Griewank(Griewank,1992;Griewank and Walther, 2000)等证明Cj为二项式分布时到达最优重算率,且与速度模型的复杂度无关.二项式方法不断的重新布置检查点从而降低重算率设置. {Bi:i=1, …, Nb}为缓存点,满足Nb≤Nc≤N,且tCNc=tBNb.
(2) 求解方程(1),从零时刻起递推到N并保存相应的缓存点状态.
(3) 重构某时刻ti的波场,先找到最近的Bk与Cj,如果tCj≠tBk,则从Bk递推到Cj并标记该点为新的Bk.从最近优化检查点Cj递推到ti.
(4) 如果tCj=tBk,则重新分布B(Yang et al., 2016b).
优化检查点法的递推过程如下图 1所示,设置时间采样N=16,2个缓存点与4个检查点.

|
图 1 优化检查点技术递推过程 Fig. 1 Optimal checkpointing technology recursive process |
优化检查点技术的计算效率与存储量受Nb和Nc的影响,Nb=N时相当于保存所有的波场,Nb=0时则每次都从0开始递推.Nb的取值越小则存储量越小,同时增大了缓存点反复递推到检查点的计算量.令Nc=rNb,r为比例因子.若r取值越小可以减少缓存点与检查点间的反复递推,然而r取小则相邻检查点间距增大,检查点到ti的反复递推量会急剧增加,从而造成优化检查点技术的重算率较高.
基于优化检查点的波场插值重构思路是根据硬件条件设置合适的缓存点个数与较小的比例因子r,减少缓存点递推到优化检查点的反复计算量.此时的反复递推主要由检查点到ti贡献.根据插值原理,从检查点到ti只需正演一次,并抽样存储波场,计算下一个时刻ti-1波场则由抽样波场插值重构而不是再次从检查点出发递推.如图 2所示的插值重构示意图:

|
图 2 插值检查点技术递推过程 Fig. 2 Interpolation checkpointing technology recursive process |
图 2中圆点为抽样存储点,叉点为通过抽样点插值重构而来,可以看出经过插值后避免了大量的波场递推.定义递推计算的重算率:

|
(3) |
其中N′为总递推次数.从图 1,2可以看出优化检查点的重算率为3.25,插值检查点的重算率为2.65.经过插值重构减少了最近的检查点到成像点的递推次数,因此可以有效的降低重算率.当时间步长N=2400时两种算法的重算率如表 1.
|
|
表 1 不同缓存点个数的重算率对比 Table 1 Comparison of the recomputation ratio of different buffer points |
从上表可以看出插值法重算率低于检查点法,当缓存点个数为5时的重算率减小为原来的1/7,极大的提高了计算效率.随着缓存点个数的增加,插值法重算率的下降幅度小于优化检查点,说明插值法对缓存点个数不敏感,因此对于三维情况可以在设置少量缓存点的情况下获得较高的计算效率.
3 波场抽样与插值重构Nyquist采样定理指出采样频率大于两倍被采样信号最大频率就能完全恢复被采样信号.设波场抽样间隔为Δtd,则:
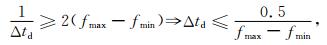
|
(4) |
其中fmin和fmax是信号的最小和截止频率,对波场进行规则抽样并满足Nyquist采样定理就能有效的重构任意时刻波场.抽样间隔Δtd是在差分格式的时间采样Δt基础上再次进行采样而来,不妨认为时间采样得到的波场为连续的信号,因此抽样间隔Δtd不必满足网格稳定性条件.对于二维交错网格稳定性条件(CFL)要求(Yang,2014b):
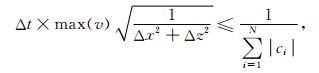
|
(5) |
其中,ci为差分格式的系数,对于四阶交错格式有Δx, 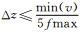
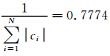

|
(6) |
从而,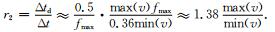
对于Marmousi模型min(v)=1500,max(v)=5500可得r2≈5.06,因此四阶交错格式满足Nyquist定理可实现至少5倍时间采样的抽样存储.
3.1 牛顿插值波场重构牛顿插值方法是一种函数逼近常用的多项式插值方法,它与Lagrange插值方法相比具有逐次生成多项式而不需要插值节点增加时全部重新计算系数的优点(李庆扬等,2008),尤其在规则采样情况下的等距节点差分牛顿插值法具有简单灵活的特点而被广泛运用.
设抽样信号为u(tk),其中tk=t0+kΔtd(k=0, 1, …, Nd-1),t0为某检查点的时刻,Δtd为抽样间隔,Nd为抽样个数.令fk=u(tk),则Δfk=fk+1-fk为一阶(前向)差分,同理有Δnfk=Δn-1fk+1-Δn-1fk为tk处的n阶差分.已证明有

|
(7) |
其中

|
(8) |
其中q为插值节点个数,t0+xΔtd为需要插值的位置.对波场位置x在tchept~tchept+1区间的任意时刻采样点t=tchept+iΔt的值,先找到该时刻临近的q个抽样波场作为插值节点,运用则波场重构为

|
(9) |
其中q个节点的选择模板如图 3所示.

|
图 3 牛顿插值示意图 (a)左边界插值过程;(b)中间插值过程;(c)右边界插值过程. Fig. 3 Newton interpolation diagram (a) The left boundary interpolation process; (b) The intermediate interpolation process; (c) The right boundary interpolation process. |
设有两个检查点ckp1和ckp2,两点间有N=16个时间采样点,若每隔2个采样点抽样存储一次则共有Nd=6个抽样点,即Δtd=3Δt.
对于q=4阶牛顿插值如图所示三种情况,图 3a:当ti<q时用前q个抽样波场作为插值节点;图 3b:当q≤ti<N-q时则用n-q/2+1到n+q/2之间的抽样点作为插值节点,其中n为ti所在的抽样区间,且n<ti<n+1;图 3c:当ti>N-q时则采用最后q个抽样值作为插值节点.
3.2 三次样条插值高次插值容易出现龙格现象,通常采用分段低次插值,特别是三次样条插值,它具有良好的收敛性与稳定性,且具有二阶光滑,理论与实际运用都有重要意义(李庆扬等,2008).
三次样条插值定义为

|
(10) |
其中的tj(j=1, …, Nd)为tchept~tchept+1之间Δtd间隔的抽样波场值,且满足:t∈[tj, tj+1].对于等间距节点的一阶导数边界条件得:

|
(11) |
其中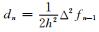
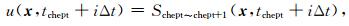
|
(12) |
其中i=0, 1, 2, …, N为tchept~tchept+1之间的时间采样.
3.3 离散傅里叶插值定义离散傅里叶变换为

|
(13) |
其中,Nd为Δtd间隔的抽样波场个数,k为信号的频率索引,m为时间采样索引,j为虚数单位.对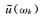

|
(14) |
值得注意的是N为tchept~tchept+1以Δt采样的波场个数,Nd为抽样波场个数,显然N>Nd,从而使Nd个样点的信号重采样为N个样点的信号,这里满足:

|
(15) |
其中*表示共轭算子,(15)式表明只需计算一半的折叠频率就能恢复出信号,因此最终的波场插值重构方程为(Yang,2016a):
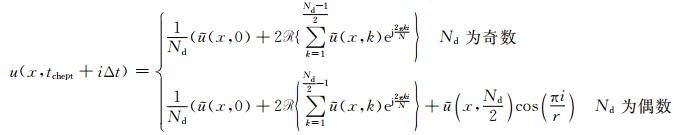
|
(16) |
其中
波场插值重构方法中相邻两检查点之间的抽样点位置(插值节点)和个数与速度模型有很大的关系,对于简单的速度模型,波场在某位置的时间方向所组成的信号在大部分时间内都为零,即信号具有稀疏性.采用非均匀分布的稀疏采样方法可以减少不必要的存储,但稀疏类方法如压缩感知(CS),凸集投影(POCS)等本质是一种最优化问题,需要反复迭代求取最优解,计算量增加较大,无法完成实时重构,计算效率反而不高,因此本文最终采用计算效率更高的等间隔抽样点方案.
4.1 波场插值重构采用网格大小为500×500的Marmousi速度模型,网格尺寸dx=dz=12 m,在(3000, 3000)m位置放置炮点.采用时间二阶空间八阶交错网格有限差分,子波为25 Hz主频雷克子波,时间采样Δt=0.001 s,步长N=650,Δtd=5Δt即5倍时间采样作为间隔抽稀存储波场.分别使用本文提出的三种插值算法重构波场.牛顿插值采用6阶多项式,傅里叶则采用快速傅里叶变化并保存一半的频点.利用上述三种插值算法重构t=0.639 s时的波场值如图 4所示.

|
图 4 三种多项式插值算法的波场重构结果与误差分布 (A)牛顿插值重构与误差;(B)三次样条插值重构与误差;(C)傅里叶插值重构与误差. Fig. 4 Wave field reconstruction of three interpolation algorithms (A) Newton interpolation reconstruction and error distribution; (B) Spline interpolation reconstruction and error distribution; (C) Fourier interpolation reconstruction and error distribution. |
图 4(a1, b1, c1)依次为牛顿插值,三次样条插值与傅里叶插值结果,可以看出三种算法都能很好的重构出波场.图 4(a2, b2, c2)依次为重构的波场与正演波场的相对误差,其中三次样条插值误差最小,达到了10-3数量级,其次为牛顿插值与傅里叶插值.抽取t=0.639 s时Depth=3000 m的波场重构值以及相对误差如图 5所示.

|
图 5 三种插值算法在Depth=3000 m上的重构误差分布 (a) Depth=3000 m剖面的实际波场值; (b)牛顿插值法重构误差分布;(c)三次样条插值法重构误差分布;(d)傅里叶插值法重构误差分布. Fig. 5 Reconstruction wave field and error distribution at z=3000 m of three interpolation algorithms (a) The real wave field signals at 3000 m; (b) Error distribution of Newton interpolation method; (c) Error distribution of Cubic spline interpolation method; (d) Error distribution of Fourier interpolation method. |
图 5a为Depth=3000 m剖面的实际波场值,图 5(b,c,d)依次为牛顿插值算法,三次样条插值法与傅里叶插值法的误差分布,可以看出经过5倍抽稀采样后三种插值算法都能很好的重构出相应的波场,其中三次样条插值的误差最小,数量级在10-3级,傅里叶插值和牛顿插值的误差分布次之.
为了研究计算效率和耗时,设计一系列的时间采样N=1000, 2000, …, 8000进行实验,同时采用检查点法与本文的插值法进行波场重构.设置缓存点Nb等间隔分布,Nc=5Nb.在相同硬件(CPU:I5 5200u)条件下得到的耗时与重算率结果如图 6所示.
|
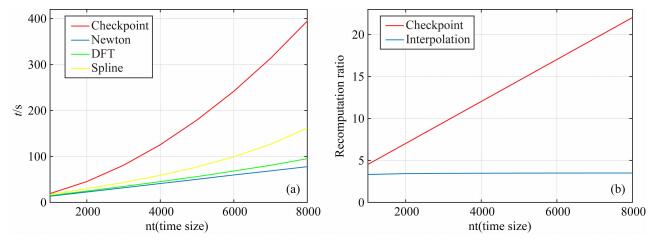
图 6 插值与检查点法计算耗时与重算率 (a)检查点法与三种插值法的计算耗时;(b)检查点法与插值法的重算率. Fig. 6 The time-consuming and recomputation ratio of interpolation and checkpointing method (a) The time-consuming of checkpointing method and three kinds of interpolation method; (b) The recomputation ratio of checkpointing and interpolation method. |
从图 6a中随着时间采样的增加,检查点法的耗时远大于插值法,而插值法中三次样条的耗时最大,傅里叶法次之,由于当插值节点变化时牛顿法只需计算新节点的插值系数,因此牛顿法耗时最小.图 6b为两种方法的重算率,检查点法随时间采样的增加快速变大,插值法增幅较小,表明插值法在计算效率上较检查点法有很大的提高.
4.2 Sigsbee模型叠前逆时偏移采用八阶交错网格有限差分与牛顿插值检查点技术波场重构,设置20层完全匹配层(PML)吸收边界,网格大小dx=dz=12 m,25 Hz主频的雷克子波,时间采样Δt=0.001 s,步长N=9800.设计25炮,每炮3201个检波点置于顶部接收,Sigsbee模型网格尺寸3201×1201并调整速度分布.成像条件为零延迟互相关成像条件并做归一化照明补偿,成像后采用Laplace算子去除低频成像噪声.插值算法采用6阶牛顿插值,设置20个缓存点与100个检查点,抽样间隔Δtd分别为5倍,10倍,15倍时间采样Δt,研究不同抽样间隔下的成像结果.图 7为提取1.571 s时的牛顿插值重构波场与误差分布,图 8为牛顿插值法的偏移结果.
|
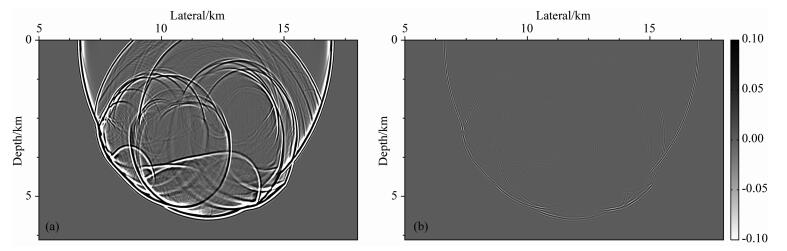
图 7 牛顿插值波场重构 (a)牛顿插值重构波场快照;(b)牛顿插值误差分布. Fig. 7 Newton interpolation wavefield reconstruction (a) Newton interpolation reconstruct wave field snapshot of Sigsbee model; (b) Newton interpolation error distribution. |
图 7a为炮点放置在Lateral=12 km,时间为1.571 s的波场插值重构快照,图 7b为对应的插值误差,可以看出插值法能很好的重构波场.图 8为Δtd=5Δt抽样情况下牛顿插值的偏移结果,其中深层两排绕射点能清晰的分辨,盐丘边界准确归位.

|
图 8 Δtd=5Δt抽样情况下牛顿插值法的偏移结果 Fig. 8 Migration result of 5 times samples Newton interpolation |
在GPU(GTX980ti)上并行实现两种方法并对比偏移一炮的耗时与重算率如表 2所示.
|
|
表 2 检查点法与插值法单炮偏移耗时与重算率 Table 2 The single shot time-consuming and recomputation ratio of Check pointing and interpolation method |
表 2中插值法耗时有大幅的减小,由于插值法避免了从检查点到成像时刻的反复递推,因此重算率较低.为了研究抽样间隔对成像结果的影响,本文设计抽样间隔Δtd分别为5倍,10倍,15倍Δt情况下的偏移结果并与检查点法的偏移结果对比如图 9所示.
|
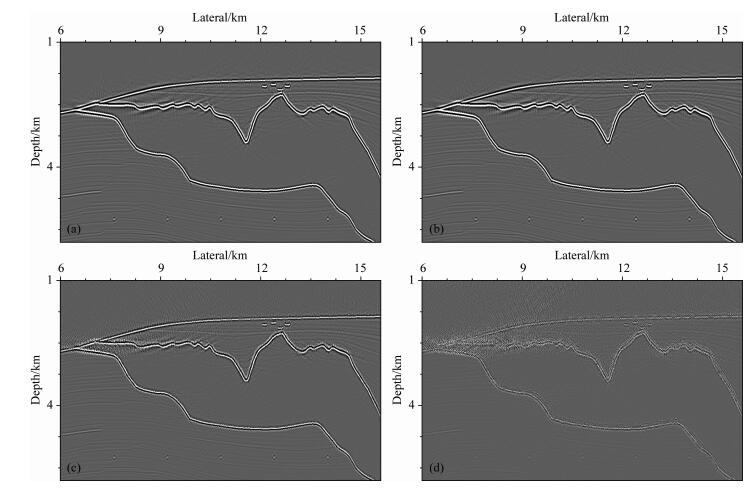
图 9 不同抽样间隔的插值法偏移结果 (a)检查点法结果;(b) 5倍抽稀插值结果;(c) 10倍抽稀插值结果;(d) 15倍抽稀插值结果. Fig. 9 The interpolation results of different sampling intervals (a) The result of Checkpointing; (b) The interpolation result of 5 times sampling intervals; (c) The interpolation result of 10 times sampling intervals; (d) The interpolation result of 15 times sampling intervals. |
图 9a为检查点法偏移得到的局部结果,图 9(b,c,d)分别为不同抽样间隔下的插值法偏移结果.从图 9b对比可知Δtd=5Δt时成像效果最好,随着抽样间隔的增大,10倍与15倍出现假频现象.图 9表明抽样间隔越小则成像效果越好,但抽样间隔小则需要存储更多的插值节点,因此应当在满足Nyquist定理前提下设置合理的抽样间隔.将检查点结果作为标准,计算不同抽样条件下每个成像点的L2范数平均误差如表 3以及图 10整体的相对误差分布:
|
|
表 3 3种抽样间隔的成像误差 Table 3 Imaging error for 3 sampling intervals |

|
图 10 5倍抽样间隔下牛顿插值法偏移结果与检查点法结果的相对误差 Fig. 10 Relative error of 5 times sampling intervals newton interpolation and optimal checkpointing method in RTM result |
表 3可以看出随着抽样间隔的增大,成像误差逐渐增大,应当选择合理的抽样间隔保证误差.图 10为5倍抽样间隔下的牛顿插值法与优化检查点法偏移结果的相对误差百分图(Kristek et al., 2002),整体重构的相对误差在2%左右,其中9~15 km的复杂构造区域误差分布大于构造相对简单区域.
4.3 重算率与存储量分析为了分析三维叠前逆时偏移不同波场重构方法的计算与存储量,设计三维速度模型网格大小nx×nz×ny=1000×1000×500,时间步长N=12000.对比分析随机边界条件,有效边界条件与优化检查点,插值检查点四种方法的重构计算量与存储情况.若采用2J等于八阶交错网格有限差分格式,插值检查点法设置Nb=15个缓存点和75个检查点,那么相邻检查点间抽样波场个数Nd=15个,单精度浮点数大小为4 Bytes,对于交错网格的波场重构需要p, px, pz, vx, vz5个波场分量,因此三种算法的存储量如表 4.
|
|
表 4 不同重构方法的存储量 Table 4 The calculation methods of storage capacity in different reconstruction methods |
从表 4可以看出插值检查点与优化检查点相比存储量的增加主要是由于保存了Nd个抽样波场三维情况的存储量与重算率如表 5.
|
|
表 5 5种重构方法对比 Table 5 Comparison of five reconstruction methods |
从表 3可以看出直接保存法的重算率为1.0,只需从零时刻开始做一次正演就能完成一炮的偏移,保存所有时刻的波场需要5722G存储量,难以运用于三维地震资料.随机边界条件不需要存储额外的波场,只需做两次的正演,因此重算率为2.0.随机边界不需要存储并且重算率较低,是一种非常经济的波场重构方法.但是随机边界条件的成像质量受随机噪声的影响较大(胡昊等,2013),而其他的重构方法不存在随机噪声问题.有效边界条件的存储量达到600 G以上,对大部分计算机而言无法满足巨大的内存需求,只能将波场写入硬盘.有效边界的重算率只有2.0,但读写硬盘极大的I/O操作量同样导致非常低的计算效率.在三维情况下优化检查点法的储存量下降为有效边界法的5.9%,存储条件得到了很好的改善,但是优化检查点法重算率达到了82.63,对于某一炮的偏移需要重复82.63次正演,计算效率非常糟糕.由于插值重构方法需要存储相邻两个检查点间的抽样波场,内存有少量的增加,但插值检查点法重算率为5.17,相比于优化检查点法下降为后者的6%,计算效率得到了显著提高.因此插值检查点法在增加少量存储的情况下可以极大的减小重算率,对于三维情况的叠前逆时偏移与全波形反演有实际意义.
5 结论本文总结了常规叠前逆时偏移中波场重构法方法的存储量与计算效率,在优化检查点技术的基础上提出一种利用插值原理的波场重构方法.考虑到压缩感知(CS),凸集投影(POCS)等非规则采样方法需要迭代求解最优化问题,不适合于实时波场插值,因此本文采用了牛顿插值,三次样条插值和离散傅里叶插值算法进行波场重构.通过数值实验表明基于插值原理的重构方法避免了优化检查点技术反复递推造成的计算效率问题,在增加少量存储的情况下大幅度降低了重算率.其中牛顿插值由于在增加插值节点时不需要重新计算插值多项式的系数从而有较小的计算代价,适合于快速重构.三次样条插值精度较高,但需要额外的开销用于求解矩阵.傅立叶插值算法的精度介于三次样条插值和牛顿插值,计算量略大于牛顿插值.本文采用计算量最小的牛顿插值法进行叠前逆时偏移,经Sigsbee模型试算和三维情况的存储与计算量分析,证明了插值算法的可行性.通过三维模型的分析,插值检查点法存储量下降为有效边界法存储量的7.1%,而与优化检查点法相比重算率降低为后者的6%,同时插值算法的重构相对误差在2%左右,具有很好的插值精度.综上所述,基于插值原理的优化检查点技术适合对三维叠前逆时偏移与全波形反演是一种有效的波场重构方案.
致谢感谢国家重大科技专项“西部盆地深层-超深层油气勘探地质理论与勘探技术”(RIRED-2015-JS-272)的资助,感谢Seiscope Consortium post-doc Pengliang Yang的讨论与帮助.
Anderson J E, Tan L J, Wang D. 2012. Time-reversal checkpointing methods for RTM and FWI. Geophysics, 77(4): S93-S103. DOI:10.1190/geo2011-0114.1 |
Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse-time migration. Geophysics, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
Clapp R G. 2009. Reverse time migration with random boundaries. //79th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Griewank A. 1992. Achieving logarithmic growth of temporal and spatial complexity in reverse automatic differentiation. Optimization Methods and Software, 1(1): 35-54. DOI:10.1080/10556789208805505 |
Griewank A, Walther A. 2000. Algorithm 799:Revolve:An implementation of checkpointing for the reverse or adjoint mode of computational differentiation. ACM Transactions on Mathematical Software, 26(1): 19-45. DOI:10.1145/347837.347846 |
Hu H, Liu Y K, Chang X, et al. 2013. Analysis and application of boundary treatment for the computation of reverse-time migration. Chinese Journal of Geophysics, 56(6): 2033-2042. DOI:10.6038/cjg20130624 |
Kristek J, Moczo P, Archuleta R. 2002. Efficient methods to simulate planar free surface in the 3D 4th-order staggered-grid finite-difference schemes. Studia Geophysica et Geodaetica, 46(2): 355-381. DOI:10.1023/A:1019866422821 |
Li Q Y, Wang N C, Yi D Y. 2008. Numerical Analysis (in Chinese). Version 5.. Beijing: Tsinghua University Press.
|
Liu H W, Liu H, Zou Z, et al. 2010. The problems of denoise and storage in seismic reverse time migration. Chinese Journal of Geophysics, 53(9): 2171-2180. DOI:10.3969/j.issn.0001-5733.2010.09.017 |
Nguyen B D, Mcmechan G A. 2015. Five ways to avoid storing source wavefield snapshots in 2D elastic prestack reverse time migration. Geophysics, 80(1): S1-S18. DOI:10.1190/geo2014-0014.1 |
Phadke S, Dhubia S, Phadke S, et al. 2012. Storage and performance issues in reverse time migration. Psychiatry & Clinical Neurosciences, 1: 363-364. |
Shen X K, Clapp R G. 2015. Random boundary condition for memory-efficient waveform inversion gradient computation. Geophysics, 80(6): R351-R359. DOI:10.1190/geo2014-0542.1 |
Shi Y, Ke X, Zhang Y Y. 2015. Analyzing the boundary conditions and storage strategy for reverse time migration. Progress in Geophysics, 30(2): 581-585. DOI:10.6038/pg20150214 |
Stumm P, Walther A. 2009. Multistage approaches for optimal offline checkpointing. SIAM Journal on Scientific Computing, 31(3): 1946-1967. DOI:10.1137/080718036 |
Sun W J, Fu L Y. 2013. Two effective approaches to reduce data storage in reverse time migration. Computers & Geosciences, 56: 69-75. |
Sun W J, Fu L Y, Yao Z X. 2015. Reducing data storage in reverse time migration. //85th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Symes W W. 2007. Reverse time migration with optimal checkpointing. Geophysics, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
Symes W W, Denel B, Cherrett A, et al. 2008. Computational strategies for reverse-time migration. //78th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Wang B L, Gao J H, Chen W C, et al. 2012. Efficient boundary storage strategies for seismic reverse time migration. Chinese Journal of Geophysics, 55(7): 2412-2421. DOI:10.6038/j.issn.0001-5733.2012.07.025 |
Wang W H, Ke X, Pei J Y. 2013. Application investigation of perfectly matched layer absorbing boundary condition. Progress in Geophysics, 28(5): 2508-2514. DOI:10.6038/pg20130529 |
Yang P L, Gao J H, Wang B L. 2014a. RTM using effective boundary saving:A staggered grid GPU implementation. Computers & Geosciences, 68: 64-72. |
Yang P L. 2014b. A numerical tour of wave propagation. Technical report, Xi'an Jiaotong University.
|
Yang P L, Brossier R, Virieux J. 2016a. Wavefield reconstruction by interpolating significantly decimated boundaries. Geophysics, 81(5): T197-T209. DOI:10.1190/geo2015-0711.1 |
Yang P L, Brossier R, Métivier L, et al. 2016b. Wavefield reconstruction in attenuating media:A checkpointing-assisted reverse-forward simulation method. Geophysics, 81(6): R349-R362. DOI:10.1190/geo2016-0082.1 |
胡昊, 刘伊克, 常旭, 等. 2013. 逆时偏移计算中的边界处理分析及应用. 地球物理学报, 56(6): 2033-2042. DOI:10.6038/cjg20130624 |
李庆扬, 王能超, 易大义. 2008. 数值分析. 5版. 北京: 清华大学出版社.
|
刘红伟, 刘洪, 邹振, 等. 2010. 地震叠前逆时偏移中的去噪与存储. 地球物理学报, 53(9): 2171-2180. DOI:10.3969/j.issn.0001-5733.2010.09.017 |
石颖, 柯璇, 张莹莹. 2015. 逆时偏移边界条件与存储策略分析. 地球物理学进展, 30(2): 581-585. DOI:10.6038/pg20150214 |
王保利, 高静怀, 陈文超, 等. 2012. 地震叠前逆时偏移的有效边界存储策略. 地球物理学报, 55(7): 2412-2421. DOI:10.6038/j.issn.0001-5733.2012.07.025 |
王维红, 柯璇, 裴江云. 2013. 完全匹配层吸收边界条件应用研究. 地球物理学进展, 28(5): 2508-2514. DOI:10.6038/pg20130529 |
 2018, Vol. 61
2018, Vol. 61


