2. 中国科学院地球科学研究院, 北京 100029;
3. 中国科学院油气资源研究院重点实验室, 北京 100029;
4. 中国科学院大学, 北京 100049;
5. 中国地震局兰州地震研究所, 兰州 730000
2. Institute of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China;
5. Lanzhou Institute of Seismology, China Earthquake Administration, Lanzhou 730000, China
地震波波场正演模拟始终是地球物理领域研究的核心内容,寻求高精确的波场正演算子是地震波成像和反演的基础.
有限差分法因其高效性是求解波动方程的常用算法,但是它本质上还是在零频处展开得到的差分系数(Dablain, 1986; Kindelan et al., 1990),对于高频波的数值模拟,其存在的时间和空间频散限制了这种算法的精度,尤其是在大网格计算的情况下.为了解决有限差分的数值频散问题,许多科学家采用不同的优化算法来提高差分算子的精度(Zhou et al., 2008; Liu and Sen, 2009; Liu et al., 2009; Kosloff et al., 2010; Zhou and Zhang, 2011), 这些方法大都是通过拟合精确的频散关系得到优化的差分系数来提高计算精度和稳定性,但是没有从根本上解决这一问题.
实现时间域波场延拓的另一种方法是谱方法(Fowler et al., 2010; Du et al., 2014).最常用的伪谱法(Kosloff and Baysal, 1982)在波数域求解空间导数,可以避免空间频散,但是由于对于时间微分项是用简单的差分近似,因此无法解决时间频散,且是条件稳定的.理论上,时间域波场延拓可以归结为对一个波数-空间混合域象征进行处理(Wards et al., 2008).关于如何近似该混合域象征,涌现了一批算法:Zhang等(2007)、Zhang Y和Zhang G Q (2009)的单步延拓法利用可分近似的方法,将该混合域象征进行展开,展开过程涉及到特征向量的计算,这种算法与单程波方法类似(Chen and Liu, 2004),计算量非常大,但是不存在稳定性问题以及数值频散;Soubaras和Zhang(2008)的双步法是利用多项式展开来逼近该混合域象征,然后利用Remez最优化方法来求取逼近系数,这种方法能够使用大时间步长进行波场延拓.快速展开法(Tal-Ezer et al., 1987)是求解波动方程的解析算法,该算法利用Chebyshev多项式来逼近混合域象征,而且没有数值频散;目前,已有科学家(Pestana and Stoffa, 2009, 2010)将这一算法运用于逆时偏移中,取得了较好的效果,但是该方法的缺点在于计算效率太低,原因在于需要进行大量的傅里叶变换.Etgen和Brandsberg-Dahl(2009)提出用拟拉普拉斯算子代替拉普拉斯算子对声波方程进行模拟,补偿因时间差分造成的误差,但是对于速度变化剧烈的速度模型,这种拟解析法在时间和空间上都具有较大的误差.Mast等(2001)提出了波数-空间混合域算法处理超声波在时间上的延拓,Tabei等(2002)将该方法扩展到耦合的一阶速度-应力方程,有效地处理了弱非均匀介质中的波场延拓问题.Liu(1995)最先将波数-空间域方法应用于弹性波,并且基于并矢格林函数解析解,推导了二阶弹性波方程的波数-空间域象征.
在求解波数-空间混合域的谱方法中,二阶时间差分算子的频散误差可以通过波数域中的谱算子进行补偿,这种补偿对于常速介质是精确的,对于一般的变速介质,该混合域象征的计算量非常大,Fomel等(2010)提出了低秩分解来近似该混合域象征算子,这种方法在每一时间步上仅需少量的几次快速傅里叶变换,这是一种计算量与网格点数呈线性关系的波场延拓方法.Song和Fomel(2011)提出低秩有限差分法解决声波方程.Fang等(2014)将低秩有限差分方法应用于交错网格上,提出交错网格低秩有限差分法,并且用来解决一阶声波方程.Han等(2016)将交错网格低秩有限差分法用来解决一阶解耦的速度应力方程.
本文致力于解决解耦的二阶弹性波位移方程,将交错网格低秩方法结合有限差分法,提出交错网格低秩有限差分法,试图改善常规交错网格有限差分法的精度.最后,数值模拟结果证明,我们提出的交错网格低秩方法和交错网格低秩有限差分法具有较高的数值模拟精度.
1 理论 1.1 解耦的弹性波方程在均匀各向同性完全弹性介质中,弹性波的传播由下述拉梅方程描述(Aki and Richards, 2009):
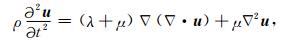
|
(1) |
式中,u =(u, v, w)为位移场,λ,μ是拉梅系数,ρ是介质的密度.▽是梯度算子.
对于拉普拉斯算符▽2u可有:
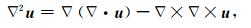
|
(2) |
于是,(1)式还可以写成:
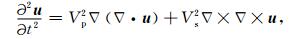
|
(3) |
其中: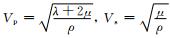
用位移向量的三个分量u,v,w描述的拉梅方程为:
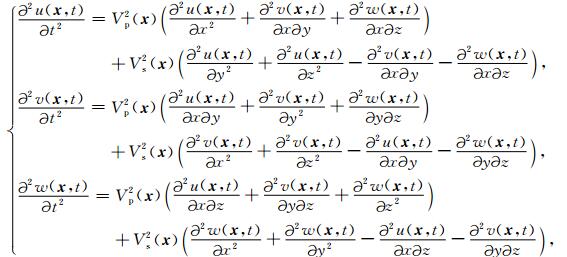
|
(4) |
式中,x =(x, y, z)代表三维空间位矢.
在三维介质中,等价的解耦弹性波方程可以写为(马德堂和朱光明,2003):
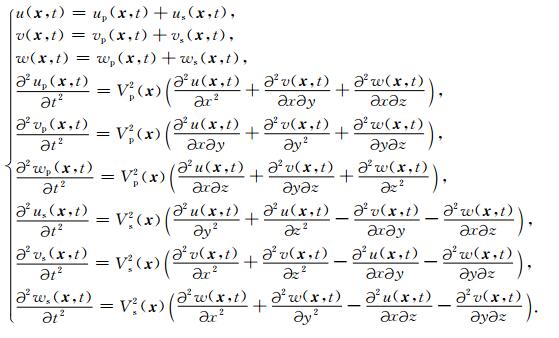
|
(5) |
在二维介质中,可以写为:
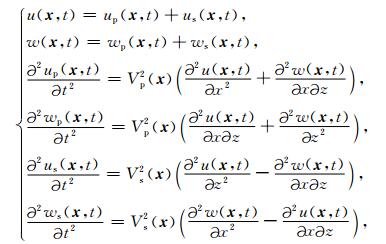
|
(6) |
(6) 式中,空间二阶微分算子可以分解成一对一阶微分算子.为了提高模拟精度,我们可以采用交错网格有限差分算子来近似一阶微分算子(陈可洋等,2009):
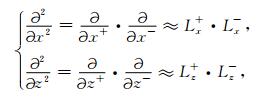
|
(7) |
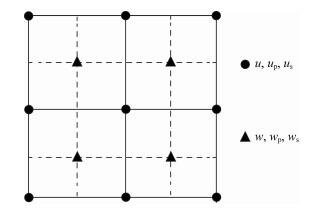
式中,Lx+和Lz+分别表示沿着x轴和z轴的前向差分算子,Lx-和Lz-分别表示沿着x轴和z轴的后向差分算子.本文中各位移分量在交错网格节点配置的方法如图 1所示:u, up, us定义在主网格节点,w, wp, ws定义在半网格节点.
|
图 1 交错网格节点配置 Fig. 1 Staggered-grid configuration |
时间微分算子通常由二阶中心差分算子Ltt近似:
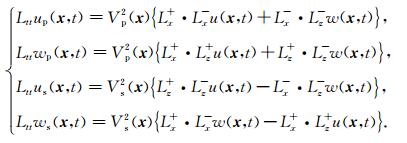
|
(8) |
利用傅里叶平移变换的性质,可以得到一阶微分算子的一种等价表示:

|
(9) |
其中,F和F -1分别代表傅里叶正、反变换,k =(kx, kz)表示波数向量.对于地震波场这样的有限带宽信号,对波场应用傅里叶变换可以准确求得波场在空间上的偏导数,可以看到,谱方法计算空间微分,由于没有任何近似,具有很高的精度.然而,我们仍然需要采用中心二阶差分计算时间微分项,受到有限差分固有的稳定性条件限制,对于大时间步长采样,会遇到不稳定问题;并且时间频散很严重(Firouzi et al., 2012).
1.2 拟微分算子与混合域象征在提出本文的方法之前,先介绍拟微分算子以及它的象征.
拟微分算子可以视为微分算子的推广,我们知道,微分与乘法对偶(齐民友等,2005),定义拟微分算子如下:
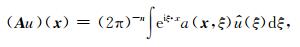
|
(10) |
其中,A称为拟微分算子,而a(x, ξ)称为拟微分算子的象征. 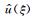
针对大步长采样不稳定问题,我们用波数-空间混合域象征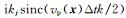
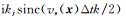
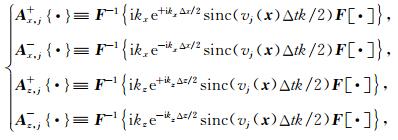
|
(11) |
其中,j=p, s.对于不均匀介质,速度随着空间位置而变化,直接采用(10)式计算,计算量是O(NxlogNx),其中Nx是总的采样点数.为了提高计算效率,Fomel等(2013), Engquist和Ying(2009)研究给出了混合域象征的低秩分解,以Wp, x=kxsinc(vp(x)Δtk/2)为例,它可以有如下的低秩分解:
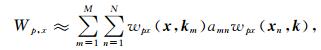
|
(12) |
其中,wpx(x, km)和wpx(xn, k)分别是从Wp, x选取M列和N行组成的子矩阵,M和N是依赖于矩阵的整数,一般是2或者3.利用(11)式,我们可以将拟微分算子Ax, p+写成:
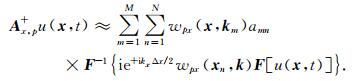
|
(13) |
同样的分解也可以用于其余三个拟微分算子.可以看到式(12)仅需N次反傅里叶变换,而直接计算Ax, p+需要Nx次反傅里叶变换,显著地减少了计算量,本文称此方法为交错低秩方法.
1.2.2 低秩有限差分近似拟微分算子注意到wpx(xn, k)是一个只与波数有关的矩阵,它可以进一步被分解为(Song et al., 2011):

|
(14) |
其中,B是L×Nk的矩阵,Nk是总的波数采样点数,L是有限差分算子的长度.它的元素形如sin((2l-1)kxΔx/2),Cpx(xn, l)是wpx(xn, k)和B的广义逆的乘积.
定义新的Nx×L矩阵:

|
(15) |
因此,可以将Ax, p+u(x, t)写成:
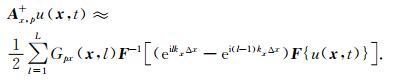
|
(16) |
利用傅里叶平移变换的移位性质,(16)式可以重新写成
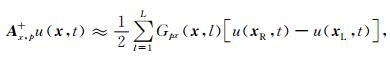
|
(17) |
其中,xR=(x+lΔx, y),xL=(x-(l-1)Δx, y),l=1, 2, …, L.类似地可以推导其余三个拟微分算子的交错低秩有限差分格式.与常规交错有限差分格式相比,差分系数Gpx是依赖于空间位置的,它随着模型参数的改变而自适应地变化,因而具有较高的模拟精度.本文称此方法为交错网格低秩有限差分法.接下来用平面波理论分析交错网格低秩有限差分法的数值频散特性,将p=ei(kx-wt)代入公式(17),并且将ξ定义为相速度的相对误差,根据频散理论,w= |k| v,以一维为例,可以得到:
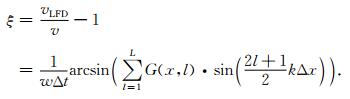
|
(18) |
利用(18)式,可以计算交错网格低秩有限差分法的频散特性.ξ如果等于0,表明不存在数值频散,ξ偏离0越大,表明数值频散越严重.
图 2对比了不同差分阶数(4,6,8,16阶)的交错网格低秩有限差分方法和常规交错网格有限差分方法的频散曲线,可以看出两种方法都随着差分阶数的提高频散减弱,注意到常规交错网格有限差分方法随着差分阶数的提高,能够精确拟合频散关系的频率范围并未增加,而对于交错网格低秩有限差分,随着有限差分阶数的增加,其精确拟合频散关系的频率范围变的更宽.

|
图 2 不同差分阶数的常规交错网格有限差分方法(a)和交错网格低秩有限差分方法(b)的频散曲线,4阶(红色),6阶(粉红色),8阶(绿色),16阶(蓝色) Fig. 2 Dispersion curves of conventional SGFD method (a) and SGLFD method (b) for different difference orders. 4th order (red), 6th order (pink), 8th order (green), 16th order (blue) |
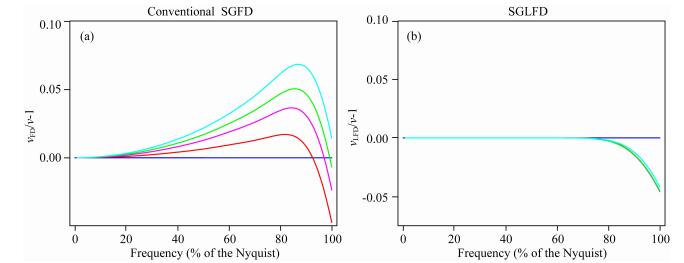
图 3对比了不同介质速度下,常规16阶交错网格有限差分和交错网格低秩有限差分的频散曲线,其中时间采样间隔是Δt=1 ms,空间采样间隔是Δx=10 m.对于一维的16阶交错网格低秩有限差分方法,L=8.图中可以看出,常规的交错网格有限差分只在零频率(波数)附近是精确的,随着频率增大,常规有限差分的频散越来越严重,而交错网格低秩有限差分能够在较宽的波数(大于70%的Nyquist波数)范围内精确地刻画频散关系,使得该方法能够较好地压制数值频散,具有较高的精度.
|
图 3 不同介质速度下,常规16阶交错网格有限差分和交错网格低秩有限差分的频散曲线对比,2500 m·s-1(红色),3500 m·s-1(粉红色),4000 m·s-1(绿色),4500 m·s-1(蓝色) Fig. 3 Comparison of 1-D dispersion curves of 16th order conventional SGFD method (a) and SGLFD method (b) for different velocities. v=2500 m·s-1 (red), v=3500 m·s-1 (pink), v=4000 m·s-1 (green), v=4500 m·s-1 (blue) |
本文中数值实验均采用海绵吸收边界条件,震源皆采用主频为20 Hz(最高频率60 Hz)的Ricker子波.
2.1 均匀模型点源测试
首先,采样2D均匀模型,测试本文提出的交错网格低秩方法与交错网格低秩有限差分法,并与常规的交错网格有限差分方法所得结果进行对比.2D模型大小为256×256,X方向和Z方向采样间隔均为10 m.横波和纵波速度分别为1500 m·s-1、3000 m·s-1. Ricker子波的主频为20 Hz,时间采样步长为1 ms.震源位于模型中心,并同时产生横波和纵波.根据Song等(2013), 我们仍然采用CFL(Courant-Friedrichs-Lewy condition)数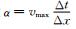
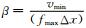
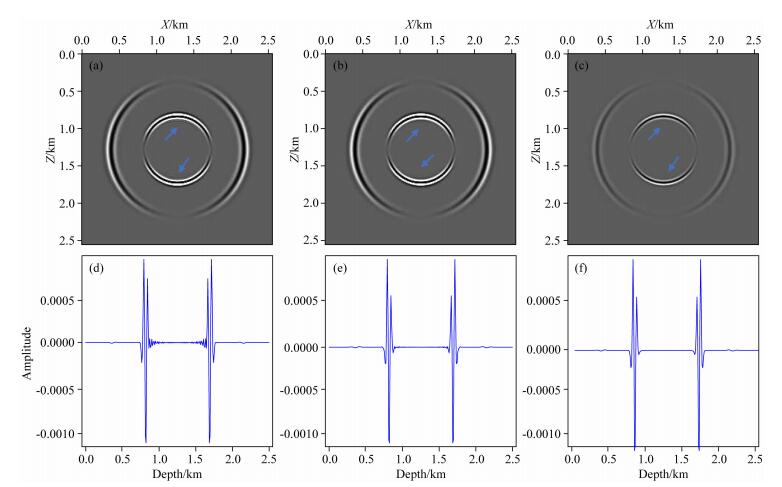
|
图 4 二维均匀弹性介质(Vp=3000 m·s-1, Vs=1500 m·s-1) t=0.4 s波场快照以及X=1250 m处的垂直道 (a) 4阶常规交错网格有限差分X分量; (b) 4阶交错网格低秩有限差分法X分量; (c)交错网格低秩方法X分量;(d)交错网格有限差分方法的垂直道;(e)交错网格低秩有限差分方法的垂直道;(f)交错网格低秩方法的垂直道. Fig. 4 Wavefield snapshots and vertical trace at distance 1250 m at 0.4 s for homogeneous media (Vp=3000 m·s-1, Vs=1500 m·s-1) (a) X-component with 4th-order SGFD; (b) X-component with 4th-order SGLFD; (c) X-component with SGL; (d) Selected vertical trace of SGFD; (e) Selected vertical trace of SGLFD; (f) Selected vertical trace of SGL. |
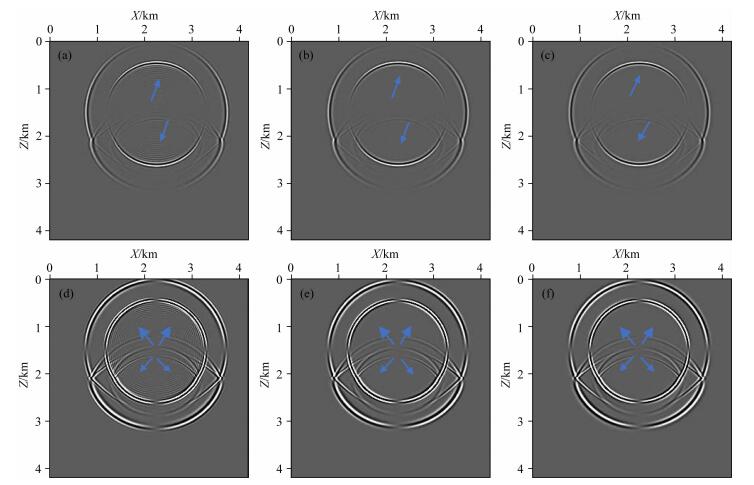
我们用层状弹性介质对比常规交错网格有限差分法和本文提出的方法.采用的模型在X方向和Z方向的空间间隔均为15 m.上层介质Vp=2500 m·s-1,Vs=1800 m·s-1.下层介质Vp=3000 m·s-1,Vs=2000 m·s-1.分界面位于Z=2100 m处.震源为主频为20 Hz的Ricker子波,位于模型(X, Z)=(2250 m, 1500 m)处.时间采样步长为2 ms.稳定性因子α=0.4,频散因子β=2.图 5a—5c显示了常规6阶交错网格有限差分法、6阶交错网格低秩有限差分法、交错网格低秩方法,X分量波场快照对比.图 5d—5f显示了常规6阶交错网格有限差分法、6阶低秩有限差分法、交错网格低秩方法,Z分量波场快照对比.从图中可以看出6阶交错网格低秩有限差分法和交错网格低秩方法得到的波场快照比常规6阶交错网格有限差分方法得到的波场快照精度更高(数值频散更弱),如蓝色箭头所示.
|
图 5 二维层状弹性介质t=0.78 s波场快照 (a) 6阶常规交错网格有限差分X分量; (b) 6阶交错网格低秩有限差分X分量; (c)交错网格低秩方法X分量;(d) 6阶常规交错网格有限差分Z分量; (e) 6阶交错网格低秩有限差分Z分量; (f)交错网格低秩方法Z分量. Fig. 5 Wavefield snapshots at 0.78 s for layered media (a) X-component with 6th-order SGFD; (b) X-component with 6th-order SGLFD; (c) X-component with SGL; (d) Z-component with 6th-order SGFD; (e) Z-component with 6th-order SGLFD; (f) Z-component with SGL. |
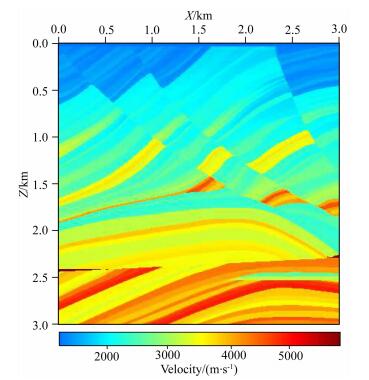
为了进一步验证本文方法的有效性,我们选择了部分Marmousi模型进行实验.图 6显示了Marmousi的纵波速度模型.横波速度与纵波速度的关系为: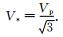
|
图 6 部分Marmousi模型纵波速度 Fig. 6 P velocity of part Marmousi model |
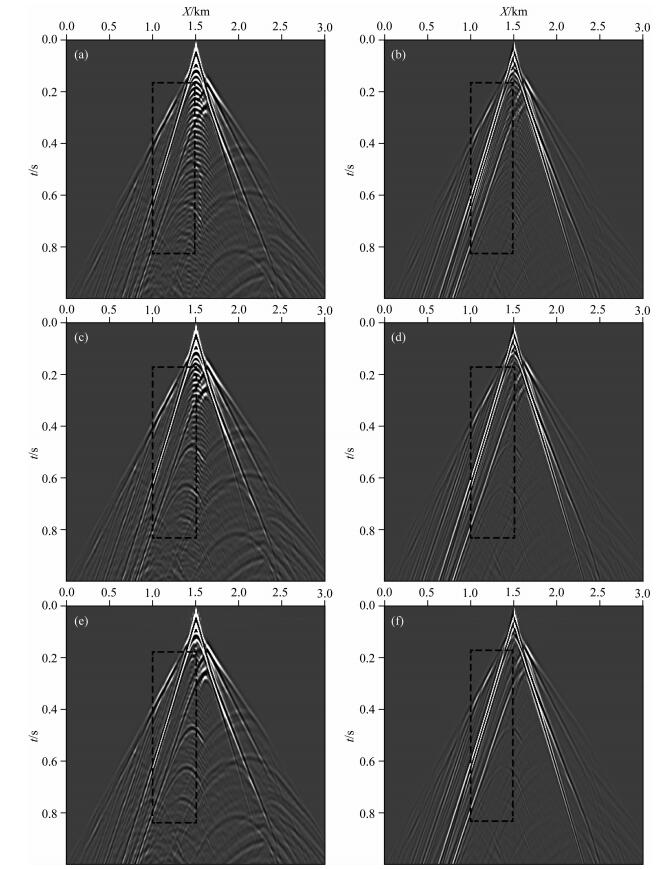
图 7a、7c、7e分别为使用常规交错网格有限差分法、交错网格低秩有限差分法、交错网格低秩方法正演得到的横波X分量地震记录.图 7b、7d、7f分别为使用常规交错网格有限差分法、交错网格低秩有限差分法、交错网格低秩方法正演得到的横波Z分量地震记录.
|
图 7 部分Marmousi模型正演得到的横波分量地震记录 (a) 8阶常规交错网格有限差分X分量; (b) 8阶常规交错网格有限差分Z分量; (c) 8阶交错网格低秩有限差分X分量; (d) 8阶交错网格低秩有限差分Z分量; (e)交错网格低秩方法X分量; (f)交错网格低秩方法Z分量. Fig. 7 Seismograms of S wavefield for part Marmousi model (a) X-component with 8th-order SGFD; (b) Z-component with 8th-order SGFD; (c) X-component with 8th-order SGLFD; (d) Z-component with 8th-order SGLFD; (e) X-component with SGL; (f) Z-component with SGL. |
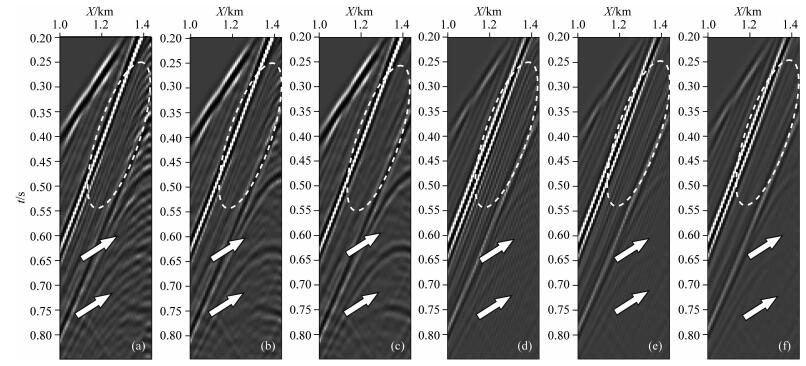
图 8为图 7中地震记录黑色虚线部分的放大图,可以看出,本文提出的交错网格低秩有限差分法和交错网格低秩方法频散更弱,精度更高.
|
图 8 从图 7中截取的地震记录窗 (a) 8阶常规交错网格有限差分X分量; (b) 8阶交错网格低秩有限差分X分量; (c)交错网格低秩方法X分量; (d) 8阶常规交错网格有限差分Z分量; (e) 8阶交错网格低秩有限差分Z分量; (f)交错网格低秩方法Z分量. Fig. 8 Zoom of the seismograms from Fig. 7 (a) X-component with 8th-order SGFD; (b) X-component with 8th-order SGLFD; (c) X-component with SGL; (d) Z-component with 8th-order SGFD; (e) Z-component with 8th-order SGLFD; (f) Z-component with SGL. |
在本文中,我们提出了交错网格低秩有限差分方法以及交错网格低秩方法求解解耦的二阶弹性波位移方程.交错网格低秩有限差分法的差分系数,是通过对波数-空间混合域的算子作低秩近似而得到的,它随着空间位置的变化而变化,相比于泰勒级数在零波数处的展开而得到传统的有限差分系数,低秩有限差分法能在高波数处拟合频散关系曲线;而交错网格低秩方法,对于均匀介质,它的解实质上就是解析解(如果不考虑矩阵低秩近似带来的微弱误差).数值结果表明:本文提出的两种方法相对于常规的交错网格有限差分法具有更高的精度,并且可以适用于复杂模型.本文的方法可以扩展到三维弹性波模型正演模拟,并且进一步应用于弹性波逆时偏移成像.
致谢感谢审稿专家和编辑提出的宝贵意见.
Aki K, Richards P G. 2002. Quantitative Seismology. 2nd ed. Sausalito, Calif. : University Science Books.
|
Chen J B, Liu H. 2004. Optimization approximation with separable variables for the one-way wave operator. Geophysical Research Letters, 31(6): L06613. DOI:10.1029/2004GL019429 |
Chen K Y, Yang W, Liu H L, et al. 2009. Wave field separation numerical modeling of second order elastic wave equation by high-precision staggered-grid finite difference scheme. Geophysical and Geochemical Exploration, 33(6): 700-703. |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. |
Du S T. 2008. Seismic Waves Dynamics Theory and Methods. Shandong Dongying: China University of Petroleum Press.
|
Du X, Fowler P J, Fletcher R P. 2014. Recursive integral time-extrapolation methods for waves:A comparative review. Geophysics, 79(1): T9-T26. DOI:10.1190/geo2013-0115.1 |
Etgen J T, Brandsberg-Dahl S. 2009. The pseudo-analytical method: Application of pseudo-Laplacians to acoustic and acoustic anisotropic wave propagation. //79th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2552-2556.
|
Engquist B, Ying L X. 2009. A fast directional algorithm for high frequency acoustic scattering in two dimensions. Communications in Mathematical Sciences, 7(2): 327-345. DOI:10.4310/CMS.2009.v7.n2.a3 |
Fang G, Fomel S, Du Q Z, et al. 2014. Lowrank seismic-wave extrapolation on a staggered grid. Geophysics, 79(3): T157-T168. DOI:10.1190/geo2013-0290.1 |
Firouzi K, Cox B T, Treeby B E, et al. 2012. A first-order k-space model for elastic wave propagation in heterogeneous media. The Journal of the Acoustical Society of America, 132(3): 1271-1283. DOI:10.1121/1.4730897 |
Fomel S, Ying L X, Song X L. 2010. Seismic wave extrapolation using lowrank symbol approximation. //80th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 3092-3096.
|
Fornberg B. 1990. High-order finite differences and the pseudospectral method on staggered grids. SIAM Journal on Numerical Analysis, 27(4): 904-918. DOI:10.1137/0727052 |
Fowler P J, Du X, Fletcher R P. 2010. Recursive integral time extrapolation methods for scalar waves. //80th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 3210-3215.
|
Han D, Du Q Z, Fang G. 2016. Elastic wave propagation on a staggered-grid using lowrank finite-difference method. //86th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 3900-3904.
|
Kindelan M, Kamel A, Sguazzero P. 1990. On the construction and efficiency of staggered numerical differentiators for the wave equation. Geophysics, 55(1): 107-110. DOI:10.1190/1.1442763 |
Kosloff D, Pestana R C, Tal-Ezer H. 2010. Acoustic and elastic numerical wave simulations by recursive spatial derivative operators. Geophysics, 75(6): T167-T174. DOI:10.1190/1.3485217 |
Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
Liu Q H. 1995. Generalization of the k-space formulation to elastodynamic scattering problems. The Journal of the Acoustical Society of America, 97(3): 1373-1379. DOI:10.1121/1.412079 |
Liu Y, Sen M K. 2009. A practical implicit finite-difference method:Examples from seismic modelling. Journal of Geophysics and Engineering, 6(3): 231-249. DOI:10.1088/1742-2132/6/3/003 |
Ma D T, Zhu G M. 2003. Numerical modeling of P-wave and S-wave separation in elastic wavefield. Oil Geophysical Prospecting, 38(5): 482-486. |
Mast T D, Souriau L P, Liu D L D, et al. 2001. A k-space method for large-scale models of wave propagation in tissue. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 48(2): 341-354. DOI:10.1109/58.911717 |
Pestana R C, Stoffa P L. 2009. Rapid expansion method (REM) for time-stepping in reverse time migration (RTM). //79th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2819-2823.
|
Pestana R C, Stoffa P L. 2010. Time evolution of the wave equation using rapid expansion method. Geophysics, 75(4): T121-T131. DOI:10.1190/1.3449091 |
Qi M Y, Wang W K, Xu C J. 2005. Introduction of Modern Partial Differential Equation. Wuhan: Wuhan University Press.
|
Song X L, Fomel S. 2011. Fourier finite-difference wave propagation. Geophysics, 76(5): T123-T129. DOI:10.1190/geo2010-0287.1 |
Soubaras R, Zhang Y. 2008. Two-step explicit marching method for reverse time migration. //78th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2272-2276.
|
Tabei M, Mast T D, Waag R C. 2002. A k-space method for coupled first-order acoustic propagation equations. The Journal of the Acoustical Society of America, 111(1): 53-63. DOI:10.1121/1.1421344 |
Tal-Ezer H, Kosloff D, Koren Z. 1987. An accurate scheme for seismic forward modelling. Geophysical Prospecting, 35(5): 479-490. DOI:10.1111/gpr.1987.35.issue-5 |
Wards B D, Margrave G F, Lamoureux M P. 2008. Phase-shift time-stepping for reverse-time migration. //78th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2262-2266.
|
Zhang Y, Yingst D, Sun J. 2007. Explicit marching method for reverse-time migration. //77th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2300-2304.
|
Zhang Y, Zhang G Q. 2009. One-step extrapolation method for reverse time migration. Geophysics, 74(4): A29-A33. DOI:10.1190/1.3123476 |
Zhou H, Liao Q, Ortigosa F. 2008. Construction and analysis of an optimized compact finite difference scheme for RTM. //78th Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts.
|
Zhou H B, Zhang G Q. 2011. Prefactored optimized compact finite-difference schemes for second spatial derivatives. Geophysics, 76(5): 87. DOI:10.1190/geo2011-0048.1 |
陈可洋, 杨微, 刘洪林, 等. 2009. 二阶弹性波动方程高精度交错网格波场分离数值模拟. 物探与化探, 33(6): 700-703. |
杜世通. 2008. 地震波动力学理论与方法. 山东东营: 中国石油大学出版社.
|
马德堂, 朱光明. 2003. 弹性波波场P波和S波分解的数值模拟. 石油地球物理勘探, 38(5): 482-486. |
齐民友, 王维克, 徐超江. 2005. 现代偏微分方程引论. 武汉: 武汉大学出版社.
|
 2018, Vol. 61
2018, Vol. 61


