2. 西安交通大学电子与信息工程学院, 西安 710049;
3. 海洋石油勘探国家工程实验室, 西安 710049;
4. 中国石化地球物理重点实验室, 南京 211103
2. School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
3. National Engineering Laboratory for Offshore Oil Exploration, Xi'an 710049, China;
4. SNOPEC Key Laboratory of Geophysics, Nanjing 211103, China
波动方程在数学上描述了地震波在介质传播过程中各个量之间的相互关系,是自然界守恒定律的数量描述(姜礼尚等,2007).地震波场模拟通过求解波动方程给出了源在激发后一段时间内地下介质的响应信息,是认识地震波在复杂介质中传播特征的重要手段.波动方程的精确高效求解在诸多地震勘探应用中至关重要,如观测系统设计、多次波压制、地震数据解释、高精度成像及建模等(Etgen and O′Brien, 2007; Ren et al., 2011).目前,地震波场模拟主要分为有限差分法、有限元法、伪谱法、体积元法以及粒子法等(黎昌成和张美根,2018;Hu and Jia, 2016).相比较而言,有限差分法具有计算量小、内存需求少和实现简单等优点,应用最为广泛(Etgen and O′Brien, 2007;黄超和董良国,2009;Yao et al., 2016).随着勘探区域的不断扩大以及储层结构越来越复杂,逆时偏移成像(Etgen et al., 2009)和全波形反演建模(Virieux and Operto, 2009; Luo et al., 2016;Luo and Xie, 2017)被广泛研究和应用,其中有限差分波场模拟占有非常重要的地位(范娜等,2018).尤其是全波形反演和最小二乘逆时偏移(Mulder and Plessix, 2004; Ren et al., 2013)广泛采用迭代求解,每个迭代均需多次求解波动方程,对波场模拟的效率和内存使用均提出更高的要求.
传统有限差分求解波动方程时,用泰勒展开近似波动方程中的偏微分项,其中的空间采样步长在整个模型所有位置处相同,即用规则网格或固定网格对介质离散(Dablain,1986).为了避免频散,网格大小是由整个模型中的最小速度对应的最短波长决定(杨凯和张剑锋,2017),此策略导致模型的高速区域出现过采样,造成计算和内存的冗余.为了提升模拟精度和效率,大量研究通过优化有限差分系数来减小最短波长内所需网格点数(Holberg, 1987; Tam and Webb, 1993; Etgen and O′Brien,2007;Liu, 2013; 刘璐等,2013;Zhang and Yao, 2013a, b;Liang et al., 2015; Ren and Liu, 2014;Yao et al., 2016).差分系数优化法通过优化策略在频率和波数尽量宽的范围内,求取使频散曲线尽量小的差分系数,并不考虑介质的结构和变化信息;另一种兼顾地震波模拟效率和精度的有效途径即变网格有限差分(Moczo,1989;朱生旺等,2007;赵海波和王秀明,2007).变网格有限差分在介质变化剧烈或者速度低的模型区域采用精细的空间网格剖分,而在介质缓变区域或者高速区采用粗网格剖分.变网格有限差分关键在于处理粗细网格区域的过渡,由此大致可分为基于插值的变网格有限差分(Jastram and Behle, 1992; Hayashi and Burns, 1999; Wang et al., 2001; Pasalic and McGarry, 2010)、基于邻域差分近似的变网格有限差分(黄超和董良国,2009;孙小东等,2012;Takekawa et al., 2015; Li et al., 2017)和基于坐标变换的变网格有限差分(Jastram and Tessmer, 1994; Atle et al., 2011; Chen and Xu, 2012).基于插值的变网格有限差分通过插值给出粗细网格分界面附近所需额外网格点信息,附加计算量小且实现简单,但插值易造成虚假反射和波场递推不稳定(Hayashi and Burns, 1999;Zhang and Yao, 2017).基于邻域差分近似的变网格有限差分将连续偏导离散近似为中心点及其邻域网格点的线性组合,网格点的放置自由灵活,但网格点差分系数一般需通过介质模型计算,增加较多额外计算量(Chen et al., 2016).基于坐标变换的变网格有限差分通过坐标映射在新的坐标系下求解波动方程,且新坐标系中仍可采用常规固定采样步长有限差分数值求解.这类方法能有效避免由不同采样区域过渡引起的虚假反射,具有附加计算量小以及网格可随速度灵活变化的优点.特别地,Chen和Xu(2012)提出梯形网格对介质进行剖分,并基于伪谱法对弹性波波场进行数值模拟,实际数据算例表明梯形网格剖分能显著减少计算量及内存消耗.
本文提出在梯形坐标系下用有限差分求解波动方程,实现一种物理横向网格采样间隔随深度增加的有限差分地震波模拟方法.后文首先给出本文所用梯形坐标系定义,然后推导二维波动方程在该梯形坐标系表达形式.由于梯形坐标系波动方程出现空间混合偏导,本文利用非正交坐标变换将混合偏导化解为非混合偏导后求解.数值试验部分将本文提出的梯形坐标系波场模拟结果首先与解析解对比,其次用两个层状模型展示本法计算结果,然后在Marmousi模型上与传统固定网格有限差分模拟结果进行对比.最后是结论和讨论.
1 方法原理 1.1 梯形坐标系Chen和Xu(2012)给出了三维梯形坐标系定义的一般形式,但由于每一维坐标变换后波动方程中所对应的偏导数项均需改变,增加了最终表达式的复杂度,本文应用了一种简化的梯形坐标系来展示其原理效果.二维情况下,其表达式为

|
(1) |
其中(x0, z0)表示直角坐标系坐标,(x, z)表示梯形坐标系坐标.梯形坐标横向位置参数a,地震波模拟中一般与源横向位置相同.γ是形状参数,与模型速度随深度变化相关.若梯形坐标系下横向采样间隔固定为Δx,则其对应的随z0变化的物理直角坐标系采样间隔Δx0(z0)可表示为

|
(2) |
若速度模型v(x0, z0)中每个深度最小速度表示为vmin(z0),且保持震源主频率下一个波长内的采样点数相同,则每个深度最大横向采样间隔可表示为
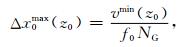
|
(3) |
其中f0为震源主频率,NG为一个波长内采样点数,可根据对模拟精度需求设定.公式(1)中对横坐标的变换为一种线性分式变换(Young, 1984),其中物理网格横向采样间隔随深度线性增加.
设Δx0(z0max)表示最深层横向采样间隔,则梯形坐标系形状参数γ可由如下表达式确定:

|
(4) |
其中Δx=Δx0(0)以及Δx0(z0max)的确定是通过构造关于z0的不超过Δx0max(z0)的线性函数.具体地,首先假定梯形坐标系在最大深度时与直角坐标系的横向覆盖范围相同,先初步令Δx0(z0max)=Δx0max(z0max)并根据Δx0(z0max)给出梯形坐标系横向采样点数以及可能最大的Δx0(0),逐渐增大梯形坐标系横向采样点数同时减少Δx0(z0max),直到最小深度的横向覆盖范围满足要求(我们一般要求最小深度的横向覆盖范围不低于直角坐标系横向覆盖范围的50%).
图 1所示为直角坐标系和梯形坐标系中对同一区域离散采样示意图.图 1a为直角坐标系一梯形区域,而在梯形坐标系下为一矩形区域(图 1b).两图中总采样点数相同且纵向采样间隔一致,但图 1a中横向采样间隔随深度逐渐增大,而图 1b中为均匀采样.两个网格覆盖区域完全相同,灰色网格表示相同采样点.

|
图 1 直角坐标系梯形网格采样(a)与梯形坐标系均匀网格采样(b)对应关系示意图其中灰色部分对应相同的采样位置. Fig. 1 (a) The trapezoid grid mesh in Cartesian coordinate and the corresponding (b) uniform grid sampling in trapezoid coordinate The gray areas represent the same sampling point. |
应用中,一般原始速度模型为均匀间隔采样,而且最终也往往要得到物理上均匀采样的波场模拟结果.本文中,速度模型在直角坐标系规则网格和梯形坐标系规则网格之间的转换通过坐标变换和线性插值实现,而波场在直角坐标系规则网格和梯形坐标系规则网格之间的转换通过坐标变换和三次样条插值实现(李乃成和梅立泉,2010).
1.2 梯形坐标系波动方程表征定义梯形坐标系与直角坐标系转换关系(公式(1))后,可写出二者之间偏导关系:

|
(5) |
利用公式(5)所描述的关系以及复合求导,可将波场关于直角坐标系(x0, z0)的偏导转化为关于梯形坐标系(x, z)的偏导.若直角坐标系压力场u(x0, z0)和梯形坐标系压力场u(x, z)分别简化为u0和u,则二者一阶偏导关系为
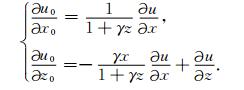
|
(6) |
公式(5)和(6)继续使用复合偏导,直角坐标系中波场二阶偏导可由梯形坐标系的一阶和二阶偏导表示为
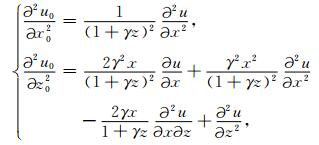
|
(7) |
直角坐标系(x0, z0)下,二维各向同性声波方程表达式为

|
(8) |
其中t为记录时间,δ(x)表示狄拉克函数,(x0s, z0s)是震源在直角坐标系中的横纵坐标,f(t)为时域震源函数.
用(7)式替换(8)式中关于空间的二阶偏导数,则由公式(8)所定义的声波方程在梯形坐标系下表示为

|
(9) |
公式(9)中等号左端出现了空间混合偏导项

|
(10) |
其逆变换为
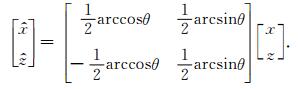
|
(11) |
公式(10)和公式(11)中θ为沿x方向的网格线与对角线的夹角(如图 2所示),且满足0 < θ < π/2.由公式(10)和公式(11)所定义的非正交坐标变换可将波动方程(9)中的混合偏导表示为
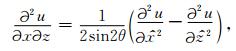
|
(12) |

|
图 2 空间混合偏导转化为非空间混合偏导非正交坐标变换示意图 Fig. 2 Illustration of the coordinate transformation for transition of mixed spatial derivatives to non-mixed derivatives |
将公式(12)代入公式(9)并整理得
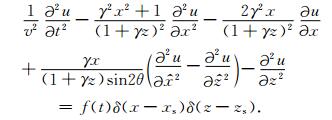
|
(13) |
为了提高模拟精度,空间偏导采用高阶有限差分格式,表示为(黄超和董良国,2009)
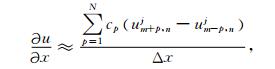
|
(14) |

|
(15) |
其中um, nj表示空间位置(xm, zn)=(x+(m-1)Δx, z+(n-1)Δz)和时刻tj=t0+(j-1)Δt处的波场,Δx和Δz是梯形坐标系横向和纵向空间采样间隔,Δt为时间采样间隔,t0为震源时延.cp和ηp(p=1, 2, …, N)分别表示空间一阶和二阶偏导差分系数,2N为空间差分精度.
如图 2所示,坐标系(

|
(16) |
所以有

|
(17) |
对公式(13)中时间采用二阶差分,将公式(14)—(17)代入并化简后,可得梯形坐标系中时间空间域二维声波方程差分方程为
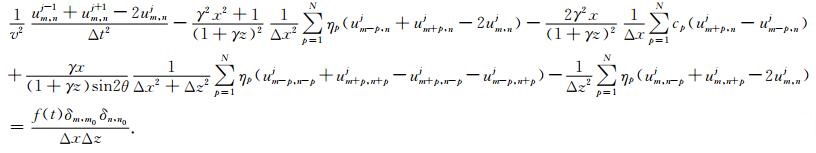
|
(18) |
式(18)为本文采用的最终差分形式,后文数值测试中空间差分精度N=8,一阶二阶差分系数cp和ηp通过泰勒展开得到(Dablain,1986).
1.3 稳定性条件根据黄超和董良国(2009),可以得到物理直角坐标系下二维声波方程在时间二阶空间2N阶有限差分稳定性条件为

|
(19) |
其中Δx0和Δz0分别为物理直角坐标系下速度模型横向和纵向采样间隔,Δt0为直角坐标系下有限差分时间采样间隔.类似地,本文通过平面波分析法给出梯形坐标系下稳定性条件为
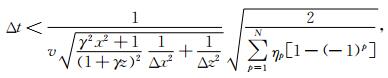
|
(20) |
其中Δx和Δz分别为梯形坐标系下速度模型横向和纵向采样间隔,Δt为梯形坐标系下有限差分时间采样间隔.
2 数值算例本部分给出不同速度模型脉冲响应来验证本方法的正确性与算法特点,并应用卷积完美匹配层避免边界的反射(Wu et al., 2018;Lan et al., 2016).首先在均匀介质模型下将梯形坐标系有限差分结果和解析解相比较,然后选择两种层状模型展示本算法在速度递增以及模型中间有高速层存在下的计算结果,最后在Marmousi模型下进行数值运算,并与常规固定采样有限差分结果进行比较.
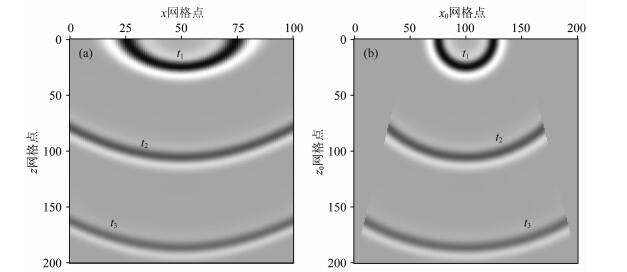
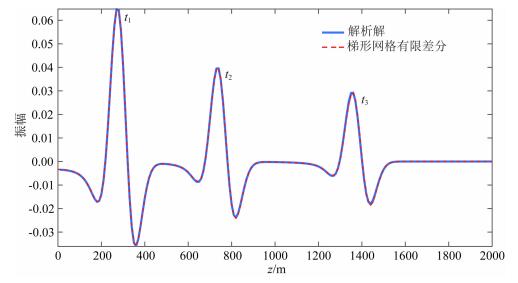
2.1 均匀介质模型数值模拟该速度模型设置为4000 m·s-1,用主频为20 Hz的Ricker子波为源放置在顶层正中间进行激发,震源时延0.075 s.Δz设置为10 m,深度方向一共201个采样点.横向采样间隔Δx为101个点,采样间隔从第一层的10 m增加至第201层的20 m(对应γ为10-5).为了避免时间频散的干扰,时间采样设置为1.3 ms.图 3显示了三个时刻的脉冲响应(t1=0.143 s,t2=0.3445 s,t3=0.546 s),其中图 3a和图 3b分别为对应梯形坐标系(x, z)和直角坐标系(x0, z0)波场快照.图 4显示的是震源处深度域波形图,其中红色虚线为梯形网格有限差分结果,蓝色实线为对应解析解(Wu et al., 2016).可以看出t1和t2时刻的脉冲响应与解析解高度吻合,在t3时刻,由于横向采样间隔的增大,可以观察到数值频散.
|
图 3 均匀速度模型三个时刻波场快照(t1=0.143 s,t2=0.3445 s,t3=0.546 s) (a)梯形坐标系;(b)直角坐标系. Fig. 3 Snapshots in constant velocity model for three time moments (t1=0.143 s, t2=0.3445 s, t3=0.546 s) (a) Trapezoid coordinate; (b) Cartesian coordinate. |
|
图 4 震源位置处深度域波形对比图 红色虚线为梯形坐标系有限差分波场模拟结果,蓝色实线为解析解(Wu et al., 2016). Fig. 4 Depth domain waveform comparison at the source location The red dash line is from trapezoid grid finite difference and the solid blue line is for the analytical solution (Wu et al., 2016). |
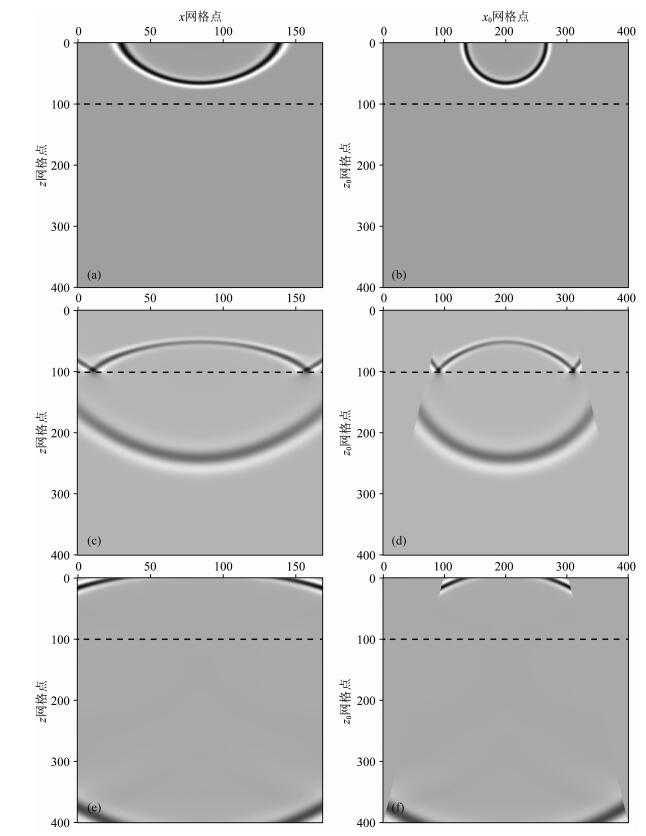
该两层模型中第一层速度为1500 m·s-1模拟水速,厚度为500 m,第二层速度为4000 m·s-1,厚度1500 m.纵向采样间隔Δz为5 m·s-1,横向采样间隔Δx从第一层的6.05 m增加至第401层11.9 m(对应γ为4.8366×10-4).震源子波与测试2.1节相同,同样放置在顶层正中间位置.梯形坐标系下有限差分时间采样间隔为0.6 ms.图 5显示了三个时刻脉冲响应,其中虚线所示为两层速度界面位置.图 5(a,b)、图 5(c,d)、图 5(e,f)分别对应时刻t1=0.3 s,t2=0.57 s和t3=0.78 s.图 5(a,c,e)和图 5(b,d,f)分别为梯形坐标系和直角坐标系下脉冲响应.从图 5可以看出梯形坐标系波场模拟的一个特点是缺失一些浅层大角度波场信息.一方面,可以通过扩大浅层孔径减少浅层信息损失;另一方面,该部分缺失信息在炮域逆时偏移成像中通常属于干扰,在后续处理中被大部分切除,因此对成像结果影响有限(Chen and Xu, 2012).
|
图 5 两层模型三个时刻波场快照:t1=0.3 s (a, b), t2=0.57 s(c, d)和t3=0.78 s(e, f) 其中左侧图形(a, c, e)和右侧图形(b, d, f)分别显示梯形坐标系和直角坐标系波场快照. Fig. 5 Snapshots for two-layer model with time moment at t1=0.3 s (a, b), t2=0.57 s (c, d) and t3=0.78 s (e, f) The left column (a, c, e) is for the trapezoid coordinate and right column (b, d, f) is for the Cartesian coordinate. |
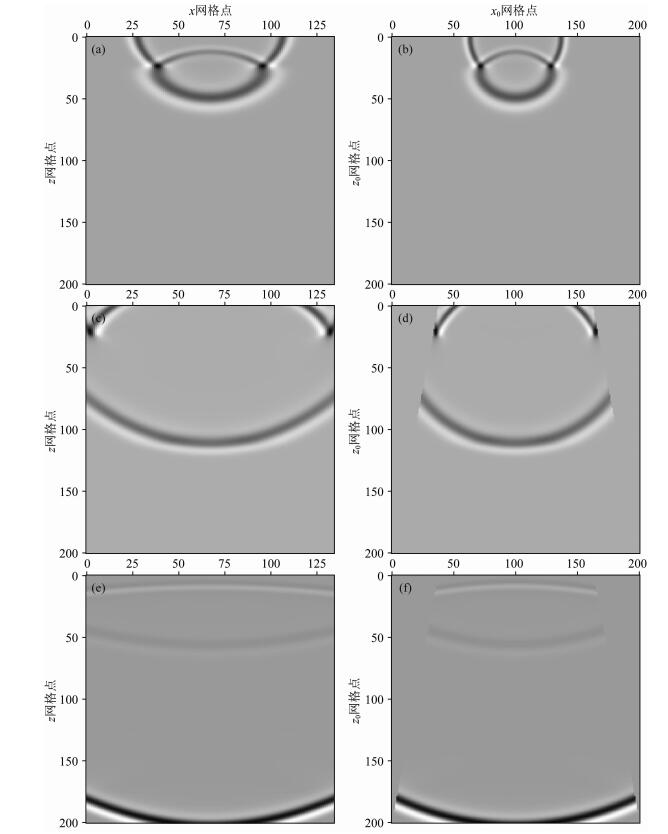
测试所用三层速度模型如图 6所示,第一层速度2000 m·s-1,厚度250 m,第二层和第三层速度分别为4000 m·s-1和3000 m·s-1,厚度均为750 m.纵向采样间隔Δz为10 m·s-1, 横向采样间隔Δx从第一层的9.33 m增加至第201层14.93 m(对应γ为3.0×10-4).震源子波和放置位置与测试2.1节和2.2节相同.梯形坐标系下有限差分时间采样间隔为1 ms.同样,图 7显示了三个时刻脉冲响应,图 7(a,b)、图 7(c,d)和图 7(e,f)分别对应时刻t1=0.265 s,t2=0.42 s和t3=0.72 s.图 7(a,c,e)和图 7(b,d,f)分别为梯形坐标系和直角坐标系下脉冲响应.测试2.2节中模型单调增加(1500 m·s-1至4000 m·s-1),横向采样间隔从最浅至最深增加1.83倍.本测试速度模型中间有高速层(4000 m·s-1),最深层速度为3000 m·s-1,为保证横向采样间隔由浅入深单调增,则中间高速层仍按深部低速层设计梯形坐标变换.因此,本测试深部是浅部横向采样间隔的1.6倍,而中间高速层被过采样.可引入纵向变网格采样进一步减少网格数量.

|
图 6 三层速度模型 Fig. 6 A three-layer velocity model |
|
图 7 三层模型三个时刻波场快照:t1=0.265s (a, b), t2=0.42s(c, d)和t3=0.72s(e, f)其中左侧图形(a, c, e)和右侧图形(b, d, f)分别显示梯形坐标系和直角坐标系波场快照. Fig. 7 Snapshots for three-layer model with time moment at t1=0.265 s (a, b), t2=0.42 s (c, d) and t3=0.72 s (e, f) The left column (a, c, e) is for the trapezoid coordinate and right column (b, d, f) is for the Cartesian coordinate. |
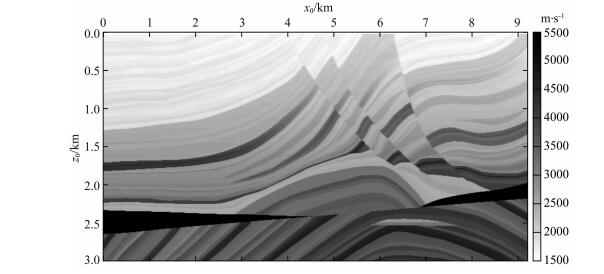
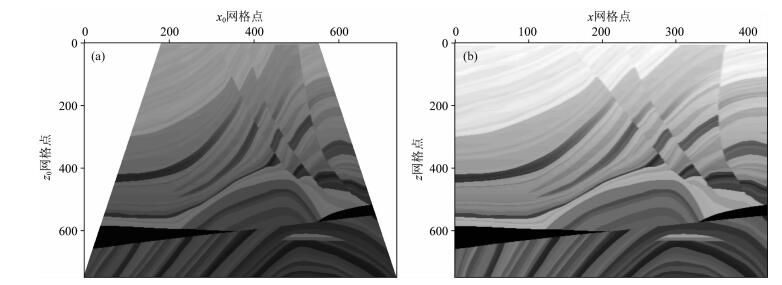
Marmousi模型被大量用于地震波模拟(黎昌成和张美根,2018)和偏移成像算法测试(吴帮玉等, 2013, 2017).该模型模拟实际地质环境,速度结构如图 8所示.该原始模型横向和纵向采样点分别为737和750,对应采样间隔分别为12.5 m和4 m.测试所用源为主频12 Hz的Ricker子波,时延0.125 s,放置于顶层中间位置.梯形坐标系下有限差分时间采样间隔为0.4 ms.实际有限差分模拟区域如图 9a所示,纵向采样点和采样间隔不变,横向采样点数为425,采样间隔经对原始速度内插重采样后从第一层的10.8979 m增加至第750层的21.6981 m(对应γ为3.3078×10-4).该区域在梯形坐标系下显示如图 9b所示.梯形坐标系下有限差分波场快照如图 10a所示.图 10b显示的是将图 10a内插至与原始速度模型相同采样间隔波场.作为对比,图 10c显示基于原始速度模型采样的固定网格传统有限差分相同时刻波场快照,与图 10b相比二者整体完全一致.为了对波形进行详细对比,图 10d—10f分别给出梯形坐标系(红色虚线)和直角坐标系下常规固定网格(蓝色实线)有限差分结果波形图.图 10d、图 10e和图 10f分别对应横向第269道、369道和469道,分别距离震源-1250 m、0 m和+1250 m.可以看出两种方法的振幅和走时完全匹配,波形高度一致.此外,对Marmousi模型,常规有限差分与梯形网格有限差分的12核CPU(Intel(R) Xeon(R) X5650 CPU, 24 GB内存)计算时间分别为147 s和256 s.结果表明虽然梯形网格有限差分的网格点数相对常规有限差分明显减少,但计算量却相对增加,这是因为梯形坐标下的波动方程相对直角坐标下的波动方程更为复杂.梯形网格有限差分计算量的问题可通过两种方式解决.一是进一步发展垂向变网格的梯形网格有限差分,这样只需在梯形坐标系下的波动方程中增加很少的项就可以换取网格点数的进一步大幅度减少;二是利用小内存的算法更适用于图形处理单元(Graphic Processing Unit, GPU)的特点,发展通过GPU进行梯形网格有限差分波场模拟的算法.
|
图 8 Marmousi速度模型 Fig. 8 Marmousi velocity model |
|
图 9 (a) 直角坐标系Marmousi模型波场模拟区域;(b)梯形坐标系Marmousi速度模型 Fig. 9 (a) The Marmousi velocity area for modeling in Cartesian coordinate; (b) The Marmousi velocity in trapezoid coordinate |

|
图 10 Marmousi模型波场快照以及深度域波形对比图 (a)梯形坐标波场快照;(b)梯形坐标系内插至直角坐标系波场快照;(c)基于传统固定网格有限差分波场模拟直角坐标系波场快照.横向第269道(d)、第369道(e)和第469道(f)深度域波形对比,其中红色虚线和蓝色实线分别表示梯形坐标系和传统固定网格有限差分模拟结果. Fig. 10 Snapshots and waveform comparison for Marmousi model (a) Trapezoid coordinate snapshot; (b) Cartesian coordinate result by interpolation from Trapezoid snapshot (a); (c) Cartesian coordinate result by modeling from traditional uniform grid finite difference; The depth domain waveform from lateral location 269 (d), 369 (e) and 469 (f) from trapezoid coordinate finite difference (red dash line) and traditional uniform grid finite difference (blue solid line). |
本文针对地震波传播速度随深度逐渐增加的一般特征,提出一种二维梯形坐标系波动方程有限差分波场模拟方法.梯形坐标系较直角坐标系更为一般,模型网格横向采样间隔可随深度逐渐线性增加,是一种变网格有限差分方法,且不会产生由于网格大小变化引起的虚假反射.梯形网格在浅层小速度区域应用细网格,深层高速区域应用粗网格,横向网格点个数不随深度变化,但由于采样间隔逐渐增大,因此横向覆盖范围随深度逐渐增加,有效减少传统固定网格有限差分对深部高速区域的过采样.本文导出了二维波动方程在本文所应用梯形坐标系中的表达式和差分格式,并应用非正交坐标变换求解其中出现的空间混合偏导数.Marmousi模型测试表明,在最深层为满覆盖情况下,梯形坐标系有限差分横向采样点仅为原始模型的57.67%.本文所提出的方法虽然可以有效减少网格点数量,但由于梯形坐标系中波动方程复杂度增加,会部分抵消网格点数量减少所减少的计算量,在本文基础上引入垂向变网格可进一步减少网格数量和计算量.梯形坐标系波动方程有限差分正演方法可推广至其他方程,且在三维情况下计算优势更加明显,具有一定的应用潜力.
致谢谨此祝贺姚振兴先生从事地球物理教学科研工作60周年.非常感谢王绵森关于梯形坐标变换性质以及尤波关于偏微分方程数值解的讨论,感谢李辉和张国伟对文章撰写提出的修改意见.
Atle A, Lencrerot R, Williamson P. 2011. TTI finite difference with variable grid in depth. //81th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts.
|
Chen F, Xu S. 2012. Pyramid-shaped grid for elastic wave propagation. //82th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts.
|
Chen Y S, Yang G W, Ma X, et al. 2016. A time-space domain stereo finite difference method for 3D scalar wave propagation. Computers & Geosciences, 96: 218-235. |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
Etgen H T, O'Brien M J. 2007. Computational methods for large-scale 3D acoustic finite-difference modeling:A tutorial. Geophysics, 72(5): SM223-SM230. DOI:10.1190/1.2753753 |
Etgen J, Gray S H, Zhang Y. 2009. An overview of depth imaging in exploration geophysics. Geophysics, 74(6): WCA5-WCA17. DOI:10.1190/1.3223188 |
Fan N, Cheng J W, Qin L, et al. 2018. An optimal method for frequency-domain finite-difference solution of 3D scalar wave equation. Chinese Journal of Geophysics, 61(3): 1095-1108. DOI:10.6038/cjg2018L0375 |
Guan H, Dussaud E, Denel B, et al. 2011. Techniques for anefficient implementation of RTM in TTI media. //81th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts.
|
Hayashi K, Burns D R. 1999. Variable grid finite-difference modeling including surface topography. //69th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts.
|
Holberg O. 1987. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophysical Prospecting, 35(6): 629-655. DOI:10.1111/gpr.1987.35.issue-6 |
Hu X L, Jia X F. 2016. A dynamic lattice method for elastic seismic modeling in anisotropic media. Geophysics, 81(3): T131-T143. DOI:10.1190/geo2015-0511.1 |
Huang C, Dong L G. 2009. High-order finite-difference method in seismic wave simulation with variable grids and local time-steps. Chinese Journal of Geophysics, 52(1): 176-186. DOI:10.1002/cjg2.v52.1 |
Jastram C, Behle A. 1992. Acoustic modelling on a grid of vertically varying spacing. Geophysical Prospecting, 40(2): 157-169. DOI:10.1111/gpr.1992.40.issue-2 |
Jastram C, Tessmer E. 1994. Elastic modelling on a grid with vertically varying spacing. Geophysical Prospecting, 42(4): 357-370. DOI:10.1111/gpr.1994.42.issue-4 |
Lan H Q, Chen J Y, Zhang Z J, et al. 2016. Application of a perfectly matched layer in seismic wavefield simulation with an irregular free surface. Geophysical Prospecting, 64(1): 112-128. DOI:10.1111/1365-2478.12260 |
Li B, Liu Y, Sen M K, et al. 2017. Time-space-domain mesh-free finite difference based on least squares for 2D acoustic-wave modeling. Geophysics, 82(4): T142-T157. |
Li C C, Zhang M G. 2018. Optimal double 9-point scheme scale wave equation simulation based on the generalized rotation method. Chinese Journal of Geophysics, 61(3): 1178-1187. DOI:10.6038/cjg2018L0143 |
Liang W Q, Wang Y F, Yang C C. 2015. Comparison of numerical dispersion in acoustic finite-difference algorithms. Exploration Geophysics, 46(2): 206-212. DOI:10.1071/EG13072 |
Liu L, Liu H, Liu H W. 2013. Optimal 15-point finite difference forward modeling in frequency-space domain. Chinese Journal of Geophysics, 56(2): 644-652. DOI:10.6038/cjg20130228 |
Li S J, Sun C Y, Ni C K, et al. 2007. Acoustic equation numerical modeling on a grid of varying spacing. Chinese Journal of Engineering Geophysics, 4(3): 207-212. |
Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78(4): T113-T132. DOI:10.1190/geo2012-0480.1 |
Luo J R, Wu R S, Gao J H. 2016. Elastic seismic envelope inversion. Journal of Seismic Exploration, 25: 103-119. |
Luo J R, Xie X B. 2017. Frequency-domain full waveform inversion with an angle-domain wavenumber filter. Journal of Applied Geophysics, 141: 107-118. DOI:10.1016/j.jappgeo.2017.04.010 |
Moczo P. 1989. Finite-difference technique for SH-waves in 2-D media using irregular grids-application to the seismic response problem. Geophysical Journal International, 99(2): 321-329. DOI:10.1111/gji.1989.99.issue-2 |
Mulder W A, Plessix R E. 2004. A comparison between one-way and two-way wave equation. Geophysics, 69(6): 1491-1504. DOI:10.1190/1.1836822 |
Pasalic D, McGarry R. 2010. A discontinuous mesh finite difference scheme for acoustic wave equations. //80th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts.
|
Ren H R, Wu R S, Wang H Z. 2011. Wave equation least square imaging using the local angular Hessian for amplitude correction. Geophysical Prospecting, 59(4): 651-661. |
Ren H R, Wang H Z, Chen S C. 2013. Least-squares reverse time migration in frequency domain using the adjoint-state method. Journal of Geophysics and Engineering, 10(3): 035002. DOI:10.1088/1742-2132/10/3/035002 |
Ren Z M, Liu Y. 2014. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes. Geophysics, 80(1): T17-T40. |
Sun X D, Li Z C, Wang X L. 2012. Pre-stack reverse-time migration using a finite difference method based on triangular grids. Progress in Geophysics, 27(5): 2077-2083. |
Takekawa J, Mikada H, Imamura N. 2015. A mesh-free method with arbitrary-order accuracy for acoustic wave propagation. Computers & Geosciences, 78: 15-25. |
Tam C K W, Webb J C. 1993. Dispersion-relation-preserving finite difference schemes for computational acoustics. Journal of Computational Physics, 107(2): 262-281. DOI:10.1006/jcph.1993.1142 |
Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26. |
Wang Y, Xu J, Schuster G T. 2001. Viscoelasticwave simulation in basins by a variable-grid finite-difference method. Bulletin of the Seismological Society of America, 91(6): 1741-1749. DOI:10.1785/0120000236 |
Wu B Y, Wu R S, Gao J H. 2013. Survey sinking prestack depth migration using local cosine basis beamlets. Chinese Journal of Geophysics, 56(2): 635-643. DOI:10.6038/cjg20130227 |
Wu B Y, Zhang G W, Zhou Q B, et al. 2016. Beamlet-domain premigration deghosting on variable-depth streamer seismic data. //86th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts.
|
Wu B Y, Wu R S, Gao J H, et al. 2017. Survey sinking migration using the time-space localized dreamlet one-way propagator. Chinese Journal of Geophysics, 60(9): 3505-3517. DOI:10.6038/cjg20170919 |
Wu B Y, Xu W H, Jia J X, et al. 2018. Convolutional perfect matched layer boundary for trapezoid grid finite difference seismic modeling. //88th Ann. Internat Met., Soc. Expi. Geophys. . Expanded Abstracts, in press.
|
Yang K, Zhang J F. 2017. Least-squares reverse time migration based on unstructured gird. Chinese Journal of Geophysics, 60(3): 1053-1061. DOI:10.6038/cjg20170318 |
Yao G, Wu D, Debens H A. 2016. Adaptive finite difference for seismic wavefield modelling in acoustic media. Scientific Reports, 6: 30302. DOI:10.1038/srep30302 |
Young N J. 1984. Linear fractional transformations in rings and modules. Linear Algebra and Its Applications, 56: 251-290. DOI:10.1016/0024-3795(84)90131-9 |
Zhang J H, Yao Z X. 2013a. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18. DOI:10.1190/geo2012-0277.1 |
Zhang J H, Yao Z X. 2013b. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. Journal of Computational Physics, 250: 511-526. DOI:10.1016/j.jcp.2013.04.029 |
Zhang J H, Yao Z X. 2017. Exact local refinement using Fourier interpolation for nonuniform-grid modeling. Earth and Planetary Physics, 1(1): 58-62. DOI:10.26464/epp2017008 |
Zhu S W, Qu S L, Wei X C, et al. 2007. Numeric simulation by grid-various finite-difference elastic wave equation. Oil Geophysical Prospecting, 42(6): 634-639. |
范娜, 成景旺, 秦雷, 等. 2018. 一种优化的频率域三维声波有限差分模拟方法. 地球物理学报, 61(3): 1095-1108. DOI:10.6038/cjg2018L0375 |
黄超, 董良国. 2009. 可变网格与局部时间步长的高阶差分地震波数值模拟. 地球物理学报, 52(1): 176-186. |
姜礼尚, 陈亚浙, 刘西垣, 等. 2007. 数学物理方程讲义. 3版. 北京: 高等教育出版社: 1-239.
|
黎昌成, 张美根. 2018. 基于广义旋转法双九点格式标量波方程数值模拟. 地球物理学报, 61(3): 1178-1187. DOI:10.6038/cjg2018L0143 |
李乃成, 梅立泉. 2010. 数值分析(西安交通大学课程讲义).
|
李胜军, 孙成禹, 倪长宽, 等. 2007. 声波方程有限差分数值模拟的变网格步长算法. 工程地球物理学报, 4(3): 207-212. |
刘璐, 刘洪, 刘宏伟. 2013. 优化15点频率-空间域有限差分正演模拟. 地球物理学报, 56(2): 644-652. DOI:10.6038/cjg20130228 |
吴帮玉, 吴如山, 高静怀. 2013. 基于局部余弦基小波束的观测系统沉降法叠前深度偏移. 地球物理学报, 56(2): 635-643. DOI:10.6038/cjg20130227 |
吴帮玉, 吴如山, 高静怀, 等. 2017. 基于时空局域化dreamlet单程波算子的观测系统沉降法偏移. 地球物理学报, 60(9): 3505-3517. DOI:10.6038/cjg20170919 |
杨凯, 张剑锋. 2017. 基于非结构化网格的最小二乘逆时偏移. 地球物理学报, 60(3): 1053-1061. DOI:10.6038/cjg20170318 |
赵海波, 王秀明. 2007. 一种优化的交错变网格有限差分法及其在井间声波中的应用. 科学通报, 52(12): 1387-1395. DOI:10.3321/j.issn:0023-074X.2007.12.005 |
朱生旺, 曲寿利, 魏修成, 等. 2007. 变网格有限差分弹性波方程数值模拟方法. 石油地球物理勘探, 42(6): 634-639. |
孙小东, 李振春, 王小六. 2012. 三角网格有限差分法叠前逆时偏移方法研究. 地球物理学进展, 27(5): 2077-2083. DOI:10.6038/j.issn.1004-2903.2012.05.031 |
 2018, Vol. 61
2018, Vol. 61


