0 引言

高精度的三维海洋磁空间背景场数据可为地磁匹配导航、水下磁性目标探测及海洋地球物理勘探等提供基础.由于实际测量资料往往是描述某一高度面的磁异常分布特征，在构建三维磁空间背景场模型时，需将已知高度面的磁异常转换到用户需求的不同高度.解析延拓是实现不同高度磁场延拓的关键技术，而向下延拓因其典型的不适定性得到广泛的重视.

目前，位场向下延拓的方法主要有直接法和迭代法.尤其是迭代法实现了较大深度的稳定向下延拓，如积分迭代法(徐世浙，2006)和泰勒级数迭代法(王彦国等，2011).由于迭代法向下延拓中延拓算子对高频噪声的放大影响，因此，出现了基于正则化的迭代方法，如Landweber迭代法(陈龙伟等，2007)、迭代Tikhonov正则化法(曾小牛等，2013)等，大大提高了延拓精度.

然而，值得注意的是采用正则化方法进行向下延拓时，正则化参数的选择对延拓结果有较大影响.目前，确定最优正则化参数的方法有基于先验策略的Morozov偏差原理、广义偏差原理等，以及基于后验策略的广义交叉校验准则(GCV)、L-曲线准则等(王彦飞，2007).先验策略需预先知道数据的噪声信息，这在实际资料处理中并不适用；而后验策略中的GCV法，在实际处理时GCV函数往往变化较平缓，无法确定其最小值(孙文等，2014)，L-曲线准则在确定曲线拐点时不仅计算复杂且有一定偏差(马涛等，2013；刘晓刚等，2014)，因此，各方法都不能保证确定的正则化参数是最优的；另外在迭代法中，迭代过程是半收敛的，迭代终止条件往往是设定某个极小值或者最大迭代次数，而在实际计算时，最优延拓结果并不一定在迭代终止前得出(姚长利等，2012).

由此可见，如何快速、准确地选取与确定最优正则化参数及最佳迭代次数有助于提高向下延拓效率及延拓效果.为此，本文尝试引入微分进化法(又称差分进化法)来确定最优正则化参数及最佳迭代次数，该方法是基于群体智能理论的优化算法，并以延拓结果的熵值为目标函数，以目标函数最小为搜索准则，实现正则化参数和迭代次数的并行全局寻优.通过实测数据分别验证了微分进化法在积分迭代法、迭代Tikhonov正则化法及Landweber迭代法中选择最优参数的有效性.

1 向下延拓原理及最优参数确定 1.1 位场向下延拓迭代法

徐世浙(2006)针对向下延拓的不适定性，利用向上延拓算子的稳定性，采用迭代思想逐渐逼近向下延拓值，提出了积分迭代法.刘东甲等(2009)将空间域迭代过程转换到频域进行，大大提高了计算效率，频域迭代公式为

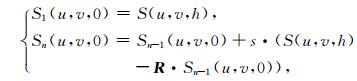
(1)

式中，S(u, v, h)为观测面z=h(h>0)上的位场频域值，u、v分别为x、y方向的圆频率，S_n(u, v, 0)为延拓面z=0上第n次迭代结果的频域值，s为迭代步长，一般取1，R为频域向上延拓算子，其表达式为

(2)

积分迭代法虽实现了20倍点距的大深度延拓，但该方法是基于向上延拓算子R的迭代，仍未解决对高频噪声的放大问题.而正则化迭代方法则有效地解决了此问题，如Landweber迭代法与迭代Tikhonov正则化法.

曾小牛等(2011)比较了以上三种向下延拓迭代方法，并采用数学归纳法推导了三种迭代法的频域延拓算子：

(a) 频域积分迭代法延拓算子

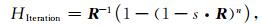
(3)

(b) 频域迭代Tikhonov正则化法延拓算子

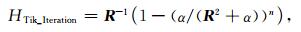
(4)

(c) 频域Landweber迭代法延拓算子

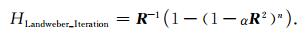
(5)

由公式(3)—(5)可以看出，相同延拓高度时，三种迭代法的延拓结果直接与正则化参数α(迭代步长s)和迭代次数n有关.而在以上三种迭代方法的计算中，通常是先采用某种准则(L-曲线法、GCV法等)确定最优正则化参数或人为给定迭代步长，再根据某种迭代终止准则确定最佳迭代次数，这是一种单路径串行求解过程，其中任意过程出现偏差，都会导致计算结果不是最优的.为此，如何快速、准确地确定最优参数仍是需要解决的问题.

1.2 微分进化法确定最优参数

微分进化法(Differential Evolution，DE)是一种随机启发式并行全局寻优算法(Storn and Price, 1996)，近年来在地球物理反演、滤波器设计及系统优化中有较好的应用(王文娟，2010；宋维琪等，2013；王天意等，2014).

利用微分进化法在迭代向下延拓过程中确定最优正则化参数及最佳迭代次数时，在一定范围内分别随机生成NP个正则化参数及迭代次数，组成二维种群向量x_ij(i=1，2，…，NP；j=1，2)，在种群个体i中随机选择三个点x_{r1, j}，x_{r2, j}，x_{r3, j}，以其中两个点的加权差加到第三个点上产生下一代的变异向量v_ij，再与原种群个体x_ij进行交叉操作后进行“自然选择”即“适者生存”，实现种群的进化.具体步骤如下：

(1) 输入参数初值

输入种群规模NP，最大进化代数G，变异算子F，交叉算子CR；以正则化参数及迭代次数为种群变量，在其取值范围内随机生成变量初值，即

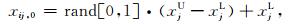
(6)

式中，rand[0, 1]表示在[0, 1]之间产生的均匀随机数，i=1，2，…，NP；j=1，2；x_j^U，x_j^L分别为种群变量的上下限.种群规模NP越大，个体多样性越多，寻优能力越强，但也因此降低了计算效率，一般取变量个数的5~10倍；

(2) 变异

对于种群向量x_{i, g}(i=1，2，…，NP；0≤g≤G)，其微分进化算法的变异公式为

(7)

式中，r₁、r₂与r₃是在i中随机选择的互不相同的向量序号，且与i也不同；变异算子F ∈[0, 2]，它控制变量偏差的放大比例，F过小容易陷入局部最优，F过大搜索效率低，一般取0.4~1.0之间；

(3) 交叉

交叉操作的目的是为了增加种群向量的多样性，通过(8)式确定交叉向量u_{ij, g+1}

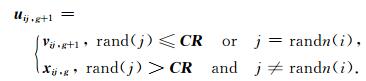
(8)

式中，rand(j) ∈ [0, 1]为均匀分布的随机数，而randn(i) ∈ (1, 2)保证该种群中至少有一个变量要进行交叉变异；交叉算子CR ∈ [0, 1]，表示子代个体从变异操作产生的向量实验个体中继承的比率，CR较好的选择是0.1，随着CR的增大，收敛速度越快，但易陷入局部最优；

(4) 地磁熵选择准则

评价交叉向量u_{ij, g+1}与上一代种群变量x_{ij, g}较优的关键在于目标函数的选择.对于位场延拓方法而言，使延拓误差最小时的参数应为最优参数，在延拓面真实值未知的情况下，如何计算延拓误差是值得思考的问题.根据信息熵的思想，熵值是衡量信息不确定度的量(徐晓苏和张逸群，2008)，延拓结果的熵值越大其不确定性越强，对应延拓误差就越大，反之误差越小.为此，将延拓结果的熵值作为目标函数，使目标函数最小的参数为最优参数，熵值计算公式为

(9)

式中，H(ΔT)为延拓结果熵值，ΔT_{i, j}为延拓方法计算值，M、N分别为网格化后的测线数与测点数，p(|ΔT_{i, j}|)为每一点磁异常概率，在一定区域范围内可由(10)式计算(孙文等，2014)

(10)

这样，根据如下准则选择目标函数较小的向量作为下一代种群，实现种群的进化.

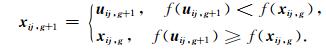
(11)

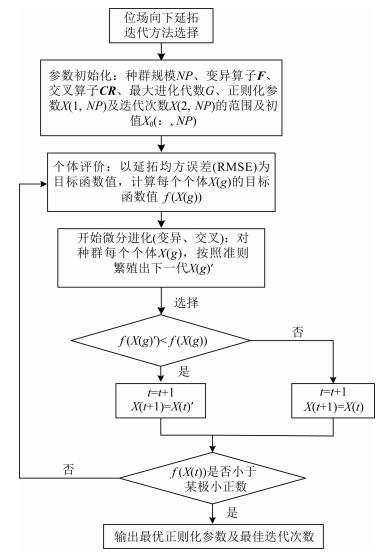
重复进行(2)—(4)的过程，直到使目标函数值小于给定的极小正数或达到最大进化代数时终止进化，输出结果.而为保证算法收敛到最优结果，最大进化代数应设置的尽量大些，一般取100~500次.微分进化法运算流程见图 1.

2 实测资料处理与对比分析

实测数据选取某次船载磁力测量资料，测区范围为10 km×10 km，主测线南北向布设，测线间距为500 m，磁测数据经常规改正后(磁测点位置改正、日变改正、船磁改正、正常场校正)进行了网格化处理，共生成201×201个磁异常点，网格间距为50 m×50 m，将其视为0 m高度磁异常真值，磁异常等值线分布见图 5a.将成果数据向上延拓500 m(10倍点距)视为航磁测量资料.因向上延拓对噪声有明显平滑作用，而实测航磁资料中不可避免含有噪声，考虑到高精度的航磁测量精度要求是1 nT(中华人民共和国国土资源部，2010)，为此，分析比较中向航磁数据中(500 m高度)加入均值为零，标准差σ_n=1.0 nT的高斯白噪声，使延拓数据更贴近实际情况.

下面分别采用积分迭代法、迭代Tikhonov正则化法、Landweber迭代法将航磁数据(500 m)向下延拓10倍点距.延拓中采用两种方案确定最优正则化参数及最佳迭代次数，通过比较三种迭代延拓方法按两种方案确定的最优正则化参数、最佳迭代次数及延拓均方误差来验证微分进化法的有效性，延拓均方误差(RMSE)计算式为

(12)

式中，ΔT_c为延拓方法计算值，ΔT_t为延拓面实际测量值，M、N分别为网格化后的测线数与测点数.

方案1，以延拓结果的熵值为目标函数，以正则化参数(或迭代步长)及迭代次数为种群变量，采用微分进化法选取最优正则化参数及最佳迭代次数；

方案2，采用较常用的L-曲线准则确定正则化参数，在此基础上通过多次试验比较延拓误差确定最佳迭代次数.

根据微分进化法运算流程，按表 1给出的控制参数进行参数初始化，三种迭代方法的迭代次数范围均为1~50次，取正则化参数(迭代步长)在0~2之间，在各参数范围内分别随机生成NP个向量作为参数初始向量.

需要说明的是，微分进化法是在给定参数取值范围内进行连续寻优计算，计算结果为参数取值范围内的非整数，而向下延拓中最佳迭代次数的确定属于整数规划问题.为此，文中对不同延拓方法确定的最佳迭代次数均按“四舍五入”原则取整.

图 2为三种迭代法采用微分进化法选取最优参数时，进化代数与目标函数的关系曲线，由图 2可知，随着种群不断进化，三种迭代方法的目标函数值均逐渐减小，最后趋于稳定.其中，积分迭代法进化23代后熵值稳定在14.07，最优参数分别为s=2，n=1.4734(取整后n=1)；迭代Tikhonov正则法进化25代后熵值稳定在12.67，最优参数分别为α=0.0075，n=1.9112(取整后n=2)；Landweber迭代法进化21代后熵值稳定在13.13，最优参数分别为α=1.8898，n=29.5987(取整后n=30).这说明微分进化法搜索结果是收敛的，且进化二十几代即使延拓结果熵值达到最小，收敛速度较快.

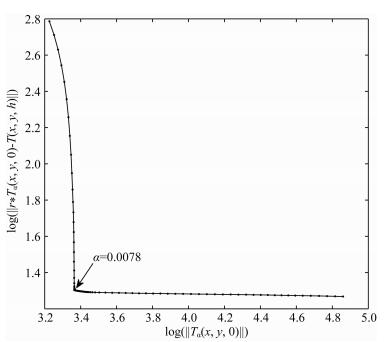
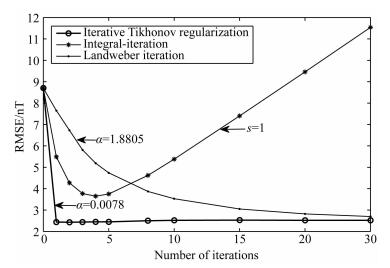
在使用迭代Tikhonov正则化与Landweber迭代法延拓时，按L-曲线准则确定最优正则化参数.如图 3为Tikhonov正则化法采用L-曲线准则确定最优正则化参数.图中拐点处对应的正则化参数为0.0078；同理Landweber迭代法确定的最优正则化参数为1.8805，而在采用积分迭代法时一般取迭代步长s=1；在此基础上，按三种迭代法的频域延拓算子进行多次延拓试验，给出了三种方法迭代次数与延拓误差的变化关系，见图 4.

由图 4知，积分迭代法在迭代步长为1时，随着迭代次数的增大，延拓误差先变小后变大，在第4次时达到最小，最小延拓误差为3.65 nT；迭代Tikhonov正则化法在正则化参数为α=0.0078时，迭代2次后延拓误差即达到最小，最小延拓误差为2.15 nT，之后保持稳定；Landweber迭代法在正则化参数为α=1.8805时，随着迭代次数增大，延拓误差逐渐减小，但变化缓慢，在迭代30次后趋于稳定，最小延拓误差为2.63 nT.为便于比较，表 2给出了三种迭代方法按两种方案确定的最优参数及按最优参数计算的延拓误差.

由表 2知，迭代Tikhonov正则化法与Landweber迭代法按两种方案确定的最优正则化参数分别只相差0.0003和0.0093，最佳迭代次数是一致的，延拓均方误差均只差0.01 nT，而积分迭代法中，方案1确定的最优迭代步长为2，迭代次数为1次，计算的延拓误差为3.55 nT，而方案2采用迭代步长为1，迭代4次后得到最小延拓误差3.65 nT，考虑到积分迭代法在处理含噪声数据时，计算精度明显低于其他两种正则化迭代方法，且积分迭代法按方案1计算的延拓误差与方案2计算的延拓误差相当，方案1确定的最优参数已经使积分迭代法达到最佳延拓效果.

综上所述，对比三种迭代方法按两种方案确定最优参数的延拓实验可知，微分进化法确定的最优参数可使所采用的延拓方法达到最佳延拓效果，且收敛速度较快，验证了微分进化法的有效性.

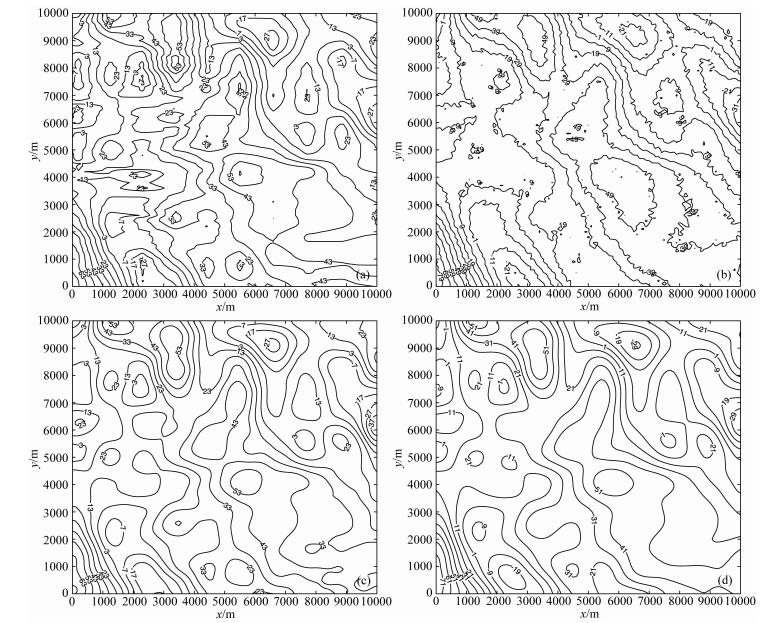
另外，采用微分进化法选择最优参数后得到的延拓结果如图 5.

由图 5，将不同方法延拓结果与0 m实际测量值比较可以看出：三种方法计算结果的总体变化趋势与0 m高度实测磁异常较接近，其中，因积分迭代法延拓算子的高频放大作用，导致延拓结果中含有大量的虚假噪声，延拓效果最差；迭代Tikhonov正则化法最接近真实值，Landweber迭代法因确定的最优正则化参数较大，延拓结果过于平滑.

3 结论

针对位场向下延拓的迭代法中，最优正则化参数(或迭代步长)及最佳迭代次数难以确定问题，引入基于群体智能理论的优化算法——微分进化法，并以延拓结果的熵值最小作为种群进化的选择准则，在实测资料处理中，与传统L-曲线准则确定最优正则化参数以及多次试验确定最佳迭代次数进行对比，结果表明：

(1) 在迭代Tikhonov正则化法与Landweber迭代法计算中，微分进化法与传统L-曲线准则确定的最优正则化参数分别只差0.0003与0.0093，最佳迭代次数是一致的，延拓误差均只差0.01 nT，验证了微分进化法的有效性.

(2) 以延拓结果熵值最小为选择准则，确定的最优参数可使所采用的延拓方法达到最佳延拓效果，且只需进化二十几代即可搜索最优解，收敛速度快，自适应性强，可明显提高迭代延拓方法的计算效率与准确性.

致谢

非常感谢审稿专家为本文提出的宝贵意见与建议.