2. 中国科学院大学, 北京 100049;
3. 中国科学院地球科学研究院, 北京 100029
2. University of Chinese Academy of Science, Beijing 100049, China;
3. Institute of Earth Science, Chinese Academy of Science, Beijing 100029, China
重力向下延拓能够增强局部异常,对位场物探技术实现由定性分析向定量解释发展具有重要的作用.由于观测噪声、边界效应以及向下延拓系数矩阵病态性等会引起向下延拓场高频振荡(Parker, 1977),为此需要在向下延拓过程中保持延拓场稳定.常用的向下延拓方法包括泰勒级数法(Peters, 1949; Trejo, 1954; Fedi and Florio, 2002)、积分迭代法(徐世浙,2006;刘东甲等,2009)、低通滤波法(侯重初,1982;梁锦文,1989)、波数域正则化法(Tikhonov and Arsenin, 1977;Pašteka et al., 2012; Zeng et al., 2013)和等效源法等.其中,等效源位场数据处理方法的物理意义明确,并且在处理过程中符合位场数学关系(拉普拉斯方程),在位场数据高精度处理中具有很高的应用价值.
等效源法被广泛用于位场数据处理,如观测数据规则化、噪声压制、位场分离、地形校正及任意曲面延拓等问题(Emilia, 1973; Bhattacharyya and Chen, 1977; Xia et al., 1993; Pawlowski, 1994; Mendonça and Silva, 1995; 管志宁等,1985;安玉林等,2013).随着重磁勘探仪器发展,等效源位场数据处理技术适用于重磁多分量数据处理(Li, 2001;Martinez and Li, 2016).
Dampney(1969)通过最小二乘法反演等效源,认为合理的等效源深度由观测步长确定.学者(Hansen and Miyazaki, 1984; Li and Oldenburg, 2010)通过在等效源反演中引入约束,提高了等效源反演的稳定性.Xia等(1993)基于实现观测数据最大平滑为准则,提出了最优等效层概念.由于时移微重力数据信噪比低,信号弱,为实现定量解释,本文将研究正则化等效源向下延拓技术.为探讨不同深度正则化等效源向下延拓算子和滤波算子的性质,本文基于数学推导和模型实验研究了正则化等效源的波数响应,并与波数域Tikhonov正则化向下延拓方法的延拓结果进行对比.针对正则化等效源向下延拓场幅值衰减问题,本文提出了迭代补偿算法.为验证方法在实测数据中的有效性,对辽河油田SAGD先导试验区时移微重力数据进行向下延拓.
1 正则化等效层(源)实现重力向下延拓 1.1 正则化等效源向下延拓方法假设观测面Z=0上有N个观测数据g0= (g1, g2, …, gN),将等效源置于Z=h面上,面源可以由M个离散化点源ρ=(ρ1, ρ2, …, ρM)近似.此时,观测重力与点源存在线性关系:
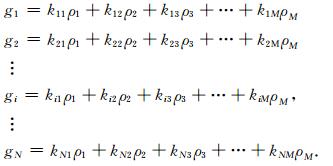
|
(1) |
其中,ki, k为系数矩阵的元素,即第k个点源处单位质量在第i个观测点处产生的重力为
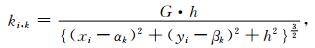
|
(2) |
其中,G为万有引力常量;xi,yi和αk,βk分别是观测数据和点源的水平坐标,Z轴向下为正.
通过方程组(1)求解等效源是典型的不适定问题,为此需要对等效源的性质进行约束.Tikhonov正则化方法通过在目标函数中引入正则项使得反演结果具有唯一解.正则化等效源的目标函数为
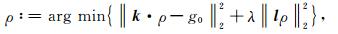
|
(3) |
式中,k为系数矩阵,λ为正则化参数,ρ为等效源,g0为观测数据,l为正则化矩阵.这里,若l为梯度矩阵,则目标函数(3)为一阶Tikhonov正则化泛函.对于Tikhonov正则化矩阵运算解表达式为
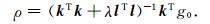
|
(4) |
正则化反演方法的关键是确定合理的正则化参数λ.L曲线法(Hansen, 1992)不需要已知数据误差,原理简单,易于计算,并在观测数据中有相关噪声时也相当稳健,被广泛应用.
基于Parseval定律将一阶Tikhonov正则化目标函数(4)变换到波数域,此时的目标函数
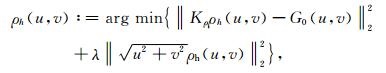
|
(5) |
其中,
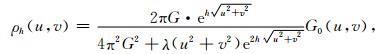
|
(6) |
由重力正演算子,在Z=h0面上向下延拓场为
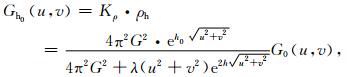
|
(7) |
则Z=h面正则化等效源在Z=h0面向下延拓算子:

|
(8) |
则在观测面Z=0上,利用等效源正演算子可以计算Z=0重力场,则得到正则化等效源滤波算子:
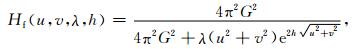
|
(9) |
延拓面Z=h0与等效源面Z=h重合时向下延拓算子:
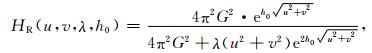
|
(10) |
式(8)(9)(10)中,可以利用ω表示为径向波数,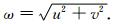
由正则化等效源向下延拓算子(8)可知,正则化等效源向下延拓算子的振幅波数响应由等效源深度h,延拓面深度h0和正则化参数λ共同确定;此外,由正则化等效源滤波算子(9)可知,其振幅波数响应由等效源深度h和正则化参数λ确定.
1.2 正则化等效源向下延拓及其迭代补偿算法利用Tikhonov正则化方法求解等效源并进行向上延拓,会使延拓重力与理想模型重力值相比幅值偏小,并且随着观测数据中噪声水平增加,向下延拓结果与理想模型重力场的差异有变大趋势.为提高向下延拓精度,这里引入正则化等效源迭代补偿向下延拓算法.
(1) 基于实际问题需要及观测数据采样间隔确定适宜的向下延拓深度,这里设延拓面处于Z=h0;
(2) 设处在延拓面(Z=h0)下方的Z=h为等效源面(图 1),在该面上设置空间间隔不大于数据采样间隔的M个点源,ρ=(ρ1, ρ2, …, ρM),计算对应的观测面上N个观测点g0=(g1, g2, …, gN)处的系数矩阵,并利用(5)式一阶Tikhonov正则化泛函计算得到Z=h面上的M个点源,这里正则化参数λ0由L曲线法得到;此时,等效源反演的波数域表达式为
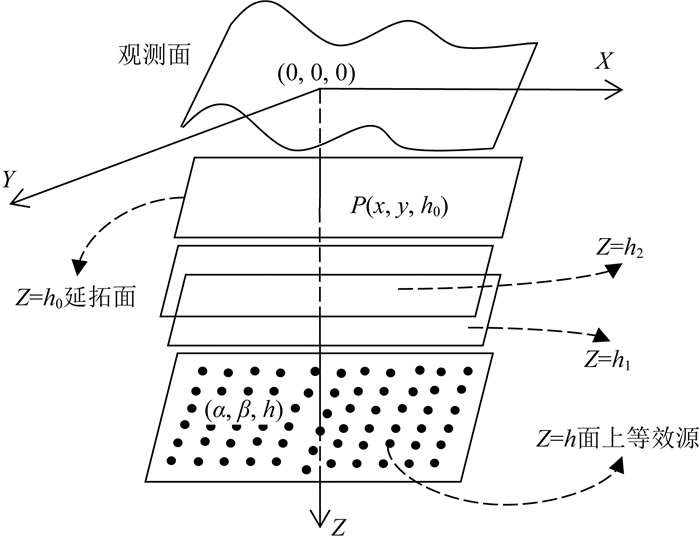
|
图 1 等效源实现向下延拓示意图 Fig. 1 Sketch map of equivalent source downward continuation method |
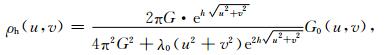
|
(11) |
其中,G为万有引力常量,ρh(u, v)和G0(u, v)分别为等效源ρh和观测重力g0的傅里叶变换.
(3) 利用Z=h面上的等效源ρh正演计算延拓面Z=h0面上的重力g0h0和观测面上的重力g01,并计算观测重力残差Δg01=g0-g01;波数域表达式为
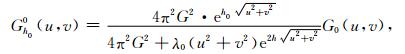
|
(12) |
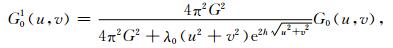
|
(13) |
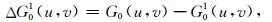
|
(14) |
其中,G0h0(u, v)、G01(u, v)分别为利用Z=h面上等效源计算的Z=h0面和Z=0面上重力场g0h0和g01的傅里叶变换,ΔG01(u, v)为经等效源滤波后观测面上重力数据残差Δg01的傅里叶变换.
(4) 在面Z=h1(图 1)构建与步骤(2)中相同M个点源(这里,h0 < h1 < h),然后对数据残差Δg01,利用步骤(2)中的正则化反演方法,得到Z=h1面上的补偿等效源;利用补偿等效源正演计算Z=h0面上的重力场Δgh01和Z=0观测面上重力残差Δg02=Δg01-Δgh1→0;此时,经补偿的向下延拓场为gh01=g0h0+Δgh01;计算Z=h0面上补偿变化量θ=‖Δgh01‖/‖g0h0‖;若θ≤ξ时(ξ是设定的小正数,这里取ξ=0.05)则迭代停止,并将此时的补偿场gh01作为向下延拓场;否则,进行步骤(5).其中,等效源反演的正则化参数λ1,补偿场的Δgh01波数域形式为
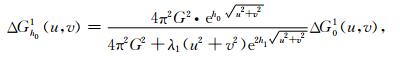
|
(15) |
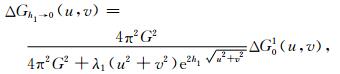
|
(16) |
(5) 与步骤(4)相同,构建Z=h2面(这里,h0 < h2 < h1)上的等效源(图 1),然后利用Z=0观测面上的残差Δg02得到补偿等效源;而后经补偿等效源正演计算Z=h0面上的补偿重力Δgh02和观测面Z=0上的重力Δgh2→0,并计算观测面上的重力残差Δg03=Δg02-Δgh2→0;此时,经补偿的延拓场为gh02=gh01+Δgh02;计算Z=h0面上的向下延拓场的相对变化量θ=‖Δgh02‖/‖gh01‖;若θ≤ξ时则迭代停止,并将此时的补偿场gh02作为Z=h0面的延拓场;否则,将等效源面设置在Z=h3面(这里,h0 < h3 < h2)重复此迭代过程.其中,等效源反演的正则化参数λ2,补偿场Δgh02的波数域形式为
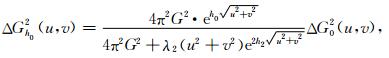
|
(17) |
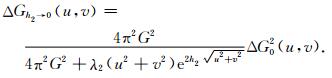
|
(18) |
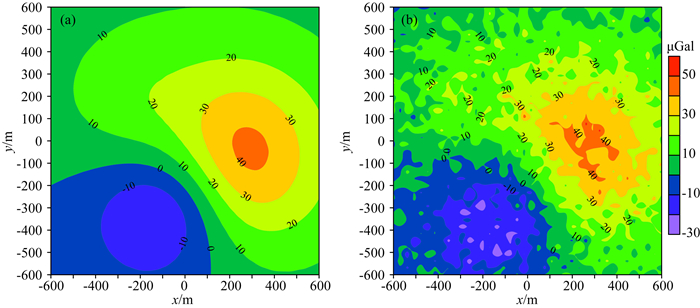
本文首先利用模型实验研究等效源深度与最优正则化参数关系(h-λ关系),等效源对观测数据的滤波波数响应(Hf),等效源向下延拓算子的波数响应(HD、HR)性质,而后验证等效源向下延拓技术及迭代补偿算法的有效性.模拟数据是由三个长方体(表 1)在Z=0 m面产生的重力场,观测的采样点线间隔30 m,共计40×40个测点,模型重力值(图 2a)加入标准差为5 μGal的高斯噪声(图 2b).
|
|
表 1 长方体模型参数 Table 1 Parameters of prism model |
|
图 2 (a) 理想模型在地表Z=0的重力值;(b)加入高斯白噪(σ=5 μGal) Fig. 2 (a) The theoretical gravity of the models at Z=0 plane; (b) Synthetic gravity with Gaussian noise (σ=5 μGal) at Z=0 plane |
利用表 1中的模型和图中的模拟观测重力数据(图 2b),并将等效源设置在不同深度h.此时,某一深度上的等效点源与观测数据水平分布一致,两个方向的水平间隔为30 m,共计40×40个点源.利用一阶Tikhonov正则化目标函数(5)式反演等效源;其中,利用L曲线法选取最优正则化参数,得到h-λ散点图(图 3a).由图可知,正则化参数λ随等效源深度h增加而呈指数衰减.
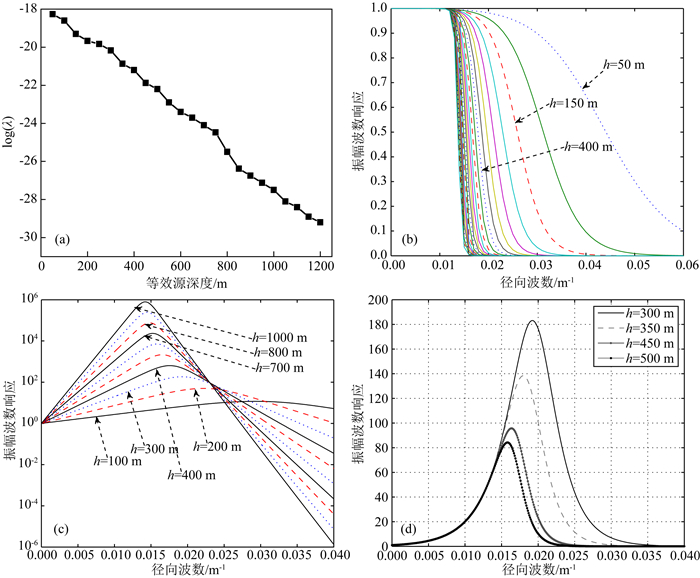
|
图 3 (a) 等效源深度h与最优正则化参数λ散点图;(b)等效源滤波器的波数响应Hf(ω, h);(c)等效源向下延拓算子波数响应HR(ω, h0);(d)在Z=300 m延拓面上波数响应HD(ω, h0=300, h) Fig. 3 (a) The scatter plot of depth of equivalent source and optimal regularization parameters; (b) The wavenumber response Hf(ω, h) of equivalent source filter; (c) The wavenumber response HR(ω, h0) of equivalent source downward continuation operator; (d) The wavenumber response HD(ω, h0=300, h) of equivalent source downward continuation operator. |
图 3b中曲线是不同深度正则化等效源的滤波响应Hf(ω, h).由曲线可知,不同深度等效源滤波算子的振幅波数特性存在差异.当等效源深度较浅时,滤波算子的截止波数较大,造成观测数据中噪声不能有效滤除;当等效源深度增加时,滤波算子的截止波数迅速减小;当深度过大时,会造成滤波后数据过于平滑.图 3c为不同深度正则化等效层向下延拓算子HR(ω, h0)的振幅波数响应,当等效源置于靠近观测面的浅层时其截止波数大,其在高频部分的放大效应明显;随着等效层深度增加,算子的截止波数变小,能够很好的抑制高频噪声,延拓面越深正则化等效源的高频抑制能力越强;但另一方面当等效源深度过大时,也会造成高频信号损失.图 3d中不同深度的正则化等效源在同一延拓面上(Z=300)的向下延拓算子的振幅波数响应HD(ω, h0=300, h),由曲线可知不同深度等效源向下延拓算子在中低频频段的波数响应重合,但随着等效层与延拓面的距离变小,算子对高频的放大能力变强.
为验证正则化等效源向下延拓方法的效果,本文对不同噪声水平下(图 2b, 图 4a)模拟观测数据进行向下延拓实验,并与波数域Tikhonov正则化向下延拓方法(Pašteka et al., 2012)进行对比.最后,利用等效源迭代补偿方法对向下延拓场进行补偿.
|
图 4 (a) Z=0面含高斯噪声模拟观测数据(σ=10 μGal);(b) Z=300 m面理想模型产生的重力场 Fig. 4 (a) The synthetic gravity of the models at Z=0 plane with Gaussian noise (σ=10 μGal); (b) Theoretical gravity field of the prim model at Z=300 m plane |
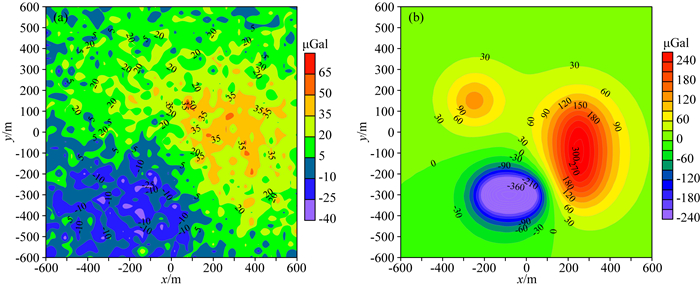
图 5a、图 5b和图 5c分别为利用波数域Tikhonov正则化向下延拓(TRDC)方法(Pašteka et al., 2012)将观测面上理想重力数据(图 2a),含标准差为σ=5 μGal(图 2b)和标准差为σ=10 μGal(图 4a)的模拟数据向下延拓至Z=300 m面上的向下延拓场.此时,由L曲线法确定的正则化参数α见表 2所示.通过与Z=300 m上的理想重力值(图 4b)相比,波数域Tikhonov正则化向下延拓场(图 5a、5b、5c)能够在一定程度上抑制高频干扰,增强重力异常,但延拓结果不够光滑,重力异常幅值衰减严重.
|
图 5 Z=300 m面上TRDC重力场和RESDC重力场 Fig. 5 The downward continuation field at Z=300 m plane obtained by TRDC and RESDC method for synthetic data at different noise levels (a) TRDC σ=0 μGal; (b) TRDC σ=5 μGal; (c) TRDC σ=10 μGal; (d) RESDC σ=0 μGal; (e) RESDC σ=5 μGal; (f) RESDC σ=10 μGal |
|
|
表 2 两种向下延拓方法在不同噪声水平下的正则化参数(α和λ) Table 2 The optimal regularization parameters of TRDC and RESDC methods |
图 5d、图 5e和图 5f分别为利用正则化等效源向下延拓(RESDC)方法对观测面上的理想模型重力数据(图 2a),含标准差分别为σ=5 μGal(图 2b)和σ=10 μGal(图 4a)的模拟数据向下延拓至Z=300 m面上的向下延拓场.正则化等效层深度设定在Z=450 m面,利用一阶Tikhonov正则化反演方法计算等效源,然后通过正演计算等效源在Z=300 m面的重力场得到向下延拓结果.此时,由L曲线法确定的正则化参数λ参数见表 2所示.
从上述模型实验可以看出,利用正则化等效源向下延拓法(RESDC)能够有效抑制高频随机噪声,实现稳定向下延拓,并且延拓结果更平滑,有效避免了噪声及边界效应造成向下延拓产生的振荡现象.由延拓结果对比可知,正则化等效源向下延拓技术(RESDC)对信号的保幅效果虽然明显优于波数域Tikhonov正则化向下延拓法(TRDC),但随着数据中噪声水平增加该方法的向下延拓场的幅值相对于理想重力数据(图 4b)仍然有较大衰减.为提高正则化等效层向下延拓精度,这里引入本文提出的正则化等效源迭代补偿方法,基于不同深度等效源向下延拓算子的频率响应实现对向下延拓场的补偿.
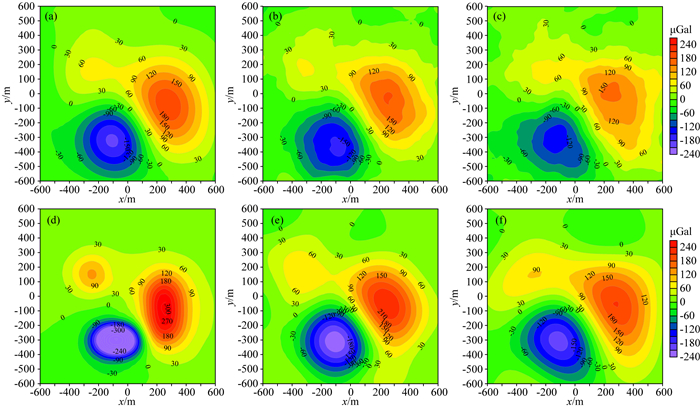
对图 2b(σ=5 μGal)和图 4a(σ=10 μGal)中模拟观测数据利用正则化等效源进行迭代补偿向下延拓.在迭代过程中等效源深度分别置于550 m和350 m,利用本文提出的算法进行迭代补偿;图 6a为对图 2b中向下延拓场经一次补偿后的向下延拓结果(λ0=4.85×10-24,λ1=4.05×10-21),图 6b是对图 4a中的向下延拓场经一次补偿后的延拓结果(λ0=1.48×10-23,λ1=2.25×10-21).

|
图 6 Z=300 m面上不同噪声水平下正则化等效层向下延拓场的迭代补偿结果 Fig. 6 The iterative compensation downward continuation field of synthetic data at different noise levels by RESDC method at Z=300 m plane (a) σ=5 μGal; (b) σ=10 μGal. |
通过上述实验可知,经迭代补偿后的正则化等效源向下延拓场(图 6a、图 6b)与正则化等效源向下延拓结果(图 5e、图 5f)对比可知,迭代方法具有一定的补偿作用,重力幅值明显增加.
3 实测时移微重力数据向下延拓蒸汽辅助重力泄油(SAGD)是通过向储层连续注入高温蒸汽降低稠油黏度,提高原油的流动性,再经水平井采出原油的开发方式.由于SAGD开发过程中蒸汽驱替原油形成蒸汽腔,造成储层内较大的密度差,这有利于采用时移微重力技术监测蒸汽腔发育,进而对生产进行动态调控,提高稠油采收率.
自2009年2月—2014年2月,项目组受油田委托对SAGD先导试验区进行了5次重力时移观测.由于时移微重力观测数据信号弱、信噪比低,为实现由定性分析到定量解释迫切需要稳定的向下延拓方法.为此,本文利用2009年2月与2014年2月的布格重力异常差数据(图 7a)进行正则化等效源向下延拓.考虑到数据观测间隔、观测范围及储层分布等因素,将向下延拓面置于Z=300 m面,初始正则化等效源深度置于Z=500 m面,然后进行正则化等效源反演,再通过迭代补偿一次后(补偿等效源在Z=400 m面)向下延拓结果如下图 7b所示.其中,最优正则化参数由L曲线法取得(λ0=3.85×10-24,λ1=4.05×10-22).
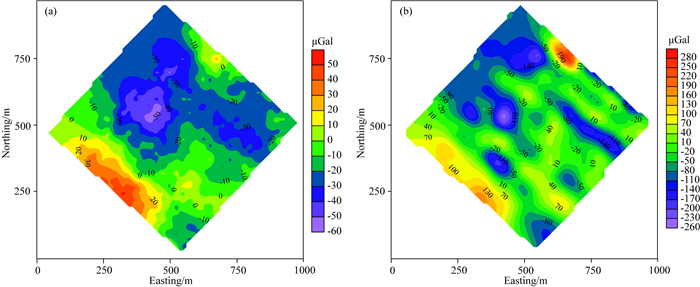
|
图 7 馆陶组SAGD先导试验区内时移微重力观测数据和向下延拓场 (a) Z=0 m观测数据等值线;(b) Z=300 m面向下延拓场(单位:μGal). Fig. 7 Time-lapse microgravity and downward continuation field at Guantao SAGD pilot field (a) The contour map of survey data; (b) The downward continuation field at Z=300 m by RESDC method. |
由正则化等效源向下延拓重力异常分布(图 7b)可知,向下延拓场在增强信号幅值的同时,延拓场比较平滑,即向下延拓受观测噪声和边界效应的影响小.因而正则化等效层向下延拓迭代补偿技术能够在大深度范围内实现低信噪比、弱信号时移微重力数据的稳定向下延拓.需要说明的是向下延拓结果还需要在后续研究中结合观察井、生产动态及其他技术手段进行验证.
4 结论本文为实现时移微重力数据稳定向下延拓引入了正则化等效层向下延拓方法,推导了正则化等效源滤波算子及向下延拓算子;针对向下延拓重力幅值衰减问题,提出了正则化等效源向下延拓的迭代补偿算法.通过模型实验验证该技术的向下延拓效果,并与波数域Tikhonov正则化向下延拓方法进行比较;最后将该技术应用于实测时移微重力数据向下延拓.本文获得了以下认识:
(1) 正则化等效源反演中正则化参数λ随等效源深度h增加呈现指数衰减规律;不同深度等效源对观测数据有不同的滤波效果,等效源深度越大对数据中的高波数成分抑制作用越大;此外,由正则化等效源向下延拓算子的波数响应HR(ω, h0)可知,等效源深度(下延深度)越大,下延算子在中低频的放大作用越强,在高频的放大能力越弱;由不同深度的正则化等效源在同一延拓面上的向下延拓算子的振幅波数响应可知,等效层与延拓面距离越小,下延算子的高频放大作用越强.由于等效源深度是决定等效源向下延拓算子振幅波数响应的重要因素,因而在后续研究中需要结合重力观测系统、异常源空间分布和形态等先验信息确定最优的等效源深度.
(2) 正则化等效源向下延拓方法能够稳定地实现较大深度的向下延拓,与波数域Tikhonov正则化向下延拓方法相比,其延拓场更平滑,延拓精度更高.正则化等效源向下延拓方法适用于结构简单异常源(孤立源)的重力数据向下延拓,对于结构复杂异常源的重力数据向下延拓,延拓结果可能会存在误差.
(3) 本文提出的正则化等效源向下延拓的迭代补偿方法在数据实验中能够对向下延拓场实现一定程度的补偿,通过迭代过程能够降低正则化参数对向下延拓结果的影响;但由于补偿效果受观测数据中噪声水平影响,在后续研究中还需要结合先验信息进一步探讨更有效的补偿方法.
致谢感谢辽河油田允许此文发表.感谢对于此工作给予重大帮助的同事们.非常感谢两位审稿专家提出的宝贵意见.特别感谢本文编辑的仔细校对和指导.
An Y L, Chai Y P, Zhang M H, et al. 2013. An optimal model of the equivalent source for reduction-to-plane of potential field on uneven surface and the new method to deduce unit potential field expression of the optimal model. Chinese Journal of Geophysics (in Chinese), 56(7): 2473-2483. DOI:10.6038/cjg20130733 |
Bhattacharyya B K, Chen K C. 1977. Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief. Geophysics, 42(7): 1411-1430. DOI:10.1190/1.1440802 |
Dampney C N G. 1969. The equivalent source technique. Geophysics, 34(1): 39-53. DOI:10.1190/1.1439996 |
Emilia D A. 1973. Equivalent sources used as an analytic base for processing total magnetic field profiles. Geophysics, 38(2): 339-348. DOI:10.1190/1.1440344 |
Fedi M, Florio G. 2002. A stable downward continuation by using the ISVD method. Geophysical Journal International, 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x |
Guan Z N, An Y L, Chen W X. 1985. Upward continuation and transformation of component of magnetic field on an undulating observed profile or surface. Acta Geophysica Sinica (in Chinese), 28(4): 419-428. |
Hansen P C. 1992. Analysis of discrete ill-posed problems by means of the L-curve. Siam Review, 34(4): 561-580. DOI:10.1137/1034115 |
Hansen R O, Miyazaki Y. 1984. Continuation of potential fields between arbitrary surfaces. Geophysics, 49(6): 787-795. DOI:10.1190/1.1441707 |
Hou Z C. 1982. A frequency method for potential field downward continuation. Geophysical and Geochemical Exploration (in Chinese), 6(1): 33-40. |
Li Y G. 2001. Processing gravity gradiometer data using an equivalent source technique. //71st Ann. Internat Mtg., Soc. Expi. Geophys. . Expanded Abstracts, 2001: 1466-1469, doi: 10.1190/1.1816382. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=SEGEAB000020000001001466000001&idtype=cvips&prog=normal
|
Li Y G, Oldenburg D W. 2010. Rapid construction of equivalent sources using wavelets. Geophysics, 75(3): 51-59. DOI:10.1190/1.3378764 |
Liang J W. 1989. Downward continuation of regularization methods for potential fields. Acta Geophysica Sinica (in Chinese), 32(5): 600-608. |
Liu D J, Hong T Q, Jia Z H, et al. 2009. Wave number domain iteration method for downward continuation of potential fields and its convergence. Chinese Journal of Geophysics (in Chinese), 52(6): 1599-1605. DOI:10.3969/j.issn.0001-5733.2009.06.022 |
Martinez C, Li Y G. 2016. Denoising of gravity gradient data using an equivalent source technique. Geophysics, 81(4): G67-G79. DOI:10.1190/geo2015-0379.1 |
Mendonça C A, Silva J B C. 1995. Interpolation of potential-field data by equivalent layer and minimum curvature:a comparative analysis. Geophysics, 60(2): 399-407. DOI:10.1190/1.1443776 |
Parker R L. 1977. Understanding inverse theory. Annual Review of Earth and Planetary Sciences, 5(1): 35-64. DOI:10.1146/annurev.ea.05.050177.000343 |
Pašteka R, Karcol R, Kušnirák D, et al. 2012. REGCONT:A Matlab based program for stable downward continuation of geophysical potential fields using Tikhonov regularization. Computers & Geoscience, 49: 278-289. DOI:10.1016/j.cageo.2012.06.010 |
Pawlowski R S. 1994. Green's equivalent-layer concept in gravity band-pass filter design. Geophysics, 59(1): 69-76. DOI:10.1190/1.1443535 |
Peters L J. 1949. The direct approach to magnetic interpretation and its practical application. Geophysics, 14(3): 290-320. DOI:10.1190/1.1437537 |
Tikhonov A, Arsenin V. 1977. Solutions of ill-posed problems. Mathematics of Computation, 32(144): 491. DOI:10.2307/2006360 |
Trejo C A. 1954. A note on downward continuation of gravity. Geophysics, 19(1): 71-75. DOI:10.1190/1.1437972 |
Xia J H, Sprowl D R, Adkins H D. 1993. Correction of topographic distortions in potential-field data:a fast and accurate approach. Geophysics, 58(4): 515-523. DOI:10.1190/1.1443434 |
Xu S Z. 2006. The integral iteration method for continuation of potential fields. Chinese Journal of Geophysics (in Chinese), 49(4): 1176-1182. DOI:10.1002/cjg2.928 |
Zeng X N, Li X H, Sun J, et al. 2013. An adaptive iterative method for downward continuation of potential-field data from a horizontal plane. Geophysics, 78(4). DOI:10.1190/geo2012-0404.1 |
安玉林, 柴玉璞, 张明华, 等. 2013. 曲化平用最佳等效源模型及其单位位场表达式推导的新方法. 地球物理学报, 56(7): 2473-2483. DOI:10.6038/cjg20130733 |
管志宁, 安玉林, 陈维雄. 1985. 曲线与曲面上磁场向上延拓和分量转换. 地球物理学报, 25(4): 419-428. |
侯重初. 1982. 位场的频率域向下延拓方法. 物探与化探, 6(1): 33-40. |
梁锦文. 1989. 位场向下延拓的正则化方法. 地球物理学报, 32(5): 600-608. |
刘东甲, 洪天求, 贾志海, 等. 2009. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报, 52(6): 1599-1605. DOI:10.3969/j.issn.0001-5733.2009.06.022 |
徐世浙. 2006. 位场延拓的积分-迭代法. 地球物理学报, 49(4): 1176-1182. |
 2018, Vol. 61
2018, Vol. 61


