2. 合肥工业大学计算机与信息学院, 合肥 230009
2. School of Computer and Information, Hefei University of Technology, Hefei 230009, China
随机噪声是地震信号中常见的不规则干扰波,频带较宽、无一定频率和视速度, 并具有在时、空域随机分布的特性.地震信号中随机噪声与有效信号重叠,使得有效信号的反射波同相轴变得模糊,因此减少随机噪声干扰、恢复有效信号,提高地震信号的信噪比显得尤为重要,并对后续地震资料的处理和解释起到至关重要的作用.近年来,地震信号中的随机噪声压制方法陆续被提出.Cao等(2005)结合第二代小波和软阈值方法对地震信号的随机噪声进行压制, 取得了较好的降噪效果.彭才等(2007)将地震信号进行小波分解形成分时分频的小波包剖面, 然后用K-L变换对小波包剖面进行降噪, 再将处理后的小波包剖面重构得到降噪后的地震剖面, 从而达到消除随机噪声的目的.Zhang等(2009)利用脊波对地震信号进行子带分解,然后在脊波域对每个子块进行非线性阈值处理,最后将处理后的数据经小波逆变换重构得到降噪后的地震信号.李雪英等(2013)将自适应阈值函数与连续硬阈值函数相结合,提出了地震信号随机噪声压制的离散小波域阈值自适应方法.Shuai等(2013)利用有效信号的自相似性,提出了一种块实现的自适应非局部均值滤波参数估计方法压制地震信号中的随机噪声.Parkan等(2014)基于完备总体经验模态分解方法将地震信号分解为一系列本征模态函数分量, 对含噪较多的高频本征模态函数分量进行阈值降噪,最后进行重构得到降噪后的地震信号.Lin等(2015)提出基于SW统计量的自适应时频峰值滤波的地震信号降噪方法.Lin等(2016)提出了一种结合Shapiro-Francia统计的最佳时空时频峰值滤波方法压制地震信号中的随机噪声.
虽然目前已经存在一些地震信号中的随机噪声压制方法,但是由于随机噪声的复杂性,它的压制方法需要进一步的深入研究.随着Fourier变换、分数阶Fourier变换和小波变换的发展,2000年瑞士学者Unser和Blu提出分数阶B样条小波.2009年刘红毅等人基于分数阶B样条小波提出了图像降噪的变分模型,取得了较好的降噪效果.2013年唐锐等人考虑小波系数之间的相关性,利用局部高斯尺度混合(Gauss Scale Mixture,GSM)模型对图像进行降噪,取得了较好的降噪效果.高国荣等(2013)在非抽样Shearlet域建立高斯尺度混合模型对图像进行降噪,不仅有效地压制随机噪声,同时增强了图像的边缘细节信息.
鉴于分数阶B样条小波具有可选的阶次,可以更灵活地调节小波系数.同时GSM模型能够很好地描述小波变换系数的边缘分布和邻域系数之间的相关性.所以本文将分数阶B样条小波与GSM模型相结合提出了一种有效的地震信号随机噪声压制方法.
1 分数阶B样条小波Unser and Blu(2000)定义了α阶因果分数B样条函数:
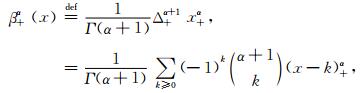
|
(1) |
其中,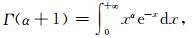

|
类似地定义了向后差分的α阶反因果分数B样条函数β_α(x):
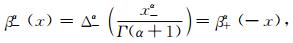
|
(2) |
其中,x-α=(-x)+α,Δ-α表示分数阶向后差分算子:
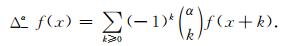
|
(3) |
基于上述两种非对称的B样条函数可以定义α阶对称分数B样条函数:
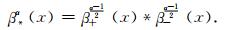
|
(4) |
这三种分数阶B样条函数具有衰减性、Riesz基、逼近性,满足双尺度方程等.这些性质使得分数阶B样条函数簇能够构成多尺度分析,构造对应的小波基函数,从而对信号进行多尺度的分解和重构.
分数阶B样条小波变换是通过滤波器组来实现的.它对应的低通滤波器H+α:
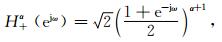
|
(5) |
进行正交化得到:
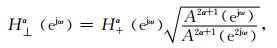
|
(6) |
其中
对应的高通滤波器为:
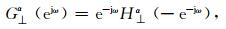
|
(7) |
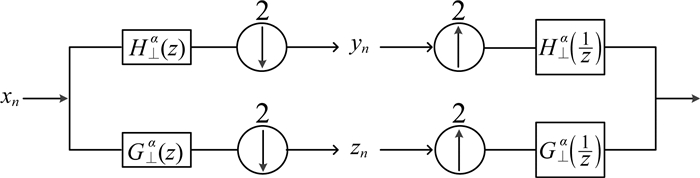
分数阶B样条小波变换的分解与合成过程,如下面的图 1所示.
|
图 1 分数阶B样条小波分解和合成示意图 Fig. 1 Schematic diagram of fractional order B spline wavelet decomposition and synthesis |
假设地震信号被标准差为σ的高斯白噪声污染,首先对含噪地震信号进行分数阶B样条小波变换.假设在分数阶B样条小波域中,含噪模型可以表示为
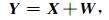
|
(8) |
其中,Y是含噪地震信号的小波系数,X为源地震信号的小波系数,W为噪声的小波系数.假设X服从高斯尺度混合分布,即:

|
(9) |
其中,
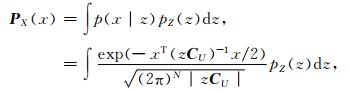
|
(10) |
其中N是U和X的维数.随机向量Y对于混合系数Z的条件分布也是零均值高斯分布的,有E(Y|Z)=0,协方差矩阵CY|Z=ZCU+CW.因此,Y的条件密度函数可以写成:
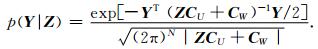
|
(11) |
对与噪声信号具有相同功率谱的脉冲信号

|
n=1, 2, …, NX, m=1, 2, …, NY, σ为噪声标准差,利用中值估计方法(Donoho,1994)来估计:
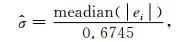
|
其中ei为小波子带系数.
若CW已知,就可以得到随机向量Y的协方差矩阵CY,求出高斯随机向量U的协方差矩阵CU.因为CY可以由CY|Z对Z取数学期望得到
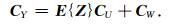
|
(12) |
若E{Z}=1,则
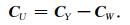
|
(13) |
因为信号的协方差矩阵是非负定的,但是上式得到的协方差矩阵可能有负的特征值,所以将负的特征值设为0,以此来保证协方差矩阵CU的非负定性.
以二次型损失函数为估计误差的测度,利用贝叶斯估计方法(Portilla et al., 2003)可以从含噪地震信号小波系数Y中估计得到Xc的估计值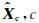
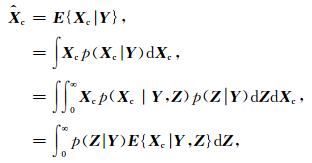
|
(14) |
上式由两部分组成,E{Xc|Y, Z}是Xc在条件Z下的贝叶斯最小二乘估计,p(Z|Y)是Z的后验概率密度函数.
下面先求E{Xc|Y, Z}.因为X|Z服从高斯分布,CY|Z=ZCU+CW,因此有

|
(15) |
其中上标-1表示矩阵的逆.
正定矩阵CW表示成CW=SST.设{Q, Λ}是矩阵S-1CUS-T的特征向量和特征矩阵,即满足S-1CUS-T=QΛQT,其中T表示矩阵的转置.那么
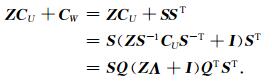
|
(16) |
简化得到:

|
(17) |
其中M=SQ, V=M-1Y.将估计限定在系数Xc,得到
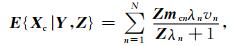
|
(18) |
其中,mi, j为矩阵M的第{i, j}个元素,λn为矩阵Λ的对角元素,vn为向量V中的元素.
接下来,求式(14)中Z的后验概率密度函数p(Z|Y),利用贝叶斯公式计算:

|
(19) |
根据式(11)得到:
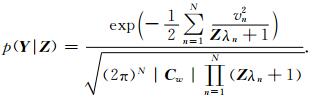
|
(20) |
尽管混合系数Z可以利用最大似然估计方法估计得到,为了简化计算,本文采用Jeffrey先验密度函数,即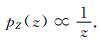
最后根据(14)式,就可以计算出降噪后地震信号的小波系数估计值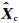
本文降噪方法实现的详细算法步骤如下:
Step 1:对含噪地震信号进行分数阶B样条小波变换.
Step 2:对每个子带小波系数,根据2.1节介绍的方法,(a)估计出噪声系数邻域协方差矩阵CW;(b)估计出含噪地震信号的小波系数邻域的协方差矩阵CY;(c)根据式CU=CY-CW求出CU;(d)计算Λ和M.
Step3:对每个邻域,对式(14)积分范围内的每个Z,(a)用式(18)计算E{Xc|Y, Z},(b)用式(20)计算p(Y|Z);(c)用式(19)计算p(Z|Y);
Step 4:用式(14)计算E{Xc|Y}得到小波系数的估计值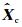
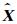
Step5:对源地震信号的小波系数估计值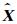
为了客观地评价降噪处理的效果,文中引入信噪比(SNR)和均方误差(MSE)作为评价标准,SNR值越大,MSE值越小,表明降噪的效果越好.设源地震信号为A,降噪后的地震信号为
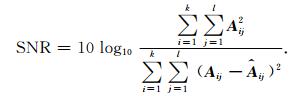
|
(21) |

|
(22) |
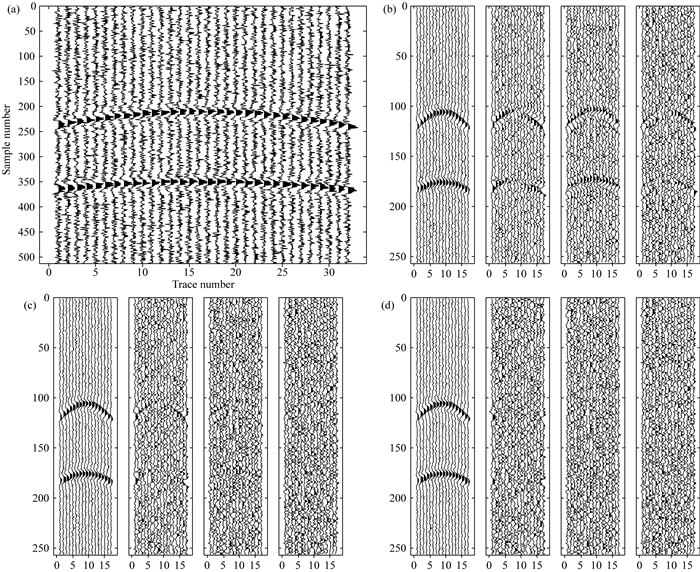
首先分析分数阶B样条小波中分数阶α对地震信号分解的影响.利用MATLAB软件编程生成合成地震信号,对合成地震信号加入标准差为70的高斯白噪声,分别选取分数阶的值为-0.4、0.01、1.5,然后对含噪合成地震信号进行一层分数阶B样条小波变换,得到的小波系数如下面的图 2所示.从图 2中可以看出,当α=-0.4时分解得到的高频系数中明显含有有效地震信号;随着α增大,高频系数中的有效信号成分逐渐减少.
|
图 2 含噪合成地震信号以及它的一层分数阶B样条小波分解系数 (a)含噪地震信号;(b) α=-0.4的低频系数和高频系数;(c) α=0.01的低频系数和高频系数;(d) α=1.5的低频系数和高频系数. Fig. 2 The noisy synthetic seismic signal and the one layer fractional B spline wavelet transform coefficients (a) The noisy seismic signal; (b) The low frequency and high frequency coefficients for α=-0.4; (c) The low frequency and high frequency coefficients for α=0.01; (d) The low frequency and high frequency coefficients for α=1.5. |
为了确定最优的分数阶α,生成5个合成地震信号,然后对其分别加入不同标准差(50、60、70)的高斯白噪声并利用本文方法对它们进行降噪分析.下面的图 3展示了参数α在-0.4, 10范围内变化时本文方法对含噪合成地震信号降噪所得的SNR值的影响.

|
图 3 参数α对SNR的影响 (a)、(b)、(c)表示噪声标准差分别为50,60,70时参数α对SNR的影响. Fig. 3 The influence of parameter α on SNR (a)、(b)、(c) The influence of parameter α on SNR with standard deviation equals to 50, 60, 70. |
图 3中(a)、(b)、(c)分别对应着标准差取50, 60, 70,每副图中5条线分别代表了利用本文方法对5个不同的合成地震信号降噪所得的信噪比随着参数α的变化而改变的情况.由图可得,参数α在[-0.4, 1.5)范围内,随着α取值的增大信噪比随之增大;当参数α≥1.5时信噪比随着α的增大而趋于平稳,并且对于加入不同程度的噪声,合成地震信号均有这一特征.同时为了简化计算,本文选取1.5作为本文方法降噪的最优分数阶.
为了验证本文方法压制地震信号中随机噪声的有效性,将本文方法与小波域GSM模型(Portilla et al., 2003)、小波软阈值(Wu et al., 2008)和小波硬阈值方法(Zhang et al., 2011)对含不同标准差σ的高斯白噪声的合成地震信号进行降噪处理.小波软阈值、小波硬阈值以及小波域GSM模型中的小波均选择Daub8小波基函数.小波分解层数均为3层.所得到的信噪比(SNR)和均方误差(MSE)如上面的表 1所示.
|
|
表 1 降噪后的SNR和MSE Table 1 SNR and MSE values after denoising |
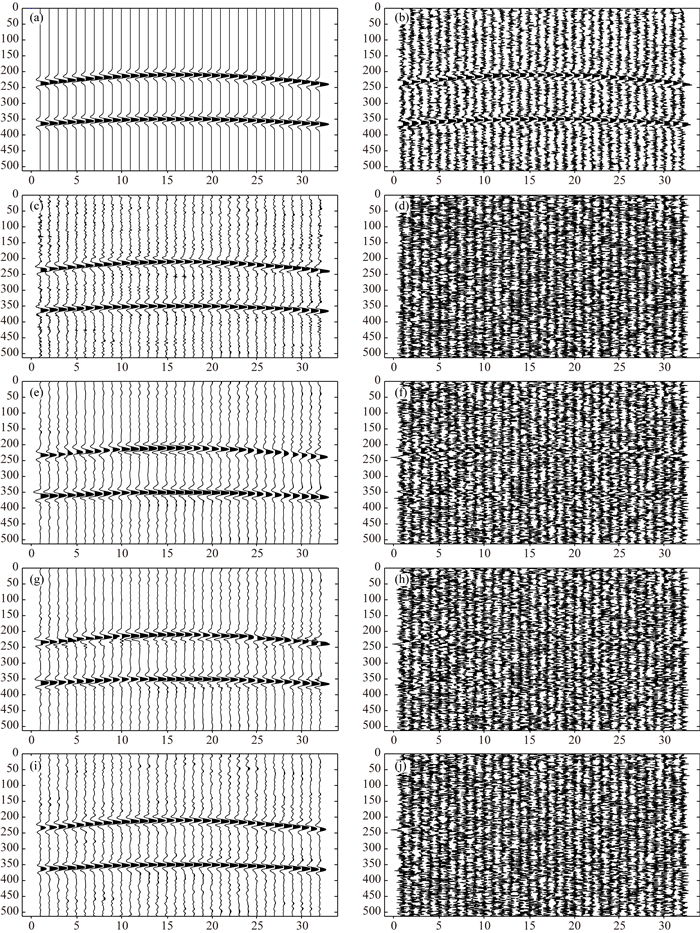
通过表 1得知,本文方法降噪得到的SNR值大于其他方法降噪得到的值,取得的MSE值小于其他方法得到的值,因此本文方法的降噪效果更好.上面的图 4为σ=70时不同方法对含噪地震信号的降噪效果图.
|
图 4 合成地震信号及降噪结果 (a)源地震信号;(b)含噪地震信号;(c)小波域GSM模型降噪后的信号;(d)小波域GSM模型降噪的差剖面;(e)小波软阈值降噪后的信号;(f)小波软阈值降噪的差剖面;(g)小波硬阈值降噪后的信号;(h)小波硬阈值降噪的差剖面;(i)本文方法降噪后的信号;(j)本文方法降噪的差剖面. Fig. 4 The synthetic seismic signal and denoised results (a) The ideal seismic signal; (b) The noisy seismic signal; (c) The denoised signal using Gaussian Scale Mixture model in wavelet domain; (d) The differential profile using Gaussian Scale Mixture model in wavelet domain; (e) The denoised signal using soft-threshold in wavelet domain; (f) The differential profile using soft-threshold in wavelet domain; (g) The denoised signal using hard-threshold in wavelet domain; (h) The differential profile using hard-threshold in wavelet domain; (i) The denoised signal using our method; (j) The differential profile using our method. |
由图 4中也可以看出本文方法具有较好的降噪效果,反射波周围的随机噪声得到了较好地压制,且较多地保留了有效信号.
为了更好地显示实验效果,选择降噪效果较好的小波域GSM模型和本文方法对单道地震信号的降噪结果进行观察.σ=70的含噪合成地震信号第20道的降噪结果如下面的图 5所示.
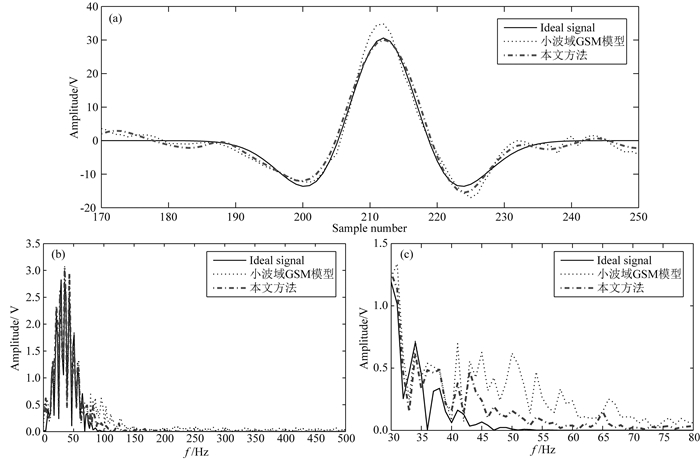
|
图 5 单道地震信号降噪结果及对应的振幅谱 (a)源地震信号、小波域GSM模型和本文方法降噪结果的局部放大比较图;(b)地震信号及其降噪后信号对应的振幅谱;(c)振幅谱的局部放大图. Fig. 5 The denoised results of single channel seismic signal and corresponding amplitude spectrum (a) The local enlarged figure of the ideal seismic signal、the denoised seismic signal using the Gaussian Scale Mixture model in wavelet domain and our method; (b) The amplitude spectrums of the seismic signal and the denoised seismic signal; (c) The local enlarged figure of the amplitude spectrum. |
从图 5可以看出,本文方法较其他降噪方法处理结果更加逼近源信号,所以本文方法能够更加有效地压制地震信号中的随机噪声.
4 实际地震信号的降噪实际地震信号为华北某地区的单炮实际地震记录,该记录每道的采样点数为1024个,采样时间间隔为4 ms,共有240道.下面的图 6是利用小波域GSM模型、小波软阈值、小波硬阈值和本文方法对单炮实际地震记录中的随机噪声进行压制的结果.

|
图 6 实际地震信号的降噪结果 (a)实际地震信号;(b)小波域GSM模型降噪后的地震信号;(c)小波域GSM模型降噪的差剖面;(d)小波软阈值降噪后的信号;(e)小波软阈值降噪的差剖面;(f)小波硬阈值降噪后的信号;(g)小波硬阈值降噪的差剖面;(h)本文方法降噪后的地震信号;(i)本文方法降噪的差剖面. Fig. 6 The denoised results of the field seismic signal (a) The field seismic signal; (b) The denoised seismic signal using the Gaussian scale mixture model in wavelet domain; (c) The differential profile using the Gaussian scale mixture model in wavelet domain; (d) The denoised signal using soft-threshold in wavelet domain; (e) The differential profile using soft-threshold in wavelet domain; (f) The denoised signal using hard-threshold in wavelet domain; (g) The differential profile using hard-threshold in wavelet domain; (h) The denoised seismic signal using our method; (i) The differential profile using our method. |
从降噪的结果来看,本文方法能够对实际地震记录中的随机噪声进行有效地压制,同相轴变得更加清晰,保留了较多的有效信号.
5 结论本文采用分数阶B样条小波对地震信号进行变换,实现对信号高效稀疏表示,然后对小波系数建立高斯尺度混合模型,再根据贝叶斯估计方法得到源地震信号小波系数估计值,最后利用分数阶B样条小波逆变换重构得到降噪后的地震信号.合成地震信号与实际地震信号的降噪结果表明本文方法能够有效地压制地震信号中的随机噪声,保留了较多的有效信号.
致谢非常感谢两位匿名评审专家提出的宝贵意见.
Andrews D F, Mallows C L. 1974. Scale mixtures of normal distributions. Journal of the Royal Statistical Society Series B-Methodological, 36(1): 99-102. |
Cao S, Chen X. 2005. The second-generation wavelet transform and its application in denoising of seismic data. Applied Geophysics, 2(2): 70-74. DOI:10.1007/s11770-005-0034-4 |
Donoho D L, Johnstone J M. 1994. Ideal spatial adaptation by wavelet shrinkage. Biometricka, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
Gao G R, Xu L P, Feng D Z. 2013. Image denoising based on the NSST domain GSM model. Geomatics and Information Science of Wuhan University (in Chinese), 38(7): 778-782. |
Li X Y, Zhang J, Kong X Q, et al. 2013. High frequency seismic nosie adaptive suppression based on discrete wavelet transform. Geophysical and Geochemical Exploration (in Chinese), 37(1): 165-170. |
Lin H B, Ma H T, Li Y, et al. 2015. Elimination of seismic random noise based on the SW statistic adaptive TFPF. Chinese Journal of Geophysics (in Chinese), 58(12): 4559-4567. |
Lin H B, Li Y, Ma H, Xu L. 2016. Simultaneous seismic random noise attenuation and signal preservation by optimal spatiotemporal TFPF. Journal of Applied Geophysics, 128: 123-130. DOI:10.1016/j.jappgeo.2016.03.013 |
Liu H Y, Wei Z H, Zhang Z R. 2009. Total variation image denoising based on fractional B-spline wavelet. Computer Engineering Applications (in Chinese), 45(11): 19-21. |
Parkan M S, Siahkoohi H R, Parkan M S, et al. 2014. The multi-dimensional complete ensemble empirical mode decomposition and its application in seismic denoising. Journal of the History of the Behavioral Sciences, 32: 297-301. |
Portilla J, Strela V, Wainwright M J, et al. 2003. Image denoising using scale mixtures of gaussians in the wavelet domain. IEEE Transactions on Image Processing, 12(11): 1338-1351. DOI:10.1109/TIP.2003.818640 |
Shuai S, Han L G, Lv Q T, et al. 2013. Seismic random noise suppression using an adaptive nonlocal means algorithm. Applied Geophysics, 10(1): 33-40. DOI:10.1007/s11770-013-0362-8 |
Tang R, Zhang J D, Zhang Q. 2013. Hybrid Fourier-wavelet image denoising using local Gaussian scale mixtures model. Laser Infrared (in Chinese), 43(5): 592-595. |
Unser M, Blu T. 2000. Fractional splines and wavelets. Siam Review, 42(1): 43-67. DOI:10.1137/S0036144598349435 |
Wu Z C, Liu T Y. 2008. Wavelet transform methods in seismic data noise attenuation. Progress in Geophysics, 23(2): 493-499. |
Zhang H, Liu T, Zhang Y. 2009. Denoising of seismic data via multi-scale ridgelet transform. Earthquake Science, 22(5): 493-498. DOI:10.1007/s11589-009-0493-4 |
Zhang Z, Cui C, Liu K. 2011. Iterative hard-threshold algorithm with momentum. Electronics Letters, 47(4): 257-259. DOI:10.1049/el.2010.2091 |
高国荣, 许录平, 冯冬竹. 2013. 利用非抽样Shearlet域GSM模型进行图像去噪. 武汉大学学报(信息科学版), 38(7): 778-782. |
李雪英, 张晶, 孔祥琦, 等. 2013. 基于离散小波变换的地震资料自适应高频噪声压制. 物探与化探, 37(1): 165-170. DOI:10.11720/wtyht.2013.1.32 |
林红波, 马海涛, 李月, 等. 2015. 基于SW统计量的自适应时频峰值滤波压制地震勘探随机噪声研究. 地球物理学报, 58(12): 4559-4567. DOI:10.6038/cjg20151218 |
刘红毅, 韦志辉, 张峥嵘. 2009. 分数阶B样条小波域的图像变分去噪. 计算机工程与应用, 45(11): 19-21. DOI:10.3778/j.issn.1002-8331.2009.11.006 |
彭才, 朱仕军, 孙建库, 等. 2007. 小波变换域K-L变换及其去噪效果分析. 石油物探, 46(2): 112-114. |
唐锐, 张敬东, 张祺. 2013. 局部高斯尺度混合模型的傅里叶-小波图像降噪. 激光与红外, 43(5): 592-595. |
 2018, Vol. 61
2018, Vol. 61

