2. 页岩油气富集机理与有效开发国家重点实验室, 北京 100083;
3. 中国石化页岩油气勘探开发重点实验室, 北京 100083;
4. 中国石化石油勘探开发研究院, 北京 100083
2. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing 100083, China;
3. SinoPEC Key Laboratory of Shale Oil/Gas Exploration and Production Technology, Beijing 100083, China;
4. SinoPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China
地下介质的物性参数(如孔隙度、泥质含量等)是用于储层描述的重要信息,然而这些参数仅能在井中直接观测得到.另一方面,地震反演能够计算弹性参数(如波阻抗、密度等的)的空间分布.岩石物理模型能够建立储层物性与弹性参数的关系,可以对地震数据进行定量解释,得到研究区域物性参数的空间分布.由于地下介质的复杂性,岩石物理模型难以准确地加以描述,并且使用的地震资料本身含有噪声,这些偏差使得储层参数反演具有不确定性.确定性反演仅给出最优解,方法本身就忽视了反演中客观存在的不确定性.已知信息(测井、地质、相邻或相似区域资料)能对反演过程加以约束以提升计算准确性和效率,却难以融入确定性反演体系中.基于贝叶斯理论的统计学反演体系能够很好地解决上述问题.在该框架下已知信息作为先验分布,岩石物理模型作为观测函数,而不确定性作为观测噪声,最终得到反演参数的后验概率分布(PDF).从该概率分布中可得出参数的最优解及估计的不确定性.
应用统计学理论进行储层参数反演的工作包括:Bachrach(2006)使用统计岩石物理模型及阻抗数据联合反演了孔隙度和饱和度,进行了参数最优估计和不确定性分析,反演过程中将地震数据中噪音的影响考虑在内.Grana和Rossa(2010)对孔隙度和饱和度进行统计学估计,并根据它们与泥质含量的统计关系对岩性进行划分.反演过程综合考虑了地震数据、岩石物理模型、井震数据尺度转化产生的偏差,得到更为准确的参数估计.Yuan等(2016)使用统计岩石物理及地震数据直接进行岩性划分,对不确定性的传递给出了全面的描述,并使用熵来衡量不确定性.上述成果对统计学反演中的偏差给予充分的考虑,但建立的多是简单的岩石物理模型,假定岩石体积模量及剪切模量的变化仅与孔隙度、饱和度等少数参数有关.为解决这一问题,有研究者将更复杂的岩石物理模型引入到反演过程.Spikes(2011)使用了广义自相容近似(SCA)模型,将组分及颗粒形状(纵横比)也考虑在内,给出了裂隙密度的最优反演结果及不确定性范围.Dupuy等(2016a, b)使用Biot-Gassmann关系式对基于多孔弹性介质模型中反演结果对各待反演参数的敏感性进行分析,并对含气饱和度进行反演.然而,上述方法基于各向同性假设进行岩石物理建模,尚未充分考虑储层的各向异性特征,模型与实际储层偏差较大,反演不确定性增强.
基于各向异性介质进行岩石物理建模,并应用地震数据进行储层参数确定性反演的技术包括Bakulin等(2000a, b, c)、张广智等(2013),但在统计学框架下进行的相关研究较少.这是因为各向异性介质中需考虑的物性参数较多,包括孔隙度、饱和度、裂缝密度、裂缝形态,甚至矿物组分等.在地震数据约束下反演如此多的未知物性参数,不仅计算量巨大,反演结果也具有很高的不确定性,因此需要使用假设或经验减少未知参数个数.Bachrach等(2009)使用叠前地震反演得到阻抗和各向异性参数数据,基于Hudson模型(Hudson,1980)反演各向异性介质的裂隙密度和孔隙度.该方法由于缺乏井数据而没有准确的先验信息,并且采用理想化假设,认为储层的弹性性质与孔隙度及裂隙密度有关.加入各向异性参数数据作为约束固然能减小反演的不确定性,但在缺乏叠前地震数据的情况下该方法无法进行.Bachrach等(2013)提出使用统计岩石物理来求取各向异性参数的方法,给叠前地震各向异性参数反演增加约束条件以减少其多解性.该研究针对泥岩和砂泥岩使用压实模型建立物性与弹性参数的联系,视孔隙度为变量,由纵波速度与孔隙度的拟合关系反演孔隙度,继而根据孔隙度求取各向异性参数.这些工作都对各向异性介质的描述进行部分简化以减少未知参数.
基于以上分析,本文拟使用地震波阻抗数据,应用统计岩石物理方法,针对中国南部龙马溪组页岩储层进行储层物性参数及各向异性参数反演.在统计岩石物理建模过程中使用压实指数(CL)来描述黏土颗粒定向排列程度的不同引起的各向异性(Guo et al., 2016),并结合对目标区域的分析,减少待反演参数.以井数据作为区域储层参数反演先验信息,反演过程考虑岩石物理模型和地震数据存在的偏差,由贝叶斯理论得到储层参数的后验概率分布.以最大后验概率准则(MAP)求取最优参数值,在寻优过程中使用模拟退火优化粒子群算法(高鹰和谢胜利,2004)提高收敛速度和计算准确性.最终得到储层参数最优值及其不确定性描述,为页岩气储层定量描述提供方法和技术.
1 方法原理 1.1 统计岩石物理正演各向异性介质储层的地震响应复杂,因此需要建立岩石物理模型描述储层物性参数与弹性参数的联系.Chapman模型(Chapman et al., 2003)基于喷射流动机制,建立了岩石弹性系数与孔隙度、裂缝密度、裂缝和裂隙纵横比等参数的定量关系.对于具有多尺度孔隙系统的岩石,其等效弹性张量表示为
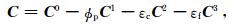
|
(1) |
其中C0是岩石基质的各向同性弹性张量;C1、C2和C3分别表示孔隙、微裂隙和裂缝附加的影响,是拉梅常数、流体和裂缝性质、频率和与喷射流动相关的松弛时间的函数.式中参数还包括圆孔隙度ϕp、微裂隙密度εc和裂缝密度εf.Chapman模型认为孔隙空间由圆孔隙、微裂隙、裂缝组成.对于大多数裂缝型实际储层,与微裂隙有关的项可以忽略,因此假设微裂隙密度为0(Chapman,2003;Maultzsch et al., 2003;Baird et al., 2013).模型中等效弹性张量的具体形式见附录.
弱各向异性介质的弹性属性可用Thomsen各向异性参数表示(Thomsen,1986):
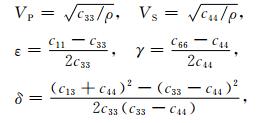
|
(2) |
其中,VP和VS为沿对称轴方向传播的纵、横波速度;c33等是刚度矩阵中的元素,矩阵具体形式见附录.公式(1)和(2)建立了储层物性参数与纵、横波速度间的联系.
Chapman(2003)模型中影响弹性系数矩阵的参数较多,包括固体矿物的弹性性质、岩石密度、孔隙度、微裂隙密度、裂缝密度、裂缝和裂隙纵横比、流体体积模量等.在实际计算中应结合研究区具体情况尽量减少自由参数的个数.
测井信息能提供部分储层参数如矿物组分、孔隙度、流体饱和度等,其他参数只能在此基础上计算得到(例如各向同性岩石基质的等效模量),或基于经验假设(例如矿物颗粒的形状).因此岩石物理模型在实际描述地下介质时存在偏差,进而公式(2)中得到的弹性参数值与实际井中观测值存在偏差:
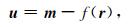
|
(3) |
其中,u表示岩石物理模型描述的偏差,是服从高斯分布且均值为0的随机误差;m表示井中弹性参数观测值;f指岩石物理模型;r是井中储层物性参数.
对于目标区域,通常已知信息有地震数据及少量井数据.井数据与地震数据中的弹性参数存在尺度差别,可使用Backus平均(Backus,1962)进行尺度转换.一些研究对尺度转换过程产生的偏差也加以考虑,但这种偏差源自于对参数取值空间进行划分(Grana and Rossa, 2010),或者对岩性分类(Yuan et al., 2016).本质是小尺度数据由于尺度提升引起分类变化,最终在求最优分类时出现偏差.本文在参数反演中使用智能寻优算法,未对参数取值空间进行分割,因此不需要考虑尺度变化引起的偏差:
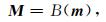
|
(4) |
其中,M是提升至地震尺度的弹性参数;B表示Backus平均.根据公式(3)和(4),在地震尺度下:
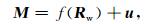
|
(5) |
其中,Rw是井位置地震尺度储层物性参数.
地震数据的采集过程包含噪声,在处理过程中也会引入偏差,在井位置:
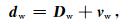
|
(6) |
其中,dw是井位置地震数据,即包含噪声的地震响应,Dw表示井位置真实地震属性;vw表示井位置地震数据的偏差,是服从高斯分布且均值为零的随机误差.
相比地震数据,测井数据和其尺度提升后数据可认为是准确的,认为是真实地震属性:
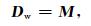
|
(7) |
井位置地震数据偏差可由公式(4)、(6)和(7)确定:

|
(8) |
对于整个目标区域,将使用井位置得到地震数据偏差,即
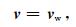
|
(9) |
其中,v指地震数据的偏差.这种代替是不准确的,但由于井数据相对于地震数据的缺乏这种情况不可避免.将公式(5)、(6)、(7)推广至整个目标区域得到:
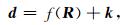
|
(10) |
其中,d是地震数据;R指储层物性参数;k=u+v,同样是服从高斯分布且均值为零的随机误差.公式(10)建立了地震数据与物性参数的统计学联系,以此可由地震数据反演物性参数.
1.2 贝叶斯框架下储层参数反演储层参数反演需要基于岩石物理模型并使用地震数据.地震数据求得的密度受偏差影响较大,一般不直接用在反演过程中(Grana and Rossa, 2010).本文选用纵波阻抗IP和横波阻抗IS数据,求得储层物性参数,并在此基础上得出各向异性参数.
公式(10)中对于给定的岩石物理模型正演值f(R), 得到观测数据d的条件概率为
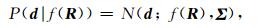
|
(11) |
其中,Σ是偏差k的协方差矩阵.而模型正演值与储层物性参数值相对应,即:
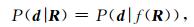
|
(12) |
则给定观测数据d时储层物性参数值R的似然概率为
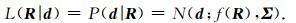
|
(13) |
对于实际工区,通常有已知信息能够提供储层物性参数的先验信息,例如地质资料、相邻区域或相似区域信息、测井数据等.另外井中储层参数反演结果也能提供部分信息.对这些信息进行统计得出储层物性参数的先验分布P(R).一般认为R代表的各参数相互独立,其具体分布形式针对不同问题会有所不同,应具体分析(Aravkin et al., 2012;印兴耀等,2014).常规确定性反演无法有效利用先验信息,而基于贝叶斯理论的统计学反演能将储层物性参数的先验信息和似然概率相结合共同约束反演结果.根据贝叶斯理论:
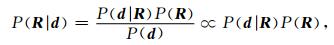
|
(14) |
其中P(R|d)为储层物性参数的后验概率分布,d在这里代表纵、横波阻抗,两者相互独立.从该后验概率分布中不仅可以得到参数的最优估计值,也能定量地描述参数估计的不确定性,这也是相对于确定性反演的优势.常用最大后验估计准则求取最优参数值,即寻找后验概率分布中概率密度最大处参数的取值.
由于岩石物理模型的复杂性,最终求得的参数后验概率分布的具体形式无法确定,需要使用蒙特卡洛(Monte Carlo)模拟方法,直接从参数空间抽取大量值计算出对应的后验概率密度描述后验概率分布,进而寻找最大概率值并确定其不确定性,但这种方法效率很低(尹彬和胡祥云,2016).对于区域地震数据,需要在每个点进行多次计算,对计算效率要求更高(Bachrach,2006).本文使用的模拟退火优化粒子群算法(SA-PSO)属于启发式蒙特卡洛方法,常用于复杂非线性问题的寻优过程.该算法结合粒子群算法实现简单、收敛快速的特点和模拟退火算法较强跳出局部极值的能力,能够快速、准确地寻找到全局最优值.对于复杂岩石物理模型引起的后验概率分布函数的强非线性,该算法能够很好地适用,能快速收敛于最大后验概率处,避免陷入局部最优,从而减小计算量.算法流程如下:
(1) 初始化参数.从参数取值区间抽取一定量随机点,被称作粒子:

|
(15) |
其中,x0i和v0i是第i个粒子的初始化位置和速度,位置也代表参数的取值;粒子可以是多维的,每个维度对应一个储层参数;U表示等概率取值;S是位置初始化区间,Su和Sd是该区间的上下界,s是速度初始化区间.初始化退火温度T,该值应足够大.
(2) 计算粒子适应度:
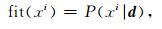
|
(16) |
其中,fit是粒子适应度函数,这里指储层物性参数的后验概率分布函数.
(3) 移动粒子:
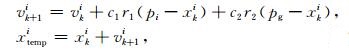
|
(17) |
其中,学习因子c1和c2是非负常数且c1+c2=4.1;r1和r2是介于[0, 1]之间的随机数;xki和vki是第k次迭代过程中对应的粒子位置和速度,vk+1i指经过本次迭代后粒子的速度;pg是全局最优值,指本次迭代时所有粒子中适应度值最大的粒子所在位置;pi是个体最优值,指单个粒子移动至今适应度最大时的位置;xtempi是本次迭代后粒子位置可能取值,粒子是否移动到该位置由以下准则判断:
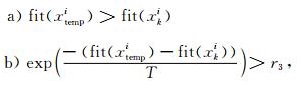
|
(18) |
其中,r3是介于[0, 1]之间的随机数.准则b)以模拟退火算法接受次优解的方式赋予了粒子群算法跳出局部极值的能力.若满足上述准则中的任何一个,粒子移动,即:
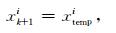
|
(19) |
否则粒子位置不变:
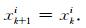
|
(20) |
(4) 降温操作.
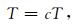
|
(21) |
其中,c是降温系数.
(5) 重复(2)—(4)步骤直到满足收敛条件.
从上述步骤(3)中可以看出模拟退火优化粒子群算法中粒子不仅能向全局最优值移动,而且此过程中对于次优值也进行了充分的搜索.粒子在移动过程中经过的每个位置都是一次蒙特卡诺模拟过程,可用来对后验概率分布进行描述,特别是在全局最优值附近.这样最终得到的不仅是最大后验概率值,对整个后验概率分布都有所描述,可用于对反演结果的不确定性进行评价.比传统蒙特卡洛模拟的方式效率更高.
综上所述,贝叶斯框架下储层参数反演步骤归纳见图 1.

|
图 1 贝叶斯框架下储层参数反演流程 Fig. 1 Workflow of reservoir parameters inversion based on Bayesian theory |
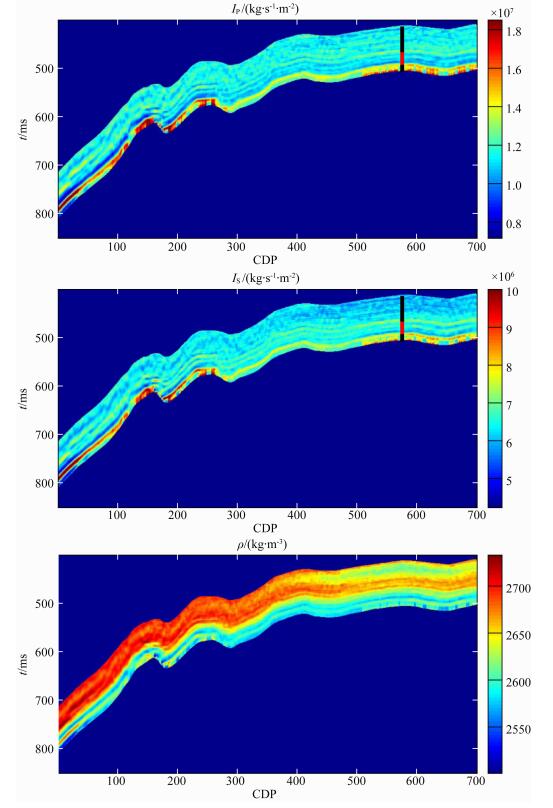
针对龙马溪组页岩气储层进行统计岩石物理反演.图 2是目标层阻抗信息剖面,由叠前地震反演得到.可以看出在目标层段纵、横波阻抗变化较小,说明该层段的储层性质变化不大,井数据提供的先验信息可适用于整个目标层.底部高阻抗低密度区域属于下反射层,用于与目标层进行对比.井位置如图所示,井数据在整个目标层段都可用,可以较准确地得到储层的先验信息.井数据的红色部分处于两个反射界面之间,为页岩气储层段,该段测井信息齐全,如图 3所示.从矿物组分体积含量可看出目标层泥质含量高,为泥质页岩.
|
图 2 目标层段纵、横波阻抗和密度剖面 (黑线表示井位置,红线部分表示页岩气储层段) Fig. 2 P- and S-wave impedances and density sections of target formation (The black line indicates the well and the red line indicates the shale gas reservoir) |

|
图 3 页岩气储层段测井数据 从左到右依次是伽马值、纵波速度、横波速度、密度、孔隙度、含水饱和度和矿物组分体积含量. Fig. 3 Well data of shale gas reservoir From left to right are gamma, P-wave velocity, S-wave velocity, density, porosity, water saturation and mineralogical volume. |
在页岩岩石物理建模的研究中,需要考虑黏土压实作用引起的各向异性(Guo et al., 2013; Bachrach et al., 2013;Qian et al., 2016).Guo等(2014)提出黏土压实指数CL,用于描述黏土颗粒定向排列引起的垂直方向纵、横波速度与各向同性情况下的偏离程度:
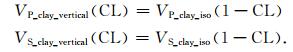
|
(22) |
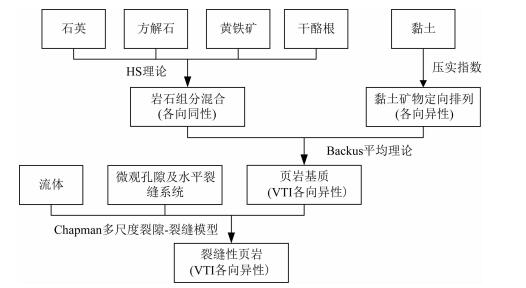
公式中CL的增加使黏土矿物垂直方向的速度降低,CL为0时对应黏土颗粒完全随机分布的各向同性情况.Guo等(2016)使用黏土压实指数,基于Chapman模型进行泥页岩岩石物理建模并反演得出各向异性参数,该模型能准确地描述泥质页岩储层.基于岩石微观结构的研究也证明了该方法的合理性(邓继新等,2015).图 4展示了其建模流程,具体步骤为
|
图 4 各向异性页岩岩石物理建模流程(Guo et al., 2016) Fig. 4 Workflow of anisotropy rock physics modeling for shale (Guo et al., 2016) |
(1) 由Hashin-Shtrikman(HS)界限(Hashin and Shtrikman, 1963)计算不含黏土的各向同性基质弹性张量Cios.
(2) 考虑黏土压实作用引起的各向异性,使用压实指数表示黏土矿物颗粒定向排列程度.计算包含黏土的各向异性基质弹性张量Cani.
(3) 在各向同性基质中考虑多尺度孔隙系统的影响,由公式(1)求得多尺度孔隙系统导致的各向异性Cf.
(4) 将多尺度孔隙系统的影响转移到各向异性基质中,则最终得到模型等效弹性张量:
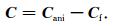
|
(23) |
在该建模流程中,黏土含量及压实指数决定基质各向异性,而裂缝属性决定多尺度孔隙系统对各向异性的影响.本文参照该建模流程,在减少待反演参数及岩石物理模型偏差的准则下,建立了适用于目标层的统计岩石物理模型.
2.2 先验信息首先对页岩气储层段进行井中储层物性参数反演,为目标层区域反演提供先验信息.在井中岩石物理建模过程中,矿物组分、孔隙度、含水饱和度等属性已知,仅考虑使用裂缝纵横比(α)和压实指数作为未知参数描述储层微观结构,其他参数由假设及经验给出.各组分属性如表 1所示,反演过程中使用实测纵、横波速度作为约束,目标函数为
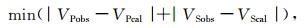
|
(24) |
|
|
表 1 页岩组分属性 Table 1 Mineralogical properties of shale |
其中,VPobs和VSobs是纵、横波速度的观测值,VPcal和VScal是岩石物理模型正演值.然后由反演出的α和CL经公式(23)和(2)得出对应各向异性参数.裂缝密度可由以下公式求得(Hudson,1980):
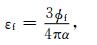
|
(25) |
其中,ϕf是裂缝体积含量.
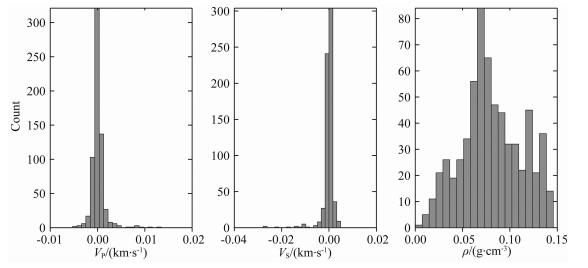
井中弹性参数反演结果与观测值偏差统计如图 5所示.由图可见模型计算出的纵、横波速度与实际值偏差较小且呈高斯分布,表明模型对目标层的适用性,能减小岩石物理模型对储层描述的偏差.密度估计值与实际值有些偏差,同地震数据类似,因此不直接使用密度而使用纵、横波阻抗作为反演约束信息.由这些信息得到岩石物理模型的偏差u,并以阻抗形式体现.这里认为纵、横波阻抗参数相互独立.
|
图 5 井中弹性参数反演结果与实际值偏差统计 (依次是纵波速度、横波速度和密度) Fig. 5 Statistics of errors between inverted elastic parameters and real data in the well (From left to right are P-wave velocity, S-wave velocity and density) |
对于整个目标层,仅有阻抗数据可用,不同于井中岩石物理建模可使用多种准确的信息.通常将井中测得矿物组分信息应用于整个储层,这种做法固然有一定偏差,但本文研究的目标层属性变化不大,使用这种替代产生的偏差较小.黏土含量对该区域岩石骨架影响大,且与各向异性参数有明显关联(邓继新等,2015),反演过程中应作为未知参数来准确确定.裂缝型含气储层中,裂缝密度对于含气饱和度并不敏感(Bachrach et al., 2009),同样目标层各处性质差别较小,储层含气饱和度完全可以使用井中数据代替.最终选用孔隙度(ϕ)、裂缝纵横比(α)、泥质含量(clay)和压实指数作为待反演参数,以尽量准确、简单地通过岩石物理模型描述目标层.
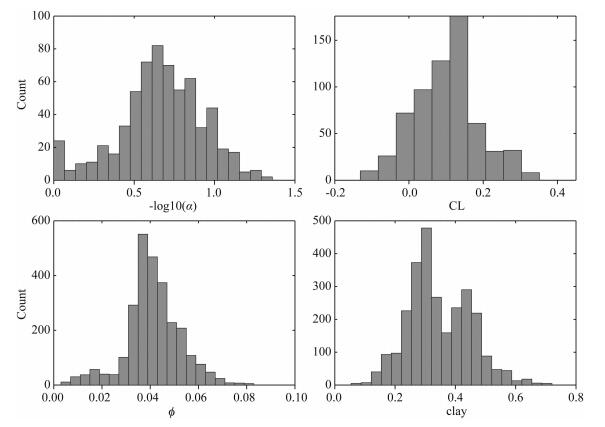
从井数据得出待反演参数的统计信息如图 6所示,其中孔隙度和泥质含量在整个目标层段可用,而反演得出的纵横比和压实指数仅在页岩气储层段可用.各参数明显呈正态分布,记为
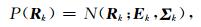
|
(26) |
|
图 6 待反演参数的统计信息 Fig. 6 Statistics of reservoir petrophysical parameters |
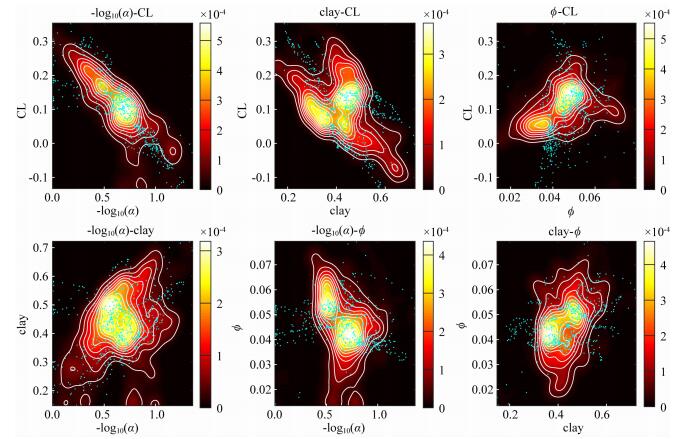
其中,Ek和Σk是第k个参数的均值和协方差,各参数间的独立性需要验证.图 7是各参数间的交汇图,其中压实指数和纵横比以及压实指数和泥质含量之间有些相关性,但并不强,其他参数无明显相关性,可认为各参数间相互独立.因此待反演参数先验分布为相互独立的四维高斯分布:
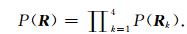
|
(27) |
|
图 7 待反演参数交汇图 Fig. 7 Cross plot of reservoir petrophysical parameters |
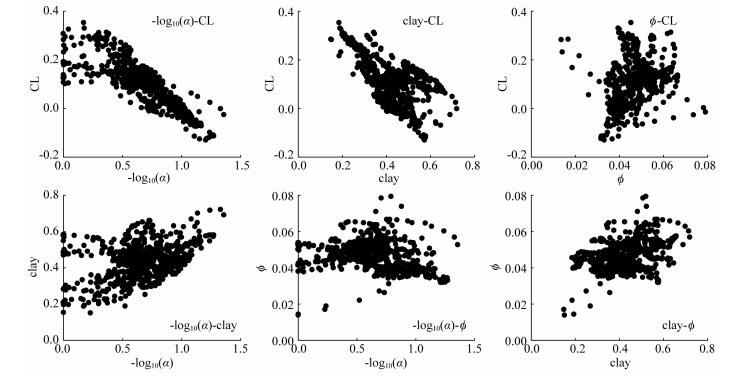
图 8展示了该四维先验分布空间的各二维剖面视图.
|
图 8 先验分布二维剖面图 (颜色对应概率) Fig. 8 2-D profiles of the prior distribution (Colors represent the probabilities) |
为确定地震数据的噪声,使用井中弹性参数数据作为准确对比信息,使用Backus平均将其提升至地震尺度.图 9是井位置地震数据与尺度提升后的测井数据对比图,图中底部为高速层,与470 ms处高速界面之间是页岩气储层段,井中反演部分在该段进行.统计各弹性参数偏差,得到阻抗数据包含的噪声v,同样认为纵、横波阻抗参数相互独立.

|
图 9 井位置地震数据(黑)和尺度提升后测井数据(红)对比 (依次是纵波速度、横波速度和密度) Fig. 9 Comparison charts of seismic data in the well location (black) and upscaled well data (red) (From left to right are P-wave velocity, S-wave velocity and density) |
至此统计学反演所需的先验分布P(R)、岩石物理模型偏差u和地震数据偏差v已经得到.岩石物理模型f可由图 4及公式(23)和(2)建立,来确定待反演储层物性参数CL、clay、ϕ、α与约束信息IP和IS的联系.从公式(14)中可以得到待反演参数的后验概率分布.
由图 6提供的统计信息可确定各待反演参数的可能取值范围,对于目标层,各参数可能取范围内任一值.我们需要在该取值范围内寻找能满足最大后验概率准则的值,在此使用模拟退火优化粒子群算法.具体操作过程中需首先确定粒子搜索区间,由各参数取值范围确定,然后从中抽取粒子:
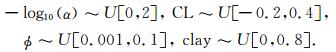
|
(28) |
注意等概率抽取粒子时,粒子对应的先验概率依然按照公式(27)求取.通常粒子可以从比搜索范围更小的区间初始化,因为最优值最可能出现在搜索区间中的部分区域,如图 6中各参数直方图的中间部分,以此可以加快收敛速度,减少计算量.本文中各参数从以下区间初始化:
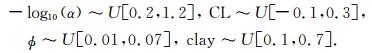
|
(29) |
算法进行过程中,粒子数N=100,迭代次数k=100,温度初值T=10000,降温系数c=0.93.为了展示整个寻优过程,我们选取目标层中某一点对其寻优迭代过程中粒子的状态进行记录.图 10分别是k=0,20,40,60,80和100时粒子状态,可以看出各参数对应的后验概率密度随着迭代次数增加逐渐变大,最终收敛于高概率处.
|
图 10 模拟退火优化粒子群算法收敛过程 (A)和(B)分别表示四维参数空间的三维视图.颜色代表概率密度,各参数最终收敛于高概率区域. Fig. 10 Optimization procedure of SA-PSO (A) and (B) are two 3-D views of the 4-D parameter space.Colors represent the probability densities, and all parameters converge to the position with high probability. |
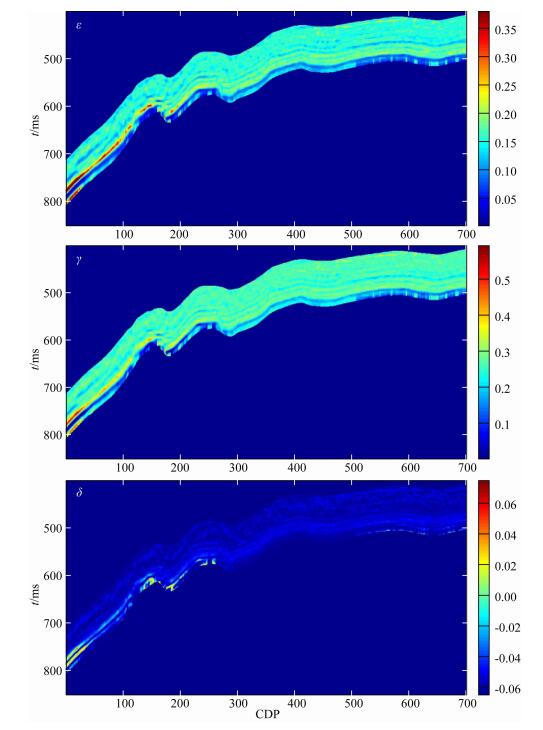
对整个目标层进行储层物性参数反演,结果如图 11所示.其中图 11(a—c)中可看出明显的分层连续性,页岩气储层段可明显辨识.图 11d中孔隙度参数值变化较小,但底界面与储层部分差别明显,说明目标层段本身孔隙度变化较小.由上述反演结果及公式(25)可得到目标层裂缝密度如图 12所示.图 13是在反演得出的储层物性参数基础上得出的Thomsen各向异性参数,同样能明显区分出储层及底界面,可用于储层描述,并可用来约束叠前地震各向异性参数反演.
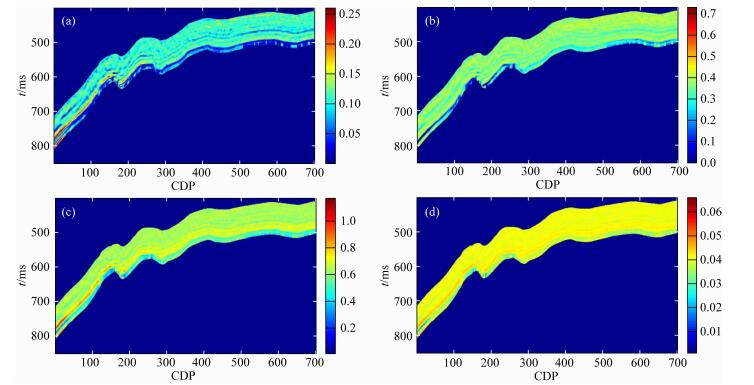
|
图 11 反演得出的储层物性参数.分别为压实指数(a)、泥质含量(b)、-log10(α)(纵横比)(c)和孔隙度(d) Fig. 11 Inversion results of reservoir petrophysical parameters, including CL (a), clay content (b), -log10 (α) (c) and porosity(d) |
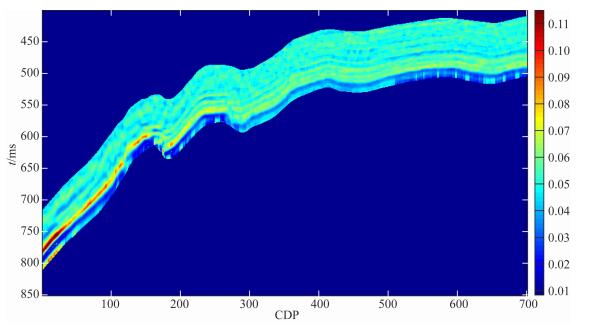
|
图 12 反演得出的裂缝密度 Fig. 12 Inverted fracture density |
|
图 13 反演出的Thomsen各向异性参数ε、γ和δ Fig. 13 Inverted Thomsen anisotropy parameters ε, γ and δ |
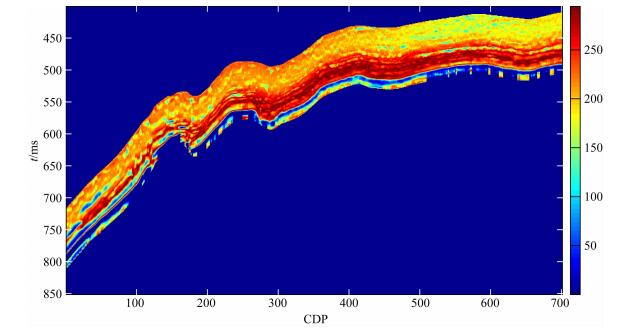
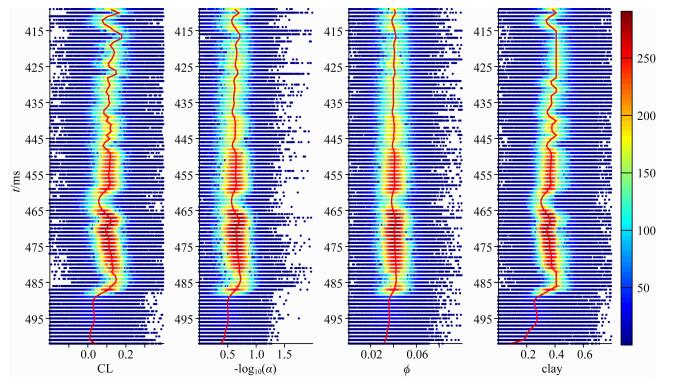
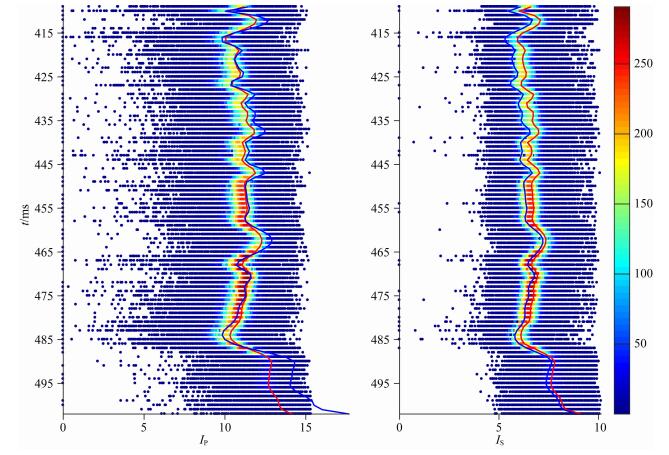
图 14显示了参数估计的最大后验概率.页岩气储层段明显概率最大,该段上部概率次之,底界面概率最小.这是因为使用的先验信息大部分来自于页岩气储层段,能准确地代表该层,而对于其他层则有所偏差.同样岩石物理模型适用于储层段,对于底界面偏差较大.这些都导致最大后验概率在不同区域差别较大.图 14表明对于先验信息充分,岩石物理模型准确的区域,参数估计的不确定性低.图 15展示了井位置储层物性参数反演值及其不确定性,图中每个点是算法迭代过程中参数的一个取值,颜色代表对应的概率密度.可以看到参数取值基本遍历了取值区间,红色高概率区域较窄,说明反演的不确定性小.同样底部概率普遍较低,页岩气储层段最高.为了证明反演的准确性,把井位置模型正演出的IP、IS和实际地震数据对比,如图 16所示.图中红色高概率区域很窄,说明反演不确定性小,真实值与正演值很接近且位于高概率区域内.底部不确定性较大,IP真实值与正演值也有些偏差,但IS值依然很准确.这是因为反演由两者共同约束且认为两者相互独立,可能出现一方很准确而另一方较准确的情况.本文中底界面仅为了与目标层进行对比.
|
图 14 目标层参数估计的最大后验概率 (颜色代表概率密度,红色为高概率区域) Fig. 14 MAP of the parameter estimation in the target formation (Colors represent the probability densities and red is the high probability area) |
|
图 15 井位置储层物性参数反演不确定性 颜色代表概率密度,红色为高概率区域,红线是最大概率值. Fig. 15 Uncertainty of the reservoir petrophysical parameters estimation in the well location Colors represent the probability densities and red is the high probability area. The red line indicates parameter values with the MAP. |
|
图 16 井位置纵、横波阻抗反演不确定性 颜色代表概率密度,红色为高概率区域,红线是最大概率值,蓝线是实际值. Fig. 16 Uncertainty of the P- and S-wave impedances estimation in the well location Colors represent the probability densities and red is the high probability area. The red line indicates parameter values with the MAP and the blue line indicates the seismic data. |
本文在贝叶斯框架下基于统计岩石物理模型,应用地震数据进行页岩储层物性参数及各向异性参数反演.方法考虑了岩石物理模型对实际储层描述的偏差,以及地震数据中的噪声的影响,也充分利用了已知井中岩石物理反演信息作为先验信息,在贝叶斯框架下进行统计学反演.从反演结果中不仅能求得最优参数值,也能得到反演不确定性的定量估计.
针对实际数据详细展示了方法的实施过程.首先经过分析选取了基于压实指数及Chapman模型的页岩岩石物理建模方法,以减少岩石物理模型对储层描述的偏差,并适当减少未知参数.然后进行了井中储层物性参数反演以提供准确的先验信息.通过对比地震数据与尺度提升后的测井数据,确定了地震数据的偏差.在求取最大后验概率过程中使用模拟退火优化粒子群算法加快收敛速度并提高准确性.最终得到了储层物性参数及各向异性参数剖面图.为储层描述提供了准确充分的信息,并可用于约束叠前地震各向异性参数反演.计算值与实际值的对比证明方法的有效性和准确性.
从结果图中可以看出在先验信息充分的区域,反演结果的不确定性较低.本文仅对目标层段进行反演,以减小先验信息不足的影响,如果对更大区域进行反演,则需要更充足的先验信息.本文提供的统计岩石物理反演方法,能够将地震属性解释为储层物性参数、各向异性参数的空间分布并提供其不确定性的定量描述,为页岩储层定量解释提供依据.
附录横向各向同性弹性介质的弹性张量可以用5个独立常数来完整描述,以刚度矩阵的形式表示为
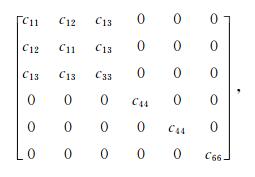
|
其中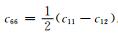
Chapman(2003)和Maultzsch等(2003)给出了矩阵中各元素表达式:
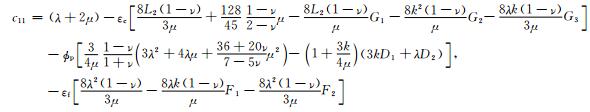
|

|
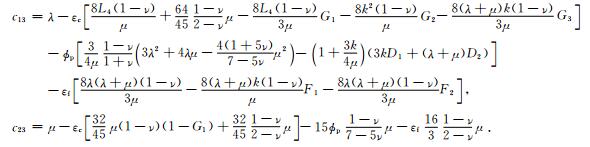
|
其中,
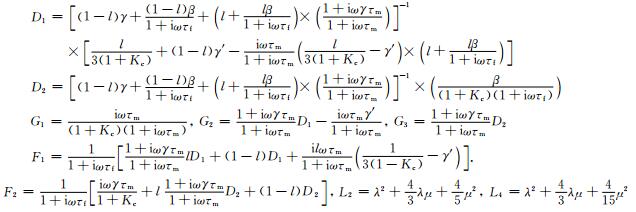
|
其中,
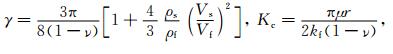
|
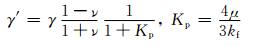
|
式中, VS指剪切波速度; Vf是流体的声波速度; ρs和ρf分别指饱和岩石密度和流体密度; kf指流体体积模量; ν是泊松比; r是微裂隙或裂缝的纵横比.假设裂缝纵横比r足够小使得Kc<<1,可得:
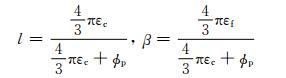
|
τm是微裂隙中流体流动弛豫时间,通过实验数据对该模型进行校准,可以估计出该值.对于野外数据的实际应用,需要根据流体和岩石性质的改变对估计的值进行进一步的校正.
当裂缝性岩石中的圆孔隙度远大于微裂隙孔隙度且研究频段低于微观喷射流动频率ωm(ωm=1/τm)时,公式(1)中与微裂隙有关的项可以被忽略,可以假设微裂隙密度为零.
Aravkin A Y, Leeuwen T V, Bube K, et al. 2012. On non-uniqueness of the student's t-formulation for linear inverse problems. //82th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 1-5.
|
Bachrach R. 2006. Joint estimation of porosity and saturation using stochastic rock-physics modeling. Geophysics, 71(5): O53-O63. DOI:10.1190/1.2235991 |
Bachrach R, SenguptaM, SalamaA, et al. 2009. Reconstruction of the layer anisotropic elastic parameters and high-resolution fracture characterization from P-wave data:a case study using seismic inversion and Bayesian rock physics parameter estimation. Geophysical Prospecting, 57(2): 253-262. DOI:10.1111/gpr.2008.57.issue-2 |
Bachrach R, Konstantin O, Dave N, et al. 2013. Applications of deterministic and stochastic rock physics modelling to anisotropic velocity model building. Geophysical Prospecting, 61(2): 404-415. DOI:10.1111/gpr.2013.61.issue-2 |
Backus G E. 1962. Long-wave elastic anisotropy producedby horizontal layering. Journal of Geophysical Research, 67(11): 4427-4440. |
BairdA F, Kendall J M, Angus D A. 2013. Frequency-dependent seismic anisotropy due to fractures:Fluid flow versus scattering. Geophysics, 78(2): WA111-WA122. DOI:10.1190/geo2012-0288.1 |
Bakulin A, Grechka V, Tsvankin I. 2000a. Estimation of fracture parameters from reflection seismic data-Part Ⅰ:HTI model due to a single fracture set. Geophysics, 65(6): 1788-1802. |
Bakulin A, Grechka V, Tsvankin I. 2000b. Estimation of fracture parameters from reflection seismic data-Part Ⅱ:Fractured models with orthorhombic symmetry. Geophysics, 65(6): 1803-1817. |
Bakulin A, Grechka V, Tsvankin I. 2000c. Estimation of fracture parameters from reflection seismic data-Part Ⅲ:Fractured models with monoclinic symmetry. Geophysics, 65(6): 1818-1830. |
Chapman M. 2003. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity. Geophysical Prospecting, 51(5): 369-379. |
Chapman M, Maultzsch S, Liu E R, et al. 2003. The effect of fluid saturation in an anisotropic multi-scale equant porosity model. Journal of Applied Geophysics, 54(3): 191-202. |
Deng J X, Wang H, Zhou H, et al. 2015. Microtexture, seismic rock physical properties and modeling of Longmaxi Formation shale. Chinese Journal of Geophysics, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
Dupuy B, Garambois S, Virieux J. 2016a. Estimation of rock physics properties from seismic attributes-Part 1:Strategy and sensitivity analysis. Geophysics, 81(3): M35-M53. DOI:10.1190/geo2015-0239.1 |
Dupuy B, GaramboisS, AsnaashariA, et al. 2016b. Estimation of rock physics properties from seismic attributes-Part 2:Applications. Geophysics, 81(4): M55-M69. |
Gao Y, Xie S L. 2004. Particle swarm optimization algorithms based on simulated annealing. Computer Engineering and Applications, 40(1): 47-50. |
Grana D, Rossa E D. 2010. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion. Geophysics, 75(3): O21-O37. |
Guo Z Q, Li X Y, Liu C, et al. 2013. A shale rock physics model for analysis of brittleness index, mineralogy and porosity in the Barnett Shale. Journal of Geophysics and Engineering, 10(2): 025006. DOI:10.1088/1742-2132/10/2/025006 |
Guo Z Q, Li X Y, Liu C. 2014. Anisotropy parameters estimate and rock physics analysis for the Barnett Shale. Journal of Geophysics and Engineering, 11(6): 065006. DOI:10.1088/1742-2132/11/6/065006 |
Guo Z Q, Liu C, Liu X W, et al. 2016. Research on anisotropy of shale oil reservoir based on rock physics model. Applied Geophysics, 13(2): 382-392. DOI:10.1007/s11770-016-0554-0 |
Hashin Z, Shtrikman S. 1963. A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics and Physics of Solids, 11(2): 127-140. DOI:10.1016/0022-5096(63)90060-7 |
Hudson J A. 1980. Overall properties of a cracked solid. Mathematical Proceedings of the Cambridge Philosophical Society, 88(2): 371-384. DOI:10.1017/S0305004100057674 |
Maultzsch S, Chapman M, Liu E R, et al. 2003. Modelling frequency-dependent seismic anisotropy in fluid-saturated rock with aligned fractures:implication of fracture size estimation from anisotropic measurements. Geophysical Prospecting, 51(5): 381-392. DOI:10.1046/j.1365-2478.2003.00386.x |
Qian K R, Zhang F, Chen S Q, et al. 2016. A rock physics model for analysis of anisotropic parameters in a shale reservoir in Southwest China. Journal of Geophysics and Engineering, 13(1): 19-34. DOI:10.1088/1742-2132/13/1/19 |
Spikes K T. 2011. Modeling elastic properties and assessing uncertainty of fracture parameters in the Middle Bakken Siltstone. Geophysics, 76(4): E117-E126. DOI:10.1190/1.3581129 |
Thomsen L. 1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
Yin B, Hu X Y. 2016. Overview of nonlinear inversion using Bayesian method. Progress in Geophysics, 31(3): 1027-1032. DOI:10.6038/pg20160313 |
Yin X Y, Zhou Q C, Zong Z Y, et al. 2014. AVO inversion with t-distribution as priori constraint. Geophysical Prospecting for Petroleum, 53(1): 84-92. |
Yuan C, Li J Y, Chen X H, et al. 2016. Quantitative uncertainty evaluation of seismic facies classification:acase study from northeast China. Geophysics, 81(3): B87-B99. DOI:10.1190/geo2015-0228.1 |
Zhang G Z, Chen H Z, Wang Q, et al. 2013. Estimation of S-wave velocity and anisotropic parameters using fractured carbonate rock physics model. Chinese Journal of Geophysics, 56(5): 1707-1715. DOI:10.6038/cjg20130528 |
邓继新, 王欢, 周浩, 等. 2015. 龙马溪组页岩微观结构、地震岩石物理特征与建模. 地球物理学报, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
高鹰, 谢胜利. 2004. 基于模拟退火的粒子群优化算法. 计算机工程与应用, 40(1): 47-50. |
尹彬, 胡祥云. 2016. 非线性反演的贝叶斯方法研究综述. 地球物理学进展, 31(3): 1027-1032. DOI:10.6038/pg20160313 |
印兴耀, 周琪超, 宗兆云, 等. 2014. 基于t分布为先验约束的叠前AVO反演. 石油物探, 53(1): 84-92. |
张广智, 陈怀震, 王琪, 等. 2013. 基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测. 地球物理学报, 56(5): 1707-1715. DOI:10.6038/cjg20130528 |
 2018, Vol. 61
2018, Vol. 61


