频率域可控源电磁法广泛应用于地下水勘探、环境调查、地质填图和油气勘探(汤井田和何继善, 2005; Constable, 2010; Streich, 2016).频率域电磁法可以分为两类:频率电磁测深法和频率电磁剖面法(李金铭, 2005).频率电磁测深法是通过改变发射频率达到测深目的的一类电磁法,典型的方法为可控源音频大地电磁法(CSAMT),采用接地长导线或不接地回线作为场源,在波区测量不同频率的相互正交的电磁场分量,并计算卡尼亚电阻率,CSAMT的工作频率范围为0.125~8000 Hz(汤井田和何继善, 2005).频率电磁剖面法是保持发射频率不变,通过改变收发距得到某一深度范围内地下电导率分布,典型的方法为海洋可控源电磁法(CSEM),采用长度为几百米的水平导线源随船拖拽移动发射低频信号,布设于海底表面的接收机阵列测量水平电场和三分量磁场响应,海洋CSEM的工作频率范围为0.1~10 Hz(Constable, 2010).
对于频率电磁测深法,在正演和反演解释过程中,为了得到一个三维模型的电磁响应,需要计算多个频率的三维正演;对于频率电磁剖面法,在勘探设计时需要计算多个频率的三维正演,用于确定一个特定三维模型的最优化发射频率.可见,频率域电磁法的勘探最优化设计和数据反演解释都需要计算多个频率的三维正演响应.目前模拟复杂三维介质的频率域电磁响应的正演算法主要有:有限差分法(Streich, 2009;殷长春等, 2014),有限元法(徐志锋和吴小平, 2010;Um et al., 2013;李建慧等, 2016;Cai et al., 2017)和有限体积法(张烨等, 2012;杨波等, 2012;Haber and Ruthotto, 2014;彭荣华和胡祥云, 2016).不论采用哪种空间离散算法,最后的离散控制方程都可以表示为以下形式:
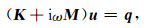
|
其中K表示离散形式的双旋度算子,M表示离散形式的电导率,u为未知的电场矢量,q为离散形式的源项.一般采用迭代法(殷长春, 2014)或直接法(Streich, 2009;彭荣华和胡祥云, 2016;Cai et al., 2017)求解上述方程.由于该方程的系数矩阵K+iωM是频率的函数,因此不论采用迭代法或直接法,不同频率的正演响应都只能独立求解,从而导致正演计算时间随发射频率个数呈线性倍数增加.
一种改进方法是针对迭代法的预处理重复利用技术(Um et al., 2013).在采用迭代法求解离散控制方程时,ILU预处理矩阵的求解需要耗费较长的计算时间.Um等(2013)提出只求解最低频率的ILU预处理矩阵,并将该预处理矩阵重复应用于其他频率的正演计算,从而减少总的正演计算时间.但该算法的改进幅度有限,而且该算法对于大的频率间隔(比如CSAMT)的正演模拟的有效性还有待验证.另一种改进方法是采用多频率并行计算(Plessix et al., 2007).由于各个频率的正演响应是相互独立的,因此可以采用多CPU的计算设备,同时计算多个频率的正演响应(彭荣华和胡祥云, 2016; Cai et al., 2017).当计算设备的CPU数量不少于发射频率数量时,其所有频率的总的正演计算时间与一个频率的正演计算时间相当.上述两种改进算法本质上都是基于不同发射频率正演响应的独立求解,当发射频率数量增加时,方程求解次数或CPU数量也需要相应增加.
更为有效的改进方法是将正演响应表示为发射频率的传递函数(蒋耀林, 2010),从而实现一定频度范围内所有频率正演响应的同时求解.但由于该传递函数的分母中包含大维度的离散系数矩阵K,难以直接求解,一般采用模型降阶方法求解该传递函数(蒋耀林, 2010).所谓模型降阶,是指在某种情况下将一个较大系统转化为一个近似的较小系统的过程,以便降低大型复杂系统的理论分析难度和减少数据运算量,同时保证降阶系统与原始系统的近似误差足够小、降阶系统保持原始系统的某些性能(蒋耀林, 2010).目前模型降阶方法因其高效快速的计算性能被广泛应用于各类大型复杂问题的数值模拟与参数最优化计算中(蒋耀林, 2010).典型的模型降阶方法是基于m维多项式Krylov子空间投影的模型降阶方法(Druskin and Knizhnerman, 1994; Druskin et al., 1999),但该算法的收敛速度依赖于计算频率范围和模型的电导率反差,对于较长的求解频率范围、存在电导率大反差模型的正演,多项式Krylov子空间的维度需要达到数千甚至上万,严重降低了该方法的计算效率.针对这一问题,Knizhnerman等(2009)提出采用基于m维有理函数Krylov子空间投影的模型降阶方法,有理函数相比多项式表现出更好的近似特性,不依赖于模型电导率反差,该算法的关键在于(1)选取最优化的m个有理函数极点,极点选取是否合适直接决定了有理函数近似特性的好坏(即m的大小);(2)构建m维有理函数Krylov子空间需要逐次求解m个关于系数矩阵和极点的方程,如何有效求解这些方程直接决定了模型降阶方法的计算效率.Knizhnerman等(2009)通过求解第三类Zolotarev问题得到了准最优化的m个(m一般为几十)不同有理函数极点,采用迭代法逐次求解m次关于系数矩阵和不同极点的方程,该算法能有效计算一定频率范围内大反差电导率模型的正演响应,但该算法构建子空间的计算量较大.
本文研究快速实现一定频度范围内所有频率的可控源电磁法三维正演响应的同时求解.首先采用基于Yee氏交错网格的拟态有限体积算法(Haber and Ruthotto, 2014)实现空间离散,将离散控制方程的解表示为传递函数的形式.然后采用基于有理函数Krylov子空间投影的模型降阶方法求解该传递函数.针对有理函数Krylov子空间构建需要多次求解关于系数矩阵和极点的线性方程组的问题,本文提出采用构建m维单个重复极点的有理函数Krylov子空间,引入直接法求解器PARDISO (Schenk and Grtner, 2004),只需要一次系数矩阵分解和m次矩阵回代即可实现有理函数Krylov子空间的构建,极大地减少了正演算法的计算量.针对最优化有理函数极点选取问题,由于本文将有理函数的极点限制为单个重复极点,极大地缩小了极点搜索范围,简化了最优化极点搜索过程.本文根据传递函数的有理函数Krylov子空间投影算法的误差分析理论(Güttel, 2010),引入关于单个重复极点的收敛率函数,通过求解有理函数的最大收敛率直接给出最优化的单个重复极点公式.最终实现了传递函数的快速计算.最后通过多个理论模型的正演计算测试验证本文算法计算多频可控源电磁法三维正演响应的精确性和高效性,并通过一个三维海洋CSEM勘探设计最优化发射频率和接收区域选取的例子进一步说明本文算法的优点.
1 正演理论 1.1 拟态有限体积空间离散算法设电磁场随时间的变化关系为eiωt,忽略位移电流,则频率域可控源电磁法对应的控制方程为
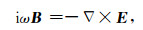
|
(1a) |
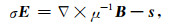
|
(1b) |
其中E是电场强度矢量,B是磁感应强度矢量,s是外加源项,σ为电导率,ω=2πf为圆频率,μ是磁导率.采用自然边界条件(Haber and Ruthotto, 2014)
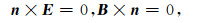
|
(2) |
与有限元方法一样,MFV方法处理弱形式的控制方程:
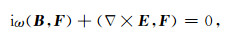
|
(3a) |
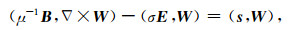
|
(3b) |
其中W与E位于相同的Sobolev空间H(Curl; Ω),F与B位于相同的Sobolev空间H(Div; Ω).内积定义为 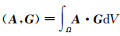
采用Yee氏交错网格进行空间离散.设定整个网格剖分区域的6个面均为规则矩形,采用正交规则矩形网格,在x、y和z三个方向上离散网格单元数为nx、ny和nz.定义网格中心为(i, j, k),网格单元如图 1所示.定义E在网格棱边中心,三个方向的场点分别为Ei, j±1/2, k±1/2x、Ei±1/2, j, k±1/2y和Ei±1/2, j±1/2, kz,定义B在网格面中心,三个方向的场点分别为Bi±1/2, j, kx、Bi, j±1/2, ky和Bi, j, k±1/2z.
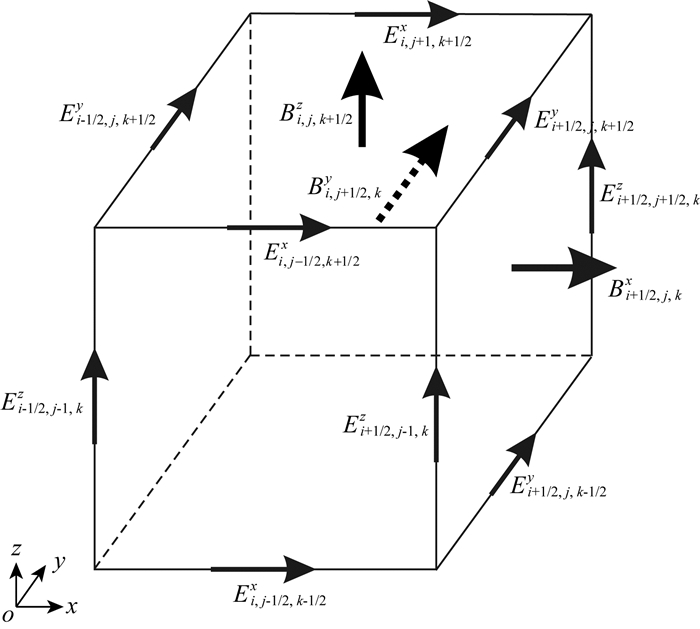
|
图 1 交错网格单元(i, j, k) Fig. 1 Grid cell (i, j, k) |
由公式(3)可知,空间离散主要包含两部分内容:旋度算子离散和空间内积离散.旋度算子离散采用积分形式的斯托克斯定理处理.考虑矩形网格单元(i, j, k),在x、y和z三个方向上的单元网格长度记为hxi、hyj和hzk.单元网格6个表面分别记为Si±1/2, j, k、Si, j±1/2, k和Si, j, k±1/2.以表面Si+1/2, j, k为例,根据中点积分规则,计算电场的旋度x方向的分量,即关于表面Si+1/2, j, k的投影为
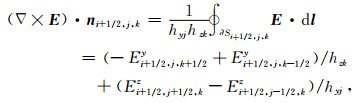
|
(4) |
同理可以得到电场旋度y方向和z方向分量的离散表示,整理将旋度算子表示为矩阵形式(Haber and Ruthotto, 2014)
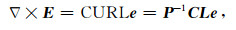
|
(5) |
其中P为包含剖分网格所有表面面积的对角矩阵,L为包含剖分网格所有棱边长度的对角矩阵,C为包含0和±1的矩阵,e是网格中电场E的矩阵表示形式.
空间内积离散包含位于面中心点的内积(B, F)和位于棱边中心的内积(σE, W).根据内积定义公式,采用中点平均即可实现空间内积离散为
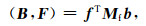
|
(6) |
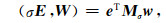
|
(7) |
其中b和f为B和F的矩阵表示形式,w为W的矩阵表示形式,Mμ和Mσ分别为单元体积的差分矩阵,具体形式见(Haber and Ruthotto, 2014).
利用旋度离散和内积离散的具体形式,消去f和w,得到控制方程空间离散的矩阵表示为
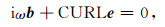
|
(8a) |
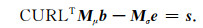
|
(8b) |
将公式(8a)代人(8b),消去b,得到关于e的离散控制方程为
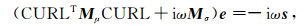
|
(9) |
令A=Mσ-1CURLTMμCURL,X=Mσ-1s,τ=iω,则方程(9)可以整理为
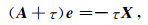
|
(10) |
方程(10)的解可以表示为
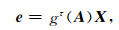
|
(11) |
其中 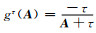
对于频率域电磁响应的正演计算,一个很重要的问题是外加源项的离散.源附近的场变化剧烈,会显著地影响正演计算精度,目前有多种方法来处理这一问题,包括散射场方法(Newman and Alumbaugh, 1995),直接离散方法(Weiss, 2013),差异场方法(Kong, 2008),虚拟场源校正方法(彭荣华和胡祥云, 2016).本文考虑采用基于有理函数Krylov子空间投影的模型降阶方法求解方程(11),实现多个频率的可控源电磁响应的快速计算.该算法要求输入X对于不同频率是保持不变的.对于不同频率的正演计算,散射场方法、差异场方法和虚拟场源校正方法都需要计算不同频率的场的解析解,导致离散源项是频率的函数.直接离散方法只是在发射源区域的网格对源进行直接离散和赋值,不需要针对不同频率进行不同的计算,当发射源的长度位置和离散网格固定时,不同频率的发射源X是不变的,本文采用Weiss(2013)的方法对发射源进行直接离散.
1.2 有理函数Krylov子空间模型降阶算法方程(11)中的传递函数gτ(A)是频率的函数,将不同的频率代入到方程(11),即可求得不同频率的正演响应,但由于传递函数的分母中含有大型稀疏矩阵A,直接求解方程(11)是困难的.本文采用有理函数Krylov子空间模型降阶算法,通过构建有理函数Krylov子空间,将大维度的传递函数投影到小维度的krylov子空间,从而实现方程(11)的快速求解.
有理函数Krylov子空间模型降阶算法本质上是一种近似算法.方程(11)的有理函数近似为
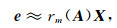
|
(12) |
其中rm(A)为有理函数,其一般形式为rm=qm-1(A)pm(A),pm是m阶非零多项式,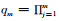
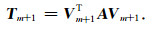
|
(13) |
则传递函数的有理函数Krylov子空间模型降阶解为(Güttel, 2010)
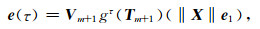
|
(14) |
其中e1=[1, 0, 0, …, 0](m+1)×1T.由于m远小于系数矩阵A的维度,因此求解gτ(Tm+1)的计算量比求解原传递函数gτ(A)的计算量要小的多,小维度传递函数可以直接求解.采用方程(14)即可快速求得不同频率的电场响应.有理函数Krylov子空间模型降阶的具体算法如表 1所示.由表 1算法可知,该算法的关键在于:(1)选择最优化极点ξj, j=1, …, m;(2)算法的主要计算量在于逐次求解m个线性方程组(A-ξjI)x=vj,如何有效求解这些线性方程组直接决定了该算法的计算效率.
|
|
表 1 计算传递函数gτ(A)X的有理函数Krylov子空间模型降阶算法 Table 1 Rational Krylov subspace model order reduction algorithm for transfer function gτ(A)X |
根据有理函数Krylov子空间模型降阶算法可知,待求的m个线性方程组的系数矩阵主要由极点确定.如果选取m个极点都相同,即采用单个重复极点,则待求的m个线性方程组的系数矩阵完全相同,结合直接法求解器PARDISO(Schenk and Grtner, 2004),只需要1次矩阵分解和m次矩阵回代即可实现m维有理函数Krylov子空间的正交基的构建.
对于最优化单个重复极点选取,根据传递函数的有理函数Krylov子空间投影算法的误差分析理论Güttel (2010),可以引入关于单个重复极点的收敛率函数:
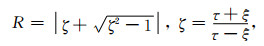
|
(15) |
其中τ是正虚数,寻找最优化的实数极点ξ0<0,保证R在传递函数的参数变化范围T=[τmin, τmax]=2iπfmin, fmax内的最小值尽可能地大.对于给定的τ,在ξ<0时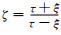
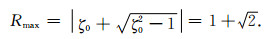
|
(16) |
当传递函数的参数变化范围为T=[τmin, τmax]时,当τ沿T范围变化时,ζ在复平面中为一个单位圆的一段圆弧.根据前面的推导已知ζ0=i时R取最大值,因此为了保证整个参数变化范围内的Rmin尽可能大,最优化单个重复极点选取为
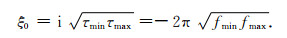
|
(17) |
对应的ζ在复平面中为关于ζ0=i对称的单位圆的一段圆弧,在τ=ξ0/i具有最大的收敛率Rmax=1+ 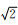
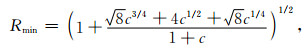
|
(18) |
其中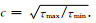
对于有理函数Krylov子空间维度m的确定,注意到采用最优化极点的有理函数Krylov子空间模型降阶算法不依赖于模型电导率反差,只依赖于求解频率范围(Güttel, 2010).因此可以通过替代算法(Börner et al., 2015)快速确定有理函数Krylov子空间的维度m,即设置一个对角矩阵W,其本征值足够密集地等间隔分布在足够大的负半轴内,逐渐增大m,分别采用直接计算方法和有理函数Krylov子空间模型降阶算法计算各个频率点对应的传递函数,从而得到有理函数Krylov子空间模型降阶算法的误差,误差不再减小或误差小于给定的误差限时对应的m值,即为有理函数Krylov子空间的维度m.
2 模型计算 2.1 算法验证首先采用典型的一维CSAMT模型和海洋CSEM模型,通过与解析解的正演结果进行比较,验证本文有理函数Krylov子空间模型降阶算法的计算精度和计算效率.本文计算所有模型三维正演的设备为32 G内存、4核主频3.6 GHz的Intel i7 CPU的台式电脑.
CSAMT方法一般采用接地长导线源作为发射源,在某一固定偏移距的接收点处,接收随频率变化的相互正交的电场和磁场,计算视电阻率和相位差(Routh and Oldenburg, 1999):
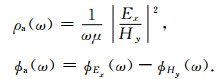
|
(19) |
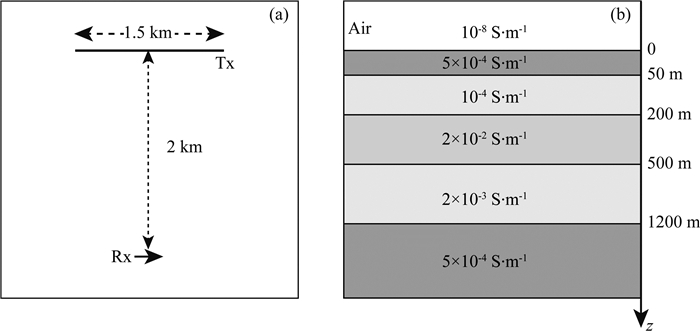
采用Routh和Oldenburg(1999)的1D层状模型,如图 2所示,为含有高阻和低阻层的5层模型,在背景电导率5×10-4S·m-1的半空间中,存在一个顶部埋深50 m、厚度150 m、电导率10-4S·m-1的高阻层,顶部埋深200 m、厚度300 m、电导率2×10-2S·m-1的低阻层,以及顶部埋深500 m、厚度700 m、电导率2×10-3S·m-1的地层.发射源(Tx)为长度1.5 km的线电流源,在偏移距2 km的位置放置接收机(Rx),接收14个频率(20~213Hz)的电场和磁场,计算不同频率对应的视电阻率和相位差.
|
图 2 CSAMT一维模型及发射-接收系统 Fig. 2 The 1D conductivity model and transmitter-receiver configuration for CSAMT |
采用替代算法(Börner et al., 2015)确定有理函数Krylov子空间模型降阶算法的子空间维度m.引入一个本征值分布足够密集的对角矩阵,本文采用区间[10-8, 108]内对数等间隔分布的维度为500的对角矩阵A,定义一个维度为500的单位向量X,求解频率范围为[20, 213]Hz,则最优化单个重复极点选取为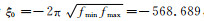
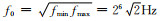
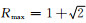
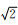
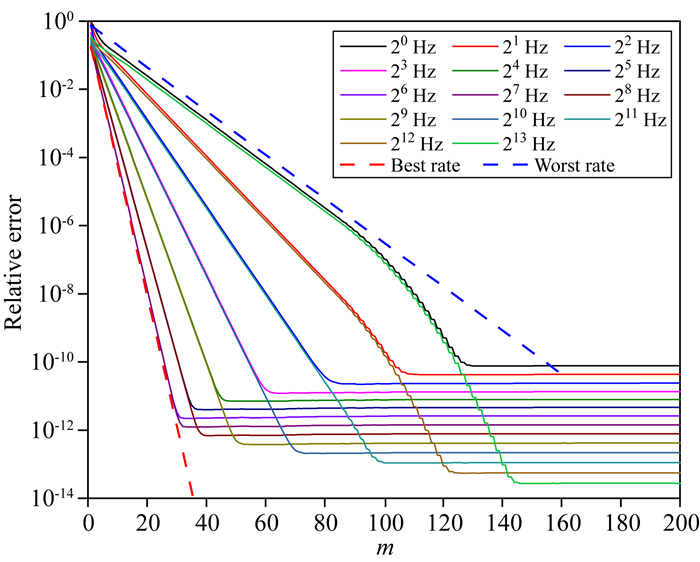
|
图 3 不同频率有理函数Krylov子空间模型降阶解的相对误差随m的变化情况 Fig. 3 Error curves of the rational Krylov method for different frequency with m |
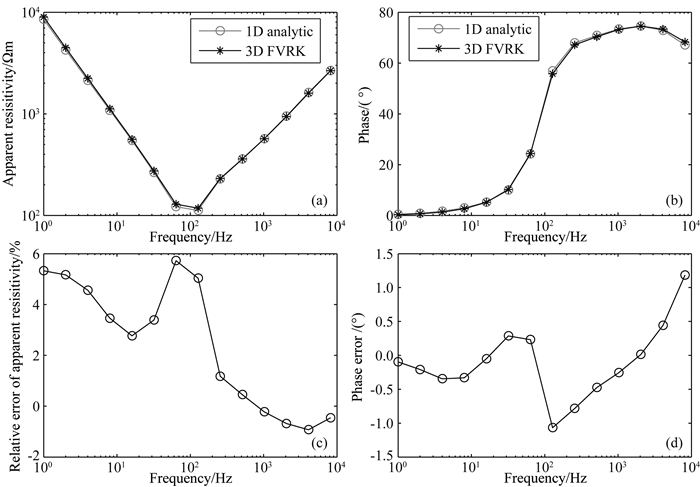
接下来采用有理函数Krylov子空间模型降阶算法计算上述CSAMT模型,拟态有限体积法进行空间离散,空气层电导率设置为10-6S·m-1,采用非均匀网格剖分,最小网格长度为15 m,网格放大系数为1.3,总的网格单元数为31×51×58.同时采用一维正演程序Dipole 1D(Key, 2009)计算该模型.总的正演计算结果如图 4所示,图 4a为视电阻率,图 4b为相位差,其中浅色点线为1D正演计算结果,黑色点线为3D算法的计算结果.图 4c为三维正演计算的视电阻率的相对误差,图 3d为三维正演计算的相位误差.从图 4a和4b可知,三维有理函数近似算法计算的CSAMT响应与解析解吻合的很好.图 4c和4d表明,各个频率的振幅响应相对误差小于6%,相位误差小于1.5°.本文的有理函数近似算法计算所有14个频率正演响应的时间为113 s,即单个频率的平均正演响应时间仅为8 s,说明本文的三维有理函数Krylov子空间模型降阶算法能够快速精确地实现多频CSAMT三维正演响应.
|
图 4 1D解析算法和3D有理函数Krylov子空间模型降阶解算法求得的CSAMT视电阻率和相位响应 Fig. 4 CSAMT apparent resistivity and phase response of the 1D model by 1D analytic method and 3D rational Krylov method |
不同于陆地CSAMT方法,海洋CSEM方法接收不同频率沿多个偏移距的电场和磁场响应,一般采用沿测线(inline)方向的电场的振幅和相位作为响应数据.本文采用Constable和Weiss(2006)的1D海洋CSEM层状模型,如图 5所示,空气层电导率为106 S·m-1,海水层深度为1000 m,电导率为0.3 S·m-1,地层电导率为1 S·m-1,在海底下方1000 m处存在一个电导率为0.01 S·m-1的高阻层.发射源位于海底上方100 m处,发射源长度为100 m,接收机位于海底表面,接收机间距500 m,计算发射频率分别为0.1 Hz、0.25 Hz、0.5 Hz、0.75 Hz、1.0 Hz时沿inline方向的电场振幅和相位响应.

|
图 5 包含高阻薄层的一维海洋CSEM模型 Fig. 5 1D marine CSEM model include the thin resistive layer |
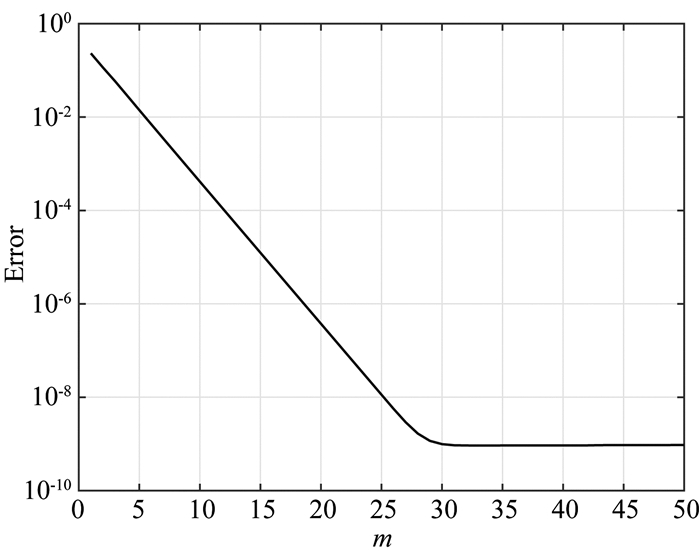
分别采用1D程序Dipole 1D(Key, 2009)和3D有理函数Krylov子空间模型降阶算法计算上述模型.采用3D算法进行正演算法时,空气层电导率设置为10-6 S·m-1,采用非均匀网格剖分,最小网格长度为20 m,网格放大系数为1.3,总的网格单元数为102×42×58.最优化极点为-1.9869,对于极点数m选取,采用替代算法(Güttel, 2010)计算最低频率fmin=0.1 Hz对应的模型降阶解的相对误差与m的关系如图 6所示,由图 6可知,当m大于30之后,模型降阶解的相对误差基本恒定,因此选取m=30.
|
图 6 频率范围[0.1, 0.25, 0.5, 0.75, 1.0]Hz时0.1 Hz的有理函数Krylov子空间模型降阶解的相对误差随m的变化情况 Fig. 6 Error curves of the rational Krylov method for 0.1 Hz with different m when frequency interval is [0.1, 0.25, 0.5, 0.75, 1.0]Hz |
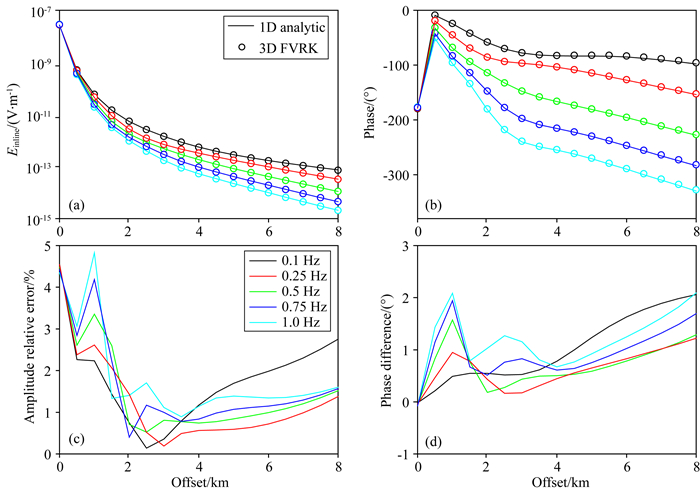
正演计算结果如图 7所示,其中黑色、红色、绿色、蓝色和青色分别为0.1 Hz、0.25 Hz、0.5 Hz、0.75 Hz、1.0 Hz的正演计算结果.图 7a为沿inline方向的电场的振幅,图 7b为沿inline方向的电场的相位,其中实线为1D正演计算结果,圆圈为3D有理函数Krylov子空间模型降阶算法的计算结果.图 7c为3D正演计算的电场振幅的相对误差,图 7d为3D正演计算的电场相位的误差.采用3D有理函数Krylov子空间模型降阶算法,只需要一次正演,即可得到所有频率的正演响应.从图 7可知,3D模型降阶算法计算的海洋CSEM响应与解析解吻合得很好,各个频率的振幅响应相对误差小于5%,相位误差小于3°.3D算法计算上述5个频率正演响应的时间为310 s,即单个频率的平均正演响应时间仅为62 s,说明本文的三维有理函数Krylov子空间模型降阶算法能够快速精确地实现多频海洋CSEM正演响应.
|
图 7 1D解析算法和3D有理函数Krylov子空间模型降阶解求得的CSEM模型沿inline方向的电场响应 Fig. 7 Inline electric field of the CSEM model by 1D analytic method and 3D rational Krylov method |
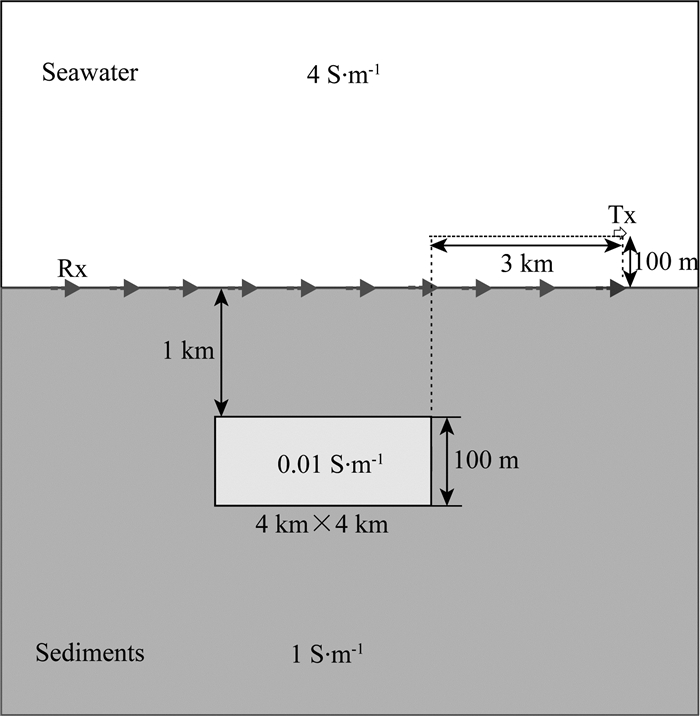
接下来分析一个典型三维海洋CSEM模型,如图 8所示,海底1 km处存在一个厚度100 m,水平尺寸4 km×4 km的矩形高阻目标体,发射源Tx为发射电流强度为1A的线电流源,位于海底上方100 m处,发射源距离海底目标体水平方向边界3 km,接收机Rx位于海底表面,接收inline方向的电场.
|
图 8 三维海洋CSEM模型 Fig. 8 3D marine CSEM model |
采用三维有理函数Krylov子空间模型降阶算法计算典型的发射频率为0.1 Hz、1 Hz的三维正演响应.采用非均匀网格剖分,最小网格长度为20 m,网格放大系数为1.3,总的网格单元数为112×48×59.最优化极点为-1.9869,对于极点数m选取,由于计算频率范围与计算图 5的一维CSEM模型的频率范围是一致的,因此其极点数仍然选取为m=30.采用模型降阶算法同时计算2个频率的正演响应,其中不含目标体的正演时间为471 s,含有目标体的正演时间为478 s.
正演计算结果如图 9所示,图 9a中虚线为不含目标体时沿inline方向的电场振幅,实线为含有目标体时沿inline方向的电场振幅,绿色虚线为深水域接收器的噪音水平5×10-16V/(Am2)(Mittet and Morten, 2013),图 9b为归一化振幅.由图 9可知,发射频率为0.1 Hz时,接收信号幅值大,在0~10 km偏移距范围内的接收信号幅值都大于噪音水平,但异常响应小,最大归一化异常为2;发射频率为1 Hz时,异常响应大,最大归一化异常大于40,但接收信号幅值小,异常响应明显的主要区域,即在偏移距大于5 km区域的接收信号幅值小于噪音水平,而偏移距小于5 km的区域,归一化异常均小于2.因此采用0.1 Hz或1 Hz的发射频率均不能得到最优化的异常响应(即大于噪音水平的信号幅值存在最大的归一化场),显然存在一个最优化的发射频率,保证接收信号大于噪音水平,同时信号的归一化幅值最大.
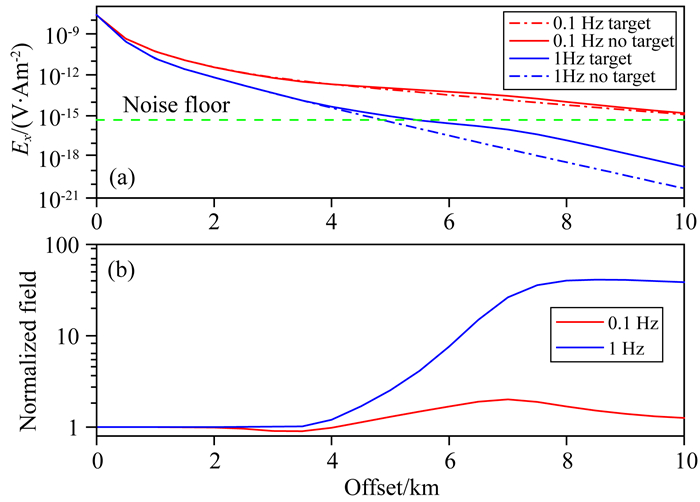
|
图 9 发射频率为0.1 Hz和1 Hz时含有和不含目标体的3D CSEM模型沿inline方向的电场响应 (a)电场振幅;(b)归一化振幅. Fig. 9 Inline electric field of the 3D model with and without target |
为了得到该模型最优化的异常响应,需要模拟不同频率的正演.采用常规正演算法需要多次正演响应,而采用本文有理函数Krylov子空间模拟降阶算法,只需要一次正演,即可得到一个频率范围内所有频率的正演响应.对于该3D模型,本文选取频率范围为0.1~2 Hz,间隔为0.1 Hz的20个频率.分别计算3D模型含有目标体和不含目标体时的响应,网格剖分仍然采用非均匀网格剖分,最小网格长度为20 m,网格放大系数为1.3,总的网格单元数为112×48×59.由于发射频率范围发生变化,最优化极点变化为-2.8099,采用替代算法(Güttel, 2010)计算的最小频率的模型降阶解的相对误差与m的关系如图 10所示,当m大于35之后,模型降阶解的相对误差基本恒定,因此选取m=35.
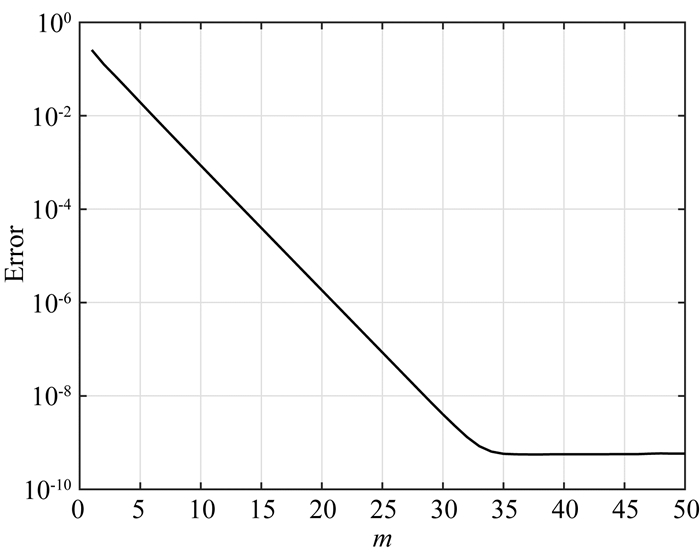
|
图 10 频率范围[0.1~2.0]Hz时0.1 Hz的有理函数Krylov子空间模型降阶解的相对误差随m的变化情况 Fig. 10 Error curves of the rational Krylov method for 0.1 Hz with different m when frequency interval is [0.1~2.0]Hz |
采用有理函数Krylov子空间模型降阶算法计算20个频率的3D正演响应,不含目标体的正演时间为495 s,含有目标体的正演时间为514 s.对比可知,计算20个频率的正演时间相比计算2个频率(0.1 Hz、1 Hz)的正演时间仅有少量增加(不含目标体的正演时间增加24 s,含有目标体的正演时间增加36 s),进一步说明了模拟降阶算法适合于计算多个频率的正演响应.
计算所有20个频率沿inline方向电场的的正演响应结果如图 11所示.图 11a为含有目标体相比不含目标体时的电场的归一化振幅,横坐标为偏移距,纵坐标为发射频率,剖面值为归一化电场振幅,图中剔除了含有目标体时测量电场振幅小于噪音水平的数据,即图中的白化区域.由图 11a可以清晰地看出,归一化电场振幅较大(大于4)的区域主要分布在发射频率为0.4~0.8 Hz、偏移距为5.5~8.5 km范围.图 11b为含有目标体相比不含目标体时的电场的相位差,横坐标为偏移距,纵坐标为发射频率,剖面值为相位差,图中同样剔除了含有目标体时测量电场振幅小于噪音水平的数据,即图中的白化区域.由图 11b可知,相位差较大(大于80)的区域主要分布在发射频率为0.1~1.0 Hz、偏移距为5.5~9.5 km范围.
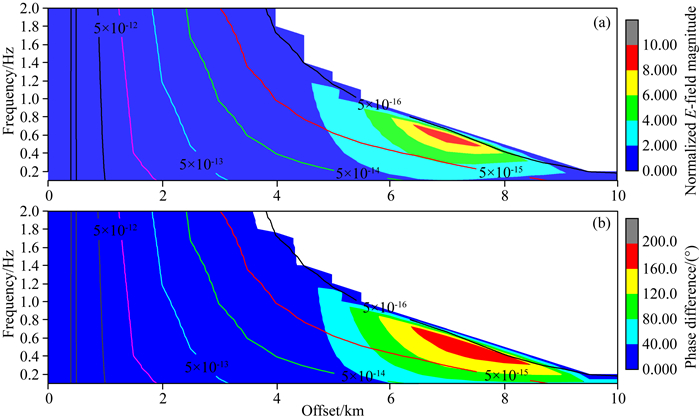
|
图 11 不同发射频率的3D CSEM模型沿inline方向的电场响应 (a)归一化电场响应;(b)相位差. Fig. 11 Inline electric field of the 3D model with different frequencies (a) Normalized electric field magnitude; (b) Phase difference. |
进一步绘制了含有目标体时测量电场振幅的等值线(图 11a和11b中的实线),偏移距越大,发射频率越高,测量电场的振幅越小.在实际采集数据时,需要保证测量电场的振幅尽可能大,从而保证测量数据质量,因此在确定最优化发射频率和偏移距时,归一化电场振幅、相位差和测量电场的振幅需要综合考虑.
3 结论本文采用有理函数Krylov子空间模型降阶算法实现了多频可控源电磁法三维正演响应的快速计算.采用基于Yee氏交错网格的拟态有限体积法实现控制方程的空间离散,从而将任意频率的电场响应表示为关于频率参数的传递函数形式.本文提出采用单个重复极点的有理函数Krylov子空间模型降阶算法求解该传递函数,并根据传递函数的有理函数Krylov子空间投影算法的误差分析理论得到了最优化的单个重复极点的计算公式,进一步结合直接法求解器PARDISO,利用Gram-Schmidt方法,将有理函数Krylov子空间模型降阶算法的计算量减少为1次系数矩阵分解和m次矩阵回代,从而实现了多个发射频率的可控源电磁法三维正演响应的快速计算.
通过与多发射频率的CSAMT和海洋CSEM层状模型的一维解析解正演结果对比,说明了本文的三维有理函数近似算法能够快速精确地计算多发射频率的可控源电磁法正演响应.对比CSAMT模型正演和海洋CSEM模型正演可知,当发射频率越多时,本文算法的计算速度优势更显著.分析了一个海洋CSEM三维模型勘探最优化设计的例子,采用本文有理函数Krylov子空间模型降阶算法,只需要2次正演(含有目标体和不含目标体),即可实现最优化频率选取.进一步说明了有理函数Krylov子空间模型降阶算法能够快速计算一定频率范围的三维正演响应,因此特别适合于勘探前最优化频率选取.
Börner R U. 2010. Numerical modelling in geo-electromagnetics:advances and challenges. Surveys in Geophysics, 31(2): 225-245. DOI:10.1007/s10712-009-9087-x |
Börner R U, Ernst O G, Güttel S. 2015. Three-dimensional transient electromagnetic modelling using Rational Krylov methods. Geophysical Journal International, 202(3): 2025-2043. DOI:10.1093/gji/ggv224 |
Cai H Z, Hu X Y, Li J H, et al. 2017. Parallelized 3D CSEM modeling using edge-based finite element with total field formulation and unstructured mesh. Computers & Geosciences, 99: 125-134. |
Constable S, Weiss C J. 2006. Mapping thin resistors and hydrocarbons with marine EM methods:Insights from 1D modeling. Geophysics, 71(2): G43-G51. DOI:10.1190/1.2187748 |
Constable S. 2010. Ten years of marine CSEM for hydrocarbon exploration. Geophysics, 75(5): 75A67-75A81. DOI:10.1190/1.3483451 |
Druskin V, Knizhnerman L. 1994. Spectral approach to solving three-dimensional Maxwell's diffusion equations in the time and frequency domains. Radio Science, 29(4): 937-953. DOI:10.1029/94RS00747 |
Druskin V L, Knizhnerman L A, Lee P. 1999. New spectral Lanczos decomposition method for induction modeling in arbitrary 3-D geometry. Geophysics, 64(3): 701-706. DOI:10.1190/1.1444579 |
Güttel S. 2010. Rational Krylov methods for operator functions. [Ph. D. thesis] Technische Universität Bergakademie Freiberg.
|
Haber E, Ruthotto L. 2014. A multiscale finite volume method for Maxwell's equations at low frequencies. Geophysical Journal International, 199(2): 1268-1277. DOI:10.1093/gji/ggu268 |
Jiang Y L. 2010. Model Reduction Method. Beijing: Science Press.
|
Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. DOI:10.1190/1.3058434 |
Knizhnerman L, Druskin V, Zaslavsky M. 2009. On optimal convergence rate of the rational Krylov subspace reduction for electromagnetic problems in unbounded domains. SIAM Journal on Numerical Analysis, 47(2): 953-971. DOI:10.1137/080715159 |
Kong F N, Johnstad S E, Røsten T, et al. 2008. A 2.5 D finite-element-modeling difference method for marine CSEM modeling in stratified anisotropic media. Geophysics, 73(1): F9-F19. DOI:10.1190/1.2819691 |
Li J H, Farquharson C G, Hu X Y, et al. 2016. A vector finite element solver of three-dimensional modelling for a long grounded wire source based on total electric field. Chinese Journal of Geophysics, 59(4): 1521-1534. DOI:10.6038/cjg20160432 |
Li J M. 2005. Geoelectric Field and Electrical Exploration. Beijing: Geological Press.
|
Mittet R, Morten J P. 2013. The marine controlled-source electromagnetic method in shallow water. Geophysics, 78(2): E6-E77. |
Newman G A, Alumbaugh D L. 1995. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophysical Prospecting, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 |
Peng R H, Hu X Y, Han B, et al. 2016. 3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method. Chinese Journal of Geophysics, 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
Plessix R E, Darnet M, Mulder W A. 2007. An approach for 3D multisource, multifrequency CSEM modeling. Geophysics, 72(5): SM177-SM184. DOI:10.1190/1.2744234 |
Routh P S, Oldenburg D W. 1999. Inversion of controlled source audio-frequency magnetotellurics data for a horizontally layered earth. Geophysics, 64(6): 1689-1697. DOI:10.1190/1.1444673 |
Ruhe A. 1994. Rational Krylov algorithms for nonsymmetric eigenvalue problems. //Golub G, Luskin M, Greenbaum A, eds. Recent Advances in Iterative Methods. The IMA Volumes in Mathematics and its Applications. New York, NY: Springer, 149-164.
|
Schenk O, Gärtner K. 2004. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Generation Computer Systems, 20(3): 475-487. DOI:10.1016/j.future.2003.07.011 |
Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy. Geophysics, 74(5): F95-F105. DOI:10.1190/1.3196241 |
Streich R. 2016. Controlled-source electromagnetic approaches for hydrocarbon exploration and monitoring on land. Surveys in Geophysics, 37(1): 47-80. DOI:10.1007/s10712-015-9336-0 |
Tang J T, He J S. 2005. Controlled-Source Audio Magnetotelluric Method and Its Application. Changsha: Central South University Press.
|
Um E S, Commer M, Newman G A. 2013. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the Earth:finite-element frequency-domain approach. Geophysical Journal International, 193(3): 1460-1473. DOI:10.1093/gji/ggt071 |
Weiss C J. 2013. Project APhiD:A Lorenz-gauged A-Φ decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous Earth. Computers & Geosciences, 58: 40-52. |
Xu Z F, Wu X P. 2010. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method. Chinese Journal of Geophysics, 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 |
Yang B, Xu Y X, He Z X, et al. 2012. 3D frequency-domain modeling of marine controlled source electromagnetic responses with topography using finite volume method. Chinese Journal of Geophysics, 55(4): 1390-1399. DOI:10.6038/j.issn.0001-5733.2012.04.035 |
Yin C C, Ben F, Liu Y H, et al. 2014. MCSEM 3D modeling for arbitrarily anisotropic media. Chinese Journal of Geophysics, 57(12): 4110-4122. DOI:10.6038/cjg20141222 |
Zhang Y, Wang H N, Tao H G, et al. 2012. Finite volume algorithm to simulate 3D responses of multi-component induction tools in inhomogeneous anisotropic formation based on coupled scalar-vector potentials. Chinese Journal of Geophysics, 55(6): 2141-2152. DOI:10.6038/j.issn.0001-5733.2012.06.036 |
蒋耀林. 2010. 模型降阶方法. 北京: 科学出版社.
|
李建慧, FarquharsonC G, 胡祥云, 等. 2016. 基于电场总场矢量有限元法的接地长导线源三维正演. 地球物理学报, 59(4): 1521-1534. DOI:10.6038/cjg20160432 |
李金铭. 2005. 地电场与电法勘探. 北京: 地质出版社.
|
彭荣华, 胡祥云, 韩波, 等. 2016. 基于拟态有限体积法的频率域可控源三维正演计算. 地球物理学报, 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
汤井田, 何继善. 2005. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社.
|
徐志锋, 吴小平. 2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 |
杨波, 徐义贤, 何展翔, 等. 2012. 考虑海底地形的三维频率域可控源电磁响应有限体积法模拟. 地球物理学报, 55(4): 1390-1399. DOI:10.6038/j.issn.0001-5733.2012.04.035 |
殷长春, 贲放, 刘云鹤, 等. 2014. 三维任意各向异性介质中海洋可控源电磁法正演研究. 地球物理学报, 57(12): 4110-4122. DOI:10.6038/cjg20141222 |
张烨, 汪宏年, 陶宏根, 等. 2012. 基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应. 地球物理学报, 55(6): 2141-2152. DOI:10.6038/j.issn.0001-5733.2012.06.036 |
 2018, Vol. 61
2018, Vol. 61

