2. 中国石化石油勘探开发研究院油气地球物理中心, 北京 100083
2. Center of Oil/gas Geophysics, Petroleum Exploration and Production Research Institute, SINOPEC, Beijing 100083, China
作为一种非常规油气资源,致密砂岩油气藏与常规砂岩储层在地质特征上有显著不同,具有孔隙结构复杂、非均质性强的特点.岩石内部不同尺度下的非均质性,一般被认为是弹性波在地下介质中传播时发生强烈固有速度频散与能量衰减的主导因素(Carcione and Picotti, 2006;Hefner and Jackson, 2010;Tisato et al., 2014),并且,孔隙结构的非均匀性及孔隙流体对波衰减和速度频散的影响,会随孔隙流体组分含量的变化而发生变化(Sherma et al., 2013).研究致密砂岩弹性波速度频散与能量衰减,可作为开展时频域储层及流体预测的关键性理论基础,同时也是解决不同地球物理测量方法(如地面地震,VSP,测井、超声波岩石观测等)之间数据匹配问题的重要方面.
波激励下诱导的局域流(wave-induced local fluid flow,简称WILFF)被认为是导致含流体岩石中弹性波固有速度频散与能量衰减的重要原因(Johnston et al., 1979;Winkler,1985;Sams et al., 1997;Pride et al., 2004;Ba et al., 2016;Spencer and Shine, 2016).引起局域流的两种类型的岩石非均匀性在前人文献中得到广泛讨论.第一种是孔隙结构的非均匀性,如当压缩波挤压岩石骨架时,孔隙流体将从较软的孔流向较硬的孔隙,引起波弛豫和伴随衰减.第二种是不相混溶流体的斑块非均匀饱和分布,具有相同压缩性但被不同流体饱和的岩石骨架,同样会在波激发下产生压力梯度与松弛效应.
绝大多数前人文献一般只考虑两种非均匀性的一种(杜启振,2007;Ba et al., 2015).Mavko和Nur(1975)通过引入流体填充平面裂纹的模型,调查了与结构非均质性有关的WILFF和非弹性特征.Dvorkin和Nur(1993)提出了Biot/squirt(BISQ)模型,将Biot摩擦机制和喷射流合并到同一组孔隙弹性方程组中.其后,BISQ模型对岩石波速与衰减的预测被证明是适用于声波与超声波频段的(Dvorkin et al., 1994, 1995).杨顶辉和陈小宏(2001)将BISQ模型推广到一般的孔隙各向异性情况,研究了孔隙各向异性介质的固-流耦合效应.邓继新等(2015)根据孔隙微观结构特征对喷射流模型进行了推广.唐晓明(2011)分析了裂隙的喷射流效应,调查了孔隙和裂隙并存情况下的弹性波传播规律.Bordakov等(1999)通过研究认为,BISQ模型不能正确预测Biot慢纵波和快纵波振幅的相对关系.Pride等(2004)提出了双重孔隙介质模型来描述具有中观非均质性岩石中的局域流,其模型中假设尺寸大于岩石粒度,但远小于地震波长的欠固结砂粒骨架被嵌入到砂岩主骨架中.巴晶等(Ba et al., 2011, 2014; 巴晶等,2013)基于哈密顿原理导出了一组双重孔隙介质岩石中的弹性波传播的Biot-Rayleigh方程,进行岩石物理建模,开展了非均质天然气藏的地震预测研究.张琳等(2017)基于Biot-Rayleigh理论方程,分析了地震波激励下,砾岩孔隙区、砂岩孔隙区以及泥岩孔隙区之间的孔隙流体局部流动,推导得出三重孔隙介质的波传播动力学方程.
White等(1975)提出了一种将球形气包嵌入到同心球壳中的斑块状饱和模型,并研究了与斑块状饱和相关的非弹性特征.Dutta和Odé(1979)重新分析了White模型,并得出了数学形式更严格的波动力学方程.Johnson(2001)改进了White模型,从理论上分析了部分饱和多孔岩石的波衰减特征.Pride等(2004)基于双重孔隙介质动力学控制方程模拟了不相混溶流体的斑块饱和特征引起的介观能量损失.Ba等(2015)将Biot-Rayleigh模型从饱和单一流体的双重孔隙介质的情况推广到可同时考虑双孔结构以及斑块状饱和的复杂情况,即双重双重孔隙介质(double double-porosity;DDP)模型.
孔隙结构和斑块状流体分布的两类非均匀性一般在储层岩石中是并存的.对于致密砂岩而言,对这两种非均匀性的重叠效应的进一步研究非常重要,因为在漫长的成藏过程中,此类岩石的低孔低渗特征,更容易诱导岩石内部流体分布的非均质性,造成气水或油水分异不明显.本文将研究利用DDP理论模型针对致密砂岩开展研究,分析预测不同频率、不同饱和度下的纵波波速频散和衰减特征,结合与实验数据的比较分析,调查相关岩石弹性波传播特性,及其与相关非均质性之间的联系.
1 致密砂岩的双双重孔隙介质特征及理论模型描述致密砂岩的孔隙结构具有强非均匀性,即岩石内部的孔隙参数是不均一的,不同形状、不同压缩性与不同渗透率的孔隙被嵌入分布于同一岩石骨架中,形成多重孔隙结构(Pettijohn et al., 1987).岩性、岩相的差异(主要是渗透率)可能会影响地质时间尺度下的流体运移,进一步导致不相混溶流体的斑块饱和与非均匀分布.
DDP模型通过考虑在背景相介质中嵌入不同孔隙度、渗透率和压缩特性的非均质体,形成一个双重孔隙固体骨架,而在此双重孔隙固体中,每一个孔隙固体组分内部还存在着斑块饱和,即含有不相混溶的流体混合物,由于每一个斑块状饱和的多孔固体均可以采用一个次一级的双重孔隙介质模型进行描述,这意味着原有的双重孔隙介质的每一个组分,仍嵌套含有一个次一级的双孔结构,即双重-双重孔隙介质模型.这是一个共含有四种不同孔隙的复合系统.
本文研究主要考虑致密砂岩的微观非均质性,即粒间孔与晶体断裂(晶体接触)组成的微观双孔结构.在此双孔骨架系统中,微裂隙尺寸小,表面不规则,包含少量泥质,由于岩石表面的亲水特性、毛细张力的作用,部分饱和气(油)与水情况下,微裂隙与晶体接触部位一般饱水(Li et al., 2001),而气(油)主要以气包(油包)的形式分布于粒间孔或晶体溶蚀孔中,进而形成部分饱和的复杂系统,而裂隙/接触内部则一般近似完全饱水,忽略其部分饱和的可能性.
1.1 DDP模型对孔隙结构非均匀性及流体饱和非均匀性的统一描述DDP理论模型的波动控制方程是由Hamilton原理推导得出的,可描述双重孔隙结构中含不相混溶流体的非饱和气包,在受到纵波激励下,发生的局域流体流动,即岩石内部的流体的局部胀缩运动.将局部流体流动相互作用并入应变能、动能和耗散能,可基于Biot-Rayleigh方程推导出相应的DDP介质波传播控制方程为(Ba et al., 2017)
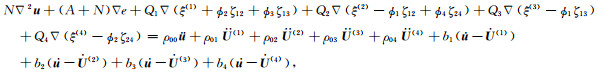
|
(1a) |
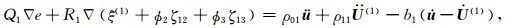
|
(1b) |
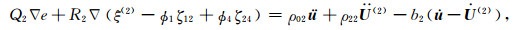
|
(1c) |

|
(1d) |
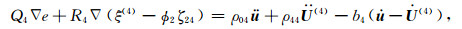
|
(1e) |
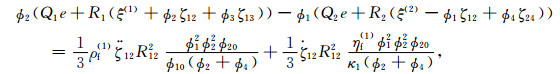
|
(1f) |
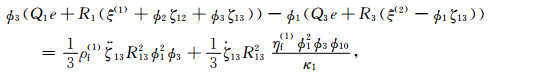
|
(1g) |
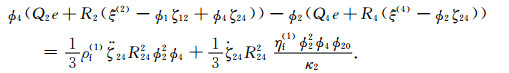
|
(1h) |
式中u, U(1), U(2), U(3)和U(4)分别为固体骨架的平均颗粒位移、流体相1(主体骨架中的主相流体),流体相2(嵌入体骨架中的主体流体),流体相3(主体骨架中的斑块内部流体)和流体相4(嵌入体骨架中的斑块内部流体)的位移;e, ξ(1), ξ(2), ξ(3)和ξ(4)是对应的5个位移散度场;ζ12, ζ13和ζ24表示局域流过程中导致的流体变化量.岩石内部由于孔隙结构的非均匀性发育两类不同孔隙,ϕ10和ϕ20是主体骨架和嵌入体骨架的局部孔隙度;κ1和κ2是主体骨架和嵌入体骨架的渗透率;R12为嵌入体骨架的半径.两种孔隙中的每一种内部,都含有两种不相混溶液体,形成四类流体相.ϕ1, ϕ2, ϕ3和ϕ4是四个流体相的绝对孔隙度.ρf(1)和ηf(1)分别为主骨架的流体密度和主相流体的黏度.R13和R24是气(油)包的半径,b1, b2, b3和b4是Biot耗散系数.
在分析前述含微观非均质性的致密砂岩的模型的过程中,主体骨架即为低孔低渗的致密砂岩主骨架,嵌入体骨架则为局部的晶体微裂隙或颗粒接触形成的软骨架,因此,若考虑亲水性的影响,部分饱和的致密砂岩中微裂隙主要含水,因此模型中的流体相4可以忽略.
1.2 裂隙及流体参数对致密砂岩频散和衰减特征的影响基于DDP理论方程模拟分析致密砂岩的波速频散和衰减特征,根据苏里格气田实际致密岩石样本进行设置(样品S35),模型中岩样的总孔隙度、背景岩石的渗透率为实验室测量值.所采用的干燥岩石模量可通过饱气岩样的纵横波速度基于Gassmann理论求取.岩石内部不同尺度的非均质性造成的不同观测频段的波的频散和衰减,可通过调节理论模型中嵌入体的半径与含量进行解释与描述.
本文在微观尺度合理范围内变换相关参数研究理论预测曲线的变化规律,所采用的模型参数如表 1所示.
|
|
表 1 致密砂岩弹性波响应特征模拟参数表(参考表 2样品S35的参数进行设置) Table 1 Modeling parameters of elastic wave response characteristics in tight sandstone (the parameters are set based on the properties of Sample S35 of Table 2) |
基于理论模型,采用平面波解析解分析方法(巴晶等,2012)进行分析,将平面波解析解代入波传播方程组,求解一元高次方程,取实部最大值为常规纵波相速度,并可计算对应的衰减逆品质因子.图 1给出了致密砂岩中不同流体及流体饱和度对于频散和衰减的影响.

|
图 1 不同流体及饱和度的情况下,致密砂岩中的纵波速度频散曲线(a)及衰减随频率的变化关系(b) Fig. 1 Velocity dispersion curves (a) and attenuation curves (b) as a function of frequency for P-waves in the tight sandstone with different saturating fluids and different saturations |
如图 1a所示的模拟结果包括饱油、饱水、饱气的三组频散曲线,油、水、气三者黏度不同,黏度越大,频散开始出现的频率越低,黏度越小,则出现的频率越高.油的黏度最大,频散最低出现于103~104 Hz范围内,是由岩石结构的非均质性引起的.图 1b显示:致密砂岩饱水、饱油、饱气三种情况下,衰减的峰值频率及衰减幅度均有差异,饱油情况下峰值频率最低,且衰减幅度最大,饱气衰减幅度最低.部分饱和气、水情况下,速度频散曲线上出现两个频散拐点,对应的衰减曲线上出现两个衰减峰值,其中较低频段内的拐点与较强峰值对应于斑块状饱和造成的非弹性,而超声频段出现的拐点与峰值则对应于岩石结构的非均质性(颗粒接触;颗粒断裂).
图 2a分析了完全饱和水的情况下,嵌入体骨架的体积比率对于致密砂岩频散及衰减特征的影响.首先嵌入体体积比率影响了频散的强度,嵌入体体积比率越大,频散越强,对应的衰减峰值也更强.如图 2b所示,嵌入体体积比率越大,衰减峰值还有略往高频端移动的趋势.

|
图 2 致密砂岩嵌入体骨架的体积比率对波速频散曲线(a)及衰减曲线(b)的影响 Fig. 2 Effects of volume ratio of inclusion solid matrix on velocity dispersion curves (a) and attenuation curves (b) versus frequency in the tight sandstone |
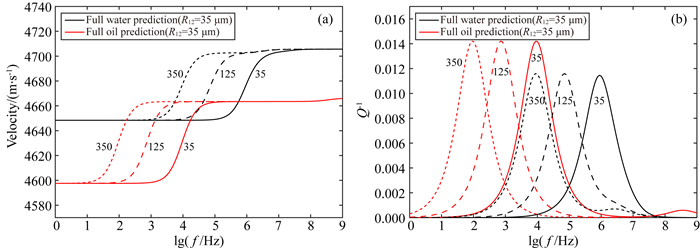
图 3给出了嵌入体半径对于致密砂岩波速频散、衰减的影响的分析结果.如图 3a、3b所示,嵌入体骨架的半径影响频散、衰减出现的特征频率,嵌入体半径越大,频散出现的频率越低,嵌入体尺寸减小,则频散拐点向高频方向移动.结果显示这种岩性非均质性的尺寸变化,并不会影响频散的强度及衰减的强度.
|
图 3 嵌入体骨架半径对频散曲线(a)及衰减曲线(b)的影响 Fig. 3 Effects of radius of inclusion solid matrix on velocity dispersion curves (a) and attenuation curves (b) versus frequency in the tight sandstone |
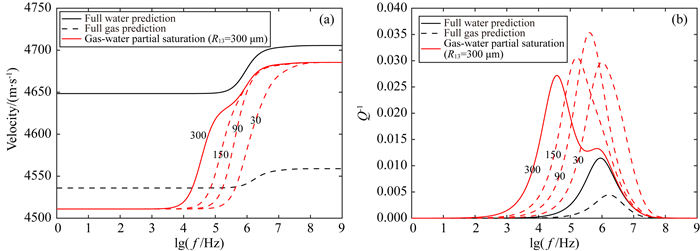
如图 4、图 5所示,分别给出了致密砂岩中主体岩石骨架内部的部分饱和斑块半径分别对气/水、油/水部分饱和情况下波速频散和衰减的影响的分析结果.对于气/水部分饱和情况(图 4),斑块尺寸大小直接影响频散曲线形态及频散拐点出现的频率,斑块越大,由于两种非均质性(岩石结构、斑块状饱和)并存导致的频散曲线上的两个拐点的特征越明显,并且对应于斑块状饱和的拐点所出现的频率越低,这是由于在模拟计算过程中固定了颗粒断裂、颗粒接触的非均质性尺度,而仅改变了斑块状饱和的气包尺寸的缘故.衰减曲线中随着斑块尺寸的减小,具有双峰值的衰减曲线逐渐融合为一个单峰值的曲线,并且最大衰减峰值有所增强.
|
图 4 致密砂岩主体岩石骨架中部分饱和的斑块半径对波速频散(a)及衰减(b)规律的影响(气/水部分饱和情况) Fig. 4 Effects of pocket radius of patchy-saturation in the host matrix on dispersion curves (a) and attenuation curves (b) versus frequency in the tight sandstone (gas-water partial saturation case) |
|
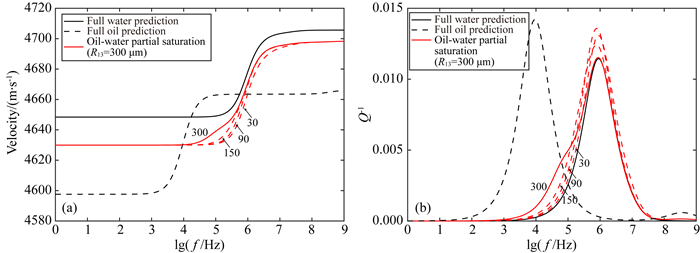
图 5 致密砂岩主体岩石骨架中部分饱和的斑块半径对波速频散(a)及衰减(b)规律的影响(油/水部分饱和情况) Fig. 5 Effects of pocket radius of patchy-saturation in the host matrix on dispersion curves (a) and attenuation curves (b) versus frequency in the tight sandstone (oil-water partial saturation case) |
对于油/水部分饱和情况(图 5),与气/水部分饱和曲线在总体规律与趋势上有相似性,但相关变化特征很不明显.油/水部分饱和曲线上由斑块状饱和造成的频散及衰减强度很弱,这主要是由于油、水两种流体之间的物理性质(特别是可压缩性)比较接近,在波激励下可能造成的局部耗散要明显弱于气/水部分饱和情况,因此此类情况下,非弹性及衰减特征可能更多的是由岩性非均质性所主导.
2 致密砂岩样本频散及衰减规律分析 2.1 岩石物理实验过程及样品相关情况本研究考虑来自鄂尔多斯盆地苏里格气田和川中须家河组气层的两个典型低孔、低渗致密砂岩气藏的岩芯,对其超声波实验数据进行对比、分析.苏里格气田的致密砂岩数据来自公开发表的结果(王大兴,2016).选取了该气田上古生界二叠系石河子组盒8段17口井的28块岩样超声波实验数据,共304组不同孔隙度、不同含水饱和度下对应的纵波速度、横波速度及弹性参数.实验设置、实验条件、实验方案与文献(伍向阳等,2000;王大兴等,2006)所采用的基本一致.实验采取的地层条件为温度105 ℃、压力29 MPa.采用超声波脉冲透射法(频率1 MHz).
盒8下段为分流河道沉积砂岩,以石英砂岩为主,填隙物以高岭石、硅质和伊利石为主,孔隙类型以次生溶孔为主.砂岩碎屑颗粒磨圆度主要为次棱状,其次是次棱-次圆状,分选较好,主要呈颗粒支撑,颗粒间以线接触为主,少量为点-线接触或凹凸接触.样品参数如表 2所示,将样品按孔隙度分为三组:孔隙度 < 5%;孔隙度5%~10%;孔隙度>10%.如表 2所示,样品序号前署S字母,表示苏里格气田的样本数据.
|
|
表 2 里格致密气砂岩物性参数(王大兴,2016) Table 2 Physical properties of Sulige tight gas sandstones(Wang, 2016) |
第二组数据来自四川盆地广安气田上三叠统须家河组致密砂岩储层,共选取10块岩样,主要为岩屑砂岩,颗粒间结晶胶结物为方解石胶结和石英次生胶结,有裂隙发育,具体物性参数如表 3所示.实验设置、实验条件、实验方案与文献(Yan等,2011)采用的一致.实验条件为温度22 ℃,有效压力35 MPa.同样将样品孔隙度分为三组:孔隙度 < 5%;孔隙度5%~10%;孔隙度>10%.如表 3所示,样品序号前署GA字母,表示广安数据.
|
|
表 3 广安致密气砂岩物性参数(来自岩石物理测试) Table 3 Physical properties of Guang′an tight gas sandstones(From rock physics experiments) |
在本文调查的致密砂岩样品中,苏里格样品石英含量较高,一般达到90%以上,岩屑次之(平均18.7%),长石含量极少(小于1%).广安样品石英含量在70%以上,以中粒石英为主,呈次棱-次圆状,含少量长石(约5%)及云母等其他矿物(小于1%).考虑致密砂岩的矿物组分为石英、泥质,岩石内部发育双重孔隙结构,即主骨架中普遍含有的粒间孔及由颗粒断裂或接触组成的软孔隙.主骨架孔隙中的主体流体为水,并含有斑块状饱和的气包,嵌入体骨架由于亲水作用而完全饱和水.采用DDP模型计算了相关样品的速度频散和衰减预测结果.在饱和一种流体情况下,频散曲线预测超声频段纵波速度与实验测量纵波速度基本吻合,部分岩样频散曲线预测超声频段纵波速度与实验测量纵波速度差异小于±5 m·s-1.表 4给出了来自苏里格样品及广安样品的三个不同孔隙度范围内的12块样品的相关模拟参数.孔隙度低于5%的第一组样品中(S5、S65、GA3、GAR1),S5与GA3孔隙度接近,S65与GAR1接近;第二组样品中,S150与GAR6接近,S6与GA8接近,S64与GAR2接近;第三组样品中,S68与GA1接近.
|
|
表 4 部分致密气砂岩样品的相关模拟参数(苏里格数据来自发表数据(王大兴,2016),广安数据来自所开展的岩石物理测试) Table 4 Relevant modeling parameters of the selected gas sandstones specimens (Sulige data are from the published data (Wang, 2016); Guang′an data are from the performed rock physics experiments) |
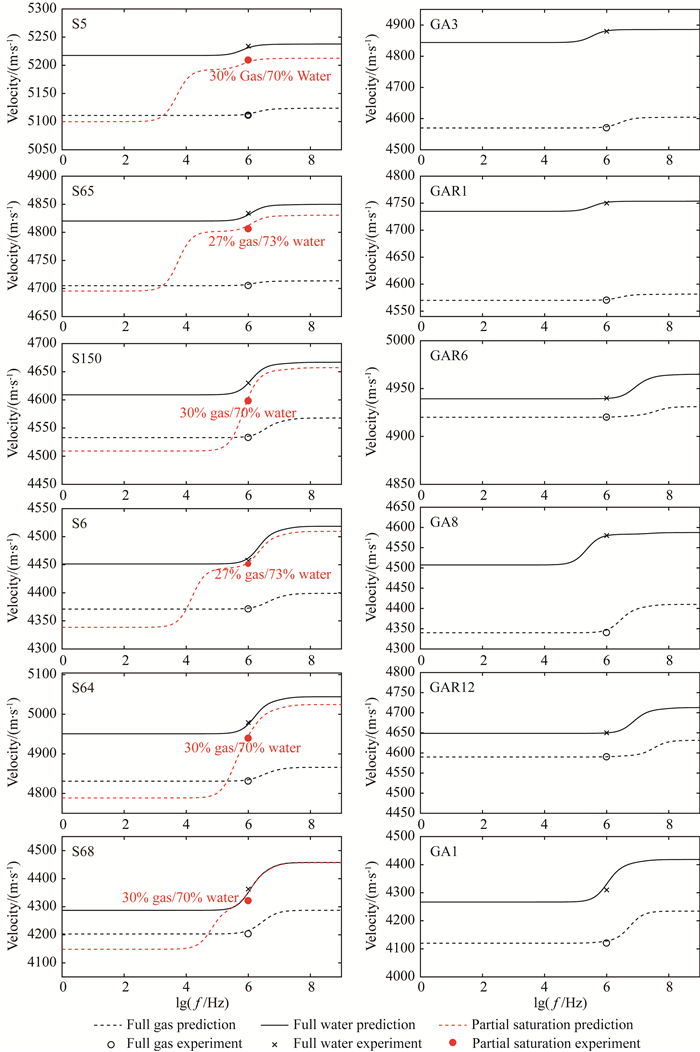
据表 1、2、3,对比两个地区目的层的典型砂岩,可知在所选样本中,广安致密砂岩相对于苏里格,总体上渗透率较低.由图 6所示,随着孔隙度增加,致密砂岩的波速频散明显呈增大的趋势.苏里格样本中,随着孔隙度增加,由气/水斑块状饱和引起的频散拐点有向高频端移动的趋势,部分情况下(样本S150、S64、S68)频率轴上的两个频散“台阶”有趋于合并的趋势,这意味着分别由孔隙结构非均匀性、流体饱和非均匀性所导致的局部流效应出现了一定程度的耦合.
|
图 6 致密砂岩纵波速度分析结果与实验数据的对比 Fig. 6 Comparisons between theoretical analysis results of P-wave velocity and experimental data in tight sandstones |
孔隙度相近的岩样,渗透率、结构的不同会在速度频率和衰减特征上造成较大差异.样品S65和GAR1孔隙度均在4.2%左右,但GAR1渗透率极低,两块样品在频散曲线规律上有明显不同.饱水状态下,GAR1处于未松弛的硬化状态下,即波速接近处于频散“台阶”上限,而S65在饱水状态下处于部分松弛状态.GAR1的频散特征与GA3接近,而部分饱和气、水情况下,S65处于斑块状饱和的硬化状态及结构非均质性的松弛状态下,与S6、S68相似,却明显与S5不同,S5在部分饱和情况下处于结构非均质性局域流诱导的硬化状态下.S150、S64的结果中,两组频散机制形成的曲线基本呈合并趋势.第一组样品(孔隙度 < 5%)在完全饱水情况下除S65外均处于局域流的完全硬化状态,S65渗透率较高,导致了结构局域流的部分松弛,从而使得速度下降.在第二组样品(孔隙度5%~10%)、第三组样品(孔隙度>10%)中,两个地区的样品在饱水情况下基本处于松弛或部分松弛状态下,仅有GAR1和GA8比较特殊,GAR1是由于其极低的渗透率导致频散拐点向频率轴左端移动所导致,而GA8的相关特征可能与其内部的岩性非均质性尺寸有关.
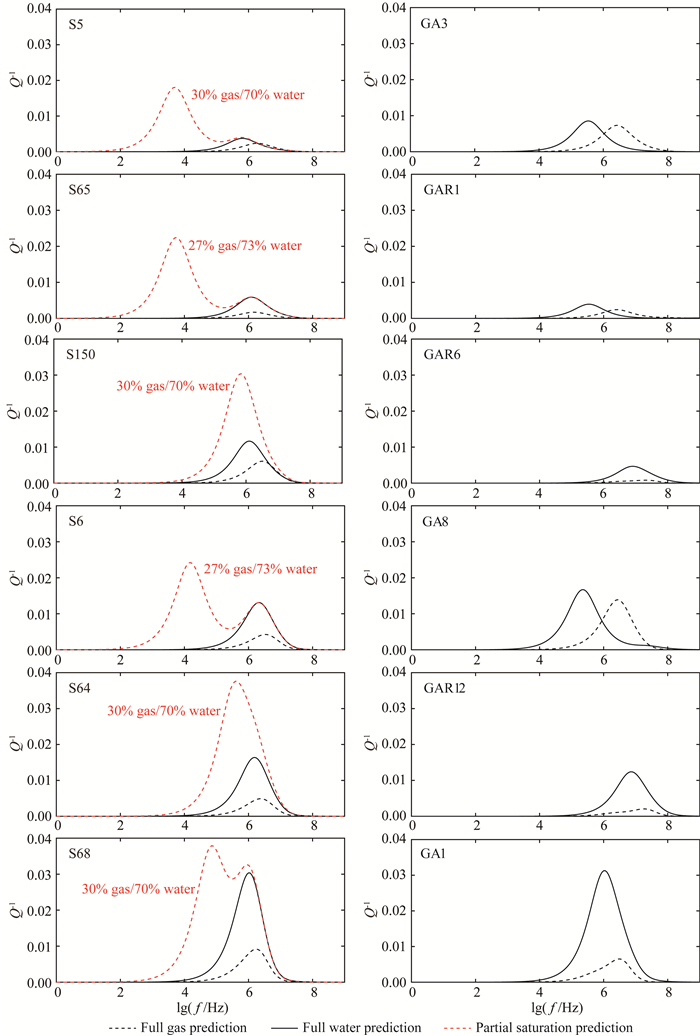
图 7对应于图 6给出了10块样本的纵波衰减随频率的变化关系.所有结果中,斑块状饱和所导致的纵波衰减均要明显强于结构非均质性所导致的纵波衰减,并且斑块状饱和所导致的衰减与结构所造成的衰减相比,出现于相对较低的频段.完全含水情况下的纵波衰减明显高于完全含气情况下的纵波衰减.随着孔隙度增大,两类机制所造成的衰减都有逐渐增强的趋势,其中由结构非均质性导致的衰减随孔隙度上升而增加的趋势更为明显,一个明显的现象是,对比第一组、第二组与第三组,孔隙度越大,在部分饱和岩石中,斑块状饱和对总衰减的贡献越低,而岩性、结构非均质性造成的衰减所占的比重越大.苏里格样本在部分饱和情况下,衰减曲线的双峰值特征非常明显,但部分样本如S150、S64中,两个衰减峰有合并以及产生一个更强的衰减峰的趋势,这与这些样本的孔渗性质以及结构特征是相关的.
|
图 7 致密砂岩的纵波衰减分析结果 Fig. 7 Theoretical analysis results of P-wave attenuation in tight sandstones |
对广安地区相关样本没有开展变饱和度情况下的超声波实验测试.图 8给出了基于DDP模型预测的苏里格样本中的纵波速度随饱和度的变化规律曲线,并给出了实验测量结果.仍采用平面波解析解分析方法求解式(1),采用的模型参数具体如表 1、表 3所示.图 8给出的相关DDP模型预测结果与各块样本的实测结果均可较好的吻合,样本S6、S64在中间饱和度范围内(40%~60%)的模型预测结果低于实测结果,这是由于这两块样本孔渗条件较好,在中间饱和度范围内主骨架内部可能形成了尺度较大的气包,从而造成频散拐点向低频端移动,以至于在超声频段内岩石呈现的是较硬的未松弛状态,高于理论模型的预测速度.

|
图 8 致密砂岩纵波速度随饱和度的变化关系曲线与实测结果对比 Fig. 8 Comparisons between theoretical prediction curves of P-wave velocity versus saturation and measured data in tight sandstones |
(1) 双重孔隙结构
针对苏里格与广安共36块砂岩开展了双双孔模型分析.其中,干岩样体积模量和剪切模量根据完全饱和状态下所测得的波速计算得到,破裂颗粒及颗粒接触体积模量取为8 GPa,矿物密度(纯石英)为2.65 g·cm-3,颗粒模量(Ks)为39 GPa.初始颗粒接触的孔隙度为ϕ20=0.09,如果矿物颗粒假设为主轴长度为140 μm的圆柱体,存在平均有效半径为10~15 μm的横向裂隙,颗粒中平均裂隙孔隙度大约为0.09.
嵌入体体积模量与背景介质体积模量比:
如图 9所示,色标给出的是嵌入体骨架体积模量与主骨架体积模量的比值.由于在相同孔隙度下,致密砂岩的主骨架体积模量变化范围不大,因此该数值的物理含义是岩石内部的颗粒接触、颗粒裂缝的柔软程度,这个数值越低,裂缝越软,且更易压.结果显示,该数值较大的岩样基本集中于低孔隙度范围内速度相对较低的一些样本.广安须家河致密砂岩样本相对于苏里格样本,其裂缝整体相对较硬.

|
图 9 苏里格气田28块岩样(圆形散点)与广安气田10块岩样(方形散点)的孔隙度-速度交会图(色标给出了嵌入体骨架与主骨架的体积模量比值) Fig. 9 Crossplot of porosity and P-wave velocity for the 28 specimens from Sulige gas field (circles) and the 10 specimens of Guang′an gas field (squares). The colorbar indicates the bulk modulus radio of the inclusion matrix and the host matrix |
(2) 孔隙含量
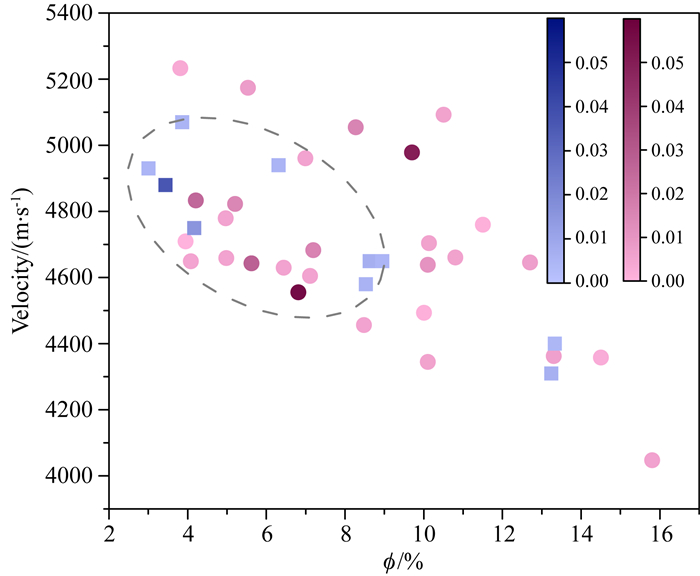
如图 10所示,色标给出的是破裂/接触颗粒与总的骨架颗粒的体积比率.该数值的物理含义是岩石内部的微裂隙/颗粒接触的体积含量.结果显示,低孔隙度范围内,裂缝的体积含量相对较高,这与致密砂岩的成岩机制、压实过程有关,若在压实过程中导致孔隙度降低,更易产生线接触、面接触以及颗粒断裂,形成易压的扁平状裂隙或孔隙.
|
图 10 苏里格气田28块岩样(圆形散点)与广安气田10块岩样(方形散点)的孔隙度-速度交会图(色标给出了破裂颗粒与总的骨架颗粒的体积比率) Fig. 10 Crossplot of porosity and P-wave velocity for the 28 specimens from Sulige gas field (circles) and the 10 specimens of Guang′an gas field (squares). The colorbar indicates the radio of volume of fractured grains and total grain volume |
(3) 结构非均质性尺度
嵌入体骨架半径R12为石英颗粒破裂或接触形成的与主骨架介质孔隙度、压缩性不同的嵌入体的有效半径,其物理意义指示的是裂隙、接触的尺度.如图 11所示,整体趋势是孔隙度越高的致密砂岩,其内部微裂隙的尺度越大,这些岩石速度较低、衰减较强.孔隙度较高的致密砂岩一般含较大的矿物颗粒,无论分选好坏与否,更倾向于发育更大的颗粒接触面.

|
图 11 苏里格气田28块岩样(圆形散点)与广安气田10块岩样(方形散点)的孔隙度-速度交会图(色标给出的是嵌入体骨架半径,单位μm) Fig. 11 Crossplot of porosity and P-wave velocity for the 28 specimens from Sulige gas field (circles) and the 10 specimens of Guang′an gas field (squares). The colorbar indicates the inclusion matrix radius (μm) |
如前述致密砂岩的结构非均匀性,尤其是孔、渗条件的空间非均匀性,可导致储层不相混溶流体的进一步非均匀分布.考虑含水的主骨架中局部分布有气包,假设软裂隙/接触中饱和水.空气密度和体积模量分别为0.16 g·cm-3、0.063 GPa,水密度和模量分别为0.97 g·cm-3、2.49 GPa(温度105 ℃、压力29 MPa).
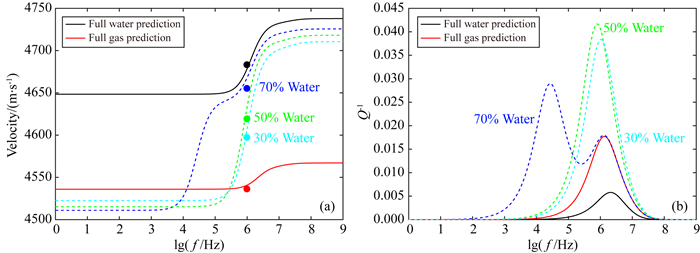
图 12给出了基于模型预测的致密砂岩纵波速度及衰减随频率的变化关系.由于两类非均质性的叠加影响,致密砂岩纵波频散与衰减主要发生的频率范围是103~107 Hz.以30%含气、70%含水的部分饱和情况为例,主骨架粒间孔中的主流体为水,而颗粒裂隙/接触中完全饱水.裂隙/接触的喷射流及粒间孔内部的斑块饱和之间存在耦合效应,导致了超声波、声波频段的两个对应衰减峰.随着含水饱和度的下降,两个频散台阶/衰减峰趋向于合并为一个.波的频散与衰减由孔隙结构及流体分布非均匀性共同控制.致密砂岩在完全饱气状态下表现出微弱频散和衰减.此外,部分饱和状态下,耦合局域流引起的波频散/衰减所发生的频带要宽于完全饱和一种流体的状态.从图 12a可知,不同饱和度下的频散和衰减的预测结果,基本与实验观测结果吻合.
|
图 12 基于DDP模型预测的样品S35纵波速度(a)及衰减(b) Fig. 12 P-wave velocity (a) and attenuation (b) in specimen S35 predicted by the DDP model |
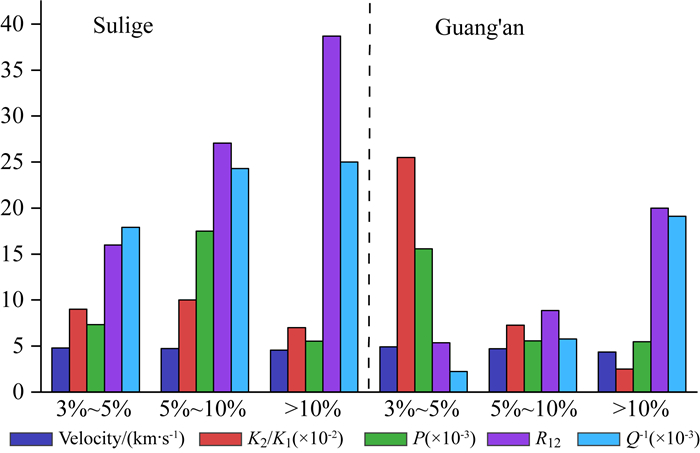
基于以上研究及分析结果,根据岩石结构参数及两个地区低孔、低渗致密砂岩样本的超声波实验数据的对比分析,如图 13所示给出了特征结果.对比三个孔隙度范围内的统计结果显示,纵波速度随孔隙度上升有减小趋势,相对而言,衰减随孔隙度增加而增加的趋势尤为明显.对比苏里格与广安的统计数据,四川盆地广安须家河的致密砂岩由于较低的渗透率,在孔隙度小于10%的范围内衰减很低,但当孔隙度增大后,衰减统计值有大幅度提高.破裂颗粒与主骨架的模量比(K2/K1)随孔隙度上升而下降,这意味着孔隙度越大的岩石,内部更容易发育更为扁平、更为易压、更容易松弛的裂隙或较大裂缝,这一点,从裂缝颗粒半径(R12)随孔隙度增大而显著增大的统计趋势上也可以清晰观察到.须家河组致密砂岩裂隙颗粒含量(P)随孔隙度上升显著减小,而苏里格致密砂岩在孔隙度5%~10%范围内微裂隙含量最高.
|
图 13 苏里格样品和广安样品的纵波速度、衰减(Q-1)、裂隙/接触与主骨架体积模量比(K2/K1)、裂隙颗粒体积比率(P)、裂隙颗粒半径(R12)在不同孔隙度区间内的分布直方图 Fig. 13 Statistical distribution histograms of P-wave velocity, P-wave attenuation (Q-1), bulk modulus radio of crack/contact matrix and host matrix (K2/K1), volume ratio of cracked grains (P), and radius of cracked grains (R12) in the different porosity ranges |
对比两个区块的致密砂岩,广安须家河组致密砂岩在孔隙度 < 5%范围内含有更多的微裂隙,但微裂隙相对比苏里格致密砂岩要“硬”.在孔隙度5%~10%范围内,苏里格样本微裂隙/接触含量最高.与苏里格样本相比,广安样本中裂隙的可压缩性随孔隙度上升而上升的趋势要明显得多,而在各个孔隙度范围内,苏里格样本的裂隙尺寸要明显大于广安样本.综上所述,广安致密砂岩在低孔隙度范围内,裂隙或扁平孔隙发育更多、更小,这样的小裂隙可压缩性相对较低,而苏里格致密砂岩发育更大的裂隙,且更为易压,这些差异性特点,是与两个地区目的层所具有的不同埋深、结构、粒径、成因等综合地质特征相关的.
3 结论致密砂岩的低孔、低渗特征可进一步诱导孔隙内部不相混溶流体的非均质分布,从而导致两种非均质性的并存,在岩石物理理论及实验研究中,必须调查二者的影响和相互耦合关系.本文采用双重双重孔隙介质模型分析了这种复杂的原位储层中的纵波传播和耗散规律,调查了两种非均质性耦合效应对波传播的影响.苏里格石盒子组和川中须家河组都是典型的低孔渗致密砂岩,属于我国西部重点勘探层系,普遍发育有气藏群构成的大气区.采用了苏里格石盒子组和川中须家河组的致密砂岩实验数据,两组岩样都是典型低孔渗致密砂岩,所属储层属于中国西部重点勘探层系,普遍发育有气藏群构成的大气区.基于理论模型对研究层系典型致密砂岩的实验结果开展分析,结果表明:
受不同性质流体的影响,频散曲线拐点出现的频率与流体黏度有关,黏度越大,拐点出现的频率越低.部分饱和气、水的致密砂岩,其频散曲线可能出现两个拐点,一般情况下,出现于较低频段的拐点对应于斑块状饱和所造成的弛豫效应.对于频散曲线出现的每个拐点,在纵波衰减曲线上存在相应频率的衰减峰值.在部分孔、渗条件比较好的致密砂岩中,两类非均质性诱发的局域流耗散机制趋向于发生耦合,对应的两个衰减峰有合并为一个更强峰值的趋势.
致密砂岩的嵌入体骨架的体积率影响了频散强度,该体积率越大,频散幅值越强.并且,伴随着嵌入体体积率的增大,波的衰减增强,频率轴上衰减曲线的峰值有向高频端移动的趋势.斑块尺寸影响了频散曲线形态及频散拐点出现的频率,斑块越大,因两种非均质性导致的频散曲线上的双拐点现象越明显,且最初拐点出现的频率越低.
将苏里格、广安两个地区的致密砂岩超声波实验测试数据按孔隙度 < 5%、5%~10%、>10%对应划分为第一组、第二组、第三组进行模型分析.第一组样品在完全饱水情况下主要处于局域流的完全硬化状态.第二组、第三组样品在饱水情况下大部分处于松弛或部分松弛的状态,其中有两块样品由于内部复杂结构的影响,导致可能处于非松弛状态.在所有样品中,斑块状饱和导致的纵波衰减明显强于结构非均质性所导致的衰减,并且前者一般出现于相对低的频段.随着孔隙度增大,两类机制所造成的衰减都有增强趋势.所有的分析结果均显示,孔隙度越大,部分饱和岩石中斑块状饱和机制对总衰减的贡献越低,而结构非均质性所占的比重则逐渐增强.
两个区块致密砂岩分析结果的对比揭示,在各孔隙度范围内,苏里格样本的裂隙尺寸都要明显大于广安样本.广安致密砂岩在低孔隙度范围内发育了更多的、更小的颗粒裂隙/接触,在相同情况下,苏里格致密砂岩裂隙尺度更大,更为易压.广安致密砂岩由于渗透率低,在低孔隙度范围内衰减较低,而微裂隙含量随孔隙度上升显著减小;苏里格致密砂岩则在孔隙度5%~10%范围内含有最高的微裂隙含量.
附录A 理论模型有关系数式(1)共含9个密度系数(ρ00,ρ01,ρ02,ρ03,ρ04,ρ11,ρ22,ρ33和ρ44)和10个需要确定的弹性系数.密度系数可根据Biot(1962)(单孔介质)和Ba等(2011)(双孔介质)确定:
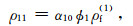
|
(A1) |
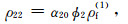
|
(A2) |
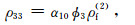
|
(A3) |
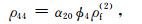
|
(A4) |
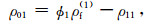
|
(A5) |
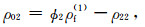
|
(A6) |
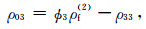
|
(A7) |
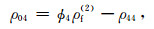
|
(A8) |
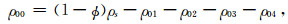
|
(A9) |
式中,ϕ是总孔隙度,ρs是固体密度,α10和α20是主体骨架和夹杂物中孔隙的弯曲度.部分饱和的致密砂岩由于假设裂隙完全饱和水,因此第四类孔隙度ϕ4为0,其余孔隙度为ϕ1=(ϕ-p(1-ϕ)ϕ20)S1,ϕ2=p(1-ϕ)ϕ20,ϕ3=(ϕ-p(1-ϕ)ϕ20)(1-S1),其中S1为含水饱和度.
各弹性系数可按如下方法确定(Johnson,1986;Ba et al., 2011):

|
(A10) |
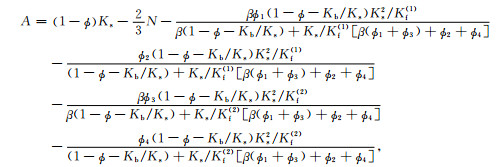
|
(A11) |
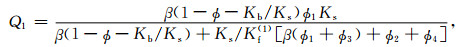
|
(A12) |
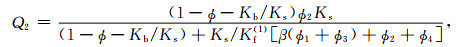
|
(A13) |
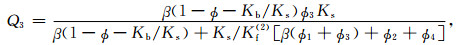
|
(A14) |

|
(A15) |
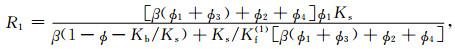
|
(A16) |
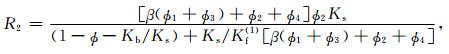
|
(A17) |
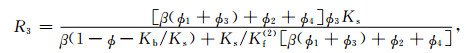
|
(A18) |
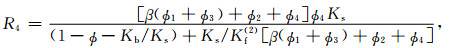
|
(A19) |
式中μb是干岩石骨架剪切模量,Ks是固体颗粒体积模量,Kb是干岩石骨架体积模量,Kf(1)和Kf(2)别是主相流体和斑块内流体的体积模量,β可根据Ba等(2011)式(40)得到.
致谢谨此祝贺姚振兴先生从事地球物理教学科研工作60周年.
Ba J, Carcione J M, Nie J.
2011. Biot-Rayleigh theory of wave propagation in double-porosity media. Journal of Geophysical Research:Solid Earth, 116(B6): B06202.
DOI:10.1029/2010JB008185 |
|
Ba J, Carcione J M, Cao H, et al.
2012. Velocity dispersion and attenuation of P waves in partially-saturated rocks:Wave propagation equations in double-porosity medium. Chinese Journal of Geophysics (in Chinese), 55(1): 219-231.
DOI:10.6038/j.issn.0001-5733.2012.01.021 |
|
Ba J, Yan X F, Chen Z Y, et al.
2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs. Chinese Journal of Geophysics (in Chinese), 56(5): 1696-1706.
DOI:10.6038/cjg20130527 |
|
Ba J, Zhang L, Sun W T, et al.
2014. Velocity field of wave-induced local fluid flow in double-porosity media. Science China Physics, Mechanics & Astronomy, 57(6): 1020-1030.
|
|
Ba J, Carcione J, Sun W T.
2015. Seismic attenuation due to heterogeneities of rock fabric and fluid distribution. Geophysical Journal International, 202(3): 1843-1847.
DOI:10.1093/gji/ggv255 |
|
Ba J, Zhao J G, Carcione J M, et al.
2016. Compressional wave dispersion due to rock matrix stiffening by clay squirt flow. Geophysical Research Letters, 43(12): 6186-6195.
DOI:10.1002/2016GL069312 |
|
Ba J, Xu W H, Fu L Y, et al.
2017. Rock anelasticity due to patchy saturation and fabric heterogeneity:A double double-porosity model of wave propagation. Journal of Geophysical Research:Solid Earth, 122(3): 1949-1976.
|
|
Biot M A.
1962. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 33(4): 1482-1498.
DOI:10.1063/1.1728759 |
|
Bordakov G A, Il'yasov K K, Sekerzh-Zenkovitch S Y, et al. 1999. Wave refraction with a porous plate in liquid-Comparison of Biot's and BISQ theories.//61st EAEG International Meeting. Expanded Abstracts, 2-3.
|
|
Carcione J M, Picotti S.
2006. P-wave seismic attenuation by slow-wave diffusion:Effects of inhomogeneous rock properties. Geophysics, 71(3): O1-O8.
DOI:10.1190/1.2194512 |
|
Deng J X, Zhou H, Wang H, et al.
2015. The influence of pore structure in reservoir sandstone on dispersion properties of elastic waves. Chinese Journal of Geophysics (in Chinese), 58(9): 3389-3400.
DOI:10.6038/cjg20150931 |
|
Du Q Z, Liu L L, Sun J B.
2007. Numerical modeling of seismic wavefield in anisotropic viscoelastic porous medium with the pseudo-spectal method. Acta Physica Sinica (in Chinese), 56(10): 6143-6149.
|
|
Dutta N C, Odé H.
1979. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model)-Part Ⅰ:Biot theory. Geophysics, 44(11): 1777-1788.
DOI:10.1190/1.1440938 |
|
Dvorkin J, Nur A.
1993. Dynamic poroelasticity:A unified model with the Squirt and the Biot mechanisms. Geophysics, 58(4): 524-533.
DOI:10.1190/1.1443435 |
|
Dvorkin J, Nolen-Hoeksema R, Nur A.
1994. The Squirt-flow mechanism:Macroscopic description. Geophysics, 59(3): 428-438.
DOI:10.1190/1.1443605 |
|
Dvorkin J, Mavko G, Nur A.
1995. Squirt flow in fully saturated rocks. Geophysics, 60(1): 97-107.
DOI:10.1190/1.1443767 |
|
Hefner B T, Jackson D R.
2010. Dispersion and attenuation due to scattering from heterogeneities of the frame bulk modulus of a poroelastic medium. The Journal of the Acoustical Society of America, 127(6): 3372-3384.
DOI:10.1121/1.3365316 |
|
Johnson D L.
2001. Theory of frequency dependent acoustics in patchy-saturated porous media. Journal of the Acoustical Society of America, 110(2): 682-694.
DOI:10.1121/1.1381021 |
|
Johnston D H, Toksöz N M, Timur A.
1979. Attenuation of seismic waves in dry and saturated rocks:Ⅱ. Mechanisms. Geophysics, 44(4): 691-711.
DOI:10.1190/1.1440970 |
|
Li X, Zhong L R, Pyrak-Nolte L J.
2001. Physics of Partially saturated porous media:residual saturation and Seismic-wave propagation. Annual Review of Earth and Planetary Sciences, 29(1): 419-460.
DOI:10.1146/annurev.earth.29.1.419 |
|
Mavko G M, Nur A.
1975. Melt squirt in the asthenosphere. Journal of Geophysical Research, 80(11): 1444-1448.
DOI:10.1029/JB080i011p01444 |
|
Pettijohn F J, Potter P E, Siever R. 1987. Sand and Sandstone. 2nd ed. Berlin:Springer-Werlag.
|
|
Pride S R, Berryman J G, Harris J M.
2004. Seismic attenuation due to wave induced flow. Journal of Geophysical Research, 109(B1): B01201.
DOI:10.1029/2003JB002639 |
|
Sams M S, Neep J P, Worthington M H, et al.
1997. The measurement of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 62(5): 1456-1464.
DOI:10.1190/1.1444249 |
|
Sharma R, Prasad M, Batzle M, et al.
2013. Sensitivity of flow and elastic properties to fabric heterogeneity in carbonates. Geophysical Prospecting, 61(2): 270-286.
DOI:10.1111/gpr.2013.61.issue-2 |
|
Spencer J W Jr, Shine J.
2016. Seismic wave attenuation and modulus dispersion in sandstones. Geophysics, 81(3): D211-D231.
DOI:10.1190/geo2015-0342.1 |
|
Tang X M.
2011. A unified theory for elastic wave propagation through porous media containing cracks-An extension of Biot's poroelastic wave theory. Science China Earth Sciences, 54(9): 1441-1452.
DOI:10.1007/s11430-011-4245-7 |
|
Tisato N, Quintal B, Chapman S, et al.
2014. Seismic attenuation in partially saturated rocks:Recent advances and future directions. The Leading Edge, 33(6): 640-646.
DOI:10.1190/tle33060640.1 |
|
Wang D X.
2016. Study on the rock physics model of gas reservoirs in tight sandstone. Chinese Journal of Geophysics (in Chinese), 59(12): 4603-4622.
DOI:10.6038/cjg20161222 |
|
Wang D X, Xin K F, Li Y M, et al.
2006. An experimental study of influence of water saturation on velocity and attenuation in sandstone under stratum conditions. Chinese Journal of Geophysics, 49(3): 908-914.
DOI:10.3321/j.issn:0001-5733.2006.03.037 |
|
White J E.
1975. Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics, 40(2): 224-232.
DOI:10.1190/1.1440520 |
|
White J E, Mikhaylova N G, Lyakhovitskiy F M.
1975. Low-frequency seismic waves in fluid saturated layered rocks. The Journal of the Acoustical Society of America, 57(S30): 654-659.
|
|
Winkler K W.
1985. Dispersion analysis of velocity and attenuation in Berea sandstone. Journal of Geophysical Research:Solid Earth, 90(B8): 6793-6800.
DOI:10.1029/JB090iB08p06793 |
|
Wu X Y, Chen Z A, Wei J X.
2000. A technique for measuring ultrasonic elocity and attenuation spectra. Chinese Journal of Rock Mechanic and Engineering (in Chinese), 19(S1): 895-898.
|
|
Yan X F, Yao F C, Cao H, et al.
2011. Analyzing the mid-low porosity sandstone dry frame in central Sichuan based on effective medium theory. Applied Geophysics, 8(3): 163-170.
DOI:10.1007/s11770-011-0293-1 |
|
Yang D H, Chen X H.
2001. BISQ model for fluid-filled, porous medium. Oil Geophysical Prospecting, 36(2): 146-159.
|
|
Zhang L, Ba J, Yin W, et al.
2017. Seismic wave propagation equations of conglomerate reservoirs:A triple-porosity structure model. Chinese Journal of Geophysics (in Chinese), 60(3): 1073-1087.
DOI:10.6038/cjg20170320 |
|
巴晶, CardioneJ M, 曹宏, 等.
2012. 非饱和岩石中的纵波频散与衰减:双重孔隙介质波传播方程. 地球物理学报, 55(1): 219–231.
DOI:10.6038/j.issn.0001-5733.2012.01.021 |
|
巴晶, 晏信飞, 陈志勇, 等.
2013. 非均质天然气藏的岩石物理模型及含气饱和度反演. 地球物理学报, 56(5): 1696–1706.
DOI:10.6038/cjg20130527 |
|
邓继新, 周浩, 王欢, 等.
2015. 基于储层砂岩微观孔隙结构特征的弹性波频散响应分析. 地球物理学报, 58(9): 3389–3400.
DOI:10.6038/cjg20150931 |
|
杜启振, 刘莲莲, 孙晶波.
2007. 各向异性粘弹性孔隙介质地震波场伪谱法正演模拟. 物理学报, 56(10): 6143–6149.
|
|
唐晓明.
2011. 含孔隙、裂隙介质弹性波动的统一理论-Biot理论的推广. 中国科学:地球科学, 41(6): 784–795.
|
|
王大兴.
2016. 致密砂岩气储层的岩石物理模型研究. 地球物理学报, 59(12): 4603–4622.
DOI:10.6038/cjg20161222 |
|
王大兴, 辛可锋, 李幼铭, 等.
2006. 地层条件下砂岩含水饱和度对波速及衰减影响的实验研究. 地球物理学报, 49(3): 908–914.
DOI:10.3321/j.issn:0001-5733.2006.03.037 |
|
伍向阳, 陈祖安, 魏建新.
2000. 一种测量岩石声波速度和衰减谱的技术. 岩石力学与工程学报, 19(S1): 895–898.
|
|
杨顶辉, 陈小宏.
2001. 含流体多孔介质的BISQ模型. 石油地球物理勘探, 36(2): 146–159.
|
|
张琳, 巴晶, 殷文, 等.
2017. 砾岩储层地震波传播方程:三重孔隙结构模型. 地球物理学报, 60(3): 1073–1087.
DOI:10.6038/cjg20170320 |
|
 2018, Vol. 61
2018, Vol. 61


