2. 南京大学 地球科学与工程学院, 南京 210023
2. School of Earth Sciences and Engineering, Nanjing University, Nanjing 210023, China
自21世纪初以来,气枪震源的应用逐步从海洋无限水体转移到陆地有限水体中(王宝善等,2011).相比传统陆地震源,气枪震源具有巨大的优势.作为一种应用于陆地区域尺度地球物理探测的新型可控人工震源,陆地大容量气枪被证明为绿色环保、效率高的理想震源,近年来越来越多的被应用到各种实验观测中来.Chen等(2008)将非调谐大容量气枪震源应用于水库、池塘等,利用内陆天然有限水体在河北省遵化市上关湖、北京市房山区马跑泉等地开展了地下介质变化的主动源探测研究试验(Wang et al., 2010),发展了针对区域尺度地球物理监测的新方法.2010年以后,先后在云南宾川、新疆呼图壁以及甘肃张掖建设气枪震源地震波发射台站(王彬等,2015;魏斌等,2016;张元生等,2016).地震波发射台站由陆地有限水体与大容量气枪组成,发射的气枪信号覆盖半径可达百公里,可以实现地震波主动激发,进行地下介质的连续高精度监测,为区域尺度问题的地震学观测提供了有力的工具.如为了探测长江沿岸地区的地下介质结构,我们于2015年在长江安徽段开展了气枪震源流动激发实验,实现了300 km距离固定台站的信号接收(徐逸鹤等,2016;张云鹏等,2016).
然而对于陆地气枪激发的机制仍然缺乏相应的理论描述.虽然半无限空间水体中气枪的激发信号方程可以由经典气泡震荡理论给出,但是由于陆地激发环境的复杂性,我们很难求出陆地有限水体中气枪激发信号的解析解.随着陆地气枪震源得到越来越广泛的应用,科学的解释陆地气枪信号激发、传播的机制显得越来越重要.经典气泡振荡理论是解释气枪激发机制的基础,一般认为,气枪子波分为压力脉冲和气泡脉冲两个部分(Ziolkowski, 1970).当气枪在水中被激发时,高压气体瞬间释放到水中,形成压力脉冲.然后气体汇聚成气泡,并在自身内压和水体静压力下做重复的膨胀收缩运动,形成气泡脉冲.Ziolkowski(1970)提出了气枪近场声波压力场的常规计算方法,Dragoset(2000)给出了气枪信号与激发条件之间的经验关系.陈浩林和於国平(2002)提出了气枪震源单枪子波修正模型的计算方法,并利用装配在枪体1 m处的检波器记录的近场子波信号计算远场子波(陈浩林等,2005).然而上述研究均针对半无限空间内进行的气枪的实验.对于陆地有限水体中的气枪激发,其结果不能很好地模拟水体边界条件对陆地气枪信号的影响. 林建民等(2010)讨论了陆地半开放性水体(上关湖水库)中大容量气枪激发信号的子波特征及变化规律,陈蒙(2014)进一步指出了水池水位等激发条件对陆上有限水体激发信号的影响,但是仅是给出了定性的规律,依然缺乏测量气枪震源的定量特征的有效手段.本文试图参照一些类似的地球物理过程及方法,寻求解决此问题的途径.
反投影方法是近年来出现的一种研究地震破裂过程的方法,其利用远距离台阵接收到的P波数据和少量先验信息,即可以得到震源破裂的时空图像.Ishii等(2005)利用Hi-Net数据得到Sumatra-Andaman地震的破裂走向、时间及速度,Krüger和Ohrnberger(2005a, b)利用不同的台站数据对同一地震得到一致的结果.由于反投影方法具有快速有效的特点,许多学者将其不断完善并加以改进,应用到更多的地球物理观测场景,如Kiser等(2011)发展了应用多震相的反投影方法来计算中深度地震的力学特征,Yao等(2012)利用迭代的反投影方法得到大震过程中子事件的分布.在陆地气枪主动源实验中,监测气枪压力场的分布与观测地震破裂过程相似.我们可以在实验场地周围布置水听器接收气枪激发的信号,利用反投影法的原理反演气枪源附近的物理场变化.本文利用人工合成的气枪数据,探讨了反投影方法应用于气枪震源监测的可行性,并提出了对反投影方法的改进方案与监测系统布置的实施方法.
1 方法和原理 1.1 改进的反投影方法反投影方法是一种信号延时叠加方法.该方法利用密集台阵所接收到的远震P波到时数据,经过预处理后,对数据进行延时叠加,以得到地震的震源破裂过程.反投影方法需要利用有限的先验数据,如所要研究地震的震源机制等,获取大致的震源破裂区域,并将此破裂区域分割为许多小的单元.之后计算各个小单元到每个接收台站的理论走时.对于每一个小单元,把所有的台站接收的数据做延时修正,延时值为对应的理论走时.最后对修正后的数据进行叠加,作为此小单元的反投影方法叠加数据.若一个小单元位于真实的地震破裂点,则叠加后的波形因相位相同而得到增强,反之则波形互相抵消而减弱.其对每一个小单元的一个叠加结果可以用下式计算得出:
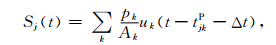
|
(1) |
其中,uk为在第k台站记录到的波形垂直分量数据,通常为速度数据,tjkP为P波从第k个台站到第j个可能破裂震源处的理论到时,Δt是由uk与参考台站相关计算得到的时间校正量,其目的是为了去除台阵下方介质不均匀性对理论到时的影响.pk与波形数据的正负有关,Ak为每个记录数据的权重.按时间顺序,依次提取所有小单元同一时刻的叠加数据,即得到该时刻整个地震破裂的能量分布状态.将反投影方法应用到陆地有限水体中气枪震源激发过程的计算中,需要针对实际物理过程的变化及应用的目的对算法进行适当的修改.
陆地气枪主动源实验通常将天然水域或人工小水体作为气枪激发池.依据反投影方法的原理,可以将激发池作为震源区域做网格化处理.测量水中波场物理量所采用的仪器通常是水听器,其记录的数据是水中的压力.我们可以在气枪激发池中布置密集的水听器,记录气枪波场的压力数据.通过计算所有水听器信号在各个网格点处的延时叠加信号,获得气枪震源的能量激发情况.另外依据气枪震源的实验条件,可以认为气枪信号是在均匀水体中传播,故而可以省略(1)式中矫正台站近处介质不均匀的Δt部分.而信号可以按照(2)式的方法叠加(Rost and Thomas, 2002),令:
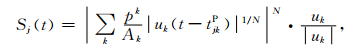
|
(2) |
其中,Sj(t)即为每个格点处的压力信号数据,N为方根调优参数.式中绝对值的运算是为了保持叠加后信号数值的符号不变.另外,基于台阵数据的传统反投影方法,采用的台站方位角均在某一很小的角度范围内,这也一定程度上造成反投影结果沿传播路径方向的分辨率不足(Walker et al., 2005).而陆地水体气枪震源实验中,可以将接收水听器均匀分布于所测水体,以在信号的每个传播方向上都获得足够的分辨率,取得理想的观测效果.综上所述,本文改进的反投影方法与传统的反投影方法相比,省去了近场到时的校正,并且接收台站的分布具有更大的可操作性.
1.2 实验方法及谱元法简介本文首先利用数值方法对气枪激发过程进行模拟,计算得到气枪震源周围密集位置的水听器接收数据.然后把此数据作为反投影方法的原始数据,进而验证反投影方法应用于气枪震源波场监测的可行性.其中数值计算方法采用谱元法(Tromp et al., 2008),在网格化的过程中,谱元法将模型剖分为多个不重叠的单元.为简洁起见并不失一般性,本文研究二维情况,采用四边形网格.在进行数值模拟时,除水面和地表是自由边界外,需要在计算区域的外侧设置人工边界条件.边界条件包括吸收边界条件、衰减边界条件等.本文的模型顶部采用自由边界条件,其余边界则采用吸收边界条件,而吸收边界条件应用了Clayton和Engquist(1980)给出的弹性波方程旁轴有理近似的一般形式.气枪震源激发信号具有丰富的高频及低频有效能量,虽然气枪子波信号可以通过数值模拟或理论计算等方法获得,但为简化起见,本文中均采用Ricker子波的一阶微分形式作为谱元法数值模拟的震源时间函数.为保持一致性,后续的反投影方法可以采用与谱元法相同的网格划分.因此,在利用谱元法进行模拟时需要采用比通常更密集的网格划分,以使得反投影方法得到更高的分辨率.
2 数据和结果与应用于反演地震震源破裂过程相比,反投影法应用于监测气枪震源激发波场的动态过程存在以下几点不同.首先研究对象的尺度不同,地震破裂过程尺度在几十千米量级,气枪震源波场尺度在百米或几十米量级,这也间接导致两种应用的监测精度不同;其次,波形传播路径的模式不同,观测系统配置不同,反演地震破裂过程台站方位角位于较窄范围内,监测气枪震源波场要求接收器方位角尽量均匀分布;再次研究的物理过程不同,地震的破裂通常沿某一方向行进,气枪的激发导致整个波场在全空间发生变化.为了验证反投影方法可应用于监测气枪震源激发过程的可行性,需要对以上多方面进行验证讨论.本文利用以下不同数值模型,分层次地逐步展开讨论.
2.1 模型1,半无限空间均匀水体中反投影方法的验证通过在激发池中布置若干水听器,记录气枪震源激发产生的波场数据,应用反投影方法对气枪激发的波场进行反演监测是一个经济简便的方法.将反投影法移植到气枪激发波场的监测,一个要考虑的问题是由气枪震源、水听器构建的监测系统与地震、传统台阵监测系统存在着配置上的不同,并且弹性波的传播路径、接收数据的类型等存在较大差异.气枪震源、水听器组成的激发监测系统是否能满足反投影法的应用条件是本文讨论问题的基础.
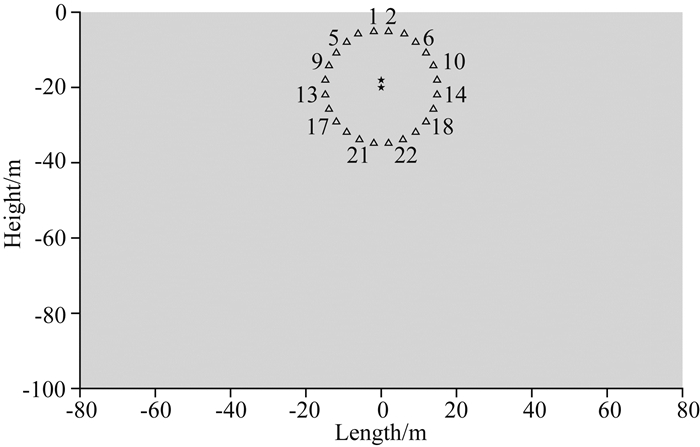
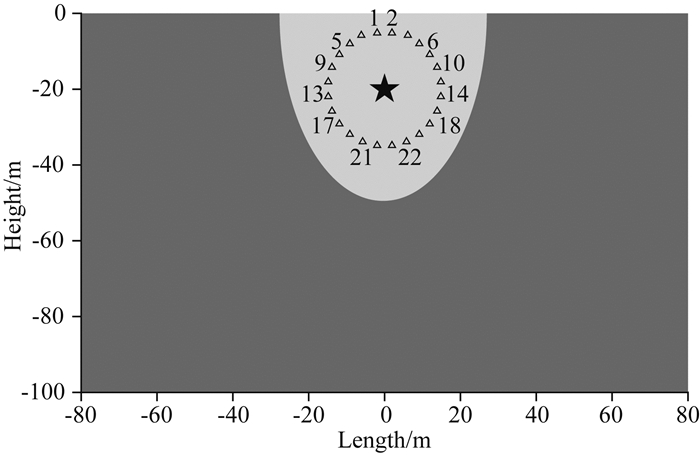
为了研究反投影方法在气枪震源、水听器构成的监测系统中的应用,建立半无限空间均匀水体二维模型,大小为100 m×160 m,共划分规则四边形网格20300个,时间步长为2×10-4s,共计模拟计算4 s,即总步数为20000步.震源采用点源,置于模型中央水下20 m深处.一般情况下,震源的主频应该设置较高,以适合模型尺寸.但是由于陆地气枪震源的主频在2~10 Hz,并且谱元法采用的震源时间函数为宽频信号,包含更高频率的信号成分,所以模拟过程中我们选择震源时间函数为主频为20 Hz的Ricker子波一阶微分形式,以对应实际气枪信号并且兼顾计算的可行性.水中波速取1200 m·s-1.共布置接收水听器24个,均匀分布在距震源约15 m的圆周上(图 1).
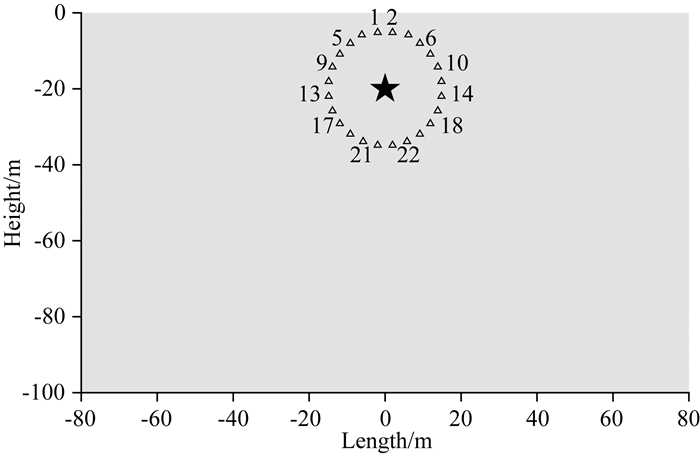
|
图 1 均匀半空间水体模型 长160 m,高100 m的半空间水体模型,三角形代表接收台站,五角星代表震源,浅灰色为水体. Fig. 1 Homogeneous half-space water body model Half-space water body model of 160 meters long and 100 meters high. Triangles represent the receivers, star indicates the airgun source and the grey part denotes the water body. |
依据图 1建立数值模型,利用谱元法模拟计算得到的各个水听器接收到的信号(见图 2).由于模型左右对称,图中仅显示了左侧部分水听器的接收信号.接收信号为归一化后的压力数据,这也是水听器实际工作中记录到的原始数据类型.由于模型结构及震源时间函数简单,各水听器接收到的信号较为相似.各个信号间的区别产生原因来源于水面反射信号路径不同.
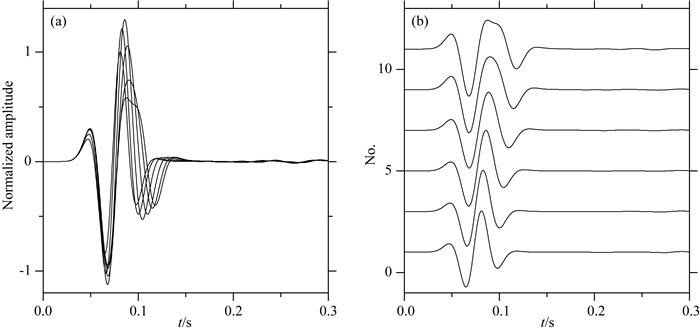
|
图 2 均匀半空间模型接收台站模拟数据 (a)纵坐标为归一化振幅; (b)纵坐标为道数.由于模型简单,模拟得到的波形形态简单. Fig. 2 Simulation data of receiving station in homogeneous half-space model Horizontal axes represent time in seconds; (a) and (b) vertical axes are normalized amplitude and trace numbers, respectively. Due to the simpleness of the model, the waveforms obtained by simulation are not complex. |
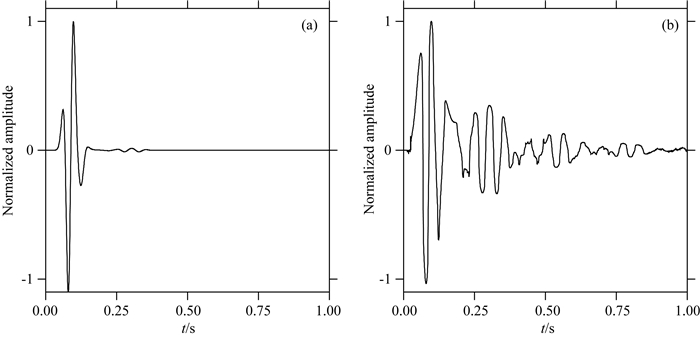
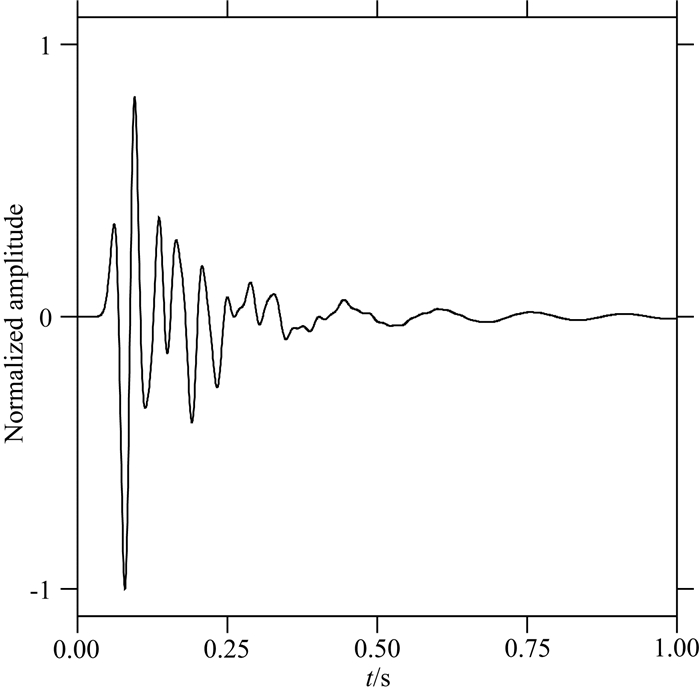
对获得的模拟数据进行反投影法计算.采用与谱元法相同的网格,对每个网格计算相应的延时叠加,得到每个小单元处的理论波形.分别采用N为1和4的情况,即对应直接叠加法与4次方根叠加方法,计算在震源处得到的波形信号(见图 3).可以看到相对于直接叠加法,反投影法中常用的4次方根法放大了微弱波形起伏,突出信号的整体起伏情况,在呈现较微弱信号的变化趋势上有较强能力,但是遗失了信号能量绝对大小的对比关系.由于数值模型简单,直接叠加方法既能呈现出信号变化的趋势,又能体现主要能量的传播特征.所以在本文的研究中,将采用直接叠加法(N=1).另外注意到,压力数据在约0.08 s和0.09 s处变化剧烈,压力数值从负的最大值跳变到正的最大值.后面的分析中,将着重考察这两个时刻的能量分布状态.
|
图 3 反投影法得到的震源处的理论波形 (a)应用直接叠加方法计算; (b)应用4次方根叠加法计算.可以看出两种叠加方法在0.1 s之前对应较好,在0.25 s之后,4次方根叠加法极大的提高了微弱信号的振幅.在约0.08 s和0.09 s处波形变化剧烈,压力数据从负变为正. Fig. 3 The theoretical waveform of the source obtained by the back-projection method (a) and (b) are derived by direct stacking method and 4th root stacking method, respectively. The results of two methods match well before 0.1 second, while the 4th root stacking method enhances the amplitude of the weak signal after 0.25 second. Both results see dramatic changes between 0.08~0.09 second with the pressure value turn from negative to positive. |
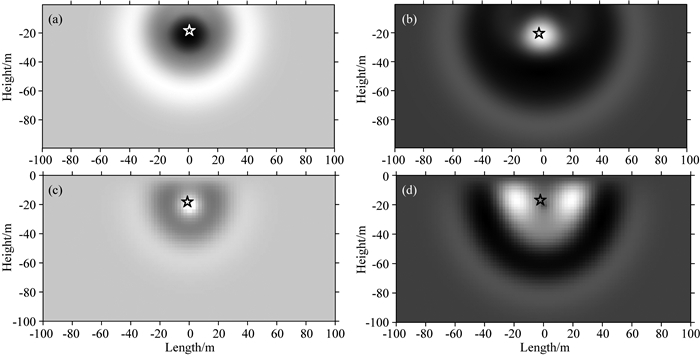
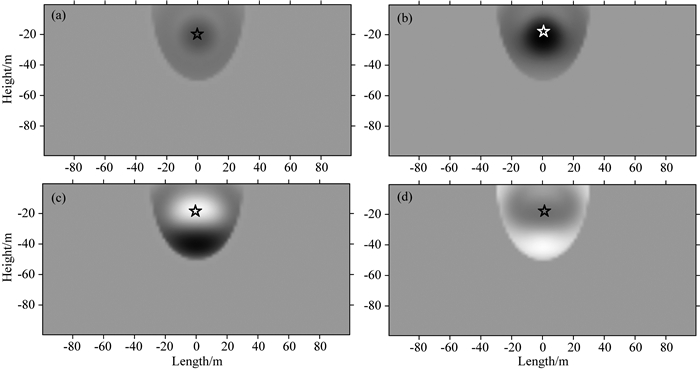
利用上面计算得到的各个小单元处的理论波形,取相同时刻各个小单元的数据,可以得到此时刻整个半无限空间水体内波场的压力分布.图 4(a, b)分别为0.08 s和0.09 s时的波场压力分布情况,对应了图 3左图中最小和最大两个极值处的时刻.可以看出,震源在20 m深处,整个波场大致呈环形分布,且重心略偏离设置的震源位置,这是可能由于自由水面(模型上界面)的影响,后面会详细介绍.为了考察反投影法计算结果的可信度,给出了谱元法模拟的结果(图 4(c,d)).通过相同时刻反投影方法计算的波场结果与谱元法计算的输入结果对比(图 4中a和c,b和d).可以看到,虽然反投影方法计算的结果与原始模拟数据总体特征相差不大,初始波场的相位信息较好地吻合,能较好地还原波场传播过程.但在细节仍处存在一定差异,如近水面处波形变形、震源处不一致等.造成这种差异的原因,可能是反投影方法仅利用部分的数据还原波场全部数据时,所引入的误差.此误差可通过更合理的水听器布置加以减弱.从此计算结果看出,反投影方法可以应用于气枪震源、水听器监测系统.
|
图 4 反投影方法与数值模拟方法的波场对照 (a)震源激发后0.08 s的压力场形态; (b)震源激发后0.09 s的压力场形态; (c, d)数值模拟结果得到的原始压力场形态,图c对应0.08 s,图d对应0.09 s.图中压力数据均经过自归一化.五角星处为震源位置.图(a, b)中均可看到因水面影响而导致的压力场形态变化,并且其形态分别与图(c, d)差别不大. Fig. 4 The wave field calculated by back-projection method compared to the results of numerical simulation (a) Wave field at 0.08 second; (b) Wave field at 0.09 second; (c) and (d) original pressure field calculated by numerical simulation at 0.08 second and 0.09 second, respectively. All the data are self-normalized. Horizontal and vertical axes are both model scale in meters. The star denotes the airgun source. The pressure field varies due to the water surface in both (a) and (b), which are very similar to those in (c) and (d), respectively. |
气枪震源激发后,气体的瞬间释放产生压力脉冲,随后气体汇集形成不断收缩膨胀的气泡,产生气泡脉冲,同时气泡震荡上浮,直至接触水面气泡破裂.根据Keller等(1956)气泡震荡衰减规律及实验观测数据,气枪气泡的能量在第三个周期时即衰减为原来的30%以下,即气枪信号的压力脉冲与前两次气泡脉冲的能量占了气枪信号总能量的大部分.因此为了模拟气枪激发过程中气泡脉冲的产生以及气泡上浮的现象,可以将气枪激发之后的物理过程,简化为两个点源分别激发,其时间间隔设为0.05 s,后一个点源在前一个点源垂向上方2 m处.由此构建半无限空间均匀水体中双震源气枪激发模型.除震源不同外,模型尺寸、介质性质、网格划分以及接收水听器布置均与图 1中模型相同.震源1采用点源,置于模型中央水下20 m深处,震源时间函数为主频为20 Hz的Ricker子波一阶微分形式,震源2亦采用点源,置于模型中央水下18 m深处,震源时间函数亦为20 Hz的Ricker子波一阶微分形式(如图 5).在某一水听器处接收到的信号如图 6中黑色波形所示.
|
图 5 半无限空间均匀水体中双震源模型 长160 m,高100 m的半空间水体模型,其中三角形代表接收台站,五角星代表震源,两震源时间间隔0.05 s,浅灰色为水体. Fig. 5 Bi-source model for homogeneous half-space water body Half-space water body model of 160 meters long and 100 meters high. Triangles represent the receivers, stars indicate the two airgun sources with 0.05 second gap and the grey part denotes the water body. |
|
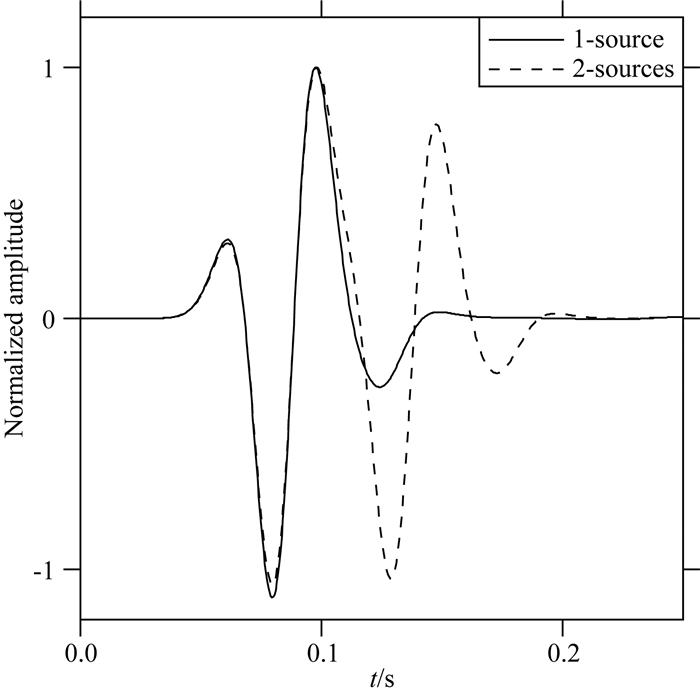
图 6 模型1与模型2模拟波形的对比 实线为模型1中谱元法模拟波形,虚线为模型2中谱元法模拟波形.对比发现,加入第二个震源后,波形前半部分一致,后部分信号得到延长. Fig. 6 Waveform comparison between Model 1 and Model 2 Simulated waveform by spectral element method is represented as solid line in Model 1 and dash line in Model 2. The comparison indicates after adding the second source, the former half of the waveform is consistent while the latter half is stretched. |
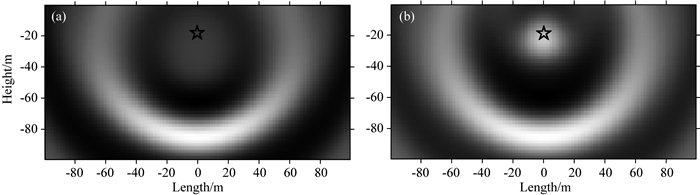
经谱元法计算理论波形后与模型1结果对比发现,增加第二个震源后,水听器接收波形仅在0.11 s后有区别(图 6).这是由于第一个震源信号与第二个震源信号在此处相互重叠的结果.与此对应,由反投影法计算得到的模型1与模型2的波场传播情况在0.11 s之前差异不大.选取0.12 s时刻的双震源波场压力分布图与单震源波场压力分布图比较(图 7),可以清晰分辨出双震源波场压力分布图中,有一明显的位于水下约20 m处的震源.这与模型设置吻合,也即说明反投影方法对气泡上浮的物理过程具有较好的模拟效果,且对气枪激发信号的波场具有较好的分辨率.
|
图 7 单震源波场分布与双震源波场分布对比 图中压力数据均经过自归一化.五角星处为震源位置,时刻均为震源激发后0.11 s. (a)模型1单震源模型中反投影法计算得到的波场压力形态; (b)模型2双震源模型中反投影法计算得到的波场压力形态.可以看出图b中第二个震源的起震. Fig. 7 Comparison of single source and bi-source wave field distribution Pressure data is self-normalized. Horizontal and vertical axes are both model scale in meters. The star denotes the airgun source. Both figures captured at 0.11 seconds. (a) Waveform is calculated by back-projection method for single source model (Model 1); (b) Waveform calculated by back-projection method for bi-source model (Model 2). The initiation of second source can be seen in (b). |
气枪的激发过程中,气泡脉冲也即气泡震荡运动是最难以数值模拟的部分.一方面,气泡存在时,反投影方法的叠加计算方法需要相应修改;另一方面由于气泡运动时存在表面压力变化,上浮以及形状改变等物理过程,使得气泡运动的数值模拟复杂而难以实现.
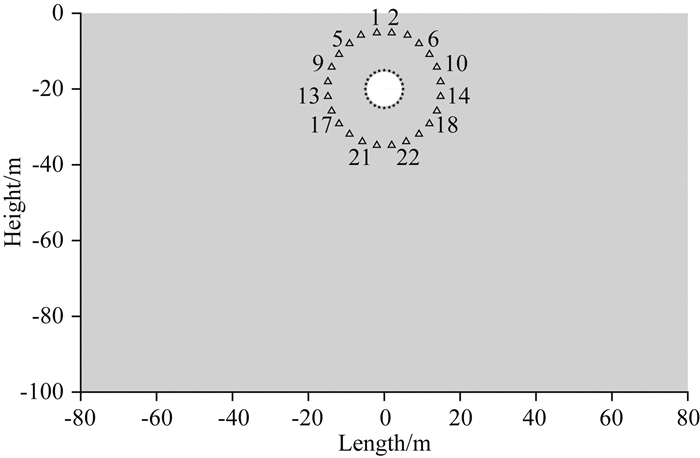
为了简化起见,本文模拟气泡运动某一时刻的物理状态,并假设气泡为规则圆形的二维情况,以忽略气泡本身上浮及形状变化的影响.在气泡膨胀的某一时刻,可以将气泡壁上某一小块区域近似为一个点源,整个气泡壁近似为由一系列点源组成的圆环.并且在气泡半径较小时,反投影计算过程中可忽略气泡存在的影响,仍然沿用之前模型的计算方法.如此,构造以下的带有气泡的半无限空间均匀水体二维模型,大小为100 m×160 m,半径为4.5 m的气泡位于模型中央距上边界20 m深处,共计划分规则四边形网格16043个,时间步长为2×10-4s.24个点源震源均匀分布,构成气泡的外边界,震源时间函数均为主频为20 Hz的Gaussian子波(其为Ricker子波的二阶微分形式,因其仅存在正方向的振幅,更适合本模型的计算).水中波速取1200 m·s-1,共布置24个水听器作为接收装置,均匀分布在与震源同圆心的半径为15 m的圆周上(如图 8).
|
图 8 半无限空间均匀水体中气泡震荡模型 模型长160 m,高100 m的半空间水体模型,其中三角形代表接收台站,五角星代表震源,浅灰色为水体,白色为空气气泡.围绕空气气泡很近的一圈密集的点源模拟气泡的膨胀运动. Fig. 8 Bubble oscillation model in homogeneous half-space water body Half-space water body model of 160 meters long and 100 meters high. Triangles represent the receivers and stars indicate the airgun sources. The grey part denotes the water body and the white part denotes the bubble. The dense point sources surrounding the bubble are used to simulate bubble expansion. |
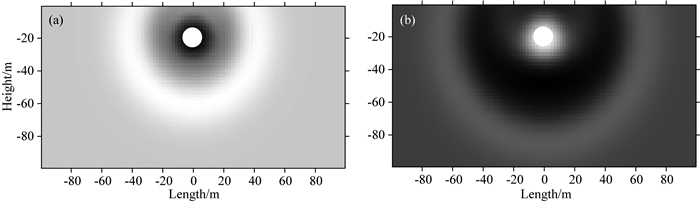
经反投影方法计算可得到对于存在气泡情况下的波场形态,图 9中分别对应震源激发后0.08 s和0.09 s时刻的波场压力分布图像.其大致与模型1中图 4a中点源情况下的压力分布相同,但在距离源约30 m处及以外的位置,压力分布更接近环形.而此结果也说明,对于气泡体积较小时的气枪激发实验,反投影法能较好地模拟其信号能量传播的方式.
|
图 9 气泡震荡模型中反投影法计算得到的波场形态 (a)震源激发后0.08 s的压力场形态; (b)震源激发后0.09 s的压力场形态.图中压力数据均经过自归一化.X轴与Y轴分别为模型尺寸,单位为m,白色圆形代表气泡.图a和图b中均可看到因水面影响而导致的压力场形态变化. Fig. 9 The wave field calculated by back-projection method with bubble oscillation model (a) Wave field at 0.08 second; (b) Wave field at 0.09 second. All the data are self-normalized. Horizontal and vertical axes are both model scale in meters. The white parts denote the bubble. The pressure field varies due to the water surface in both (a) and (b). |
通过分析前面3个模型的计算结果,可以证明反投影方法可以应用于半无限空间水体中气枪波场形态的测量,利用24个水听器组成的观测系统接收的数据可以有效地重建气枪激发压力场的物理过程.但是在实际操作过程中,观测仪器的布置可能难以达到如此多的数量,抑或是水听器的沉放位置可能与规则的圆环存在偏差.要回答如何用较少的仪器达到满意的测量结果,就要求对不同的观测仪器配置加以讨论.
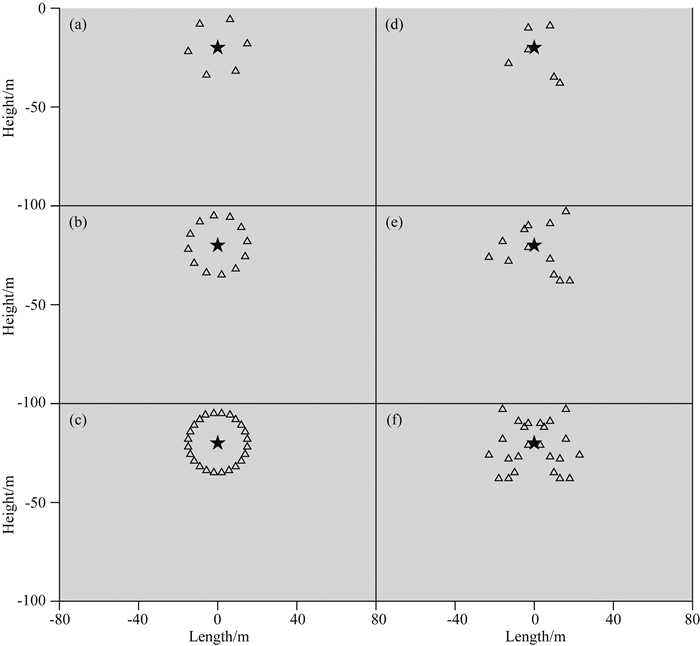
为达到上述目的,参考模型1中的模型,模型4设置与之相同的震源参数、模型尺寸、介质性质和网格划分,而水听器布置则采用多种不同的配置方案(图 10).本文采用了规则圆环状位置与随机位置的水听器布置,并且分别实验了不同水听器数目情况下的计算结果.如图 10所示,每个三角形点代表一个水听器.其中,图 10(a, b, c)为均匀圆环状布置水听器时的情况,各点均匀分布在距离震源15 m的圆环上,其中图 10a中共6个水听器,图 10b中12个水听器,图 10c中24个水听器.图 10f为随机位置的12个水听器以及他们各自相对于x=0轴的对称位置布置的水听器,即共24个随机的水听器位置,而图 10(d, e)则为由从图 10f中分别随机选择的6个与12个水听器组成的观测系统.
|
图 10 不同的水听器配置方案 图中为6个不同水听器配置方案对应的6个半无限空间水体模型.模型长160 m,高100 m的半空间水体模型,其中三角形代表接收台站,五角星代表震源,浅灰色为水体.(a,d) 6个水听器; (b,e) 12个水听器; (c,f) 24个水听器.其中图a, b, c中的模型水听器均匀分布,而图d, e, f中对应的模型水听器随机分布,但依然左右对称. Fig. 10 Different hydrophone configurations Each figure corresponds to one hydrophone configuration. Each model is 160 meters long and 100 meters high. Triangles represent the receivers and stars indicate the airgun sources. The grey part denotes the water body. (a) and (d) 6 hydrophones; (b) and (e)12 hydrophones; (c) and (f) 24 hydrophones. (a), (b) and (c) uniform distributed hydrophones; (d), (e) and (f) randomly but vertically symmetrical distributed hydrophones. |
对以上六种水听器布置情况分别做反投影方法计算,并选取与模型1中相同时刻的数据进行对比,如图 11所示.图 11A与图 11B分别为气枪激发后0.08 s与0.09 s时刻的压力能量聚焦状态.图 11中各子图的相对位置与图 10中对应,(a—c)为圆环状接收装置接收数据的计算结果,(d—f)为随机位置的接收装置接收数据的计算结果,从上到下则对应不同水听器数目的情况,分别为6个,12个以及24个.图 11Ac和图 11Bc则与模型1中图 4中两图相同.从图 11中可以看出,均匀分布的水听器布置方案结果均优于随机分布的水听器布置方案.在水听器随机布置的情况下,波场形态变形较大,水听器数目较少时(如6和12)则不能较好的反映出波场应有的形态,只有在水听器数目达到较大时(如24)才可大致反映出较为可靠的波场形态.而在规则布置水听器的情况下,12个水听器即可达到较好的计算效果,与24个水听器的计算结果仅有细微差别,但在水听器的数目下降到6个时,波场形态依然出现了明显的畸变.
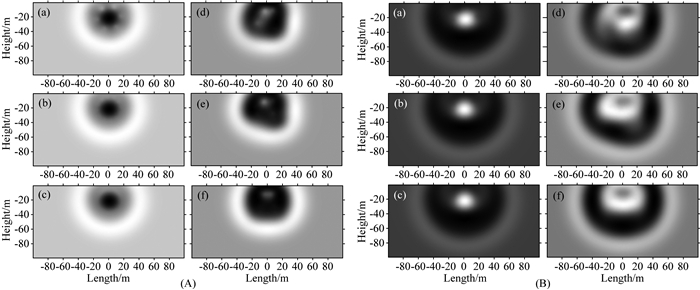
|
图 11 不同水听器配置方案对应反投影方法计算结果 图中压力数据均经过自归一化.五角星处为震源位置.(A)为0.08 s时刻波场压力形态,(B)为0.09 s波场压力形态.每幅图中的编号与图 10对应.对比发现,对于均匀分布的水听器配置方案,数目为12时就可以达到较好的效果.而对于非均匀排列的水听器配置方案,则需要更多的数目. Fig. 11 Results of back-projection method for different hydrophone configurations All pressure data are self-normalized. Horizontal and vertical axes are both model scale in meters. Stars indicate the airgun sources. The left figure is captured at 0.08 second, while the right figure at 0.09 second. The figure sequence is the same as Fig. 10. Comparison shows that 12 hydrophones are enough for the uniformly distributed configuration. However, more hydrophones are needed for randomly distributed configuration. |
从该模型试验,可以看到反投影方法本质上是一种缺失数据重建的方法,在小区域陆地有限水体的应用中,其采集数据的仪器需要满足一定的条件.一方面在空间上仪器应当尽量均匀地布置,使得仪器相对于震源的入射角尽量布满整个空间,另一方面,接收仪器的数量应在经济简捷的条件下尽可能地多,以防止因接收仪器数量不足而引起的结果畸变.
2.5 模型5,陆地水体实验中气枪震源激发实验的反投影方法的验证实际陆地气枪激发实验中,由于存在水池底对气枪波场的影响,尤其是不规则形状的天然水池底部复杂水-固界面,以及水下介质性质的变化,会对气枪激发信号的反射折射产生影响.这里仅考虑坚实水底的情况,并假设水池底剖面为抛物面的形状,以研究在天然水池中气枪激发实验中,应用反投影法监测气枪震源波场特征的可行性.
为此,建立模型如下,半无限空间均匀固体二维模型,大小为100 m×160 m,介质密度2 kg·m-3,P波速度3000 m·s-1,S波速度1700 m·s-1.在此模型中央,有一形状为抛物面的水体,其深度50 m,开口60 m.水中P波波速1200 m·s-1.共计划分四边形网格20300个,时间步长为2×10-4s,共计模拟计算4 s,即总步数为20000步.为简单起见,模型采用单震源点源,置于模型中央水下20 m深处,震源时间函数为主频为20 Hz的Ricker子波一阶微分形式.共布置接收水听器12个,均匀分布在距震源约15 m的圆周上(具体设置如图 12所示).
|
图 12 陆地有限小水体模型 模型长160 m,高100 m的半空间水体模型,其中三角形代表接收台站,五角星代表震源,浅灰色为水体,深灰色为固体介质. Fig. 12 Land limited water body model Half-space water body model of 160 meters long and 100 meters high. Triangles represent the receivers, star indicates the airgun source, the light grey part denotes the water body and the dark grey denotes solid medium. |
气枪信号传播到固体介质的过程中,在固-液界面会产生折射等现象,导致信号的理论到时计算比较复杂,且本文侧重考察水体中气枪震源波场的特征,故而这里只计算水体中波场的情况,对固体介质中的波形反投影结果不加以详细讨论.利用反投影方法,我们计算模型中水体涵盖的各个小单元格的波场波形,其中图 13为反投影方法计算得到的震源位置处的波形数据.可以看出,由于水底固体界面的反射,接收信号震相较前两个模型的震相更为丰富,在约0.1 s之后出现明显的反射波与多次反射波.这也说明,由于水体底面的影响,水体中气枪震源波场的传播更为复杂.图 14(a—d)分别为震源激发后0.06 s,0.08 s,0.11 s和0.13 s的水中压力波场情况.图 14a,显示有位于水下20 m深处的震源开始激发,图 14b为震源激发过程中,对应图 13中接收数据最小极值时刻,与前两个模型中的波场形态类似,但由于水面和水底的共同影响,其波场部分偏离环形状态.图 14c显示了水面及水底导致的波场形变,具体表现为波场的形态趋近于水体的物理轮廓,图 14d显示了水面与水-固界面交界处的尖锐区域对波场分布的影响.
|
图 13 陆地有限小水体模型接收台站模拟数据 横纵坐标为归一化振幅.相比模型1,可见由于固液界面的反射作用,波形变得复杂. Fig. 13 Simulation data of receiving station in land limited water body model Horizontal axis represents time in seconds; the vertical axis is normalized amplitude. Compared to Model 1, the waveform is more complicated due to the reflection at the solid-liquid boundary. |
|
图 14 陆地水体模型中反投影法计算得到的压力场分布 图中压力数据均经过自归一化.五角星处为震源位置,其中背景中的浅灰色为固体介质.图(a, b, c, d)分别为模型5中反投影法计算得到的震源激发后0.06 s,0.08 s,0.11 s和0.13 s后的波场压力形态,其特征反映了水体固液界面形状对波场的影响.图(b)和(d)中锯齿状的边界为网格划分时网格单元边界. Fig. 14 The distribution of pressure field calculated by back-projection method with land water body model All pressure data are self-normalized. Horizontal and vertical axes are both model scale in meters. Stars indicate the airgun sources and the light grey represents solid medium. (a)—(d) are the wave field calculated by back-projection method at 0.06, 0.08, 0.11 and 0.13 second respectively, which reflect the influence of the solid-liquid boundary to waveform. |
从图中可以看出,反投影法的结果可以清晰地构建出实际水池中气枪震源激发波场的形态.从所得到的波场分布,与前文中均匀半空间水体中结果对比,可以清晰地看到有限小水体的固液界面对波场能量传播的影响.
3 分析和讨论气枪震源是区域尺度探测的优良震源,了解气枪震源的性质对气枪震源的有效利用有着重要的意义.本文提出的计算气枪震源波场分布的反投影方法,监测系统布置简单,数据获取和结果计算简捷可靠.通过上文中的模型实验,可以看出利用反投影方法可以得出较好的波场能量分布的计算结果.在气枪震源波场监测工作中,该方法快速了解气枪震源激发能量的传播方式,为评估气枪震源的性能以及实时调整提供参考.另一方面,本文提出的计算方法中,用于观测的水听器可以围绕震源均匀布置,使得计算结果在信号传播的各个方向上均有较好的分辨率.针对较为复杂的水体,结合水体形状适当加密重点监测部位的水听器布置,可以更精确地分辨水体的变化对气枪震源波场的影响.
本文提出的方法在实际应用中存在一定误差,并存在可供选择的改进方案.一方面,在实地的气枪激发实验中,气枪的激发条件比本文中模型设置的情况更加复杂.尤其天然水体中的气枪激发实验,其水体形状不规则,水底及侧壁经常出现起伏的情况,并且水底为孔隙度变化的双多孔相介质.但是本文目的是为了验证反投影方法应用于气枪震源监测的可行性,所以对复杂介质的情况并未加以讨论.相应地,基于以上简化,我们也仅能得到水体中的能量分布状态.如果想一并研究水体外介质中反投影法应用的效果,则需要考虑实际情况,引入信号传播路径计算等.这也会极大地增加该算法的计算成本,将在今后的工作中加以考虑.另一方面,本文的实验方案中仅选择了水听器作为信号接收装置.由于水听器的规格等限制,用于检测地震波动会存在诸多限制,而野外地震科考实验中最常用的仪器仍然是地震仪.如何在实验系统中,有效利用近场地震计的数据,借鉴波场逆向延拓的方法处理复杂界面的情况,是一个值得讨论的话题,这将包括如何布置地震仪以及如何更改反投影算法.
从本文中应用反投影法计算得到的波场压力分布图可以看到,气枪震源位置与压力场对称中心点并不总是重合.这是由于水面的反射导致的压力场变化.需要指出的是,气枪的信号实际上可以分为压力脉冲信号与气泡震荡信号两个部分,其中压力脉冲信号部分频率较高(大于20 Hz),气泡震荡部分频率较低(5~15 Hz).本文的模拟计算均将用到的震源时间函数主频设置为20 Hz的Ricker子波一阶微分形式.根据Ricker子波一阶微分形式的性质,其信号为宽频信号,包含了20 Hz以下所有的频率成分,也即较高频的震源时间函数将同时模拟了压力脉冲和气泡震荡两个部分的信号.另外,由于低频成分波长较大(200 m),在其尺度大于的水体尺度的情况下,水体中低频成分的波场分布不会获得足够的空间分辨率.不过这并不影响在水体中波场计算的精确性.
本文提出的方法隐含一个前提假设,即气枪的激发并未导致水听器附近介质物理性质的明显改变,如附近水体的激烈震荡或者附近泥沙的运移等.而在未来的实地实验操作过程中,需要对水听器合理布置,要求水听器必须布置在离气枪震源足够远的安全距离上,以保证水听器位置的稳定.在模型4实验中,仅比较了环状排列与随机排列的水听器布置方案.对于是否存在其他更适合的布置方案,需要进一步的研究.另外本文中所有数据均来源于数值模拟实验,下一步的研究将会更多的采用实际实验数据,在新疆呼图壁或云南大银甸气枪激发池中布置水听器,采集数据并对反投影方法进行验证与应用.
4 结论本文提出了一种改进的反投影方法,使之适用于陆上气枪震源的波场监测.通过数值模拟实验,证明了利用布置在水体中的水听器接收到的信号,该方法可以有效地监测到气枪信号激发后能量的传播方式.该方法布置方便,计算迅速,结果可靠,可以有效及时地对气枪震源的效果做出评估,可以对更充分地利用气枪震源提出有益的指导.
Chen H L, Yu G P.
2002. Computer simulation for single air-gun signature. Equipment for Geophysical Prospecting, 12(4): 241-244.
|
|
Chen H L, Quan H Y, Liu J, et al.
2005. Simulation of far-field wavelet based on near-field measuring gun-array. Oil Geophysical Prospecting, 40(6): 703-707.
|
|
Chen M. 2014. Explore and monitor regional-scale subsurface structure using untuned large volume airgun array[Ph. D. thesis](in Chinese). Beijing: Institude of Geophysics, China Earthquake Administration.
|
|
Chen Y, Liu L B, Ge H K, et al.
2008. Using an airgun array in a land reservoir as the seismic source for seismotectonic studies in northern China:experiments and preliminary results. Geophysical Prospecting, 56(4): 601-612.
DOI:10.1111/j.1365-2478.2007.00679.x |
|
Clayton R W, Engquist B.
1980. Absorbing boundary conditions for wave-equation migration. Geophysics, 45(5): 895-904.
DOI:10.1190/1.1441094 |
|
Dragoset B.
2000. Introduction to air guns and air-gun arrays. The Leading Edge, 19(8): 892-897.
DOI:10.1190/1.1438741 |
|
Ishii M, Shearer P M, Houston H, et al.
2005. Extent, duration and speed of the 2004 Sumatra-Andaman earthquake imaged by the Hi-Net array. Nature, 435(7044): 933-936.
DOI:10.1038/nature03675 |
|
Kiser E, Ishii M, Langmuir C H, et al.
2011. Insights into the mechanism of intermediate-depth earthquakes from source properties as imaged by back projection of multiple seismic phases. Journal of Geophysical Research:Solid Earth, 116(B6): B06310.
DOI:10.1029/2010JB007831 |
|
Krüger F, Ohrnberger M.
2005a. Spatio-temporal source characteristics of the 26 December 2004 Sumatra earthquake as imaged by teleseismic broadband arrays. Geophysical Research Letters, 32(24): L24312.
DOI:10.1029/2005GL023939 |
|
Krüger F, Ohrnberger M.
2005b. Tracking the rupture of the MW=9.3 Sumatra earthquake over 1, 150 km at teleseismic distance. Nature, 435(7044): 937-939.
DOI:10.1038/nature03696 |
|
Keller J B, Kolodner I I.
1956. Damping of underwater explosion bubble oscillations. Journal of Applied Physics, 27(10): 1152-1161.
DOI:10.1063/1.1722221 |
|
Lin J M, Wang B S, Ge H K, et al.
2010. Characters of large volume air-gun source excitation. Chinese J. Geophys., 53(2): 342-349.
DOI:10.3969/j.issn.0001-5733.2010.02.012 |
|
Reasenberg P, Aki K.
1974. A precise, continuous measurement of seismic velocity for monitoring in situ stress. Journal of Geophysical Research, 79(2): 399-406.
DOI:10.1029/JB079i002p00399 |
|
Rost S, Thomas C.
2002. Array seismology:methods and applications. Reviews of Geophysics, 40(3): 2-1.
|
|
Tromp J, Komattisch D, Liu Q.
2008. Spectral-element and adjoint methods in seismology. Communications in Computational Physics, 3(1): 1-32.
|
|
Walker K T, Ishii M, Shearer P M.
2005. Rupture details of the 28 March 2005 Sumatra MW8.6 earthquake imaged with teleseismic P waves. Geophysical Research Letters, 32(24): L24303.
DOI:10.1029/2005GL024395 |
|
Wang B S, Yang W, Yuan S Y, et al.
2010. An experimental study on the excitation of large volume airguns in a small volume body of water. Journal of Geophysics and Engineering, 7(4): 388-394.
DOI:10.1088/1742-2132/7/4/005 |
|
Wang B S, Wang W T, Ge H K, et al.
2011. Monitoring subsurface changes with active sources. Advances in Earth Science, 26(3): 249-256.
|
|
Wang B, Wu G H, Su Y J, et al.
2015. Site selection and construction process of Binchuan earthquake signal transmitting seismic station and its preliminary observation result. Journal of Seismological Research, 38(1): 1-6.
|
|
Wei B, Su J B, Wang H T, et al.
2016. Site selection and construction of Hutubi airgun source signal transmitting seismic station and its characteristic of source. Earthquake Research in China, 32(2): 222-230.
|
|
Xu Y H, Wang B S, Wang W T.
2016. Characteristics of airgun signals excited in the Yangtze River from analysis of permanent stations' data. Earthquake Research in China, 32(2): 282-294.
|
|
Yao H J, Shearer P M, Gerstoft P.
2012. Subevent location and rupture imaging using iterative backprojection for the 2011 Tohoku MW9.0 earthquake. Geophysical Journal International, 190(2): 1152-1168.
DOI:10.1111/gji.2012.190.issue-2 |
|
Zhang Y P, Wang B S, Wang W T, et al.
2016. Preliminary result of tomography from permanent stations in the Anhui air-gun experiment. Earthquake Research in China, 32(2): 331-342.
|
|
Zhang Y S, Guo X, Qin M Z, et al.
2016. The construction ofactive source repeated monitoring in the Qilian Mountains of Gansu province. Earthquake Research in China, 32(2): 209-215.
|
|
Ziolkowski A.
1970. A method for calculating the output pressure waveform from an air gun. Geophysical Journal International, 21(2): 137-161.
DOI:10.1111/j.1365-246X.1970.tb01773.x |
|
陈浩林, 於国平.
2002. 气枪震源单枪子波计算机模拟. 物探装备, 12(4): 241–244.
|
|
陈浩林, 全海燕, 刘军, 等.
2005. 基于近场测量的气枪阵列模拟远场子波. 石油地球物理勘探, 40(6): 703–707.
|
|
陈蒙. 2014. 利用水库大容量非调制气枪阵列进行区域尺度地下结构探测和监测[博士论文]. 北京: 中国地震局地球物理研究所.
http://cdmd.cnki.com.cn/Article/CDMD-85401-1014405982.htm |
|
林建民, 王宝善, 葛洪魁, 等.
2010. 大容量气枪震源子波激发特性分析. 地球物理学报, 53(2): 342–349.
DOI:10.3969/j.issn.0001-5733.2010.02.012 |
|
王宝善, 王伟涛, 葛洪魁, 等.
2011. 人工震源地下介质变化动态监测. 地球科学进展, 26(3): 249–256.
|
|
王彬, 吴国华, 苏有锦, 等.
2015. 宾川地震信号发射台的选址、建设及初步观测结果. 地震研究, 38(1): 1–6.
|
|
魏斌, 苏金波, 王海涛, 等.
2016. 新疆呼图壁人工水体大容量气枪信号发射台性能研究. 中国地震, 32(2): 222–230.
|
|
徐逸鹤, 王宝善, 王伟涛.
2016. 利用固定台站分析长江激发气枪信号特征. 中国地震, 32(2): 282–295.
|
|
张云鹏, 王宝善, 王伟涛, 等.
2016. 安徽气枪实验固定台层析成像初步结果. 中国地震, 32(2): 331–342.
|
|
张元生, 郭晓, 秦满忠, 等.
2016. 甘肃祁连山主动源重复探测项目建设及震源重复性分析. 中国地震, 32(2): 209–215.
|
|
 2018, Vol. 61
2018, Vol. 61


