0 引言

全波形反演(Full Waveform Inversion, FWI)通过最小化计算波场和观测波场的残差来更新地下速度结构，其最初是在声波近似下提出的(Tarantola, 1984). 然而，地震波在地下传播过程中，不只有纵波，还会产生转换波，因此弹性介质比声波介质更能接近地下真实的介质情况. Tarantola (1986, 1988)和Mora (1987, 1988)最早发展了弹性波全波形反演的理论和方法. Crase等(1990)最早将弹性波全波形反演方法应用于实际数据的反演. 但是，弹性波全波形反演计算效率比声波低很多，很长时间以来限制了其发展和应用. 近年来，随着计算机硬件的发展，弹性波全波形反演的方法研究(Brossier et al., 2009; 孙宏宇等, 2015; 王毓玮等, 2016)和应用研究(Sears et al., 2008; Prieux et al., 2013; Vigh et al., 2014)得到很大发展.

在波恩近似框架下，全波形反演问题可以采用局部优化算法求解(Tarantola, 1984; Virieux and Operto, 2009)，这决定了常规全波形反演必须靠很多次的迭代来接近真解. 迭代过程的梯度可以采用伴随状态法求取(Tarantola, 1984; Zhou et al., 1995; Sheng et al., 2006; Plessix, 2006)，基本做法是利用震源正传波场与残差(伴随源)反传波场的互相关求取；也可以采用散射积分法直接计算核函数-向量乘求取目标函数的梯度(Liu et al., 2015). 但无论哪种方法，全波形反演的计算量主要消耗在正演上. 同时震源技术可以大大提高正演的计算效率，进而提高全波形反演的计算效率(Vigh and Starr, 2008). 但是，记录的混叠会在应用成像条件时引入串扰噪声. 对震源进行随机编码可以有效压制串扰噪声. Krebs等(2009)首次将动态震源编码方法引入全波形反演，并提出了随机正负相位编码. 随后，震源编码方法也被拓展到频率域全波形反演(Moghaddam and Herrmann, 2010；van Leeuwen et al., 2011；Li et al., 2012). Boonyasiriwat和Schuster (2010)提出了双随机动态编码方法，在每次迭代时同时改变震源的位置和极性. Moghaddam等(2013)考虑到随机震源反演时梯度的随机性，将随机最优化方法引入到混合震源的全波形反演中. Hu等(2016)提出了一种混合的动态相位编码方式，并将其用于声波介质多级全波形反演的计算. 以上编码方式对于压制多震源声波全波形反演的串扰噪声有显著效果. 但是，在弹性介质情况下，波场成分更复杂，引入的串扰噪声干扰比声波时更严重. 为了压制和离散弹性波全波形反演过程中的串扰噪声，本文提出了一种综合的动态随机编码策略.

单纯靠震源编码策略，在弹性介质情况下，无法完全消除串扰噪声的影响，尤其在反演后期会有很多串扰噪声残留. 本文在分析了这些残留串扰噪声的特殊形态后，引入全变分(Total Variation, TV)约束来进行压制. TV约束方法是图像去噪和复原领域常用的一种方法，能用于图像的去噪、去模糊和缺失部分恢复等(Rudin et al., 1992; Acar and Vogel, 1994; Beck and Teboulle, 2009b; Yuan and Wang, 2013). TV范数约束问题将模型的梯度作为约束项，能使结果中模型的边界更尖锐且层内更平滑. TV约束用于消除混合震源最小二乘偏移过程中的串扰噪声，取得了很好的效果(卢昕婷等, 2015; 卢昕婷, 2016). Askan等(2007)首次将TV范数作为正则项约束地震全波形反演问题，消除介质高震荡成分的同时保持了介质的不连续性. Burstedde和Ghattas (2009)对比了几种TV范数约束的一维全波形反演问题，发现primal-dual TV正则化在模型存在不连续时效果最好，并提出了反演前期用吉洪诺夫正则化，后期用TV正则化的反演策略. Anagaw和Sacchi (2011)将TV正则化方法应用于频域全波形反演，验证了其对于保持模型边界和不连续面的作用. Lin和Huang (2015)、Gao等 (2015)将常规全波形反演问题分解为吉洪诺夫正则化问题和TV正则化问题，提出了基于改进的TV约束的全波形反演方法，并分别在声波介质、弹性波介质和各向异性介质中进行了应用. Esser等 (2015)在TV约束反演过程中，对梯度加以限制使其主要在垂向更新，该方法对于反演强速度扰动的盐丘模型取得了好的效果. Liu等 (2016)提出将TV正则化方法用于声波介质同时震源的反演，能同时提高反演的计算效率和结果的分辨率. Qiu等 (2016)提出了一种灵活的TV正则化反演方法，可以根据模型的速度反差选择不同强度的正则化. 可见，将TV约束引入到多震源弹性波FWI中，用以消除残留的串扰噪声，并锐化模型界面，具有很好的应用潜力.

本文提出了基于各向异性TV约束和新的多震源动态混合编码的弹性波全波形反演策略. 为克服跳周现象，将基于稀疏约束的多尺度方法引入基于TV约束的弹性波全波形反演算法中. 模拟数据反演结果表明，本文提出的反演方法抗噪能力强且反演速度得到很大的提升.

1 常规弹性波全波形反演原理

在二维各向同性介质中，用位移-应力表示的弹性波方程可以表示为

$\left\{ {\begin{aligned}& {\rho \displaystyle\frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = \frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\sigma _{x{\textit z}}}}}{{\partial {\textit z}}}},\\& \rho \displaystyle\frac{{{\partial ^2}{u_{\textit z}}}}{{\partial {t^2}}} = \frac{{\partial {\sigma _{x{\textit z}}}}}{{\partial x}} + \frac{{\partial {\sigma _{{\textit z}{\textit z}}}}}{{\partial {\textit z}}},\\& {\sigma _{xx}} = {C_{11}}\displaystyle\frac{{\partial {u_x}}}{{\partial x}} + {C_{13}}\frac{{\partial {u_{\textit z}}}}{{\partial {\textit z}}},\\& {\sigma _{{\textit z}{\textit z}}} = {C_{13}}\displaystyle\frac{{\partial {u_x}}}{{\partial x}} + {C_{33}}\frac{{\partial {u_{\textit z}}}}{{\partial {\textit z}}},\\& {\sigma _{x{\textit z}}} = {C_{44}}\displaystyle\frac{{\partial {u_{\textit z}}}}{{\partial x}} + {C_{44}}\frac{{\partial {u_x}}}{{\partial {\textit z}}},\end{aligned}} \right.$

(1)

其中，ρ为介质密度，u_x和u_z分别为介质中质点在水平方向和垂直方向的位移分量，t为时间，σ_xx、σ_zz和σ_xz为应力分量，C_ij为弹性刚度张量元素，且 ${C_{11}} = {C_{33}} = \lambda + 2\mu $ ， ${C_{13}} = \lambda $ ， ${C_{44}} = \mu $ ，λ和μ为拉梅常数. 本文采用时间二阶空间十阶差分格式进行正演模拟.

本文采用多分量地震记录进行弹性波全波形反演，即接收记录中同时包含u_x和u_z分量. 采用常密度，构建L2范数的目标函数为

$\begin{split}E\left( {\lambda ,\mu } \right) =& \frac{1}{2}\sum\limits_{{x_{\rm s}}} {\sum\limits_{x_{\rm r}} {\int_0^T {\left[ {{{u}_{{\rm{cal}}}}\left( {t,{x_{\rm{r}}},{x_{\rm{s}}},\lambda ,\mu } \right) } \right.} } } \\& - {\left. {{{u}_{{\rm{obs}}}}\left( {t,{x_{\rm{r}}},{x_{\rm{s}}}} \right)} \right]^2}{\rm{d}}t,\end{split}$

(2)

其中，E为目标函数，x_s和x_r分别代表震源和检波点位置，T为记录时间，u_cal和u_obs分别表示合成和观测的地震记录.

根据伴随状态法(Plessix, 2006)，并结合链式法则，可得到目标函数相对于介质纵、横波速度的梯度公式为

$\begin{split}\frac{{\partial E}}{{\partial {V_{\rm P}}}} & = \frac{{\partial E}}{{\partial \lambda }} \cdot \frac{{\partial \lambda }}{{\partial {V_{\rm P}}}} = 2\rho {V_{\rm P}} \cdot \frac{{\partial E}}{{\partial \lambda }} \\& = -2\rho {V_{\rm P}}\int_0^T {\left( {\frac{{\partial {u_x}}}{{\partial x}} + \frac{{\partial {u_z}}}{{\partial z}}} \right)\left( {\frac{{\partial u_x^ + }}{{\partial x}} + \frac{{\partial u_z^ + }}{{\partial z}}} \right){\rm d}t,} \end{split}$

(3)

$\begin{split}\frac{{\partial E}}{{\partial {V_{\rm S}}}} = & \frac{{\partial E}}{{\partial \lambda }} \cdot \frac{{\partial \lambda }}{{\partial {V_{\rm S}}}} + \frac{{\partial E}}{{\partial \mu }} \cdot \frac{{\partial \mu }}{{\partial {V_{\rm S}}}} \\& \!\!\!\!\! = - 4\rho {V_{\rm S}} \cdot \frac{{\partial E}}{{\partial \lambda }} + 2\rho {V_{\rm {\rm S}}} \cdot \frac{{\partial E}}{{\partial \mu }}\\& \!\!\!\!\! = 4\rho {V_{\rm S}}\int_0^T{\left( {\frac{{\partial {u_x}}}{{\partial x}} + \frac{{\partial {u_{\textit z}}}}{{\partial {\textit z}}}} \right)\left( {\frac{{\partial u_x^ + }}{{\partial x}} + \frac{{\partial u_{\textit z}^ + }}{{\partial {\textit z}}}} \right){\rm d}t} \\ & \quad - 2\rho {V_{\rm S}}\int_0^T{{\left[ {2\left( {\frac{{\partial {u_x}}}{{\partial x}} \cdot \frac{{\partial u_x^ + }}{{\partial x}} + \frac{{\partial {u_{\textit z}}}}{{\partial {\textit z}}} \cdot \frac{{\partial u_{\textit z}^ + }}{{\partial {\textit z}}}} \right) } \right.} } \\ & \quad + \left. {\left( {\frac{{\partial {u_{\textit z}}}}{{\partial x}} + \frac{{\partial {u_x}}}{{\partial {\textit z}}}} \right)\left( {\frac{{\partial u_{\textit z}^ + }}{{\partial x}} + \frac{{\partial u_x^ + }}{{\partial {\textit z}}}} \right)} \right]{\rm d}t,\end{split}$

(4)

其中，V_P和V_S分别表示纵、横波速度， $u_x $ 和 $ u_{\textit z}$ 分别表示正传波场的x和z分量， $u_x^ + $ 和 $u_{\textit z}^ + $ 分别表示伴随波场的x和z分量.

本文采用共轭梯度法计算模型的更新方向(Mora, 1987; Luo and Schuster, 1991; Crase et al., 1992; Sheng et al., 2006)，第k次更新方向为

${{\mathit{\boldsymbol{d}}}_k} = - {{\mathit{\boldsymbol{g}}}_k} + {\beta _k}{{\mathit{\boldsymbol{d}}}_{k - 1}},$

(5)

${\beta _k} = \frac{{{\mathit{\boldsymbol{g}}}_k^{\rm T} \cdot {{\mathit{\boldsymbol{g}}}_k}}}{{{\mathit{\boldsymbol{g}}}_{k - 1}^{\rm T} \cdot {{\mathit{\boldsymbol{g}}}_{k - 1}}}},$

(6)

其中，d_k为第k次的速度模型更新方向，g_k为第k次的梯度，β_k为共轭梯度法的系数. 第k次的速度模型更新公式为

${{\mathit{\boldsymbol{v}}}_k} = {{\mathit{\boldsymbol{v}}}_{k - 1}} + \alpha \cdot {{\mathit{\boldsymbol{d}}}_k},$

(7)

其中，α为步长.

2 动态多震源弹性波反演策略

多震源模拟技术将多个单炮记录进行随机编码，形成超级炮记录，正演计算时采用相应的超级炮震源函数，使得一个超级炮的计算时间大约为一个单炮记录的正演时间(Zhang et al., 2015). 假设一个超级炮中包含n个单炮记录，那么一次超级炮正演大约比常规正演提速n倍. 但是，多震源的混叠将在计算梯度时产生成像串扰噪声，影响反演的最终结果. 本文首先采用动态混合编码技术在一定程度上压制串扰噪声，并使剩余串扰噪声呈离散分布的随机噪声状态. 然后通过TV约束，进一步压制剩余串扰噪声. 本文提出了一种综合的混合编码方法，其中一个超级炮震源可以写作

${\mathit{\boldsymbol{S}}} = \mathop \sum \limits_{i = 1}^{{N_{\rm s}}} {A_{\rm rand}} \cdot {\rm P}{{\rm H}_{\rm rand}}\left[ {{{\mathit{\boldsymbol{s}}}_i}\left( {{x_{\rm rand}},t} \right)*\delta \left( {t - \Delta {t_{\rm rand}}} \right)} \right],$

(8)

其中，N_s表示超级炮中的单炮个数，i为单炮震源序号，A_rand表示随机的振幅值， ${{{\mathit{\boldsymbol{s}}}_i}\left( {{x_{\rm rand}},t} \right)}$ 表示在随机震源位置x_rand的震源函数， ${\delta \left( {t - \Delta {t_{\rm rand}}} \right)}$ 表示随机延时为∆t_rand的δ函数，·代表乘积，*代表褶积. PH_rand(·)表示随机相位编码算子，可以表示为

${\rm P}{{\rm H}_{\rm rand}}\left( {\mathit{\boldsymbol{a}}} \right) \!=\! {\rm cos} \left( {\frac{{{\theta _{\rm rand}}\!\cdot \! \pi }}{{180}}} \right) \!\! \cdot{\mathit{\boldsymbol{a}}} \!+\! {\rm sin} \! \left( {\frac{{{\theta _{\rm rand}}\cdot\pi }}{{180}}} \right)\!\! \cdot H\left( {\mathit{\boldsymbol{a}}} \right),$

(9)

其中，θ_rand代表随机的相位旋转角，H(a)代表信号a的希尔伯特变换.

本文的动态多震源全波形反演算法是首先将观测记录进行编码，同时得到相应的超级炮震源. 然后，在全波形反演过程中，每次都采用超级炮震源进行正演，与超级炮观测记录进行对比和求取残差. 由于编码为随机采取，会导致照明的不均匀，因此，每隔5~10次迭代更换一次随机编码，能提高照明的均匀性，这是本文采取的动态编码方式.

本文提出的动态多震源反演策略，在压制串扰噪声和提高收敛性上都较前人的方法有所改进. Krebs等(2009)首次提出了动态随机相位编码的FWI方法，在每次迭代中都对震源采用不同的正负相位编码方式，而且每次对所有震源进行一次编码形成一个超级炮，虽然能大大提高计算效率，但是将产生较强的串扰噪声. Boonyasiriwat和Schuster(2010)对其进行了改进，将所有震源编码成多个超级炮，每个超级炮采用随机震源位置和随机相位编码，这样可以进一步压制多震源同时反演产生的串扰噪声. 但是，前人的动态编码策略在串扰噪声的压制上还可以进一步改进，而且其收敛性也存在一定的问题. 由于弹性波场成分比声波波场更为复杂，因此有必要进一步增加混叠震源之间的非相干性. 本文提出的方法同时采用四种编码方式：随机位置编码，随机相位编码，随机能量编码和随机时间延迟编码. 这样，对于超级炮中的每一道记录来说，来自不同震源的信号的非相干性更强，产生的串扰噪声更弱. 另外，如果每次迭代更换随机编码方式，会存在收敛性问题，因为不同随机编码方式得到的目标函数值可能不一样，因此无法简单地根据两次迭代的目标函数值判断当前编码方式是否收敛. 本文的动态编码反演方法对每一组随机编码都迭代5~10次再更换编码，这样既能有效利用当前编码信息稳定地更新模型，又能方便地判断当前编码方式是否收敛.

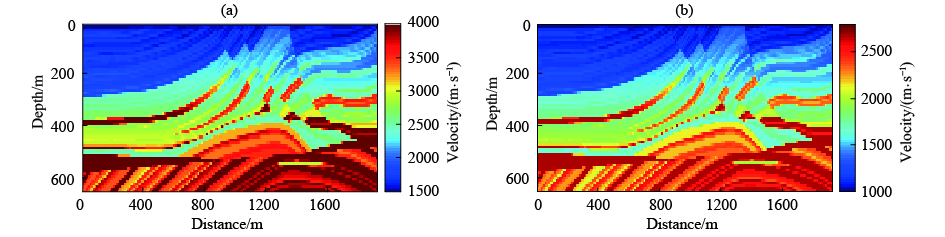
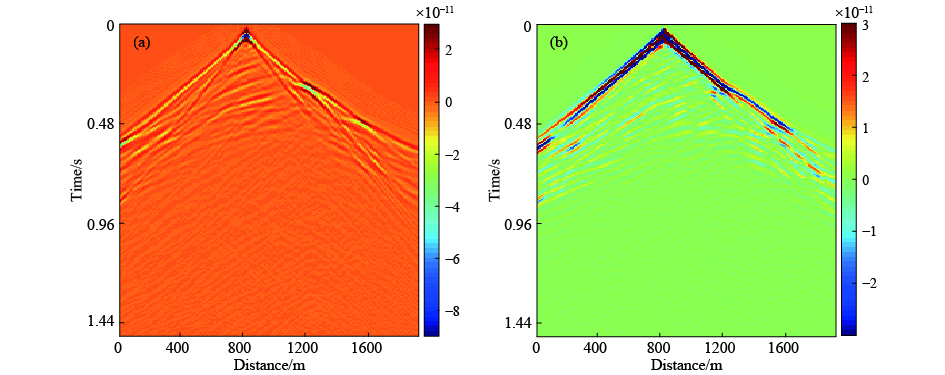
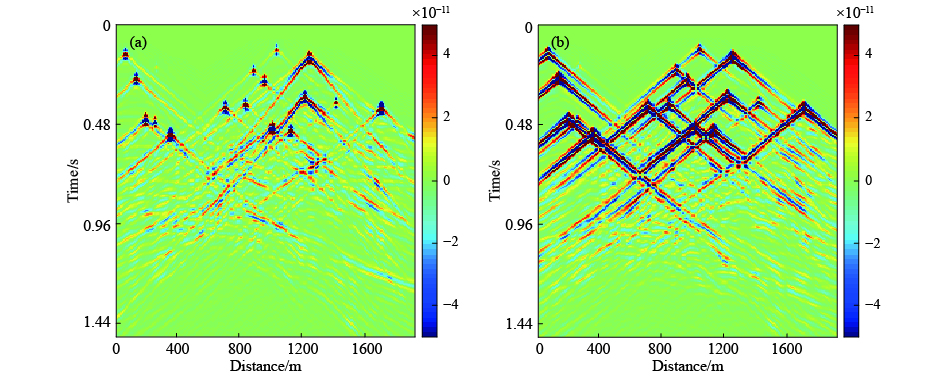
采用如图1所示的Marmousi模型，纵波和横波速度模型分别如图1a和1b所示. 模型大小为65×192，网格间距为10 m. 首先模拟单炮记录. 检波器布设在地表，间距为10 m. 炮点选在地表x=810 m处. 子波采用主频为20 Hz的雷克子波，震源采用压力震源. 采样间隔为0.8 ms. 记录1.5 s的位移垂直分量(Z分量)和水平分量(X分量)分别如图2a和图2b所示. 可见，两个分量的记录中均包含清晰的直达波和反射波信息. 然后，采用公式(8)构建超级炮震源，一个超级炮含有19个单炮震源. 用超级炮震源在图1的模型上进行正演，得到的Z分量和X分量的超级炮记录分别如图3a和图3b所示. 可见，随机编码使得超级炮中的各单炮记录能量、相位、激发时间和激发位置各不相同，这将有利于压制梯度计算时的串扰噪声.

3 基于各向异性TV约束的弹性波全波形反演 3.1 基于各向异性TV约束的弹性波反演策略

串扰噪声是多炮地震记录在应用成像条件时，不相关炮记录成像导致的. 对多炮进行随机编码，则串扰噪声也将是随机的，这可以在一定程度上离散串扰噪声. 而本文提出的动态多震源反演策略，每隔几次迭代会更换一次编码，这会进一步增加串扰噪声的离散程度，使最终残留的串扰噪声呈现随机分布的噪声状态. 这些噪声对模型浅部和层内速度的均匀性影响较大. 可引入TV约束来压制反演后期这些残留的串扰噪声. 本文提出的TV约束速度模型最优化问题的目标函数可以表示为

$J = \left\| {{\mathit{\boldsymbol{m}}}_k^* - \left( {{\mathit{\boldsymbol{m}}}_{k - 1}^* + \alpha \cdot\Delta {\mathit{\boldsymbol{m}}}} \right)} \right\| + 2\lambda {\left\| {{\mathit{\boldsymbol{m}}}_k^*} \right\|_{\rm TV}},$

(10)

其中， ${\mathit{\boldsymbol{m}}}_k^*$ 和 ${{\mathit{\boldsymbol{m}}}_{k - 1}^*}$ 分别为第k次和第k-1次TV去噪后的更新模型，这里代表纵波速度模型和横波速度模型，α为步长，∆m为模型更新量，λ为TV约束的权系数. 模型的各向同性TV范数可以写为

$\begin{split}{\left\| {\mathit{\boldsymbol{m}}} \right\|_{\rm TV}} \!=\!\!\! \mathop \sum \limits_{i = 1}^{n{\textit z} \! - 1} \mathop \sum \limits_{j = 1}^{nx - 1} \!\! \sqrt {{{\left( {{{\mathit{\boldsymbol{m}}}_{i,j}} - {{\mathit{\boldsymbol{m}}}_{i + 1,j}}} \right)}^2} \!\!+\! {{\left( {{{\mathit{\boldsymbol{m}}}_{i,j}} \!-\! {{\mathit{\boldsymbol{m}}}_{i,j + 1}}} \right)}^2}} \\\;\;\;\;\;\;\; + \mathop \sum \limits_{i = 1}^{n{\textit z} - 1} \left| {{{\mathit{\boldsymbol{m}}}_{i,{{nx}}}} \!\!- {{\mathit{\boldsymbol{m}}}_{i + 1,nx}}} \right| \!+ \mathop \sum \limits_{j = 1}^{nx - 1} \left| {{{\mathit{\boldsymbol{m}}}_{n{\textit z},j}} \!- {{\mathit{\boldsymbol{m}}}_{n{\textit z},j + 1}}} \right|,\end{split}$

(11)

其中，nz和nx分别为模型垂向和横向的网格点数. 模型的各向异性TV范数可以写作

$\begin{split} {\left\| {\mathit{\boldsymbol{m}}} \right\|_{\rm TV}} = & \sum\limits_{i = 1}^{n{\textit z} - 1} {\sum\limits_{j = 1}^{nx - 1} {\left\{ {\left| {{{\mathit{\boldsymbol{m}}}_{i,j}} - {{\mathit{\boldsymbol{m}}}_{i + 1,j}}} \right| } \right.} } \\ & + \left. {\left| {{{\mathit{\boldsymbol{m}}}_{i,j}} - {{\mathit{\boldsymbol{m}}}_{i,j + 1}}} \right|} \right\} + \sum\limits_{i = 1}^{n{\textit z} - 1} {\left| {{{\mathit{\boldsymbol{m}}}_{i,nx}} - {{\mathit{\boldsymbol{m}}}_{i + 1,nx}}} \right|} \\& + { \sum\limits_{j = 1}^{nx - 1} {\left| {{{\mathit{\boldsymbol{m}}}_{n{\textit z},j}} - {{\mathit{\boldsymbol{m}}}_{n{\textit z},j + 1}}} \right|} .}\end{split}$

(12)

以上两种TV约束问题都可以通过快速梯度投影(Fast Gradient Projection, FGP)算法求解(Beck and Teboulle, 2009b).

定义L为一个线性算子，表示为

$\begin{split}L{\left( {{\mathit{\boldsymbol{p}}},{\mathit{\boldsymbol{q}}}} \right)_{i,j}} = & {p_{i,j}} + {q_{i,j}} - {p_{i - 1,j}} - {q_{i,j - 1}},\;\\& \!\!\!\! i = 1, \cdots, n{\textit z}, \,\, j = 1, \cdots ,nx.\end{split}$

(13)

L的共轭算子可以写为 ${L^{\rm T}}\left( x \right) = \left( {{\mathit{\boldsymbol{p}}},{\mathit{\boldsymbol{q}}}} \right)$ ，其中

$\left\{ \begin{aligned}& {p_{i,j}} \!\!=\! {x_{i,j}} \!-\! {x_{i + 1,j}},\;i \!=\! 1, \cdots ,n{\textit z} - 1,\;\;j \!=\! 1, \cdots ,nx,\\& {q_{i,j}} \!\!=\! {x_{i,j}} \!-\! {x_{i,j + 1}},\;i \!=\! 1, \cdots ,n{\textit z},\;\;j \!=\! 1, \cdots ,nx - 1.\end{aligned} \right.$

(14)

定义P_C为集合C内的正交投影算子，集合C的上下界分别为u和l. P_C可以表示为

${P_C}{\left( x \right)_{i,j}} = \left\{ {\begin{aligned}{l\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_{i,j}} < l,}\\{{x_{i,j}}\;\;\;\;\;\;\;l \leqslant {x_{i,j}} \leqslant u,}\\{u\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_{i,j}} > u.}\end{aligned}} \right.$

(15)

基于TV约束的全波形反演算法流程可以表示为：

第1步：设置初始模型v₀，震源子波S，最大迭代次数M，以及其他FWI参数，k=1.

第2步：当迭代次数k>M，跳到第7步；当迭代次数k≤M，根据公式(5)计算模型更新量∆m，令ks=1.

第3步：计算步长α.

第4步：如果ks<10，设置TV约束权重λ和FGP算法最大迭代次数N的值，令t₁=1，r₁，s₁，p₀，q₀为零矩阵，i=1；如果ks≥10，跳到第7步.

第5步：当i≤N时，执行以下FGP算法；当i>N时，执行第6步.

$\begin{split}\left( {{{\mathit{\boldsymbol{p}}}_i},{{q}_i}} \right) = & {P_\xi }\left\{ {\left( {{{r}_i},{{s}_i}} \right)} \right.\\& + \frac{1}{{8\lambda }}{L^T}\left. {\left( {{P_C}\left[ {\left( {{m}_{k - 1}^* + \alpha \cdot \Delta {m}} \right) - \lambda \cdot L\left( {{{r}_i},{{s}_i}} \right)} \right]} \right)} \right\},\end{split}$

(16)

${t_{i + 1}} = \frac{{1 + \sqrt {1 + 4t_i^2} }}{2},\quad \quad \quad \quad \quad \quad \quad \quad \quad $

(17)

$\begin{split}&\left( {{{\mathit{\boldsymbol{r}}}_{i + 1}},{{\mathit{\boldsymbol{s}}}_{i + 1}}} \right) = \\& \quad \quad \quad \left( {{{\mathit{\boldsymbol{p}}}_i},{{\mathit{\boldsymbol{q}}}_i}} \right) + \left( {\frac{{{t_i} - 1}}{{{t_{i + 1}}}}} \right)\left( {{{\mathit{\boldsymbol{p}}}_i} - {{\mathit{\boldsymbol{p}}}_{i - 1}},{{\mathit{\boldsymbol{q}}}_i} - {{\mathit{\boldsymbol{q}}}_{i - 1}}} \right),\\& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad{i = i + 1.}\end{split}$

(18)

第6步：计算 ${\mathit{\boldsymbol{m}}}_k^* = {P_C}\left[ {\left( {{\mathit{\boldsymbol{m}}}_{k - 1}^* + \alpha \cdot\Delta {\mathit{\boldsymbol{m}}}} \right) - \lambda L\left( {{{\mathit{\boldsymbol{p}}}_N},{{\mathit{\boldsymbol{q}}}_N}} \right)} \right]$ . 当目标函数 ${E_k} > {E_{k - 1}}$ 时，令步长 $\alpha = 0.5\alpha $ ， $ks = ks + 1$ ，返回第4步；当目标函数 ${E_k} < {E_{k - 1}}$ 时，k=k+1，返回第2步.

第7步：输出最终结果 ${\mathit{\boldsymbol{m}}}_k^*$ .

以上算法流程使用各向同性TV约束和各向异性TV约束的求解过程是一样的，只是投影算子P_ξ的计算不同. 令 ${P_\xi }\left( {{\mathit{\boldsymbol{p}}},{\mathit{\boldsymbol{q}}}} \right) = \left( {{\mathit{\boldsymbol{r}}},{\mathit{\boldsymbol{s}}}} \right)$ ，如果使用各向同性TV约束，投影算子的计算为

${r_{i,j}} = \left\{ {\begin{aligned}& \frac{{{p_{i,j}}}}{{\rm max\left\{ {1,\sqrt {p_{i,j}^2 + q_{i,j}^2} } \right\}}}\\& \quad \quad i = 1, \cdots ,n{\textit z} - 1,\;j = 1, \cdots ,nx - 1,\\& \frac{{{p_{i,nx}}}}{{{\rm max}\left\{ {1,\left| {{p_{i,nx}}} \right|} \right\}}}\\& \quad \quad i = 1, \cdots ,n{\textit z} - 1,\end{aligned}} \right.$

(19)

${s_{i,j}} = \left\{ {\begin{split}& \frac{{{q_{i,j}}}}{{\rm max\left\{ {1,\sqrt {p_{i,j}^2 + q_{i,j}^2} } \right\}}}\\& \quad \quad i = 1, \cdots ,n{\textit z} - 1,\;j = 1, \cdots ,nx - 1,\\& \frac{{{q_{n{\textit z},j}}}}{{{\rm max}\left\{ {1,\left| {{q_{n{\textit z},j}}} \right|} \right\}}}\\& \quad \quad j = 1, \cdots ,nx - 1.\end{split}} \right.$

(20)

如果使用各向异性TV约束，投影算子的计算为

${r_{i,j}} \!\!=\!\! \frac{{{p_{i,j}}}}{{{\rm max}\left\{ {1,\left| {{p_{i,j}}} \right|} \right\}}}\;\;\;i \!\!=\!\! 1, \cdots ,n{\textit z},\;j \!\!=\!\! 1, \cdots ,nx,$

(21)

${s_{i,j}} \!\!=\!\! \frac{{{q_{i,j}}}}{{{{\rm max}}\left\{ {1,\left| {{q_{i,j}}} \right|} \right\}}}\;\;\;i \!\!=\!\! 1, \cdots ,n{\textit z},\;j \!\!=\!\! 1, \cdots ,nx.$

(22)

以上算法流程中有两个迭代停止条件，分别为k>M和ks≥10. k>M表示当迭代次数大于最大迭代次数时，迭代终止. ks≥10表示当减小步长至很小，仍然无法保证收敛的情况下，迭代终止. 流程第3步的步长计算方法是首先给出一个试探步长，使最大速度更新量限制在一定范围之内，然后根据需要采用二分法逐步减小步长，减小的方法在流程的第6步中.

流程第5步为FGP算法的核心. 公式(16)为常规的梯度投影算法公式，其表示在约束范围内按梯度方向搜索，当梯度搜索方向超出约束范围时，将迭代方向投影到约束边界上搜索. 其中，线性算子L为一个散度算子，计算方法见式(13)，其共轭算子L^T可以看作一个梯度算子，计算方法见式(14). 算子P_C是为了限制结果的上下界，其计算见式(15). P_ξ为投影算子，对于不同TV约束方法，P_ξ的计算见式(19)—(22). FGP算法的公式(17)和公式(18)是对常规梯度投影算法的改进，通过引入中间变量t、r和s来加速算法收敛. 该加速方法是Beck和Teboulle (2009b)在借鉴快速迭代收缩阈值算法的基础上，对常规梯度投影算法改进得到的.

由以上分析可知，动态多震源反演后期串扰噪声主要呈现离散的随机噪声状态. 另外，当地震数据中含有噪声时，反演结果中也将存在离散的随机噪声. 下面对速度模型加入强随机噪声来测试各向同性TV和各向异性TV约束对随机噪声的压制效果. 对图1a所示的纵波速度模型加入强随机噪声，如图4a所示. 因为噪声较强，这里采用较大的TV约束权重来压制噪声和突出模型界面. 采用的TV约束权重为λ=200，迭代1000次，各向同性TV约束和各向异性TV约束对噪声的压制结果分别如图4b和4c所示，图中红、黑、蓝箭头所示的三处为对比较为明显的细节结构. 可见，各向异性TV约束在保持细节构造连续性方面的效果要好于各向同性TV约束. 对黑箭头和蓝箭头所示的两个细节界面的横向局部抽线对比结果如图4d所示，可见，由于噪声较强，两种TV约束去噪后的速度值都有些偏离真实速度值，但是对噪声的压制效果很明显，各向异性TV约束能更好地保留真实速度在界面上的连续性. 因此，各向异性TV约束对噪声的压制和模型的恢复程度好于各向同性TV约束. 本文基于TV约束的弹性波全波形反演算法采用的都是各向异性TV约束.

3.2 新的多尺度反演策略

由于前文介绍的动态多震源反演策略和TV约束反演算法的主要作用是压制反演过程的串扰噪声，不具有明显的抑制跳周的作用. 为了保证反演在高主频震源时能得到好的效果，这里我们将基于稀疏约束的多尺度反演策略(Zhang et al., 2016, 2017)引入到各向异性TV约束的弹性波全波形反演中.

假设地震子波是非时变和非空变的稳定子波，将地震记录看作是宽带的地下反射脉冲响应和有限带宽的地震子波的褶积. 构建L1范数约束问题，并采用稀疏算法求解，可得到一系列尖脉冲，即为地下反射脉冲响应. 提取反射脉冲响应的过程需要已知地震子波. 在声波情况下，Zhang等(2017)提出首先用常规方法估计子波，然后结合稀疏盲反褶积算法校正子波的振幅和时移误差，从而能同时获得较好的反射脉冲响应和子波估计结果. 因此，本文提取反射脉冲响应的过程都是在假设观测记录子波已知的情况下进行的. 将得到的宽带地下反射脉冲响应褶积上低主频子波，即可重构得到相应的低主频地震记录. 依次将得到的低主频地震记录作为观测记录，即可进行多尺度全波形反演. 将该方法与上文基于TV约束的全波形反演流程结合即为一种新的相应于TV约束的多尺度全波形反演算法. 由于该方法在低频缺失时具有低频重构的作用，因此较常规基于滤波的多尺度方法(Bunks et al., 1995; Boonyasiriwat et al., 2009)具有明显的优势.

研究发现，对于多震源弹性波全波形反演来说，低主频数据反演效果稳定，串扰噪声较弱. 随着主频的增高，串扰噪声增强，经过动态多震源反演策略后噪声的离散性增强. 因此在多尺度反演的不同尺度，TV约束的权重不同. 多尺度对应的主频越高，需要去除的串扰噪声越强，所用的TV约束的权重越大.

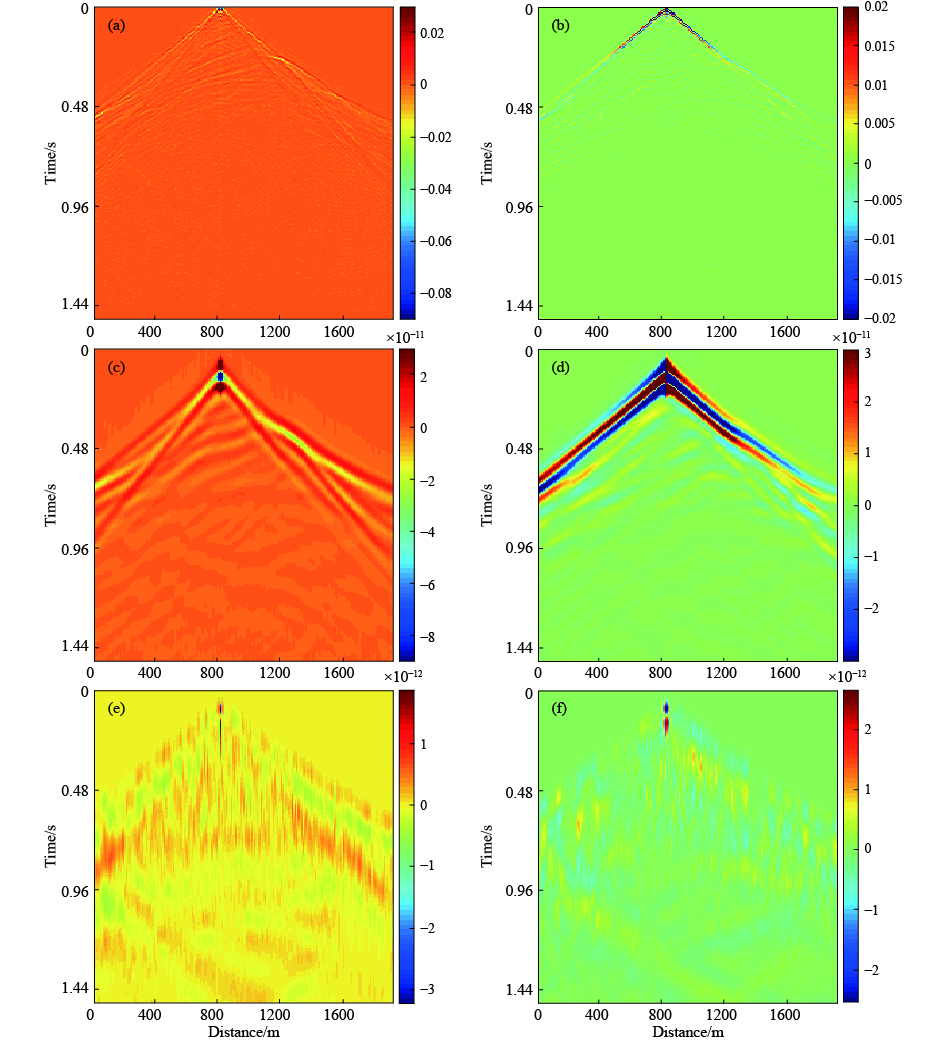
下面用弹性波地震记录对这种低频重构算法进行测试. 对于图2中所示弹性波记录，采用快速迭代收缩阈值算法(Fast Iterative Shrinkage-Thresholding Algorithm, FISTA)(Beck and Teboulle, 2009a)提取反射脉冲响应，得到的Z分量和X分量脉冲响应分别如图5a和5b所示. 可见，脉冲响应相当于地震记录波形被压缩的结果. 将其分别褶积上主频为8 Hz的雷克子波，得到重构的低频地震记录，Z分量和X分量结果分别如图5c和5d所示. 利用8 Hz主频的雷克子波做有限差分正演模拟，得到低频参考记录. 计算重构记录与参考记录的差剖面，Z分量和X分量的差剖面分别如图5e和5f所示. 可见，除了震源处残留能量较大外，其他波场信息残留较小，说明重构记录包含了真实低主频记录的绝大部分信息. 这也说明了，这种基于稀疏约束的低频重构算法，对于弹性波记录仍然适用. 下文中基于TV约束的全波形反演方法都是基于此多尺度策略进行的，较低尺度的观测数据都是由该低频重构算法生成.

4 数值算例 4.1 稀疏约束多尺度与常规多尺度反演策略

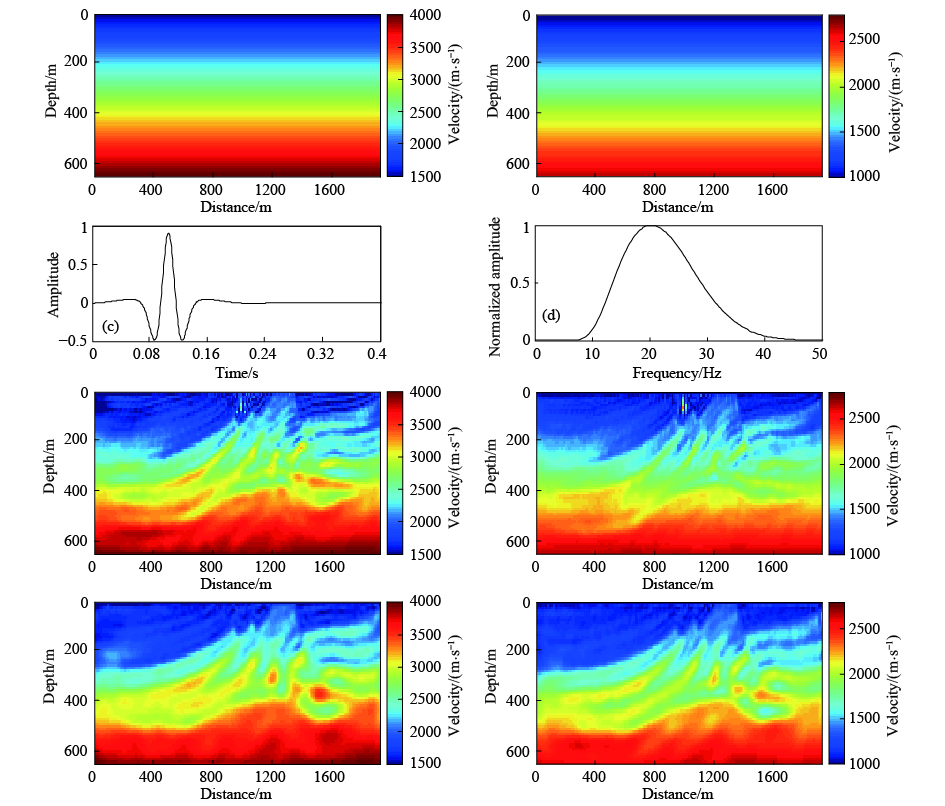
本文提出的稀疏约束多尺度反演策略相对于常规滤波多尺度反演策略有两个明显的优势：(1)稀疏约束多尺度方法无需对子波进行滤波处理，因此无需考虑低通滤波子波与低通滤波数据的匹配问题，而且褶积重构得到的地震记录的子波是确定已知的，能减小子波不确定对反演结果的影响；(2)在低频缺失情况下，基于稀疏约束的方法可以重构出部分缺失的低频信息，使反演能在较低的频带进行，而常规滤波多尺度方法只能在已有的频带中提取较低频段的信息. 本节在低频缺失的情况下对比稀疏约束多尺度与常规多尺度反演方法. 采用如图1所示的Marmousi模型作为真实模型，初始模型采用线性梯度模型，初始V_P和V_S模型分别如图6a和6b所示. 采用20 Hz主频且缺失7 Hz以下信息的雷克子波作为震源子波，子波的波形和频谱分别如图6c和6d所示. 首先进行常规滤波多尺度反演，采用巴特沃斯低通滤波器提取低频信息，低通滤波参数采用10 Hz. 由于滤波器具有一定的频率截断宽度，因此保留的有效信息在7~15 Hz之间. 进行该尺度的反演，迭代200次，得到的V_P和V_S反演结果分别如图6e和6f所示. 可见，常规滤波多尺度反演由于缺乏超低频信息，模型左侧边界附近和浅部均出现局部极小值，且该方法对深部构造的反映模糊. 采用稀疏约束多尺度反演，首先重构出相应8 Hz主频的观测记录，相应的有效能量在1~15 Hz之间. 在该尺度下反演，迭代200次，得到的V_P和V_S反演结果分别如图6g和6h所示. 可见，稀疏约束多尺度反演浅部没有出现明显的局部极小值，且深部构造和低速层较常规多尺度方法有更好的显示. 因此，本文提出的稀疏约束多尺度反演策略在低频缺失情况下，比常规基于滤波的多尺度反演具有比较明显的优势.

4.2 无噪情况下多尺度TV约束反演测试

下面在无噪情况下测试以上基于各向异性TV约束的弹性波全波形反演方法和基于稀疏约束的多尺度反演策略，并对比其与常规全波形反演的效果. 采用的纵波速度和横波速度初始模型分别如图6a和6b所示，均为线性梯度模型. 检波器布设在地表全偏移距接收，震源采用20 Hz主频的雷克子波. 反演过程都采用动态多震源全波形反演策略. 首先，直接对20 Hz主频的观测记录进行全波形反演，迭代300次，得到的纵波和横波速度模型分别如图7a和7b所示. 可见，反演过程跳周严重，串扰噪声使得结果层内光滑度很低. 然后，采用基于稀疏约束的多尺度反演策略，并应用TV约束. 先反演8 Hz主频的尺度，再反演20 Hz主频的尺度. 在低频尺度反演时，由于结果中界面信息不明显，因此TV约束权重λ=0. 在20 Hz主频尺度反演时，采用λ=0.5. 总共迭代300次，得到的纵波和横波速度模型结果分别如图7c和7d所示. 可见，反演过程的跳周问题被很好地克服，模型深部和浅部构造均得到较好的恢复. TV约束使反演结果构造更清晰，浅部的离散噪声被很好地压制，且模型层内速度较为均匀.

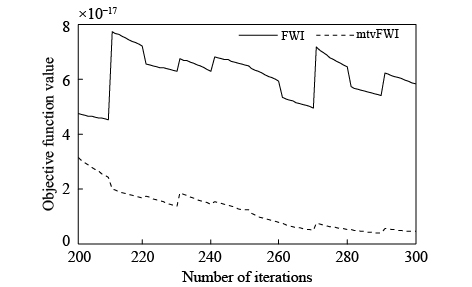
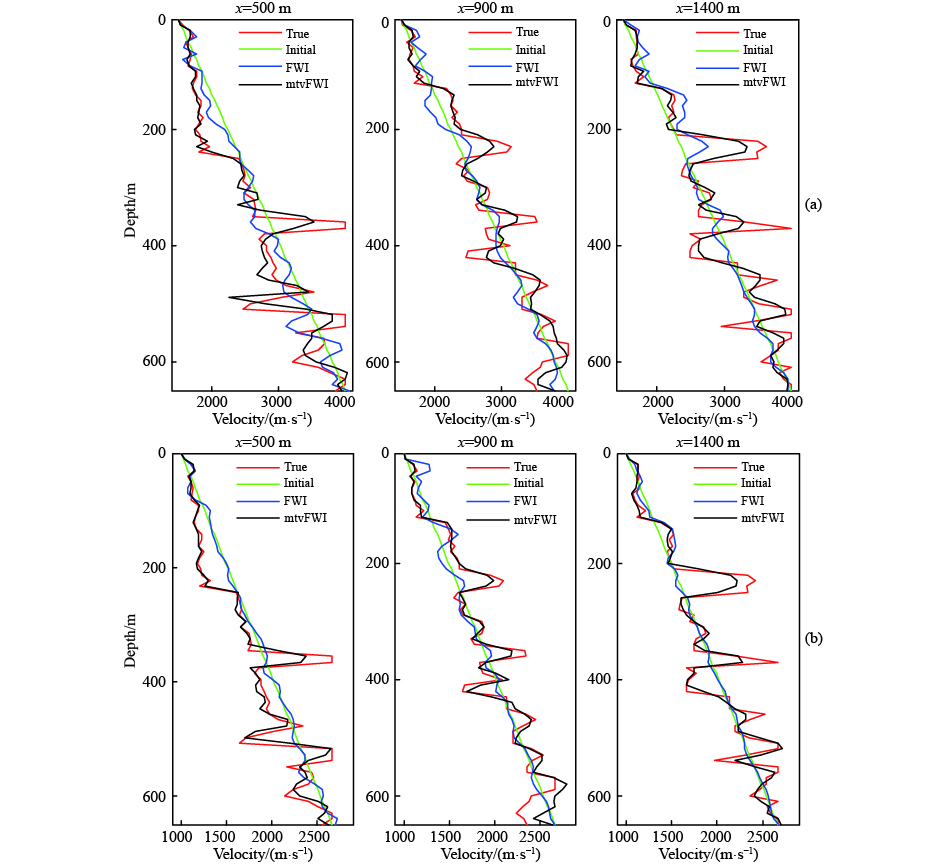
反演过程的目标函数如图8所示. 由于TV约束是在最后100次迭代加入的，因此这里只对比最后100次迭代的收敛曲线. 可见，常规FWI的目标函数曲线(FWI曲线)虽然在每个动态超级炮迭代中能下降，但是整体已没有下降趋势. 加入TV约束的稀疏约束多尺度反演的目标函数曲线(mtvFWI曲线)仍能较快地下降. 抽取图7中反演结果的单道进行对比，如图9所示. 可见，常规FWI反演结果偏离真实值很远. 加入了TV约束的稀疏约束多尺度反演结果(mtvFWI曲线)的V_P值和V_S值均较接近真实模型的速度曲线，且浅部和深部均未出现随机噪声干扰. 可见，在较差的初始模型下，本文提出的方法仍然能得到较好的反演结果.

4.3 含噪情况下多尺度TV约束反演测试

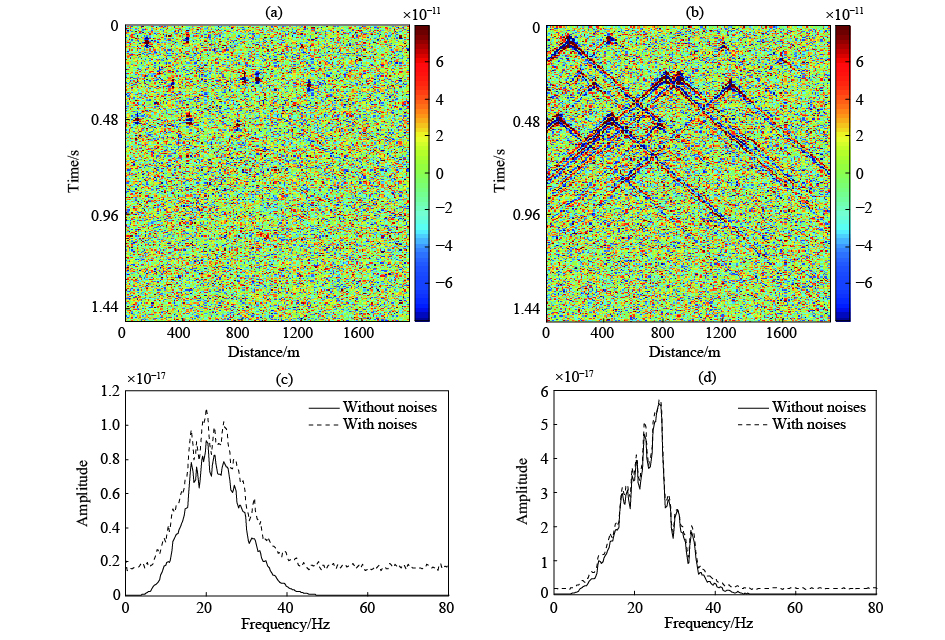
下面对本文的方法进行抗噪性测试. 无噪观测记录是由20 Hz主频的雷克子波采用随机编码生成的超级炮记录. 对观测记录加入高斯噪声，加噪后的Z分量和X分量的超级炮记录分别如图10a和10b所示. 可见，Z分量记录信息严重地淹没在噪声中，X分量记录可以看到直达波，而反射信息被淹没在噪声中. 加噪前后地震记录Z分量和X分量的频谱分别如图10c和10d所示. 可见，加入的噪声是全频带的.

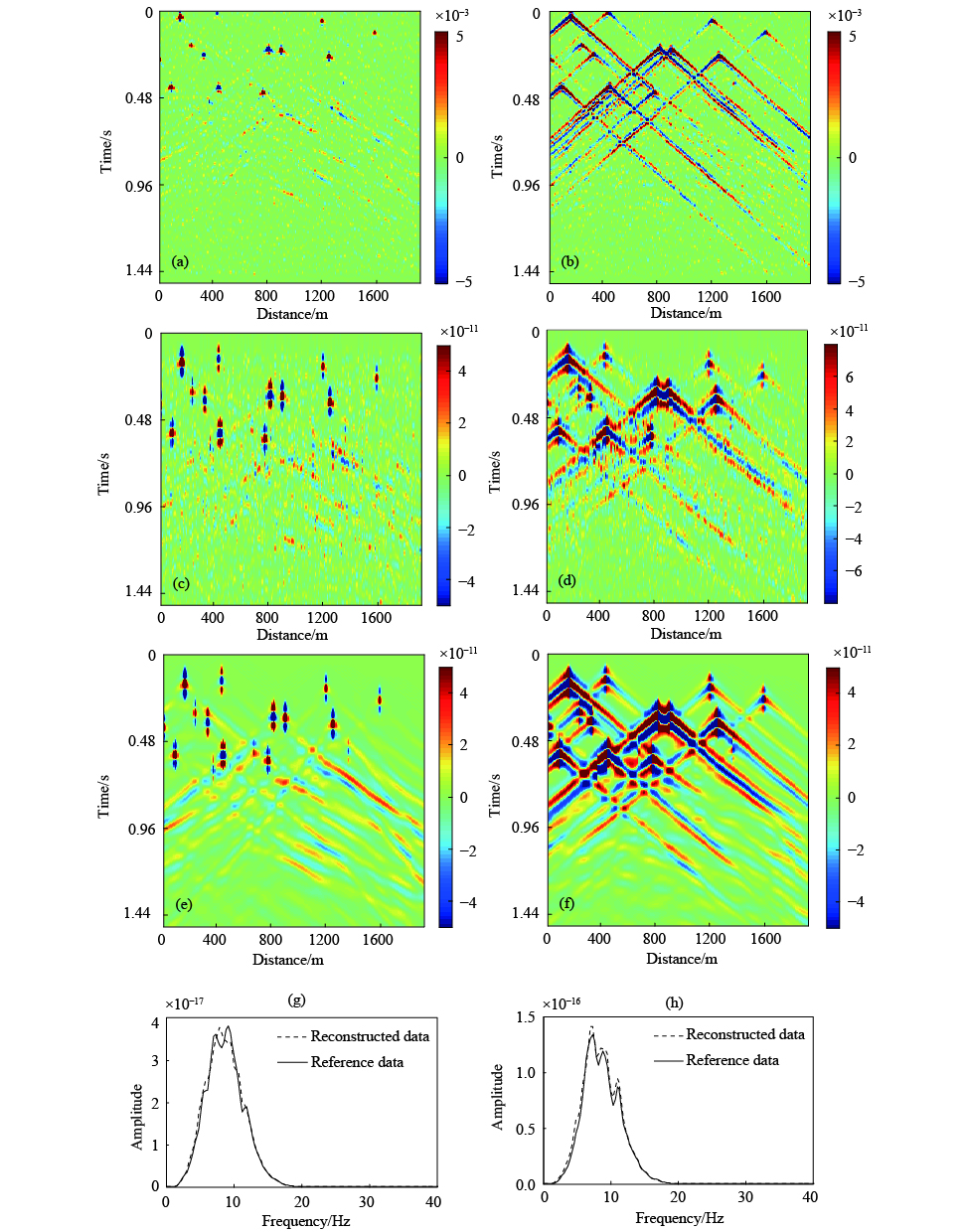
本文的稀疏约束低频重构方法对于含噪记录的重构，具有两个主要的优势：(1)增加稀疏约束的权重可以增强反射脉冲响应的比重，从而提高重构记录的信噪比；(2)提取得到的反射脉冲响应是全频带的，包含很多高频噪声，与低频子波的褶积相当于一个带通滤波过程，可以去除无效频带内的噪声干扰. 下面对噪声观测记录采用稀疏约束方法进行重构，得到相应主频为8 Hz的地震记录. 由于噪声的影响，提取得到的原始Z分量和X分量反射脉冲响应含有很多的异常值干扰，这些干扰主要是一些放大的高频噪声. 这里对原始反射脉冲响应30 Hz的低通滤波进行显示，Z分量和X分量的反射脉冲响应结果分别如图11a和11b所示. 可见，反射脉冲响应的信噪比有所提高，直达波能量明显. 重构得到的8 Hz主频的地震记录Z分量和X分量分别如图11c和11d所示. 可见，高斯噪声在重构记录中已被大大压制，呈现较弱的低频噪声干扰. 模拟8 Hz主频的参考记录，分别如图11e和11f所示. 对比可知，虽然重构结果的反射信息也被噪声掩盖，但是相对于原始含噪记录来说，噪声的干扰已经被大大削弱了，记录整体反射信息形态与参考记录接近. 对重构记录和参考记录进行频谱分析，Z分量和X分量的频谱对比分别如图11g和11h所示. 可见，相对于图10c和10d，重构记录中噪声的能量已被大大压制，重构记录频谱能量分布与参考记录频谱接近. 这相对于原始含噪观测记录来说，对反演是有利的.

对加噪后的地震记录进行全波形反演，初始模型仍然采用图6a和6b的线性模型. 首先进行常规全波形反演，迭代300次的结果如图12a和12b所示. 可见，高主频和噪声的影响使得反演结果跳周严重，且结果中包含很多噪声干扰. 应用多尺度反演策略, 并且加入TV约束，依次反演8 Hz和20 Hz主频两个尺度. 在低频尺度反演时，由于结果中界面信息不明显，因此TV约束权重λ=0. 在20 Hz主频尺度反演时，采用λ=0.8. 总共迭代300次的纵波和横波速度结果分别如图12c和12d所示. 可见，反演过程的跳周现象被大大压制，最终结果的浅部和深部构造均较为清晰. 数据中的观测噪声和震源混叠的串扰噪声的影响均被较好地压制.

反演过程的目标函数曲线如图13所示. 由于反演后期常规FWI目标函数的绝对数值与本文方法反演的目标函数值相差大约一个数量级，因此分别显示在图13a和13b中. 由于TV约束仍然是在最后100次迭代中加入的，因此只对比最后100次迭代的目标函数曲线. 常规FWI目标函数曲线整体已经没有了下降趋势，只在每个动态超级炮内部下降. 加入TV约束的稀疏约束多尺度反演(mtvFWI曲线)目标函数曲线仍然有较好的下降趋势，说明加入TV约束的反演过程仍然能够很好地收敛. 图12中反演结果的抽道对比结果如图14所示. 对比V_P和V_S的单道结果可知，常规FWI反演结果偏离真实结果很远，只在浅部有一定的结果. mtvFWI的反演结果中，V_P和V_S的浅部和深部速度均比FWI结果更接近真实值. 可见，本文提出的反演策略具有较强的抗噪性，能同时压制观测噪声和串扰噪声对反演结果的影响.

5 结论

针对提高弹性波全波形反演计算效率的问题，本文提出了一种新的动态混合震源编码策略. 该策略能大大提高正演的计算效率，并且在有效压制和离散串扰噪声的同时保证照明的均匀性. 经过动态反演策略后，多震源产生的残留串扰噪声呈现离散分布的随机状态. 本文提出了基于TV约束的全波形反演方法来压制剩余串扰噪声. 将各向异性TV约束引入弹性波全波形反演过程中，可以更有效地去除残留串扰噪声对结果的影响，并使结果层内速度均匀. 本文首次对基于稀疏约束的多尺度方法在弹性介质上进行测试，取得好的效果，说明这种基于稀疏约束的低频重构方法对于弹性波仍然适用.

数值算例表明：(1)本文提出的动态随机编码方式能较好地压制多震源弹性波全波形反演过程中的串扰噪声，并且能在保证照明均匀性的同时提高反演过程的收敛性；(2)本文提出的稀疏约束多尺度反演策略在低频缺失情况下，比常规基于滤波的多尺度反演具有比较明显的优势；(3)将各向异性TV约束引入混合震源弹性波全波形反演过程，可以在有效压制串扰噪声的同时保持较好的模型构造信息；(4)噪声测试说明本文提出的方法不仅对于压制多震源导致的串扰噪声有效，对于压制数据中的观测噪声对反演结果的影响也有很好的效果.

 

致谢　感谢美国加州大学圣克鲁兹分校(UCSC)吴如山老师和谢小碧老师在本研究过程中给予的帮助和建议. 感谢两名审稿专家和编辑老师对本文的建议和贡献. 感谢中国地质大学(北京)尤加春博士的讨论和建议. 本研究得到国家留学基金资助.