地球物理学报  2018, Vol. 61 Issue (12): 5044-5051 |
 PDF
|
, XU DengHui1
, GUO JunXin2, YANG Long3, WANG ZhenLin4, ZHANG Da5, LUO XingPing4, NIE JunGuang1, LI Hao1, JIANG JiaYang1
砂岩储层是一类分布广泛的重要储层，孔隙度、渗透率和孔隙结构等参数控制砂岩储层的产能，而砂岩的压实和胶结作用对这些性质具有重要的影响(David et al., 1994；Walderhaug，1996；Chen et al., 2011).因此，建立定量表征压实和胶结作用的统一声波速度模型对于应用地震和测井资料识别砂岩的有利储层、定量评价孔隙度以及开展横波速度预测等极为重要.
前人(Dvorkin et al., 1991, 1994；Agersborg et al., 2011)在分析声波测井和地震勘探的响应特征发现，压实和胶结作用会显著影响砂岩储层的弹性性质，因而可以通过建立岩石物理模型来将视压实率、视胶结率与砂岩的弹性性质联系起来.至今，前人提出了很多岩石物理模型来研究压实和胶结作用对砂岩(或颗粒介质)弹性性质的影响.Hertz(1882)研究了静水压力条件下颗粒介质的压实作用，提出了两种颗粒之间法向刚度的概念.Mindlin(1949)考察了切向力作用下两种颗粒之间的切向滑动，并给出了切向接触刚度的表达式.基于法向和切向接触刚度，可以计算颗粒介质(如砂岩)的体积和剪切模量.与Hertz-Mindlin模型中颗粒大小相同的假设不同，Brandt(1955)考察了颗粒粒径变化对颗粒介质弹性性质的影响并且提出了相应的体积模量计算模型.Digby(1981)假设两个颗粒存在初始的接触面积并且推导了净水围压条件下这种颗粒介质的弹性性质.Walton(1987)考察了颗粒介质切向滑动和法向位移同时发生的情况，分别给出了接触表面粗糙、光滑的颗粒介质的弹性模量计算模型.相对于之前的理论，Jenkins等(2005)的假设中允许颗粒之间的相对运动，这与之前理论中有关均匀应力场的假设不同，最终计算出的剪切模量比之前理论的计算结果更小.Agersborg等(2011)基于表层有附着物的包含体模型提出了一种定量表征压实作用的模型，模型计算结果与其他模型计算结果比较吻合.近期，Li和Han(2015)考察了颗粒接触面上的局部摩擦及非均匀应力场，在此基础上给出了疏松砂岩的弹性性质.
前面提到的理论只考虑了压实作用对砂岩(或颗粒介质)的影响，一些相关的模型也考虑了胶结作用的影响.Dvorkin等(1991, 1994)分析了分布在颗粒表面的胶结物对已固结颗粒介质弹性性质的影响，并针对胶结物含量较小的情况提出了接触胶结(CCT)模型.然后，Dvorkin和Yin(1995)将CCT模型拓展到颗粒之间有一定接触面积的情况下.为了克服原有CCT模型中胶结物含量较小的应用限制，Dvorkin等(1999)结合CCT模型和自洽理论(SCA)进一步拓展了CCT理论.Madadi和Christy(2012)修正了自洽相干势近似(CPA)，考察了配位数和颗粒接触区域弹性性质对颗粒介质整体弹性性质的影响.Madadi和Christy的模型预测结果与CCT模型的预测结果较为接近.韩学辉等(2014)、Guo和Han(2016)修正了原始的CCT模型，考察了胶结厚度对颗粒砂岩性质的影响.近期，Madadi和Saadatfar(2017)应用有限元数值模拟的方法同样考察了胶结厚度对砂岩弹性性质的影响，并给出了一系列砂岩弹性性质的经验计算公式.
虽然前人已经提出很多模型来研究压实或胶结作用对砂岩(或颗粒介质)弹性性质的影响，但是并没有综合考察这两种作用对于砂岩(或颗粒介质)弹性性质的影响.在很多砂岩中，压实作用和胶结作用对它们的弹性性质都有着显著的影响.本次研究，选取视压实率和视胶结率定量表征砂岩成岩作用，通过建立视压实率与颗粒配位数的关系将压实作用的影响引入修正的CCT模型(考虑了胶结作用对岩石模量及声波速度的影响)，最终建立了一种能够定量表征压实和胶结作用对砂岩声波速度影响的岩石物理模型，通过实例定量考察了压实作用和胶结作用对声波速度的影响.最后，为了验证理论模型，将理论预测结果与人工样品、天然样品的实验测量声波速度进行了对比，取得了较好的结果.
1 理论模型为了建立定量表征压实作用和胶结作用声波速度模型，本次研究以定量表征胶结作用的CCT模型(Dvorkin et al., 1994)为基础，通过建立配位数与压实作用关系来定量表征压实作用，最终建立定量表征压实、胶结作用的砂岩统一声波速度模型.
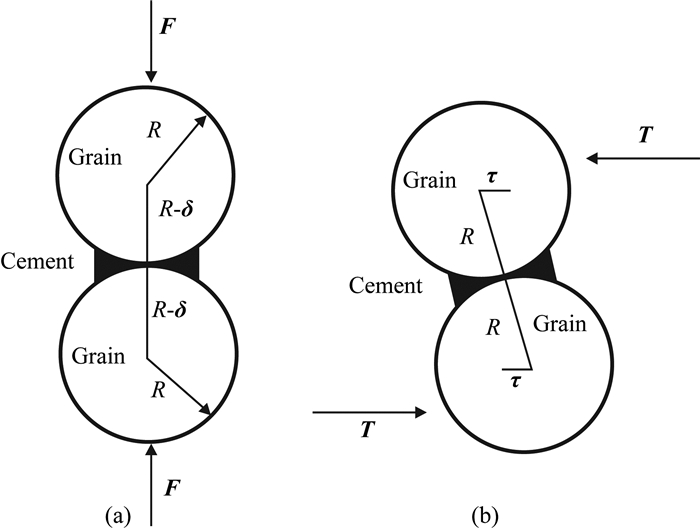
1.1 接触胶结模型(CCT)及修正的CCT模型 1.1.1 接触胶结模型(CCT)Dvorkin等(1994)提出了CCT模型来定量表征胶结作用对砂岩弹性性质的影响.在这个理论中，颗粒和胶结物的分布状态如图 1所示.法向应力和切向应力作用于颗粒与胶结物的组合体中并产生了相应的法向和切向位移(图 1).因此，根据法向和切向刚度的定义可以得到颗粒-胶结物组合体的法向和切向刚度.公式为
|
图 1 作用在颗粒和胶结物组合体上的法向(a)和切向应力(b)及相应的法向和切向位移 Fig. 1 The application of the normal (a) and tangential forces (b) on the grain-cement combination and the corresponding normal and tangential displacements relative to the grain contact point |
|
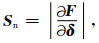
(1) |
|
(2) |
式中，F和T分别是作用在颗粒-胶结物组合体的法向和切向应力；δ和τ分别是颗粒中心点相对颗粒接触点的法向和切向位移.
应用法向刚度和切向刚度，砂岩的体积模量和剪切模量可以用式(3)、(4)计算得到(Winkler，1983)：
|
(3) |
|
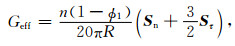
(4) |
式中，Keff和Geff分别是砂岩的体积和剪切模量，n为配位数，ϕ1为孔隙度，R为颗粒半径.
因此，胶结砂岩的纵波和横波速度可以用式(5)、(6)计算得到：
|
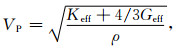
(5) |
|
(6) |
式中，VP和VS分别是砂岩的纵波和横波速度；ρ是砂岩的密度.
1.1.2 修正的CCT模型Dvorkin等(Dvorkin et al., 1994; Dvorkin and Nur, 1996)忽略了胶结厚度(颗粒之间的最小胶结层厚度)的影响并且假设在CCT模型中，颗粒之间的接触方式为点接触.然而，韩学辉等(2014)认识到天然的岩心特别是基底式胶结泥质砂岩存在胶结厚度并不为零的情况.通常情况下，砂岩颗粒之间并不总是直接接触，而当胶结厚度不为零时，它会对砂岩的弹性性质产生显著的影响.因此，考虑到胶结厚度的影响，他们修正了原有的CCT模型.当考虑胶结厚度的影响时，砂岩的体积和剪切模量可以通过式(7)、(8)计算得到(Dvorkin et al., 1994；韩学辉等，2014)：
|
(7) |
|
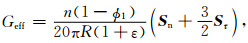
(8) |
式中，ε是根据颗粒半径R归一化的胶结厚度，n为配位数.
根据计算得到的体积模量与剪切模量，应用式(5)和式(6)可以计算得到砂岩的纵波速度和横波速度.
1.2 基于修正的CCT模型的综合考察压实和胶结作用的岩石物理模型为了定量表征压实和胶结作用对砂岩弹性性质的影响，定义视压实率γ作为压实前后的相对孔隙体积变化，定义视胶结率β为胶结物占据的体积与总孔隙体积的比值(Houseknecht，1987).因此，视压实率γ和视胶结率β的表达式为
|
(9) |
|
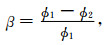
(10) |
式中，ϕ0和V0分别是砂岩压实前的孔隙度和总体积，V1是压实后砂岩的体积，ϕ1是压实后粒间孔隙度，ϕ2是胶结物的百分含量.
既然修正的CCT模型定量表征了胶结作用对砂岩弹性性质的影响，可以用视胶结率直接替换修正的CCT模型中的相应参数来更好地反映胶结作用的影响.将式(10)带入归一化胶结半径的表达式中(Dvorkin et al., 1994; Dvorkin and Nur, 1996，韩学辉等，2014)中，可以得到两种胶结方式的归一化胶结半径表达式.式(11)为胶结物仅分布在颗粒之间时的归一化胶结半径表达式，式(12)为胶结物均匀分布在颗粒周围时的归一化胶结半径表达式.应用式(11)、式(12)可以定量表征胶结作用对砂岩弹性性质的影响.式(11)、(12)为
|
(11) |
|
(12) |
压实作用会降低砂岩的孔隙度，增加配位数(Murphy Ⅲ，1982).式(7)和式(8)表明砂岩的弹性模量会随着孔隙度的减小、配位数的增加而增大.为了定量表征压实作用对砂岩弹性性质的影响，本文考虑建立视压实率与配位数的关系.
首先，假设压实过程中砂岩的颗粒体积保持恒定，砂岩总体积的变化全部由孔隙体积的变化引起，可以得到关系式为
|
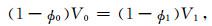
(13) |
|
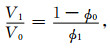
(14) |
将式(12)带入式(9)中，有：
|
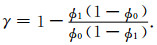
(15) |
其次，假设砂岩颗粒具有相同的粒径，可以应用Smith的关系式(Smith et al., 1929)建立砂岩临界孔隙度ϕ1与配位数n的关系，表达式为
|
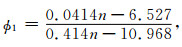
(16) |
将式(16)带入式(15)中，可以得到视压实率和配位数的关系式为
|
(17) |
最后，将式(17)带入式(7)和式(8)当中，就可以考察压实作用对砂岩弹性性质的影响.因此，基于修正的CCT模型，可以得到能够定量表征压实、胶结作用对砂岩弹性性质影响的统一的岩石物理模型.
2 数值算例 2.1 参数设定为了考察压实和胶结作用对砂岩弹性性质的影响，分析了一种由石英砂和黏土胶结物组成的砂岩样品.计算参数设定如下：石英砂颗粒的体积模量是37 GPa，剪切模量是44 GPa，密度是2.65 g·cm-3；胶结物的体积模量为21 GPa，剪切模量为7 GPa，密度是2.6 g·cm-3.假设胶结物仅仅分布在颗粒接触处或者均匀分布在颗粒周围，胶结厚度为0.02.同时假设砂岩的原始孔隙度为0.38.根据这些参数及前述计算模型，可以计算出不同视压实率和视胶结率的砂岩的纵波和横波速度.
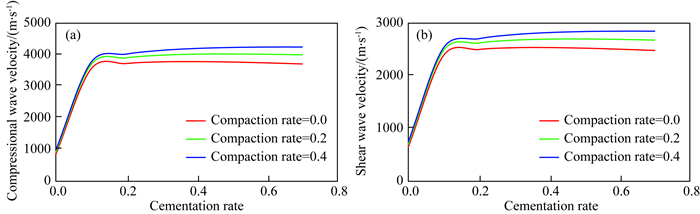
2.2 声波速度随视压实率和视胶结率的变化图 2给出了当胶结物仅分布在颗粒接触处(第一种胶结方式)时砂岩声波速度随视压实率和视胶结率的变化趋势.从图 2中可以看出，当视胶结率较小时，纵波速度和横波速度随视胶结率的增大而迅速增大.原因是当视胶结率较小时，砂岩的法向和切向刚度对胶结物含量非常敏感.因此，胶结物含量的微小变化就会显著增加砂岩的法向和切向刚度，提高砂岩的纵波和横波速度.随着视胶结率的继续增加，纵波速度和横波速度会出现轻微的下降.这是因为视胶结率继续增加，砂岩弹性模量随视胶结率的增加速度显著减慢，砂岩密度随视胶结率的增加速度大于弹性模量的增加速度.根据式(5)和式(6)，砂岩的声波速度会随着视胶结率的增加缓慢的下降.轻微下降之后，随着视胶结率的增加砂岩的声波速度将趋于定值.这说明此时随着视胶结率的增加，弹性模量的增大速度和密度的增大速度相同.
|
图 2 当胶结物仅分布在颗粒接触处时，纵波(a)和横波(b)速度随压实率、胶结率的变化 Fig. 2 The variations of the compressional (a) and shear (b) wave velocities with the cementation and compaction degrees when the cement is only distributed at the grain contacts |
对比不同视压实率的砂岩声波速度可以发现，随视压实率增大，纵波速度和横波速度逐渐增大.因为在本文中考虑的是相对较弱的压实作用，压实作用的主要影响是增大颗粒配位数，而配位数的增加会提高砂岩的弹性模量和声波速度.当视胶结率较低时，视压实率对砂岩声波速度的影响较小；当视胶结率较高时，视压实率的影响变得显著.产生这一现象的原因是本文主要研究弱压实作用对砂岩声波速度的影响，其主要影响颗粒配位数进而改变砂岩弹性性质.当视胶结率较低时，砂岩的法向和切向刚度较小.因此，根据式(7)和式(8)，配位数的增加不会引起砂岩声波速度的显著变化.然而，随着视胶结率的增加，法向和切向刚度会逐渐变大，配位数的增加就会显著提高砂岩的声波速度.
图 3给出了当胶结物均匀分布在颗粒表面时砂岩声波速度随视压实率和视胶结率的变化趋势.图中可以看出压实和胶结作用对声波速度的影响与第一种胶结方式相同.然而，第二种胶结方式的砂岩，压实和胶结作用对声波速度的整体影响要小于第一种胶结方式的砂岩.这是因为在第二种胶结方式下，分布在颗粒接触处的胶结物更少，砂岩的刚度和声波速度随视胶结率的增长速度比较缓慢.正如上面所讨论的，在砂岩法向刚度和切向刚度较小的时候，压实作用对声波速度的影响也会较小.
|
图 3 当胶结物均匀分布在颗粒表面时，纵波速度(a)和横波速度(b)随压实率、胶结率的变化 Fig. 3 The variations of the compressional (a) and shear (b) wave velocities with the cementation and compaction degrees when the cement is evenly distributed around the grain surface |
为了验证本次提出的模型，选取人造砂岩样品、天然砂岩样品分别进行了理论模型预测和实验测量，并对比了模型预测结果和实验观测声波速度.
3.1 人造砂岩的理论数据与实验测量数据对比 3.1.1 人造砂岩的理论声波速度获取方法人造砂岩是由石英颗粒和胶结物制作而成.石英颗粒的体积模量为38 GPa，剪切模量为44 GPa，密度是2.65 g·cm-3.胶结物是黏土与环氧树脂的混合物，胶结物的等效体积模量是2.24 GPa，剪切模量为1.57 GPa，密度为1.38 g·cm-3.
首先，根据薄片鉴定结果可以得到样品的胶结类型及胶结厚度.其中，归一化的胶结厚度的分布范围为0~0.05.
其次，样品的原始孔隙度可以通过Beard-Weyl的关系得到(Scherer，1987)，表达式为
|
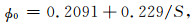
(18) |
式中，S是根据粒度累积曲线可以计算出样品的分选系数.
再次，综合实验确定的氦气法孔隙度、原始孔隙度及薄片照片图像分析得到的胶结物含量可以确定样品的视压实率和视胶结率(徐登辉等，2018).
最后，根据式(11)、式(12)和式(17)可以得到样品的归一化胶结半径和颗粒配位数.根据上述参数及前面提出的模型就可以计算人造砂岩的纵波和横波速度(临界孔隙度可通过骨架颗粒及样品体积模量来确定，本次取值为0.4).
3.1.2 人造砂岩声波速度的实验测量方法采用脉冲透射法测量样品的纵横波速度.纵波探头和横波探头的频率分别是0.25 MHz和0.12 MHz.纵波速度测量的相对误差小于0.5%，横波速度测量的相对误差小于1%(韩学辉等, 2013, 2014).
3.1.3 结果对比图 4给出了实测纵横波速度与理论预测纵横波速度的对比关系.从图中可以看出，理论预测与实验数据基本一致(数据点分布在交会图的45°线上).实验数据和理论预测的微小差距可能是样品的非均质性引起——在理论模型中，假设样品是均匀的，砂岩的性质(如配位数、粒径等)在样品中是不变的.然而，实际样品存在非均质性，这可能是理论预测值与实测测量值存在偏差的主要原因.此外，在理论模型中，假设颗粒为理想的球形.然而，实际样品是由不同形状的颗粒组成的，而不会是理想的球形，这可能是实验数据与理论数据不一致的另一个原因.
|
图 4 人造砂岩样品实验测量与模型预测的声波速度对比 (a)纵波速度对比；(b)横波速度对比. Fig. 4 Comparison of the measured and predicted P- and S-wave velocities for the synthetic sandstone samples (a) P-wave velocities; (b) S-wave velocities. |
除了用本文提出的理论模型进行声波速度预测，也用修正的CCT模型对样品的声波速度进行了预测，并在图 4中还给出了修正的CCT模型的预测结果.修正CCT模型中使用的配位数是样品压实率为0时对应的配位数.因此，两种模型的声波速度预测结果对比体现了压实作用对声波速度的影响.结果表明：新提出的理论模型的声波速度预测结果略高于修正后的CCT模型.人造砂岩制作时围压较低，压实作用较弱，因此两种模型的声波速度预测结果差异不大.从图中可以看出，在考虑压实作用以后，理论模型的预测结果与实验测量结果更为接近，特别是纵波的结果.
3.2 天然砂岩样品的理论数据与实验数据对比为了进一步验证理论模型，用同样的方法实验测量了某地区天然砂岩样品的声波速度.这些砂岩样品的埋深是4000~5700 m，孔隙度从5%到24%不等.理论计算声波速度采用的输入参数和计算方法为：石英颗粒骨架的体积模量为38 GPa，剪切模量为44 GPa，密度为2.65 g·cm-3；胶结物是黏土、碳酸盐岩和石英的混合物，组成胶结物的各组分弹性模量和密度如表 1所示.根据砂岩样品中不同的胶结物组分，可以使用Voigt-Reuss-Hill平均公式来计算胶结物的等效弹性模量(Mukerji et al., 2009).胶结物的等效密度是各组分密度的体积平均值，各样品胶结物的有效模量和密度如表 2所示；样品的临界孔隙度值ϕ1为0.36(Dvorkin and Nur, 1996)，原始孔隙度ϕ2由Beard-Weyl关系式得到(见公式(18))(Scherer，1987)，视压实率、视胶结率的确定方法和人工样品的方法一样(徐登辉等，2018)，从薄片鉴定结果中确定胶结厚度和胶结类型.根据上述参数及前面提出的模型就可以计算天然样品的纵波和横波速度.
|
表 1 天然样品中胶结物组分的弹性模量和密度(Mukerji et al., 2009) Table 1 Elastic moduli and densities of the cement components in the natural sandstone samples (Mukerji et al., 2009) |
|
|
表 2 天然砂岩样品中胶结物的弹性模量和密度 Table 2 Effective elastic moduli and densities of the cement in the natural sandstone samples |
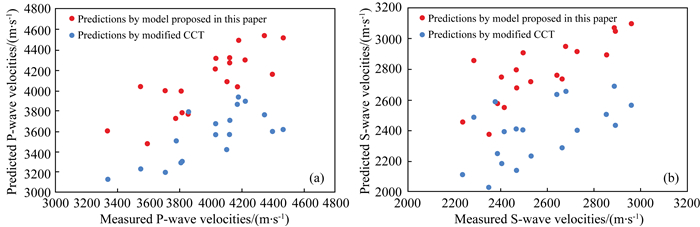
图 5给出了天然样品的理论预测声波速度及实验测量声波速度的对比结果.结果表明：理论预测结果与实验数据吻合得较好.与人造砂岩一样，理论预测值与实验数据之间的差异可能是砂岩样品的非均质性和砂岩颗粒偏离理想球体所致.此外，除了石英颗粒外，样品中还含有少量的其他矿物颗粒，这也会导致理论结果与实验数据的偏差.为了体现压实作用对声波速度的影响，图 5中同时给出了修正的CCT模型的声波速度预测结果.结果表明：修正CCT模型预测的声波速度明显低于新模型所预测的声波速度.因此，在天然样品中，压实作用对声波速度的影响显著高于对人造砂岩样品的影响.这是因为天然样品的埋深为4000~5700 m，颗粒会在较高的围压下变得更加致密.考虑了压实作用后，理论预测值与实验数据之间更为接近.另外，理论模型预测的横波速度比实测值稍高，可能的原因也如上所述.
|
图 5 天然样品实验测量声波速度与理论预测声波速度的对比 (a)纵波速度对比；(b)横波速度对比. Fig. 5 Comparison of the measured and predicted P- and S-wave velocities for the natural sandstone samples (a) P-wave velocities; (b) S-wave velocities. |
本次研究，提出了一个能够表征压实、胶结作用对砂岩声波速度影响的岩石物理模型.该模型基于修正的CCT模型，通过建立视压实率与配位数的联系，将压实作用的影响引入到了原有模型中，最终建立了定量表征压实作用和胶结作用的砂岩统一声波速度模型，可用来预测不同视压实率、视胶结率的砂岩的声波速度.定量研究压实和胶结作用对砂岩声波速度影响的数值算例结果表明：声波速度随着视胶结率增加而先迅速增加然后保持不变.同时，声波速度随着视压实率的增加也会逐渐增大，这一速度的变化会受到胶结率的影响，在胶结率高的情况下声波速度变化尤为明显.应用理论模型预测声波速度与人造砂岩、天然砂岩的实验测量声波速度吻合得很好，表明本次研究理论模型的适用性.
本文提出的模型能够定量表征压实、胶结作用对砂岩声波速度的影响，便于使用，预测声波速度结果准确，并在砂岩储层有利区的预测以及孔隙度等物性参数的反演等方面有很好的应用潜力，可用于砂岩储层的勘探和描述.
Agersborg R, Johansen T A, Mavko G, et al. 2011. Modeling of elasticity effects of sandstone compaction using coated inclusions. Geophysics, 76(3): E69-E79. DOI:10.1190/1.3565050 |
Brandt H. 1955. A study of the speed of sound in porous granular media. Journal of Applied Mechanics, 22: 479-486. |
Chen G J, Du G H, Zhang G C, et al. 2011. Chlorite cement and its effect on the reservoir quality of sandstones from the Panyu low-uplift, Pearl River Mouth Basin. Petroleum Science, 8(2): 143-150. DOI:10.1007/s12182-011-0127-z |
David C, Wong T F, Zhu W, et al. 1994. Laboratory measurement of compaction-induced permeability change in porous rocks:Implications for the generation and maintenance of pore pressure excess in the crust. Pure and Applied Geophysics, 143(1-3): 425-456. DOI:10.1007/BF00874337 |
Digby P J. 1981. The effective elastic moduli of porous granular rocks. Journal of Applied Mechanics, 48(4): 803-808. |
Dvorkin J, Berryman J, Nur A. 1999. Elastic moduli of cemented sphere packs. Mechanics of Materials, 31(7): 461-469. DOI:10.1016/S0167-6636(99)00009-5 |
Dvorkin J, Mavko G, Nur A. 1991. The effect of cementation on the elastic properties of granular material. Mechanics of Materials, 12(3-4): 207-217. DOI:10.1016/0167-6636(91)90018-U |
Dvorkin J, Nur A. 1996. Elasticity of high-porosity sandstones:Theory for two North Sea data sets. Geophysics, 61(5): 1363-1370. DOI:10.1190/1.1444059 |
Dvorkin J, Nur A, Yin H Z. 1994. Effective properties of cemented granular materials. Mechanics of Materials, 18(4): 351-366. DOI:10.1016/0167-6636(94)90044-2 |
Dvorkin J, Yin H Z. 1995. Contact laws for cemented grains:implications for grain and cement failure. International Journal of Solids and Structures, 32(17-18): 2497-2510. DOI:10.1016/0020-7683(94)00279-6 |
Guo J X, Han X H. 2016. Rock physics modelling of acoustic velocities for heavy oil sand. Journal of Petroleum Science and Engineering, 145: 436-443. DOI:10.1016/j.petrol.2016.05.028 |
Han X H, Guo J X, Li F B, et al. 2013. Modified acoustic velocity model for basal cemented loose sandstone based on contact cement theory. Journal of China University of Petroleum (in Chinese), 37(4): 76-82. |
Han X H, Guo J X, Li F B, et al. 2014. Generalization of the expression of cementation radius in contact cement theory and its application. Chinese Journal of Geophysics (in Chinese), 57(4): 439-449. DOI:10.6038/cjg20140718 |
Hertz H. 1882. Uber die Berührung fester elastischer Körper (On the contact of elastic solids). Journal fur die Reine und Andgewandte Mathematik, 92: 156-171. |
Houseknecht D W. 1987. Assessing the relative importance of compaction processes and cementation to reduction of porosity in sandstones. AAPG Bulletin, 1987(71): 633-642. |
Jenkins J, Johnson D, La Ragione L, et al. 2005. Fluctuations and the effective moduli of an isotropic, random aggregate of identical, frictionless spheres. Journal of the Mechanics and Physics of Solids, 53(1): 197-225. DOI:10.1016/j.jmps.2004.06.002 |
Li H, Han D H. 2015. Rock physics modeling of unconsolidated sands:Accounting for partial friction grain contacts and heterogeneous stress field. Journal of Computational Acoustics, 23(4): 1540001. DOI:10.1142/S0218396X15400019 |
Madadi M, Christy A G. 2012. A modified coherent potential approximation:Grain-contact moduli and coordination-number effect. Geophysics, 77(3): WA141-WA148. |
Madadi M, Saadatfar M. 2017. A finite-element study of the influence of grain contacts on the elastic properties of unconsolidated sandstones. International Journal of Rock Mechanics and Mining Sciences, 93: 226-233. DOI:10.1016/j.ijrmms.2017.02.008 |
Mindlin R D. 1949. Compliance of elastic bodies in contact. Journal of Applied Mechanics, 16: 259-268. |
Mukerji T, Mavko G, Dvorkin J. 2009. The Rock Physics Handbook:Tools for Seismic Analysis of Porous Media. 2nd ed. Cambridge: Cambridge University Press.
|
MurphyⅢ W F. 1982. Effects of microstructure and pore fluids on the acoustic properties of granular sedimentary materials[Ph. D. thesis]. Stanford: Stanford University.
|
Scherer M. 1987. Parameters influencing porosity in sandstones; a model for sandstone porosity prediction. AAPG Bulletin, 71(5): 485-491. |
Smith W O, Foote P D, Busang P F. 1929. Packing of homogeneous spheres. Physical Review, 34(2): 1271-1274. |
Walderhaug O. 1996. Kinetic modeling of quartz cementation and porosity loss in deeply buried sandstone reservoirs. AAPG Bulletin, 80(5): 731-745. |
Walton K. 1987. The effective elastic moduli of a random packing of spheres. Journal of the Mechanics and Physics of Solids, 35(2): 213-226. DOI:10.1016/0022-5096(87)90036-6 |
Winkler K W. 1983. Contact stiffness in granular porous materials:comparison between theory and experiment. Geophysical Research Letters, 10(11): 1073-1076. DOI:10.1029/GL010i011p01073 |
Xu D H, Wang Y, Han X H, et al. 2018. Experimental method for quantitative characterization of apparent compaction rate and apparent cementation rate. Progress in Geophysics (in Chinese), 33(1): 274-278. DOI:10.6038/pg2018BB0114 |
韩学辉, 郭俊鑫, 李峰弼, 等. 2013. 基于CCT模型的基底式胶结疏松砂岩声波速度修正模型. 中国石油大学学报(自然科学版), 37(4): 76-82. DOI:10.3969/j.issn.1673-5005.2013.04.011 |
韩学辉, 郭俊鑫, 李峰弼, 等. 2014. 连续胶结声速理论胶结半径表达式的一般性推广及应用. 地球物理学报, 57(4): 439-449. DOI:10.6038/cjg20140718 |
徐登辉, 王燕, 韩学辉, 等. 2018. 一种实用的定量表征岩石视压实率和视胶结率的实验方法. 地球物理学进展, 33(1): 274-278. DOI:10.6038/pg2018BB0114 |
表 1
Table 1
