2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
从海量的数据中准确高效的提取地震信号是进行地震数据分析的基础.准确的波形到时拾取有助于更精确的分析震源位置、震源深度、震源类型、地层参数等.同时其可以用于余震的分析与提取,这为建立余震序列、分析地震发生规律以及后续防震减灾工作提供数据基础.但由于震源与介质的复杂性导致地震信号在时间、频率域形态上均表现出复杂的特征(Johnston, 1979;Ramos-Martínez et al., 2000;张建中和陈世军, 2003;周磊等, 2013).到时提取本质上是对波形特征进行分析处理,复杂的地震波形态使得传统特征分析方法难以进行.传统的时间域、频率域方法所提取的固定特征难以适用于复杂的地震波形态,其在到时分析过程之中依赖于人工进行特征定义与分析.这使得特征的完备性与普适性有所欠缺,因此传统波形拾取方法在提取到时方面会遇到困难.
早期工作中提取波形到时主要依靠人工识别,这种方式在处理少量数据时是可行的.但随着观测仪器的改进与地震台站的增多,地震数据量出现了较大程度的增长.与此同时滑坡、次生灾害等不同方向上的研究逐渐增多,这对于波形拾取的精度和速度需求也在不断地提高.早期的人工拾取在速度上很难满足需要(陈金焕等, 2015).因此波形自动拾取方法得到了发展并逐渐成为主流(Allen, 1982, 1978;Baer and Kradolfer, 1987;Cichowicz, 1993;Gibbons et al., 2008),自动拾取方法是对波形特征进行提取并量化,之后通过设定阈值的方式决定信号的取舍.这个过程之中使用的特征包括时间域特征、频率域特征、综合特征.而阈值的设定早期是人为给定的,在后续的工作之中则逐渐地依赖于机器学习方法习得.
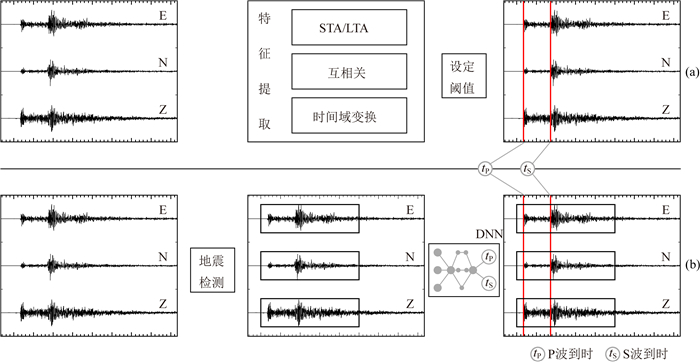
图 1a展示了自动到时提取的过程,这其中关键过程是对于波形特征的提取.对于信号本身特征形态而言,使用相应的形态的波形进行直接比对是合理的,因此互相关算法(Molyneux and Schmitt, 1999;Peraldi and Clement, 1972)在波形本身具有很高相似性的情况下有良好的效果.在信噪比比较高的情况下,使用简单的STA/LTA方法(Stevenson, 1976;Tong and Kennett, 1996)就能够得到很好的效果,此方法使用了时窗能量特征.为了应对低信噪比场景,需要对特征进行增强,由此引入了多种特征函数(Allen, 1982, 1978;Baer and Kradolfer, 1987;Earle and Shearer, 1994;高淑芳等,2008).通过分析信号的分形维数、波形统计等特征产生出了用于到时拾取的分形维数法(Boschetti, 1996;Hayward et al., 1989;Russ, 1994)、AR-AIC方法(Leonard and Kennett, 1999;Sleeman and Eck, 1999;Takanami and Kitagawa, 1991;常旭和刘伊克,1998).变换域分析过程之中比较有代表性的是短时傅里叶变换(STFT)方法,此方法时窗固定的情况下时间、频率分辨率无法同时达到最佳(胡明顺等, 2009).小波变换方法克服了短时傅里叶变换的缺陷,使用小波变换系数来刻画特征进行到时拾取,用小波特征进行到时拾取有很多相关研究(Grossmann and Morlet, 1984;高静怀等, 1997;何小波和周蕙兰, 2005;滕云田等, 2006).综上在基于特征的到时拾取算法之中可以理解为如下过程:
|
图 1 波形搜索方法示意 (a)基于阈值的波形到时提取过程;(b)神经网络方式计算到时过程. Fig. 1 Sketch for searching method (a) Threshold based method to pick the onset time of seismic phase; (b) NN based method to calculate the onset time of seismic phase. |
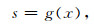
|
(1) |
其中x为原始地震信号,g(·)为对信号进行某种变换的函数,变换后所得为特征向量s.计算过程可以根据s来计算是否符合某一震相特征.通常而言这属于条件概率问题:p(y|s),在具有特征s后计算属于某种波形y的概率.而计算概率的过程是一个利用人工、机器选择的过程,对于传统的方法而言,这个模型可以更进一步地描述为:p(y|s, θ),其中θ为人为所设定的阈值,或者通过机器学习方法所得到的参数.前面说到,由于震源的复杂性会使得固定特征的提取出现较多变化,这种变化表现为特征s的分布变化q(s),因此在对于某一数据集进行统计分析而得到的最佳结果可能在面对新的数据集时无法达到理想效果.举个例子来说,对于STA/LTA方法来讲在高信噪比情况下所得特征分布为q0(s),此时设定阈值为θ0.而在面对低信噪比数据时,此时特征分布为另外的形式q1(s),显然在高信噪比情况下所得的参数θ,在适用于低信噪比场景可能会带来预测准确度降低的问题.不同震源、介质等因素均会对特征分布产生影响.解决方式是使得数据分布尽可能地接近预测数据.但是单一特征提取所使用的可变参数量θ过少,单纯的增加数据会使得整个模型欠拟合.为了解决这个问题引入了综合性方法,综合不同特征进行地震波形拾取(Bai, 2000),综合性方法之中最常用的方式就是多层神经网络方法(Dai and Macbeth, 1997;Gentili and Michelini, 2006;Mccormack et al., 1993;Murat and Rudman, 1992;Wang and Teng, 1995;Zhao and Takano, 1999).多层神经网络所提取的特征更多,包括峰值振幅、时窗内均方根振幅比、噪声信号比值以及前面提到的时域、频域特征.这些特征的引入使得神经网络方法可以适用于更广泛的场景.
在整个地震到时自动拾取过程之中依赖于人工特征s的提取,这些特征提取的有效性直接决定了最终模型预测的有效性.随着计算性能的提升,特征的提取也可以依赖计算机完成,由此到时拾取模型变为p(t|x),此时可以直接使用原始信号进行输入,而特征计算则依赖于神经网络自动完成.这用到的算法包括多层全链接网络(FC), 卷积神经网络(CNN).此时神经网络直接输入x计算,建模过程使用了用于特征提取的CNN、FC层,这使得神经网络层数增加.但是为了更细致地描述特征,需要更多的可训练参数θ,因此深度网络的架构是适用的(Canziani et al., 2016),深度神经网络模型引入了更多的可训练参数θ,用于波形特征的构建.为了解决训练过程之中出现的难于优化的问题,本文在深度神经网络在子结构中采用了Inception结构,这种网络结构在人脸识别、物体识别等计算视觉领域表现出了较好的效果(Szegedy et al., 2015).由于传统的多层CNN感受野相对固定,使得其在特征尺度上的拾取上受到了限制,而Inception层中加入了不同大小的卷积核心,这样使得卷积核心对于特征提取更加完整,同时可以对不同尺度特征进行提取.最终模型输出并非是某一波形y概率,而是直接对到时进行输出:p(ti|x),其中ti代表不同波形到时.
1 方法原理本文基于深度神经网络方法进行P和S波到时的拾取工作.深度神经网络在计算机图形学、自然语言处理、图像分类等方面均证明是有效的.不同于简单的地震波形检测任务,地震到时拾取任务中所需分析的特征信息更多,这些特征在时域上表现为持续时间与波形振幅比的差异,而在频率域表现为不同特征频率之间的差异.在时间域、频率域均表现出差异的情况下,特征尺度上可能因此出现较大程度的差异.这就需要神经网络具有处理较长时间依赖的能力,也就是需要神经网络具有较大感受野.这可以通过增加网络深度的方式来解决,但是传统CNN结构在网络较深的情况下难以进行训练(Szegedy et al., 2015).因此本文参考了用于人脸分类问题的的Inception网络结构,将其进行修改用于到时拾取.而Inception层的加入也有效地减少了参数数量,减少训练难度,增加运算速度(Krizhevsky et al., 2012).
1.1 网络结构Inception层本质上属于多层卷积网络的融合(Krizhevsky et al., 2012),其在简单的卷积层之上融入了不同大小的卷积核心,并将卷积结果向量进行连接,这样使得不同尺度的特征得以提取并保存,Inception层中部分池化子层将卷积核心大小设为1,用于不同特征之间的计算输出,实验表明选取不同长度的池化层可以更好地提取特征.本文为适应地震波形处理任务所用卷积核心大小与图像处理所用卷积核心相比有所增加.
如图 2神经网络的输入层为固定长度的地震三分量数据,将其记为向量v(v∈Rn·l·3),其中n为批尺寸(BATCHSIZE),l为波形长度.输出为p和s波到时记为y(y∈Rn·2).在训练过程中直接利用二范数作为损失函数来表示样本偏差,但由于截取过程中S波相对到时普遍比P波相对到时长三倍左右(基于训练数据统计),因此为了保持数值均衡P和S波到时采用加权的形式:
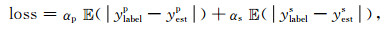
|
(2) |

|
图 2 深度神经网络结构 Fig. 2 The structur of deep neural network |
其中ylabel为震相实际到时,yest为神经网络估计到时,
Inception层中存在的连接操作属于矩阵运算:
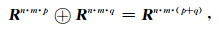
|
(3) |
其中⊕为连接运算符,其保留了inception层中多个卷积核心所输出的特征.表 1所表示的整个深度神经网络的自由参数个数在106量级,在这个量级上可以完整地提取波形特征信息,进而可以形成更好的预测超曲面进行地震到时预测.为了增强特征提取的有效性,加快计算速度,所用的激活函数为修正线性函数:
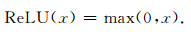
|
(4) |
|
|
表 1 神经网络参数* Table 1 The parameters of network |
参数初始化过程采用随机数值进行权值的初始化,随机数均值为0,方差0.1.初始化之后,有部分神经元处于未激活状态,这对于训练是有利的.同时由于激活函数选取的相对简单,所以可以加快训练过程以及模型应用过程.最后的两层是全连接层,全链接层输出向量长度为2,用于输出到时,其所选取的激活函数为sigmoid(Mhaskar and Micchelli, 1993):
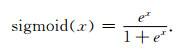
|
(5) |
在线性层中选取ReLU激活函数会有一定机会导致迭代不收敛,所以在到时拾取过程中将激活函数定义为sigmoid,这需要对于时间标签信息进行归一化处理.
1.2 数据预处理训练数据的数据预处理对于神经网络的训练是十分重要的.预处理过程直接影响了神经网络的收敛,同时部分影响了训练模型的预测效果(Haykin, 2009).神经网络的波形特征提取是基于时间域特征而言的,因此地震数据的预处理不应当大幅度改变波形的形态.对于滤波处理,在传统的识别方法中将相当一部分频率的信号当做干扰信息进行排除,因此需要带通滤波,而神经网络中同样也需要滤波,但是滤波目的有所区别.
地震信号中存在的干扰包括零点漂移与超低频干扰,显然这对于地震信号的提取是没有价值的,其来源于人为确定的干扰或仪器本身原理所致(罗新恒等, 2003),而零漂与超低频干扰本身会使得神经网络特征计算出现问题,过大的零漂会使得激活函数饱和,同时压制有效信号.由于深度神经网络中采用字典学习等无监督学习的方式进行特征拾取,显然零点漂移与超低频干扰会使得无用信号特征值过大,从而无法有效提取特征,因此神经网络数据预处理中需要着重对以上干扰进行处理,处理的方式为极低频滤波.而地震信号中的高频的噪声,由于高频噪声的存在可以增强神经网络的泛化能力,在后续的处理中为了防止过拟合也需要对训练数据加入适量的噪声,因此在这里不对高频噪声进行处理(Haykin, 2009).
在输入神经网络之前需要对数据进行归一化处理,这是由于原始波形信息的幅度值变化范围较大,而幅值显然并非波形识别中的有效特征,因此归一化处理并不会引起有效特征的减少:
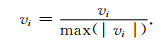
|
(6) |
在产生训练数据的过程中除了需要对于波形数据进行上述预处理之外,还需要进行一系列的变换以扩充训练集.增加训练集可以有效地增强神经网络泛化能力,这些处理包括波形平移、拉伸、加噪声(Hayakawa et al., 1995;Schroff et al., 2015).
对于训练集的平移操作比较简单,就是对时窗进行平移,使得时窗内P和S波的相对到时发生相应变化,拉伸就是对于波形进行一定尺度的拉伸变换,这里限定拉伸范围为0.5~1.5,过大的拉伸比会使得地震的特征频率发生明显的变化,在一定程度上可能导致拉伸后产生非地震信号,这会使得神经网络学习到非地震信号特征,这对于网络的应用是不利的.最后在时序数据中添加一定量的白噪声,噪声的加入可以有效增强神经网络的泛化能力.
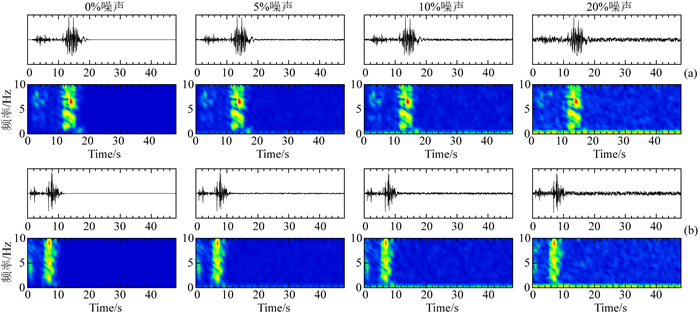
图 3为经过加噪声处理后的训练集,这里随机选择出8个波形绘图.可以看到经过变换扩充训练集后,训练集得到了扩充,但是由于人工标注数据需要大量人力,因此在方法发展初期并未累计足够数量的样本,而对于训练样本直接进行数据集扩充所得特征数量依然有所欠缺.因此引入了正演模拟的方式扩充训练集.
|
图 3 训练数据波形与频谱特征 (a)(b)为随机选择的两个地震波形分别加入0.0%、5%、10%、20%比例的随机噪声(比例定义为最大振幅所对应比例). Fig. 3 Waveform and spectrum of training datas (a)(b) are two samples random selected with 0.0%, 5%, 10%, 20% noise (The ratio of the noise and the maximum amplitude). |
相比于神经网络参数量而言,训练集数量依然比较欠缺,因此在其训练过程中加入了正演计算的结果,正演结果的加入使得训练集可以在较大程度上得到扩充,正演方法采用波数法,地层速度模型采用一维速度模型,这在地震学中证明可以有效地产生理论地震图.而震源深度、震源参数也在一定范围内变化,用以产生不同形式的地震波形数据用以扩充训练集,用以增强神经的泛化能力.
由表 2可以看到,正演结果提供了一个比较大范围、不同震源、深度的地震波形,因此地震波形特征得到了比较大的扩充.但是正演数在计算过程中并未考虑地形、地下不均匀体、破裂过程与噪声等问题,因此在模拟波形中与实际所得有所区别,对于地震波形识别而言,利用一维底层模型所生成的地震波形数据已经可以很好地模拟真实的地震震动情况,因此利用其作为神经网络的训练数据是可以建立预测模型,从而提取地震波形到时.
|
|
表 2 正演模拟参数选取 Table 2 The parameters of forward modeling |
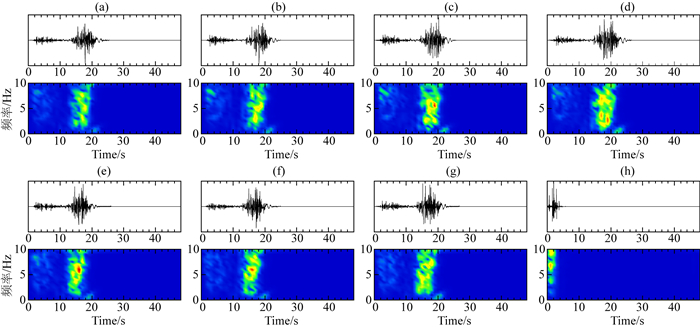
由图 4可以看到地震波形态上相比于单纯的拉伸变换产生出了更多的波形特征用于深度神经网络的训练,所以说正演计算方式扩充训练集是可行的.但是训练数据频率特征相比于原始地震信号在频率上较为单一,同时时间域形态上也相对简单,这是由于模型和正演方法所决定的.训练过程中同样对产生的地震信号进行加噪声处理.这种处理只是在训练集不足时的补救的方式,为完全解决问题需要在之后的工作中对识别出的地震波形人工拾取之后再次加入训练集中,这是一个迭代完善的过程,因此神经网络精度并非是固定的,而是一个随着有效数据量增多而不断改善的过程.
|
图 4 正演模拟生成训练数据与频率特征 (a)—(h)为8个随机选择的正演波形. Fig. 4 Waveform and spectrum of forward modeling (a)—(h) are eight diffent waveform generated by forward modeling. |
神经网络的参数调整是一个复杂的过程,首先对于卷积网络而言最主要的就是卷积核心的大小,在图像识别中卷积核心大小选取通常从3~5范围内变换,这综合了“感受野”以及计算效率的因素,而对于地震波形数据而言其特征长度(特征)与图像特征长度存在一定区别,其特征尺寸通常比图像特征尺寸大:
由表 3可以看到在前六层纯卷积网络中,大的卷积核感受野比小卷积核心感受野大了2倍,达到了50,这所对应的时间长度是2.5 s(以0.05 s为采样间隔计),在这个尺度上是可以提取P和S波等波形细节特征的,而小核心选取则无法完整包含完整波形特征信息.但是在这个尺度上再增加核心长度的话虽然感受野更加广,但是增加了大量自由参数数目,在计算过程中所需计算量也更大,因此卷积核心的选取应当综合性能与效果考虑,本文中将其选择为6.
|
|
表 3 不同卷积核心感受野对比(采样间隔:0.05 s) Table 3 Different field of vision of diffenent CNN kernels(Sampling interval:0.05 s) |
由于文中训练集相对有限,这是在神经网络方法拾取波形方法初期所不得不面对的,因此应更加重视过拟合问题.过拟合问题很大程度上是由于训练集与训练参数数量相差过大所导致的.本文中所采取的避免过拟合的方式除了上文中提到的用正演数据进行训练、对标签数据进行拉伸、平移、添加噪声外,还包含了神经网络训练中常用的避免过拟合的方式,包括正则化、dropout、操作对每层结果进行处理.
数据在通过卷积层后进行正则化处理,由于ReLU函数没有上限,因此进行正则化处理避免了训练特征过度增长,同时避免了梯度消失的问题.而dropout属于训练过程中的技巧,训练过程中随机选取部分神经元不进行训练,这种操作可以有效地避免过拟合问题.
但最有效的增强神经网络泛化能力的方式依然是添加足够的样本,而标签样本的积累是一个长期的工作,因此神经网络的优化也是随着样本的积累不断地提高累积的过程.
2 训练过程神经网络的训练算法选取为(Adaptive Moment Estimation)Adam算法(Kingma and Ba, 2014),自适应算法使得迭代收敛过程较为平稳,对内存需求较小,可以对不同计算参数自适应学习速率.训练中所用硬件为E3-1225(4cores),内存8G.学习速率设置为0.001,过大的学习速率在测试过程中会使得迭代不收敛,而过小的学习率在学习过程中收敛过于缓慢,对于纯随机情况下,由于用于预测时间的归一化到时均在0~1之间变化,因此在这种情况下有

|
(7) |
在迭代2000次后,用时40 h,代价函数收敛于0.0025,此时对应时间精度为±0.2 s(2个采样点),也就是神经理论上对于PS波到时误差精度平均可以到0.2 s(2个采样点)量级.这个结果是针对于所训练数据而言的,因此带有一定的训练数据的特征,也就是说对于训练数据集或者波形接近于训练数据的地震数据神经网络的预测精度可能会很高,但是对于与训练数据相差比较大的数据而言,到时拾取的精度可能并不理想.
2.1 卷积核心选择影响卷积核心的选取对于神经网络的精度和计算效率有一定影响,对于地震数据而言由于采样率较高,在重采样处理之后为了保存地震波形特征仍然有较大数据量输入.本文中输入神经网络的波形向量为长度1000的三分量数据,对于不同长度的地震波将其重载样,波形时间长度范围为50~200 s,对于地震数据而言代表了近震波形数据,对于图像图里中传统核心大小无法满足需求.因此本文选取了三种不同的卷积核心大小进行了测试.
由表格 4可以看到,对于长度为3的卷积核心,其最小内存消耗是比较小的,相应的迭代过程计算较快,但是由于跟地震波形特征尺度不匹配使得精度结果并不理想,由于卷积核心较少,因此受到噪声的影响较大,在信噪比较大的情况下有机会出现不收敛的情况.对于12长度的卷积核心,由于增加了四倍的自由参数数量,使得训练过程最小内存消耗变大,最小内存用于维持系统开销以及存储变量,相应的单次迭代过程时间消耗也相应变大,大的卷积核心也会影响到训练完成后的到时计算的时间消耗.对于地震波形的特征尺度而言,长度为6的卷积核心已经可以很好地提取地震波形特征,并且具有了一定的抗干扰能力.由此在地震到时拾取的神经网络模型中将卷积核心长度选择为6.
|
|
表 4 不同卷积核心选择对于结果影响 Table 4 The iterative process affected by different CNN kernels |
在参数选取过程中BATCHSIZE对于收敛与耗时影响较大.在BATCHSIZE过小时无法抵消随机性对于梯度的影响,而过大的BTACHSIZE虽然可以更好地预测梯度,但是在迭代过程中会增加计算消耗,这种消耗是随着BATCHSIZE大小变化近似线性增加的,如表 5所示.
|
|
表 5 不同BATCHSIZE选择对于结果影响 Table 5 The iterative process affected by different batchsize |
在小的BATCHSIZE下,由于样本不足梯度随机性增加,使得迭代过程有一定几率收敛缓慢甚至于不收敛,而在BATCHSIZE增大到100时,几乎每次迭代都能得到收敛结果.但是过大的BATCHSIZE会使得迭代过程的时间消耗显著增加,同时所需最大内存也不断增加,但对于梯度方向已经很好的估计,因而对于达到相同精度所需迭代步数影响已经很小.由表格可以看到,在大的BATCHSIZE下,迭代步数与100样本的时候数量接近,甚至于稍多一些,这是因为随机性的影响.因此权衡性能与精度将BATCHSIZE的大小选择为100.
神经网络训练曲线是从0.25开始不断减少的,在多次迭代之后继续降低,开始时收敛较快,但是在0.008之后收敛速度明显降低,最终收敛于0.003,但是这个数值是一个动态变化的过程,数值从0.0025到0.004之间不断的跳动,这个变化是由于训练数据本身的不确定性所导致的.
如图 5所示,在训练过程中采取了逐步增加噪声的形式,初始加入较大比例的噪声会使得迭代收敛缓慢,不利于训练过程,因此在训练过程中加入噪声采用步进的方式,开始迭代的500次未加入噪声,此时精度随着迭代不断升高,最终到达0.01量级,在之后噪声逐步增加,初始加入噪声后由于神经网络健壮性较弱,精度不甚理想,随着迭代增多对于噪声数据的容忍度也在增强,这表现为精度不断提升,随后再增加噪声进行训练直到最大振幅的20%,在加入最大振幅的20%后,最终精度在0.004:

|
图 5 训练曲线 Fig. 5 Training curve |
如表 6所示噪声训练过程中采用5次递进,初始训练过程由纯随机情况下的精度0.25经过800次迭代后精度到达0.003,之后加入少量噪声使得精度上升到了0.012.由于未加噪声的训练使得神经网络泛化能力很弱,在之后训练中逐步提高噪声,用以增强神经网络的泛化能力,最终噪声水平设定为0.2.图 6是初始训练和最终训练对于预测结果的影响,两个模型分别为带噪声与不带噪声训练所得的对于两种噪声情况的预测结果.
|
|
表 6 加入训练噪声比例 Table 6 Adding different ratio of noise |
|
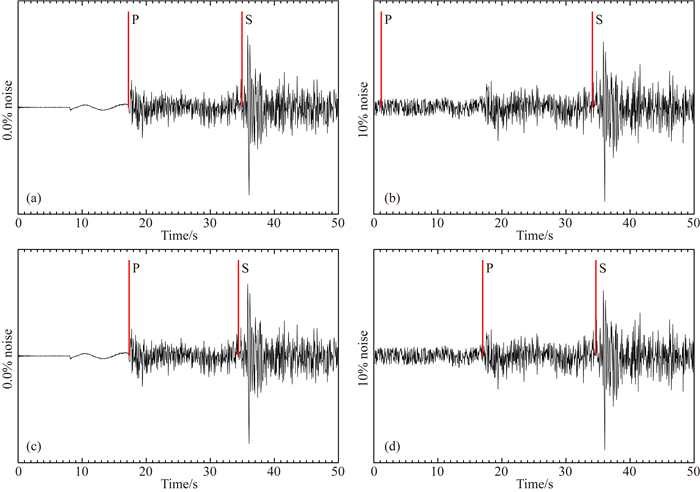
图 6 噪声训练对比 (a)不带噪声模型预测无噪声数据;(b)不带噪声模型预测噪声数据;(c)带噪声模型预测无噪声数据;(d)带噪声模型预测噪声数据;带噪声模型指的是训练数据加入了噪声进行训练. Fig. 6 Comparison of different noise ratio (a) Noizeless model predict thenoizeless data; (b) Noizeless model predict the noize data; (c) Noize model predict the noizeless data; (d)Noize model predict the noizeless data; Noize model is trained with noise data. |
由图 6可以看到加入噪声训练使得整个神经网络的泛化能力得到了极大的提升.在未进行噪声训练之前神经网络对于P波的拾取出现了较大程度的偏差,这是由于P波信号本身幅度比较小,在拾取过程中容易被背景噪声所覆盖,而在非噪声训练中训练结果处于局部最优解之中,对P波到时拾取特征不完整.而利用噪声训练后对于P波特征的拾取更加完整,因此预测效果很好.同时可以看到对于S波而言由于波形持续时间比较长因此对于其特征拾取比较完整,对于噪声的忍耐度天然高于P波.而利用噪声步进的方式进行训练避免了初始迭代无法收敛的问题.
3 模型应用模型训练好之后可以直接输入地震波形数据计算输出P和S波到时,在单机情况下对于100条波形数据提取P和S波到时所用时间在4s左右.在到时提取结果中对于P波数据直接用STA/LTA方法进行对比,而对于S波,则用地震台网数据进行对比分析.
3.1 方法准确性与稳定性为了验证方法的准确性与稳定性,本文选取了100个数据加入噪声进行与到时信息进行对比输出,将到时误差定义为预测到时与理论到时之差:
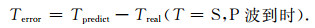
|
(8) |
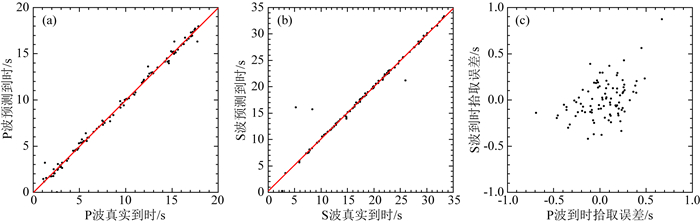
将理论到时Treal、预测到时Tpredict、到时误差Terror绘制成图, 如图 7所示.
|
图 7 PS波理论与实际到时统计 (a)理论P波到时与预测到时相关性;(b)理论S波到时与预测到时相关性;(c) P、S到时误差统计. Fig. 7 The statistics of P and S arrival time (a) The theoretical and predicted arrival time of P wave; (b) The theoretical and predicted arrival time of S wave; (c) The statistics of P and S arrival time error. |
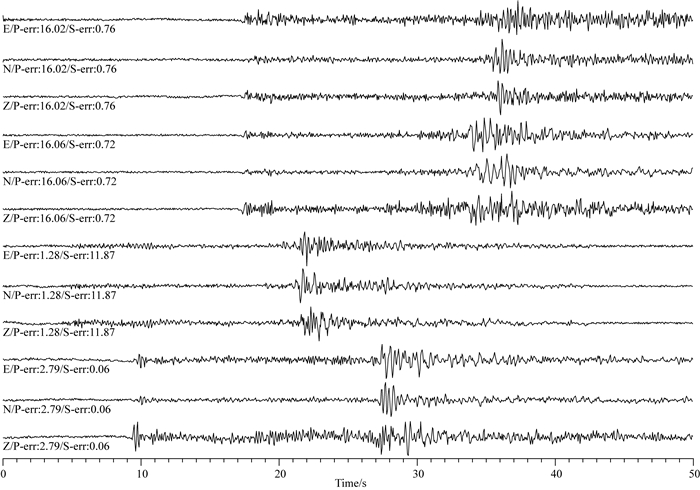
由图 7看到神经网络在P波寻找过程中出现了较大偏差,而S波到时寻找则相对比较准确,这是与传统方法不同的地方,传统方法中P波到时提取较为准确.这是因为S波形振幅较大,持续时间较长,更容易进行特征的提取.同时可以看到对于统计信息而言其均值在0附近,也就是说通过大量到时数据进行平均可以更加接近于理论到时.同时也出现了一些偏差较大的数据,对于出现较大偏差的数据将其绘制成图, 见图 8.
|
图 8 较大误差样本三分量数据 Fig. 8 Samples with larger error |
由图 8可以看到对于较大偏差数据的原因,P、S波并不相同,首先对于P波来说,出现较大偏差是因为信噪比过低,使得在计算过程中无法提取有效特征,这是因为在提取P波的过程中,虽然加入的噪声是随机的,但是依然可能存在局部噪声特征与P波特征相吻合.S波由于振幅和持续时间的原因,使得特征提取相比于P波容易,但是依然出现了一定偏差,这是由于震中距相差较大,使得到时提取过程中受到了其他波形信息的干扰.这部分问题需要在后续的工作中利用更多的波形去训练,提升深度神经网络的预测能力与抗干扰能力.单一波形对于噪声的容忍度见图 9.
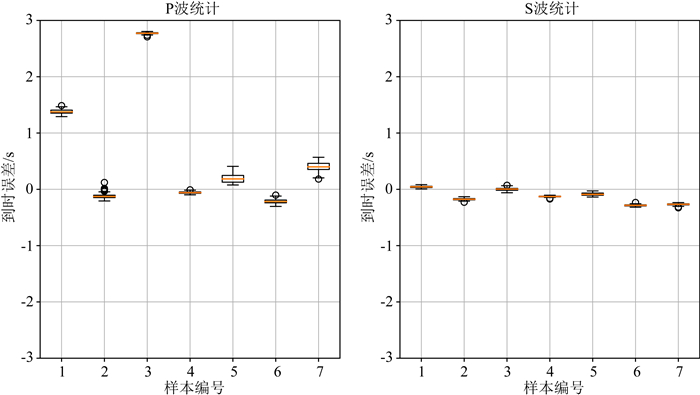
|
图 9 单一样本不同噪声影响(取自七个不同的样本,每个样本形成100个测试数据,每个测试数据由相应样本加入10%的随机噪声,统计每个加噪声事件的预测到时误差,借以估计神经网络对于噪声的鲁棒性) Fig. 9 Single sample affected by noise (Here are seven different event. Every event form 100 samples. Every sample is generated by that event adding 10% noise. The statistics are for estimating the robustness of DNN) |
如图 9可以看到噪声数据对于识别的影响极小,标准差在0.1 s(两个采样点)左右,可以说神经网络方法对于噪声的容忍度很高,这是神经网络具有比较大实用性的地方.但是在计算P到时时有些情况会出现误差较大的情况,前面分析P波相比于S波更难于提取特征,因此在信噪比比较大的情况下,P波到时提取会遇到波动较大的情况.
3.2 AR-AIC+STA/LTA方法对比本文使用AR-AIC+STA/LTA方法(Akazawa, 2004)作为对比.STA/LTA方法对于振幅变化是敏感的,但是易于受噪声干扰,AR-AIC方法对于频率、相位较为敏感.二者结合使得算法对于波形到时的拾取更加精确.对比过程之中选择三个不同的地震波形,已人工标注P、S波到时.对原始波形加入不同比例噪声(信号最大振幅与噪声最大振幅比例),每种比例噪声加入1000个样本进行测试.对同一样本、同一噪声水平下的样本使用不同的方法拾取到时误差进行统计分析.从而分析不同方法在噪声情况下的稳定性与可靠性.
由图 10可以看到,在小的信噪比情况下两种方法均获得了比较理想的结果,而随着信噪比的减少P波到时拾取精度也在不断地降低.对于P波到时在低信噪比条件下,两种方法均表现出了一定条件的性能损失.虽然相比于AR-AIC方法深度神经网络在P波拾取上表现出了相对较高的稳定性(低方差),但是拾取准确度上二者并未有明显区别.对于S波而言在低信噪比情况下二者都表现出了比P波更好的性能,相比较而言深度神经网络的稳定性更好,比AR-AIC方法方差低一个数量级,而且拾取精度更高,在±0.1 s(2个采样点)量级.总体而言,S波到时拾取相比于P波而言的偏差、方差均较低.

|
图 10 STA/LTA与神经网络方法在不同信噪比情况下拾取地震P、S波误差统计 NN代表神经网络方法;AR代表AR-AIC+STA/LTA方法. Fig. 10 Comparison of STA/LTA and DNN method with different noise ratio NN stands for Deep neural work, AR stands for AR-AIC+STA/LTA method. |
本节中利用地震目录中到时进行提取,选取地震为USArray地震目录数据,地震震级为MW5.7, 震源深度7.3 km.随机选取部分波形绘拾取到时,如图 11所示.
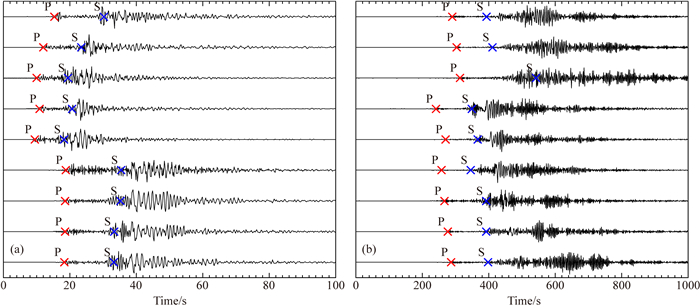
|
图 11 神经网络对于P、S波到时拾取 (a)近震数据; (b)远震数据. Fig. 11 DNN picks the arrival time of P and S wave (a) Near earthquake; (b) Distant earthquake. |
由图 11可以看到,由于训练数据、训练集震中距均小于500 km,因此对于近震数据可以较好地完成到时拾取任务,而对于远震数据而言,由于训练数据的缺失,导致对于波形拾取出现了问题,准确率相对较低,由于卷积神经网络后为一个全链接网络,这使得波形拾取带有全局的特征,因此P、S波形之后的数据对于到时的拾取有一定的干扰.同时可以看到对于P、S波到时提取准确性相比于人工提取仍然有差距,这是由训练数据所决定的,也是需要在后续工作中不断改进之处,神经网络方法可以通过数据积累不断地提升提取到时精度.整个计算过程并无人工干预与设定阈值,这是神经网络方法相比于其他方法的优势所在.阈值的选取带有很大的不确定性,这种不确定性无法具体地量化形成通用的规则,神经网络方法基于自适应的提取波形特征,使得对于地震到时提取更加有针对性.
神经网络作为震相自动拾取工具,其表现出了相比于传统方法的优越性.在计算震相到时的过程中避免了人为的影响,不需要根据特定条件进行相关阈值的设定.而现有模型定时精度可以满足定位和其他处理的需要,而且可以随着标签样本的累计不断地再训练以提高精度.同时可以看到,在计算速度方面由于卷积核心选取得当,其定时精度在单机情况下已经达到了可用的程度,虽然相比于其他方法速度方面仍有所欠缺.但是在自动化程度与抗干扰方面则表现出了一定优势.
当然,现有神经网络方法仍然存在部分问题,就是识别精度并不理想.神经网络输出的误差包括方差(输出对于噪声的敏感程度)与偏差(输出均值与真实值之差).由于深度神经网络的可训练参数较多,在数据量不足的情况下可以很容易形成高方差,低偏差的结果.解决此问题可以使用“集成学习”的思想:同时使用不同的初始化参数训练网络,取平均结果,这样可以在很大程度上消除输出方差.由于神经网络输出是以格值计算的,因此为减少输出偏差可以减少采样间隔.但提升精度最有效的方式在于不断地累计标注数据,在现有模型的基础上继续进行训练.这是深度神经网络的优势:模型精度在训练完成后可以继续训练提升精度,这是一个长期的过程.
Akazawa T. 2004. A technique for automatic detection of onset time of P-and S-Phases in strong motion records.//13th World Conference on Earthquake Engineering. Vancouver, B.C., Canada. International Association for Earthquake Engineering, paper, 2004 (786).
|
Allen R. 1982. Automatic phase pickers:Their present use and future prospects. Bulletin of the Seismological Society of America, 72(6B): S225-S242. |
Allen R V. 1978. Automatic earthquake recognition and timing from single traces. Bulletin of the Seismological Society of America, 68(5): 1521-1532. |
Baer M, Kradolfer U. 1987. An automatic phase picker for local and teleseismic events. Bulletin of the Seismological Society of America, 77(4): 1437-1445. |
Bai C Y. 2000. Automatic phase-detection and identification by full use of a single three-component broadband seismogram. Bulletin of the Seismological Society of America, 90(1): 187-198. DOI:10.1785/0119990070 |
Boschetti F. 1996. A fractal-based algorithm for detecting first arrivals on seismic traces. Geophysics, 61(4): 1095-1102. DOI:10.1190/1.1444030 |
Canziani A, Paszke A, Culurciello E. 2016. An analysis of deep neural network models for practical applications. arXiv preprint arXiv:1605.07678. |
Chang X, Liu Y K. 1998. Distinguishing seismic first break by means of hausdorff fractal dimension. Chinese Journal of Geophysics (in Chinese), 41(6): 826-832. |
Chen J H, Cao Y S, Sun C L, et al. 2015. The algorithm for automatic first-breaks picking on seismic traces based on Dichotomy. Progress in Geophysics (in Chinese), 30(2): 688-694. DOI:10.6038/pg20150228 |
Cichowicz A. 1993. An automatic S-phase picker. Bulletin of the Seismological Society of America, 83(1): 180-189. |
Dai H C, Macbeth C. 1997. The application of back-propagation neural network to automatic picking seismic arrivals from single-component recordings. Journal of Geophysical Research:Solid Earth, 102(B7): 15105-15113. DOI:10.1029/97JB00625 |
Earle P S, Shearer P M. 1994. Characterization of global seismograms using an automatic-picking algorithm. Bulletin of the Seismological Society of America, 84(2): 366-376. |
Gao J H, Wang W B, Zhu G M. 1997. Wavelet transform and instantaneous attributes analysis. Chinese Journal of Geophysics (in Chinese), 40(6): 821-832. |
Gao S F, Li S Y, Wu D P, et al. 2008. An automatic identifcation method of seismic phase based on modified STA/LTA algorithm. World Earthquake Engineering (in Chinese), 24(2): 37-41. |
Gentili S, Michelini A. 2006. Automatic picking of P and S phases using a neural tree. Journal of Seismology, 10(1): 39-63. DOI:10.1007/s10950-006-2296-6 |
Gibbons S J, Ringdal F, Kværna T. 2008. Detection and characterization of seismic phases using continuous spectral estimation on incoherent and partially coherent arrays. Geophysical Journal International, 172(1): 405-421. DOI:10.1111/gji.2008.172.issue-1 |
Grossmann A, Morlet J. 1984. Decomposition of hardy functions into square integrable wavelets of constant shape. SIAM Journal on Mathematical Analysis, 15(4): 723-736. DOI:10.1137/0515056 |
Hayakawa Y, Marumoto A, Sawada Y. 1995. Effects of the chaotic noise on the performance of a neural network model for optimization problems. Physical Review E(Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics), 51(4): R2693-R2696. |
Haykin S S. 2009. Neural Networks and Learning Machines. Upper Saddle River, NJ: Pearson.
|
Hayward J, Orford J D, Whalley W B. 1989. Three implementations of fractal analysis of particle outlines. Computers & Geosciences, 15(2): 199-207. |
He X B, Zhou H L. 2005. Arrival time measurements of first phases P and PKIKP using the method of fixed scale wavelet transformation ratio. Acta Seismologica Sinica (in Chinese), 27(4): 385-393. |
Hu M S, Pan D M, Xu H L, et al. 2009. The comparative study and application of several time-frequency analysis methods in the coal field. Geophysical and Geochemical Exploration, 33(6): 691-695, 709. |
Johnston D H. 1979. The attenuation of seismic waves in dry and saturated rocks[Ph. D. thesis]. Cambridge: Massachusetts Institute of Technology.
|
Kingma D P, Ba J. 2014. Adam:A Method for Stochastic Optimization. arXiv preprint arXiv:1412.6980. |
Krizhevsky A, Sutskever I, Hinton G E. 2012. ImageNet classification with deep convolutional neural networks.//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc, .
|
Leonard M, Kennett B L N. 1999. Multi-component autoregressive techniques for the analysis of seismograms. Physics of the Earth and Planetary Interiors, 113(1-4): 247-263. DOI:10.1016/S0031-9201(99)00054-0 |
Luo X H, Zhang Z, Liu G S. 2003. A kind of high pass digital filter for the reduction of zero drift. Seismological and Geomagnetic Observation and Research (in Chinese), 24(3): 49-52. |
Lv P, Ding Z F, Zhu L P. 2011. Application of double-difference relocation technique to aftershocks of 2008 Wenchuan earthquake using waveform cross-correlation. Acta Seismologica Sinica (in Chinese), 33(4): 407-419. |
Mccormack M D, Zaucha D E, Dushek D W. 1993. First-break refraction event picking and seismic data trace editing using neural networks. Goophysics, 58(1): 67-78. DOI:10.1190/1.1443352 |
Mhaskar H N, Micchelli C A. 1993. How to choose an activation function.//Proceedings of the 6th International Conference on Neural Information Processing Systems. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
|
Molyneux J B, Schmitt D R. 1999. First-break timing:Arrival onset times by direct correlation. Geophysics, 64(5): 1492-1501. DOI:10.1190/1.1444653 |
Murat M E, Rudman A J. 1992. Automated first arrival picking:A neural network approach. Geophysical Prospecting, 40(6): 587-604. DOI:10.1111/gpr.1992.40.issue-6 |
Peraldi R, Clement A. 1972. DIgital processing of refraction data study of first arrivals. Geophysical Prospecting, 20(3): 529-548. DOI:10.1111/gpr.1972.20.issue-3 |
Ramos-Martínez J, Ortega A A, Mcmechan G A. 2000. 3-D seismic modeling for cracked media:Shear-wave splitting at zero-offset. Geophysics, 65(1): 211-221. |
Russ J C. 1994. Fractal Surfaces. New York: Springer: 275-290.
|
Schroff F, Kalenichenko D, Philbin J. 2015. FaceNet: A unified embedding for face recognition and clustering.//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA: IEEE, 815-823.
|
Sleeman R, Van Eck T. 1999. Robust automatic P-phase picking:An on-line implementation in the analysis of broadband seismogram recordings. Physics of the Earth and Planetary Interiors, 113(1-4): 265-275. DOI:10.1016/S0031-9201(99)00007-2 |
Stevenson P R. 1976. Microearthquakes at Flathead Lake, Montana:A study using automatic earthquake processing. Bulletin of the Seismological Society of America, 66(1): 61-80. |
Szegedy C, Vanhoucke V, Ioffe S, et al. 2015. Rethinking the inception architecture for computer vision.//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA: IEEE, 2818-2826.
|
Takanami T, Kitagawa G. 1991. Estimation of the arrival times of seismic waves by multivariate time series model. Annals of the Institute of Statistical Mathematics, 43(3): 407-433. DOI:10.1007/BF00053364 |
Takanami T, Kitagawa G. 2003. Multivariate time-series model to estimate the arrival times of S-waves. Computers & Geosciences, 19(2): 295-301. |
Teng Y T, Wang X Z, Wang X M, et al. 2006. P wave onset time picking with the B-spline biorthogonal wavelet. Acta Seismologica Sinica (in Chinese), 28(3): 329-333. |
Tong C, Kennett B L N. 1996. Automatic seismic event recognition and later phase identification for broadband seismograms. Bulletin of the Seismological Society of America, 86(6): 1896-1909. |
Wang J, Teng T L. 1995. Artificial neural network-based seismic detector. Bulletin of the Seismological Society of America, 85(1): 308-319. |
Zhang J Z, Chen S J. 2003. Numerical modeling of seismic first break in complex media. Chinese Journal of Computation Physics (in Chinese), 20(5): 429-433. |
Zhao Y, Takano K. 1999. An artificial neural network approach for broadband seismic phase picking. Bulletin of the Seismological Society of America (in Chinese), 89(3): 670-680. |
常旭, 刘伊克. 1998. Hausdorff分数维识别地震道初至走时. 地球物理学报, 41(6): 826-832. DOI:10.3321/j.issn:0001-5733.1998.06.013 |
陈金焕, 曹永生, 孙成龙, 等. 2015. 基于二分法的地震波初至自动拾取算法. 地球物理学进展, 30(2): 688-694. DOI:10.6038/pg20150228 |
高静怀, 汪文秉, 朱光明. 1997. 小波变换与信号瞬时特征分析. 地球物理学报, 40(6): 821-832. DOI:10.3321/j.issn:0001-5733.1997.06.011 |
高淑芳, 李山有, 武东坡, 等. 2008. 一种改进的STA/LTA震相自动识别方法. 世界地震工程, 24(2): 37-41. |
何小波, 周蕙兰. 2005. 利用定尺度小波变换比方法测量远震极远震P和PKIKP震相到时. 地震学报, 27(4): 385-393. DOI:10.3321/j.issn:0253-3782.2005.04.004 |
胡明顺, 潘冬明, 徐红利, 等. 2009. 几种时频分析方法对比及在煤田地震勘探中的应用. 物探与化探, 33(6): 691-695, 709. |
罗新恒, 张哲, 刘桂生. 2003. 数字地震监测技术开发与应用论文(二)一种滤除零点漂移的高通数字滤波器. 地震地磁观测与研究, 24(3): 49-52. DOI:10.3969/j.issn.1003-3246.2003.03.009 |
吕鹏, 丁志峰, 朱露培. 2011. 结合波形互相关的双差定位方法在2008年汶川地震余震序列中的应用. 地震学报, 33(4): 407-419. DOI:10.3969/j.issn.0253-3782.2011.04.001 |
张建中, 陈世军. 2003. 复杂介质地震初至波数值模拟. 计算物理, 20(5): 429-433. DOI:10.3969/j.issn.1001-246X.2003.05.011 |
周磊, 申重阳, 韦进, 等. 2013. gPhone重力仪记录的汶川8.0地震高频信号研究. 大地测量与地球动力学, 33(S1): 16-19. |
滕云田, 王喜珍, 王晓美, 等. 2006. 用B-样条双正交小波拾取P波到时. 地震学报, 28(3): 329-333. DOI:10.3321/j.issn:0253-3782.2006.03.013 |
 2018, Vol. 61
2018, Vol. 61


