2. 重庆大学, 重庆 400044
2. Chongqing University, Chongqing 400044, China
2008年10月6日发生的西藏当雄MW6.3地震的宏观震中位于近南北向的亚东—谷露裂谷羊易盆地的北部(吴中海等,2009).据Global_CMT震源机制解,MW6.3主震为正断破裂,并且10月6日与10月8日相继发生的MW5.2与MW5.5余震也均以正断破裂为主(表 1).西藏当雄MW6.3地震发生后,一些学者利用InSAR测量技术进行了同震干涉形变提取及断层滑动反演研究(乔学军等,2009;冯万鹏等,2010;Elliott et al., 2010;Liu et al., 2012),主要的研究成果表明西藏当雄MW6.3地震的发震断层位于羊易盆地东侧,走向近南北向,倾向西,倾角介于47°~60°之间,断层滑动分布以正倾滑为主.由于SAR卫星在时间分辨率上无法将2008年的MW6.3、MW5.2与MW5.5三次地震进行区分,因此同震干涉形变场实际上包括了MW5.2与MW5.5余震的影响.
|
|
表 1 2008年10月6日当雄地震与主要余震震源机制解 Table 1 Focal mechanism of the October 6th 2008 Damxung Earthquake and Major aftershocks |
然而,距离2008年10月6日MW6.3级主震发生后约2年,2010年11月30日在该区域再次发生以正断破裂为主的MW5.3级余震(图 1,表 1).仅仅研究当雄MW6.3同震形变与同震破裂机理不足以揭示主震与余震之间的联系.获取间隔约2年的当雄MW6.3级主震与MW5.3级余震之间的地表形变场,是进一步认识主余震发震机理的重要前提.鉴于此,本文利用ENVISAT ASAR卫星数据,通过小基线集干涉测量、大气误差校正、轨道误差校正与基于小波变换的MInTS(Hetland et al., 2012)技术,提取了2008年西藏当雄MW6.3地震后约2年的地表形变场,并基于SDM方法(Wang et al., 2013)反演了震后余滑分布.结果表明:当雄MW6.3地震的震后形变场具有明显的对数函数衰减特征;震后余滑的地震矩与矩震级在时间演化上具有指数函数递增规律;当剪切模量μ=32 GPa,震后665天的余滑地震矩能量约1.92×1017,约为同震滑动释放矩能量的4.8%,相当于矩震级MW5.46;虽然部分余滑已经延伸到断层中南段0~5 km的浅部区域,但是浅部的弱余滑并没有改变断层浅部的滑动亏损现象.
|
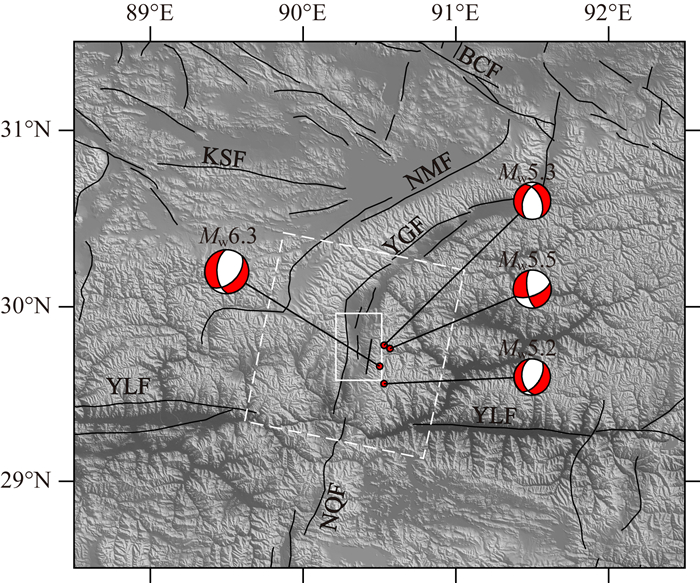
图 1 2008年西藏当雄MW6.3地震构造背景 白色虚线框为ENVISAT ASAR数据覆盖范围;白色实线框为当雄地震形变区域;BCF:崩错断裂;NMF:纳木错东南岸断裂;YGF:亚东—谷露断裂;NQF:念青唐古拉东麓断裂;YLF:雅鲁藏布江断裂;KSF:克玛如青—色丁断裂. Fig. 1 Seismic tectonic background of the 2008 Damxung MW6.3 Earthquake The white dashed frame is the coverage of ENVISAT ASAR data, and the white solid frame is the deformation region of the Damxung Earthquake; BCF, Bengcuo Fault; NMF, the Southeast Namucuo Lake Fault; YGF, Yadong-Gulu Fault; NQF, the eastern Nianqingtanggula Fault; YLF, Yaluzangbu River Fault; KSF, Kemaruqing-Seding Fault. |
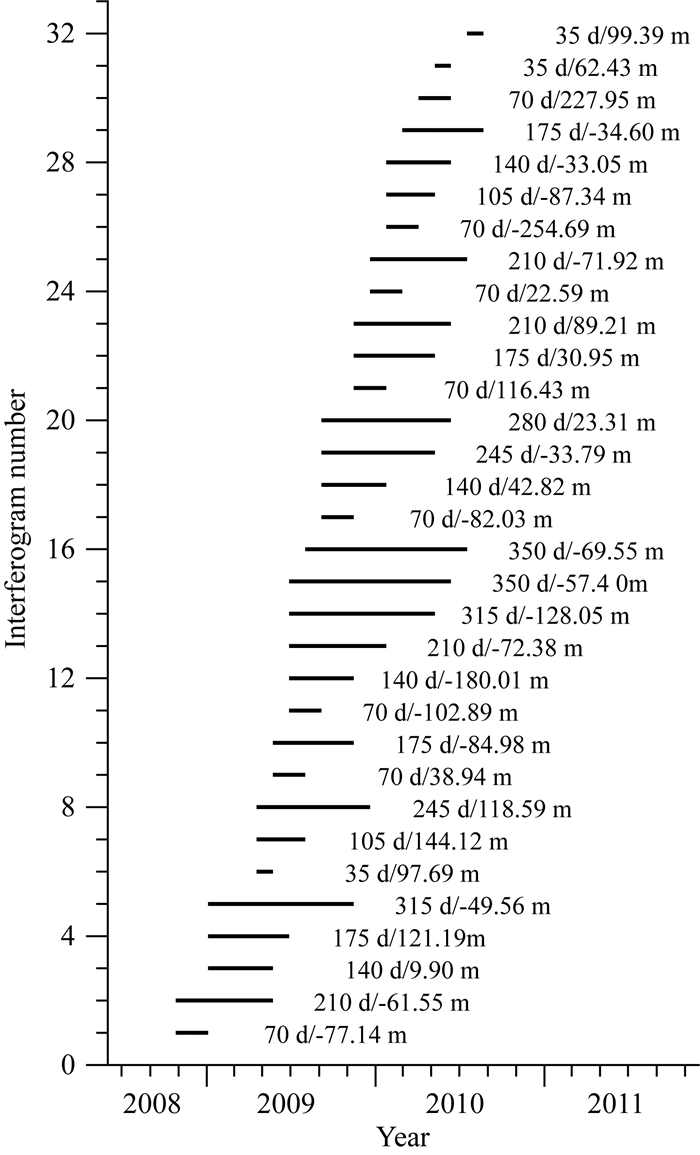
本文采用2008年10月26日至2010年08月22日之间的16期ENVISAT ASAR数据进行干涉测量处理,数据覆盖范围见图 1.ENVISAT ASAR数据为C波段,波长约5.6 cm.为了减少时空失相干的影响,本文采用小基线集组合策略(Hooper, 2008),共挑选出32组小基线干涉像对(图 2),除两组干涉像对的垂直基线距大于200 m之外,其他均小于200 m;所有干涉像对的时间基线距均小于365天.利用开源软件ROI_PAC对32组小基线干涉像对分别进行处理,处理时需要先将32组干涉像对进行严格配准,利用DORIS精密轨道减少轨道误差影响,通过SRTM3"DEM数据(空间分辨率约90 m)去除地形相位贡献,利用SNAPHU(Chen and Zebker, 2002)方法进行干涉相位解缠,并将解缠相位进行统一地理编码.
|
图 2 干涉像对小基线集 横坐标表示SAR数据时间,纵坐标表示干涉像对编号,一共有32组干涉像对;黑线右侧数值表示干涉像对的时间基线距与垂直基线距,如70d/-77.14m表示时间基线距为70天,垂直基线距为-77.14 m. Fig. 2 The small baseline interference pairs The horizontal axis is acquisition time of SAR data, the vertical axis is the number of the interference pairs, and there are 32 interference pairs in total. The values at right of black lines are the time baseline and vertical baseline of the corresponding interference pairs, for example, 70d/-77.14 m means 70 days for time baseline and -77.14 meters for vertical baseline. |
InSAR测量的大气误差主要包括电离层与对流层两部分.电离层误差对于波长较长的L/P波段卫星干涉测量是不可忽略的,而对于相对波长较短的C波段的影响较弱(Gray et al., 2000).由于采用的为C波段ENVISAT ASAR数据,本文仅考虑对流层的大气影响校正.采用Jolivet等(2011, 2014)提出的利用全球气象再分析资料进行大气误差校正的方法,可以克服获取其他气象卫星数据或地面实测资料的困难(Xu et al., 2010, Li et al., 2012),以及经验滤波模型带来的不确定性(Doin et al., 2009).LOS向单程路径对流层延迟δLLOSs(z)是地表高程z和参考高程Zref之间的空气折射率的积分,其数学模型为(Baby et al., 1988)
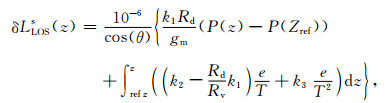
|
(1) |
LLOSs(z)代表高程z的像元点InSAR测量单次沿LOS向穿过对流层的大气延迟量,θ代表区域入射角,Rd=287.05 J·kg-1·K-1与Rv=461.495 J·kg-1·K-1分别代表干性大气与水气分子特定气体常数,gm代表高程Z与Zref之间的重力加速度加权均值,一般取值9.8 m·s-2,P代表干噪大气气体压力(单位Pa),e代表水蒸气气体压力(单位Pa),T代表气体温度(单位K).k1=0.776 K·Pa-1, k2=0.716 K·Pa-1, k3=3.75·103·K2·Pa-1为常数项(Smith and Weintraub, 1953).Zref通常取值10000 m,设定在这高度之上的大气折散系数的变化可以忽略不计.公式的第一项对应于对流层延迟的干性大气部分,第二项对应于大气湿气部分.
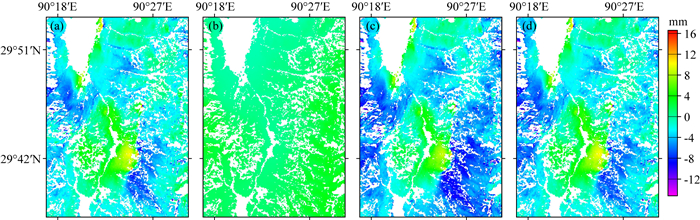
本文采用的全球气象再分析资料为ERA-Interim大气模型.ERA-Interim日模型每天提供4个UTC时间的模型数据,水平分辨率约0.75°,在垂直方向上共分37层压力等级.ERA_Interim大气模型的重力位势高度、相对温度、温度与压力等级4个参量是InSAR大气误差校正需要的输入参数.根据干涉像对SAR数据拍摄的UTM时间,获取与之时间上最接近的ERA-Interim日模型,分别计算32对干涉像对的大气延迟相位,进而从解缠相位中将大气延迟误差进行剔除(图 3a—3c).
|
图 3 干涉测量大气与轨道误差校正 (a)校正前干涉形变;(b) ERA_Interim模型大气延迟;(c)大气延迟校正结果;(d)轨道误差校正结果. Fig. 3 An example of atmospheric and orbital error correction for interferometry (a) The uncorrected interference deformation image; (b) The atmosphere delay from the ERA_Interim model; (c) The image after atmospheric correction; (d) The image after orbit error correction. |
虽然在干涉处理时引入DORIS精密轨道,但是仍然会存在残余的轨道误差影响.本文利用最佳拟合曲面方法(Cavalié et al., 2007),在大气延迟误差校正的基础上去除残余轨道误差的影响(图 3d).单个干涉像对的轨道误差相位可以用下式来估计:
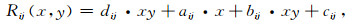
|
(2) |
ij代表组成干涉像对的SAR图像序号,(x, y)代表干涉图像的像元位置,aij,bij,cij,dij分别代表干涉像对ij的轨道误差校正系数.在轨道误差估计时,需要根据相干性与形变先验信息进行掩膜,以避免低相干点区域与形变区域对校正参数估计的影响.为了确保干涉网络中单个SAR图像具有一致性的轨道误差校正系数,需要通过最小二乘方法对轨道误差校正系数进行后修正.
1.4 震后形变反演将32组小基线集干涉像对进行干涉处理、大气误差校正与轨道误差校正后,利用Hetland等(2012)提出的MInTS时间序列分析方法进行震后形变反演.MInTS方法是基于空间域与时间域的小波分解技术,使用交叉验证、最小二乘、正规化最小二乘反演方法,在小波域对地表形变进行反演.Agram等(2013)将MInTS算法进行改进,可以直接支持InSAR数据域分析,避免了针对解缠相位的小波分解与重构过程,提高了计算效率.假设每个像元(m, n),可以构建如下的反演方程:
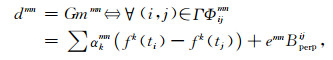
|
(3) |
Γ表示所有干涉像对集ij(ij,表示干涉像对的SAR数据序号),ti与tj表示SAR数据拍摄时间,Φijmn表示干涉像对ij的像元相位值,Bperpij表示干涉像对集ij的垂直基线距,emn表示地形误差.fk表示用户定义的形变函数集,可以包括季节性波动的形变函数、二次多项式函数、B样条函数、综合B样条函数、阶跃函数、指数函数、对数函数等,αkmn表示对应的系数.在实际反演中,可以有正则化最小二乘方法与非正规化最小二乘方法.非正则化最小二乘方法,针对每一个像元(m, n),通过最小化权值函数Fcmn来实现,Fcmn如下式:

|
(4) |
正规化最小二乘方法的函数Fcmn如下式:
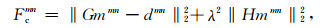
|
(5) |
H是拉普拉斯算子.利用广义奇异值分解方法选择阻尼参数λ.
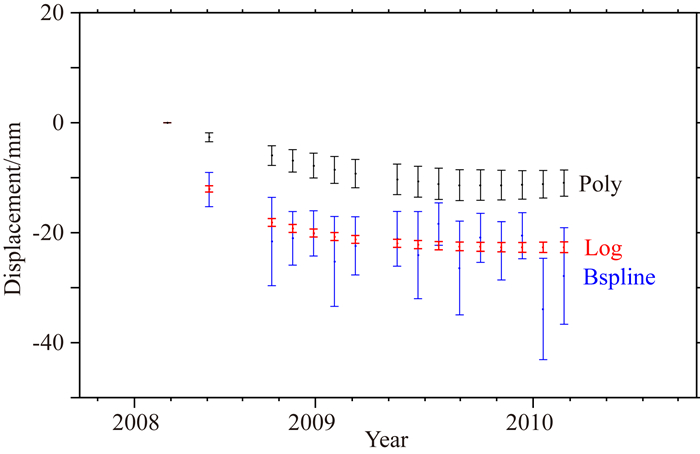
MInTS方法的优势是可以自定义形变函数模型,有利于提高形变解算的合理性.由于震后形变一般符合对数函数衰减的形变规律,本文采用对数函数模型进行2008年西藏当雄MW6.3地震的震后形变场解算,获得的震后形变序列如图 4所示.为了验证采用的对数函数模型是否合理,本文也尝试利用二次多项式与B样条曲线函数模型分别进行震后形变解算.然后,通过Jackknife方法(Quenouille, 1949, 1956; Efron and Stein, 1981)对形变序列解算的标准差进行评估.Jackknife方法是一种统计学上的重采样方法,它通过将某个T时刻的形变从整个形变数据集中抽离,利用剩余时刻的形变数据组成N个子集,结合形变经验模型(Hetland et al., 2012)与重采样方法,估计被抽离的T时刻形变的均值与标准差,并将标准差作为T时刻形变的不确定性,本文将这种不确定性称之为误差.通过Jackknife方法可以对不同函数模型解算的震后形变序列进行误差估计.从单点的形变序列及误差分析,发现基于二次多项式与B样条曲线函数模型的震后形变解算的误差明显大于对数函数模型(图 5).因此,采用对数函数模型进行震后形变场解算更加合理.通常,经验函数模型的选择,需要根据待研究对象的形变特征先验认识来确定.二次多项式与B样条曲线函数模型可能更适合于其他类型的形变信号提取;针对震后形变,对数函数模型显然更符合要求.

|
图 4 基于对数函数模型解算的当雄MW6.3地震震后形变场 以震后第1期SAR影像为参考,计算其他SAR影像与参考影像的成像时间差值作为震后天数;震后形变场没有明显的斑点噪声,主要表现为LOS向沉降. Fig. 4 The post-seismic deformation field of the Damxung MW6.3 earthquake based on the log function model The first SAR image acquired after the earthquake is assigned as the reference image, and the time difference between the other SAR images and the reference image are calculated as the post-seismic days; the post-seismic deformation field are mainly contributed by LOS subsidence. No obvious speckle noise in the deformation field. |
|
图 5 点形变序列及误差对比 点坐标为90.4120°E, 29.7096°N,具体位置见图 4的震后665天形变场的红色三角形;黑色、蓝色与红色点形变序列及标准差区间分别为采用二次多项式、B样条曲线与对数函数模型反演的结果. Fig. 5 The contrast of point deformation sequences and errors The coordinate of the point is 90.4120°E, 29.7096°N. The point is represented as a red triangle in the post-seismic 665 days image of the Fig. 4; The black, the blue, and the red point deformation sequences and errors are the results resolved by quadratic polynomial, B spline curve, and logarithmic function models, respectively. |
震后形变解算一共利用了震后16期ASAR观测数据,以震后第1期观测数据作为参考,可以解算得到15期的震后形变序列(图 4).根据雷达影像与参考影像的拍摄日期差值,可以计算15期震后形变序列的震后天数,有利于在时间维上分析震后形变序列的演化特征.震后70天,InSAR已经可以测量到明显的当雄震后形变信号,其LOS向的沉降形变量可达14 mm;震后665天,当雄震后形变最为明显,其LOS向的沉降形变量可达32 mm.在空间分布上,震后形变场没有出现明显的斑点噪声效应,震后形变区主要位于断层西侧,以LOS向沉降为主;断层东侧为LOS向隆升,但形变量相对较小.在时间演化上,震后形变序列符合对数函数衰减规律,大部分的震后形变集中在震后约1年内,1年后震后形变渐趋于稳定(图 5).
2 震后余滑分布反演为了提高余滑反演的效率,采用四叉树采样方法(Jónsson et al., 2002)对震后形变场进行降采样.由于不同时期的震后形变场具有相似的形变分布规律(图 4),本文首先利用震后665天的形变场进行四叉树降采样,形变点数量从38590降到2237;然后采用相同的四叉树降采样格网对其它时期的震后形变场进行降采样,使15期震后形变场经过降采样后具有同样的观测点,有利于在余滑反演时进行比较.
断层模型是进行震后余滑反演的重要参数.一般情况下,余滑反演的断层模型可以参考同震形变非线性反演的断层参数.考虑到现有同震断层几何模型参数的差异(表 2).本文直接根据震后形变场及同震形变场的图像特征确定断层在地表的投影位置,从而设定断层起点、终点与走向参数,断层倾角则直接利用GCMT解,上边界埋深则根据滑动分布反演的经验设置为0 km.
|
|
表 2 当雄MW6.3同震滑动反演的断层几何参数 Table 2 The fault geometry parameters of Damxung MW6.3 earthquake resolved by coseismic slip inversion |
利用SDM方法(Wang et al., 2013)进行震后余滑反演.由于分层地壳模型比均匀地壳模型更加合理,本文采用Crust1.0(Laske et al., 2013)地壳分层模型进行断层余滑反演,并利用EDGRN软件(Wang et al., 2003)计算格林函数.利用折中曲线的方法选择余滑反演的光滑因子.由于以震后第一期SAR观测为参考,因此2008年10月26日的震后形变场为0值,不参与反演.利用断层模型对其余15期震后形变场(图 4)分别进行余滑分布反演,模拟的震后形变场及残差如图 6所示,反演的余滑分布如图 7所示.模拟的震后形变场与InSAR测量的震后形变场具有较高的相似度,反演残差得到有效控制.震后主形变区域的模拟误差主要集中分布在远离断层的西侧.发震断层附近也存在一定残差影响,可能与余滑反演时采用的直线断层模型过于简化有关,也可能与震后粘弹性松驰效应有关.

|
图 6 震后余滑的模拟形变场与残差 (a, b, c, d)分别为震后70天,245天,455天与655天的InSAR形变场;(a', b', c', d')分别为对应的模拟形变场;(a", b", c", d")分别为对应的模拟残差;另外11期的模拟形变与残差特征与此类似;注意不同时间图像的色标范围不同. Fig. 6 The simulated post-seismic deformation fields and the residuals based on the after-slip (a, b, c, d) are respectively the InSAR deformation fields of 70, 245, 455, 655 days after earthquake; (a', b', c', d') are the corresponding simulated deformation fields, respectively; (a", b", c", d") are the corresponding residuals, respectively; and the other 11 periods of simulated deformation fields and residuals are similar; Note that the color bar for different time images are different. |
|
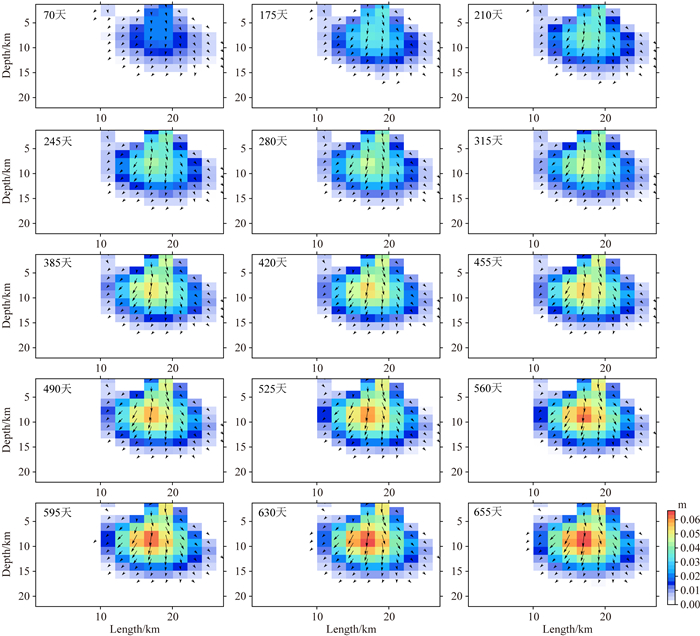
图 7 MW6.3级当雄地震的震后余滑分布 横坐标表示断层长度,纵坐标表示断层垂向深度;箭头长短表示余滑量相对大小,箭头方向表示余滑方向;震后余滑表现为单滑动中心,以正倾滑为主,随震后时间推移余滑量逐渐增加. Fig. 7 The afterslip distribution of Damxung MW6.3 earthquake The horizontal axis and vertical axis are respectively fault length and fault vertical depth; The length and the direction of the arrows indicate the relative magnitude and the direction of after-slips, respectively; The fault after-slips exhibit a single slip center, mainly normal dip slip, and increase gradually over time. |
从2008年10月26日至2010年08月22日,一共可以反演得到15期的震后余滑分布,结果如图 7所示.震后余滑表现为单一滑动中心,余滑主要集中于断层垂向深部0~15 km处,并在大致相同的位置出现由弱至强的递变过程.2010年08月22日即震后665天的余滑最明显,余滑最大量可达0.07 m,位于断层垂向深部约9.28 km,滑动角约-103°.另外,震后余滑主要出现在断层中南段,断层北段未发现明显的余滑过程.从震后余滑的滑动方向来分析,余滑主要表现为正倾滑,这与当雄MW6.3地震的同震滑动分布特征(乔学军等,2009;冯万鹏等,2010;Elliott et al., 2010;Liu et al., 2012)相类似.
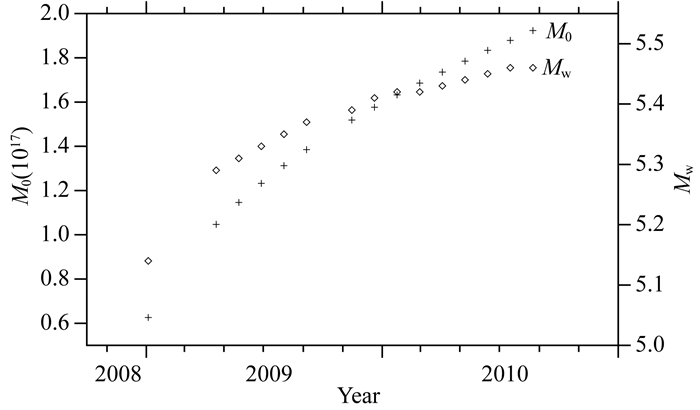
利用反演的震后余滑分布,可以计算不同时间的震后余滑地震矩及矩震级,结果如图 8所示.当剪切模量μ=32 GPa,2009年01月04日(震后70天)的震后余滑地震矩约为0.625×1017N·m,相当于矩震级MW5.14;2010年08月22日(震后665天)的震后余滑地震矩约为1.92×1017 N·m,相当于矩震级MW5.46.震后余滑引起的地震矩及矩震级均呈现较明显的指数函数递增变化特征,即表现为先快速增加再逐渐趋于平缓的过程.在时间演化上,震后余滑的地震矩及矩震级的指数变化规律(图 8)恰好与震后形变场的对数函数规律(图 5)相对应,这也表明震后余滑反演的结果是合理的.
|
图 8 震后余滑的地震矩与矩震级 当μ=32 GPa时,根据断层震后余滑计算的地震矩M0与矩震级MW均具有指数函数递增规律. Fig. 8 The earthquake moment and the moment magnitude of the after-slip When μ=32 GPa, both the seismic moment M0 and the moment magnitude MW calculated by the fault afterslip increase exponentially over time. |
关于同震滑动反演的研究已经有较多的成果(乔学军等,2009;冯万鹏等,2010;Elliott et al., 2010;Liu et al., 2012),主要包括断层几何参数的非线性反演及断层滑动分布反演.本文采用与Elliott等(2010)相同的ENVISAT ASAR数据进行同震形变场提取及同震滑动反演.ENVISAT ASAR升轨T26条带的震后数据观测时间为2008年10月15日,降轨T176条带的震后数据观测时间为2008年10月26日,避免了与震后形变场的时间重叠.同震差分干涉处理、大气延迟校正、轨道误差校正及四叉树降采样的方法与震后形变场提取过程中用到的方法类似,不再赘述.
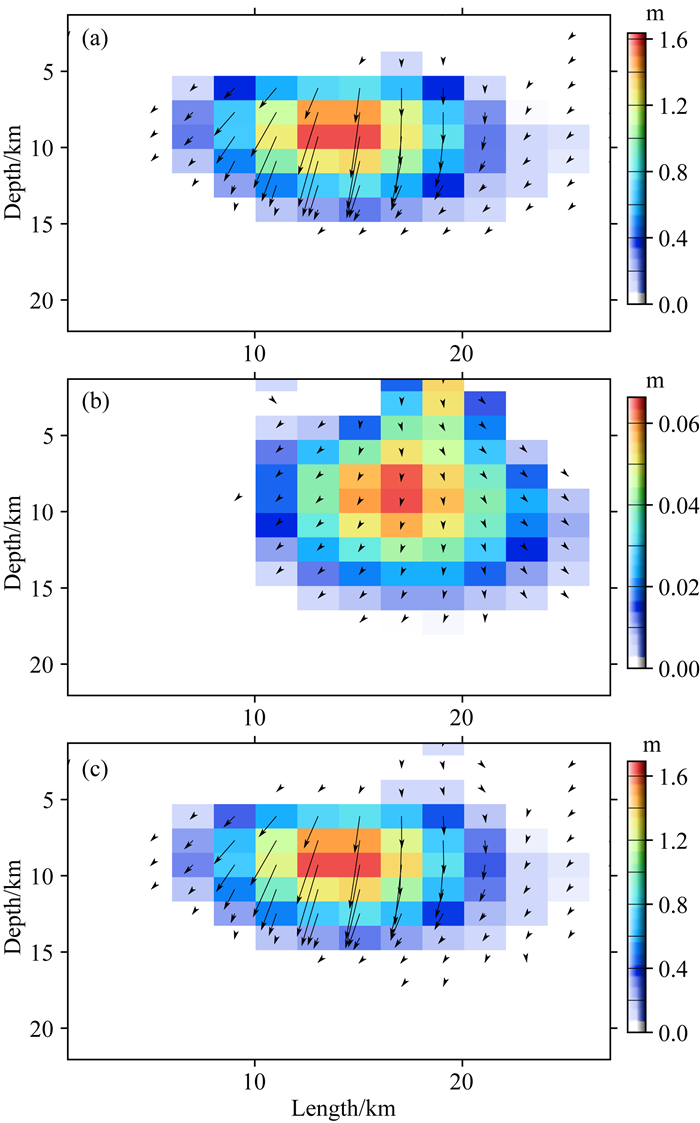
采用与震后余滑反演相同的地壳分层模型Crust1.0与断层模型,通过SDM方法进行同震滑动分布反演,结果如图 9a.同震滑动主要分布于断层深部5~15 km之间,断层浅部并没有出现明显的同震滑动.最大的同震滑动位于断层深部9.28 km处,滑动量可达1.64 m,滑动角约99.8°;断层同震滑动的平均滑动角约-108.8°,平均滑动量约0.16 m;当剪切模量μ=32 GPa时,反演的同震滑动地震矩M0约4.0×1018N·m,相当于地震矩MW6.34.而震后665天的余滑地震矩约1.92×1017N·m,约占同震滑动地震矩的4.8%.
|
图 9 同震及震后断层滑动分布 (a)同震滑动分布;(b)震后665天的余滑分布;(c)(a)与(b)叠加后的滑动分布.横坐标表示断层走向长度,纵坐标表示断层垂向深度;箭头长短表示滑动相对大小,箭头方向表示滑动方向. Fig. 9 The distribution of the coseismic and the postseismic slips along fault (a) The co-seismic slip distribution; (b) The after-slip distribution on post-seismic 665 days; (c) The slip distribution of sum of (a) and (b). The horizontal axis and the vertical axis are fault length and fault vertical depth, respective. The length and the direction of the arrow indicate the relative slip magnitude and the slip direction, respectively. |
将2010年08月22日(震后665天)的断层震后余滑与同震滑动进行叠加,结果如图 9c所示.由于震后665天的余滑最大值仅为0.07 m,而同震滑动最大值可达1.64 m,震后余滑相对于同震滑动显得并不明显.震后余滑与同震滑动的极值区均位于断层深部约9.28 km,导致大部分的震后余滑区与同震滑动区相互重叠(图 9).因此,虽然震后余滑使发震断层在同震滑动的基础上有进一步加剧滑动的趋势,但在总体上并没有改变断层同震滑动分布的特征.
值得注意的是,震后余滑虽然形变量相对较小,但是已经延伸到断层中南段的浅部区域(图 7).不过,从同震滑动与震后余滑叠加结果来分析,断层中南段浅部区域0~5 km的滑动量相对较小,仍然存在滑动亏损的现象;另外,断层中北段的滑动亏损更加明显(图 9c).
4 讨论与结论 4.1 讨论本文利用震后形变场及同震形变场的图像特征确定了断层走向值189°,与乔学军等(2009)利用同震形变干涉条纹确定的断层走向相同.在进行余滑分布反演时,断层走向对反演残差的影响最明显.本文尝试过利用其他研究成果(冯万鹏等,2010;Elliott et al., 2010;Liu et al., 2012)的断层走向参数进行震后余滑反演,发现在SDM方法反演时,利用其它断层走向参数的反演残差均大于本文采用189°断层走向的反演残差.
由于本文采用了更加合理的震后形变提取方法,与Bie等(2014)相比,本文的当雄MW6.3地震震后形变场在空间上并没有出现明显的斑点噪声影响,在时间序列上也更加符合震后余滑的对数衰减规律,震后形变场的精度得到有效提高.基于本文提取的震后形变场进行约束,利用SDM法反演的震后余滑在断层不同深度并没有出现多个滑动中心或分块的现象(Bie et al., 2014),而是集中分布在断层浅部0~15 km之间.另外,本文反演得到的震后不同时期的余滑地震矩能量M0略小于Bie等(2014)反演的结果,但两者处在同一数量级.
在震后约2年的时间内,当雄地震的震后形变场有可能还受到部分黏弹性松驰效应的影响(Bie et al., 2014).但是,InSAR测量的形变为2008年10月6日MW6.3地震的近场震后形变,在震后不到2年时间内的近场震后形变主要以余滑机制为主.Bie等(2014)在考虑黏弹性松驰效应时,以反演残差与震后InSAR形变场的相似性作为依据,从而大致判断地壳黏滞系数的下边界,也说明黏弹性松驰引起的地表形变并不能对该地震的近场震后形变起主导作用.因此,本文并没有进一步考虑黏弹性松驰效应的影响.
地震波形数据的同震滑动反演(高星等,2010)与InSAR数据同震滑动反演(冯万鹏等,2010;Elliott et al., 2010;Liu et al., 2012)均揭示同震滑动主要出现在断层面深部4~5 km以下.然而,震后余滑可以延伸到断层中南段的浅部区域0~5 km.但是,由于震后余滑量相对较小,综合考虑震后余滑和同震滑动分布,发现在断层浅部0~5 km区域仍然存在明显的滑动亏损,特别是断层北段的滑动亏损更加明显.因此,同震滑动的断层浅部亏损,并没有在震后余滑中得到有效补偿,这可能是随后100天左右2010年11月30日MW5.3级余震发生的主要原因之一.
4.2 结论本文利用小基线集干涉测量与MInTS技术提取了2008年西藏当雄MW6.3地震的震后形变场,通过SDM方法反演了2008年10月26日至2010年08月22日之间的震后余滑分布演化过程,并分析了震后余滑与同震滑动的相互关系,主要结论如下:
(1) 当雄MW6.3地震的震后形变场主要位于断层西侧,以LOS向沉降为主,震后665天的最大LOS向沉降量可达32 mm;在时间演化上,震后形变符合对数函数衰减规律;
(2) 震后665天的余滑量最大可达0.07 m,位于断层垂向深度约9.28 km处,滑动角约-103°;震后665天余滑释放的地震矩能量M0约为1.92×1017N·m,相当于矩震级MW5.46;
(3) 震后余滑反演的地震矩与矩震级在时间演化上具有指数函数递增规律,与震后形变的对数函数衰减规律相呼应;
(4) 震后余滑主要发生在断层深部0~15 km的中南段,同震滑动主要发生在断层深部5~15 km;震后665天的余滑地震矩相当于同震滑动地震矩的4.8%;
(5) 虽然震后余滑已经延伸到断层浅部区域并接近地表,但由于余滑量相对较小,并没有改变同震滑动在断层浅部区域的滑动亏损现象.
致谢 评审老师对本研究提出了宝贵建议,汪荣江老师提供了SDM反演程序,欧洲航天局(European Space Agency,ESA)提供了ENVISAT ASAR科学研究共享数据(C1P.5623),文中图件为GMT程序绘制,在此一并致谢.
Agram P S, Jolivet R, Riel B, et al. 2013. New radar interferometric time series analysis toolbox released. Eos, Trans. AGU, 94(7): 69-70. |
Baby H B, Golé P, Lavergnat J. 1988. A model for the tropospheric excess path length of radio waves from surface meteorological measurements. Radio Science, 23(6): 1023-1038. DOI:10.1029/RS023i006p01023 |
Bie L D, Ryder I, Nippress S E J, et al. 2014. Coseismic and post-seismic activity associated with the 2008 MW6.3 Damxung earthquake, Tibet, constrained by InSAR. Geophysical Journal International, 196(2): 788-803. DOI:10.1093/gji/ggt444 |
Cavalié O, Doin M P, Lasserre C, et al. 2007. Ground motion measurement in the Lake Mead area, Nevada, by differential synthetic aperture radar interferometry time series analysis:Probing the lithosphere rheological structure. Journal of Geophysical Research, 112: B03403. DOI:10.1029/2006JB004344 |
Chen C W, Zebker H A. 2002. Phase unwrapping for large SAR interferograms:statistical segmentation and generalized network models. IEEE Transactions on Geoscience and Remote Sensing, 40(8): 1709-1719. DOI:10.1109/TGRS.2002.802453 |
Doin M P, Lasserre C, Peltzer G, et al. 2009. Corrections of stratified tropospheric delays in SAR interferometry:Validation with global atmospheric models. Journal of Applied Geophysics, 69(1): 35-50. |
Efron B, Stein C. 1981. The jackknife estimate of variance. The Annals of Statistics, 9(3): 586-596. DOI:10.1214/aos/1176345462 |
Elliott J R, Walters R J, England P C, et al. 2010. Extension on the Tibetan plateau:recent normal faulting measured by InSAR and body wave seismology. Geophysical Journal International, 183(2): 503-535. DOI:10.1111/j.1365-246X.2010.04754.x |
Feng W P, Xu L S, Li Z H. 2010. Fault parameters of the October 2008 Damxung MW6.3 earthquake from InSAR inversion and its tectonic implication. Chinese J. Geophys. (in Chinese), 53(5): 1134-1142. DOI:10.3969/j.issn.0001-5733.2010.05.014 |
Gao X, Duan Z Q, Wang W M, et al. 2010. Rupture process of the Oct.6 Damxung earthquake, Tibet, China. Chinese J. Geophys (in Chinese), 53(9): 2083-2090. DOI:10.3969/j.issn.0001-5733.2010.09.008 |
Gray A L, Mattar K E, Sorko G. 2000. Influence of ionospheric electron density fluctuations on satellite radar interferometry. Geophysical Research Letters, 27(10): 1451-1454. DOI:10.1029/2000GL000016 |
Hetland E A, Musé P, Simons M, et al. 2012. Multiscale InSAR Time Series (MInTS) analysis of surface deformation. Journal of Geophysical Research, 117: B02404. DOI:10.1029/2011JB008731 |
Hooper A. 2008. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophysical Research Letters, 35: L16302. DOI:10.1029/2008GL034654 |
Jolivet R, Grandin R, Lasserre C, et al. 2011. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophysical Research Letters, 38: L17311. DOI:10.1029/2011GL048757 |
Jolivet R, Agram P S, Lin N Y, et al. 2014. Improving InSAR geodesy using Global Atmospheric Models. Journal of Geophysical Research:Solid Earth, 119(3): 2324-2341. DOI:10.1002/2013JB010588 |
Jónsson S, Zebker H, Segall P, et al. 2002. Fault slip distribution of the 1999 MW7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bulletin of the Seismological Society of America, 92(4): 1377-1389. DOI:10.1785/0120000922 |
Laske G, Masters G, Ma Z T, et al. 2013. Update on CRUST1.0-A 1-degree global model of earth's crust.//EGU General Assembly 2013. Vienna, Austria.
|
Li Z W, Xu W B, Feng G C, et al. 2012. Correcting atmospheric effects on InSAR with MERIS water vapour data and elevation-dependent interpolation model. Geophysical Journal International, 189(2): 898-910. DOI:10.1111/j.1365-246X.2012.05432.x |
Liu Y, Xu C J, Wen Y M, et al. 2012. Fault rupture model of the 2008 Dangxiong (Tibet, China) MW6.3 earthquake from Envisat and ALOS data. Advances in Space Research, 50(7): 952-962. DOI:10.1016/j.asr.2012.06.006 |
Qiao X J, You X Z, Yang S M, et al. 2009. Study on dislocation inversion of MS6.6 Damxung earthquake as constrained by InSAR measurement. Journal of Geodesy and Geodynamics (in Chinese), 29(6): 1-7. |
Quenouille M H. 1949. Problems in plane sampling. The Annals of Mathematical Statistics, 20(3): 355-375. DOI:10.1214/aoms/1177729989 |
Quenouille M H. 1956. Notes on bias in estimation. Biometrika, 43(3-4): 353-360. DOI:10.1093/biomet/43.3-4.353 |
Smith E K, Weintraub S. 1953. The constants in the equation for atmospheric refractive index at radio frequencies. Proceedings of the Ire, 41(8): 1035-1037. DOI:10.1109/JRPROC.1953.274297 |
Wang R J, Martín F L, Roth F. 2003. Computation of deformation induced by earthquakes in a multi-layered elestic crust-FORTRAN programs EDGRN/EDCMP. Computers & Geosciences, 29(2): 195-207. |
Wang R, Parolai S, Ge M, et al. 2013. The 2011 MW9.0 Tohoku Earthquake:Comparison of GPS and strong-motion data. Bulletin of the Seismological Society of America, 103(2B): 1336-1347. DOI:10.1785/0120110264 |
Wu Z H, Ye P S, Wu Z H. 2009. The seismic intensity, seismogenic tectonics and mechanism of the MS6.6 Damxung earthquake happened on October 6, 2008 in southern Tibet, China. Geological Bulletin of China (in Chinese), 28(6): 713-725. |
Xu C J, Liu Y, Wen Y M, et al. 2010. Coseismic slip distribution of the 2008 MW7.9 Wenchuan Earthquake from joint inversion of GPS and InSAR data. Bulletin of the Seismological Society of America, 100(5B): 2736-2749. DOI:10.1785/0120090253 |
冯万鹏, 许力生, 李振洪. 2010. 2008年10月当雄MW6.3级地震断层参数的InSAR反演及其构造意义. 地球物理学报, 53(5): 1134-1142. DOI:10.3969/j.issn.0001-5733.2010.05.014 |
高星, 段宗奇, 王卫民, 等. 2010. 2008年10月6日当雄MS6.6级地震破裂过程. 地球物理学报, 53(9): 2083-2090. DOI:10.3969/j.issn.0001-5733.2010.09.008 |
乔学军, 游新兆, 杨少敏, 等. 2009. 当雄Ms6. 6地震的InSAR观测及断层位错反演. 大地测量与地球动力学, 29(6): 1-7. |
吴中海, 叶培盛, 吴珍汉. 2009. 2008年10月6日西藏当雄MS6.6级强震的地震烈度控震构造和发震机理. 地质通报, 28(6): 713-725. DOI:10.3969/j.issn.1671-2552.2009.06.005 |
 2018, Vol. 61
2018, Vol. 61


