地球物理学报  2018, Vol. 61 Issue (12): 4746-4757   PDF    
引用本文
黄谟涛, 刘敏, 邓凯亮, 等. 2018. 基于向上延拓的航空重力向下解析延拓解. 地球物理学报, 61(12): 4746-4757, doi: 10.6038/cjg2018L0594.  
Huang M T, Liu M, Deng K L, et al. 2018. Analytical solution of downward continuation for airborne gravimetry based on upward continuation method. Chinese J. Geophys. (in Chinese), 61(12): 4746-4757, doi: 10.6038/cjg2018L0594.  
基于向上延拓的航空重力向下解析延拓解
黄谟涛1, 刘敏2, 邓凯亮1,3, 欧阳永忠1, 陆秀平1, 翟国君1, 吴太旗1, 陈欣1     
1. 海军海洋测绘研究所, 天津 300061;
2. 信息工程大学地理空间信息学院, 郑州 450001;
3. 国防科技大学机电工程与自动化学院, 长沙 410073
收稿日期 2017-09-08, 2017-10-31 收修定稿
基金项目: 国家自然科学基金（41804011，41474012），国家重点研发计划（2016YFC0303007，2016YFB0501704）和国家重大科学仪器设备开发专项（2011YQ12004504）共同资助
第一作者简介: 黄谟涛, 男, 1961年生, 博士生导师, 研究方向为海洋重力场测定理论方法.E-mail:Ouyangyz@sohu.com
通讯作者: 邓凯亮, 男, 1983年生, 博士, 研究方向为海空重力测量理论及应用技术.E-mail:dengkailiang036@163.com
摘要：位场向下与向上延拓之间存在固有的内在联系，向上延拓解算具有稳定可靠的优良特性，本文据此提出了借助向上延拓信息实现航空重力向下延拓稳定解算的两种方法，分别建立了点对点向下解析延拓模型和最小二乘向下解析延拓模型.其核心思想是，依据泰勒级数展开模型，将位场向下延拓解算过程转换为向上延拓计算和垂向偏导数解算两个步骤，通过第一步的处理有效抑制数据观测噪声对解算结果的干扰，通过第二步的处理成功实现向下延拓反问题的稳定解算，较好地解决了向下延拓解算固有的不适定性问题.分析研究了两种解析延拓模型的计算精度及适用条件，利用超高阶位模型EGM2008建立的模拟标准场数据对两种模型解算结果的合理性和有效性进行了数值验证，证明本文新方法实用易行，具有较高的应用价值.
关键词: 航空重力测量      向上与向下延拓      泰勒级数展开      垂向偏导数      精度估计     
Analytical solution of downward continuation for airborne gravimetry based on upward continuation method
HUANG MoTao1, LIU Min2, DENG KaiLiang1,3, OUYANG YongZhong1, LU XiuPing1, ZHAI GuoJun1, WU TaiQi1, CHEN Xin1     
1. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China;
2. Institute of Geographic Space Information, Information Engineering University, Zhengzhou 450001, China;
3. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China
Abstract: There exists an inherent link between upward and downward continuation of potential field data. It is undoubted that the upward continuation procedure can give a stable and reliable solution. Based on this excellent property of upward continuation, we propose two methods to obtain a stable solution for downward continuation of airborne gravity data using the information of upward continuation. Then a point-to-point analytical model and a least-squares analytical model of downward continuation are established. The key view of the new approaches is that a downward continuation process can be transformed to an upward continuation procedure and the computation of vertical derivatives by means of Taylor series expansion. The effect of data noise on the solution of downward continuation will be suppressed by the operation of first step. And a stable solution of downward continuation can be obtained by the operation of second step. So we avoid the ill-posedness problem of downward continuation successfully. The solution accuracy and applicability of the new models are analyzed and discussed. Finally, a numerical test using a synthetic airborne gravity data set from ultra-high-degree geopotential model EGM2008 has been made to prove the reasonableness and validity of the suggested models. It is shown that the new methods are practical and easy to be realized, and will be of great value to the application of airborne gravimetry.
Keywords: Airborne gravimetry    Upward and downward continuation    Taylor series expansion    Vertical derivatives    Accuracy estimation    
0 引言

位场向上和向下延拓是地球物理和大地测量数据分析应用中最重要的技术环节之一.位场向下延拓的目的是将数据观测面外推到更接近于位场源体，通过改善观测数据的信噪比，增强地球内部浅层质量分布异常的映射强度，来凸显地球重力场或磁场的局部变化特征，以提高位场数据解释推断的可靠性(Trompat et al., 2003；陈生昌和肖鹏飞，2007；骆遥和吴美平，2016).但我们知道，位场向下延拓在数学上属于典型的不适定反问题，其延拓算子对高频噪声具有明显的放大作用，很小的观测噪声也会引起延拓解算结果严重偏离真实的问题解(Martinec, 1996；王彦飞, 2007).针对此问题，国内外学者已经开展了广泛而深入的研究工作，提出了许多富有成效的处理方法.在重力场向下延拓研究领域，归纳起来主要有三种解决途径：第一种是直接求逆泊松(Poisson)积分方程(包括迭代求解和非迭代求解法、FFT法)，人们主要围绕求逆过程引起的不稳定性问题开展不同形式的正则化方法研究，代表成果包括：Hansen和O′Leary(1993)提出的L-曲线法；Xu(1998)提出的截断奇异值分解法(TSVD)；Kern(2003)、Alberts和Klees(2004)对包括正则化和非正则化在内的不同类型向下延拓算法的适用性作了比较全面的分析和比较；王兴涛等(2004a, 2004b)研究解析了重力向下延拓的正则化算法及其谱分解式，定量评估了几种常用向下延拓方法的应用效果；王振杰(2006)给出了不适定问题正则化解法的统一表达式；顾勇为和归庆明(2010)分析研究了基于信噪比的重力向下延拓正则化解法；邓凯亮等(2011)提出了重力向下延拓的Tikhonov双参数正则化算法；蒋涛等(2011)分析比较了Tikhonov、岭估计和广义岭估计三种正则化算法的技术特点及应用效果；孙文等(2014)提出了基于波数域迭代的向下延拓Tikhonov正则化算法；刘晓刚等(2014)研究探讨了位场数据向下延拓中最优正则化参数的选择问题.解决重力向下延拓问题的第二种途径是间接求逆法，包括最小二乘配置法(Moritz，1980；Hwang et al., 2007)、点质量方法(李建成等，2003；黄谟涛等，2005)、多尺度边缘变换法(Boschetti et al., 2004；宁津生等，2005)和矩谐分析法(蒋涛等，2013)等，此类方法虽然避开了直接求逆Poisson积分方程，但仍涉及矩阵求逆过程，因此也不可避免存在不稳定性问题(黄谟涛等, 2013, 2015a).第三种途径可统称为非求逆法，代表成果包括：石磐和王兴涛(1997)提出的利用航空重力测量和DEM确定地面重力场的直接代表法；黄谟涛等(2014, 2015b)提出的联合使用超高阶位模型和地形信息确定向下延拓改正数的方法等，此类方法不受传统求逆过程不稳定性的影响.Novák和Heck(2002)依据航空重力测量数据固有的带限(band-limited)频谱特性，提出了向下延拓的直接积分公式，并将其推广应用于大地水准面的直接解算，其计算过程也避开了方程求逆问题.刘敏等(2016)分析检验了当前国内外最具代表性的几种向下延拓模型的计算效果，得出了比较明确的量化分析结论.

针对磁场数据向下延拓问题，国内外学者也陆续推出了系列化的研究成果，Bateman(1946)、Peters(1949)最早提出采用泰勒(Taylor)级数法作位场的延拓计算；栾文贵(1983)、梁锦文(1989)和Cooper(2004)很早就将正则化方法引入到位场向下延拓领域；Fedi和Florio(2002)提出了基于组合二阶垂直梯度(ISVD)的位场延拓模型；Trompat等(2003)提出了改进的位场延拓模型；徐世浙(2006, 2007)创新提出了位场向下延拓的积分-迭代法；陈生昌和肖鹏飞(2007)、张辉等(2009)、刘东甲等(2009)分别提出了位场向下延拓的波数域广义逆算法、正则化方法及迭代算法；卞光浪(2011)提出了磁异常稳健向下延拓的改进泰勒级数法；骆遥和吴美平(2016)提出了位场向下延拓的最小曲率方法.很显然，上述各类方法的提出和应用，都在一定程度上改善了位场向下延拓解算的不稳定性和精确度.但不可否认的是，这些方法在实际应用中仍存在一些不足或改进的余地，有些新方法可能只停留在理论研究和仿真试验阶段，缺少实测数据的解算验证；有的方法可能理论上很严密，但因实现过程过于复杂而受到应用上的制约.Vaníček等(2017)依据法国数学家Hadamard的理论，推断位场向下延拓具有物理意义上的适定性，存在有限的唯一解.该文作者甚至认为，任何指望通过物理意义上的正则化方法来改善向下延拓解的想法都是徒劳的，因为在存在观测噪声干扰的情形下，寻求向下延拓的精确解是没有实际意义的，应当把向下延拓作为一个统计问题来处理，寻求该问题的最优估计.

由上述综合分析结果得知，关于位场向下延拓问题，国内外学者虽然已经提出了许多各具特色的解算模型和方法，但至今未能推出一种统一通用的解决方案，仍有一些理论上和应用上的难点问题需要研究解决.本文主要针对航空重力向下延拓稳定性和实用性两个方面的应用需求，探讨借助向上延拓信息改善向下延拓不稳定性和解算精度的可能性，同时达到简化向下延拓解算过程的目的.

1 向下延拓解算模型及适用性分析 1.1 基于向上延拓的点对点解析解

泰勒级数展开式是最经典的位场解析延拓模型之一.假设海拔高度为ho的待求地球表面O点的重力异常为Δgo，已知对应飞行高度面hp(P点)上的空中重力异常为Δgp，则由重力场解析延拓理论得知(Moritz, 1980)，Δgo和Δgp之间的关系可表示为

(1)

式中，Δhpo=hp－ho代表空间P点相对于地面O点的高度差；代表空中重力异常Δgp在P点的n阶垂向偏导数；δΔgpo代表重力异常Δgp到Δgo的向下延拓改正数.由式(1)知，实现航空重力向下延拓计算的关键是，准确获取重力异常沿垂直方向的各阶偏导数.当此条件无法得到满足时，需要寻求其他的替代方案.这里首先给出一种比较简单的近似处理方法.

假设位于飞行高度面上方、海拔高度为hq(Q点)处的空中重力异常为Δgq，令Δhqp=hq－hp，那么，根据重力场解析延拓理论，同样可以将Δgq和Δgp之间的关系表示为

(2)

式中，δΔgpq代表重力异常Δgp到Δgq的向上延拓改正数，其他符号意义同前.如果人为取Δhqp=Δhpo，那么将式(1)和(2)两式相加并略加整理得

(3)

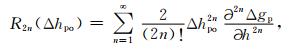
(4)

这里称R2n(Δhpo)为向下延拓改正数的余项.如果忽略该余项的影响，即令

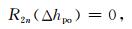
(5)

那么就得到如下近似的点对点向下解析延拓计算式：

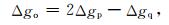
(6)

式中，航空重力异常Δgp是已知的，Δgq可依据Poisson积分方程由Δgp向上延拓计算得到.可见，延拓计算式(6)的实现过程是稳定可靠的，不存在向下延拓固有的不适定性问题.由Δgp向上延拓计算Δgq的Poisson积分公式为(Heiskanen and Moritz, 1967)

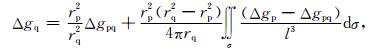
(7)

式中，rp=R+hp，rq=R+hq，R为地球椭球平均半径；Δgpq代表与计算点Q相对应的飞行高度面上的重力异常；Δgp为飞行高度面流动点的重力异常；为计算点与流动点之间的空间距离，ψ为计算点与流动点之间的球面角距.使用式(7)进行向上延拓计算可避开常见的积分奇异性问题.

实际上，不难证明，通常使用的一阶梯度解模型只是前面给出的向下解析延拓模型(即式(6))的主项.根据Heiskanen和Moritz(1967)，飞行高度面上与地面O点、空中Q点相对应的重力异常一阶垂向梯度积分式可表示为

(8)

式中，，其他符号意义同前.把式(8)代入式(1)得

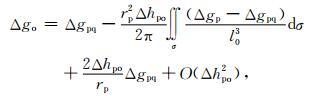
(9)

式中，O(*)为Landau符号.把式(7)代入式(6)得

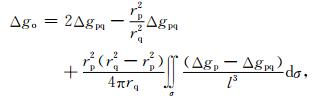
(10)

进一步做下列简化：

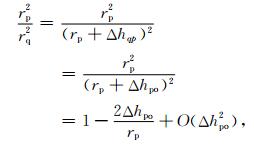
(11)

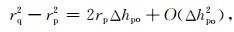
(12)

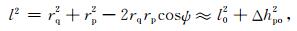
(13)

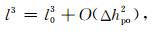
(14)

将式(11)、(12)和(14)代入式(10)，并做简单的整理就得到式(9).由此可见，在只顾及到延拓高度差(Δh)一阶项影响条件下，两种向下延拓计算模型是等价的.也就是说，对应于式(9)的一阶梯度解只是式(10)模型解的主项.使用式(10)(也就是式(6))作为向下延拓解算模型既可顾及到延拓高度差(Δh)高阶项的影响，同时可利用向上延拓算子的低通滤波特性，对观测量中的高频噪声进行有效的抑制.

需要指出的是，使用式(10)作为向下延拓模型虽然顾及了一部分高阶项的影响，但也忽略了另一部分高阶项的影响.对比式(1)、(2)和(6)不难看出，等式(5)完全等价于下面的等式：

(15)

上式说明，忽略余项R2n(Δhpo)的影响就意味着把重力向上延拓改正数近似等同于向下延拓改正数.我们也因此将式(6)称为点对点解析延拓模型，其近似处理带来的误差大小(见式(4))取决于二阶及以上偶阶项重力异常垂向偏导数和延拓高度差(Δh)的量值.目前国内外航空重力测量的精度水平在1~5 mGal(10-5m·s-2)之间(Alberts，2009；孙中苗等，2013；欧阳永忠等，2013)，根据误差传播理论，为确保向下延拓计算模型误差不显著影响航空重力测量成果的质量，应尽可能将计算模型的单项误差控制在数据观测误差的四分之一以内.这里将观测误差量值设定为2 mGal(新型航空重力仪一般可达到此指标)，取计算模型单项误差限差为0.5 mGal，依据模型解式(10)所对应的截断误差表达式(4)，可分别确定在不同延拓高度差条件下，满足单项误差限差要求的不同阶次重力异常垂向偏导数所允许的变化幅度.其中，二阶和四阶垂向偏导数允许变化幅度的计算式分别为

(16)

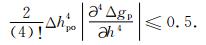
(17)

对应于5个不同延拓高度差的具体计算结果如表 1所示.当已知某一区域的重力异常垂向偏导数量值大小时，也可由式(16)和(17)确定误差限差允许下的向下延拓计算高度.

表 1 误差限差允许下的重力异常垂向偏导数变化幅度 Table 1 Ranges of gravity vertical derivatives under allowable error

在实际应用中，我们可依据表 1给出的计算对比结果，分析评估向下延拓模型解式(10)对于不同变化特征重力场的适应能力，可事先对预定的测量区域开展航空重力测量技术设计，以确定合适的测量飞行高度.

1.2 基于向上延拓的最小二乘解析解

如前所述，依据泰勒级数展开式(1)进行航空重力向下延拓计算的关键，是准确获取重力异常沿垂直方向的各阶偏导数.前面给出了不需要直接计算重力异常垂向梯度，借助向上延拓信息就能实现向下延拓稳定解算的近似处理方法.该方法虽然简便易行，但由于模型解的截断误差随延拓高度差增大而快速增大，因此其适用范围受到了一定的限制，只能应用于较低飞行高度的航空重力向下延拓计算.为了突破上述近似模型解的限制，这里进一步提出借助向上延拓信息，通过最小二乘方法计算重力异常不同阶次的垂向偏导数，从而实现向下延拓的严密和稳定解算.

关于位场观测量沿垂直方向各阶导数的计算问题，国内外学者已经开展了许多卓有成效的研究工作(Fedi and Florio, 2002；Cooper，2004；翟国君等，2011；卞光浪，2011)，但已有研究成果的解算思路几乎都是基于位场强度沿垂直和水平方向的二阶偏导数之间满足拉普拉斯(Laplace)方程这一基本假设，通过借助水平方向的偏导数来计算垂向偏导数的，并通常采用频率域方法进行这样的转换.该方法理论上较为完善，但频率域中的响应函数相当于高频放大器，对观测数据中的噪声具有显著的放大作用，且存在较强的边缘效应，因此需要对相关算法做相应的改化(Trompat et al., 2003；卞光浪，2011).本文提出了完全有别于上述传统的由水平向转换到垂直向的解算思路，具体解算过程如下.

首先在航空重力测量飞行高度面上方，以一定的间隔选取M个高度面(Q1，Q2，…，QM)，它们相对于飞行高度面的高度差为：Δh1，Δh2，…，ΔhM.然后利用飞行高度面上的重力异常观测量(Δgp)，依据向上延拓积分式(7)分别计算上述M个高度面上的重力异常(ΔgQ1，ΔgQ2，…，ΔgQM).将计算得到的M个高度面上的重力异常作为过渡观测量代入泰勒级数展开式(2)，可得到一系列以重力异常垂向偏导数作为未知数的观测方程.对于飞行高度面上的某个P点，使用处于不同高度面但在同一垂线方向上的M个重力异常(Δgq1，Δgq2，…，ΔgqM)，可建立M个相对应的观测方程.考虑到航空重力测量分辨率的有限性和观测噪声干扰的现实性，这里取泰勒级数展开式(2)的最高阶数N=4，由此可建立如下形式的观测误差方程：

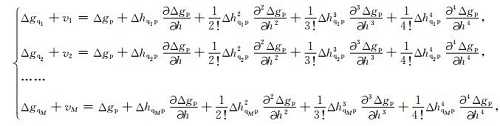
(18)

式中，vi代表重力异常观测误差和向上延拓计算误差的综合影响.令

可将式(18)表示为如下矩阵形式：

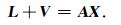
(19)

取M>N，可求得式(19)的最小二乘解为

(20)

这里把由式(20)一次性求出所有未知数的解法称为整体解.需要指出的是，当飞行高度面上的重力异常观测量(Δgp)存在较大的观测误差时，由其计算得到的M个高度面上的重力异常(ΔgQ1，ΔgQ2，…，ΔgQM)也必然会受到较大的干扰，此时由式(20)解算得到的高阶垂向偏导数可能存在较高的不确定性.为了解决此类问题，本文提出如下分步求解不同阶次垂向偏导数的数值解法(简称分步法)：以N=4为例，首先按照式(20)确定一阶和二阶垂向偏导数x1和x2，然后把x1和x2作为已知量，同时把四阶项影响视为误差干扰，使用下式计算三阶垂向偏导数：

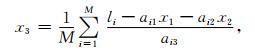
(21)

此后，可进一步把x1、x2和x3作为已知量，使用下式计算四阶垂向偏导数：

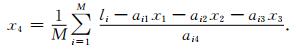
(22)

通过降低未知数解算过程的相关性，以提高解算结果的稳定性，是上述分步计算高阶垂向偏导数做法的主要目的，其实际效果将在后面的数值试验中做进一步的验证.最后将单独由式(20)或由式(20)—(22)联合计算得到的重力异常垂向偏导数代入式(1)，即完成了航空重力向下延拓解析模型的构建，依据该模型可实现任意高度差下的向下延拓解算.但在多大的高度差范围内，相对应的向下延拓解算结果才是有效的，取决于多方面的影响因素.

由式(1)和(18)知，航空重力向下延拓计算过程不仅涉及原始的重力观测量(Δgp)，还涉及两个不同层次的过渡计算量即向上延拓计算值(Δgqi)和重力异常垂向偏导数.可见，向下延拓模型的解算精度不仅取决于航空重力的观测精度和垂向偏导数的计算精度，还取决于模型展开式的截断阶数(N)和向上延拓值(Δgqi)的计算精度，它们之间相互交叉影响，具有较强的相关性，因此很难使用传统的精度估计公式来精确表征上述解算过程的误差传播规律.实际上，除了数据观测误差、过渡量计算误差和模型截断误差以外，在向下延拓模型中还隐含一个与计算区域重力场变化特征相关的代表误差因素的影响，因为我们知道，泰勒级数展开式是以展开点处的各阶偏导数为基础建立起来的，计算点距离展开点越远，重力场变化特征越显著，各阶偏导数的代表误差就越大，展开式的计算误差也就越大.由此可见，上述向下延拓模型的有效性不仅取决于重力数据观测精度水平的高低，还取决于计算区域重力场变化的剧烈程度，两个方面的因素都直接影响该延拓模型的适用高度.

为了进一步了解和掌握向下延拓模型的适用性与垂向偏导数解算精度和向下延拓有效高度之间的制约关系，这里参照前面建立误差限差方程式(16)和(17)时的研究思路，同样将对应于式(1)的向下延拓解析模型的单项误差限定为0.5mGal，用公式形式表示为

(23)

式中，Δxj代表偏导数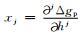的误差量.式(23)与式(16)和(17)的区别主要体现为：前者限制的是偏导数的综合计算误差(含代表误差)，后者限制的则是偏导数自身的大小.同样，可由式(23)分别确定在不同延拓高度差条件下，满足单项误差限差要求的不同阶次偏导数综合计算精度指标.对应于5个不同延拓高度差的具体计算结果如表 2所示.表中数据所体现的不同参数之间的制约关系，可为我们选择合适的向下延拓模型和延拓高度提供量化的参考依据.

表 2 误差限差允许下的重力异常垂向导数综合计算精度要求 Table 2 Ranges of computation accuracy of vertical derivatives under allowable error
2 数值计算检验与分析 2.1 试验方案设计

为了检验前面提出的两种向下延拓模型的解算效果，这里采用超高阶位模型作为标准场开展数值计算检验及分析比较研究.以美国本土西部一个3°×3°区块(φ:37°N—40°N；λ:248°E—251°E)作为试验区，选用EGM2008位模型模拟产生不同高度面2′×2′网格重力异常及其垂向偏导数的“真值”.选择美国本土作为试验区，是考虑到EGM2008位模型在美国地区具有更高的逼近度(章传银等，2009；Pavlis et al., 2012).该区块属于地形变化比较剧烈的大山区，试验效果具有一定的代表性.由EGM2008位模型计算空中网格重力异常的公式为(Heiskanen and Moritz, 1967)

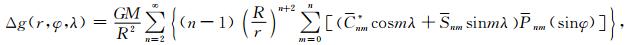
(24)

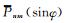
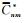
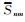
式中，GM为地球引力常数，R为地球椭球平均半径，r=R+h，h为计算点高度. 为完全规格化缔合勒让德函数，和为完全规格化位系数.连续对式(24)求r的偏导数，可得到不同阶次的垂向偏导数计算模型.

这里取R=6371 km, hi=ikm(i=0, 1，…，10)，使用EGM2008模型(以360阶次作为参考场)分别计算11个对应于ri=R+hi球面上的2′×2′网格重力异常“真值”Δgi(tru)，同时计算5 km高度面(r5=R+h5)上的垂向偏导数.表 3列出了4个不同高度面上的EGM2008位模型(361~2160阶次)残差重力异常的统计结果，表 4列出了5km高度面垂向偏导数计算值的统计结果.本文采用的试验方案具体设计为：以5 km高度面作为航空重力测量的观测面，即假设Δg5(tru)是已知的观测量，依次采用不同的向下延拓模型，由Δg5(tru)分别计算4 km、3 km、2 km、1 km和0 km高度面上的重力异常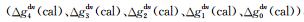，将计算值与相对应的“真值”Δgi(tru)(i=0, …，4)作比较，从而获得对应延拓模型解算精度的评估参数.

表 3 不同高度面位模型残差重力异常统计结果(单位：10-5m·s-2) Table 3 Residual anomalies from EGM2008 on different flying altitudes (unit: 10-5m·s-2)
表 4 5 km高度面垂向偏导数统计结果 Table 4 Vertical derivatives of anomalies from EGM2008 on 5 km altitudes level
2.2 点对点解析模型计算检验

为了检验点对点延拓模型解式(6)的计算效果，首先使用向上延拓积分式(7)，由Δg5(tru)分别计算6 km、7 km、8 km、9 km和10 km高度面上的重力异常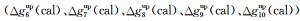，求计算值与相对应“真值”Δgi(tru)(i=6，…，10)的互差，可得到向上延拓计算模型的精度评价，具体结果见表 5.其中，积分半径统一取为ψ0=30′.为了减小积分边缘效应对评估结果的影响，计算区域边缘30′范围内的数据不参加对比分析，这个区域的数据也不再参加下一步的向下延拓计算检验(下同).

表 5 向上延拓模型计算精度检核(单位：10-5m·s-2) Table 5 Accuracy test of upward continuation model (UCM) on different altitude(unit:10-5m·s-2)

由表 5结果看出，当观测数据不存在噪声干扰时，向上延拓模型计算结果可以达到很高的精度水平，即使是1km的延拓高度差，计算误差也不超过0.3 mGal.分别将前面计算得到的6个高度面的向上延拓重力异常(Δgiup(cal))和飞行高度面上的观测重力异常Δg5(tru)代入向下延拓计算式(6)，可求得相对应延拓高度差下的向下延拓重力异常：

(25)

求上述计算值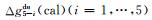相对应“真值”Δgi(tru)的互差，可得到向下延拓计算式(6)的精度评价，具体结果见表 6.

表 6 点对点向下延拓模型计算精度检核(单位：10-5m·s-2) Table 6 Accuracy of point-to-point downward continuation model (DCM) on different altitudes (unit:10-5m·s-2)

表 6中延拓高度差为ikm对应于计算面的高度为(5－i)km.由表 6结果看出，虽然向上延拓模型的计算误差随计算高度的增大而减小，但点对点向下延拓模型的计算精度随延拓高度差的增大而降低，说明向下延拓模型的截断误差对延拓计算结果有较大影响.只有当延拓高度差小于3 km时，该模型的计算精度才优于1 mGal.对比表 1和表 4计算结果可以看出，就本试验数据源所对应的重力场变化特征而言，如果以0.5 mGal作为单项误差限定值，那么在表 1所列的所有延拓高度差范围内，都可以略去四阶垂向偏导数项的影响，但只能在2 km高度差内略去二阶垂向偏导数项的影响.如果单项误差限定值放宽到1 mGal，那么可略去二阶垂向偏导数影响项的高度差也可相应增大到3 km.不难看出，上述分析结论与表 6的计算检核结果完全吻合.

为了进一步考察数据观测噪声对向下延拓计算结果的影响，这里人为在模拟观测量Δg5(tru)中分别加入±1 mGal、±3 mGal和±5 mGal的白噪声，对应生成三组带噪声的观测量，并重复前面的计算和比对检核过程.上述误差量值与当前国内外航空重力测量的精度水平基本相当(Alberts，2009；孙中苗等，2013；欧阳永忠等，2013)，因此其检验结论具有实用意义.加入观测噪声后，与表 5相对应的向上延拓模型计算精度检核结果(这里只列出互差均方根值(rms)，下同)如表 7所示，与表 6相对应的向下延拓模型计算精度检核结果如表 8所示.

表 7 噪声影响下的向上延拓误差均方根值(单位：10-5m·s-2) Table 7 Accuracy (rms) of UCM with noisy data (unit:10-5m·s-2)
表 8 噪声影响下的点对点向下延拓误差均方根值(单位：10-5m·s-2) Table 8 Accuracy (rms) of point-to-point DCM with noisy data (unit:10-5m·s-2)

对比表 5和表 7数值结果可以看出，数据观测噪声对向上延拓计算结果的影响很小，几乎不改变计算参数的变化形态，说明向上延拓模型作为低通滤波器的作用相当明显.进一步对比表 6和表 8结果可以看出，得益于向上延拓模型抑制高频噪声的优良特性，点对点向下延拓模型计算结果也几乎不受数据观测噪声的影响，在延拓高度差小于3 km的高度内，仍可获得1 mGal左右的计算精度.

2.3 最小二乘解析模型计算检验

下面重点讨论基于公式(20)整体解的模型检验问题.考虑到最小二乘解析模型对输入数据的特殊要求，首先在5 km飞行高度面的上方，以0.5 km的间隔选取20个计算高度面(即计算高度延伸到15 km)，使用向上延拓积分式(7)，由Δg5(tru)分别计算对应于上述20个高度面上的重力异常(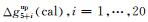；前期已经计算过的高度面不再计算).以每一个2′×2′网格点作为计算单元，将前面计算得到的同一点但在不同面上的20个重力异常值代入式(20)，解算得到相对应的重力异常垂向偏导数，并将其代入式(1)，进一步依据设定的延拓高度差(与前面的试验取值相同)即可求得想要的向下延拓值.求上述计算值与相对应“真值”的互差，可得到最小二乘解析延拓模型的精度评价.由于选用不同数量的观测数据(向上延拓计算值是一种过渡性的观测量)和不同阶次的垂向偏导数，都会对向下延拓模型解算结果产生一定的影响，故需要做必要的对比试验和分析，以选择合适的模型计算参数.我们对试算初步结果作分析后发现，总体而言，模型解算精度随使用观测数据数量的增多而逐步提高，但观测数据达到一定数量后，模型解算结果趋于稳定.其中，模型阶数取的越低，解算结果趋于稳定所要求的数据量越少，当模型阶数取为N=1和N=2时，使用5.5 km至10 km高度段内的10个观测数据即可达到解算结果稳定要求.当模型阶数取为N=3和N=4时，模型解算结果的变化规律则略有不同，需要区别对待.因向上延拓高度越低，相对应的向上延拓数据计算精度也越低，故较高阶次的向下延拓模型对向上延拓高度较低的“观测”数据具有更高的敏感度，此时如果加入这一部分观测数据反而会在一定程度上降低向下延拓模型的解算精度.为此，在构建N=3和N=4的向下延拓模型时，我们对原有20个高度面的观测数据进行了缩减，最后只保留7 km至14 km高度段内的15组观测数据参加重力异常垂向偏导数解算.这里依次取垂向偏导数最高阶次为：N=1, 2, 3, 4，分别解算得到4组相对应的向下延拓模型解.4组模型解所对应的向下延拓计算精度检核结果如表 9所示.

表 9 最小二乘解析模型误差均方根(单位：10-5m·s-2) Table 9 Accuracy of least-squares DCM on different altitudes (unit:10-5m·s-2)

由表 9结果看出，最小二乘解析延拓模型的计算精度随垂向偏导数最高阶次取值的增大而逐步提高，但当最高阶次增大到N=4时，计算精度反而有所下降，这个结果一方面说明增加高阶项对提高解析延拓模型的计算精度具有重要作用，另一方面也说明增加高阶项越多，对数据观测质量的要求也越高.就本试验数据源而言，尽管形式上我们使用了2′×2′分辨率的数据，但由于EGM2008模型的最高阶次为2160，对应的数据分辨率只有5′×5′，故实际使用的数据分辨率远达不到试验设计的要求.表 9结果说明，使用这样的数据源只能有效确定三阶及以下的垂向偏导数，三阶以上高阶项解算结果的可靠性无法得到保证，因为现有数据源包含的有限的高频成分不足以分离出三阶以上高阶项信息.实际上，对比表 2和表 4结果不难看出，本试验数据源四阶偏导数自身的量值已经远远小于计算误差限差的要求，故舍去四阶及以上高阶项的影响应当在情理之中.对比表 6和表 9结果还可以看出，在4 km高度差以内，点对点解析延拓模型的计算精度要略优于一阶最小二乘解析模型，这个结果与前面的分析结论即通常使用的一阶梯度解模型只是点对点解析延拓模型的主项是相吻合的.

采用类似于点对点解析延拓模型的检验思路，在模拟观测量Δg5(tru)中分别加入±1 mGal、±3 mGal和±5 mGal的白噪声，然后重复前面的计算和比对检核过程.加入观测噪声后，与表 9相对应的向下延拓模型计算精度检核结果如表 10所示.表 11则有选择地列出了当N=4时，观测噪声分别取为0 mGal、1 mGal、3 mGal和5 mGal四种情形下的不同阶次垂向偏导数计算精度检核结果(计算值与表 4真值互差均方根值).

表 10 噪声影响下的最小二乘解析模型误差均方根值(单位：10-5m·s-2) Table 10 Accuracy (rms) of least-squares DCM with noisy data (unit: 10-5m·s-2)
表 11 不同阶次垂向偏导数计算精度检核 Table 11 Accuracy(rms) of vertical derivatives of different orders

由表 10结果看出，观测噪声对解析延拓模型计算精度的影响随垂向偏导数阶数的增高而加大，观测噪声越大，其影响随阶数增大的趋势更加明显.这一结果说明，随着观测噪声的增大，观测数据所对应的信噪比发生了显著的变化，观测噪声的量值已经足以淹没掉有用的高频观测信息，因此，无法准确分离出所要求的高阶偏导数.就本试验数据源的变化特征而言，只有当数据观测噪声小于1mGal时，选用最高阶次N=3的解析延拓模型才是有效的，否则，应当选择最高阶次N=2的解析延拓模型.从表 10不难看出，较低阶次的解析延拓模型对观测噪声和计算高度差大小的敏感度都远低于较高阶次的模型，前者比后者具有更加稳定的模型解算精度.考虑到航空重力测量数据不可避免会受到观测噪声的干扰，其影响量值可达1~5 mGal的水平，因此在实际应用中，优先选用N=2的解析延拓模型是比较稳妥的.此外，对比分析表 11和表 2，同时联系对比表 9和表 10中对应于N=4的计算统计结果，不难看出，除了四阶偏导数由于自身量值过小，比对结果失去参考意义以外，其他三个阶次偏导数的计算结果基本反映了表 2所列的误差限差、延拓高度差与偏导数计算精度要求之间的制约关系.

为了检验联合使用式(20)—(22)分步求解高阶重力垂向偏导数的实际效果及其对向下延拓模型计算精度的影响，本文在使用式(20)解算得到一阶和二阶垂向偏导数基础上，进一步使用式(21)和(22)分别计算三阶和四阶偏导数，并按照同样的方式完成垂向偏导数计算精度和向下延拓计算效果的检核.表 12和表 13分别列出了与表 10和表 11相对应的分步法数值检验结果，因两种解算方法在选用一阶和二阶偏导数时不存在差异，故表 12只列出N=3和N=4情形下的比对结果.表 13则是N=4、观测噪声分别取1 mGal、3 mGal和5 mGal三种情形下的不同阶次垂向偏导数计算精度检核结果.

表 12 带噪声的分步最小二乘解析模型误差均方根值(单位：10-5m·s-2) Table 12 Accuracy of step by step least-squares DCM with noisy data (unit:10-5m·s-2)
表 13 对应于分步法的不同阶次垂向偏导数计算精度检核 Table 13 Accuracy (rms) of vertical derivatives of different orders from step by step method

对比表 10和表 12可以看出，只有观测噪声取1 mGal、N=3一种情形，最小二乘整体解的计算精度略优于分步法，其他情形后者都一致优于前者，观测噪声越大，后者的优势更为明显.就本算例而言，相比于N=2时的最小二乘整体解，尽管通过分步法将泰勒级数展开式拓展到三阶和四阶，对提高向下延拓精度并未起到实质性的作用，但表 10和表 12对比结果已经证明，分步解算方法具有抑制噪声干扰、提升计算稳定性的作用是显而易见的.这一点从表 11和表 13计算结果的对比中也能得到验证.在延拓模型中增加三阶和四阶项影响之所以对计算精度没有改善效果，还是因为本算例中的三阶和四阶偏导数量值过小，其计算误差已经超过或接近偏导数自身的大小(具体见表 4和表 13所列的数值结果)，因此，即使采用分步解算方法也无法准确分离出所要求的高阶偏导数.当实际重力观测场的变化特征比较明显，且又包含较大的观测误差时，可期待分步解算法能够给出理想的向下延拓计算结果.

3 结论

基于位场向上延拓解算过程稳定可靠的优良特性，本文提出了借助向上延拓信息实现航空重力向下延拓稳定解算的两种方法，分别建立了点对点向下解析延拓模型和最小二乘向下解析延拓模型.通过前面的理论分析和数值计算检验，可得出以下基本结论：

(1) 利用泰勒级数展开模型，将位场向下延拓解算过程转换为向上延拓计算和垂向偏导数解算两个步骤，可有效抑制数据观测噪声对解算结果的干扰，较好地解决了向下延拓解算固有的不适定性问题，具有较高的实用性.

(2) 点对点向下解析延拓模型解算过程简单易行，计算精度优于传统的一阶梯度解模型，特别适用于高度差小于2 km的低空向下延拓问题解算，对应解算精度优于1 mGal.

(3) 最小二乘向下解析延拓模型虽然解算过程略显复杂，但计算精度更高，适用范围更广.在存在观测噪声干扰条件下，适宜选用顾及二阶偏导数的向下解析延拓模型，当观测噪声为3 mGal时，对应于4 km高度差的向下延拓计算精度可达1 mGal.当实际重力观测场的变化特征比较明显，且又包含较大的观测误差时，可考虑采用分步法计算高阶次垂向偏导数，以提高解算过程的稳定性.

(4) 在实际应用中，为了减小积分计算边缘效应的影响，同时解决因数据观测区域不规则或存在空白区引起的数据填充问题，建议采用超高阶位模型(如EGM2008)作为参考场，以位模型延拓改正数作为向下延拓解算的初始解(黄谟涛等，2014)，以航空观测重力异常余差作为观测量，按照本文提出的计算步骤求解向下延拓问题的精确解.

References
Alberts B, Klees R. 2004. A comparison of methods for the inversion of airborne gravity data. Journal of Geodesy, 78(1-2): 55-65.
Alberts B. 2009. Regional gravity field modeling using airborne gravimetry data[Ph. D. thesis]. Delft: Netherlands Geodetic Commission.
Bateman H. 1946. Some integral equations of potential theory. J. Appl. Phys., 17(2): 91-102. DOI:10.1063/1.1707698
Bian G L. 2011. Research on the precise detection theory and algorithm of underwater small-scale magnetic target[Ph.D. thesis] (in Chinese). Dalian: PLA Dalian Naval Academy.
Boschetti F, Therond V, Hornby P. 2004. Feature removal and isolation in potential field data. Geophys. J. Int., 159(3): 833-841. DOI:10.1111/gji.2004.159.issue-3
Chen S C, Xiao P F. 2007. Wavenumber domain generalized inverse algorithm for potential field downward continuation. Chinese Journal of Geophysics (in Chinese), 50(6): 1816-1822.
Cooper G. 2004. The stable downward continuation of potential field data. Exploration Geophysics, 35(4): 260-265. DOI:10.1071/EG04260
Deng K L, Huang M T, Bao J Y, et al. 2011. Tikhonov two-parameter regulation algorithm in downward continuation of airborne gravity data. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(6): 690-696.
Fedi M, Florio G. 2002. A stable downward continuation by using the ISVD method. Geophys. J. Int., 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x
Gu Y W, Gui Q M. 2010. Study of regularization based on signal-to-noise index in airborne gravity downward to the Earth surface. Acta Geodaetica et Cartographica Sinica (in Chinese), 39(5): 458-464.
Hansen P C, O'Leary D P. 1993. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput., 14(6): 1487-1503. DOI:10.1137/0914086
Heiskanen W A, Moritz H. 1967. Physical Geodesy. San Francisco: W. H. Freeman and Company.
Huang M T, Zhai G J, Guan Z, et al. 2005. Determination and Application of Marine Gravity Field (in Chinese). Beijing: Surveying and Mapping Press.
Huang M T, Ouyang Y Z, Zhai G J, et al. 2013. Tikhonov regularization collocation for multi-source gravity data fusion processing. Hydrographic Surveying and Charting (in Chinese), 33(3): 6-12.
Huang M T, Ouyang Y Z, Liu M, et al. 2014. Practical methods for the downward continuation of airborne gravity data in the sea area. Geomatics and Information Science of Wuhan University (in Chinese), 39(10): 1147-1152.
Huang M T, Ouyang Y Z, Liu M, et al. 2015a. Regularization of point-mass model for multi-source gravity data fusion processing. Geomatics and Information Science of Wuhan University (in Chinese), 40(2): 170-175.
Huang M T, Ning J S, Ouyang Y Z, et al. 2015b. Downward continuation of airborne gravimetry on land using geopotential model and terrain information. Acta Geodaetica et Cartographica Sinica (in Chinese), 44(4): 355-362.
Hwang C, Hsiao Y S, Shih H C, et al. 2007. Geodetic and geophysical results from a Taiwan airborne gravity survey:data reduction and accuracy assessment. Journal Geophysical Research, 112(B4): B04407. DOI:10.1029/2005JB004220
Jiang T, Li J C, Wang Z T, et al. 2011. Solution of ill-posed problem in downward continuation of airborne gravity. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(6): 684-689.
Jiang T, Dang Y M, Zhang C Y, et al. 2013. Downward continuation of airborne gravity data based on rectangular harmonic analysis. Acta Geodaetica et Cartographica Sinica (in Chinese), 42(4): 475-480.
Kern M. 2003. An analysis of the combination and downward continuation of satellite, airborne and terrestrial gravity data[Ph.D. thesis]. Calgary: University of Calgary.
Li J C, Chen J Y, Ning J S, et al. 2003. Theory of the Earth's Gravity Field Approximation and Determination of China Quasi-Geoid 2000 (in Chinese). Wuhan: Wuhan University Press.
Liang J W. 1989. Downward continuation of regularization methods for potential fields. Acta Geophysica Sinica (in Chinese), 32(5): 600-608.
Liu D J, Hong T Q, Jia Z H, et al. 2009. Wave number domain iteration method for downward continuation of potential fields and its convergence. Chinese Journal of Geophysics (in Chinese), 52(6): 1599-1605. DOI:10.3969/j.issn.0001-5733.2009.06.022
Liu M, Huang M T, Ouyang Y Z, et al. 2016. Test and analysis of downward continuation models for airborne gravity data with regard to the effect of topographic height. Acta Geodaetica et Cartographica Sinica (in Chinese), 45(5): 521-530.
Liu X G, Li Y C, Xiao Y, et al. 2014. Optimal regularization parameter determination method in downward continuation of gravimetric and geomagnetic data. Acta Geodaetica et Cartographica Sinica (in Chinese), 43(9): 881-887.
Luan W G. 1983. The stabilized algorithm of the analytic continuation for the potential field. Acta Geophysica Sinica (in Chinese), 26(3): 263-274.
Luo Y, Wu M P. 2016. Minimum curvature method for downward continuation of potential field data. Chinese Journal of Geophysics (in Chinese), 59(1): 240-251. DOI:10.6038/cjg20160120
Martinec Z. 1996. Stability investigations of a discrete downward continuation problem for geoid determination in the Canadian rocky mountains. Journal of Geodesy, 70(11): 805-828. DOI:10.1007/BF00867158
Moritz H. 1980. Advanced Physical Geodesy. Karlsruhe: Herbert Wichmann Verlag.
Ning J S, Wang H H, Luo Z C. 2005. Downward continuation of gravity signals based on the multiscale edge constraint. Chinese Journal of Geophysics (in Chinese), 48(1): 63-68.
Novák P, Heck B. 2002. Downward continuation and geoid determination based on band-limited airborne gravity data. Journal of Geodesy, 76(5): 269-278. DOI:10.1007/s00190-002-0252-y
Ouyang Y Z, Deng K L, Lu X P, et al. 2013. Tests of multi-type airborne gravimeters and data analysis. Hydrographic Surveying and Charting (in Chinese), 33(4): 6-11.
Pavlis N K, Holmes S A, Kenyon S C, et al. 2012. The development and evaluation of the Earth gravitational model 2008 (EGM2008). Journal Geophysical Research, 117(B4): B04406. DOI:10.1029/2011JB008916
Peters L J. 1949. The direct approach to magnetic interpretation and its practical application. Geophysics, 14(3): 290-320. DOI:10.1190/1.1437537
Shi P, Wang X T. 1997. Determination of the terrain surface gravity field using airborne gravimetry and DEM. Acta Geodaetica et Cartographica Sinica (in Chinese), 26(2): 117-121.
Sun W, Wu X P, Wang Q B, et al. 2014. Wave number domain iterative Tikhonov regularization method for downward continuation of airborne gravity data. Acta Geodaetica et Cartographica Sinica (in Chinese), 43(6): 566-574.
Sun Z M, Zhai Z H, Xiao Y, et al. 2013. Systematic error compensation for airborne gravimetry. Chinese Journal of Geophysics (in Chinese), 56(1): 47-52. DOI:10.6038/cjg20130105
Trompat H, Boschetti F, Hornby P. 2003. Improved downward continuation of potential field data. Exploration Geophysics, 34(4): 249-256. DOI:10.1071/EG03249
Vaníček P, Novák P, Sheng M, et al. 2017. Does Poisson's downward continuation give physically meaningful results?. Studia Geophysica et Geodaetica, 61(3): 412-428. DOI:10.1007/s11200-016-1167-z
Wang X T, Shi P, Zhu F Z. 2004a. Regularization methods and spectral decomposition for the downward continuation of airborne gravity data. Acta Geodaetica et Cartographica Sinica (in Chinese), 33(1): 33-38.
Wang X T, Xia Z R, Shi P, et al. 2004b. A comparison of different downward continuation methods for airborne gravity data. Chinese Journal of Geophysics (in Chinese), 47(6): 1017-1022.
Wang Y F. 2007. Computational Methods for Inverse Problems and Their Applications (in Chinese). Beijing: Higher Education Press.
Wang Z J. 2006. Regularization Methods for Ill-posed Problem in Survey (in Chinese). Beijing: Science Press.
Xu P L. 1998. Truncated SVD methods for discrete linear ill-posed problems. Geophys. J. Int., 135(2): 505-514. DOI:10.1046/j.1365-246X.1998.00652.x
Xu S Z. 2006. The integral-iteration method for continuation of potential fields. Chinese Journal of Geophysics (in Chinese), 49(4): 1176-1182.
Xu S Z. 2007. A comparison of effects between the iteration method and FFT for downward continuation of potential fields. Chinese Journal of Geophysics (in Chinese), 50(1): 285-289.
Zhai G J, Bian G L, Huang M T. 2011. A new method to calculate the vertical derivatives of total field magnetic anomaly. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(6): 671-678.
Zhang C Y, Guo C X, Chen J Y, et al. 2009. EGM2008 and its application analysis in Chinese mainland. Acta Geodaetica et Cartographica Sinica (in Chinese), 38(4): 283-289.
Zhang H, Chen L W, Ren Z X, et al. 2009. Analysis on convergence of iteration method for potential fields downward continuation and research on robust downward continuation method. Chinese Journal of Geophysics (in Chinese), 52(4): 1107-1113. DOI:10.3969/j.issn.0001-5733.2009.04.028
卞光浪. 2011.水下小尺度磁性目标精密探测理论与方法研究[博士论文].大连: 海军大连舰艇学院.
陈生昌, 肖鹏飞. 2007. 位场向下延拓的波数域广义逆算法. 地球物理学报, 50(6): 1816-1822. DOI:10.3321/j.issn:0001-5733.2007.06.023
邓凯亮, 黄谟涛, 暴景阳, 等. 2011. 向下延拓航空重力数据的Tikhonov双参数正则化法. 测绘学报, 40(6): 690-696.
顾勇为, 归庆明. 2010. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究. 测绘学报, 39(5): 458-464.
黄谟涛, 翟国君, 管铮, 等. 2005. 海洋重力场测定及其应用. 北京: 测绘出版社.
黄谟涛, 欧阳永忠, 翟国君, 等. 2013. 融合多源重力数据的Tikhonov正则化配置法. 海洋测绘, 33(3): 6-12. DOI:10.3969/j.issn.1671-3044.2013.03.002
黄谟涛, 欧阳永忠, 刘敏, 等. 2014. 海域航空重力测量数据向下延拓的实用方法. 武汉大学学报·信息科学版, 39(10): 1147-1152.
黄谟涛, 欧阳永忠, 刘敏, 等. 2015a. 融合海域多源重力数据的正则化点质量方法. 武汉大学学报·信息科学版, 40(2): 170-175.
黄谟涛, 宁津生, 欧阳永忠, 等. 2015b. 联合使用位模型和地形信息的陆区航空重力向下延拓方法. 测绘学报, 44(4): 355-362.
蒋涛, 李建成, 王正涛, 等. 2011. 航空重力向下延拓病态问题的求解. 测绘学报, 40(6): 684-689.
蒋涛, 党亚民, 章传银, 等. 2013. 基于矩谐分析的航空重力向下延拓. 测绘学报, 42(4): 475-480.
李建成, 陈俊勇, 宁津生, 等. 2003. 地球重力场逼近理论与中国2000似大地水准面的确定. 武汉: 武汉大学出版社.
梁锦文. 1989. 位场向下延拓的正则化方法. 地球物理学报, 32(5): 600-608. DOI:10.3321/j.issn:0001-5733.1989.05.012
刘东甲, 洪天求, 贾志海, 等. 2009. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报, 52(6): 1599-1605. DOI:10.3969/j.issn.0001-5733.2009.06.022
刘敏, 黄谟涛, 欧阳永忠, 等. 2016. 顾及地形效应的重力向下延拓模型分析与检验. 测绘学报, 45(5): 521-530.
刘晓刚, 李迎春, 肖云, 等. 2014. 重力和磁力测量数据向下延拓中最优正则化参数确定方法. 测绘学报, 43(9): 881-887.
栾文贵. 1983. 场位解析延拓的稳定化算法. 地球物理学报, 26(3): 263-274. DOI:10.3321/j.issn:0001-5733.1983.03.007
骆遥, 吴美平. 2016. 位场向下延拓的最小曲率方法. 地球物理学报, 59(1): 240-251. DOI:10.6038/cjg20160120
宁津生, 汪海洪, 罗志才. 2005. 基于多尺度边缘约束的重力场信号的向下延拓. 地球物理学报, 48(1): 63-68. DOI:10.3321/j.issn:0001-5733.2005.01.011
欧阳永忠, 邓凯亮, 陆秀平, 等. 2013. 多型航空重力仪同机测试及其数据分析. 海洋测绘, 33(4): 6-11. DOI:10.3969/j.issn.1671-3044.2013.04.002
石磐, 王兴涛. 1997. 利用航空重力测量和DEM确定地面重力场. 测绘学报, 26(2): 117-121. DOI:10.3321/j.issn:1001-1595.1997.02.004
孙文, 吴晓平, 王庆宾, 等. 2014. 航空重力数据向下延拓的波数域迭代Tikhonov正则化方法. 测绘学报, 43(6): 566-574.
孙中苗, 翟振和, 肖云, 等. 2013. 航空重力测量的系统误差补偿. 地球物理学报, 56(1): 47-52. DOI:10.6038/cjg20130105
王兴涛, 石磐, 朱非洲. 2004a. 航空重力测量数据向下延拓的正则化算法及其谱分解. 测绘学报, 33(1): 33-38.
王兴涛, 夏哲仁, 石磐, 等. 2004b. 航空重力测量数据向下延拓方法比较. 地球物理学报, 47(6): 1017-1022.
王彦飞. 2007. 反演问题的计算方法及其应用. 北京: 高等教育出版社.
王振杰. 2006. 测量中不适定问题的正则化解法. 北京: 科学出版社.
徐世浙. 2006. 位场延拓的积分-迭代法. 地球物理学报, 49(4): 1176-1182. DOI:10.3321/j.issn:0001-5733.2006.04.033
徐世浙. 2007. 迭代法与FFT法位场向下延拓效果的比较. 地球物理学报, 50(1): 285-289. DOI:10.3321/j.issn:0001-5733.2007.01.035
翟国君, 卞光浪, 黄谟涛. 2011. 总强度磁异常各阶垂向导数换算新方法. 测绘学报, 40(6): 671-678.
章传银, 郭春喜, 陈俊勇, 等. 2009. EGM2008地球重力场模型在中国大陆适用性分析. 测绘学报, 38(4): 283-289. DOI:10.3321/j.issn:1001-1595.2009.04.001
张辉, 陈龙伟, 任治新, 等. 2009. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究. 地球物理学报, 52(4): 1107-1113. DOI:10.3969/j.issn.0001-5733.2009.04.028