2. 吉林交通职业技术学院, 长春 130012
2. Jilin Communications Polytechnic, Changchun 130012, China
基于波动方程高频近似的射线类偏移成像技术由于采用几何射线理论计算波场的振幅以及相位信息,从而实现波场的延拓成像,具有较高的计算效率和灵活性,因此在工业界得到了广泛应用.但在应用该算法实现偏移成像的过程当中,为了满足射线追踪系统(运动学和动力学),要求速度模型必须具有二阶连续的导数,而实际给定的速度模型往往比较复杂,具有不连续的速度突变间断面和很强的速度梯度,而且以网格的形式被离散地给定在各个网格节点上.为了能够应用射线理论保证射线追踪的可行性,需要对速度模型进行特殊处理来减小速度的突变和梯度来保证射线追踪的可行性,而目前常用的处理手段就是对速度模型进行光滑处理来克服这种速度模型中波速突变的间断面或强的速度梯度变化对成像的影响(韩复兴,2009;韩复兴等,2011).
关于速度模型的光滑处理对偏移成像的影响,1996年,Lailly在其文章中讨论了应用叠前深度偏移对复杂地质结构进行反射层析成像时(Lailly and Sinoquet, 1996),应用平滑的速度模型相对于块状模型能够获得更好的层析成像效果;2000年,Larner在其文章深度偏移前对速度模型进行光滑处理的利弊中也讨论了速度模型光滑处理虽然会改变原始速度模型的空间结构(Larner and Pacheco, 2000),但其适度的改变可以一定程度上获得更加清晰的成像结果;同年Gray针对3种较为复杂、变化剧烈的SEG/EAGE岩丘模型、Marmousi速度模型和加拿大Foothills模型,讨论了不同程度的模型光滑处理对偏移成像的影响(Gray, 2000),其结果表明:相对于原始速度模型来说,对3种模型进行适度的光滑后,不但不会破坏原始速度模型的空间结构,而且可以获得较好的成像结果,但相反对速度模型进行过度光滑则会改变原模型的地质结构,造成错的成像结果.2011年韩复兴在其文章中从射线追踪方程组成立的前提条件、射线理论成立的高频近似理论以及菲涅尔带等不同角度着手,分析了速度模型光滑的理论基础以及速度模型光滑前后对地震波走时和射线路径的影响(韩复兴等,2011).
对速度模型进行光滑处理,通常采用的主要方式是卷积类光滑算子(韩复兴,2009;Ettrich and Gajewski, 1996)、三点平均算子以及五点平均算子,这些算子在对速度模型进行光滑处理时,都是对速度模型进行局部光滑处理,并没有很好地考虑速度模型整体的空间变化.对此,本文将近几年在数字图像处理当中发展起来的基于偏微分方程的模型平滑处理技术(Gabor, 1965; Koenderink, 1984; Hummel, 1987; Kass et al., 1987; Carmona and Zhong, 1998; Perona and Malik, 1990; Catte et al., 1992; Alvarez et al., 1992; Caselles and Morel, 1998)引入到射线类偏移成像中,实现速度模型的平滑处理.偏微分方程法自20世纪80年代引入图像处理中,90年代得到了很好的发展,该方法主要是数学方法在空间域内图像处理中的应用,由于偏微分方程方法具有线性叠加特性、偏微分方程模型解的唯一性、局部特征保持性能(Perona and Malik, 1990; Catte et al., 1992; Alvarez et al., 1992; ),因此通过方程迭代处理图像可以在保持边缘特征的同时较好地重建平滑特征区域(Perona and Malik, 1990; Alvarez et al., 1992),因此该模型处理算法对实现不破坏原始速度模型空间结构的波场计算和精确成像结果都具有十分重要的研究价值和广阔的应用前景.
1 偏微分方程模型光滑处理算法偏微分方程(Partial Differential Equation)对图像的平滑过程可以表示为:以u0:R2→R表示一幅灰度图像,灰度值为u0(x, y).引入时间因子t,则对图像的处理以偏微分方程表示可写为
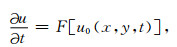
|
(1) |
其中u(x, y, t):R2×[0, τ)→R为变化过程中的图像,F:R→R表达了某给定算法,通常依赖于图像及其空间上一、二阶导数.原始图像u0为初始条件.偏微分方程的解u(x, y, t)即给出了迭代t次时的图像.通常在得到满意的图像时即停止迭代.这就是偏微分方程表达的图像处理过程.
根据以上偏微分方程对图像的平滑处理,对于射线类偏移成像当中速度模型的光滑处理,也可以用变分方法导出基于速度平滑的偏微分方程模型,其过程如下:考虑如下形式的能量函数:
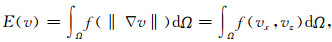
|
(2) |
Ω为速度模型的大小,f(·)≥0为递增函数.在速度模型横向和纵向变化比较剧烈的区域,速度梯度的模就越大,因此,要达到图像平滑的目的就要最小化能量函数E(v).
下面用变分方法来求解这个能量极小化问题,容易得到
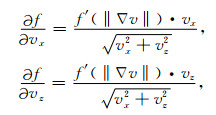
|
(3) |
从而,相应的Euler-Lagrange方程为

|
(4) |
利用最速下降法求解以上的Euler-Lagrange方程,得
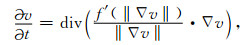
|
(5) |
令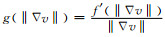
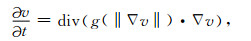
|
(6) |
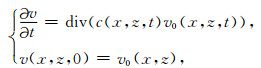
|
(7) |
扩散系数表达式:
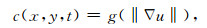
|
(8) |
其中g(s)是单调递减函数,g(0)= 1,
下面以简单的2层速度模型为例,说明基于偏微分方程的光滑处理对模型空间的改造.速度模型大小100×200,网格间距为5 m×5 m,取dt=0.05,分别应用PDE算法对原始速度模型迭代处理1次、5次、10次、20次、30次后的速度模型以及相对误差如图 1所示.

|
图 1 PDE算法对速度模型的光滑处理 (a)两层原始速度模型及对分界面光滑处理后的两层速度模型; (b)不同迭代次数处理后的速度模型与原始速度模型在分界面处速度的相对误差分布. Fig. 1 Smooth processing velocity model using Partial Differential Equation algorithm (a) The two layer original and smoothed interface velocity model using PDE algorithm; (b) Relative error of the original and after Different Iteration Smoothing velocity model. |
通过应用PDE算法对以上2层模型的光滑处理分析可以看出,随着迭代次数的增加,PDE算法对速度模型两层之间的光滑处理从迭代1次时的z方向上5 m范围内速度值会改变到迭代30次时的z方向上30 m范围内速度值会发生改变,在30次迭代z方向上30 m的范围速度值得变化内与原始速度其相对误差最大达到20%,然而z方向上的空间结构点速度的改变只是在96点到102点之间的区域,说明了偏微分方程具有很好的局部特征保持性能,这种空间结构的改变可以为实际应用过程中对速度模型的光滑处理提供参考.
2 计算测试 2.1 速度模型空间结构以Marmousi模型为例,分析原始速度模型和应用PDE和卷积算光滑算子光滑30次后速度模型空间结构的变化情况.二维Marmousi速度模型大小384×122,网格间距为24 m×24 m.原始速度模型以及光滑后的速度模型如图 2所示.
|
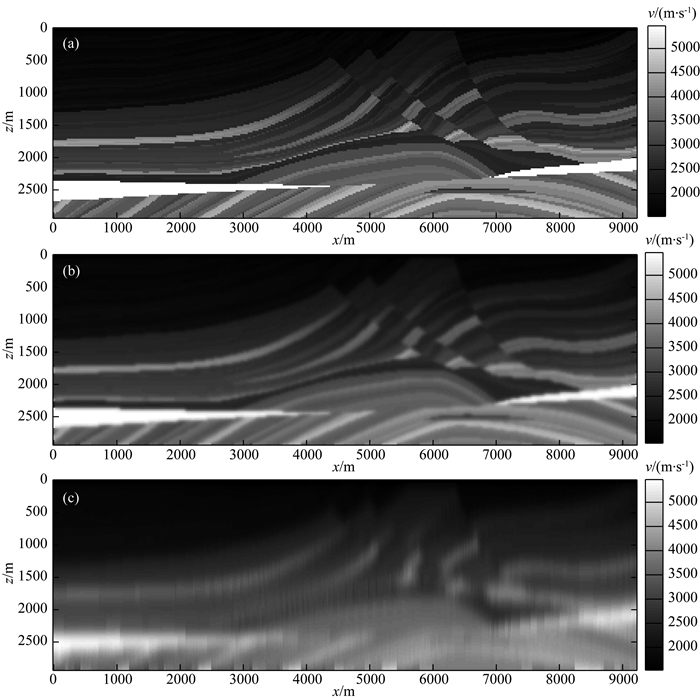
图 2 Marmousi原始速度模型以及光滑处理后的速度模型 (a)原始Marmousi速度模型; (b)应用PDE光滑处理迭代30次后的速度模型; (c)卷积算子光滑30次后的速度模型. Fig. 2 The original and smoothing velocity model using PDE algorithm of Marmousi (a) Original velocity model of Marmousi; (b) The velocity model of Smoothing iteration 30 times using Partial Differential Equation algorithm; (c) The velocity model of Smoothing 30 times using Convolution Operator. |
对于以上原始速度模型以及应用PDE算法和卷积类算子光滑处理30次后的速度模型,取z=100点位,x方向所有点的速度值以及x=192点位,z方向上的所有速度值进行空间结构的对比如图 3所示.
|
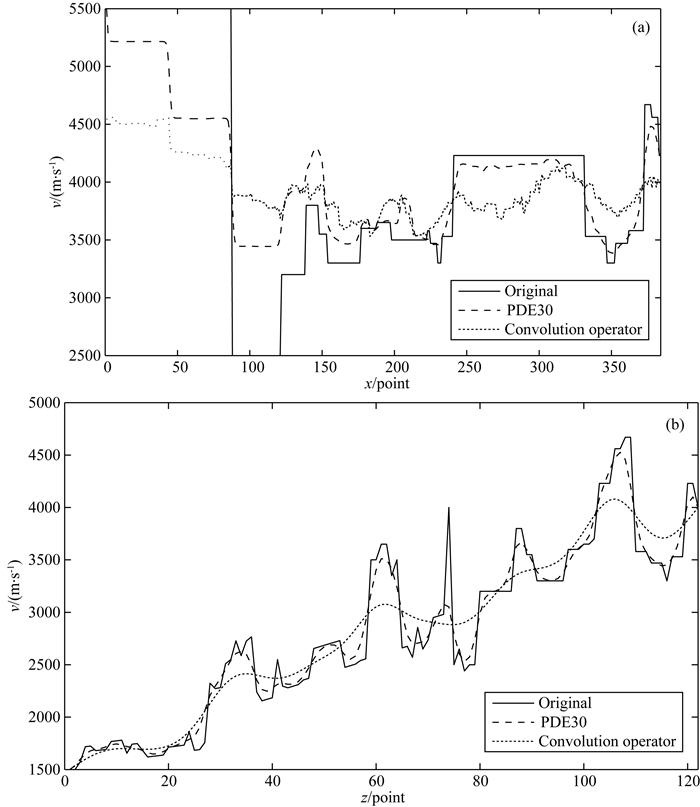
图 3 原始Marmousi速度模型以及光滑处理后速度模型在x方向和z方向上的空间结构对比 (a) z=100点位,x方向所有点的速度值对比; (b) x=192点位,z方向上的所有速度值对比. Fig. 3 Contrast spatial structure of original and smoothing velocity model using PDE algorithm of Marmousi velocity model (a) z=100 point, the velocity difference of all points in the x direction; (b) x=100 point, the velocity difference of all points in the z direction. |
通过以上图 2的速度模型整体平滑以及图 3看出,不管是x方向还是z方向上的速度分布,应用PDE算法对原始速度模型进行光滑,其速度模型的空间分布与应用卷积算子对速度模型光滑处理后对比,PDE算法光滑后的速度模型更加吻合原始速度模型的空间分布.
2.2 走时误差分析下面取震源点位于(192, 1),分别在原始Marmousi速度模型以及应用PDE算法和卷积算子对原始速度光滑处理30次后的速度模型上计算地震波走时.其时间场分布以及相对误差如图 4所示.

|
图 4 光滑处理前后Marmousi速度模型上地震波走时以及相对误差 (a)原始Marmousi速度模型和光滑处理后的速度模型走时对比; (b) PDE算法光滑处理后的走时相对误差; (c)卷积算子光滑处理后的走时相对误差. Fig. 4 Seismic travel time and relative error distribution of Marmousi model (a) Travel time distribution of original and smoothing velocity model; (b) Traveling Time Relative Error using PDE algorithm; (c) Traveling Time Relative Error using Convolution Operator. |
通过图 4的时间场分布以及PDE算法和卷积算子光滑后模型的走时相对误差可以看出,PDE算法对速度模型进行光滑处理后的走时与原始速度模型走时相比其相对误差最大为3%,而卷积算子光滑后的走时相对误差为16%.说明应用PDE算法对模型地光滑处理能够很好的保持原始速度模型的空间分布.
2.3 射线路径对比同样取震源点位于(192, 1),分别在原始Marmousi速度模型以及应用PDE算法和卷积算子对原始速度光滑处理30次后的速度模型上计算射线路径.原始速度模型、PDE算法及卷积算子光滑处理后模型上的射线路径对比如图 5所示.
|
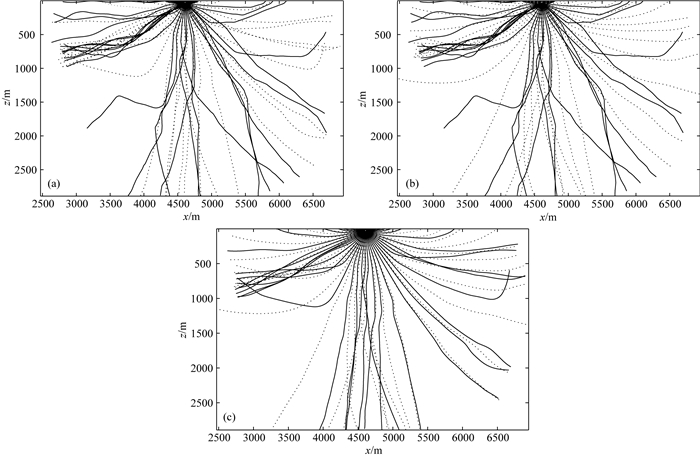
图 5 原始Marmousi速度模型、PDE算法及卷积算子光滑处理后模型上的射线路径对比 (a)原始速度模型及PDE算法光滑处理后的射线路径对比(实线为原始速度模型); (b)原始速度模型及卷积算子光滑处理后的射线路径对比(实线为原始速度模型); (c) PDE算法以及卷积算子光滑处理后的射线路径对比(实线为PDE光滑后的模型射线路径, 虚线为卷积算子). Fig. 5 The difference ray paths of original velocity model and using PDE Algorithm Convolution Operator (a) The difference ray paths of original and smoothing velocity model using PDE Algorithm(Solid line is original velocity model); (b) The difference ray paths of original and smoothing velocity model using Convolution Operator (Solid line is original velocity model); (c) The difference ray paths of velocity model using PDE Algorithm and Convolution Operator (Solid line is PDE Algorithm). |
通过图 5射线路径的对比可以看出,由于所采用的模型光滑算法不同对速度模型空间结构的改变不同,因此导致应用PDE算法以及卷积算子光滑处理后的模型射线路径差异比较大,但整体上还是PDE模型光滑算法所获得射线路径与原始速度模型比较接近.
3 在偏移成像中的应用下面以南海海底较为复杂的大水深速度模型说明海水速度差异对偏移成像中深层的影响.模型大小为3200×3000,网格间距为2.5 m×2.5 m,海水深度3750 m,海水下面地层起伏变化,速度变化从2900 m·s-1到4900 m·s-1,如图 6所示.在海水里面加入声道进行波场数值模拟,数值模拟炮点位置位于(200, 4)、(600, 4)、(1000, 4)、(1400, 4)、(1800, 4)、(2200, 4)、(2600, 4)、(3000, 4),共8炮,每炮640道接收,道间距为12.5m.应用PDE算法对原始速度模型光滑迭代10次后,在原始速度模型以及光滑处理后的速度模型上应用所获得地震记录进行偏移成像,偏移结果如图 7所示.

|
图 6 原始大水深速度模型以及应用PDE光滑处理后的速度模型 (a)原始速度模型; (b) PDE光滑处理后的速度模型(t=10). Fig. 6 The original complex seabed model and smoothing velocity model using PDE algorithm (t=10) (a) The original complex seabed velocity model; (b) Smoothing velocity model using PDE algorithm (t=10). |
|
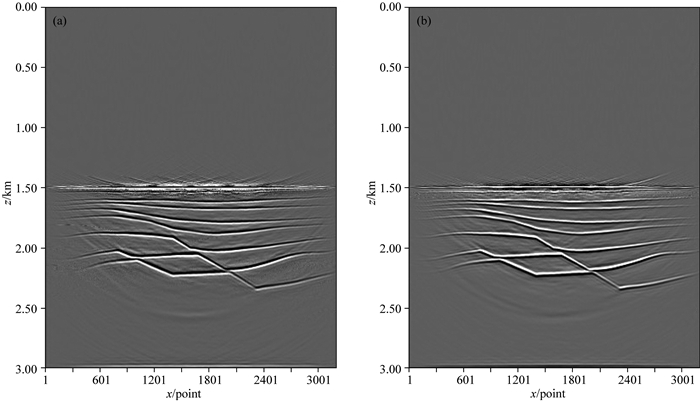
图 7 原始速度模型以及光滑处理后的速度模型上的偏移成像结果 (a)原始速度模型的偏移结果; (b) PDE算法光滑处理后模型的偏移结果. Fig. 7 The migration imaging results of the original and smoothing using PDE algorithm (t=10) (a) The migration imaging results of the original velocity model; (b) The migration imaging results of smoothing velocity model using PDE algorithm (t=10). |
通过图 7的成像结果可以看出,对于相对简单,地层层位分布明确的速度模型,PDE对速度模型光滑处理后所获得成像结果与原始速度模型成像结果对比,其层位更加清晰,层与层之间的干扰更少.
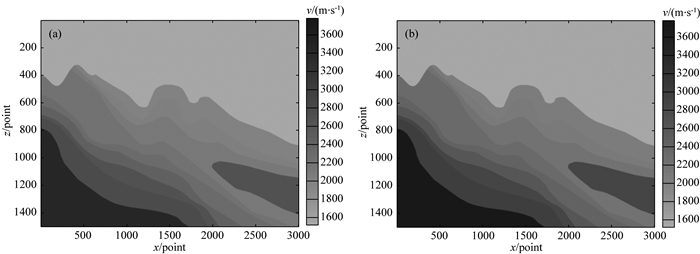
下面再以南海某区域崎岖海底大陡坡速度模型为例,说明PDE算法在偏移成像速度模型光滑中的作用.崎岖海底大陡坡模型大小为3001×1501,网格间距为2.5 m×2.5 m,海水深度存在较大的变化,原始速度模型以及应用PDE光滑处理30次后的速度模型如图 8所示.数值模拟炮点从点位1到3000,炮间距500 m,共16炮,每炮601道,道间距12.5 m,时间采样间隔2 ms.原始速度模型以及经过PDE光滑处理后的速度模型以及偏移成像结果如图 9所示.
|
图 8 原始速度模型以及应用PDE光滑处理30次后的速度模型 (a)原始崎岖海底大陡坡速度模型; (b) PDE光滑处理30次后崎岖海底大陡坡速度模型. Fig. 8 The original and smoothing velocity model using PDE algorithm (t=30) (a) The original rough and steep slope rugged seabed velocity model; (b) The rough and steep slope rugged seabed velocity model smoothed using PDE algorithm (t=30). |
|
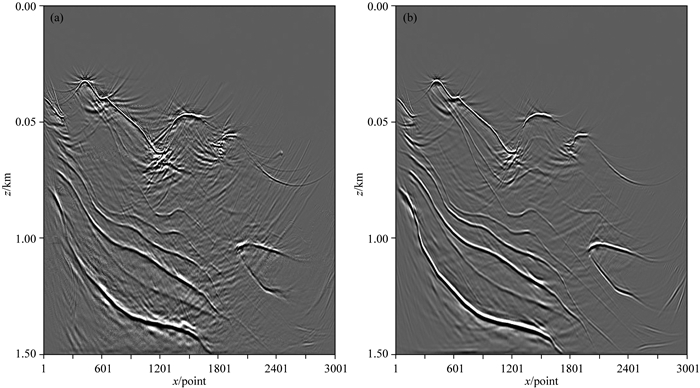
图 9 原始崎岖海底大陡坡速度模型以及光滑处理后的速度模型上的偏移成像结果 (a)原始崎岖海底大陡坡速度模型偏移成像结果; (b) PDE光滑处理30次后崎岖海底大陡坡速度模型偏移结果. Fig. 9 The migration imaging results of the original rough and steep slope rugged seabed velocity model and smoothed using PDE algorithm (t=30) (a) The migration imaging results of the original rough and steep slope rugged seabed velocity model; (b) The migration imaging results of smoothing rough and steep slope rugged seabed velocity model using PDE algorithm (t=30). |
在原始崎岖海底大陡坡速度模型和应用于PDE光滑处理后的速度模型上采用高斯波束叠前偏移处理后的剖面如图 9所示.
通过图 9的成像结果可以看出,对于海水深度剧烈变化的崎岖海底大陡坡速度模型,PDE对速度模型光滑处理后所获得成像结果其层位清晰可见, 尤其是在崎岖海底界面和速度模型底部,光滑处理后模型所获得成像效果要远远优于原始速度模型的成像效果.
4 结论在基于波动方程高频近似的射线类偏移成像中,速度模型的光滑处理对地震波走时、射线路径和振幅有着十分重要的影响,不同程度的光滑处理会对速度模型的空间结构带来不同程度的改变,进而影响到地震波走时、射线路径,最终影响到偏移成像的质量.本文就射线类偏移当中的速度模型光滑处理问题,引入了基于偏微分的光滑处理算法实现尽量不破坏原始速度模型空间结构的速度光滑处理,通过在原始Marmousi速度模型以及应用PDE算法光滑处理速度模型上分析速度模型的空间结构、计算地震波走时以及射线路径对比分析,证实了基于偏微分方程法在图像光滑处理当中的效果,通过在大水深速度模型以及崎岖海底大陡坡速度模型上的偏移成像结果,也说明了在射线类偏移成像当中应用PDE算法对速度模型进行光滑处理能够获得较好的成像结果.
Alvarez L, Lions P L, Morel J M. 1992. Image selective smoothing and edge detection by nonlinear diffusion.Ⅱ. SIAM Journal on Numerical Analysis, 29(3): 845-866. DOI:10.1137/0729052 |
Carmona R A, Zhong S F. 1998. Adaptive smoothing respecting feature directions. IEEE Transactions on Image Processing, 7(3): 353-358. DOI:10.1109/83.661185 |
Caselles V, Morel J. 1998. Introduction to the special issue on partial differential equations and geometry-driven diffusion in image processing and analysis. IEEE Transactions on Image Processing, 7(3): 269-273. DOI:10.1109/TIP.1998.661176 |
Catte F, Coll T, Lions P L, et al. 1992. Image selective smoothing and edge detection by nonlinear diffusion.Ⅰ. SIAM Journal on Numerical Analysis, 29(3): 182-193. |
Ettrich N, Gajewski D. 1996. Wave front construction in smooth media for prestack depth migration. Pure and Applied Geophysics, 148(3-4): 481-502. DOI:10.1007/BF00874576 |
Gabor D. 1965. Information theory in electron microscopy. Laboratory Investigation:A Journal of Technical Methods and Pathology, 14: 801-807. |
Gray S H. 2000. Velocity smoothing for depth migration: how much is too much?.//70th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Han F X. 2009. On some computational problems in wavefront construction method [Ph. D. thesis] (in Chinese). Changchun: Jilin University.
|
Han F X, Sun J G, Wang K. 2011. Analysis of velocity model smoothing. Journal of Jilin University (Earth Science Edition) (in Chinese), 41(5): 1610-1616, 1645. |
Hummel R. 1987. Representations based on zero-crossing in scale-space. Readings in Computer Vision, 753-758, Published by Courant Institute of Mathematical Sciences, New York University, in New York.
|
Kass M, Wiltkin A, Terzopoulos D. 1987. Snakes:active contour models. International Journal of Computer Vision, 1(4): 321-331. |
Koenderink J J. 1984. The structure of image. Biological Cybernetics, 50(5): 363-370. DOI:10.1007/BF00336961 |
Lailly P, Sinoquet D. 1996. Smooth velocity models in reflection tomography for imaging complex geological structures. Geophysical Journal International, 124(2): 349-362. DOI:10.1111/gji.1996.124.issue-2 |
Larner K, Pacheco C. 2005. Velocity smoothing before depth migration:Does it help or hurt?. Seg Technical Program Expanded Abstracts, 24(1): 1970. |
Perona P, Malik J. 1990. Scale-space and edge detection usinganisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7): 629-639. DOI:10.1109/34.56205 |
韩复兴. 2009.论波前构建法中的几个计算问题[博士论文].长春: 吉林大学.
|
韩复兴, 孙建国, 王坤. 2011. 速度模型的光滑处理分析. 吉林大学学报(地球科学版), 41(5): 1610-1616, 1645. |
 2018, Vol. 61
2018, Vol. 61


