2. 中国石油集团东方地球物理勘探有限责任公司, 河北涿州 072751;
3. 中国石油勘探开发研究院, 北京 100083
2. DBGP Inc, China National Petroleum Corporation, Zhuozhou Hebei 072751, China;
3. Sinopec Petroleum Exploration and Production Research Institute, Beijing 100083, China
可控源音频大地电磁法(controlled source audio electromagnetic, CSAMT)由于具有分辨率高、勘探深度大及野外工作效率高等优点,已被广泛应用于矿产与油气资源勘探(Bastani et al., 2009;Hu et al., 2013)、地热资源勘查(Wu et al., 2012)、地下水文调查(Carlson et al,2005)以及浅地表环境与工程勘察(Asch and Sweetkind, 2011)等领域,成为一种重要的地球物理电磁勘探技术.传统的CSAMT测量继承了大地电磁观测方式,为满足远区测量要求,通常需要在距离发射源3~5倍趋肤深度以外的区域内接收正交的水平电磁场信号来获得卡尼尔视电阻率和相位信息(汤井田和何继善,2005).然而,在野外实际施工中,由于测区场地条件的限制,有时难以满足远区测量的要求;另外,人工源激发的电磁场会随着传播距离的增大迅速衰减,当存在较强人文干扰时,会使得远区测量的数据信噪比降低,数据质量难以控制.这些因素均阻碍了CSAMT的进一步发展.
广域电磁法(wide field electromagnetic method, WFEM)是在CSAMT基础上发展起来(何继善,2010).一方面广域电磁法沿用了CSAMT采用人工场源的特点,从而克服了大地电磁天然场源信号随机性大和易受干扰的缺点;另一方面,广域电磁法采用全区视电阻率定义,有效克服了CSAMT必须在远区测量的要求,并通过将非平面波区(近区或过渡区)纳入到可测量区域,极大拓展了可控源电磁法的观测范围(何继善,2010).除此之外,广域电磁法采用伪随机信号作为发射场源信号,可以同时发送包含多个主频率的激励信号,相比CSAMT,显著提高了观测速度和工作效率(李帝铨和胡艳芳,2015).
目前无论CSAMT还是广域电磁数据解释多采用一维或二维反演技术.但考虑到发射场源的影响(如阴影效应,陈明生和闫述,2005),以及随着野外电磁勘探越来越多地进入复杂地质构造环境,通过一维或二维(Tong et al., 2018)反演可能难以获得三维电性目标体全方位的空间展布情况.三维正反演技术对于获得精确的地下电性分布信息变得必不可少.正演是反演的引擎,因此,可控源电磁数据的三维反演解释首先需要发展有效的三维正演方法.从数值模拟的角度看,目前常用的电磁法三维正演方法包括积分方程法(Avdeev et al., 2002;Zhdanov et al., 2006;王若等,2009)、有限差分法(Mackie et al., 1994;Newman and Alumbaugh, 1995;沈劲松,2003)、有限体积法(Haber and Ascher 2001;Weiss and Constable, 2006;彭荣华等,2016)和有限单元法(Cai et al., 2014, 2017;Ren et al,2014;杨军等,2015;Ansari and Farquharson, 2014).这些方法由于所依据的数学理论不同,求解过程和求解效率也不尽相同.具体数值方法的选择,不仅需考虑所模拟的地质构造的复杂性,还需考虑计算资源的消耗.总体而言,当前电磁三维正演算法研究仍集中于提高计算精度和计算效率(Börner,2010).
为获得稳定且高精度的三维正演数值结果,本文将麦克斯韦方程组转化为库伦规范条件下的磁矢势和电标势耦合方程,并采用散射场(scattering field)方法来降低场源奇异性对数值结果的影响.使用交错网格有限体积法(Staggered-grid Finite Volume, SFV)对势场方程进行离散化,实现了基于二次耦合势的广域电磁法三维正演计算.最后,通过与一维层状模型准解析解对比验证了本文算法的有效性,并进一步对比分析了CSAMT与广域电磁法对典型三维目标体的响应特征及探测能力.
1 方法理论 1.1 势场控制方程假定电磁场的时谐因子取为eiwt,在准静态极限条件下,频率域Maxwell方程组可表示为
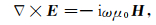
|
(1a) |
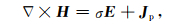
|
(1b) |
其中,E为电场强度,H为磁场强度,ω为角频率.σ为介质电导率,μ0为真空中磁导率.Jp为人工激发场源的电流密度.对(1a)式两边取旋度并将其代入(1b)式,消去磁场强度H,得到关于电场E的二阶矢量Helmholtz方程为
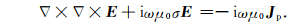
|
(2) |
随着频率的降低,电场控制方程(2)式的近似求解会出现低感应数问题(Low induction number, LIN).LIN不仅会导致迭代求解的收敛速度降低,增加计算时间;而且会由于数值计算中的舍入误差而导致伪解的出现(Newman and Alumbaugh, 2002).为克服低感应数问题,一种有效的方法是采用势场公式作为求解的控制方程(Badea et al., 2001;Haber et al., 2000;Weiss,2013;蔡红柱等,2015).该方法利用Helmholtz定理将电场分解为标量势(无旋场)和矢量势(无源场)的叠加.一方面,该方法通过释放旋度算子的零空间来有效改善系数矩阵的条件数,从而显著提升迭代求解的收敛速度(Weiss and Newman, 2002);另一方面,由于显式地加入了散度条件,可以避免因数值舍入误差所引起的伪解对计算精度的影响(Jiang et al., 1996).
考虑到磁场H为无源场,则可将磁场H表示为一个矢量场的旋度:
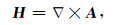
|
(3) |
其中A称为磁矢量势.将(3)式代入到(1a)中可得
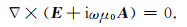
|
(4) |
由矢量恒等关系则电场可表示为
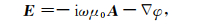
|
(5) |
其中φ称为电标量势.将(3)和(5)式代入(1b)式可得

|
(6) |
为确保势函数的唯一性,采用库伦规范条件:
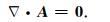
|
(7) |
利用矢量恒等式∇×∇×A≡∇(∇·A)-∇2A并结合(7)式,则(6)式可改写为
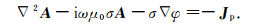
|
(8) |
为避免伪解的出现,对(1b)两边取散度来确保势场方程满足电流连续性条件,并结合(5)式得到

|
(9) |
为克服人工场源的空间奇异性对数值结果的影响,采用可控源电磁模拟中常用的二次场方法,将总场分解为由背景模型σ0(一般为均匀半空间模型或一维层状模型)在人工场源Jp激发下所产生的一次场(Ep, Ap, φp)和剩余模型(实际模型相对于参考模型的差异)所产生的二次场(Es, As, φs)的叠加.则二次势场所满足的控制方程为
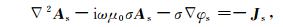
|
(10a) |
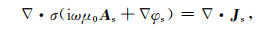
|
(10b) |
其中Js=(σ-σ0)Ep为二次电流密度.
由于人工场源的局部性,并且地下介质为损耗介质,二次电磁场会随传播距离的增加迅速衰减.因此,可采用理想导体边界条件,即场源所激发的二次电磁场在足够远的区域内可以忽略不计,此时相对应的二次耦合势的边界条件可表示为
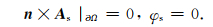
|
(11) |
其中n为边界处的外法向向量.
1.2 有限体积离散化为求解二次势场控制方程(10)式,本文采用交错网格有限体积法来对其进行离散化.与常用的有限差分法相比,SFV是在控制体积内对微分方程进行积分.考虑到电磁场在局部可能存在剧烈变化(如发射场源附近),通过积分离散化能更准确地表示电磁场的分布(Weiss and Constable, 2006).
首先将整个计算区域剖分成一系列规则的长方体单元,x、y、z方向上的节点分别为xi∈[x1, x2, …, xNx],yj∈[y1, y2, …, yNy]和zk∈[z1, z2, …, zNz],然后在网格单元上交错地对磁矢势和电标势进行采样.采用如图 1a所示的采样方式,其中磁矢势位于网格棱边中心,电标势位于网格节点处.这种交错采样方式能够使磁矢势A与电标势梯度位于相同采样点(即网格棱边中心),确保了相邻网格间电场切向分量的连续性(Weiss,2013).此外,此种交错采样方式使得对(10)式进行有限体积离散时,需对磁矢势的三个分量和电标势分别定义控制网格单元:
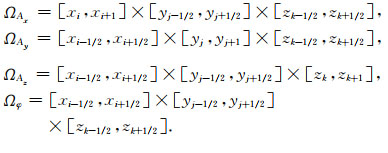
|
(12) |

|
图 1 有限体积离散示意图 (a)耦合势交错采样网格;(b)磁矢势x分量控制体积;(3)电标势控制体积.图中蓝色方框为交错网格,灰色方框为势场的控制网格. Fig. 1 (a) Staggered discretization of FV; (b) Integration volume for x-component of the magnetic potential; (c) Integration volume for the electrical potential |
图 1中展示了磁矢势x分量(图 1b)和电标势的控制体积(图 1c).对(10a)式进行有限体积离散化,由于其为矢量方程,以x分量为例,在ΩAx控制网格单元内积分:

|
(13) |
为求解(13)式积分,采用七点公式对左端第一项进行离散化,并利用中心差分对左端第三项进行离散化,然后在控制单元体积内求积可得
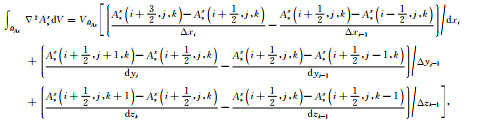
|
(14a) |
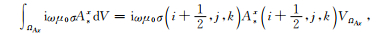
|
(14b) |
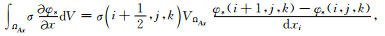
|
(14c) |
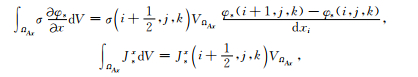
|
(14d) |
其中
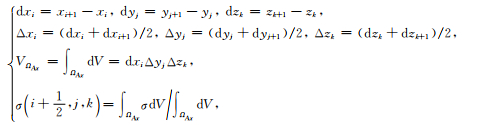
|
(15) |
对(10a)中的y分量和z分量进行类似的离散化过程,然后在各自控制网格内总体合成,则可以得到
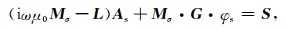
|
(16) |
其中符号L为拉普拉斯算子的离散式,G为梯度算子的离散式,S为二次电流密度的离散式,Mσ为电导率离散式.
接着对(10b)式进行有限体积离散化,在Ωφ控制网格单元内对(10b)进行积分:
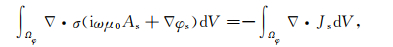
|
(17) |
利用高斯公式,则(17)式可转换为
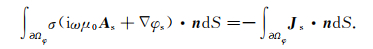
|
(18) |
为求解(18)式积分,同样利用中心差分对左端第二项进行离散化,然后在控制单元内求积可得
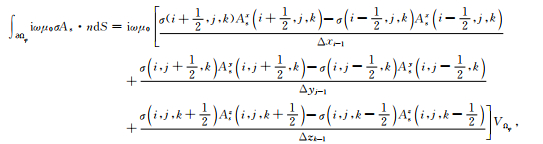
|
(19a) |
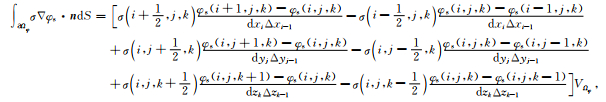
|
(19b) |
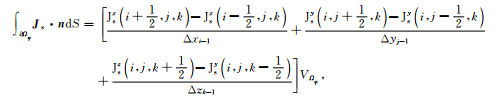
|
(19c) |
其中
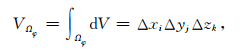
|
(20) |
利用(19)式在整个控制网格内进行总体合成可得
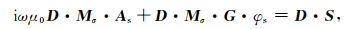
|
(21) |
其中D为散度算子的离散式.
结合(16)式和(21)式,则离散化的二次势场方程(10)式可表示为

|
(22) |
二次势场方程的SFV离散式(22)可简化成矩阵形式为
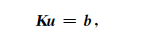
|
(23) |
其中系数矩阵K为大型、对称、稀疏复矩阵,待求解的未知量u的个数约为4Nx·Ny·Nz(Nx、Ny、Nz分别为x、y、z方向上的网格数).对于三维地电模型来说,未知量的个数很容易达到几十万到上百万个,如何高效求解(23)式一直是当前数值计算研究的热点.目前主要有迭代求解法和基于矩阵分解的直接求解法.直接解法的求解时间和数值精度基本不受系数矩阵条件数的影响,且主要开销集中在系数矩阵的分解阶段,特别适合多场源问题(韩波等,2015b).因此近年来开始应用于可控源电磁三维模拟,特别是海洋可控源电磁三维正反演计算(Streich, 2009;Schwarzbach and Haber, 2013).但直接解法中系数矩阵的分解需要消耗大量的计算内存和计算时间,随着系数矩阵未知量个数的增加,直接解法在普通计算平台上(如PC单机)往往难以进行.与之对比,迭代解法只涉及系数矩阵与向量的乘积,所需计算机内存较小,被广泛应用于当前各类电磁法三维数值计算中.但迭代解法的收敛性和求解精度极大地受系数矩阵条件数影响,如网格的剖分方式或介质电性差异都有可能影响数值计算结果,此时需要对系数矩阵进行预条件处理来改善其条件数.
由于本文采用势场控制方程,通过释放旋度算子的零空间有效改善了系数矩阵的条件数,并且CSAMT或广域电磁法只涉及单一或较少发射源问题,因此本文采用非完全LU分解(ILU)预条件子的稳定双共轭梯度迭代法(BiCGSTAB)来求解(23)式.
1.4 广域视电阻率利用不同的场源形式或观测参数,广域电磁法可形成多种工作方式.考虑到野外实际情况和工作效率,目前应用最为广泛的是采用水平电流源作为发射源,只观测沿测线方向的水平电场Ex分量,构成E-Ex观测系统.不同于传统的CSAMT测量,由于只观测单个电场分量,广域电磁法只利用电场分量来定义广域视电阻率.
为计算广域视电阻率,考虑均匀大地表面水平电流源产生的电磁场,其电场Ex分量可表示为(何继善,2010)
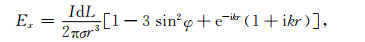
|
(24) |
其中,I为电偶极源的电流强度;dL为电偶极源的长度;σ为均匀半空间的电导率;r为接收点与发射源中心径向矢量的长度;φ为x轴与径向矢量之间的夹角;k为电磁波的波数.由(24)式便可得到E-Ex工作方式的广域电磁视电阻率为
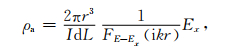
|
(25) |
其中FE-Ex(ikr)=1-3sin2φ+e-ikr(1+ikr)称为广域电磁法的电磁效应函数,是一个与发射频率、介质电磁性质以及收发距相关的函数,反映了电磁波在地下的传播特性(何继善,2010).在(25)式中,由于电磁效应函数也含有未知的电阻率参数,广域电磁法的视电阻率无法通过常用的代数方法来求取.因此需要迭代求解(25)式,通过多次迭代,逐步逼近来获得最佳的视电阻率值.为便于对比,CSAMT测量所采用的卡尼亚视电阻率和阻抗相位为
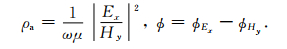
|
(26) |
本节通过对多个理论模型正演数值结果的对比分析来检验本文所开发的正演算法对广域电磁法模拟计算的准确性及有效性.
2.1 一维层状模型的对比测试为了验证本文算法的准确性,考虑具有准解析解的一维层状模型.图 2为一个典型陆地三层H型模型,其中第一层厚度为400 m,电阻率为100 Ωm;第二层厚度为200 m,电阻率为10 Ωm;第三层电阻率为1000 Ωm.水平发射电偶极子位于坐标原点处,发射频点数为16个,频率在0.25~8192 Hz之间呈对数等间隔分布.模型网格剖分为56×96×40,最小网格尺寸为100 m ×100 m × 50 m,空气层电阻率设为106 Ωm.用于一次场计算的背景模型选为100 Ωm的均匀半空间.层状模型的正演和一次场的计算均采用基于Hankel变换的准解析法(Key,2009).
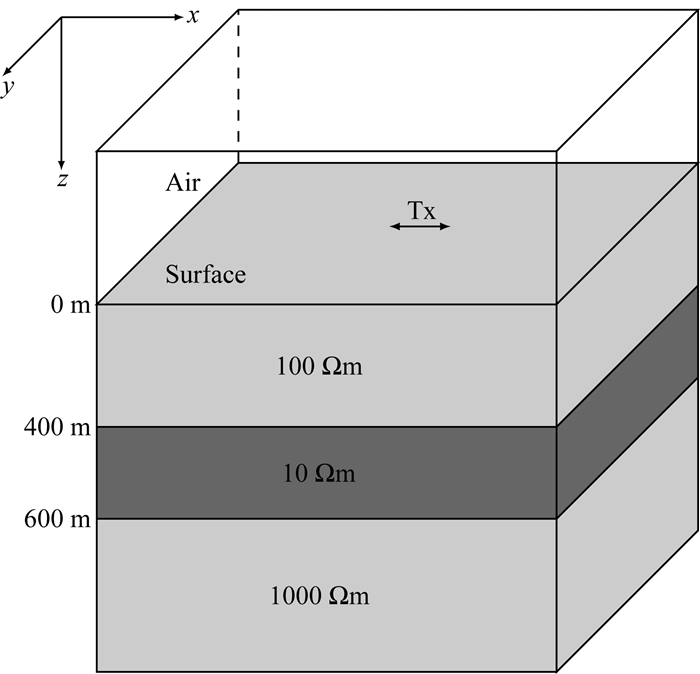
|
图 2 三层H型模型示意图 Fig. 2 Sketch of 1D layered model |
图 3给出了坐标为(0, 6000 m, 0)测点处所有频率的电磁场数值解与准解析解的对比.从图中可以看出,所有频点的数值解与准解析解相当一致(图 3a, b).在中高频段(>64 Hz)电磁场分量的振幅误差均在1%以内(图 3c),随着频率的降低,Ex分量的振幅误差有所增加,但保持在3%以内,而Hy分量振幅误差仍在1%以内;在整个发射频率范围内,除个别频点外,电磁场相位误差均在0.5°以内(图 3d).
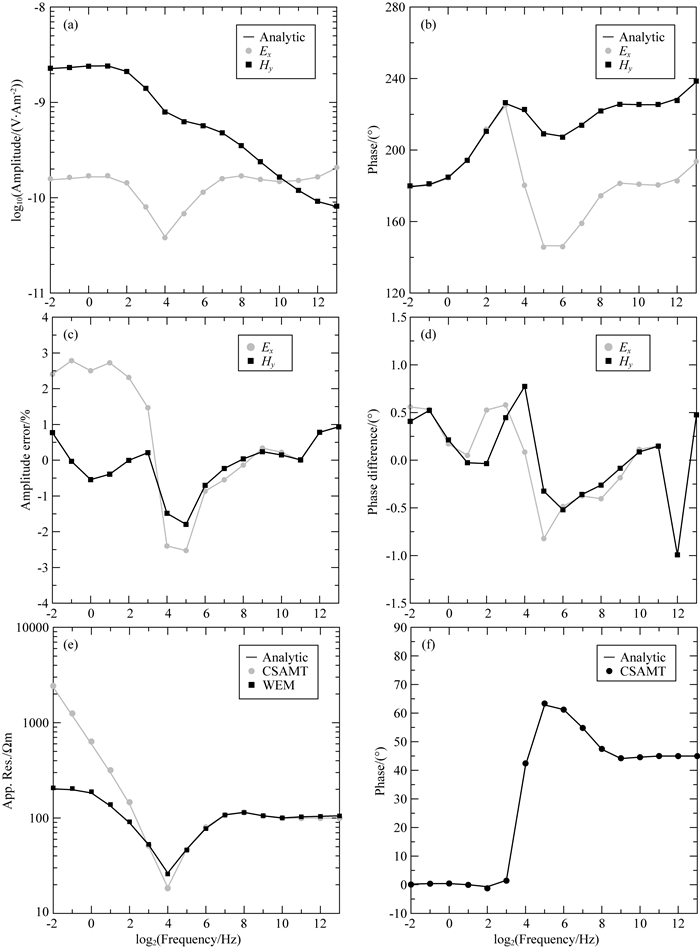
|
图 3 水平H型模型广域电磁数值解与准解析解对比 (a)电磁场振幅; (b)电磁场相位; (c)振幅相对误差; (d)相位相对差异; (e)视电阻率; (f)阻抗相位. Fig. 3 Comparison between SFV numerical solutions and quasi-analytic solutions for 1D layered model |
从电磁场分量的相位图中可以看出(图 3b),当发射频率小于8 Hz时,Ex分量和Hy分量的相位基本重合,此时对应的卡尼亚视电阻率(图 3e)在对数坐标系中呈现倾斜上升,而阻抗相位(图 3f)接近于零,表明此时测点已进入过渡区和近区,CSAMT测量将不再具有测深能力.与之对比,广域视电阻率曲线变化稳定,大体反映了真实地层电阻率的变化.因此,在相同的观测系统下,广域电磁法能够反映出过渡区和部分近区的地电特征,勘探深度要远大于CSAMT,这对于提升野外可控源电磁法的工作效率及勘探深度具有重要意义.
2.2 三维低阻体模型为对比广域电磁法与CSAMT的探测能力,设计如图 4所示的三维低阻体模型.在100 Ωm的均匀半空间中赋存一个尺寸为600 m×600 m×600 m的低阻异常体,其埋深为400 m,电阻率为10 Ωm.取低阻异常体中心在地表的投影为坐标原点O.采用沿x方向的水平电偶极子作为发射源,偶极子中心坐标为(0, 6000 m, 0),发射频点数为12个,频率在0.25~512 Hz之间呈对数等间隔分布.测线与发射源偶极方向一致.模型网格剖分为42×84×40,最小网格尺寸为100 m×100 m×50 m.

|
图 4 三维低阻体模型及观测系统示意图 Fig. 4 Sketch of 3D conductive model and data acquisition geometry |
图 5给出了不同测线上卡尼亚视电阻率与广域视电阻率拟断面图,其中测线A位于低阻体的正上方,距场源中心水平距离为6000 m;测线B位于低阻体外,距场源中心水平距离为6600 m.从图中可以看出,在主测线A上,卡尼亚视电阻率(图 5a)和广域视电阻率(图 5b)均较好反映出低阻异常体的空间轮廓.但对于卡尼亚视电阻率响应,当发射频率小于2 Hz时,测线上视电阻率均已超过100 Ωm;随着频率的降低,视电阻率进一步增大.这是因为随着发射频率的降低,电磁波在低阻体与背景介质中的趋肤深度增大,此时测线所在的位置不再满足远区测量条件,卡尼亚视电阻率公式无法适用.与之对比,广域视电阻率响应(图 5b)在低频处仍能有效反映出地下低阻体空间轮廓,并未受到远区测量条件限制.对于测线B,尽管其位于低阻异常体外,但会受到场源阴影效应的影响(陈明生和闫述,2005).对比图 5c和图 5d可以发现,场源阴影效应对于卡尼亚视电阻率的影响范围比较大,对整体测线均有影响;而对于广域视电阻率响应,场源阴影效应主要局限于低阻异常区域.这对于准确推断异常体的空间位置具有重要作用.
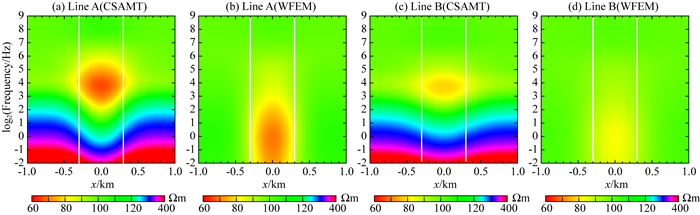
|
图 5 不同测线下卡尼亚视电阻率与广域视电阻率拟断面对比图,图中白色虚线为真实模型横向边界 Fig. 5 Pseudo-sections of Cagniard apparent resistivity and wide field apparent resistivity responses |
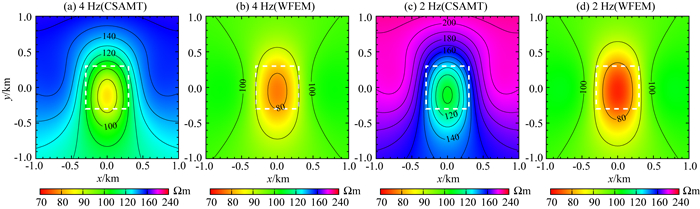
图 6给出了频率分别为4 Hz和2 Hz时卡尼亚视电阻率和广域视电阻率响应切片图.对比图 6a和图 6c可以发现,随着趋肤深度的变化,卡尼亚视电阻率响应会发生相应变化,特别是当测点位置不再满足远区测量条件时,此时卡尼亚视电阻率无法准确反映出地下电性分布情况.与之对比,随着频率的降低,在低阻异常区域,广域视电阻率响应进一步降低(图 6d),准确反映出地下异常体的空间分布和电性特征,表明广域电磁对于低阻体的深部信息仍能较好地反映.
|
图 6 不同频率下卡尼亚视电阻率与广域视电阻率切片对比图,图中白色虚线方框为真实模型位置 Fig. 6 Slices of Cagniard apparent resistivity and wide field apparent resistivity responses at specified frequencies |
图 7分别给出了沿X=0剖面上卡尼亚视电阻率(图 7a)与广域视电阻率响应(图 7b).我们利用电距离p(收发距与趋肤深度的比值,汤井田和何继善,2005)来定量描述最佳响应间距,图中黑实线为背景地层中电距离等值线.从图中可以看出,卡尼亚视电阻率对低阻目标体的最佳响应收发距大于3倍的趋肤深度,这与野外CSAMT测量中所要求的远区条件是一致的.与之对比,广域视电阻率对低阻目标体的最佳响应间距要小于3倍趋肤深度,并且在过渡区(p≈1),广域视电阻率响应仍能够准备反映低阻目标体的特征.由于可控源电磁信号强度随收发距增大呈三次方迅速衰减,因此对于广域电磁法来说,在野外测量时可以减小收发距,将非平面波区(近区或过渡区)纳入到可测量区域.这对于提高强干扰环境下数据的信噪比具有重要意义.另外,图 7c给出了X=0剖面上(0,0)测点处的卡尼亚视电阻率和广域电阻率视电阻率曲线对比图.当发射频率小于16 Hz时,对应的卡尼亚视电阻率开始快速上升,而广域视电阻率曲线变化稳定,近似反映出地下真实电阻率的变化.这表明在相同观测条件下,广域视电阻率具有更优的探测能力.

|
图 7 (a) X=0剖面的卡尼亚视电阻率拟断面图;(b) X=0剖面的广域视电阻率拟断面图; (c)地表测点(0,0)处的卡尼亚视电阻率和广域电阻率视电阻曲线对比图.图中白色虚线为真实模型横向边界,黑色实线为电距离等值线. Fig. 7 (a) Pseudo-section of Cagniard apparent resistivity at X=0 km; (b) Pseudo-section of wide field apparent resistivity at X=0 km; (c) Comparison between Cagniard apparent resistivity and wide field apparent resistivity at surface observation site (0, 0) |
本文依据Helmholtz定理,将麦克斯韦方程组转化为库伦规范条件下的磁矢势和电标势耦合方程,采用散射场方法避免了场源奇异性对数值结果的影响,并通过强加散度条件来消除电场伪解的影响.利用交错网格有限体积法对二次耦合势场方程进行离散化,实现了频率域可控源电磁三维正演计算.通过与一维水平层状模型的准解析解对比,验证了本文所开发的正演算法的准确性及有效性,并进一步对比分析了CSAMT与WFEM对典型三维低阻目标体的响应特征,结果表明,WFEM有效克服了CSAMT远区测量的要求,在非平面波区(过渡区或近区)仍能够准确反映地下目标体特征,极大拓展了可控源电磁法的观测范围,对于野外测量具有重要指导作用.
Ansari S, Farquharson C G. 2014. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids. Geophysics, 79(4): E149-E165. DOI:10.1190/geo2013-0172.1 |
Asch T H, Sweetkind D S. 2011. Audiomagnetotelluric characterization of range-front faults, Snake Range, Nevada. Geophysics, 76(1): B1-B7. DOI:10.1190/1.3511358 |
Avdeev D B, Kuvshinov A V, Pankratov O V, et al. 2002. Three-dimensional induction logging problems, Part Ⅰ:An integral equation solution and model comparisons. Geophysics, 67(2): 413-426. DOI:10.1190/1.1468601 |
Badea E A, Everett M E, Newman G A, et al. 2001. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials. Geophysics, 66(3): 786-799. DOI:10.1190/1.1444968 |
Bastani M, Malehmir A, Ismail N, et al. 2009. Delineating hydrothermal stockwork copper deposits using controlled-source and radio-magnetotelluric methods:A case study from northeast Iran. Geophysics, 74(5): B167-B181. DOI:10.1190/1.3174394 |
Börner R U. 2010. Numerical modelling in geo-electromagnetics:Advances and challenges. Surveys in Geophysics, 31(2): 225-245. DOI:10.1007/s10712-009-9087-x |
Cai H Z, Xiong B, Han M R, et al. 2014. 3D controlled-source electromagnetic modeling in anisotropic medium using edge-based finite element method. Computers & Geosciences, 73: 164-176. |
Cai H Z, Xiong B, Zhdanov M. 2015. Three-dimensional marine controlled-source electromagnetic modelling in anisotropic medium using finite element method. Chinese Journal of Geophysics (in Chinese), 58(8): 2839-2850. DOI:10.6038/cjg20150818 |
Cai H Z, Hu X Y, Li J H, et al. 2017. Parallelized 3D CSEM modeling using edge-based finite element with total field formulation and unstructured mesh. Computers & Geosciences, 99: 125-134. |
Carlson N R, Paski P M, Urquhart S A. 2005. Applications of controlled source and natural source audio-frequency magnetotellurics to groundwater exploration.//18th EEGS Symposium on the Application of Geophysics to Engineering and Environmental Problems. Atlanta, Georgia: The Environmental & Engineering Geophysical Society, 18: 585-595. http://www.researchgate.net/publication/269122987_Applications_of_Controlled_Source_and_Natural_Source_Audio-Frequency_Magnetotellurics_to_Groundwater_Exploration
|
Chen M S, Yan S. 2005. Analytical study on field zones, record rules, shadow and source overprint effects in CSAMT exploration. Chinese Journal of Geophysics (in Chinese), 48(4): 951-958. |
Haber E, Ascher U M, Aruliah D A, et al. 2000. Fast simulation of 3D electromagnetic problems using potentials. Journal of Computational Physics, 163(1): 150-171. DOI:10.1006/jcph.2000.6545 |
Haber E, Ascher U M. 2001. Fast finite volume simulation of 3D electromagnetic problems with highly discontinuous coefficients. SIAM Journal on Scientific Computing, 22(6): 1943-1961. DOI:10.1137/S1064827599360741 |
Han B, Hu X Y, Schultz A, et al. 2015a. Three-dimensional forward modeling of the marine controlled-source electromagnetic field with complex source geometries. Chinese Journal of Geophysics (in Chinese), 58(3): 1059-1071. DOI:10.6038/cjg20150330 |
Han B, Hu X Y, Huang Y F, et al. 2015b. 3-D frequency-domain CSEM modeling using a parallel direct solver. Chinese Journal of Geophysics (in Chinese), 58(8): 2812-2826. DOI:10.6038/cjg20150816 |
He J S. 2010. Wide Band Electromagnetic Method and Pseudo Random Signal Electrical Method (in Chinese). Beijing: Higher Education Press.
|
Hu X Y, Peng R H, Wu G J, et al. 2013. Mineral Exploration using CSAMT data:Application to Longmen region metallogenic belt, Guangdong Province, China. Geophysics, 78(3): B111-B119. DOI:10.1190/geo2012-0115.1 |
Jahandari H, Farquharson C G. 2014. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids. Geophysics, 79(6): E287-E302. DOI:10.1190/geo2013-0312.1 |
Jiang B N, Wu J, Povinelli L A. 1996. The origin of spurious solutions in computational electromagnetics. Journal of Computational Physics, 125(1): 104-123. |
Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. DOI:10.1190/1.3058434 |
Li D Q, Hu Y F. 2015. A comparison of wide field electromagnetic method with CSAMT method in strong interferential mining area. Geophysical and Geochemical Exploration (in Chinese), 39(5): 967-972. |
Mackie R L, Smith J T, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite-difference equations:The magnetotelluric example. Radio Science, 29(4): 923-935. DOI:10.1029/94RS00326 |
Newman G A, Alumbaugh D A. 1995. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences. Geophysical Prospecting, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 |
Newman G A, Alumbaugh D L. 2002. Three-dimensional induction logging problems, Part 2:A finite-difference solution. Geophysics, 67(2): 484-491. DOI:10.1190/1.1468608 |
Peng R H, Hu X Y, Han B, et al. 2016. 3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method. Chinese Journal of Geophysics (in Chinese), 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2014. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling. Geophysics, 79(6): E255-E268. DOI:10.1190/geo2013-0376.1 |
Schwarzbach C, Haber E. 2013. Finite element based inversion for time-harmonic electromagnetic problems. Geophysical Journal International, 193(2): 615-634. DOI:10.1093/gji/ggt006 |
Shen J S. 2003. Modeling of 3-D electromagnetic responses in frequency domain by using staggered-gridfinite difference method. Chinese Journal of Geophysics (in Chinese), 46(2): 281-288. |
Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy. Geophysics, 74(5): F95-F105. DOI:10.1190/1.3196241 |
Tang J T, He J S. 2005. ControllableSource Audio Magnetotelluric Method and Its Application (in Chinese). Changsha: Central South University Press.
|
Tong X Z, Liu J X, Li A Y. 2018. Two-dimensional regularized inversion of AMT data based on rotation invariant of Central impedance tensor. Earth Planet. Phys., 2(5): 430-437. DOI:10.26464/epp2018040 |
Wang R, Di Q Y, Wang M Y, et al. 2009. Research on the effect of 3D body between transmitter and receivers on CSAMT response using integral equation method. Chinese Journal of Geophysics (in Chinese), 52(6): 1573-1582. DOI:10.3969/j.issn.0001-5733.2009.06.019 |
Weiss C J, Newman G A. 2002. Electromagnetic induction in a fully 3-D anisotropic earth. Geophysics, 67(4): 1104-1114. DOI:10.1190/1.1500371 |
Weiss C J, Constable S. 2006. Mapping thin resistors and hydrocarbons with marine EM methods, Part Ⅱ:Modeling and analysis in 3D. Geophysics, 71(6): G321-G332. DOI:10.1190/1.2356908 |
Weiss C J. 2013. Project AphiD:A Lorenz-gauged A-Φ decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous Earth. Computers & Geosciences, 58: 40-52. |
Wu G J, Hu X Y, Huo G P, et al. 2012. Geophysical exploration for geothermal resources:An application of MT and CSAMT in Jiangxia, Wuhan, China. Journal of Earth Science, 23(5): 757-757. DOI:10.1007/s12583-012-0282-1 |
Yang J, Liu Y, Wu X P. 2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids. Chinese Journal of Geophysics (in Chinese), 58(8): 2827-2838. DOI:10.6038/cjg20150817 |
Zhdanov M S, Lee S K, Yoshioka Y. 2006. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity. Geophysics, 71(6): G333-G345. DOI:10.1190/1.2358403 |
蔡红柱, 熊彬, Zhdanov M. 2015. 电导率各向异性的海洋电磁三维有限单元法正演. 地球物理学报, 58(8): 2839-2850. DOI:10.6038/cjg20150818 |
陈明生, 闫述. 2005. CSAMT勘探中场区、记录规则、阴影及场源复印效应的解析研究. 地球物理学报, 48(4): 951-958. DOI:10.3321/j.issn:0001-5733.2005.04.031 |
韩波, 胡祥云, Schultz A, 等. 2015a. 复杂场源形态的海洋可控源电磁三维正演. 地球物理学报, 58(3): 1059-1071. DOI:10.6038/cjg20150330 |
韩波, 胡祥云, 黄一凡, 等. 2015b. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报, 58(8): 2812-2826. DOI:10.6038/cjg20150816 |
何继善. 2010. 广域电磁法和伪随机信号电法. 北京: 高等教育出版社.
|
李帝铨, 胡艳芳. 2015. 强干扰矿区中广域电磁法与CSAMT探测效果对比. 物探与化探, 39(5): 967-972. |
彭荣华, 胡祥云, 韩波, 等. 2016. 基于拟态有限体积法的频率域可控源三维正演计算. 地球物理学报, 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
沈金松. 2003. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报, 46(2): 280-288. DOI:10.3321/j.issn:0001-5733.2003.02.032 |
汤井田, 何继善. 2005. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社.
|
王若, 底青云, 王妙月, 等. 2009. 用积分方程法研究源与勘探区之间的三维体对CSAMT观测曲线的影响. 地球物理学报, 52(6): 1573-1582. DOI:10.3969/j.issn.0001-5733.2009.06.019 |
杨军, 刘颖, 吴小平. 2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827-2838. DOI:10.6038/cjg20150817 |
 2018, Vol. 61
2018, Vol. 61


