地球物理学报  2018, Vol. 61 Issue (10): 4007-4020   PDF    
引用本文
谢志南, 郑永路, 章旭斌. 2018. 常Q滞弹性介质地震波动数值模拟——时域本构优化逼近. 地球物理学报, 61(10): 4007-4020, doi: 10.6038/cjg2018L0704.  
Xie Z N, Zheng Y L, Zhang X B. 2018. Optimized approximation for constitution of constant Q viscoelastic media in time domain seismic wave simulation. Chinese J. Geophys. (in Chinese), 61(10): 4007-4020, doi: 10.6038/cjg2018L0704.  
常Q滞弹性介质地震波动数值模拟——时域本构优化逼近
谢志南, 郑永路, 章旭斌     
中国地震局工程力学研究所, 中国地震局地震工程与工程振动重点实验室, 哈尔滨 150080
收稿日期 2017-11-13, 2018-03-20 收修定稿
基金项目: 国家科技支撑计划课题（2015BAK17B01），国家自然科学基金（51678539），黑龙江省国家科技重大专项和重点研发项目省级资助资金（GX16C006）资助
第一作者简介: 谢志南, 1984年生, 男, 博士, 副研究员, 研究方向为工程地震.E-mail:wla_2012@163.com
摘要：在地震波动模拟中计入常Q滞弹性阻尼，可有效降低模拟波形的误差.就时域有限差分和有限元模拟而言，常基于广义标准线性体建立阻尼介质的时域本构逼近.广义标准线性体由若干标准线性体并联得到，增加标准线性体个数能有效提高模拟精度，但计算量及计算存储将成倍增长.目前尚未有普适的标准线性体个数优化取值方案.本文基于广义标准线性体参数的非线性优化拟合方法，详细分析了时域本构逼近误差的影响因素，清楚揭示了逼近误差仅取决于频带宽度，与频带上下限取值无关这一特性，阐明了构建具有普适性标准线性体个数优化取值方案的可行性.论证了波形模拟精度主要取决于波传播距离与模拟波长的比值以及标准线性体的个数取值.综合考虑上述两个控制因素，结合在波动正反演问题中广为采纳的波形时频误差衡量准则，对不同Q值介质给出了标准线性体个数优化取值表.进一步，本文提出采用不同个数标准线性体以近似不同Q值的阻尼介质时域本构，解决了以往波动数值模拟中统一采用相同个数标准线性体而导致的计算量及计算存储浪费或模拟精度低下等问题，并基于数值实验验证了这一方法的精度.本文工作对推进滞弹性介质波动数值模拟及其在全波形反演问题中的应用具有理论价值和实践意义.
关键词: 滞弹性      地震波动模拟      常Q      广义标准线性体      时域本构     
Optimized approximation for constitution of constant Q viscoelastic media in time domain seismic wave simulation
XIE ZhiNan, ZHENG YongLu, ZHANG XuBin     
Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
Abstract: Taking into account viscoelastic damping effect of media with constant Q, the error of the synthetic waveform can be effectively reduced in seismic wave simulation. In term of time domain finite difference or finite element method for wave simulation, the generalized standard linear body (GSLS), consisted of several standard linear bodies (SLS) connected in parallel, is used to approximate the constitution of viscoelastic media. Via increasing the number of SLS, the accuracy of simulation can be effectively improved but simultaneously increasing the amount of both computational work and memory by times. It is not available yet a general instruction for the choices of the number of SLS in viscoelastic wave simulation, which is the main focus of this paper. The factors that impact on the GSLS approximation error are firstly analyzed with the parameter of GSLS fitted by a nonlinear optimization approach. Via clarifying that the error depends on the bandwidth but not the specific value of upper and lower limits of frequency interval, the feasibility of deriving such an instruction is illustrated. Moreover, for given bandwidth and the given number of SLS used in GSLS, the accuracy of synthetic waveform simulation is demonstrated to be impacted by both the factor of the ratio of wave propagation distance to the interested wavelength in simulation and the factor of the Q value of the media. Incorporating of the two factors, the table for optimal choice of the SLS number for medium with different Q value is established by using a generally applied criterial for measurement of time-frequency goodness-of-fit of the synthetic and the observed waveform. On basis of the new table, a method of using GSLS with different number of SLS for modelling media with different Q values is proposed to avoid the waste of the computational work and memory or the deterioration of the accuracy of simulation caused by using the same number of SLS in GSLS to approximate media with large spanned Q value, which is usually presented in seismic wave simulation. Finally, the accuracy and the efficiency of new method are validated by numerical tests. The work of this paper could further promote the wide application of viscoelastic wave simulation in forward problem and in inverse problem using full waveform inversion technique.
Keywords: Viscoelasticity    Seismic wave simulation    Constant Q    Generalized standard linear solid    Time-domain constitution    
0 引言

地震波在实际介质中传播时，除波阵面扩展、非均匀体散射等几何因素引起的衰减外(张立彬等，2011)，介质内耗(Internal friction)阻尼也会导致地震波衰减，传播过程中介质的非弹性形变将部分地震波能量耗散为热能.地震学常基于线性滞弹性阻尼理论(葛庭燧, 2000)描述介质阻尼：介质非弹性应变可完全恢复，不产生永久形变；应力-应变关系(本构)由Boltzmann卷积表示；介质阻尼大小用无量纲参数——品质因子Q衡量.基于观测记录分析结果，常假定介质Q值与频率无关(Kjartansson, 1979；Aki and Richards, 2002).大量地震波动数值模拟的实验表明，准确计入常Q滞弹性阻尼，可有效改善地震波模拟精度，大幅降低模拟记录与实测记录之间的误差方差(Olsen et al., 2003)，解决基于弹性介质波动理论难以解释观测记录中P波质点行进轨迹呈椭圆状等问题(Marcellini and Tento, 2011).

就大型复杂地震波动时域数值模拟而言，直接计入介质常Q阻尼将导致难以承受的计算量与计算存储，因卷积本构计算需存储以往所有计算时刻的节点位移.为此，研究人员提出采用弹簧阻尼模型在有限宽的频带范围实现对常Q阻尼介质时域本构的近似(Liu et al., 1976).广义Maxwell体(Emmerich and Korn, 1987)和广义标准线性体(Carcione et al., 1988)是当前广为采用的弹簧阻尼模型，但二者相互等价(Moczo and Kristek, 2005；Cao and Yin, 2014).广义标准线性体(Generalized Standard Linear Solid, GSLS)由若干标准线性体(SLS)并联得到：SLS应变与总应变一致，总应力为SLS应力的叠加.GSLS时域本构可由一阶常微分方程组表示，因此基于GSLS建立常Q介质时域本构近似规避了卷积计算的困难，便于在时域波动数值模拟中实现.GSLS中弹簧和阻尼元件的弹性模量和黏滞系数可基于优化方法拟合常Q介质时域本构得到.除仅适用于Q值较大情形的常τ方法外(Blanch et al., 1995)，大多优化方法在拟合过程中没有确保弹性模量应为正值这一物理特性，拟合所得弹性模量可能为负值(Emmerich and Korn, 1987).这将导致时域波动数值模拟失稳，模拟波场呈现不符合物理实际的快速增长(Blanc et al., 2016)，该问题对Q值较小情形(Q≤5)尤为突出(Blanc et al., 2016).为此，Blanc等(2016)提出了一种基于非线性优化的GSLS参数拟合方法，通过施加弹性模量和黏滞系数必须为正值这一约束，实现了对常Q介质时域本构的收敛逼近，收敛精度随SLS个数增加而稳步提升.

对任意给定的有限宽频带范围，增加GSLS中SLS的个数均可实现对常Q介质时域本构的收敛逼近，但SLS个数增加会导致计算量及计算存储成倍增长.为解决这一问题, 针对均匀滞弹性介质地震波模拟，Day(1998)建议了一种分布式滞弹性阻尼模拟方法，该方法将均匀滞弹性介质等效为周期性空间分布的非均匀滞弹性介质，空间分布周期长度小于四分之一个模拟波长.与常规方法不同，该方法不直接在计算节点处基于GSLS近似阻尼介质本构，而是通过在单一计算节点上采用SLS，在周期长度覆盖的体积范围实现对常Q介质本构的等效近似.目前，该方法已应用至有限差分(Graves and Day 2003)，线性集中质量有限元(Ma and Liu, 2006)，轴对称勒让德谱元地震波动模拟(van Driel and Nissen-Meyer, 2014).然而，Kristek和Moczo(2003)明确指出：该方法不适用于介质阻尼存在显著差异的分界面模拟.

另外，Zhu等(2013)针对浅地表勘探时域地震波动数值模拟，对给定模拟频带范围[5, 125]Hz, 基于数值实验结果讨论了SLS个数选取对波动数值模拟精度的影响.其结果表明：在其给定频带范围内，对Q值较大介质(Q≥100)地震波动数值模拟，或者是对模拟区中仅包含小范围Q值较小介质的地震波动数值模拟问题，单个SLS即可实现对常Q介质时域本构的有效近似.为此Zhu等(2013)建议采用单个SLS以降低计算量及计算存储.与以往相关研究工作类似，对其他模拟频带范围，Q值较小介质，在保证波动模拟精度前提下，作者并未给出SLS个数取值建议.

综上所述，目前尚未有普适的标准线性体个数优化取值方案.本文研究围绕这一取值方案的建立展开.基于Blanc等(2016)提出的非线性优化方法详细讨论了SLS个数对常Q滞弹性阻尼时域本构逼近误差的影响，阐明了误差仅取决于频带宽度，与频带范围的上下限取值无关且误差随带宽减小而减小这一概念.该概念是建立具有普适性的SLS个数优化取值方案的基础.本文清楚揭示了波形模拟精度主要取决于传播距离与模拟波长的比值以及SLS个数取值.结合Kristeková等(2009)提出的波形拟合精度时频衡量准则，综合考虑上述两个控制因素，建立了SLS个数优化取值表.在此基础上，本文提出采用包含不同个数SLS的GSLS以近似不同Q值的阻尼介质时域本构，SLS个数选取由本文建议SLS个数优化取值表给出.解决了以往波动数值模拟中统一采用相同个数SLS而导致的计算量及计算存储浪费或模拟精度低下的问题.

文中第一节给出滞弹性介质波动方程.第二节简要介绍基于GSLS建立常Q阻尼介质时域本构的方法及GSLS参数的非线性拟合方法.第三节详细分析GSLS时域本构逼近误差及其对波动模拟精度的影响.第四节结合地震波动谱元模拟阐明采用不同SLS个数的GSLS近似不同Q值介质的时域本构可提高计算效率以及降低计算存储.最后给出本文工作小结.

1 滞弹性介质波动方程

在小应变前提假定下，地震波在滞弹性介质中的传播满足运动平衡方程：

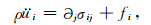
(1)

式中ρ为介质密度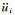，为xi方向加速度，σij为外法线矢量为ni平面上的应力沿xj方向的分量. ∂j表示xj方向空间偏导数，∂j=∂/∂xj.fi为施加在xi方向上的体力.

滞弹性介质时域本构由Boltzmann卷积表示：

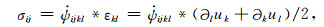
(2)

ψijkl为满足因果律的应力松弛函数.

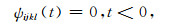
(3)

对应地，频域本构可表示为

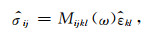
(4)

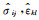
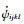
式中, Mijkl(ω)分别表示σij，εkl，的傅里叶变换.复弹性模量Mijkl(ω)的实部和虚部满足Kramers-Krönig关系.

就各向同性介质而言，有

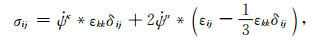
(5)

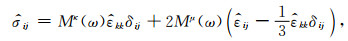
(6)

式中δij为二阶狄拉克张量. Mκ(ω)，Mμ(ω)分别为复膨胀模量和复剪切模量.(5), (6)式可分解为两个一维介质本构:

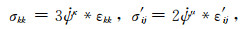
(7)

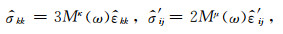
(8)

式中.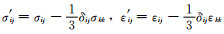

因此，描述各向同性滞弹性介质的品质因子分两类，即膨胀模量品质因子和剪切模量品质因子:

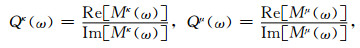
(9)

式中Re[z]，Im[z]分别表示复数z的实部与虚部.

2 常Q滞弹性介质时域本构近似

因各向同性滞弹性介质本构由两个独立的一维形式本构所组成，本节给出一维常Q滞弹性介质时域本构的GSLS近似及其参数的非线性拟合方法.

由N个SLS所构成GSLS(图 1)的复弹性模量可表示为

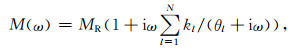
(10)

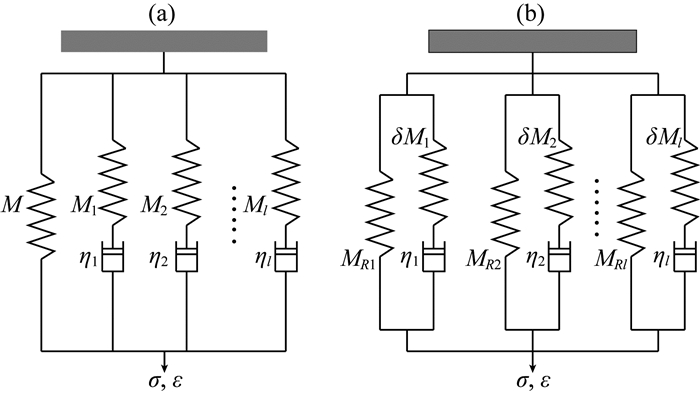
图 1 广义Maxwell体(a)与广义标准线性体(GSLS, b)示意图 Fig. 1 Sketch of the generalized Maxwell body (a), and the generalized standard linear solid (GSLS, b)

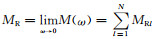
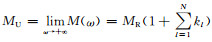
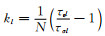
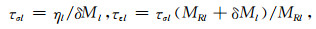
式中MR为松弛模量，，未松弛模量，下标l代表SLS的编号. ，θl=1/τσl，其中τσl，τεl分别为第l个SLS对应的应力松弛时间和应变蠕变时间:

(11)

GSLS对应Q值可表示为

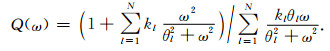
(12)

基于(10)式可得GSLS应力松弛函数为

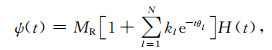
(13)

式中，H(t)为单位阶跃函数.由此可得GSLS时域本构

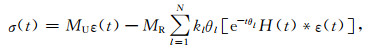
(14)

通过引入辅助变量ϕl(t)=e-tθlH(t)*ε(t)，可将(14)式简化为

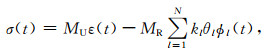
(15)

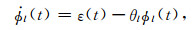
(16)

GSLS时域本构便于在时域数值模拟中实现，规避了卷积计算.

基于优化方法拟合GSLS Q值与介质Q值之间误差的最小值可得kl，θl，l=1, …, N.本文采用Blanc等(2016)提出的非线性优化方法.与其他方法不同，该方法对kl，θl二者施加了严格大于0的前提条件，避免了因二者为负值导致的数值模拟失稳问题.另外，该方法扩大了θl的允许取值范围，极大提高了拟合精度.

考虑在模拟频带[ωmin, ωmax]中的4N个频率离散点上拟合GSLS系数.介质Q值的取值为常数Q0.离散频率点分布由下式给出：

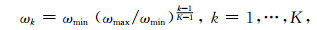
(17)

K=4N.令(12)式离散频率点取值等于Q0，整理得到

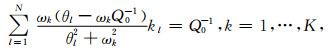
(18)

为保证参量kl，θl为正值，令

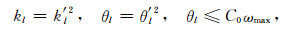
(19)

式中C0一般取为100左右大小的实数，避免拟合所得θl过大而导致(16)式转化为刚性微分方程.将(19)式代入(18)式，整理得到(18)式两端取值之间残差的平方和为

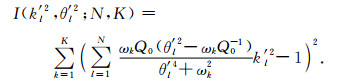
(20)

基于SolvOpt算法，拟合得到令残差I(k′l2, θ′l2; N, K)取值最小的k′l，θ′l值.具体过程参照文献Blanc等(2016).广义标准线性体MR参数的取值可通过令GSLS与目标介质在参考频率ωref处波传播的相速度相等得到：

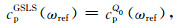
(21)

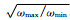
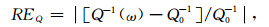
cpGSLS，cpQ0详细表达式见附录A.常用ωref取值为ωmin .在后续章节，为简化表述，将cpQ0(ωref)简写为cref.拟合所得GSLS的Q-1值相对误差与相速度相对误差为

(22)

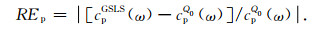
(23)

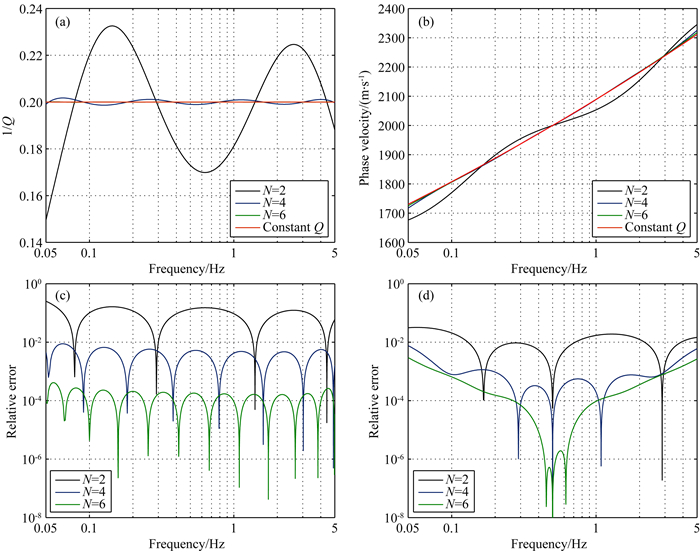
图 2给出基于N取值等于2, 4, 6的GSLS建立常Q阻尼介质本构逼近对应的Q-1值和相速度随频率的变化关系及相对误差.结果表明，通过增加SLS的个数，可实现对常Q介质时域本构的收敛逼近.收敛精度随SLS增加稳步提升.

图 2 基于SLS个数为2, 4, 6的GSLS建立常Q阻尼介质本构逼近对应的Q-1值(a)和相速度(b)随频率变化曲线，(c)和(d)为Q-1值和相速度相对误差.模拟频带为0.05~5 Hz，Q0=5, cref=2000 m·s-1 Fig. 2 (a, b) Reciprocal of the quality factor and the phase velocity of constant Q media and its approximation GSLS with N=2, N=4 and N=6. (c, d) The corresponded relative error of inverse quality factor and the phase velocity. The frequency interval of 0.05~5 Hz, Q0=5 and cref=2000 m·s-1 are considered
3 时域本构逼近误差及其对波动数值模拟精度的影响分析

以往研究表明时域本构逼近误差及其对波动数值模拟精度的影响由五个因素控制：模拟频带取值，目标Q0值大小，SLS个数取值，cref取值，波传播距离.误差随Q0值和SLS个数的增加而减小.但大多研究是针对某一具体给定的频带进行，所得结果不具有普适性.本节将系统分析上述因素对逼近误差以及波形模拟精度的影响.首先阐明误差仅取决于频带宽度，与频带上下限取值无关这一概念.这使得建立普适的SLS个数优化取值方案成为可能.进一步，通过论证波形模拟精度主要取决于传播距离与模拟波长的比值以及SLS个数取值这两个关键因素，结合Kristeková等(2009)提出的波形拟合精度时频衡量准则，对不同Q0值介质，建立了SLS个数的优化取值表.最后解释了Zhu等(2013)建议采用单个SLS近似常Q时域本构以降低计算量及计算存储这一方法的适用范围.

3.1 时域本构逼近误差影响因素分析

本节阐明模拟频带，Q0值，SLS个数取值，cref取值对逼近误差的影响.从Q-1值相对误差、相速度相对误差表达式容易看出，这两类误差大小与cref取值无关.下面分析其余两个因素对误差的影响.

首先阐明逼近误差大小仅取决于模拟频带带宽，与频带上下限取值无关.进一步结合SLS的Q值分布特征阐明带宽变窄时，误差将随着减小.固定频带宽度ωmax/ωmin，引入比例系数β，可将任一给定带宽的模拟频带表示为[βωmin, βωmax].为此，可将(20)式改写为

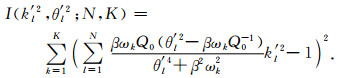
(24)

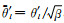
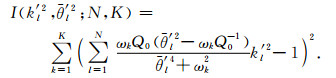
引入参数，整理(24)式得到

(25)

因(24)式等同于(25)式，这意味着拟合(24)式与拟合(25)式所得k′l2是一致的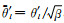，，对应地，Q-1值相对逼近误差也是一致的.因此，给定模拟频带宽度，逼近误差与频带上下限取值无关.当模拟频带宽度变窄时，相同SLS个数GSLS的Q-1值相对逼近误差将随之减小(图 3)，这是由于SLS对应Q值呈单峰分布所决定的.以单个SLS为例，当模拟频带很窄时，SLS的Q值在其峰值附近近似为常数(Liu et al., 1976).为此，对模拟频带较窄情形，单个SLS即可实现对常Q介质时域本构的较好近似；然而，对于模拟频带较宽情形，单个SLS难以满足对常Q介质时域本构的近似精度.

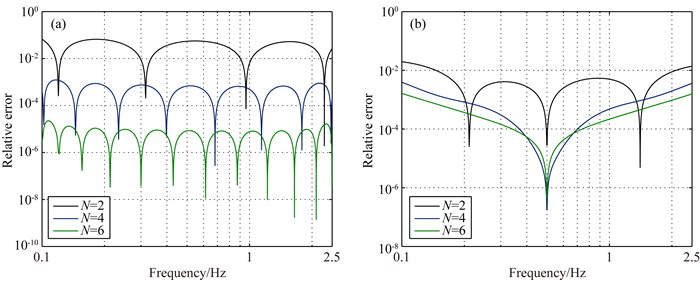
图 3 (a, b)基于GSLS(N=2, 4, 6)近似常Q阻尼介质的Q-1值和相速度相对误差.模拟频带取为0.1~2.5 Hz，Q0=5 Fig. 3 (a, b) the relative error curve of inverse quality factor and the phase velocity when using GSLS with N=2, 4, 6 for constant Q approximation. The frequency interval of 0.05~5 Hz and Q0=5 are considered

逼近误差随SLS个数取值增加而减小.因SLS个数与相对误差大小之间呈强非线性关系，难以解析论证二者之间关系.这里基于算例分析SLS个数取值对相对误差的影响.表 1给出N取值等于2, 3, 4情形，GSLS的Q-1值相对误差以及相速度相对误差.GSLS中弹簧和阻尼元件的弹性模量和黏滞系数由Blanc等(2016)提供非线性优化方法拟合得到.从表 1可知，给定Q0值，Q-1相对误差随N增加而快速减小.给定N，Q-1相对误差大小随Q0值增加而缓慢减小，当Q0≥100，相对误差近似不变.相速度相对误差变化规律与Q-1值相对误差变化规律基本一致，但相速度相对误差普遍小于Q-1值相对误差，对Q0≥50，后者比前者大十倍以上.下面针对Q0值较大情形，给出Q-1相对误差近似不变的证明.首先给出Q值相对误差具体表达式

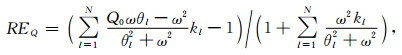
(26)

表 1 GSLS (N=2, 3, 4)近似常Q阻尼介质的Q-1值和相速度的最大相对误差值.模拟频带取为0.05~5 Hz，Q0=5, 25, 50, 100, 200, 500, 1000.括号内数值为相速度最大相对误差值 Table 1 The maximum relative error of inverse quality factor and the phase velocity (shown in bracket) when using GSLS with N=2, 3, 4 for constant Q approximation. The frequency interval of 0.05~5 Hz and Q0=5, 25, 50, 100, 200, 500, 1000 are considered

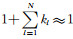
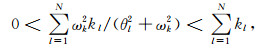
对Q0值较大情况，因MU/MR接近1，即.因

(27)

进而可将(26)式简化为

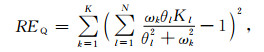
(28)

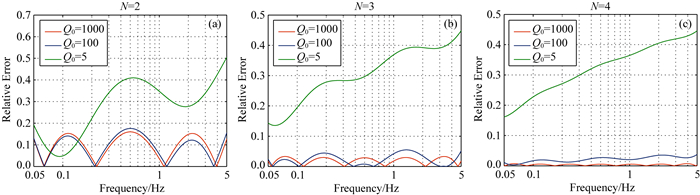
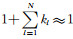
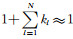
式中Kl=Q0kl.同样地，基于(28)式，可采用非线性优化方法拟合得到θl、Kl的取值，二者取值与Q0无关，这意味对Q0值取值较大情形，Q-1相对逼近误差与Q0无关.值得一提的是这一简化条件的引入，极大简化了不同Q0值对应GSLS参数回归的工作量，因Kl不随Q0发生变化，kl=Q0/Kl，在相同频带宽度范围内拟合不同Q值对应的kl值可一次性完成. 这一简化条件仅适用于Q0值较大(Q0≥100)情形.即便Q0≥100，当N＞3时直接基于拟合所得Kl计算kl也是不合适的(图 4).为提高Q值拟合精度，Blanch等(1995)一文建议采用Kl= Q0kl代替Kl=Q0kl以计算kl，其中Q0≤Q0.然而，截止目前并没有相关研究工作明确地给出Q0的取值准则.

图 4 红线为通过非线性优化方法求出Q0 =1000时N为2, 3, 4的GSLS在目标频带0.05~5 Hz范围内拟合常Q介质的Q-1相对误差曲线，蓝线和绿线分别为根据Q0 =1000的系数按比例得到的Q0 =100、Q0 =5时N为2, 3, 4的GSLS拟合常Q介质的Q-1相对误差曲线 Fig. 4 The red line shows Q-1 relative error of GSLS with 2, 3, 4 relaxation mechanisms for target Q0=1000 approximation in frequency interval 0.05~5 Hz using nonlinear optimization approach, and the blue and green lines shows Q-1 relative error of GSLS with 2, 3, 4 relaxation mechanisms for target Q0=100 and Q0=5 approximation via calculating coefficients according to the proportion of Q0 value
3.2 时域本构逼近对波动模拟精度的影响分析

本节集中讨论时域本构逼近对波动模拟精度的影响，仍考虑一维滞弹性介质波动模型(附录A)，介质本构分别由常Q阻尼介质本构以及GSLS本构给出，采用Kristeková等(2009)提出的波形时频误差(misfit)衡量准则(表 2)衡量SLS取值对波形拟合精度的影响.该准则不仅考察了波形的相位拟合误差(Misfit of phase)，同时考虑了在幅值拟合误差(Misfit of envelop)，目前被广泛应用于波动正反演问题.根据该表，波形相位拟合度(Phase goodness of fit, PG)以及幅值拟合度(Envelop goodness of fit，EG)在8分以上为拟合度极好，6~8分为较好，4~6分为一般，4分以下为差.

表 2 时频误差(misfit)衡量准则取值及口头评价标准 Table 2 Time-frequency goodness-of-fit criteria and four verbal degrees

就常Q阻尼介质时域本构而言，一维模型的谐波解可表示为

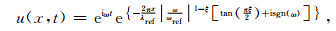
(29)

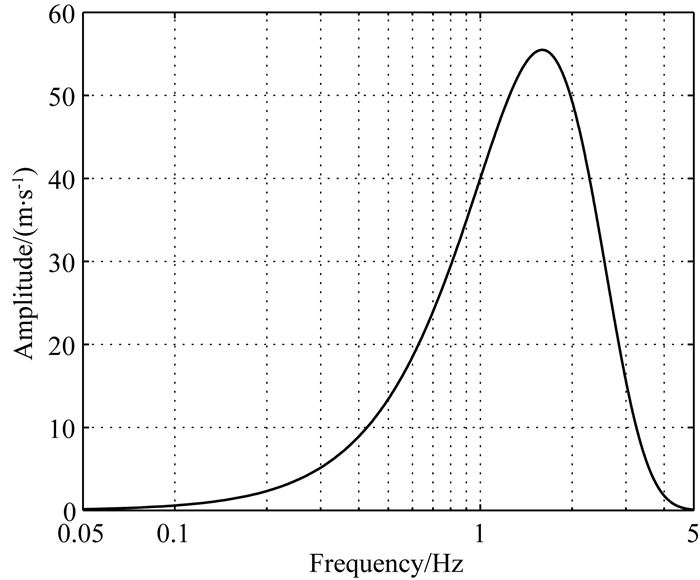
式中λref=2πcref/ωref.u(0, t)=eiωt，对激励施加在原点x=0情形.(29)式对应于源函数为2δ(t)的脉冲激励下一维波形模型的右行波解格林函数.将格林函数与源函数卷积即可得到原点右侧不同位置观测点处位移时程，模型参数做归一化无量纲处理，ωref=π，cref=1，ρ=1.同样地，基于上述方法可得到基于GSLS近似常Q阻尼介质时域本构的一维波动模型的解析解.将模拟频带宽度取为地震波动数值模拟常用带宽，即100，模拟频带为[0.05 Hz, 5 Hz].考虑傅里叶谱为如下形式的脉冲激励源A0(ω)=1.5e-iω-ω2/(32π)ω2 (图 5).为降低非模拟频带范围谐波在远距离对模拟误差分析的影响，这里采用平滑窗函数H(ω)对激励源进行频域滤波，该函数的表达式为

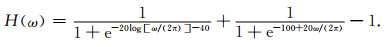
(30)

图 5 激励源时间函数傅里叶频谱 Fig. 5 The Fourier spectra of the source time function

同时将时域波形误差定义为

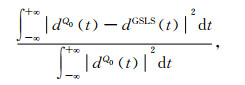
(31)

式中dQ0(t)，dGSLS(t)分别表示基于常Q介质本构以及基于GSLS本构计算所得观测点波形.直接计算(31)式较为困难，可根据Parseval定理，时域波形误差可表示为

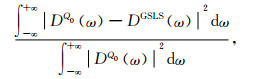
(32)

其中，D(ω)为d(t)的傅里叶变换. (32)式对于给定模拟参数可求出其误差值，以此作为量化标准，对给定模拟精度要求，可以得到SLS个数的取值.基于(29)，(32)式可得单频波模拟误差可表述为

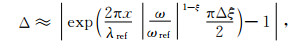
(33)

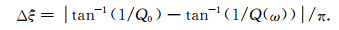
(34)

(33) 式清楚揭示了波形模拟精度主要取决于传播距离与模拟波长的比值以及Q值拟合误差Δξ，在给定模拟带宽的前提下，后者大小由标准线性体的个数唯一确定.另外，从(33)式不难看出，对频率大于参考频率的单频波形拟合误差要高于频率小于参考频率情形.因此在应用本文SLS个数优化取值表时，激励源主频应设置在参考频率以下或稍大于参考频率的范围.

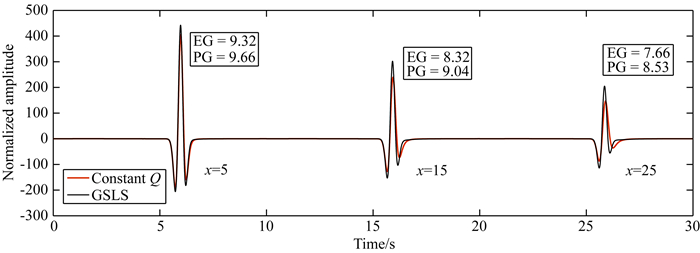
基于单个SLS拟合常Q阻尼介质本构，图 6给出了GSLS介质本构与常Q阻尼介质本构对应一维模型在x=5, 15, 25处的位移波形以及其对应的相位拟合度以及幅值拟合度.从图中可以看出波形包络误差，相位误差随波传播距离增加而逐渐增加.由(33)式可知，波形模拟精度受Q值拟合精度、波传播距离x、参考波速取值cref，模拟主频ωref的影响.基于大量分析、计算，在保证波形相位拟合度PG以及幅值拟合度EG均大于9的前提下，对模拟带宽取值为100，本文给出了不同Q值，x/λref取值下，SLS个数的优化取值建议表(见表 3).为保证模拟波形精度，与表 2不同，这里令PG与EG的取值均大于9，原因在于表 2大多应用于衡量波动反问题中波形拟合精度的衡量，考虑到反演问题的复杂性，Kristeková等(2009)相应地降低了对波形拟合度的要求，基于数值模拟实验结果，本文作者认为EG与PG均大于8且小于9情形，模拟波形与实测波形仍存在较大误差，这对于构建高精度波动正演问题数值模拟方案不适用.同时，考虑到在勘探地震波动数值模拟中模拟频带较窄这一特点，由上述分析可知，对于这一情形，在达到同等波形模拟精度的前提下，可减小SLS个数的取值.为此本文附录亦给出了模拟频带带宽取值为25和10的SLS个数优化取值建议表(附表 1, 2).另外，就滞弹性介质波动模拟而言，因其模拟误差既包含时域本构逼近引入的误差，同时存在数值离散引入的误差.因此在采用本文优化取值建议表时应保障数值离散的精度，即需要采用合理的空间及时间离散步长.

图 6 距源x=5、15、25处一维波动模型解析解.介质本构分别采用常Q阻尼本构(红线)和GSLS本构(黑线). 方框数值分别表示波形幅值拟合度(EG)以及波形相位拟合度(PG).模拟频带0.05~5 Hz, Q0=100 Fig. 6 The analytical wave solution of the one-dimensional wave model located at x=5, 15, 25. The red line and black line show respectively the waveforms obtained via using constant Q constitution and SLS constitution. The value of envelop goodness of fit and the phase goodness of fit are shown in the bracket. The frequency interval of 0.05~5 Hz and Q0=100 are considered
表 3 基于GSLS建立常Q滞弹性介质时域本构近似的SLS个数优化取值表，适用于模拟频带带宽小于或等于100情形 Table 3 For frequency bandwidth equals or less than 100, the suggested optimized value of SLS number when using GSLS for approximating constant Q constitution

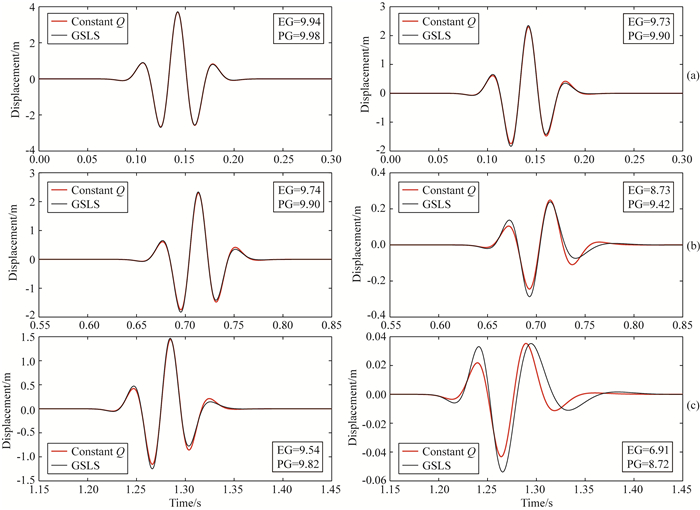
Zhu等(2013)建议采用单个SLS近似常Q时域本构以降低计算量及计算存储.基于全空间二维滞弹性声波模拟算例，通过比对不同接收点位移模拟波形与解析模型之间的相对误差，针对Q0=100以及Q0=20，作者基于算例验证了对于前者采用单个SLS近似阻尼介质时域本构能有效保障数值模拟精度.其数值模拟采用的模拟频带范围为5~125 Hz，ωref=25 Hz.激励源为中心频带等于16 Hz的四阶Ricker子波.参考波速cref=3.5 km·s-1，观测点距离源点位置分别为0.5 km，2.5 km，4.5 km.然而，基于表 3可知对Q0=100情形，由于观测点对应的无量纲值x/λref分别等于3.57, 12.8, 28.5，因此除第一个观测点外，采用单个SLS不能保证其余两个观测点的波形拟合精度.其原因在于作者采用了带宽极窄的四阶Ricker子波作为激励源，且源的中心频带低于参考频率，对于激励源频带较窄且主要位于参考频率附近的情形，基于峰值拟合方法建立常Q介质时域本构的单个SLS近似具有更高的精度.与Zhu等(2013)不同，本文对单个SLS的Q值逼近并没有采用峰值拟合方法，而是与GSLS参数非线性拟合方法一致，统一采用残差值最小方法.由上述讨论可知对模拟频带较窄情形，单个SLS即可实现对常Q介质时域本构的有效近似.为更清晰阐述这一问题，本文基于一维模型，激励源采用为中心频带等于16 Hz的四阶Ricker子波，分析距离源点0.5 km，2.5 km，4.5 km观测点上位移波形的拟合度(图 7)，结果表明对源激发频带较窄，且主频低于参考频率情形，基于单个SLS的峰值拟合方法可有效实现Q=100阻尼介质时域本构的近似.观测所得波形对应的PG以及幅值拟合度EG均大于9.0.但单个SLS对Q=20情形并不适用，由表 3可知，为保证第二、第三观测点的波形拟合精度，SLS个数应取为3，因此即便对源激发频带较窄，且主频低于参考频率情形单个SLS无法保证波形模拟精度要求.值得一提的是，本文在构建SLS个数优化取值建议表时，考虑了源主频设置的问题，并且将源主频设置在高于参考频率位置处，有效保障了整个模拟频带的模拟精度.

图 7 距源x=500 m(a)、2500 m(b)、4500 m(c)处一维波动模型解析解.介质本构分别采用常Q阻尼本构(红线)和GSLS本构(黑线).方框数值分别表示波形幅值拟合度(EG)以及波形相位拟合度(PG).模拟频带5~125 Hz, Q0=100(左栏), Q0=20(右栏) Fig. 7 The analytical wave solution of the one-dimensional wave model located at x=500 m (a), 2500 m (b), 4500 m (c). The red line and black line show respectively the waveforms obtained using constant Q constitution and SLS constitution. The value of envelop goodness of fit and the phase goodness of fit are shown in the bracket. The frequency interval of 0.05~5 Hz, Q0=100 (left) and Q0=20 (right) are considered
4 滞弹性介质波动数值模拟计算效率优化方案及其精度验证

滞弹性介质地震波动数值模拟常统一采用包含相同个数SLS的GSLS近似不同Q值阻尼介质的时域本构.若SLS个数参照低Q值介质时域本构近似所需SLS个数取值，则导致模拟计算量及计算存储的浪费.反之，若统一取为高Q值阻尼介质近似所需SLS个数，则将损失波形模拟精度.为此在保证模拟精度的前提下，本文提出采用基于包含不同个数SLS的GSLS近似不同Q值阻尼介质以降低计算量及计算存储，SLS个数参照优化取值表选取.下面基于数值算例验证该方法的精度.

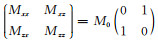
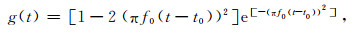
考虑二维水平层状介质模型.模型上覆沉积层介质参数为：密度ρ1=2000 kg·m-3，P波参考波速V1P= 1800 m·s-1，S波参考波速V1S=1040 m·s-1，膨胀模量品质因子Q1κ=12，剪切模量品质因子Q1μ=5，覆盖层厚度为1 km.下卧基岩半空间介质参数为：ρ2=2550 kg·m-3，V2P=4500 m·s-1，V2S=2630 m·s-1，Q2κ=680，Q2μ=263.二维剪切位错震源设置在垂直方向距离水平自由地表 5 km深度处，地震矩张量为，M0为地震矩，这里令其等于矩震级为3.3小震释放的地震矩，即1.0×1021 dyne·cm.震源时间函数为主频为1Hz的Ricker子波:

(35)

式中f0=1 Hz.基于人工边界截取有限计算区，为规避人工边界条件设置带来的精度问题.这里统一采用固定边界条件.分别在水平方向距震源左侧5 km，以及右侧45 km处设置垂直固定边界；在垂直方向下方距震源4 km设置水平固定边界截取有限计算区域.采用25节点正方形勒让德谱元对模型进行空间离散，单元长度为100 m：时间离散采用Newmark-Beta预估校正法(β=0, γ=1/2)，时间离散步长取为8×10-4s.基于勒让德谱元构建所得滞弹性介质波动数值模拟方案的详细过程见Savage等(2010).

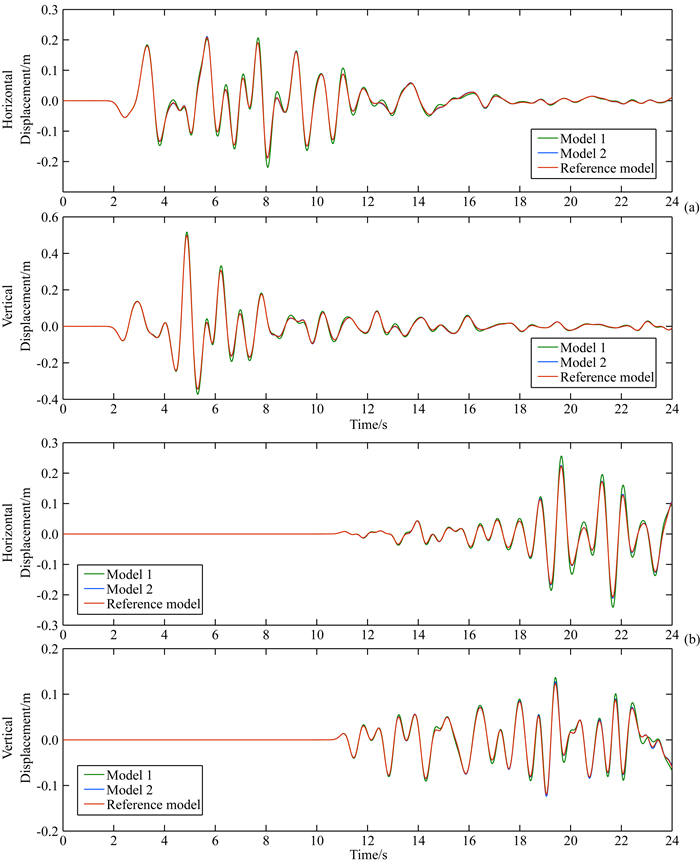
为保证波形模拟精度，考虑到直达波在上覆土层介质传播的最远直线距离约等于9 km，对应无量纲取值x/λref约为9.0 km/1.04 km≈8.7，依照表 3，对上覆土层阻尼介质时域本构包含3个SLS的GSLS近似.同样地，考虑到直达波下卧基岩传播的最远直线距离为45 km，对应无量纲值x/λref为45 km/2.63 km≈17.2，采用包含3个SLS的GSLS近似下卧基岩阻尼介质的时域本构(model 2).为对比分析，同时给出了统一采用2个(model 1)以及5个SLS (reference model)的GSLS近似阻尼介质时域本构的数值模拟结果，后者作为参考数值精确解.图 8给出了位于震源右侧，水平距离分别为0 km以及44 km处观测点水平向以及垂直向位移时程.基于波形时频拟合误差衡量准则，得到震源上方观测点水平位移分量对应的EG=9.25(9.90)，PG= 9.82(9.97)，垂直位移分量对应的EG=9.37(9.92)，PG=9.85(9.98).震源左侧观测点水平位移分量EG=8.59(9.82)，PG=9.79(9.98)，垂直位移分量对应EG=9.13(9.79)，PG=9.75(9.94).括号内、外分别为model 1和model 2模拟波形的时频拟合度分值.根据表 3可知，除model 1外，model 2和reference model均能满足整体波动数值模拟精度要求，图 8所示波形记录也佐证了这一结论.另外，垂直位移分量波形拟合度优于水平位移分量的原因是后者波形成分中P波占优的缘故.因此采用包含不同个数SLS的GSLS以近似不同Q值阻尼介质时域本构在有效降低滞弹性波动数值模拟计算量及计算存储的同时，保证了波动模拟的精度.

图 8 与震源水平距离分别为0 km (a)以及44 km (b)处观测点处水平向以及垂直向位移时程对比.红线为两层均采用包含5个SLS的GSLS近似滞弹性本构，绿线为两层介质均采用包含2个SLS的GSLS，蓝线为上层介质采用包含3个SLS的GSLS、下层介质采用包含2个SLS的GSLS，蓝线与红线基本完全重合 Fig. 8 Comparison of displacement time-history in horizontal and vertical orientation at the distance 0 km and 44 km from the source. Red and green lines show the displacement time-history which are obtained based on GSLS viscoelastic constitution using 2 and 5 SLS in two layers respectively, blue line is obtained based on GSLS viscoelastic constitution using 3 and 2 SLS in top and bottom layer respectively
5 结论

本文详细分析了基于GSLS建立常Q滞弹性阻尼介质本构近似的误差及其对时域波动数值模拟精度的影响.明确提出本构近似误差仅取决于频带宽度，与频带上下限取值无关这一概念.在此基础上，结合Kristeková等(2009)提出的波形拟合精度衡量准则，在保证波形时频模拟精度的前提下，考虑Q值、波传播距离、波速大小因素，给出了SLS个数的优化取值建议表.该表清楚揭示了对于Q值较小、波传播距离与感兴趣模拟波长比值较大情形均需增加SLS以提高精度.给出了基于不同SLS个数近似阻尼介质本构对应的适用范围.解释了Zhu等(2013)建议采用单个SLS近似常Q时域本构以降低计算量及计算存储这一手段的适用范围：该手段仅适用于波传播距离与感兴趣模拟波长较小，且激励源频带与单个SLS的Q值峰值所在频带基本重合情形.

针对滞弹性介质地震波动时域数值模拟，本文给出了一种提高计算效率以及降低计算存储的有效途径，即采用不同个数SLS的GSLS逼近不同Q值介质的时域本构，并基于数值验证了这一方法的精度.本文工作围绕各向同性常Q滞弹性阻尼介质波动数值模拟展开，但文中结果对各向异性常Q滞弹性阻尼介质波动数值模拟亦具有参考价值，有助于推进滞弹性介质波动数值模拟以及其在全波形反演问题中的进一步应用(Komatitsch et al., 2016).

在后续研究工作中，有必要深入研究阻尼介质本构逼近对滞弹性介质中非均匀波传播特性的影响.另外，在地震波动有限差分以及有限元波动数值模拟中引入伪谱模拟中对滞弹性阻尼本构的优化模拟方法(Zhu and Carcione, 2014)以进一步降低模拟计算量以及计算存储也值得深入研究.

附录A 一维滞弹性波动模型及其谐波解

一维情形下滞弹性时域、频域本构和波动方程可表示为

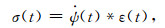
(A1)

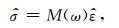
(A2)

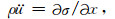
(A3)

基于频域分析，可得(A3)齐次谐波解

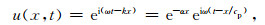
(A4)

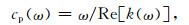
(A5)

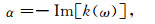
(A6)

式中.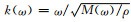

对常Q滞弹性介质, 应力松弛函数和复模量为(Kjartansson, 1979)

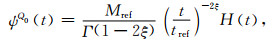
(A7)

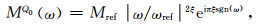
(A8)

Γ表示Gamma函数，tref=1/ωref，Mref为参考模量，ξ=tan-1(1/Q0)/π≈1/(πQ0)，sgn表示符号函数，ωref参考圆频率，Mref是参考模量，常Q滞弹性介质的品质因子与频率无关:

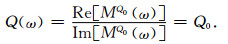
(A9)

谐波沿行进方向的衰减因子α以及其传播的相速度cp与频率相关：

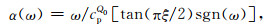
(A10)

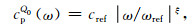
(A11)

cref为参考波速：.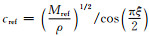

基于GSLS建立常Q阻尼介质本构近似，GSLS复模量式(10)，实部和虚部分别为

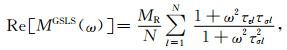
(A12)

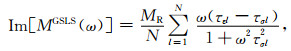
(A13)

根据复数运算法则和式(A4), 有

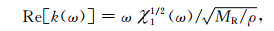
(A14)

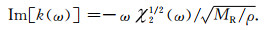
(A15)

可得采用GSLS时，一维波动模型谐波解的衰减因子αGSLS以及传播相速度的取值cpGSLS为

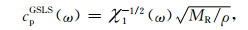
(A16)

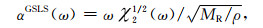
(A17)

其中

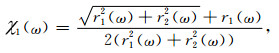
(A18)

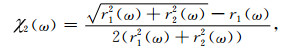
(A19)

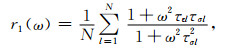
(A20)

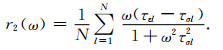
(A21)

附录B 模拟频带带宽为25及10情形, 标准线性体个数优化取值表
附表 1 基于GSLS建立常Q滞弹性介质时域本构近似的SLS个数优化取值表，适用于模拟频带带宽小于或等于25情形 AppendixTable 1 For frequency bandwidth equals or less than 25, the suggested optimized value of SLS number when using GSLS for approximating constant Q constitution
附表 2 基于GSLS建立常Q滞弹性介质时域本构近似的SLS个数优化取值表，适用于模拟频带带宽小于或等于10情形 AppendixTable 2 For frequency bandwidth equals or less than 10, the suggested optimized value of SLS number when using GSLS for approximating constant Q constitution
致谢  感谢匿名审稿专家对本文提出的宝贵意见.感谢南京航空航天大学陈少林教授对本文的仔细审阅.感谢廖振鹏研究员一直以来对作者工作的支持.
References
Aki K, Richards P G. 2002. Quantitative Seismology. California: University Science Books.
Blanc E, Komatitsch D, Chaljub E, et al. 2016. Highly accurate stability-preserving optimization of the Zener viscoelastic model, with application to wave propagation in the presence of strong attenuation. Geophysical Journal International, 205(1): 427-439.
Blanch J O, Robertsson J O A, Symes W W. 1995. Modeling of a constant Q:Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique. Geophysics, 60(1): 176-184. DOI:10.1190/1.1443744
Cao D P, Yin X Y. 2014. Equivalence relations of generalized rheological models for viscoelastic seismic-wave modeling. Bulletin of the Seismological Society of America, 104(1): 260-268. DOI:10.1785/0120130158
Carcione J M, Kosloff D, Kosloff R. 1988. Wave propagation simulation in a linear viscoelastic medium. Geophysical Journal International, 95(3): 597-611. DOI:10.1111/j.1365-246X.1988.tb06706.x
Day S M. 1998. Efficient simulation of constant Q using coarse-grained memory variables. Bulletin of the Seismological Society of America, 88(4): 1051-1062.
Emmerich H, Korn M. 1987. Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics, 52(9): 1252-1264. DOI:10.1190/1.1442386
Ge T S. 2000. Foundation of Solid Internal Friction Theory:Grain-Boundary Relaxation and Structure (in Chinese). Beijing: Science Press.
Graves R W, Day S M. 2003. Stability and accuracy analysis of coarse-grain viscoelastic simulations. Bulletin of the Seismological Society of America, 93(1): 283-300. DOI:10.1785/0120020094
Kjartansson E. 1979. Constant Q-wave propagation and attenuation. Journal of Geophysical Research:Solid Earth, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737
Komatitsch D, Xie Z N, Bozdaǧ E, et al. 2016. Anelastic sensitivity kernels with parsimonious storage for adjoint tomography and full waveform inversion. Geophysical Journal International, 206(3): 1467-1478. DOI:10.1093/gji/ggw224
Kristek J, Moczo P. 2003. Seismic-wave propagation in viscoelastic media with material discontinuities:A 3D fourth-order staggered-grid finite-difference modeling. Bulletin of the Seismological Society of America, 93(5): 2273-2280. DOI:10.1785/0120030023
Kristeková M, Kristek J, Moczo P. 2009. Time-frequency misfit and goodness-of-fit criteria for quantitative comparison of time signals. Geophysical Journal International, 178(2): 813-825. DOI:10.1111/gji.2009.178.issue-2
Liu H P, Anderson D L, Kanamori H. 1976. Velocity dispersion due to anelasticity; implications for seismology and mantle composition. Geophysical Journal International, 47(1): 41-58. DOI:10.1111/j.1365-246X.1976.tb01261.x
Ma S, Liu P. 2006. Modeling of the perfectly matched layer absorbing boundaries and intrinsic attenuation in explicit finite-element methods. Bulletin of the Seismological Society of America, 96(5): 1779-1794. DOI:10.1785/0120050219
Marcellini A, Tento A. 2011. Explosive sources prove the validity of homogeneous isotropic linear viscoelastic models. Bulletin of the Seismological Society of America, 101(4): 1576-1583. DOI:10.1785/0120100269
Moczo P, Kristek J. 2005. On the rheological models used for time-domain methods of seismic wave propagation. Geophysical Research Letters, 32(1): 1-5.
Olsen K B, Day S M, Bradley C R. 2003. Estimation of Q for long-period (> 2 sec) waves in the Los Angeles basin. Bulletin of the Seismological Society of America, 93(2): 627-638. DOI:10.1785/0120020135
Savage B, Komatitsch D, Tromp J. 2010. Effects of 3D attenuation on seismic wave amplitude and phase measurements. Bulletin of the Seismological Society of America, 100(3): 1241-1251. DOI:10.1785/0120090263
van Driel M, Nissen-Meyer T. 2014. Optimized viscoelastic wave propagation for weakly dissipative media. Geophysical Journal International, 199(2): 1078-1093. DOI:10.1093/gji/ggu314
Zhu T Y, Carcione J M, Harris J M. 2013. Approximating constant-Q seismic propagation in the time domain. Geophysical Prospecting, 61(5): 931-940. DOI:10.1111/gpr.2013.61.issue-5
Zhu T Y, Carcione J M. 2014. Theory and modelling of constant-Q P-and S-waves using fractional spatial derivatives. Geophysical Journal International, 196(3): 1787-1795. DOI:10.1093/gji/ggt483
Zhang L B, Wang H Z, Ma Z T. 2011. Analysis of absorption and dispersion characteristics of anelastic medium. Oil Geophysical Prospecting (in Chinese), 46(2): 252-258.
葛庭燧. 2000. 固体内耗理论基础:晶界弛豫与晶界结构. 北京: 科学出版社.
张立彬, 王华忠, 马在田. 2011. 非完全弹性介质的地震波吸收与频散问题研究. 石油地球物理勘探, 46(2): 252-258.