2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;
3. 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083
2. The Key Laboratory of Metallogenic Prediction of Nonferrous Metals of Ministry of Education, Central South University, Changsha 410083, China;
3. The Key Laboratory of Non-ferrous Resources and Geological Hazard Detection, Changsha 410083, China
勘探地球物理存在众多方法,如磁法、重力、地震、直流电及电磁勘探等(Dai et al., 2016; Ren et al., 2017a, 2017b, 2017c, 2018b; Chou and Chouteau, 2016; Attias et al., 2016), 人们常根据勘探需求选择不同的方法.直流电阻率法(Maillet, 1947)是一种可以有效探测地表浅部的电导率结构的地球物理探测方法,它利用地表观测的电势分布,反演地下结构的电导率分布(Pain et al., 2003; Greenhalgh et al., 2009).随着野外采集仪器的快速发展和数值算法及其理论的快速提高,高精度、高效地求解带地形复杂三维直流电阻率模型是目前研究的热点和难点.考虑地下介质各向异性会带来更多的计算参数(Yin, 2000),因此目前的正反演算法通常只考虑地下介质的电各向同性或者简化的电导率各向异性(Pain et al., 2003; Linde and Pedersen, 2004).然而即使最后反演得到的模型与野外数据完全吻合,也会隐含不能忽视的错误(Asten, 1974; Yin and Weidelt, 1999; Linde and Pedersen, 2004).当遇到具有层理面的岩石或者裂缝等具有方向依赖性(Greenhalgh, 2009)的物质结构时,直流电阻率模拟必须考虑地下电导率各向异性.
正演是反演的关键,首先,必须开发考虑地下电导率各向异性的高精度直流电阻率正演模拟算法.对于一些简单的各向异性模型,有学者计算了均匀半空间倾斜各向异性介质的解析解(Habberjam, 1975)以及各向异性层状介质的地电响应(Yin and Weidelt, 1999; Yin and Maurer, 2001; Wait, 1990; Li and Uren, 1997).然而对于复杂各向异性电导率模型时,我们只能寻求数值解法.目前主要有以下几种数值解法,分别是积分方程法(Li and Stagnitti, 2004; Li and Uren, 1999, Ren et al., 2014, 任政勇等, 2017d),有限差分法(Wang and Fang, 2001; Hou et al., 2006),谱元法(Zhou et al., 2009)和有限元法(Bibby, 1978; Li and Spitzer, 2005; Wang et al., 2013; 严波, 2013).如果考虑带地形复杂几何模型时,基于非结构化网格的有限元法成为最优化的选择,因此本文选择基于非结构化网格的有限元算法来处理任意起伏地形复杂直流电阻率问题(Li and Pek, 2008; Wang et al., 2013).
众所周知,源电极附近快速变化的电位导致源附近电位较大的数值误差.为了提高源附近场的精度,一般采用二次场的求解策略(Lowry et al., 1989).传统的二次场求解方法要求一次场满足背景模型的边值问题(Li and Spitzer, 2002; Blome et al., 2009; 徐世浙等, 1994).然而背景场带起伏地形时,一次场不存在解析解只能通过高阶有限元近似或其他需要付出较大计算成本的数值方法来计算(Rücker et al., 2006).本文基于Penz等(2013)从直流电阻率各向同性模型提出的概念,扩展到各向异性模型,利用均匀半空间各向异性模型的解析解(Li and Uren, 1997; Penz et al., 2013)作为一次场,建立了直流电阻率各向异性问题的“虚拟场边界值问题”,即有效地去除了源奇异性现象,也正确地处理了任意起伏地形情况,从而达到精度的最优化方案.
为了达到速度的最优化方案,我们采用了面向目标的自适应有限元算法来求解上述新的“虚拟场边界值问题”.求解上述“虚拟场边界值问题”,可采用基于先验信息的人工有限元网格加密算法(Li and Spitzer, 2002; Rücker et al., 2006)、基于后验误差估计的全局自适应有限元法(Babuška and Rheinboldt, 1979; Zienkiewicz, 2006; 胡恩球等, 1997; 王建华等, 2000)和面向目标的自适应有限元算法.对于复杂的模型,很难确定场变化剧烈程度等先验信息,从而难以设计出能够真实模拟复杂场变化的有限元网格,全局自适应有限元法(Franke et al, 2007; Ren and Tang, 2010; 任政勇和汤井田, 2009; 王飞燕, 2009)采用全局的后验误差估计算法(Ainsworth and Oden, 1997),即所有的网格单元误差具有相同的权重,来达到降低全局网格上平均数值误差的目的.对于直流电阻率勘探问题来说,我们既需要降低全局网格的数值误差,更需要测量电极处的数值解达到足够的精度.全局自适应有限元法所导致的全局网格再分配方案往往不能有效提供测点附近的数值解精度,并且存在浪费计算量的情况.面向目标的自适应有限元算法首次由Oden和Prudhomme提出(Oden and Prudhomme, 2001),通过增加测量区域的误差权重,从而达到大幅度提高测点处数值解精度的目的.由于其优越性,面向目标的自适应有限元算法在勘探地球物理领域得到越来越多的应用.Kerry和Weiss(2006)首先利用面向目标的自适应有限元算法解决了2D大地电磁问题.Li and Kerry(2007)利用面向目标的自适应有限元算法解决了2.5D可控源电磁问题.Ren等(2013)利用面向目标的自适应有限元算法解决了3D大地电磁问题.Ren和Tang(2014)利用面向目标的自适应有限元算法解决了3D直流电阻率各向同性问题.对于直流电阻率各向异性问题,目前最新的研究成果为Wang等(2013)利用基于非结构化网格的有限元算法,因此,本文提出的面向目标自适应有限元算法可被看作高精度求解直流电阻率各向异性问题的进一步延伸.
另外,本文的另一目的为测试基于电流密度法向分量的不连续性的后验误差估计算法求解稳态直流电阻率法的能力.后验误差估计算法是指导面向目标的自适应有限元网格自适应修正的关键.在电阻率不连续分界面上,电流密度法向分量呈连续状态,由于网格的不合理性,有限元算法计算出的电流密度法向分量在电阻率不连续分界面上一般呈不连续状态.在前期的大地电磁问题研究中,我们发现基于这一物理现象构建出的后验误差估计算法具有非常优良的性能,能够有效计算出有限元解的数值误差,从而驱动网格的自适应加密.这一研究发现,也被Yin等(2016)成功应用了航空电磁法的高精度计算,另外这一后验误差与其他种类后验误差的对比见我们最新的研究成果(Ren et al., 2018a).
本文从考虑电导率各向异性情况出发,建立了直流电阻率各向异性问题的“虚拟场边值问题”,利用基于电流密度法向分量的不连续性的后验误差估计算法,提出了可以大幅度提高数值解精度、大幅度减小计算消耗的面向目标的自适应有限元算法,利用非结构化网格和高效的并行线性方程组求解器Pardiso,成功地实现了带起伏地形复杂各向异性直流电阻率三维问题高精度、低计算消耗的求解目的.最后,三组电阻率各向异性模型验证了本文算法的正确性和适应性.
1 理论 1.1 电导率张量
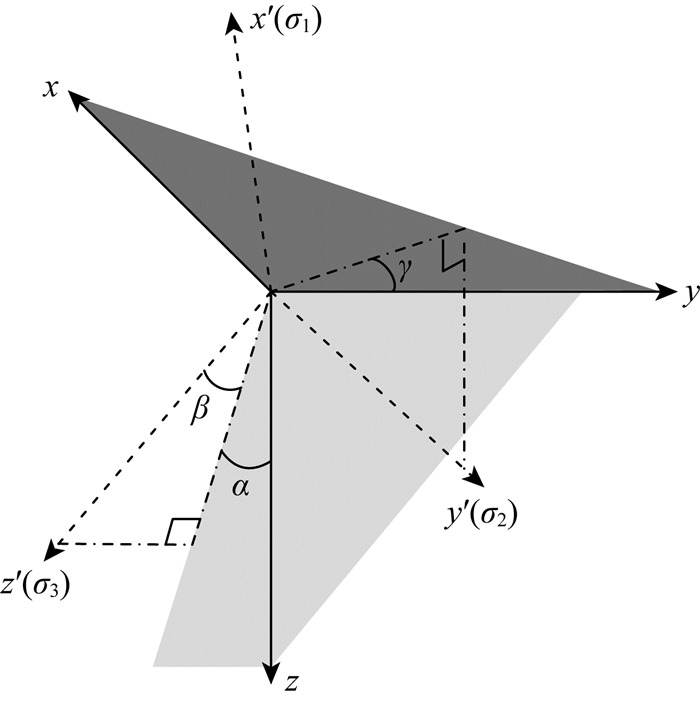
对于任意各向异性的地下介质,电导率σ是一个具有6个独立分量的张量,其为实对称正定矩阵(Yin, 2000),可以通过三次旋转变换转化为正对角矩阵.如图 1所示,x′, y′, z′表示主轴坐标系,对应岩石的自然结构,x, y, z为测量坐标系,表示测点的地理坐标.由测量坐标系变换到主轴坐标系共需要确定三个欧拉角(Yin, 2000;Greenhalgh, 2009;Zhou et al., 2009),首先固定x轴,以角α顺时针旋转平面(y, z),变换矩阵为


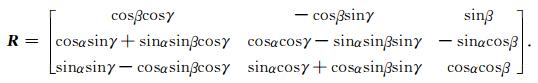
|
(1) |
|
图 1 各向异性电导率主轴坐标系和测量坐标系框架 Fig. 1 The measuring coordinate frame and principal axis frame of anisotropic conductivity |
由于电导率各向异性的存在,向地下供入电流之后电流密度的方向不再与电场强度的方向一致,但是在主轴坐标系下电流密度J′和电场强度E′方向相同:J′=σ′·E′.测量坐标系下电流密度J和电场强度E都可以通过主轴坐标系下的电流密度和电场强度变换得到:J=R·J′, E=R·E′.根据电流密度和电场强度的关系:J=σ·E可以得到电导率张量的表达式:

|
(2) |
式中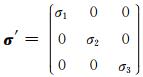
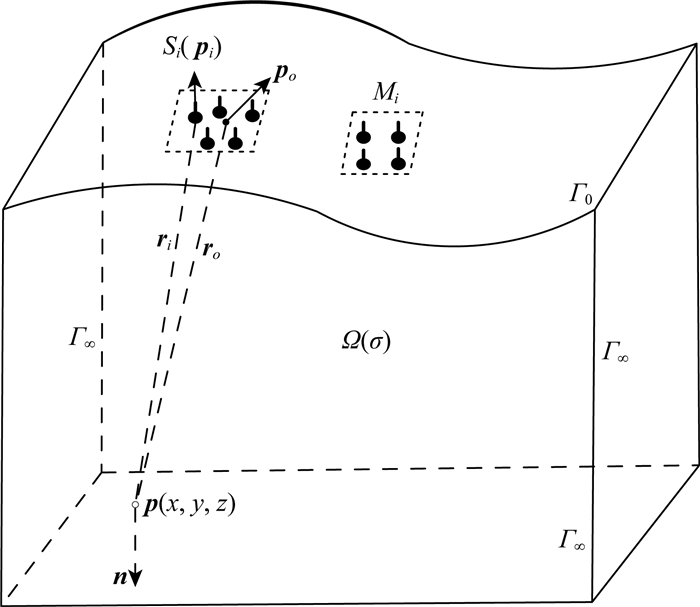
如图 2所示的模型,Γ0是地表面,Γ∞是无穷远边界,围绕封闭区域Ω.{Si}(i=1, 2, …, s)和{Mi}(i=1, 2, …, m)分别表示源电极群和测量电极群,在地表面Γ0上共布置s个源电极和m个测量电极,源电极Si的坐标是pi,点po是源电极群{Si}的中心;p, n分别表示边界上任一点及其对应的外法向向量,σ是地下介质的电导率张量,矢量ri和ro分别表示:ri=p-pi和ro=p-po.在Si处注入电流I,其引发电流密度Ji=J(x, y, z),基于全电流定律(Stratton, 2007),忽略位移电流,有:
|
图 2 带地形三维各向异性直流电阻率模型图 Fig. 2 3D anisotropic DC resistivity model with topography |
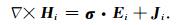
|
(3) |
对方程(3)两边取散度,结合电荷守恒定律的微分形式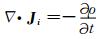

|
(4) |
由于源附近场变化迅速,直接求解总场会产生很大的数值误差,为了避免源的奇异性,我们采用特别的二次场法(Penz et al., 2013),其中一次场采用各向异性均匀半空间的解析解,我们将总场分解为
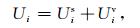
|
(5) |
式中Uis, Uiv分别表示一次奇异场和剩余的二次场.在平滑的地表Γ0,如果Si的邻域足够小,那么它可视作各向异性的均匀半空间,其电位解析解有以下形式(Li and Uren, 1997):
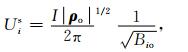
|
(6) |
式中Bio=riT·ρo·ri,ρo是源电极Si附近邻域的张量电阻率,如果邻域足够小,那么ρo可以假设为一个常张量,在实际计算中,将源电极邻域定义为一系列包含源电极Si的小区域,常电阻率张量作为该邻域的平均电阻率.此处对于源电极的位置不做任何限制,如果源位于带地形的地表,一次场采用源点处的切向平面往地下延伸构成的均匀半空间作为背景场.将总场减去邻域的一次奇异场,剩余的二次场因为不满足地表的齐次诺依曼条件被命名为二次虚拟场.
与总场类似,我们可以得到源电极Si产生的奇异场所满足的控制方程:
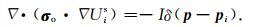
|
(7) |
将(7)式与(5)式代入方程(4)定义的总场满足的方程,我们可以得到虚拟电势满足的微分方程:

|
(8) |
源电极Si向地下供电时由于空气无穷大的电阻率,没有电流通过地表流到空气中,所以地表电位的诺依曼条件成立:
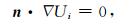
|
(9) |
式中n是由地表外法向向量.将(5)式代入(9)式,在地表Γ0,有

|
(10) |
在无穷远边界Γ∞上,地形以及不均匀电导体的影响可以忽略,参照各向异性均匀半空间的解析解(Li and Uren, 1997)及类比各向同性的情况(Dey and Morrison, 1979),假设位于平滑地表的点电源Si在无穷远边界Γ∞上产生的总场电位(Li and Uren, 1997)以如下的形式衰减:

|
(11) |
式中Bi=riT·ρ·ri,C是一个常数.结合总场的分解方程(5)和一次场的奇异解析式(6),我们得到位于边界Γ∞上关于虚拟场的混合边界条件:

|
(12) |
综上所述,关于源电极Si,对于二次虚拟场的边值问题如下所示:

|
(13) |
基于虚拟场的微分方程,由伽里金有限单元法(Zienkiewicz and Taylor, 2000),可得:

|
(14) |
式中T是一个测试函数,且T属于希尔伯特函数空间H1(Ω)(Brenner and Scott, 2007),该空间中函数及其梯度都是有限的,应用格林恒等式再代入边界条件(13)式,将虚拟场在各个单元上应用线性形函数插值(Jin, 2014),采用形函数作为测试函数T,且当点p位于无穷远边界Γ∞上,即距点源Si足够远时,ri≈ro,这样便可忽略单个源的特殊性,从而形成适用于多源系统的线性方程组(Ren and Tang, 2014):

|
(15) |
式中K是所有源共用的系数矩阵,Fi是只与源Si有关的右端项,他们都包含各个单元的面积分和体积分,我们使用开源代码(Si, 2015)将模型域剖分成Delaunay四面体网格,采用高斯积分规则(Zhu et al., 2005)计算各个积分项,最后使用基于Intel MKL的精确高效的直接LU求解器PARDISO(Schenk and Gärtner, 2004)求解大型稀疏矩阵线性方程组.K和Fi具体表达式如下:

|
(16) |
式中Bi=riT·ρ·ri & Bo=roT·ρ·ro.
1.3 面向目标的后验误差估计技术有限元初始网格并不能保证其数值解达到足够的精度,我们需要估计单元基本误差并对初始网格进行修正即自适应计算.目前自适应有限元方法中主要存在两类后验误差估计技术被广泛采用,分别是基于梯度恢复技术的后验误差估计方法和基于残差的后验误差估计方法(Ainsworth and Oden, 1997).残差型的后验误差估计技术利用局部区域的残值(Ainsworth and Oden, 1993)来估计后验误差,这里采用由于数值误差引起的边界条件的不连续性来估计单元的基本误差,这些数值误差来源于模型误差,网格离散误差,线性形函数插值误差等因素.在计算区域Ω上我们假定其中一个网格单元为Ωk,它的一个邻元为Ωkne,我们将Ωk和Ωkne上的电导率和电势分别用σ, Ui和σne, Uine标记.在他们的共面上,其上电流密度的不连续性可以表示如下(Stratton, 2007):
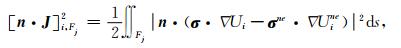
|
(17) |
式中[·]表示L2范数操作,n为由单元Ωk指向单元Ωkne的单位法向量,i表示源Si,Fj表示单元Ωk的第j个邻面,据此我们可以计算网格单元的基本残差Ek:
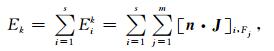
|
(18) |
式中s, m分别指代源的数量、单元Ωk邻面的个数.
式(18)对单元相对误差的计算属于全局型的误差估计,即所有网格单元的基本数值误差具有相同的误差权重,然而在测量剖面处通常需要获得更高的数值精度,即需要增加测量区域的误差权重.为了解决这一问题,应用面向目标的概念(Oden and Prudhomme, 2001),可由此导出面向目标的后验误差.
大型线性方程组(15)可以写成双线性形式:

|
(19) |
式中Uiv, T∈H1(Ω),H1(Ω)表示希尔伯特函数空间(Brenner and Scott, 2007),b(T, Uiv)表示未知项,S(T)表示源项,两者表达式如下:
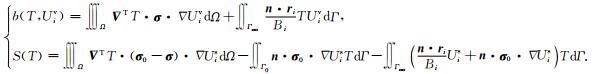
|
(20) |
通过构造虚拟场变分公式(19)的对偶问题可以得到影响函数W(Ren and Tang, 2014)的分布.应用对偶加权误差估计法(Oden and Prudhomme, 2001),为了构造式(19)的对偶变分,我们定义误差项E(eU)(Ren and Tang, 2014):
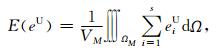
|
(21) |
式中eiU指代源Si产生的虚拟场有限元数值解的误差,E(eU)是虚拟电位总的数值误差项的函数,它衡量的是在子域集合ΩM内所有源产生的虚拟电位误差的平均值,在实际计算中我们将各个测点的邻域统称为子域集ΩM.将方程(19)中源项S(T)用误差项E(eU)替换,并基于偶函数b(, )的自我伴随特征(Ren et al., 2013),我们可以得到下面的变分形式:
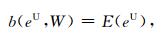
|
(22) |
式中W∈H1(Ω),W被称为影响函数(Oden and Prudhomme, 2001),它对产生面向目标的概念起着关键作用,(22)式可以写成矩阵形式:
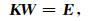
|
(23) |
所以影响函数W离散解与Uiv的有限元数值解具有相同的系数矩阵K,它的计算基于和Uiv相同的网格.
经过换算,影响函数的变分公式(22)对应的微分形式为

|
(24) |
由上式我们可以看出影响函数W具有满足地表齐次诺依曼边界条件的电位分布.对于单个源Si,如果考虑所有测量电极处的虚拟电位误差项,则是在所有测点所在的邻域中分别注入单位幅度电流I,在整个域Ω所产生的电位分布.将影响函数W分成数值解WFEM和误差项eW,基于方程(22),我们可计算测量剖面总的数值误差Θ为

|
(25) |
基于伽里金正交性(Brenner and Scott, 2007),忽略双线性形式b(, )(式(20))中的面积分项,有

|
(26) |
式中Θk用于衡量每个单元的基本误差,利用柯西不等式(Brenner and Scott, 2007; Ren et al., 2013),上式变为
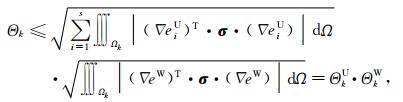
|
(27) |
式中ΘkU, ΘkW分别反映了虚拟场的误差和影响函数的误差,由式(24)我们意识到在测点区域附近影响函数的变化十分迅速,所以相对其他区域,测量剖面由于影响函数产生的误差ΘkW也会更大,这表明在考虑了全局数值误差ΘkU的基础上,使测量区域的单元基本误差在所有单元中占有更高的权重,从而有目的地加密测量电极处的网格,在后面的模型计算中我们将会佐证这一点.由于梯度误差ΔeiU和ΔeiW不容易获得,我们采用电流密度的法向分量残差的L2范数来替代相应的能量范数,即使用式(18)来分别估计虚拟场和影响函数场的电流密度法向分量残差,这种根据场的变化规律设置的后验误差估计将能更好地模拟物性界面.
为了实现特定单元的网格加密,我们定义一个单元相对误差指标(Ren and Tang, 2014):
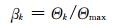
|
(28) |
式中Θmax是所有单元误差中的最大值,标记单元相对误差βk大于设定的阈值βs的网格单元,在下一次网格再生中进行加密,可以通过设置更小的阈值βs来增加每次网格修正的单元数以缩减算法的收敛时间.流程图 3给出了自适应算法(Ren and Tang, 2014)的具体实现.

|
图 3 网格自适应修正框架流程图 Fig. 3 The flow chart of adaptive mesh refinement procedure |
本文算法的终止条件包含总的单元数值误差阈值、最大允许迭代次数、最多未知数个数,我们通常使用后两者作为程序的终止条件.如果循环终止条件达到要求,获得基于最终网格的虚拟场,加上一次奇异场电位便可得到测量电极处的总场,然后可用于计算不同排列装置的标量视电阻率或张量视电阻率(Bibby, 1986;Bibby and Hohmann, 1993).
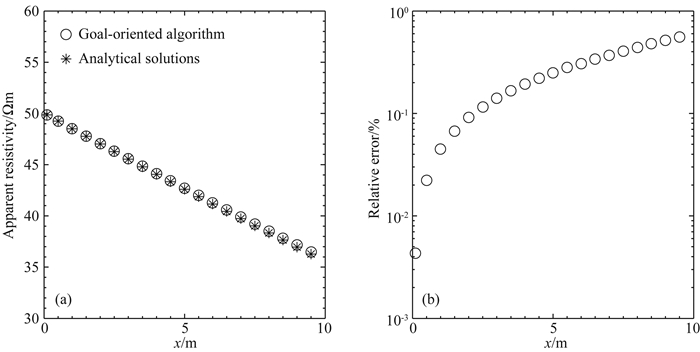
2 算例 2.1 代码验证本文算例的运行平台为:Intel(R) Core(TM) i5-4590 CPU @3.30GHz(4 cores)和8GB RAM.我们首先采用各向异性的两层模型(图 4)来验证代码的精度,两层介质具有相同的水平各向异性,源电极位于坐标原点,沿x轴正方向以间隔为0.5 m的间距布设20个测量电极,σ1表示第一层介质电导率张量的三个主轴电导率及三个旋转欧拉角:σ1:ρ1=100 Ωm, ρ2=ρ3=25 Ωm, α=0°, β=0°, γ=90°,σ2表示第二层介质的有关参数:σ2:ρ1=10 Ωm, ρ2=ρ3=2.5 Ωm,α=0°, β=0°, γ=90°.采用pole-pole装置,参照解析解(Wait, 1990),我们计算得到了测量剖面的视电阻率和相对误差曲线图,如图 5所示,本文算法计算的结果与解析解有极好的一致性,计算节点数为28373,最大误差小于0.556%.

|
图 4 两层各向异性模型示意图 Fig. 4 Illustration of two-layer anisotropic modle |
|
图 5 两层各向异性模型上面向目标自适应加密算法结果与解析解对比 Fig. 5 Comparison of the apparent resistivity computed by goal-oriented adaptive algorithm for two-layer anisotropic model against analytical solution |
下面我们将使用山脉峡谷模型证明本算法对于带地形各向异性模型的有效性,如图 6所示,该模型为均匀半空间中嵌入一个带地形的倾斜各向异性(Li and Spitzer, 2005)的异常体,其中山脉和峡谷的最大地形都为10 m且关于顶点对称,我们将源电极布于A处,沿x轴正方向以间距10 m布设19个测量电极经过山顶和谷底,异常体的电阻率为倾斜各向异性,电导率相关参数见图 6,均匀半空间的背景电阻率为100 Ωm.

|
图 6 山脉峡谷模型示意图 Fig. 6 Illustration of mountain-valley model |
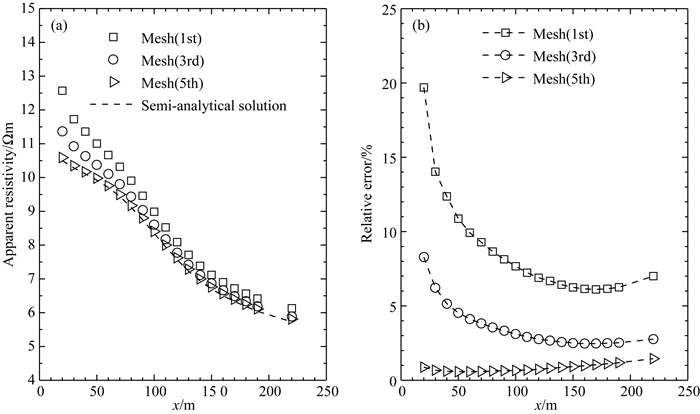
图 7测试了面向目标自适应算法的收敛性,计算了其三次网格的视电阻率和相对误差曲线,因为该模型没有解析解,所以采用全局网格同等加密的方式加密至网格节点数达到11037605的数值解作为拟解析解(Ren et al., 2013).图 7可以看出视电阻率曲线向准解析解迭代收敛.表 1是三次网格水平的单元参数及统计误差,经过四次迭代,视电阻率的最大相对误差从8.72%极大地减少到了0.82%,表明本文提出的算法可以有效处理地形,非结构化网格可以很好地自适应拟合地形的变化.
|
图 7 山脉峡谷模型上不同迭代网格沿测线上的视电阻率收敛情况及相对误差曲线 Fig. 7 Convergence of apparent resistivity and relative error curves along survey profile computed on different mesh levels for mountain-valley model |
|
|
表 1 山脉峡谷模型三次网格参数对比 Table 1 Mesh parameters of three mesh levels for mountain-valley model |
图 8(a)、(b)是初始网格和第五次网格的相对单元误差βk的网格等值线图,具体视角是做y=50 m的切片后将(y, z)平面旋转一定角度.图 8a中源电极附近单元相对误差值较大,表明该区域需要加密,所以在图 8b中得到了细密的剖分,从而消除了源附近的奇异性.图 8b中山脉和峡谷处以及电导率的分界面上都具有稠密的网格密度,而在远离异常体的区域则网格较为稀疏.山脉峡谷地形起伏大需要极小的网格单元才可以精确地拟合,电导率分界面上由于急剧变化的场导致电流密度法向分量的数值误差相对更大,因此这些区域会得到重点加密,其他区域较为稀疏的网格密度下线性插值已经可以模拟出场的变化趋势.此外,图中测点周围得到了细密的网格剖分,这将极大地改善数值解.因为网格单元加密到一定的程度时,测量剖面的精度严重依赖于局部的网格密度(Brenner and Scott, 2007),所以面向目标的算法可以通过加密测点局部区域从而实现高精度的收敛性.
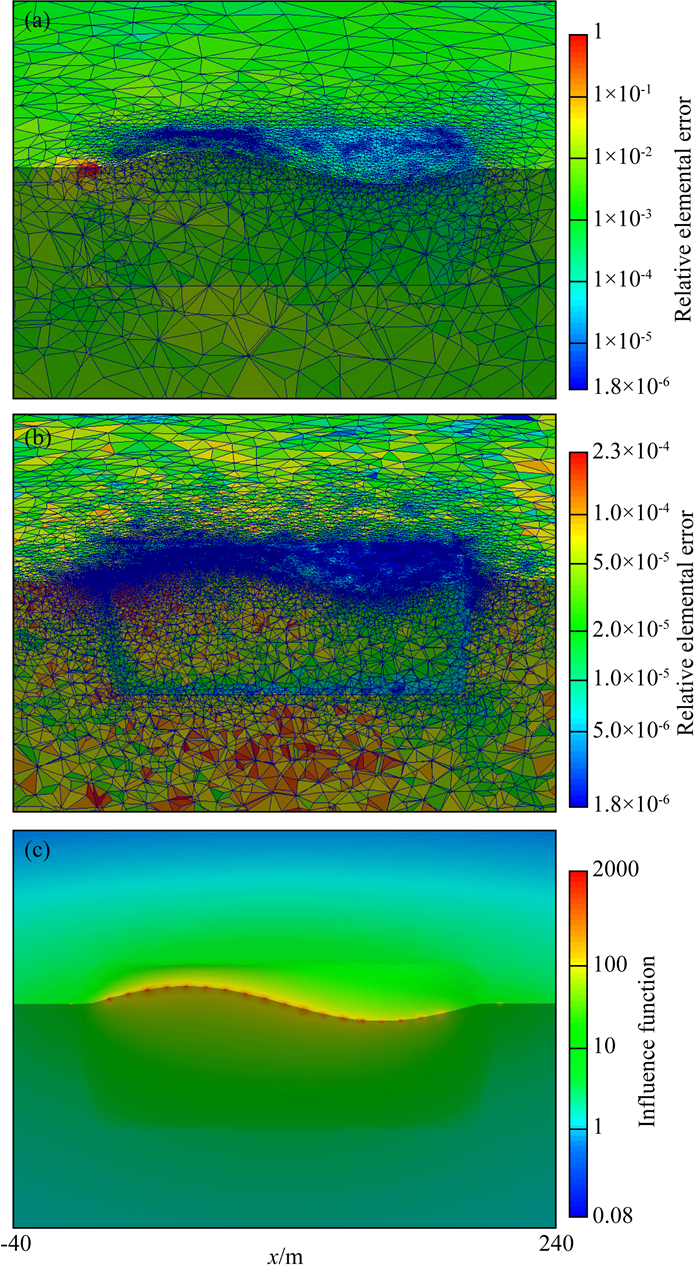
|
图 8 山脉峡谷模型自适应加密网格(第一次网格(a), 第五次网格(b))上单元相对误差分布图,第五次网格影响函数W的分布图(c) Fig. 8 Adaptive refining mesh of relative elemental error for mountain-valley model(the first mesh (a), the fifth mesh (b)), the distribution of influence function W based on the fifth mesh |
图 8c是由基于第五次网格计算得到的影响函数W的网格密度分布,由于其服从地表齐次诺依曼边界条件的电位分布(见方程(24)),所以在图中测量剖面上测点处出现红色的亮点,这表明了由对偶变分构造的虚拟源的存在,因而可以产生在测点附近着重加密的面向目标效应.
2.3 埋藏多个各向异性的立方块最后我们简要分析一下地下埋藏多个各向异性异常体的情况.如图 9所示,均匀半空间中嵌入四个埋深和尺寸相同的立方块A、B、C、D,其中心埋深和尺寸均为3 m,为了排除异常体的特征随源取向的影响,采用两对偶极源S1-S2, S3-S4用于张量视电阻率的测量(Bibby, 1986; Bibby and Hohmann, 1993).如图 10所示,首先通过偶极子S1-S2测量测点P处的电场分量E11, E12,然后测量偶极子S3-S4产生的电场分量E21, E22.根据电场与电流密度的关系:E=ρ·J,即:
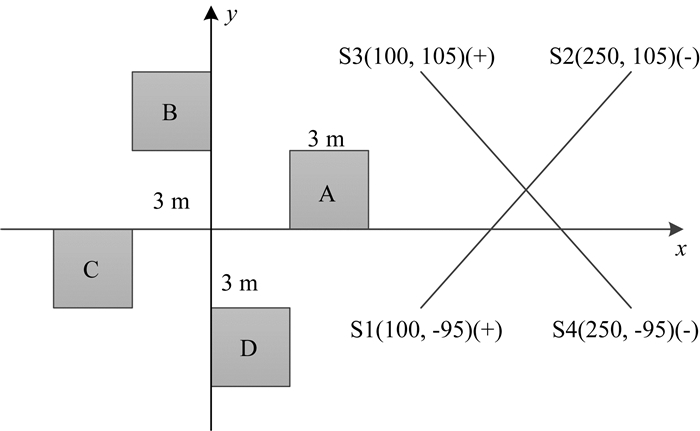
|
图 9 张量视电阻率测量 Fig. 9 Measurement of tensor apparent resistivity |
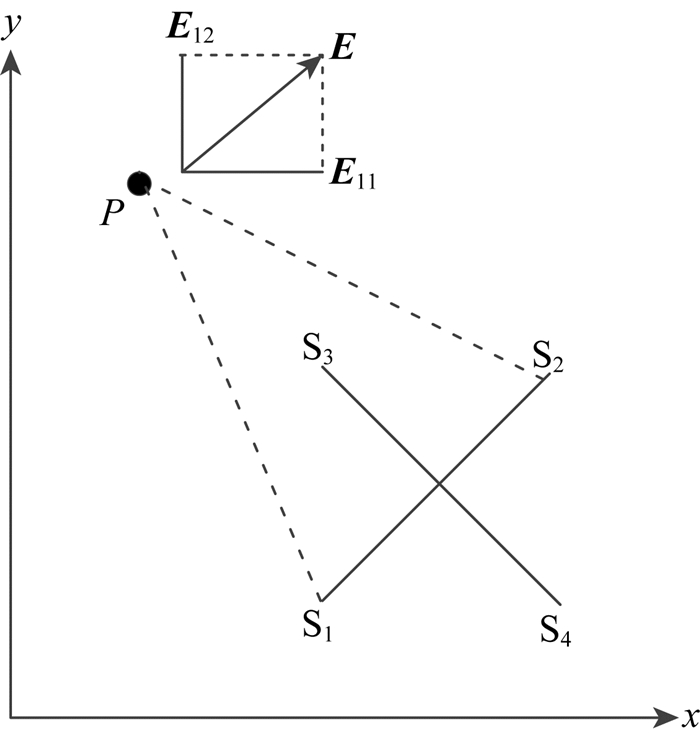
|
图 10 双偶极子源测量装置(Bibby,1986) Fig. 10 The measurement of double bipole source |

|
(29) |
式中J11, J12和J21, J22分别是各向同性的均匀半空间中偶极子S1-S2和S3-S4产生的电流密度分布.由式(29)我们可以得到P2旋转不变量(Bibby and Hohmann, 1993; Li and Spitzer, 2005; Wang et al., 2013)的表达式:
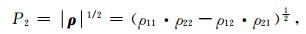
|
(30) |
P2不变量具有与标量视电阻率相同的量纲,各向同性均匀半空间下两者等效(Wang et al., 2013).
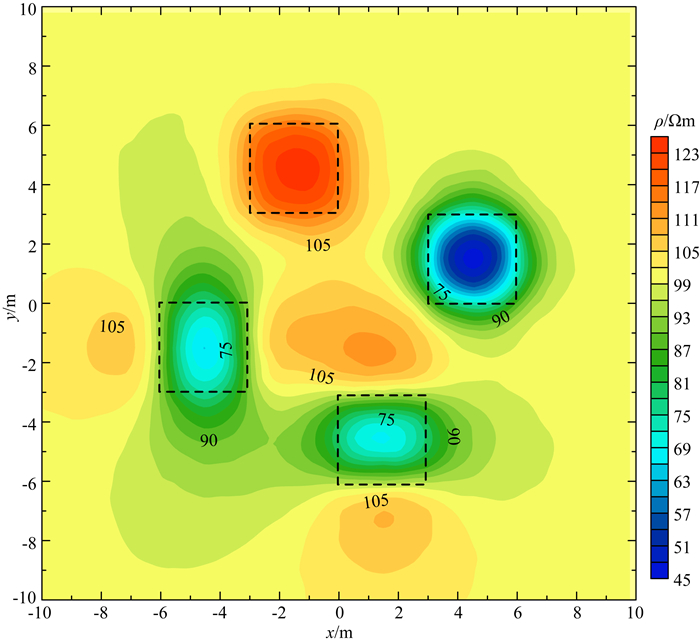
图 11中展示了P2不变量的地表等值线图,黑色的虚线框是立方块在地表的投影,背景均匀半空间的电阻率为100 Ωm,图中四个立方块异常体的电阻率相关参数分别为:A:10、B:1000、C:ρ1/ρ2/ρ3=10/100/10, α/β/γ=0°/0°/0°、D:ρ1/ρ2/ρ3=10/100/10,α/β/γ=0°/0°/90°.立方块A,B分别是各向同性的低阻和高阻异常体,在图中得到了较为准确的响应,立方块的中心位置和大概范围都得到了很好的刻画,C, D表示方位角γ相差90°的水平各向异性立方块,在图中立方块C和D都得到了一定程度的对称拉伸,两者拉伸的方向与主轴电阻率的大小及方位角γ有关,立方块C拉伸较大的方向为其垂直层理面的方向,相对应的横向电阻率相对于高阻背景电性差异较小,从而使得该方向电流密度较大,而立方块D为C旋转90°的方向,故其拉伸方向也相差90°,这也是各向异性悖论的体现(李金铭,2005).此时立方块C,D的中心位置仍然得到了准确的反映,但在两个低阻的各向异性立方块之间存在相对高阻的假异常.
|
图 11 A和B为各向同性,C和D为各向异性情况下的张量视电阻率的P2旋转不变量等值线图 Fig. 11 P2 rotation variable contour lines of tensor apparent resistivity with A and B of isotropy, C and D of anisotropy |
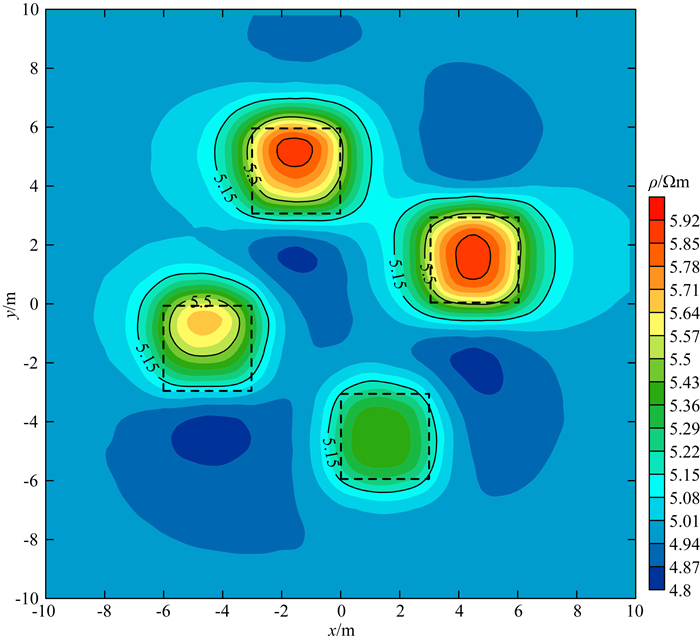
图 12则是四个不同倾斜各向异性立方块的P2不变量响应,背景均匀半空间的电阻率为5 Ωm,四个立方块具有相同的主轴电阻率:ρ1/ρ2/ρ3=10/100/10,倾角不同:A:α/β/γ=0°/0°/0°,B:α/β/γ=30°/0°/0°,C:α/β/γ=60°/0°/0°,D:α/β/γ=90°/0°/0°.总的来看,随着倾角增大,各个立方块的等值线拉伸幅度逐渐减少,且逐渐呈现为更加低阻的异常.立方块A倾角为0°,此时对应水平各向异性,在图中表现为对称的拉伸椭圆,由于立方块A的纵向电阻率与低阻背景的电性差异相对较小使得该方向的电流密度分布更为密集,所以其拉伸方向为平行层理面的方向.随着倾角增大至30°,立方块B呈现不对称的拉伸,拉伸方向与A相同,此时异常的中心偏移了立方块的投影中心.倾角继续增大至60°,立方块C也呈现不对称的拉伸,但拉伸幅度有所减少,当倾角达到90°时,D立方块的P2等值线表现为无拉伸的圆形异常,且其中心与立方块的投影中心吻合,此时倾斜各向异性已经转化为垂直各向异性,在地表水平方向不能检测到各向异性.
|
图 12 A, B, C, D均为各向异性情况下的张量视电阻率的P2旋转不变量等值线图 Fig. 12 P2 rotation variable contour lines of tensor apparent resistivity with A, B, C and D of anisotropy |
由上述复杂模型可知,地下电阻率各向异性介质在直流电阻率法野外观测数据中具有不可忽略的反映,不同的各向异性排列方式会产生不同幅度的地表响应.但是,目前仍缺乏一种从观测数据中判断地下各向异性的有效方案,这一问题需要进一步深入研究.
3 结论本文提出的基于非结构化网格的面向目标的自适应有限元算法,可以处理带起伏地形的任意复杂三维直流电阻率问题.不同于传统的二次场法,本文的一次场采用各向异性均匀半空间的解析解,减去这个简单的一次奇异背景场,可导出满足带任意地形的二次虚拟场的边值问题,在两层模型中验证了算法的高精度以及在山脉峡谷模型中证明了算法对地形的有效性.
通过估计电流密度法向分量的不连续性作为后验误差,可以很好地指导非结构化网格自动加密以适应物性界面场的急剧变化.结合面向目标的概念,使算法在考虑全局数值误差的基础上着重加密测点区域,可以实现测量剖面更高效地达到收敛精度,极大地节约了计算成本.
在对于产生面向目标特性起到关键作用的影响函数的网格密度分布图中(图 8c),当测点离源电极的距离逐渐加大时,由对偶变分(Oden and Prudhomme, 2001)构造的虚拟源的特性逐渐减弱,即在远离源的测点处的局部加密能力得到削弱.我们可以考虑关于距离的加权因子,以提升远点的面向目标特性,为大范围的电法勘探提供高精度的数值解,这需要进一步的研究与测试.
致谢感谢Mark Blome博士构建了最初的山脉峡谷模型.
Ainsworth M, Oden J T.
1993. A unified approach to a posteriori error estimation using element residual methods. Numerische Mathematik, 65(1): 23-50.
DOI:10.1007/BF01385738 |
|
Ainsworth M, Oden J T.
1997. A posteriori error estimation in finite element analysis. Computer Methods in Applied Mechanics and Engineering, 142(1-2): 1-88.
DOI:10.1016/S0045-7825(96)01107-3 |
|
Asten M W.
1974. The influence of electrical anisotropy on mise a la masse surveys. Geophysical Prospecting, 22(2): 238-245.
DOI:10.1111/gpr.1974.22.issue-2 |
|
Attias E, Weitemeyer K, Minshull T A, et al.
2016. Controlled-source electromagnetic and seismic delineation of subseafloor fluid flow structures in a gas hydrate province, offshore Norway. Geophysical Journal International, 206(2): 1093-1110.
DOI:10.1093/gji/ggw188 |
|
Babuška I, Rheinboldt W C.
1979. Adaptive approaches and reliability estimations in finite element analysis. Computer Methods in Applied Mechanics and Engineering, 17-18: 519-540.
DOI:10.1016/0045-7825(79)90042-2 |
|
Bibby H M.
1978. Direct current resistivity modeling for axially symmetric bodies using the finite element method. Geophysics, 43(3): 550-562.
DOI:10.1190/1.1440836 |
|
Bibby H M.
1986. Analysis of multiple-source bipole-quadripole resistivity surveys using the apparent resistivity tensor. Geophysics, 51(4): 972-983.
DOI:10.1190/1.1442155 |
|
Bibby H M, Hohmann G W.
1993. Three-dimensional interpretation of multiple-source bipole-dipole resistivity data using the apparent resistivity tensor. Geophysical prospecting, 41(6): 697-723.
DOI:10.1111/gpr.1993.41.issue-6 |
|
Blome M, Maurer H R, Schmidt K.
2009. Advances in three-dimensional geoelectric forward solver techniques. Geophysical Journal International, 176(3): 740-752.
DOI:10.1111/gji.2009.176.issue-3 |
|
Brenner S, Scott R. 2007. The Mathematical Theory of Finite Element Methods. Dordrecht:Springer.
|
|
Chou T K, Chouteau M, Dubé J S.
2016. Intelligent meshing technique for 2D resistivity inverse problems. Geophysics, 81(4): IM45-IM56.
DOI:10.1190/geo2015-0177.1 |
|
Dai R H, Zhang F C, Liu H Q.
2016. Seismic inversion based on proximal objective function optimization algorithm. Geophysics, 81(5): R237-R246.
DOI:10.1190/geo2014-0590.1 |
|
Dey A, Morrison H F.
1979. Resistivity modeling for arbitrarily shaped three-dimensional structures. Geophysics, 44(4): 753-780.
DOI:10.1190/1.1440975 |
|
Franke A, Börner R U, Spitzer K.
2007. Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography. Geophysical Journal International, 171(1): 71-86.
DOI:10.1111/gji.2007.171.issue-1 |
|
Greenhalgh M S. 2009. DC resistivity modelling and sensitivity analysis in anisotropic media[Ph. D. thesis]. Adelaide:The University of Adelaide.
|
|
Greenhalgh S, Zhou B, Greenhalgh M, et al.
2009. Explicit expression s for the Fréchet derivatives in 3D anisotropic resistivity inversion. Geophysics, 74(3): F31-F43.
DOI:10.1190/1.3111114 |
|
Habberjam G M.
1975. Apparent resistivity, anisotropy and strike measurements. Geophysical Prospecting, 23(2): 211-247.
DOI:10.1111/gpr.1975.23.issue-2 |
|
Hou J S, Mallan R K, Torres-Verdín C.
2006. Finite-difference simulation of borehole EM measurements in 3D anisotropic media using coupled scalar-vector potentials. Geophysics, 71(5): G225-G233.
DOI:10.1190/1.2245467 |
|
Hu Q E, Chen X Z, Zhou K D.
1997. A new posterior error estimate and adaptivity approach for electromagnetic field finite element computations. Proceedings of the CSEE, 17(2): 78-83.
|
|
Jin J M. 2014.
The Finite Element Method in Electromagnetics. New York: John Wiley & Sons.
|
|
Key K, Weiss C.
2006. Adaptive finite-element modeling using unstructured grids:The 2D magnetotelluric example. Geophysics, 71(6): G291-G299.
DOI:10.1190/1.2348091 |
|
Li J M. 2005.
Geoelectric Field and Electrical Exploration. Beijing: Geological Publishing House.
|
|
Li P, Uren N F.
1997. Analytical solution for the point source potential in an anisotropic 3-D half-space I:two-horizontal-layer case. Mathematical and Computer Modelling, 26(5): 9-27.
DOI:10.1016/S0895-7177(97)00155-6 |
|
Li P, Uren N F.
1999. The modelling of direct current electric potential in an arbitrarily anisotropic half-space containing a conductive 3-D body. Journal of Applied Geophysics, 38(1): 57-76.
|
|
Li P, Stagnitti F.
2004. Direct current electric potential in an anisotropic half-space with vertical contact containing a conductive 3D body. Mathematical Problems in Engineering, 2004: 63-77.
DOI:10.1155/S1024123X04201016 |
|
Li Y G, Spitzer K.
2002. Three-dimensional DC resistivity forward modelling using finite elements in comparison with finite-difference solutions. Geophysical Journal International, 151(3): 924-934.
DOI:10.1046/j.1365-246X.2002.01819.x |
|
Li Y G, Spitzer K.
2005. Finite element resistivity modelling for three-dimensional structures with arbitrary anisotropy. Physics of the Earth and Planetary Interiors, 150(1-3): 15-27.
DOI:10.1016/j.pepi.2004.08.014 |
|
Li Y G, Key K.
2007. 2D marine controlled-source electromagnetic modeling:Part 1-An adaptive finite-element algorithm. Geophysics, 72(2): WA51-WA62.
DOI:10.1190/1.2432262 |
|
Li Y G, Pek J.
2008. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media. Geophysical Journal International, 175(3): 942-954.
DOI:10.1111/gji.2008.175.issue-3 |
|
Linde N, Pedersen L B.
2004. Evidence of electrical anisotropy in limestone formations using the RMT technique. Geophysics, 69(4): 909-916.
DOI:10.1190/1.1778234 |
|
Lowry T, Allen M, Shive P N.
1989. Singularity removal:A refinement of resistivity modeling techniques. Geophysics, 54(6): 766-774.
DOI:10.1190/1.1442704 |
|
Maillet R.
1947. The fundamental equations of electrical prospecting. Geophysics, 12(4): 529-556.
DOI:10.1190/1.1437342 |
|
Oden J T, Prudhomme S.
2001. Goal-oriented error estimation and adaptivity for the finite element method. Computers & Mathematics with Applications, 41(5-6): 735-756.
|
|
Pain C C, Herwanger J V, Saunders J H, et al.
2003. Anisotropic resistivity inversion. Inverse Problems, 19(5): 1081-1111.
DOI:10.1088/0266-5611/19/5/306 |
|
Penz S, Chauris H, Donno D, et al.
2013. Resistivity modelling with topography. Geophysical Journal International, 194(3): 1486-1497.
DOI:10.1093/gji/ggt169 |
|
Rücker C, Günther T, Spitzer K.
2006. Three-dimensional modelling and inversion of dc resistivity data incorporating topography-I. Modelling. Geophysical Journal International, 166(2): 495-505.
DOI:10.1111/gji.2006.166.issue-2 |
|
Ren Z Y, Tang J T.
2009. Finite element modeling of 3-D DC resistivity using locally refined unstructured meshes. Chinese Journal of Geophysics, 52(10): 2627-2634.
|
|
Ren Z Y, Tang J T.
2010. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method. Geophysics, 75(1): H7-H17.
DOI:10.1190/1.3298690 |
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al.
2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718.
DOI:10.1093/gji/ggt154 |
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al.
2014. A hybrid boundary element-finite element approach to modeling plane wave 3D electromagnetic induction responses in the Earth. Journal of Computational Physics, 258: 705-717.
DOI:10.1016/j.jcp.2013.11.004 |
|
Ren Z Y, Tang J T.
2014. A goal-oriented adaptive finite-element approach for multi-electrode resistivity system. Geophysical Journal International, 199(1): 136-145.
DOI:10.1093/gji/ggu245 |
|
Ren Z Y, Chen C J, Tang J T, et al.
2017d. A new integral equation approach for 3D magnetotelluric modeling. Chinese Journal of Geophysics, 60(11): 4506-4515.
DOI:10.6038/cjg20171134 |
|
Ren Z Y, Qiu L W, Tang J T, et al.
2018a. 3-D direct current resistivity anisotropic modelling by goal-oriented adaptive finite element methods. Geophysical Journal International, 212(1): 76-87.
DOI:10.1093/gji/ggx256 |
|
Ren Z Y, Chen C J, Pan K J, et al.
2017a. Gravity Anomalies of Arbitrary 3D Polyhedral Bodies with Horizontal and Vertical Mass Contrasts. Surveys in Geophysics, 38(2): 479-502.
DOI:10.1007/s10712-016-9395-x |
|
Ren Z Y, Tang J T, Kalscheuer T, et al.
2017b. Fast 3D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multi-level fast multipole method. Journal of Geophysical Research:Solid Earth, 122(1): 79-109.
DOI:10.1002/2016JB012987 |
|
Ren Z Y, Chen C J, Tang J T, et al.
2017c. Closed-form formula for full magnetic gradient tensor of a homogeneous polyhedral body:a tetrahedral grid example. Geophysics, 82(6): WB21-WB28.
DOI:10.1190/geo2016-0470.1 |
|
Ren Z Y, Zhong Y Y, Chen C J, et al.
2018b. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics, 83(1): G1-G13.
DOI:10.1190/geo2017-0219.1 |
|
Schenk O, Gärtner K.
2004. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Generation Computer Systems, 20(3): 475-487.
DOI:10.1016/j.future.2003.07.011 |
|
Si H.
2015. TetGen, a delaunay-based quality tetrahedral mesh generator. Acm Transactions on Mathematical Software, 41(2): 1-36.
|
|
Stratton J A. 2007.
Electromagnetic Theory. New York: John Wiley & Sons.
|
|
Wait J R.
1990. Current flow into a three-dimensionally anisotropic conductor. Radio Science, 25(5): 689-694.
DOI:10.1029/RS025i005p00689 |
|
Wang F Y. 2009. 2.5D DC resistivity modeling by the adaptive finite-element method with unstructured triangulation[Master's thesis] (in Chinese). Changsha:Central South University.
|
|
Wang J H, Yang L, Shen W P.
2000. Advances of posteriori error estimation for FEM. Advances in Mechanics, 30(2): 175-190.
|
|
Wang T, Fang S.
2001. 3-D electromagnetic anisotropy modeling using finite differences. Geophysics, 66(5): 1386-1398.
DOI:10.1190/1.1486779 |
|
Wang W, Wu X P, Spitzer K.
2013. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids. Geophysical Journal International, 193(2): 734-746.
DOI:10.1093/gji/ggs124 |
|
Xu S Z, Liu B, Ruan B Y.
1994. The finite element method for solving anomalous potential for resistivity surveys. Chinese Journal of Geophysics, 37(2): 511-515.
|
|
Yan B. 2013. 2.5D DC resistivity numerical modeling by adaptive finite-element method[Master's thesis] (in Chinese). Qingdao:Chinese Marine University.
|
|
Yin C C, Weidelt P.
1999. Geoelectrical fields in a layered earth with arbitrary anisotropy. Geophysics, 64(2): 426-434.
DOI:10.1190/1.1444547 |
|
Yin C C.
2000. Geoelectrical inversion for a one-dimensional anisotropic model and inherent non-uniqueness. Geophysical Journal International, 140(1): 11-23.
DOI:10.1046/j.1365-246x.2000.00974.x |
|
Yin C C, Maurer H M.
2001. Electromagnetic induction in a layered earth with arbitrary anisotropy. Geophysics, 66(5): 1405-1416.
DOI:10.1190/1.1487086 |
|
Yin C C, Zhang B, Liu Y H, et al.
2016. A goal-oriented adaptive finite-element method for 3D scattered airborne electromagnetic method modeling. Geophysics, 81(5): E337-E346.
DOI:10.1190/geo2015-0580.1 |
|
Zhou B, Greenhalgh M, Greenhalgh S A.
2009. 2. 5-D/3-D resistivity modelling in anisotropic media using Gaussian quadrature grids. Geophysical Journal International, 176(1): 63-80.
|
|
Zhu J, Taylor Z, Zienkiewicz O. 2005.
The Finite Element Method:Its Basis and Fundamentals. Burlington, VT: Butterworth-Heinemann.
|
|
Zienkiewicz O C, Taylor R L. 2000.
The Finite Element Method:Solid Mechanics. Oxford: Butterworth-Heinemann.
|
|
Zienkiewicz O C.
2006. The background of error estimation and adaptivity in finite element computations. Computer Methods in Applied Mechanics and Engineering, 195(4-6): 207-213.
DOI:10.1016/j.cma.2004.07.053 |
|
胡恩球, 陈贤珍, 周克定.
1997. 电磁场有限元计算后验误差估计与自适应新方法. 中国电机工程学报, 17(2): 78–83.
|
|
李金铭. 2005.
地电场与电法勘探. 北京: 地质出版社.
|
|
任政勇, 汤井田.
2009. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟. 地球物理学报, 52(10): 2627–2634.
DOI:10.3969/j.issn.0001-5733.2009.10.023 |
|
任政勇, 陈超健, 汤井田, 等.
2017d. 一种新的三维大地电磁积分方程正演方法. 地球物理学报, 60(11): 4506–4515.
DOI:10.6038/cjg20171134 |
|
王飞燕. 2009. 基于非结构化网格的2. 5-D直流电阻率法自适应有限元数值模拟[硕士论文]. 长沙: 中南大学.
|
|
王建华, 杨磊, 沈为平.
2000. 有限元后验误差估计方法的研究进展. 力学进展, 30(2): 175–190.
DOI:10.6052/1000-0992-2000-2-J1998-015 |
|
徐世浙, 刘斌, 阮百尧.
1994. 电阻率法中求解异常电位的有限单元法. 地球物理学报, 37(2): 511–515.
|
|
严波. 2013. 2. 5维直流电阻率自适应有限元数值模拟[硕士论文]. 青岛: 中国海洋大学.
|
|
 2018, Vol. 61
2018, Vol. 61


