煤储层渗透率是影响煤层气开发的主要因素之一(李俊乾等,2013),煤储层渗透率的准确预测是煤层气开发成功与否的关键因素,也是当今研究的热点.
目前,煤储层渗透率预测模型主要是以单轴应变假设(水平应变为零、垂直应变不为零)为基础建立的,其代表模型有ARI模型(Sawyer et al., 1990)、S & H模型(Seidle and Huitt, 1995)、P & M模型(Palmer and Mansoori, 1998;Palmer et al., 2007;Palmer,2009)、S & D模型(Shi and Durucan, 2004)以及Gongda Wang模型(Wang et al., 2014)等.随着人们对煤层气储运机理认识的深入,煤储层渗透率预测模型逐步发展并趋于完善.但在指导煤储层渗透率预测实践中仍存在诸多困难,例如在模型参数获取方面,上述模型用到孔隙压缩系数ccleat、计算因子f和几何因子g等一个或几个基本参数,其取值通过实验室试验很难获得,大都凭主观经验或间接方式获得,使得模型预测存在一定难度.在2009年国际煤层气会议上,美国和澳大利亚学者(Massarotto et al., 2009)指出随着煤层气的开采,煤层体积保持不变,提出体积不变基本假设,并通过试验和现场勘测数据论证了这一假设的正确性.鉴于此Ma等(2011)学者以体积不变假设为基础,建立煤储层渗透率动态变化模型,即M & H模型.该模型参数简单易获取,但M & H模型只考虑煤基质收缩和有效应力两个方面对渗透率的影响,忽略了克林伯格效应的影响.
Harpalani和Chen(1997)研究发现当储层压力从900 Psi降低到100 Psi时,渗透率增大了17倍,其中12倍是由有效应力变化引起的,5倍由克林伯格效应引起.Wei和Zhang(2010)研究指出当储层压力较低时,克林伯格效应对渗透率的贡献大于有效应力和煤基质收缩.Wang等(2015)、Kazemi和Takbiri-Borujeni(2015)等研究也均证实了克林伯格效应的存在,并指出其对渗透率的影响.Klinkenberg (1941)通过实验和理论推导给出了考虑克林伯格效应的渗透率公式为
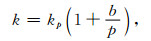
|
(1) |
其中,kp为储层压力为p时的绝对渗透率,单位为m2;p为储层压力,单位为MPa,b为克林伯格系数,单位为MPa,其表达式为

|
(2) |
式中,c是常数,一般取0.9;μ为流体的黏性系数,单位为Pa·s;M为分子量,单位为kg·mol-1;rpore为孔隙平均宽度,单位为m;R为普适气体常数,单位为J/(mol·K);T是温度,单位为K.
克林伯格系数b是影响克林伯格效应的主要参数,因此各国学者对克林伯格系数b进行了大量的研究工作,并给出了不同的计算克林伯格系数b的表达式(Heid et al., 1950;Jones and Owens, 1979;Florence et al., 2007;罗瑞兰等,2007)及实验获取克林伯格系数的方法(图 1).

|
图 1 克林伯格系数实验测量方法 Fig. 1 Experimental measurement method of Klinkenberg coefficient |
目前对煤储层克林伯格效应的研究大都认为气测渗透率与压力倒数为单一线性关系,其克林伯格系数b为常数.但王勇杰等(1995)、Moghadam和Chalaturnyk(2014)研究了低渗透性储层气测渗透率与压力的关系,分析了气体滑脱物理机制,研究发现气测渗透率随储层压力的增大而减小,并指出气测渗透率与压力倒数并非单一线性关系,即克林伯格系数b并不是一个固定常数.
从Klinkenberg给出的克林伯格系数计算公式中也不难发现,克林伯格系数b不仅与气体本身属性有关,还与储层孔隙平均半径rpore有关.Javadpour(2009)研究并证实了克林伯格效应和rpore的关系,并指出随着rpore越小,克林伯格效应越明显.Karniadakis和Beskok(2002)研究指出多孔介质平均孔径与孔隙率成反比.汪吉林等(2012)指出在储层压力降低过程中,煤储层孔隙率不是一成不变的,其随有效应力增加而减小,随煤基质收缩而增大.因此,采用固定克林伯格系数b对煤储层渗透率进行预测势必会造成一定误差,应考虑在储层压力降低过程中克林伯格系数b的动态变化过程.
鉴于此,本文以体积不变假设为基础,基于火柴棍模型,分析在储层压力降低过程中,克林伯格系数的动态变化规律及影响因素,建立考虑动态克林伯格系数的煤储层渗透率动态变化模型,采用实验室易获取的物理力学参数更加准确的预测煤储层渗透率动态变化规律.
1 渗透率模型的建立 1.1 模型基本假设(1) 体积不变假设(Massarotto et al., 2009).所谓体积不变假设是指在煤层气开采过程中,储层压力降低,煤储层的整体体积保持不变,即水平应变为零,垂直应力、应变也为零.
(2) 煤基质体孔隙对渗透率不产生影响,即煤储层渗透率主要取决于微裂隙的影响.
(3) 不考虑基质体与裂隙之间压力传递损耗,即煤基质体中压力与裂隙压力相等
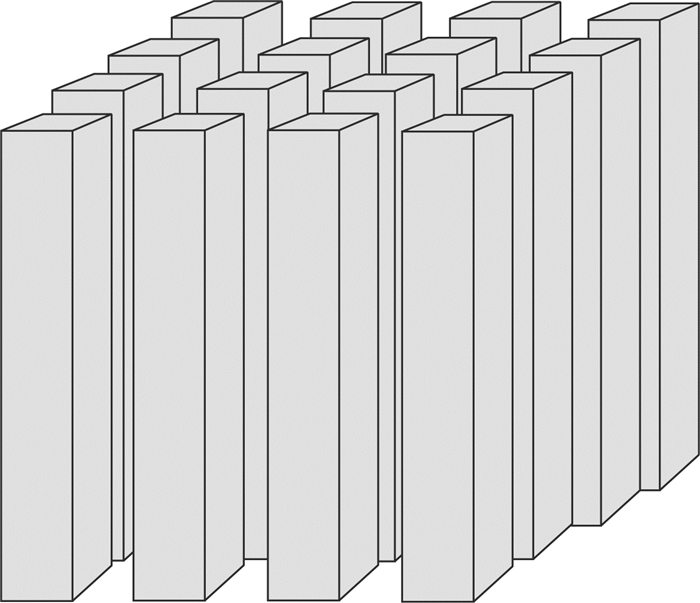
(4) Matchstick群假定(Reiss, 1980).煤层被理想化为一个火柴棍的集合体,火柴棍模型中的有效空间代表煤的孔隙,每一个火柴棍体代表煤基质,如图 2.
|
图 2 Matchstick模型 Fig. 2 Matchstickmodel |
(5) 假设火柴棍块体为弹性体.
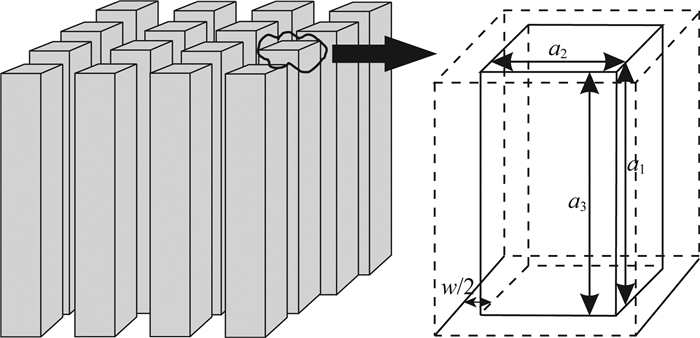
1.2 模型理论推导 1.2.1 孔隙率随储层压力变化关系在体积不变的情况下,假设火柴棍体的两个水平边边长a1和a2相等,其值均为a0,即a1=a2= a0,如图 3,那么在储层压力为p时,煤的孔隙率及渗透率可表示为(Reiss, 1980):

|
(3) |
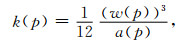
|
(4) |
|
图 3 火柴棍模型中微裂隙变化示意图 Fig. 3 Sketch of micro-crack change in Matchstick model |
式中w(p)为储层压力为p时孔隙平均宽度,a(p)为储层压力为p时火柴棍模型中煤基质体边长.
在煤储层压力降低的过程中,假设由有效应力引起的流通路径宽度变化量为Δa1,由煤基质收缩引起的煤基质体变形量为Δa2,由于a0远大于Δa1和Δa2,则:

|
(5) |
将式(5)代入式(3)得:
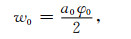
|
(7) |
式中w0为初始储层压力时煤储层孔隙平均宽度,a0为初始储层压力时煤基质体边长.
将式(5)、(7)代入式(3),则孔隙率可近似表示为

|
(8) |
在火柴棍模型假设及体积不变基本假设条件下,由有效应力引起的火柴棍体边长变形量Δa1为(马强,2011):
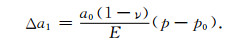
|
(9) |
由煤基质收缩引起的变形量Δa2为(马强,2011):
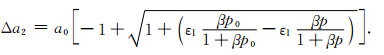
|
(10) |
将式(9)、(10)代入式(8)中可得煤储层孔隙率随储层压力变化关系为:
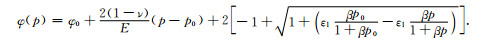
|
(11) |
将式(11)代入式(4)中得煤储层绝对渗透率为
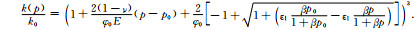
|
(12) |
已知Poiseuille孔隙直径公式为

|
(13) |
将式(13)代入式(2)得:
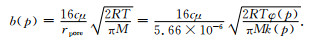
|
(14) |
将式(11)、(12)代入式(14)得克林伯格系数b的表达式为
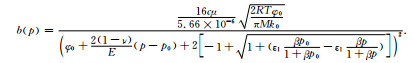
|
(15) |
1941年克林伯格通过实验证明多孔介质中气体流动存在克林伯格效应,并给出了考虑克林伯格效应渗透率表达式(式(1)).在考虑动态克林伯格系数b时,式(1)可写为
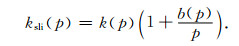
|
(16) |
将式(12)、(15)代入式(16)得考虑动态克林伯格系数的渗透率模型为
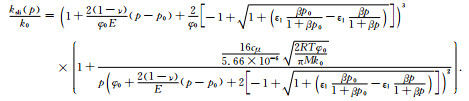
|
(17) |
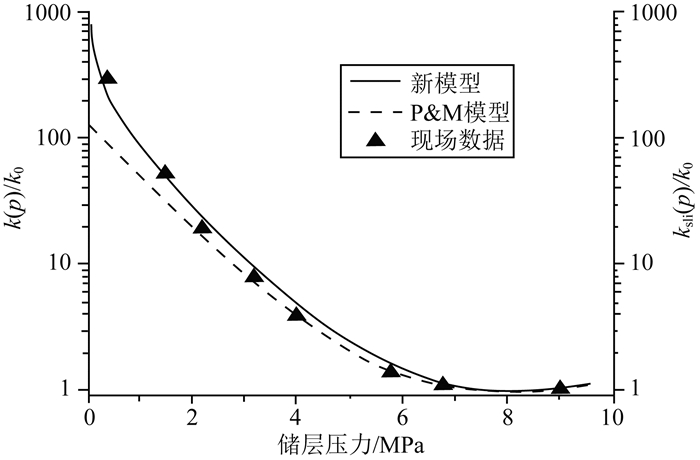
本文中的现场实测渗透率数据来自于圣胡安盆地28口抽采试验井测试数据(Giehart et al., 2006).表 1中的基本参数来自于P & M模型对圣胡安盆地渗透率模拟预测时采用的最佳参数(Palmer et al., 2007).图 4为P & M模型、新模型对圣胡安盆地煤储层渗透率的模拟预测结果与现场实测数据的比较.从图 4可以看出,随储层压力的降低,圣胡安盆地煤储层渗透率逐步增加,在储层压力大于2 MPa时,新模型和P & M模型预测结果差异不大,其预测结果与实测数据符合度均较好;但在储层压力小于2 MPa后,新模型预测结果与实测数据更为接近,其预测结果较P & M模型更为精确.
|
|
表 1 模型验证参数 Table 1 Parameter used for model verification |
|
图 4 渗透率随储层压力变化曲线 Fig. 4 Variation of permeability with reservoir pressure |
为了验证动态克林伯格系数b对渗透率的影响,本文分别以储层压力为0.5 MPa和8.5 MPa时不变的克林伯格系数计算在储层压力降低的过程中渗透率变化规律,如图 5.

|
图 5 不同固定克林伯格系数下渗透率随储层压力变化曲线 Fig. 5 Variation of permeability with increasing reservoir pressure under different Klinkenberg coefficients |
从图 5中可以看出,0.5 MPa下的固定克林伯格系数的所预测的渗透率小于8.5 MPa下的固定克林伯格系数所预测的渗透率.这是由于在有效应力、基质收缩的共同作用下,0.5 MPa时孔隙率大于8.5 MPa时孔隙率,导致其克林伯格系数较小,渗透率值小于8.5 MPa下的固定克林伯格系数的渗透率,尤其在储层压力小于2 MPa后,两者差异更加明显.由此可以看出,以固定的克林伯格系数预测渗透率变化必然会造成误差,储层压力越小,其预测结果误差越大.因此,在建立渗透率预测模型时,不可以忽略克林伯格系数的动态变化.
3 动态克林伯格系数影响因素分析根据克林伯格系数计算公式(15),选取表 1中的参数为基本参数,经MATLAB编程,计算分析储层压力、渗透率、温度等对克林伯格系数的影响.
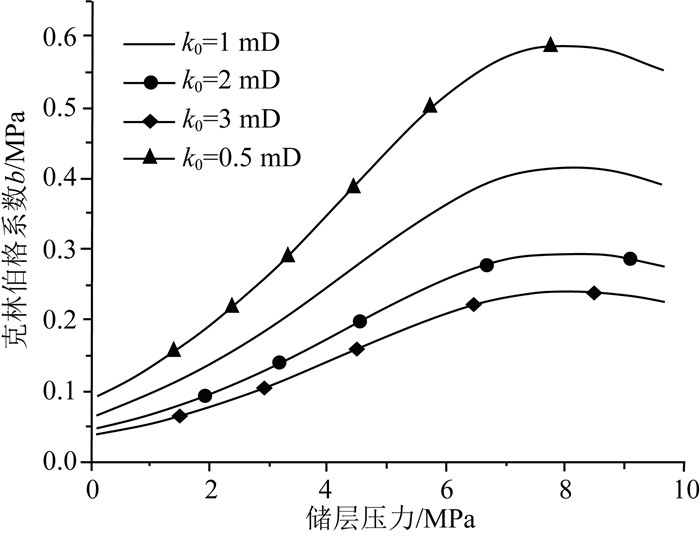
图 6为不同渗透率下克林伯格系数随储层压力变化关系曲线.由图 6可以看出:在储层压力降低过程中,克林伯格系数呈先增大后减小的变化趋势.这是因为克林伯格系数是与孔隙率φ(p)的函数,随着储层压力的降低,有效应力和基质收缩共同对煤储层孔隙率产生作用,有效应力使得储层孔裂隙减小,基质收缩使孔裂隙增加,在储层压力降低初期,有效应力作用效果强于基质收缩作用,其孔隙率呈减小趋势,克林伯格系数b增大;随着孔隙压力的进一步减小,基质收缩作用大于有效应力,煤储层孔隙率增加,克林伯格系数减小.
|
图 6 不同初始渗透率下克林伯格系数随储层压力变化关系 Fig. 6 Relationship between Klinkenberg coefficient and reservoir pressure under different initial permeability values |
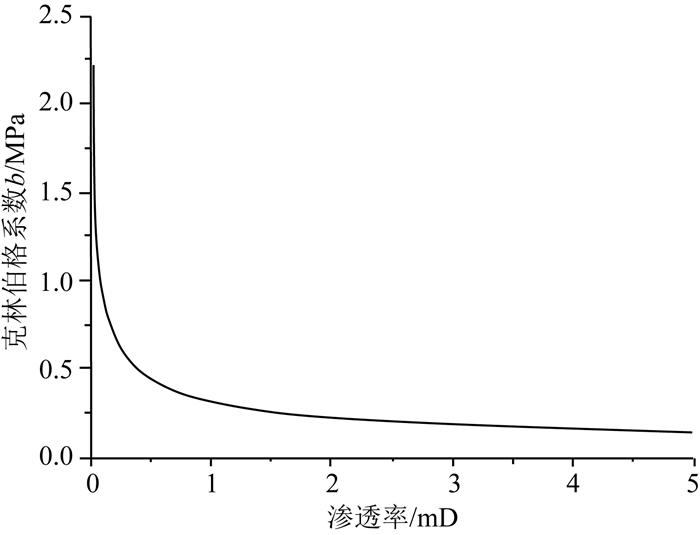
图 7为储层压力为5 MPa时克林伯格系数随渗透率变化关系曲线.由图 7可以看出:克林伯格系数与煤储层渗透率呈负指数关系;渗透率越小克林伯格系数越大,克林伯格效应越明显.这是由于在其他参数相同的情况下,渗透率越小,储层平均孔径越小,其克林伯格系数值越大.
|
图 7 储层压力为5 MPa时克林伯格系数与渗透率关系曲线 Fig. 7 Curve of Klinkenberg coefficient versus permeability at 5 MPa reservoir pressure |
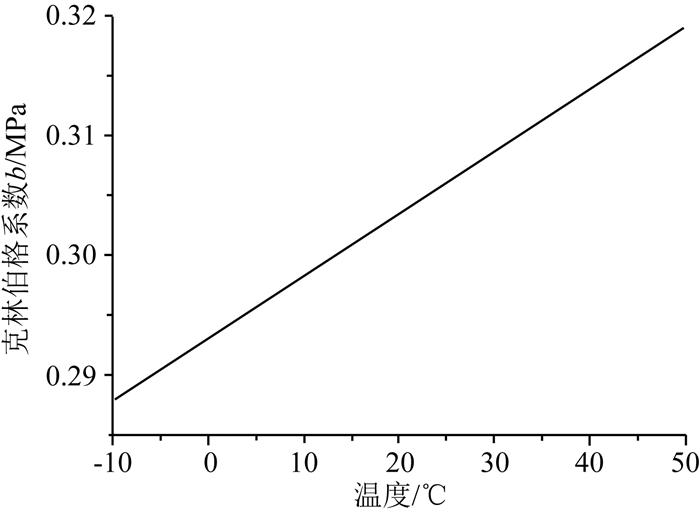
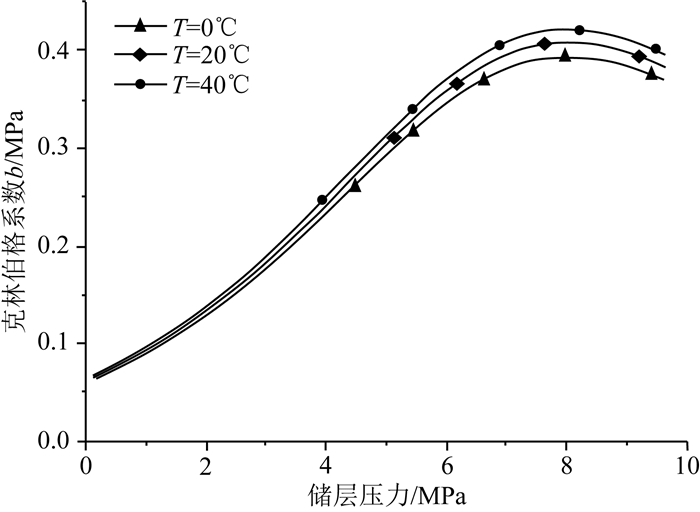
图 8为储层压力为5 MPa时,克林伯格系数随温度变化关系曲线.从图 8中可以看出:在储层压力不变时,克林伯格系数b随温度的升高逐渐增大.这是由于在相同储层压力下,温度越高,其平均分子自由程越大,克林伯格效应越明显,克林伯格系数b越大.图 9为温度为0 ℃、20 ℃和40 ℃下克林伯格系数随储层压力变化关系曲线.从图 9中可以看出:在高储层压力阶段,相同储层压力下,温度越高其克林伯格系数b值越大;在低储层压力阶段,随储层压力的降低,温度变化对克林伯格系数b影响越来越小.这是由于在高储层压力阶段,相同储层压力下,温度越高气体分子运动越活跃,气体分子平均自由程越大,其克林伯格效应越明显;在低储层压力阶段,气体储层压力对分子自由程的影响远大于温度变化对其影响,温度变化对克林伯格系数的影响程度较小,因此低储层压力阶段,克林伯格系数b随温度变化不明显.
|
图 8 储层压力为5 MPa时克林伯格系数随温度变化关系曲线 Fig. 8 Relationship between Klinkenberg coefficient and temperature with reservoir pressure 5 MPa |
|
图 9 不同温度下克林伯格系数随储层压力变化关系曲线 Fig. 9 Curves of Klinkenberg coefficient versus reservoir pressure at different temperatures |
本文以体积不变假设为基础,基于火柴棍应力-应变分析模型,建立了考虑动态克林伯格系数的渗透率预测模型,并对克林伯格系数随储层压力的变化规律及影响因素进行了分析,其结论如下:
(1) 考虑在储层压力降低过程中克林伯格系数b的动态变化,给出了动态克林伯格系数b的计算公式,并建立考虑动态克林伯格效应的渗透率预测模型.该模型只用基本物理学参数,实现对煤储层渗透率预测,该模型实用性和操作性强,具有更高的理论和实用价值.
(2) 以圣胡安盆地基础工程数据为背景,分别采用新模型和P & M模型对其渗透率进行预测,并与实际工程数据进行比较.结果表明:高储层压力阶段(大于2 MPa)两者预测结果差异不大,均与实测数据符合良好;在低储层压力阶段(小于2 MPa),新模型考虑了动态考虑伯格效应的影响,其预测结果与实测结果符合度高于P & M模型,进而验证了新模型的正确性及优越性.
(3) 以圣胡安盆地煤储层数据为基础,分析了克林伯格系数的影响因素.结果表明随储层压力的降低,克林伯格系数呈先增大后减小变化趋势;在储层压力相同时,克林伯格系数随渗透率的减小呈指数形式变化,随温度的升高呈线性变化趋势.
Florence F A, Rushing J, Newsham K E, et al. 2007.Improved permeability prediction relations for low permeability sands.//SPE 107954. Rocky Mountain Oil & Gas Technology Symposium.Denver, Colorado, USA:SPE.
|
|
Giehart R, Gips G, Seidle J. 2006. San Juan Basin Fruitland coal pressure dependent permeability observations.//Proceedings, SPE Applied Technology Workshopon Unconventional Gas.Keystone, Cololardo:SPE.
|
|
Harpalani S, Chen GL.
1997. Influence of gas production induced volumetric strain on permeability of coal. Geotechnical & Geological Engineering, 15(4): 303-325.
|
|
Heid J G, McMahon J J, Nielsen RF, et al. 1950.
Study of the Permeability of Rocks to Homogenous Fluids. New York: API Drilling & Production Practice Press: 230-246.
|
|
Javadpour F.
2009. Nanopores and apparent permeability of gas flow in mudrocks(shales and siltstone). Journal of Canadian Petroleum Technology, 48(8): 16-21.
DOI:10.2118/09-08-16-DA |
|
Jones F O, Owens W W.
1979. A laboratory study of low-permeability gas sands. Journal of Petroleum Technology, 32(9): 1631-1640.
|
|
Karniadakis G E, Beskok A. 2002.
Micro Flows:Fundamentals and Simulation. Berlin: Springer.
|
|
Kazemi M, Takbiri-Borujeni Ai.
2015. An analytical model for shale gas permeability. International Journal of Coal Geology, 146: 188-197.
DOI:10.1016/j.coal.2015.05.010 |
|
Klinkenberg L J. 1941. The permeability of porous media to liquids and gases.//Proceedings of Drilling and Production Practice.New York:American Petroleum Institute, 200-213.
|
|
Li J Q, Liu D M, Yao Y B, et al.
2013. Controls of gas slippage and effective stress on the gaspermeability of coal. Natural Gas Geoscience, 24(5): 1074-1078.
|
|
Luo R L, Cheng L S, Zhu H Y, et al.
2007. Problems on the study of slippage effect in low-permeability gas reservoirs. Natural Gas Industry, 27(4): 92-94.
|
|
Ma Q. 2011. Study on theory and experiment of permeability changes discipline in CBM reservoir[Ph. D. thesis](in Chinese). Beijing:China University of Mining & Technology (Beijing).
http://cdmd.cnki.com.cn/Article/CDMD-11413-1011184674.htm |
|
Ma Q, Harpalani S, Liu S M.
2011. A simplified permeability model for coalbed methane reservoirs based on matchstick strain and constant volume theory. International Journal of Coal Geology, 85(1): 43-48.
DOI:10.1016/j.coal.2010.09.007 |
|
Massarotto P, Golding S D, Rudolph V. 2009. Constant volume CBM reservoirs:An important principle.//Proceedings of 2009 International Coalbedand Shale Gas Symposium/RPSEA Forum.Tuscaloosa, Alabama:University of Alabama.
|
|
Moghadam A A, Chalaturnyk R.
2014. Expansion of the Klinkenberg's slippage equation to low permeability porous media. International Journal of Coal Geology, 123: 2-9.
DOI:10.1016/j.coal.2013.10.008 |
|
Palmer I, Mansoori J.
1998. How permeability depends on stress and pore pressure in coalbeds:A new model. SPE Reservoir Evaluation & Engineering, 1(6): 539-544.
|
|
Palmer I, Mavor M, Gunter B. 2007. Permeability changes in coal seams during production and injection.//International Coalbed Methane Symposium. Tuscaloosa, Alabama:University of Alabama.
|
|
Palmer I.
2009. Permeability changes in coal:Analytical modeling. International Journal of Coal Geology, 77(1-2): 119-126.
DOI:10.1016/j.coal.2008.09.006 |
|
Reiss L H. 1980.
The Reservoir Engineering Aspects of Fractured Formations. Houston: Gulf Publishing Co.
|
|
Sawyer W K, Paul G W, Schraufnagel R A. 1990.Development and application of a 3-D coalbed simulator.//Proceedings of International Technical Meeting Hosted Jointly by the Petroleum Society of CIM and the Society of Petroleum Engineers.Calary, Alberta, Canada:Petroleum Society of Canada, 90-119.
|
|
Seidle J P, Huitt L G. 1955. Experimental Measurement of coal matrix shrinkage due to gas desorption and implications for cleat permeability increases.//International Meeting on Petroleum Engineering.Beijing, China:Society of Petroleum Engineers, 575-579.
|
|
Shi J Q, Durucan S.
2004. Drawdown induced changes in permeability of coalbeds:A new interpretation of the reservoir response to primary recovery. Transport in Porous Media, 56(1): 1-16.
|
|
Wang G D, Ren T, Wang K, et al.
2014. Improved apparent permeability models of gas flow in coal with Klinkenberg effect. Fuel, 128: 53-61.
DOI:10.1016/j.fuel.2014.02.066 |
|
Wang J L, Qin Y, Fu X H.
2012. Dynamic changes laws of the coal reservoirs permeability under the superimposition of multi influential factors. Journal of China Coal Society, 37(8): 1348-1353.
|
|
Wang Y, Liu S M, Elsworth D.
2015. Laboratory investigations of gas flow behaviors in tight anthracite and evaluation of different pulse-decay methods on permeability estimation. International Journal of Coal Geology, 149: 118-128.
DOI:10.1016/j.coal.2015.07.009 |
|
Wang Y J, Wang C J, Gao J B.
1995. A research of gas slip in low permeability porous media. Acta Petrolei Sinica, 16(3): 101-105.
|
|
Wei Z J, Zhang D X.
2010. Coupled fluid-flow and geomechanics for triple-porosity/dual-permeability modeling of coalbed methane recovery. International Journal of Rock Mechanics and Mining Sciences, 47(8): 1242-1253.
DOI:10.1016/j.ijrmms.2010.08.020 |
|
李俊乾, 刘大锰, 姚艳斌, 等.
2013. 气体滑脱及有效应力对煤岩气相渗透率的控制作用. 天然气地球科学, 24(5): 1074–1078.
|
|
罗瑞兰, 程林松, 朱华银, 等.
2007. 研究低渗气藏气体滑脱效应需注意的问题. 天然气工业, 27(4): 92–94.
|
|
马强. 2011. 煤层气储层渗透率变化规律理论与实验研究[博士论文]. 北京: 中国矿业大学(北京).
http://cdmd.cnki.com.cn/Article/CDMD-11413-1011184674.htm |
|
汪吉林, 秦勇, 傅雪海.
2012. 多因素叠加作用下煤储层渗透率的动态变化规律. 煤炭学报, 37(8): 1348–1353.
|
|
王勇杰, 王昌杰, 高家碧.
1995. 低渗透多孔介质中气体滑脱行为研究. 石油学报, 16(3): 101–105.
DOI:10.7623/syxb199503015 |
|
 2018, Vol. 61
2018, Vol. 61


