2. 中国科学院页岩气与地质工程重点实验室, 北京 100029;
3. 中国科学院地球科学研究院, 北京 100029;
4. 中国科学院大学, 北京 100049;
5. 长江大学地球物理与石油资源学院, 武汉 432100;
6. 日本地球环境产业技术研究所, 日本东都 6190292
2. Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Institute of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China;
5. College of Geophysics and Petroleum Resource, Yangtze University, Wuhan 430100, China;
6. Research Institute of Innovative Technology for the Earth, Kyoto 6190292, Japan
在微地震研究中,最基础也是最重要的环节是进行震源定位.震源定位的精度是影响震源机制反演的重要因素(Aki and Richards, 2002; Song and Toksöz, 2011).因此,震源定位不仅对传统地震学研究具有重要意义,而且在非常规油气开发中,是评价压裂效果、研究裂缝空间分布的重要依据(Daniels et al., 2007; Maxwell et al., 2015),也是研究水力压裂诱发的微地震震源破裂类型的基础数据(Eisner et al., 2010).微地震震源定位面临两大难题,一是发震时刻难以确定,二是微地震事件的信号难以识别.为了克服这两大难题,微地震震源定位发展了两大类方法,一类是震源成像的方法,另一类是基于微地震事件走时的方法.基于震源成像的方法可以在发震时刻未知的条件下进行计算,同时避免对微地震事件初至走时的拾取,近年来震源成像的方法中大多采用地震干涉原理,例如Sava等提出的在波动方程偏移基础上利用干涉成像条件对震源成像的方法(Sava and Poliannikov, 2008),Poliannikov等发表了利用地震干涉原理的水力压裂微地震定位方法(Poliannikov et al., 2011),此外,采用能量聚焦方法也可实现震源成像,例如Artman等提出的波场时间域反向传播叠加法(Artman et al., 2010),另外TRM(Time Reverse Mirror)作为一种高分辨率的能量聚焦震源成像方法也用于微地震震源定位的研究(Hanafy et al., 2009).上述方法面临的困难是需要利用计算量较大的波动方程,目前在实际应用中还存在一定的困难.基于走时的方法对微地震事件初至拾取的精度要求很高,面临的困难是难以处理低信噪比微地震数据,因此,在基于走时的震源定位方法中,前人提出了微地震事件走时自动拾取的方法(刘劲松等,2013;王鹏等,2014),用来拾取淹没在噪声中的微地震事件.其中,双差定位法(Waldhauser and Ellsworth, 2000;Zhang and Thuber, 2003)利用相邻震源到达不同检波器的时差,提高了基于走时震源定位方法的精度和抗干扰性.干涉走时定位法(王璐琛等,2016)利用同一震源事件对不同检波点的地震波干涉来消除震源发震时刻在反演中的影响,提高了微地震事件的定位效果.上述方法都不可避免地需要进行难度较大的走时的拾取.
另一方面,在震源定位中,介质的复杂性也同样影响走时的准确拾取.我们研究的地层在许多情况下并非理想的完全弹性介质,地震波在非弹性介质中传播形成地震波的衰减.由于地震波传播过程中衰减的影响,加剧了微地震事件走时拾取的困难.地震波在吸收介质中每传播一个波长的距离,能量和频率成分的损失可以认为是固定的,损失的多少与介质的品质因子Q值(Quality Factor)相关.本文分析了地震波在传播过程中频率衰减随传播距离的变化关系,据此假设同一个震源信号在传播到不同的地震道上,会表现出不同的振幅频率衰减特征,当衰减量得到相应的补偿后,这些不同地震道的信号就会在空间某一个位置显示振幅频率的最佳一致性,此时的空间位置即是我们需要计算的震源位置.在这一条件下,我们探讨利用地震波的频率衰减补偿对微地震事件进行定位的方法,给出了理论计算方法,通过数值模拟和误差分析证明了这一方法的合理性和有效性.
1 频率衰减补偿方法原理微地震波的频率很高,在传播过程中衰减很严重,衰减程度与传播距离以及地层的Q值密切相关.在微地震震源的定位计算中,我们可以利用地震波频率成分的衰减信息,对微地震记录在频率域实施频率衰减补偿,使得补偿后的信号与震源信号的频谱特征一致,如图 1所示.

|
图 1 频率衰减补偿法微地震震源定位的原理 Fig. 1 Frequency attenuation compensation method of micro seismic source localization principle diagram |
在图 1中,微地震波从震源传播到3个检波器,震源子波的频谱位于图 1右上角.震源破裂后,微地震波按照各自的传播时间到达检波器G1,G2和G3.在检波器端接收到的微地震信号表现为不同程度的衰减,如图中左侧示意了不同的频谱特征.我们的方法是将各个检波器的接收信号沿着传播路径反向延拓,在反向延拓中对信号进行频率衰减补偿.当补偿后的各个信号的频谱一致时,我们就得到了震源子波的原始频谱,同时可获得反向延拓的时间,即检波器记录到的微地震信号返回到震源的走时,进而确定出微地震的空间位置.
本文提出的方法不再直接拾取微地震事件的初至信息,而是将微地震记录变换到频率域,计算其振幅谱.虽然将微地震信号从时间域变换到频率域时,微地震事件的初至信息不会出现在频率域的振幅谱中,但微地震事件的走时信息将在频率衰减补偿计算中获得.频率衰减补偿的计算过程相对于LTA/STA等(Allen, 1978; Baer and Kradolfer, 1987)走时拾取的方法不需要更多的计算时间.
地震波衰减公式可表示为
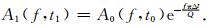
|
(1) |
(1) 式中,A0(f, t0)为震源子波的振幅谱,Δt为微地震波从震源传播到检波器的时间,A1(f, t1)为检波器端接收到的微地震事件的频谱特征.
频率衰减补偿是(1)式的逆运算,补偿公式可表示为
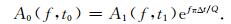
|
(2) |
首先,我们利用(1)式对地震信号的衰减过程进行模拟,考察频率衰减与传播距离的关系.理论计算采用主频为800 Hz的雷克子波,采样频率为4000 Hz.设模型为均匀介质,地震波速度为4500 m·s-1;观测段长度为1000 m,在此观测段上等间距放置检波器,检波器间隔为5 m.
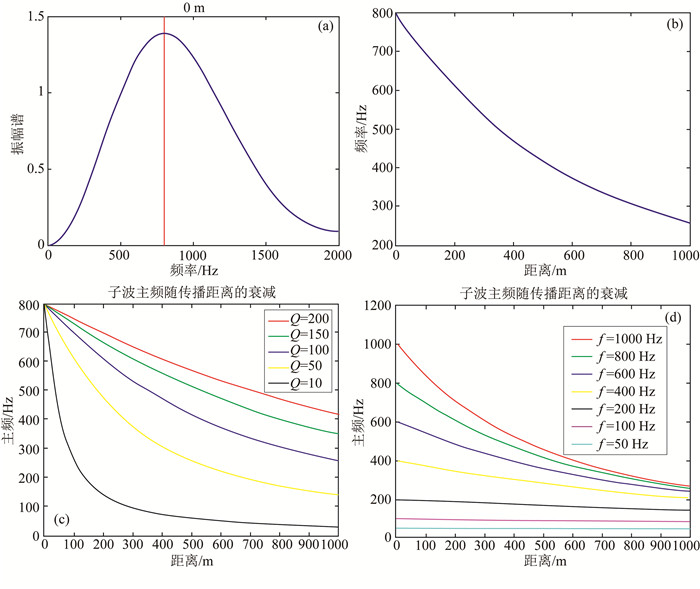
图 2是利用一个均匀模型计算的不同Q值和不同频率子波在传播过程中,频率随传播距离的变化.图 2a表示主频为800 Hz的雷克子波;图 2b表示800 Hz雷克子波在Q值为100的介质中频率随传播距离衰减的情况;图 2c是设定不同Q值条件下信号主频的衰减变化过程;图 2d是不同初始信号主频在同一Q值条件下信号主频的衰减过程.从图 2可以看出:当震源子波主频一定,介质的Q值越大,地震信号主频衰减越慢.在低Q值条件下,主频衰减量与传播距离之间呈指数关系.在高Q值条件下,主频衰减量与传播距离之间呈近似线性关系.另一方面,当介质Q值一定,初始子波主频越高,信号主频衰减越快,主频衰减与传播距离之间的指数关系越明显.上述这一地震波传播过程中频率衰减的基本特征可以用来进行震源定位.当我们获得了介质的Q值(这与我们利用走时计算震源位置时需要首先获得介质的速度是等价的),我们就可以对地震波的传播进行Q值补偿,当多个地震道的信号在Q值补偿过程中频率趋向一致时的空间位置,即是震源的位置.这里需要说明的是,对于频率较低的地震信号的定位,例如天然地震的定位,低频信号的衰减在短距离内的变化并不像高频信号那样明显,如图 2d所示,关于这一点将在讨论与小结一节中论述.
|
图 2 微地震信号主频随传播距离的变化 (a)雷克子波,主频为800 Hz;(b)主频为800 Hz的雷克子波频率随传播距离的变化,Q为100;(c)主频为800 Hz的雷克子波频率随传播距离的变化,Q分别为10,50,100,150,200;(d)主频为50 Hz,100 Hz,200 Hz,400 Hz,600 Hz,800 Hz,1000 Hz的雷克子波频率随传播距离的变化,Q为100. Fig. 2 Micro-seismic signal frequency varies with the change of the propagation distance (a) Ricker wavelet, the frequency of 800 Hz; (b) Using 800 Hz Ricker wavelet calculated the frequency varies with the change of the propagation distance, Q value is 100; (c) Using 800 Hz Ricker wavelet calculated the frequency varies with the change of the propagation distance, Q value are 10, 50, 100, 150, 200 respectively; (d) Using the 50 Hz, 100 Hz, 200 Hz, 400 Hz, 600 Hz, 800 Hz and 1000 Hz of Ricker wavelet, calculated the frequency varies with the change of the propagation distance, Q value is 100. |
在进行频率补偿的计算中,我们需要判断相邻地震道补偿后频率成分的相似性.对于两个信号的相似程度的判断,采用归一化互相关法NCC(Normalized Cross-Correlation)(Lu et al., 2007)来进行计算:
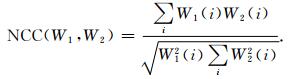
|
(3) |
(3) 式中,W1(i),W2(i)分别为两信号的振幅谱,NCC(W1, W2)表示两信号的相似程度,当NCC的值等于1时,表示两个信号完全一致.
当对多个信号求相似度时,例如对4个信号求相似度的情况,(3)式变形为
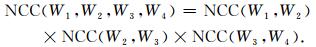
|
(4) |
上式可被理解为:当对多个信号求其相似度时,可先分别求相邻两个信号的相似度,再将所有计算结果相乘.若所有信号是完全相同的,那么各个相邻信号间的NCC值都为1,此时(4)式等于1,表示微地震信号已由接收点的频率补偿至震源点的频率,计算至此可停止.
有两种方法可实现本文提出的频率衰减补偿微地震震源定位.
(1) 全程补偿法
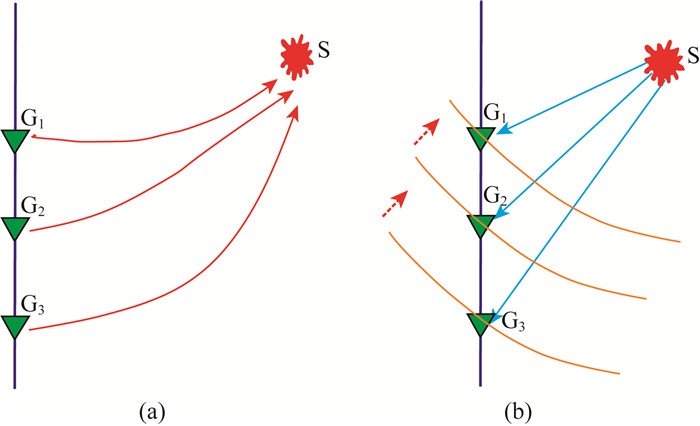
全程补偿法是同时对多个地震记录在频率域进行衰减补偿,直到每个地震记录的频谱特征相一致.如图 3a所示,同时对检波器G1,G2和G3的微地震信号频谱进行补偿.各地震道地震记录的补偿关系可表示为
|
图 3 确定微地震震源位置 (a)全程补偿法;(b)道间时差补偿法. Fig. 3 Locate the micro-seismic source (a) Full path compensation method; (b) Time difference compensation method. |
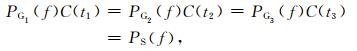
|
(5) |
其中,P(f)为频谱特征函数,C(t)为补偿函数,t1,t2和t3分别是检波器G1,G2和G3地震记录的衰减补偿时间,PS(f)为震源的频谱特征函数.(5)式中的补偿函数C(t)可用(2)式表示,这里为了简化起见表示为C(t),在计算中,可预先预设一个t0作为震源发震时刻,第i个地震道的衰减补偿时间ti通过搜索频谱一致性获得.
(2) 道间时差补偿法
全程补偿法需要计算微地震事件延拓至震源点的全程时间,观测距离越大计算量越大,不适合快速反演计算.为此,本文给出一种对同一微地震事件的道间时差进行补偿的方法.
道间时差补偿法仅计算相邻检波器间频率衰减之差的补偿关系.如图 3b所示,图中蓝线表示由微地震波从震源到达各个检波器的路径,桔黄线表示微地震波场的波前面.将第n个检波器地震记录的频谱特征依次补偿到第n-1个检波器地震记录的频谱.补偿公式可表示为
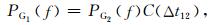
|
(6) |
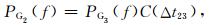
|
(7) |
其中,PG1,PG2和PG3分别为检波器G1,G2和G3的频谱特征,Δt12表示波前面由G1到G2的传播时间,即这两个检波器间的补偿时差,Δt23表示波前面由G2到G3的传播时间.
相对于全程补偿法,道间时差补偿法所需要的计算时间较少,因此可实现相对快速的定位,另外,补偿时间缩短表示可以降低计算步长,进一步提高反演定位的精度.
3 理论计算本文采用二维均匀模型进行方法验证,模型如图 4所示.
|
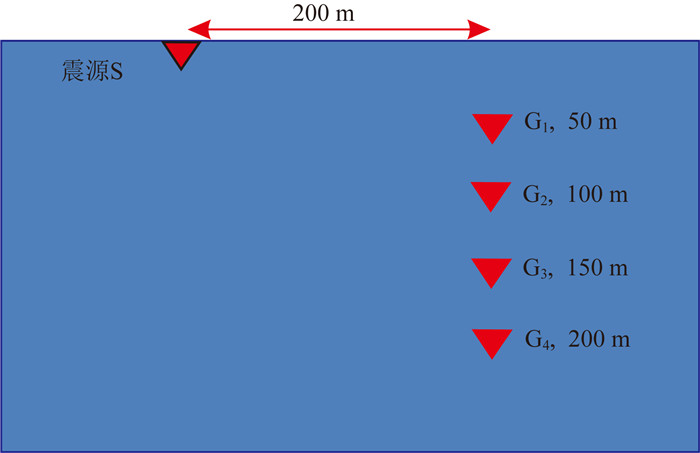
图 4 二维均匀模型 Fig. 4 Two-dimensional uniform model |
在图 4中,以震源S为坐标原点(0,0)建立坐标系,检波器G1,G2,G3与G4的横向坐标是200 m,纵向坐标分别为50 m,100 m,150 m和200 m.模型速度设定为3000 m·s-1,Q值设定为100.震源信号为雷克子波,原始信号主频为800 Hz.
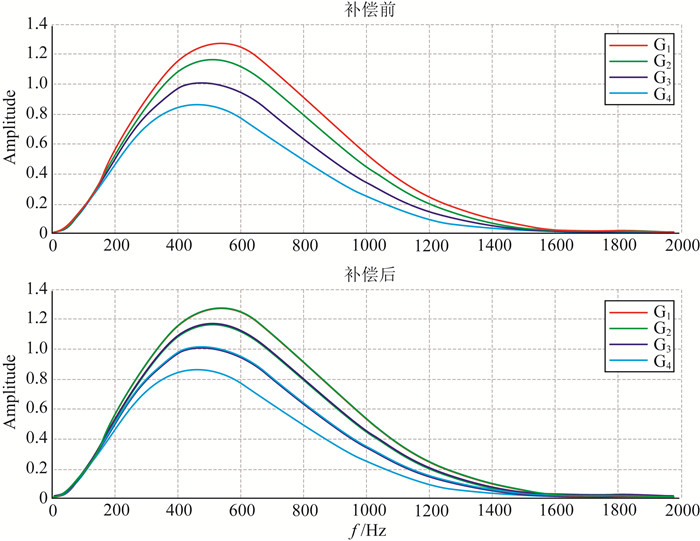
采用道间时差补偿法对微地震震源进行反演:在图 5中,上图是地震记录G1,G2,G3和G4的频谱特征曲线,即震源信号经过不同传播路径,衰减以后的频谱特征;下图为相邻检波器的频谱特征经过补偿后的结果.理想情况下,补偿后地震记录的频谱特征与补偿前相邻地震记录的频谱特征一致,我们对补偿后的第n道地震记录的频谱用Fn表示,补偿前第n道的地震记录频谱用fn表示,则有
|
图 5 道间时差补偿法理论计算结果 Fig. 5 Theoretical calculations result using time difference compensation method |
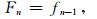
|
(8) |
依此类推.这一理想情况在图 5的下图中表示为:青色频谱特征曲线与原始蓝色频谱特征曲线重合,蓝色频谱特征曲线与绿色频谱特征曲线重合.经过道间时差补偿的计算,就可得到道间时差.
在均匀速度模型下的微地震震源定位公式可表示为
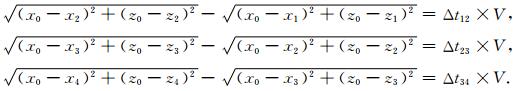
|
(9) |
(9) 式中,(x0, z0)表示震源坐标,(x1, z1),(x2, z2),(x3, z3)和(x4, z4)分别是检波器G1,G2,G3和G4的坐标,Δt12,Δt23和Δt34分别是利用频率衰减补偿方法得到的相邻地震道的时差,V是模型速度.
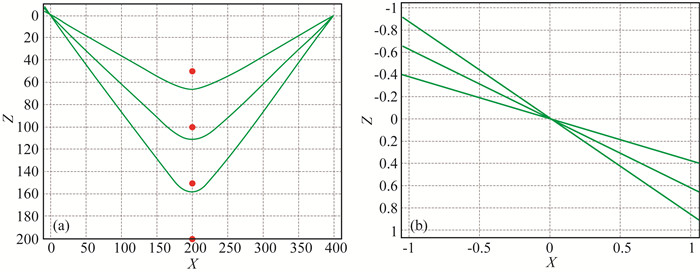
在(9)式中,仅震源位置(坐标)是未知量,其余各个变量为已知量或可通过道间时差补偿法计算获得.例如速度模型是各种利用走时进行震源定位的方法都需要定义的,(9)式中的相邻道时差Δt可用本文方法获得,不需要进行走时拾取.(9)式方程组的解可表示为三条双曲线的交点,图 6所示是公式(9)的理论解,计算结果表明,三条双曲线准确地相交于表示震源位置的坐标原点(0,0),与模型给出的初始震源位置完全一致.
|
图 6 均匀模型微地震震源定位方法 (a)根据(9)式计算出三条双曲线,其焦点位于左上部位坐标原点处;(b)左图左上部三条双曲线交点邻域的放大. Fig. 6 Determined micro-seismic source location (a) Three hyperbolic curves calculated from formula (9); (b) Zoom in on the three curves cross-point area. |
(4) 式的NCC是补偿计算的理论停机条件,在实际资料处理中,NCC的值不可能为1,因此我们采用实际资料计算时NCC最大值与NCC理论值之差的最小二乘解,并根据需要给出残差的取值作为停机条件.定义补偿计算步长dt=Δt/N,Δt是补偿计算所需要的总时长,N表示计算的步数.
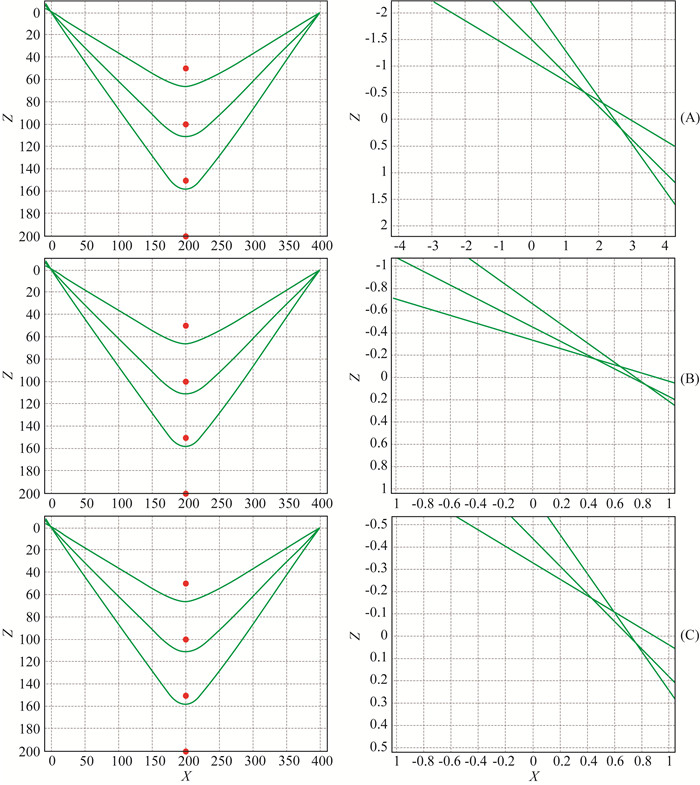
图 7给出了不同的补偿计算步长和补偿停机条件对定位精度的影响,这对于实际微地震数据的定位具有参考意义.图 7a表明,当补偿计算的步长为0.1 μs,补偿停机时残差为10-7时,三条双曲线各自相交,形成三个交点,横向误差在2 m左右,纵向误差小于0.5 m.图 7b表明,当补偿计算步长1 μs,补偿停机时的残差为10-8时,反演精度得到提高,横向误差小于1 m,纵向误差小于0.2 m.图 7c表明,当补偿计算步长10 μs,补偿停机时的残差为10-8时,相对于图 7b的条件,图 7c增加了补偿计算步长,补偿停机条件的精度保持不变,最终的反演精度依然较高,横向误差小于1 m,纵向误差小于0.2 m.
|
图 7 频率衰减补偿计算步长以及补偿停机条件对震源定位精度的影响 (A)、(B)、(C)分别表示不同的补偿步长和补偿停机条件计算的结果,右列图是左列图的局部放大. Fig. 7 The influence on location accuracy by algorithm step and stopping criteria The top, middle and bottom figures show the results computation by different step and different stopping criteria, respectively. The left column is the three hyperbolic curves, and the right column is zoom in on the three curves cross-point area. |
通过对比以上三组补偿计算步长和补偿停机条件下的震源位置反演结果,可知反向补偿停机条件相对于补偿计算步长来说,对震源位置反演精度影响更大.
5 讨论与小结通常情况下, 水力压裂诱发的微地震波频率较高,可以达到200~1000 Hz.正如本文图 2所示的计算结果,这种高频的微地震波在可观测距离上的衰减十分显著,因此,利用频率衰减补偿的方法实现震源定位的条件是充分的.需要说明的是,如果接收到的微地震信号频率较低,就需要对观测系统和地震波频率的衰减进行分析,判断频率衰减与观测系统的相关性(频率衰减随传播距离的变化),当地震波的衰减与观测系统具有明显的相关性时,本文方法就可以适用.正如图 2d所示,在1000 m范围内,低于100 Hz的地震波的频率衰减是不明显的,本文方法对于较低频率的信号必须通过计算给出足够的观测距离,而这一观测距离在实际观测中是可实现的,本文方法才能适用.
关于补偿函数.本文提出不需要拾取微地震事件走时的频率衰减补偿微地震定位方法,利用理论计算证明了该方法的合理性.在此基础上对本文方法用于实际资料处理时可能产生的定位误差进行了探讨,对补偿计算的步长和影响频谱相似性判定的因素(补偿计算的停机条件)进行了分析,为实际资料的处理提供了参考.本文的方法对于层状介质和三维模型的情况, 以及地面微地震数据也同样适用.
Aki K, Richards P. 2002.
Quantitative Seismology. (2nd ed). Sausalito: University Science Books.
|
|
Allen R V.
1978. Automatic earthquake recognition and timing from single traces. Bulletin of the Seismological Society of America, 68(5): 1521-1532.
|
|
Artman B, Podladtchikov I, Witten B.
2010. Source location using time-reverse imaging. Geophysical Prospecting, 58(5): 861-873.
DOI:10.1111/j.1365-2478.2010.00911.x |
|
Baer M, Kradolfer U.
1987. An automatic phase picker for local and teleseismic events. Bulletin of the Seismological Society of America, 77(4): 1437-1445.
|
|
Daniels J L, Waters G A, LeCalvez J H, et al. 2007. Contacting more of the Barnett shale through an integration of real-time microseismic monitoring, petrophysics, and hydraulic fracture design.//77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
|
Eisner L, Williams-Stroud S Y, Hill A, et al.
2010. Beyond the dots in the box:Microseismicity-constrained fracture models for reservoir simulation. The Leading Edge, 29(3): 326-333.
DOI:10.1190/1.3353730 |
|
Hanafy S M, Cao W P, McCarter K, et al.
2009. Using super-stacking and super-resolution properties of time-reversal mirrors to locate trapped miners. The Leading Edge, 28(3): 302-307.
|
|
Liu J S, Wang Y, Yao Z X.
2013. On micro-seismic first arrival identification:A case study. Chinese Journal of Geophysics, 56(5): 1660-1666.
DOI:10.6038/cjg20130523 |
|
Lu W K, Zhang Y S, Zhang S W, et al.
2007. Blind wavelet estimation using a zero-lag slice of the fourth-order statistics. Journal of Geophysics and Engineering, 4(1): 24-30.
DOI:10.1088/1742-2132/4/1/004 |
|
Maxwell S C, Chorney D, Goodfellow S D.
2015. Microseismic geomechanics of hydraulic-fracture networks:Insights into mechanisms of microseismic sources. The Leading Edge, 34(8): 904-910.
DOI:10.1190/tle34080904.1 |
|
Poliannikov O V, Malcolm A, Djikpesse H, et al.
2011. Interferometric hydrofracture microseism localization using neighboring fracture. Geophysics, 76(6): WC27-WC36.
DOI:10.1190/geo2010-0325.1 |
|
Sava P, Poliannikov O.
2008. Interferometric imaging condition for wave-equation migration. Geophysics, 73(2): S47-S61.
DOI:10.1190/1.2838043 |
|
Song F, Toksöz M N.
2011. Full-waveform based complete moment tensor inversion and source parameter estimation from downhole microseismic data for hydrofracture monitoring. Geophysics, 76(6): WC103-WC116.
DOI:10.1190/geo2011-0027.1 |
|
Waldhauser F, Ellsworth W L.
2000. A double-difference earthquake location algorithm:Method and application to the northern Hayward fault, California. Bulletin of the Seismological Society of America, 90(6): 1353-1368.
DOI:10.1785/0120000006 |
|
Wang L C, Chang X, Wang Y B.
2016. Locating micro-seismic events based on interferometric traveltime inversion. ChineseJournal of Geophysics, 59(8): 3037-3045.
DOI:10.6038/cjg20160826 |
|
Wang P, Chang X, Wang Y B, et al.
2014. Automatic event detection and event recovery in low SNR microseismic sifnals based on time-frequency sparseness. Chinese Journal of Geophysics, 57(8): 2656-2665.
DOI:10.6038/cjg20140824 |
|
Zhang H J, Thurber C H.
2003. Double-difference tomography:the method and its application to the Hayward Fault, California. Bulletin of the Seismological Society of America, 93(5): 1875-1889.
DOI:10.1785/0120020190 |
|
刘劲松, 王赟, 姚振兴.
2013. 微地震信号到时自动拾取方法. 地球物理学报, 56(5): 1660–1666.
DOI:10.6038/cjg20130523 |
|
王鹏, 常旭, 王一博, 等.
2014. 基于时频稀疏性分析法的低信噪比微震事件识别与恢复. 地球物理学报, 57(8): 2656–2665.
DOI:10.6038/cjg20140824 |
|
王璐琛, 常旭, 王一博.
2016. 干涉走时微地震震源定位方法. 地球物理学报, 59(8): 3037–3045.
DOI:10.6038/cjg20160826 |
|
 2018, Vol. 61
2018, Vol. 61

