2. 有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Changsha 410083, China
勘探地球物理存在众多方法,如磁法、重力、地震、直流电及电磁勘探等, 人们常根据勘探需求选择不同的方法(Ren et al., 2017).在电磁勘探中,人们在20世纪70年代针对天然场源具有信号弱、极化方向随机、易受噪声干扰等缺点,提出了可控源电磁法(Controlled source electromagnetic method,CSEM) (Goldstein and Strangway, 1975).由于人工场源的加入,可控源电磁法具有信号强度大、数据信噪比高的优点,在近几十年来发展很快且是很有发展前景的勘探方法,在中深部隐伏矿体查明、复杂地区页岩气勘探、地热资源寻找及海洋油气勘探等领域都取得了良好效果(何继善, 1990).
对于一般地电模型来说,可控源电磁法不具备简单的解析解,往往需要寻求可靠的数值解.传统的可控源电磁数值解求解方法可归纳为体积积分法、边界积分法、有限差分法及有限单元法等四种主要算法.有限单元法以网格多样性、计算精度高的特点,被广大学者所采纳.从Coggon (1971)开创了地电磁问题有限元模拟先河后,有限元计算在该领域得到了极大的发展(Pridmore et al., 1981; Unsworth et al., 1993; Stalnaker and Everett, 1999; Mitsuhata, 2000; Badea et al., 2001; 闫述, 2003; 底青云等, 2004; 王若等, 2007; Li et al., 2007; 张继峰, 2008; Kong et al., 2008; 公劲喆, 2009, 汤井田等, 2014; 徐志峰等, 2010; 刘颖, 2011; De Silva et al., 2012; 范翠松, 2013; Ren et al, 2013, 2014; Chung et al., 2014; 汤文武等, 2015; 李勇等, 2015; 杨军等, 2015; 黄威等, 2016).Pridmore等(1981)首先讨论了三维地电磁场的有限单元模拟问题.Unsworth等(1993)对简单2.5维可控源电磁法模型进行了有限元数值模拟.Stalnaker和Everett (1999)采用四面体线性有限单元对三维可控源电磁模拟进行了探索.Mitsuhata (2000)模拟了2.5维可控源电磁法正演模型,分析了场源和地形对电磁场响应的影响.闫述(2003)采用电偶极子源进行了三维可控源电磁模型有限元计算.Li和Key (2007)采用自适应有限元方法实现2.5D海洋可控源电磁法正演.Kong等(2008)利用有限元法实现了2.5D各向异性介质海洋可控源电磁正演.De Silva等(2012)和Chung等(2014)利用矢量有限元法实现了三维可控源电磁正演模拟.Ren等(2013, 2014)分别采用面向目标的自适应有限元法和混合边界元-有限元法实现了平面波区域地电磁法正演模拟.黄威等(2016)采用矢量有限元法实现了基于航空电磁法正演模拟.
上述研究存在一个共同特点:有限元计算基本采用传统截断边界,即在一个相对较大的区域内,将无穷边界问题近似为有限区域进行,这一特点往往造成有限元计算区域大、节点数多、存储量大和计算耗时等问题.较合理的边界处理策略应该为将计算区域限制在较小的目标区域内,减少单元与节点个数,实现节约计算资源和提高计算速度的目的.混合有限元-无限元法为实现这一策略提供了可能.混合有限元-无限元的核心思路是用“无限单元”取代传统截断边界,通过坐标映射将“无限单元”沿某一方向无限扩展,实现电磁场在无限单元中快速衰减为零,最后结合有限元离散内部小区域,从而快速正演模拟.
Ungless (1973)最早给出了无限元基本概念并实现了衰减型无限单元.Zienkiewicz等(1977)提出了Bettes型映射无限元,并将其用于表面水波衍射和折射问题的研究.Astley等(1994)发展出波包映射无限元,并将其应用到无穷边界问题的处理中.之后,无限元在岩土工程、工程力学、电磁散射、声学以及地球物理等众多领域中得到了一定的应用.而在地球物理领域中,无限元思想主要应用于地震、测井和直流电领域.Fu和Wu (2000)应用无限元处理了弹性波吸收边界条件.张玉娥等(2001)和姜忻良等(2004)利用无限元研究了隧道地震反应.Cecot等(2003)、朱军等(2008)应用无限元来处理测井中无穷边界问题. 孙跃(2005)应用无限元模拟了三维直流电阻率法.Blome等(2009)应用Astley无限元处理了直流电法边界问题.公劲喆(2009)在三维直流中成功应用了有限元-无限元耦合法.但在可控源电磁法中,混合有限元-无限元的相关研究鲜为报道,汤井田等(2014)采用迭代法初步实现了基于电场总场公式的3D CSEM混合有限元-无限元计算,初步结果表明:借助无限元思想,计算区域可以大幅度减小,从而提高计算速度.为了开发出更为高效的CSEM 3D正演算法,本研究尝试开发基于二次场的混合有限元-无限元计算算法,进而达到精度与速度的双重提高,另外还借助于目前特别适合于多源CSEM问题的最新并行直接求解技术,进一步加速正演计算速度.
为了达到上述精度与速度的双重提高目的,本文首先从二次电场双旋度方程出发,利用“无限单元”代替传统截断边界条件,采用Garlerkin有限元法通过八节点六面体有限元将“无限单元”耦合,采用散度校正避免节点型有限元伪解现象,采用Pardiso并行直接求解器实现了高精度、低未知数三维CSEM快速正演计算.最后,通过层状模型解析解验证了预期效果.
2 理论 2.1 基本方程水平电偶极子(时间因子e-iωt,ω为角频率)在各向同性导电介质中产生的电场E满足双旋度方程(Nabighian, 1991):
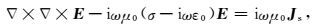
|
(1) |
其中σ为电阻率,Js为电偶极子电流密度矢量, 取空气中和地下介质的磁导率为真空磁导率μ0,介电常数为真空介电常数ε0.
电偶极子源存在奇异性,将总电场分解为背景场(一次场) Ep和感应场(二次场) Es之和,背景场Ep直接利用一维地电模型求解(Kaufman, 1983),Es采用有限元进行求解,从而避免源的奇异性计算:
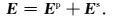
|
(2) |
背景场Ep同样满足电场双旋度方程,式(1) 和式(2) 可得基于二次场Es的双旋度方程:
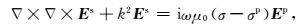
|
(3) |
其中k2=-iωμ0(σ-iωε0),式(3) 为本文的出发方程.一次场Ep利用均匀半空间表面水平电偶极子产生的电磁场进行计算.我们知道,在电性分界面上,电场的法向不连续,节点型有限元要求电磁场法向上必须是连续的,因此求解得到的有限元解往往不准确,需要进行求解校正.在有源区,节点有限元的电场解不满足▽·(εE)=-▽·(J/iω);在无源区域不满足:▽·(εE)=0.需在方程(3) 中加入散度校正条件(Jin, 2002):
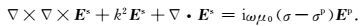
|
(4) |
基于加权余值有限元法(Jin,2002),建立式(4) 的残差公式:
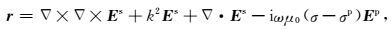
|
(5) |
取任意测试函数V,在区域Ω上令
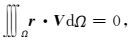
|
则有:
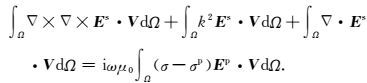
|
(6) |
设S为区域Ω外边界表面.采用无限元代替传统截断边界条件.在无限单元内电磁场衰减为零,因此有:
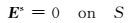
|
(7) |
通过第一矢量Green定理可将式(6) 简化为:
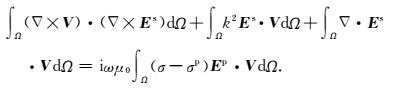
|
(8) |
利用有限元对内部计算区域进行离散.假设内部计算区域内有n个节点,对于第j个测试函数可取:
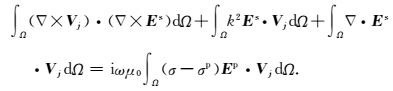
|
(9) |
混合有限元-无限元算法将整个求解区域分为有限元区域和无限元区域,用无限元区域代替传统的外边界,在两个区域分别采取有限元分析和无限元分析,通过总体刚度矩阵组装将两者结合起来从而进行数值求解.
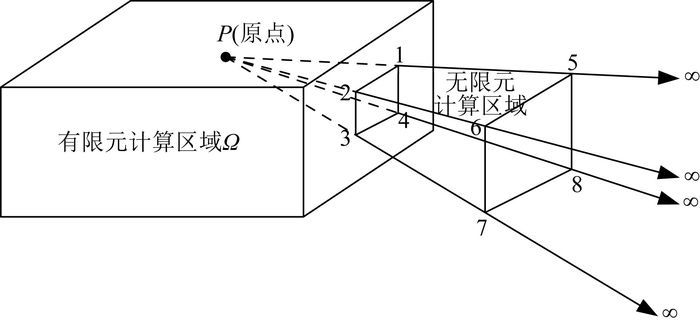
图 1为有限元和无限元计算区域划分示意图.图中有限元区域为目标区域,包含场源、目标体及测点等;无限元区域为有限元区域边界至无穷远,为边界计算区域.无限元分析就是在该区域的某一方向上,采用无限元映射和形函数,将整体坐标映射到局部坐标上来,其原理与有限元分析相同.
|
图 1 有限元和无限元计算区域划分示意图 Fig. 1 Sketch of the calculation domain division of the finite and infinite element method |
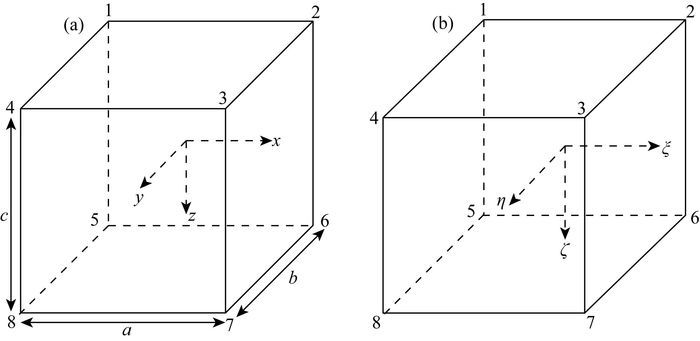
有限元单元分析时,采用矩形六面体进行区域离散,单元节点编号及坐标如图 2所示.
|
图 2 有限元映射示意图 (a)子单元;(b)母单元. Fig. 2 Mapping sketch of the finite element (a) Sub-element; (b) Parent element. |
图 2中子母单元坐标对应关系为:
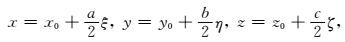
|
(10) |
其中x0,y0,z0为子单元的中点, a, b, c为子单元的三个边长.矩形六面体形函数表达式如下:
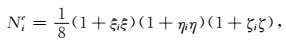
|
(11) |
式中ξi,ηi,ζi是子单元节点i在母单元中的坐标.
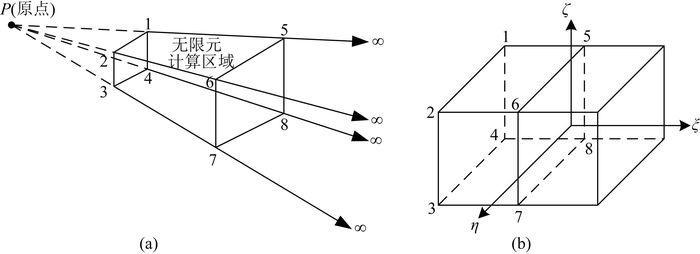
2.3.2 无限元分析无限元单元分析时,采用三维八节点Astley型无限元.图 3为三维无限元映射示意图,图中节点1、2、3、4、5、6、7、8为无限元基本要素.P点为坐标原点,节点1、2、3和4为有限元边界上某单元的四个节点,P点到节点5,6,7,8的距离分别为P点到节点1、2、3、4距离的两倍.无限元分析就是通过无限元映射将无穷坐标映射到图 3b中的局部坐标上.图 3b中无限单元最外围的四个节点为无穷远,其场值为零.
|
图 3 无限元映射示意图 (a)子单元;(b)母单元. Fig. 3 Mapping sketch of the infinite element (a) Sub-element; (b) Parent element. |
图 3b中ξ方向表示无限元映射方向,在ζ-η平面内,无限单元与有限单元采用相同的映射形式和形函数.无限元坐标映射为:
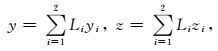
|
(12) |
其中:Li为四边形面积, 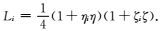
再结合ξ方向的坐标映射关系式,可得到八节点无限单元坐标映射函数:
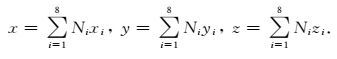
|
(13) |
其中: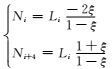
对于无限元形函数,其具体表达式如下:
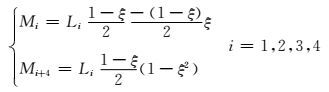
|
(14) |
该形函数是Astley映射无限单元理论(Astley et al., 1994)中采用的形函数中的系数(1-ξ)/2与二阶Lagrange插值多项式的乘积.
有限元与无限元单元分析基本一致,都为八节点单元,因此在数值模拟中,可将无限元和有限元完美结合起来,保证刚度矩阵的对称性,从而使得求解简单、方便.
2.4 方程组求解在CSEM三维数值模拟中,单节点具有x、y、z三个自由度,因此取:
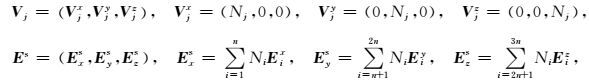
|
(15) |
其中Nj为第j个测点的形函数,其具体形式详见式(11) 和(14).
式(9) 可写成:

|
(16) |
根据矢量旋度公式及散度公式可将式(16) 进行化简并写成矩阵形式:

|
(17) |
其中:

|

|
式(17) 为三维CSEM混合有限元-无限元正演模拟最终形成的大型、稀疏、对称的复系数线性方程组,其中矩阵A为混合有限元-无限元总体刚度矩阵,为3×Nx×Ny×Nz阶方阵,Nx、Ny、Nz分别为x、y、z三个方向上节点总数,矩阵A中每行最多有81个非零元素;x为各节点待求解的电场值;b为右端项,包含异常体和一次场.本文采用性能良好、高度并行化的开源求解器Pardiso求解大型稀疏线性方程组, Pardiso采用LU分解(LU分解是把矩阵分解为上三角矩阵L和下三角矩阵U的乘积)直接求解,特别适合处理多源CSEM问题.
3 精度验证 3.1 三层模型验证采用三层模型.设第一层与第三层电阻率相同,第二层为异常层,以三层层状解析解与均匀半空间解析解之差,构造二次场解析解,将模型三维无限元数值解与二次场解析解进行对比分析,验证程序的正确性.以下数值计算平台均为Intel (R) Xeon (R) CPU 3.10 G,256 GB RAM,16CPUs.
第一层和第三层电阻率为100 Ωm.异常层电阻率为10 Ωm,埋深225 m,层厚100 m.水平电偶极子沿x轴布设,其中心为坐标原点,偶极子长1 m,发射电流为1 A.区域离散采用矩形六面体进行网格剖分,x方向剖分区域为-3000~3000 m,对称剖分,共计120个节点;y方向剖分区域为-3000~3000 m,共计66个节点;z方向剖分区域为-2000~2000 m,共计39个节点,由于电磁场在空气中衰减较慢,因此空气中网格剖分较为稀疏,共计11层;计算频率为256 Hz.网格和计算数据如表 1所示.
|
|
表 1 三层层状模型网格和计算数据 Table 1 Mesh of a three-layer model and calculation data |
图 4为基于本文算法的正演模拟结果与解析解对比图,从图中可以看出,在测线y=1500 m上,二次场值Ex和Ey的数值大小及变化趋势与解析解高度重合.通过误差分析可以看出,二次场Ex实部和虚部最大相对误差为2%,并随着测点靠近中垂线,场值实部虚部相对误差呈现规律性减小,在目标观测区域内相对误差都在1%以内,满足正演精度要求.在图 4d中,二次场值Ey虚部相对误差在1%以下,满足精度要求,但其实部误差较大,约为4%,特别是随着测点靠近中垂线,其相对误差逐渐增大,分析其主要原因:一方面是由于节点有限元方程中直接加入电场散度校正条件造成的,对比分析散度校正前后的结果,发现散度校正降低了中垂线附近Ey实部的精度,但极大地提高了中垂线附近场值Ex的精度;另一方面中垂线附近Ey解析解场值趋近于零、数值小,分析相对误差时分母数值小,所以其相对误差数值较大.通过与解析解对比可以得出,本文算法是正确可靠的,其计算精度在1%以内.

|
图 4 三层层状模型数值解与解析解对比 (a) Ex数值解与解析解对比;(b) Ey数值解与解析解对比;(c) Ex相对误差;(d) Ey相对误差. Fig. 4 Comparison of numerical solution with analytical solution based on a three-layer model (a) Comparison of numerical solution with analytical solution based on Ex; (b) Comparison of numerical solution with analytical solution based on Ey; (c) Relative error of Ex; (d) Relative error of Ey. |
为更好测试本文提出的新的基于二次场CSAMT混合有限元-无限元算法(Secondary field based finite-element and infinite element method, SFEIE)优点,以上述三层层状模型为例,对比了其与基于总场混合有限元-无限元算法(Total field based finite-element and infinite elment method, TFEIE)、基于总场有限元算法(Total field based finite-element method, TFE)、基于二次场有限元算法(Secondary field based finite-element method, SFE)等三种方法的计算性能.
TFEIE算法具体为采用无限元代替传统截断边界条件,直接求解电场总场(汤井田等,2014).TFE算法具体为采用传统截断边界条件,将源附近和边界节点场值作为第一类边界条件直接求解电场总场(汤井田等,2014).SFE算法具体为采用二次电场方案,采用传统截断边界条件,近似认为边界上电场衰减为零,从而数值求解二次电场,与本文提出的SFEIE算法区别在于设置极大的计算区域,采用传统截断边界.
对于以上四种方法采用相同的输入网格,即在目标计算区域内有限元法与混合有限元-无限元法网格剖分相同.图 5为四种算法的精度分析.基于总场和二次场有限元算法场值Ex相对误差明显高于基于总场和二次混合有限元-无限元算法.基于总场混合有限元-无限元算法其相对误差在中垂线附近较大,且存在严重的跳变,这是由于总场法中未加入散度校正条件及场源的加载精度造成的.基于二次场混合有限元-无限元算法其相对误差整体变化平稳,规律性强,相对误差数值小,且全在1%以内.因此,通过四种算法精度对比可以得出,本文提出的基于二次场混合有限元-无限元算法精度最高.

|
图 5 四种算法数值解与解析解对比 (a)场值Ex与解析解对比;(b)四种方法相对误差. Fig. 5 Comparison of numerical solution with analytical solution of four methods (a) Comparison of numerical solution with analytical solution based on Ex; (b) Relative errors of four methods. |
表 2为四种方法的相关计算数据.表 2中可以看出,基于总场混合有限元-无限元算法和基于二次场混合有限元-无限元算法两者离散区域极小,计算区域仅为基于总场和二次场有限元法的1%,相应两者网格单元数和自由度总数也减少了27.03%.在计算内存上,基于二次场混合有限元-无限元算法为四种方法中占用内存最小的,相对于有限元算法其内存减少了42.89%;在计算时间上,混合有限元-无限元算法仅为基于总场有限元法和基于二次场有限元法的45%左右.因此可以说,基于总场和二次场混合有限元-无限元两种方法相对于传统大区域的有限元法具有离散区域小、计算节点少、求解速度快等明显优势.
|
|
表 2 四种方法相关计算数据对比 Table 2 Comparison of related calculation dat of four methods |
综合表 2和图 5可以得出,在四种算法中,本文提出的基于二次场混合有限元-无限元算法其计算性能和求解精度最高,具有离散区域小、计算节点少、求解速度快、计算精度高等明显优势.
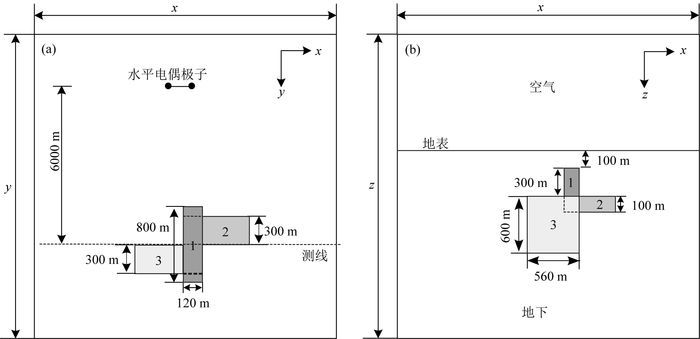
4 模型计算 4.1 三维复杂地电模型复杂地电模型为均匀半空间中存在三个目标异常体,均匀半空间电阻率为100 Ωm,异常体1电阻率为10 Ωm,异常体2电阻率为1 Ωm,异常体3电阻率为10000 Ωm,三个异常体空间位置及尺寸分布详见图 6.
|
图 6 复杂3D地电模型示意图 (a)平面图;(b)断面图. Fig. 6 Sketch of 3D complex geoelectric model (a) Plan; (b) Cross section. |
设直角坐标原点位于水平电偶极子中心,电偶极子AB长1 m,发射电流I为1 A.采用矩形六面体进行网格剖分,x方向剖分区域为-2000~2000 m,对称剖分,共计74个节点,y方向剖分区域为-3000~8000 m,共计61个节点.z方向剖分区域为-3200~2000 m,共计41个节点.采用本文提出的基于二次场无限元法进行正演模拟,计算频率共计21个,具体为(单位Hz):8192、4096、2048、1024、724、512、362、256、181、128、90、64、46、32、23、16、11、8、4、2、1.单频点计算时间约为134 s,正演计算共耗时2810 s.其正演模拟结果拟断面图如图 7所示.

|
图 7 视电阻率拟断面图 (a) 5400线;(b) 5800线;(c) 6200线;(d) 6700线. Fig. 7 Pseudo-section of apparent resistivity (a) Line 5400; (b) Line 5800; (c) Line 6200; (d) Line 6700. |
根据CSEM电磁响应规律,当测线位于异常体上方时,视电阻率会产生相应的电磁响应.从图 7a中可以看出,当测线位于复杂地电模型和源之间时,受复杂地电模型边界效应的影响,正演结果对低阻异常体1和2有轻微的电磁响应;当测线横跨低阻异常体1和2时,图 7b中正演模拟结果对低阻异常体1和低阻异常体2有清晰的响应.但当测线横跨低阻异常体1和高阻异常体3时,即图 7c,正演模拟结果对低阻异常体1有较强的响应,但对高阻异常体3基本没有响应,同时受低阻异常体2的边界效应影响,在拟断面图中右下方中低频段出现一假低阻异常,受低阻体1和2的影响,高阻体3电磁响应全部被低阻响应淹没;随着测线远离异常体,复杂地电模型电磁响应逐渐变小直至消失,如图 7d所示.通过上述研究,可以说基于二次场的无限元程序能够进行三维复杂地电模型的正演模拟.
4.2 场源阴影效应场源阴影效应是指测点和场源之间存在异常地质体,当异常体尺寸足够大时,会对CSAMT测点测深数据造成影响,常常影响人们正确判断地下介质真实情况的一种现象,因此开展场源阴影效应的研究是十分必要的.
图 8所示为场源阴影效应模型.在场源和测线之间存在异常地质体,取异常体电阻率1或10000 Ωm,背景电阻率100 Ωm,异常地质体具体空间位置及大小详见图 8.设直角坐标系原点位于水平电偶极子中心,电偶极子AB长1 m,发射电流I为1 A.采用矩形六面体剖分,异常体x方向共剖分41个网格单元;y方向共剖分16个网格单元;z方向共剖分16个网格单元.主测线位于y=4500 m处.采用基于二次场的无限元法进行正演计算.
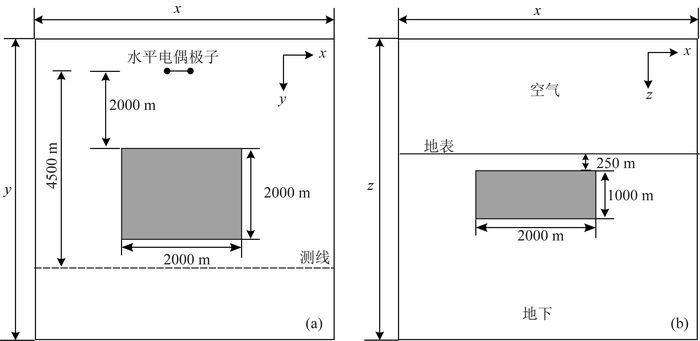
|
图 8 场源阴影效应模型 (a)平面图;(b)剖面图. Fig. 8 Model of source shadow effect (a) Plan; (b) Cross section. |
图 9中测点A坐标为(25 m, 4500 m, 0 m),其中图 9a和图 9b分别为测线与场源间存在低阻地质体和高阻地质体时的视电阻率测深曲线图.从图 9中可以看出,不管是高阻或低阻异常体,在场源阴影效应的影响下,测点A处卡尼亚视电阻率测深曲线在高频段基本重合,在中低频段发生分离.存在低阻地质体时,场源阴影效应较强,使得测点A处视电阻率曲线快速下降,视电阻率值比实际预期低,过渡带及近区特征被低阻淹没.存在高阻地质体时,场源阴影效应强度较弱,视电阻率测深曲线中低频段发生轻微的抬升,视电阻率数值较实际预期高,同时在频率为256 Hz时,测深曲线出现一极小值,可能为CSAMT过渡带特征,与实际测深曲线相比,测点进入过渡带频率提早.
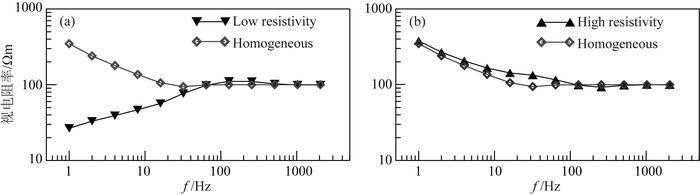
|
图 9 地下异常体的场源阴影效应 (a)低阻体视电阻率测深曲线图; (b)高阻体视电阻率测深曲线图. Fig. 9 Source shadow effect of a subsurface anomalous body (a) Sounding curve of a low-resistivity anomalous body; (b) Sounding curve of a high-resistivity anomalous body. |
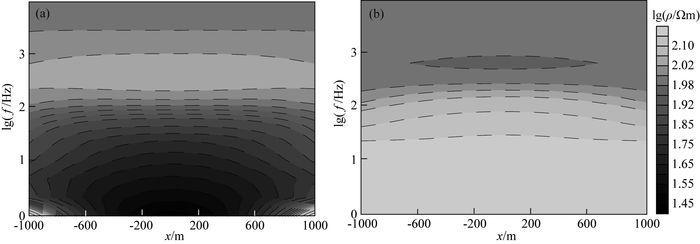
图 10为测线y=4500 m处视电阻率频率拟断面图.从图中可以看出,当频率大于100 Hz时,场源阴影效应基本不存在.当频率低于100 Hz,在测线中低频段出现一假低阻异常,与图 9a中测深曲线低频段数值减小特征吻合,为场源阴影效应影响造成.图 10b中高阻地质体时,场源阴影效应不明显.
|
图 10 场源阴影效应下4500线视电阻率频率拟断面图 (a)低阻地质体; (b)高阻地质体. Fig. 10 Pseudo-section of line 4500 under the source shadow effect (a) Low-resistivity anomalous body; (b) High-resistivity anomalous body. |
综合图 9和10可知,当场源和测线之间存在异常地质体时,场源阴影效应都对测点低频段数据造成分离影响,其分离方向与地质体的视电阻率高低是一致的.低阻体的阴影效应使得测点低频段视电阻率数值严重降低,高阻体的阴影效应使得测点低频段视电阻率升高.但低阻地质体场源阴影效应强于高阻地质体.
5 结论本文从二次电场双旋度控制方程出发,采用Garlerkin法得到了节点型有限元系数矩阵表达式.通过施加散度校正,克服了节点型有限元伪解,采用无限单元代替传统截断边界条件,并通过与有限元结合,极大地缩小了离散区域,实现了低未知数的求解策略,采用直接法求解方程组,实现了小区域基于二次场的三维CSAMT快速高精度正演模拟.
三层层状模型测试表明本文提出的基于二次场CSAMT混合有限元-无限元算法是正确的.数值解与解析解相对误差分析表明:在观测区域内电场Ex分量实部和虚部相对误差均小于1%.而场值Ey由于在中垂线附近为零,其实部相对误差较大在4%以内,虚部相对误差小于1%,满足精度要求.
通过文中四种算法的精度及计算分析表明:本文提出的基于二次场CSAMT混合有限元-无限元模拟新算法相对于传统大区域有限元法,其离散区域仅占1%,节点自由度总数减少27.03%,计算所耗内存减少42.89%,计算时间缩减55%,并且其计算精度最高.因此本文提出的CSAMT模拟新算法具有离散区域小、计算节点少、求解速度快、计算精度高等显著优势.
场源阴影效应模拟表明当测线和场源之间存在异常体时,场源阴影效应会使得测点低频段视电阻率测深曲线发生分离.当测线和场源之间存在低阻异常体时,视电阻率下降,高阻体时,视电阻率升高,且低阻体场源阴影效应强,高阻体场源阴影效应弱.因此为了更好地解释CSAMT数据,必须考虑场源阴影效应的影响.
| Astley R J, Macaulay G J, Coyette J P. 1994. Mapped wave envelope elements for acoustical radiation and scattering. Journal of Sound and Vibration, 170(1): 97-118. DOI:10.1006/jsvi.1994.1048 | |
| Badea E A, Everett M E, Newman G, et al. 2001. Finite-element analysis of controlled-source electromagnetic induction using Coulomb gauged potentials. Geophysics, 66(3): 786-799. DOI:10.1190/1.1444968 | |
| Blome M, Maurer H R, Schmidt K. 2009. Advances in three-dimensional geoelectric forward solver techniques. Geophysical Journal International, 176(3): 740-752. DOI:10.1111/gji.2009.176.issue-3 | |
| Cecot W, Rachowicz W, Demkowicz L. 2003. An hp-adaptive finite element method for electromagnetics. Part 3:A three-dimensional infinite element for Maxwell's equations. International Journal for Numerical Methods in Engineering, 57(7): 899-921. | |
| Chung Y, Son J S, Lee T J, et al. 2014. Three-dimensional modelling of controlled-source electromagnetic surveys using an edge finite-element method with a direct solver. Geophysical Prospecting, 62(6): 1468-1483. DOI:10.1111/gpr.2014.62.issue-6 | |
| Coggon J H. 1971. Electromagnetic and electrical modeling by the finite element method. Geophysics, 36(1): 132-155. DOI:10.1190/1.1440151 | |
| De Silva N V D, Morgan J V, MacGregor L, et al. 2012. A finite element multifrontal method for 3D CSEM modeling in the frequency domain. Geophysics, 77(2): 101-115. DOI:10.1190/geo2010-0398.1 | |
| Di Q Y, Unsworth M, Wang M Y. 2004. 2.5D CSAMT modeling with the finite element method over 2D complex earth media. Chinese Journal of Geophysics, 47(4): 723-730. | |
| Fan C S. 2013. Research on complex resistivity forward and inversion with finite element method and its application[Ph. D. thesis] (in Chinese). Changchun:Jilin University. | |
| Fu L Y, Wu R S. 2000. Infinite boundary element absorbing boundary for wave propagation simulations. Geophysics, 52(2): 596-602. | |
| Goldstein M A, Strangway D W. 1975. Audio-frequency magnetotellurics with a grounded electric dipole source. Geophysics, 40(4): 669-683. DOI:10.1190/1.1440558 | |
| Gong J Z. 2009. Application of finite-infinite element coupling method on 3D direct current and electromagnetic numerical modeling[Master's thesis] (in Chinese). Changsha:Central South University, 34-47. | |
| He J S. 1990. Controlled Source Audio-frequency Magnetotellurics Method. Changsha: Central South University Press: 74-90. | |
| Huang W, Yin C C, Ben F, et al. 2016. 3D forward modeling for frequency AEM by vector finite element. Earth Science-Journal of China University of Geosciences, 41(2): 331-342. DOI:10.3799/dqkx.2016.025 | |
| Jiang X L, Tan D, Jiang N. 2004. 3D Finite and infinite element analysis for seismic response of intersecting tunnel. Journal of Tianjin University, 37(4): 307-311. | |
| Jin J. 2002. The Finite Element Method in Electromagnetics. Wiley. | |
| Kaufman A A. 1983. Frequency and Transient Soundings. Amsterdam:Elsevier Science Ltd. | |
| Kong F N, Johnstad S E, Rosten T, et al. 2008. A 2.5D finite-element-modeling difference method for marine CSEM modeling in stratified anisotropic media. Geophysics, 73(1): F9-F19. DOI:10.1190/1.2819691 | |
| Li Y, Wu X P, Lin P R. 2015. Three-dimensional controlled source electromagnetic finite element simulation using the secondary field for continuous variation of electrical conductivity within each block. Chinese Journal of Geophysics, 58(3): 1072-1087. DOI:10.6038/cjg20150331 | |
| Li Y G, Key K. 2007. 2D marine controlled-source electromagnetic modeling:Part 1-An adaptive finite-element algorithm. Geophysics, 72(2): WA51-WA62. DOI:10.1190/1.2432262 | |
| Liu Y. 2011. Frequency Domain Controlled Source Electromagnetic 3D Finite Element Modeling Based on MPI[Master's thesis] (in Chinese). Changsha:Central South University. | |
| Mitsuhata Y. 2000. 2-D electromagnetic modeling by finite-element method with a dipole source and topography. Geophysics, 65(2): 465-475. DOI:10.1190/1.1444740 | |
| Nabighian M N. 1991. Electromagnetic Methods in Applied Geophysics:Volume 2, Application, Parts A and B. Society of Exploration Geophysicists. | |
| Pridmore D F, Hohman G W, Ward S H, et al. 1981. An investigation of finite element modeling for electrical and electromagnetic data in three dimensions. Geophysics, 46(7): 1009-1024. DOI:10.1190/1.1441239 | |
| Ren Z Y, Chen C J, Pan K J, et al. 2017. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surveys in Geophysics, 38(2): 479-502. DOI:10.1007/s10712-016-9395-x | |
| Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal, 194(2): 700-718. DOI:10.1093/gji/ggt154 | |
| Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2014. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling. Geophysics, 79(6): E255-E268. DOI:10.1190/geo2013-0376.1 | |
| Stalnaker J L, Everett M E. 1999. Finite element analysis of controlled-source electromagnetic induction for near-surface geophysical prospecting. Seg Technical Program Expanded Abstracts, 21(1): 2478. | |
| Sun Y. 2005. Numerical analysis for three-dimensional resistivity model by using finite element infinite element methods. Chinese Journal of Geotechnical Engineering, 27(7): 733-737. | |
| Tang J T, Zhang L C, Gong J Z, et al. 2014. 3D frequency domain controlled source electromagnetic numerical modeling with coupled finite-infinite element method. Journal of Central South University (Science and Technology), 45(4): 1251-1260. | |
| Tang W W, Li Y G, Liu J X, et al. 2015. Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element using secondary electric field. Geophysical Prospecting for Petroleum, 54(6): 665-673. | |
| Ungless R F. 1973. Infinite elements[Master's thesis]. Columbia:University of British Columbia. | |
| Unsworth M J, Travis B J, Chave A D. 1993. Electromagnetic induction by a finite electric dipole source over a 2-D Earth. Geophysics, 58(2): 198-214. DOI:10.1190/1.1443406 | |
| Wang R, Wang M Y, Lu Y L. 2007. Preliminary study on 3D3C CSAMT method modeling using finite element method. Progress in Geophysics, 22(4): 579-585. DOI:10.3969/j.issn.1004-2903.2007.02.035 | |
| Xu Z F, Wu X P. 2010. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method. Chinese Journal of Geophysics, 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 | |
| Yan S. 2003. Studies on the electrical and electromagnetic prospecting based on three-dimensional finite element numerical modeling[Ph. D. thesis] (in Chinese). Xi'an:Xi'an Jiaotong University, 55-60. | |
| Yang J, Liu Y, Wu X P. 2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids. Chinese Journal of Geophysics, 58(8): 2827-2838. DOI:10.6038/cjg20150817 | |
| Zhang J F. 2008. Three dimensional controlled source electromagnetic numerical simulation based on electric field double curl equation using finite element method[Ph. D. thesis] (in Chinese). Changsha:Central South University, 83-107. | |
| Zhang Y E, Niu R M. 2001. Studying on the response of subway tunnel subjected to earthquake loading. Journal of Shijiazhuang Railway Institute, 14(3): 71-74. | |
| Zhu J, Tang Z H, Dun Y Q, et al. 2008. Application of infinite element method (IEM) to 3D electric logging calculation. Natural Gas Industry, 28(11): 59-61. | |
| Zienkiewicz O C, Kelly D W, Bettess P. 1977. The coupling of the finite element method and boundary solution procedures. International Journal for Numerical Methods in Engineering, 11(2): 355-375. DOI:10.1002/(ISSN)1097-0207 | |
| 底青云, UnsworthM, 王妙月. 2004. 复杂介质有限元法2. 5维可控源音频大地电磁法数值模拟.地球物理学报, 47(4): 723–730. | |
| 范翠松. 2013. 基于有限元法的复电阻率正反演研究及应用[博士论文]. 长春: 吉林大学. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013193112.htm | |
| 公劲喆. 2009. 有限元-无限元耦合法在三维直流电和电磁数值模拟中的应用[硕士论文]. 长沙: 中南大学, 34-47. https://max.book118.com/html/2015/0107/11159488.shtm | |
| 何继善. 1990. 可控源音频大地电磁法. 长沙: 中南工业大学出版社: 74-90. | |
| 黄威, 殷长春, 贲放, 等. 2016. 频率域航空电磁三维矢量有限元正演模拟. 地球科学——中国地质大学学报, 41(2): 331–342. | |
| 姜忻良, 谭丁, 姜南. 2004. 交叉隧道地震反应三维有限元和无限元分析. 天津大学学报, 37(4): 307–311. | |
| 李勇, 吴小平, 林品荣. 2015. 基于二次场电导率分块连续变化的三维可控源电磁有限元数值模拟. 地球物理学报, 58(3): 1072–1087. DOI:10.6038/cjg20150331 | |
| 刘颖. 2011. 基于MPI的频率域可控源电磁法三维有限元数值模拟[硕士论文]. 长沙: 中南大学. http://d.wanfangdata.com.cn/Thesis/Y1916247 | |
| 孙跃. 2005. 直流电阻率法的三维有限元无限元数值分析. 岩土工程学报, 27(7): 733–737. | |
| 汤井田, 张林成, 公劲喆, 等. 2014. 三维频率域可控源电磁法有限元-无限元结合数值模拟. 中南大学学报(自然科学版), 45(4): 1251–1260. | |
| 汤文武, 李耀国, 柳建新, 等. 2015. 基于二次电场的可控源电磁法三维矢量有限元正演模拟. 石油物探, 54(6): 665–673. | |
| 王若, 王妙月, 卢元林. 2007. 三维三分量CSAMT法有限元正演模拟研究初探. 地球物理学进展, 22(4): 579–585. DOI:10.3969/j.issn.1004-2903.2007.02.035 | |
| 徐志锋, 吴小平. 2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931–1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 | |
| 杨军, 刘颖, 吴小平. 2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827–2838. DOI:10.6038/cjg20150817 | |
| 张继峰. 2008. 基于电场双旋度方程的三维可控源电磁法有限单元法数值模拟[博士论文]. 长沙: 中南大学, 83-107. http://cdmd.cnki.com.cn/article/cdmd-10533-2009208502.htm | |
| 张玉娥, 牛润明. 2001. 引入无限元的地铁区间隧道地震反应分析. 石家庄铁道学院学报, 14(3): 71–74. | |
| 朱军, 唐章宏, 顿月芹, 等. 2008. 无限元法在三维电测井计算中的应用. 天然气工业, 28(11): 59–61. DOI:10.3787/j.issn.1000-0976.2008.11.016 | |
| 闫述. 2003. 基于三维有限元数值模拟的电和电磁探测研究[博士论文]. 西安: 西安交通大学, 55-60. | |
 2017, Vol. 60
2017, Vol. 60


