2. 中国科学院大学, 北京 100049;
3. 苏黎世联邦理工学院, 苏黎世 8092, 瑞士;
4. 唐山学院, 河北唐山 063020
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ETH, Zurich 8092, Switzerland;
4. Tangshan College, Hebei Tangshan 063020, China
地震波波场模拟(地震正演)和成像(逆时偏移)是勘探地球物理领域两个重要研究方向.高效高精度地震正演算子是地震成像和反演的基础和关键.常用的地震波波场模拟方法可以分为:有限差分法、有限元法、伪谱法和积分方程法等.
有限差分法,具有计算效率高、占用内存较小等优点,且对均匀介质、非均匀介质、各向异性介质均适用,因此被广泛应用于地震正演、偏移成像及反演.Alterman和Karal(1968)首先提出利用有限差分法模拟地震波波场.Virieux(1984)提出了弹性波二阶(时间和空间)交错网格有限差分格式.Bayliss等(1986)采用空间四阶近似精度有限差分算子对弹性波进行了模拟.Levander(1988)将Virieux(1984)的方法发展为时间二阶、空间四阶交错网格有限差分法,提高了计算精度.Crase(1990)发展了任意阶的高阶交错网格有限差分法,提高了地震波波场模拟的精度和稳定性,但计算量和内存要求相比于低阶交错网格有限差分法大幅增加.Graves(1996)、董良国等(2000)、裴正林和牟永光(2003)等将高阶交错网格有限差分法用于模拟三维弹性波传播问题.Robertsson等(1994)提出有限差分法模拟任意起伏地表弹性和黏弹性介质中地震波传播.然而,由于常规有限差分通过泰勒级数展开得到差分系数(Dablain, 1986),在数值计算中需要注意数值频散和稳定性.为了优化基于泰勒级数展开得到的有限差分系数,国内外地球物理学者提出了许多改进方法,其核心思想是采用优化的有限差分算子减小数值频散(Takeuchi and Geller, 2000; Chu et al., 2009).Liu和Sen(2009)基于时间-空间域的频散关系和平面波理论,提出了求解双程波动方程的有限差分格式,随后又提出自适应的变长度空间算子(Liu and Sen, 2011),在保证精度的前提下,节省了计算量.杜启振等(2010)通过引入强约束条件和弱约束条件,构造不同的Lagrange函数得到优化的差分系数.上述优化方法都是通过拟合精确的频散关系得到优化差分系数,能够提高计算精度和稳定性.为了抑制数值频散,空间网格的大小通常比地震波长小8~10倍.而为了满足稳定性条件,时间采样间隔需取得较小.因此,为了达到地震波波场模拟精度,基于泰勒级数展开的有限差分方法,由于空间和时间采样不能太大,导致其计算量很大.
伪谱法由Gazdag(1981)、Kosloff和Baysal(1982)把它应用到勘探地球物理领域,首次利用伪谱法对声波波动方程进行了地震波波场数值模拟,并与解析解和超声波物理模拟结果作了比较,证明了该方法的有效性.伪谱法可以看作是二阶近似差分法的推广,该算法在求解方程时,通过对空间坐标的微分实施快速傅里叶变换,避免了对空间坐标的差分运算,只在时间上作差分计算,从而大大加快了计算速度,并节省大量计算内存.Fornberg(1987)讨论了伪谱法的基本特性,并与有限差分法进行了比较.Tessmer等(1992)则通过引入映射函数处理起伏地表,并采用伪谱法进行了弹性波波场模拟.与有限差分方法相比,伪谱法通过对空间坐标的微分实施快速傅氏变换,求取空间导数.因此,在空间采样上可以达到Nyquist采样极限,具有很高的空间精度.由于伪谱法多次利用快速傅里叶正变换和反变换,其计算量相对于有限差分有所增加.但随着高性能计算集群和GPU的发展,伪谱法多次快速傅里叶正反变换的计算量可得以缓解.然而,由于伪谱法二阶时间差分格式在时间方向上精度较低,且对于大步长时间采样间隔,伪谱法仍然存在数值误差和不稳定现象.
针对上述伪谱法缺点,拟解析法解决了常规伪谱法中二阶时间差分格式精度较低的问题.拟解析法首先由Etgen和Brandsberg-Dahl(2009)提出,类似于Lax-Wendroff方法的补偿思想:利用空间导数项,近似补偿时间二阶导数离散产生的误差(Chen, 2011).Lax-Wendroff方法利用空间的高阶导数项来近似代替高阶时间差分, 补偿时间二阶差分近似所造成的误差,从而提高了时间精度(Lax and Wendroff, 1960; Carcione et al., 2002; Chen, 2007).拟解析法(Etgen and Brandsberg-Dahl, 2009; Crawley et al., 2010a, b)可以在波数域修正拉普拉斯算子.在波数-空间域,利用拟Laplacian算子,可以补偿因时间二阶差分而造成的解析误差,从而压制时间方向二阶差分格式造成的误差.在速度变化缓慢的情况下,拟解析法可以有效地消除时间方向的数值频散.对于速度变化不是太剧烈的模型,拟解析法可以通过级联几个恒定补偿速度的拟拉普拉斯算子,补偿由于二阶时间差分引起的误差.但当速度变化较为剧烈时,Etgen和Brandsberg-Dahl(2009)指出可采用多个常速下的拟Laplacian算子进行速度插值,近似变速的拟Laplacian算子.虽然采用速度插值策略(3~5个参考补偿速度)对于各向同性介质可取得较好效果,但对于各向异性介质(VTI或TTI)效果较差,因拟Laplacian算子不仅包括速度,而且还包含各向异性等参数,其需要组合速度和各向异性参数对拟Laplacian算子进行插值,不仅计算量增大,且拟解析法在时间和空间上均会产生较大误差.
针对:(1) 常规伪谱法在时间方向上二阶差分格式精度较低,且对于大步长时间采样间隔,伪谱法不稳定;(2) 拟解析法对于速度变化剧烈的模型,模拟出的地震波场在时间和空间上均有较大的误差.在声波拟解析法的基础上,本文提出了一种求解弹性波解耦二阶位移方程的优化拟解析法,该方法将声波归一化拟拉普拉斯算子改进为弹性波优化归一化拟拉普拉斯算子,利用弹性波拟微分算子表示弹性波优化归一化拟拉普拉斯算子,该算子不仅包括原始拟微分算子的谱估计,而且还包含一个时间补偿项.弹性波优化拟微分算子不能直接应用空间快速傅里叶变换进行计算,若直接计算,其计算量较大.为了减少计算量,本文对弹性波优化拟微分算子中的象征,采用低秩分解近似方法进行分解.最后,分别采用2-D均匀模型、层状模型和部分盐丘模型正演模拟,测试本文方法在时间和空间上的精度和计算效率,并与常规的伪谱法和拟解析法进行对比.
2 方法理论 2.1 二阶位移P波、S波解耦弹性波方程二阶位移常密度弹性波方程式为:
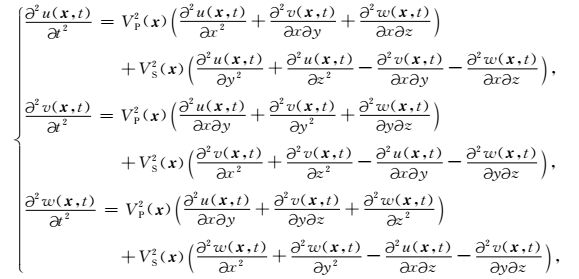
|
(1) |
其中,x为空间矢量,VP(x)和VS(x)分别为纵波速度与横波速度,u(x, t)、v(x, t)、w(x, t)分别为质点在混合波场作用下,在三个方向上产生的位移分量.
在式(1) 中,位移分量时间二阶差分的计算,不仅与纵波速度VP(x)有关,还与横波速度VS(x)有关,使得我们不能直接应用下文所提出的弹性波优化拟微分算子,所以将式(1) 分解为与其等效的P波、S波解耦的弹性波方程(马德堂和朱光明, 2003),公式为:
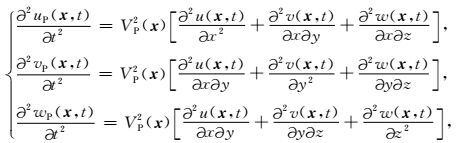
|
(2) |
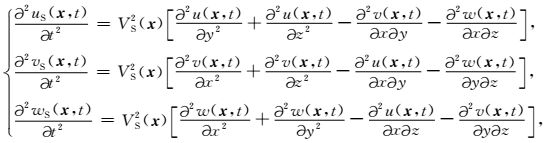
|
(3) |
其中,式(2) 为P波解耦弹性波方程,式(3) 为S波解耦弹性波方程.uP (x, t)、vP (x, t)、wP (x, t)分别为质点在P波作用下,在三个垂直方向产生的位移分量;uS(x, t)、vS(x, t)、wS(x, t)分别为质点在S波作用下,在三个方向产生的位移分量.那么,质点在混合波场作用下,在三个方向的位移分量u(x, t)、v(x, t)、w(x, t)以及P波、S波波场p(x, t)、s(x, t)可以表示为:
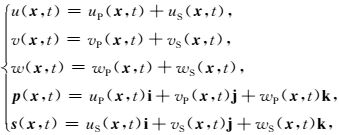
|
(4) |
其中,i、j、k为分别为坐标单位矢量.
空间位移矢量为:

|
(5) |
上述解耦的弹性波方程可以在延拓矢量波场的同时,分解并延拓纯纵波和纯横波波场.
2.2 弹性波优化拟微分算子各向同性常密度声波方程可写为:

|
(6) |
其中,U(x, t)为地震声压波场,v(x)为地震波波速,▽2为拉普拉斯算子.
在v(x)=v(常数)的假设条件下,拟拉普拉斯算子(二阶波数-空间算子)(Etgen and Brandsberg-Dahl, 2009)F(k)为:
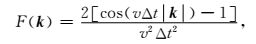
|
(7) |
其中,k为空间波数矢量.
由式(6) 和式(7) 可得波数-空间域拟解析法公式为:

|
(8) |
在时间-空间域,拟解析法表达式为:

|
(9) |
其中,FFT表示空间快速傅里叶正变换,FFT-1表示空间快速傅里叶反变换.
对于均匀介质,式(9) 中的空间快速傅里叶反变换可直接应用,并且式(9) 可提供解析解或近似解析解;对于非均匀介质,速度随空间变化时,不能直接应用(9) 式中空间快速傅里叶反变换.
为了更为精确地补偿二阶有限差分引起的时间误差,本文将式(7) 中拟拉普拉斯算子的恒定补偿速度v,替换为随空间变换的真实速度v(x).那么,拟拉普拉斯算子可改写为:
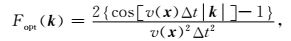
|
(10) |
其中,Fopt(k)称为优化拟拉普拉斯算子(Yan and Liu, 2016),是波数矢量k的函数,且与空间网格坐标有关,即与速度有关.
将式(10) 中的余弦函数使用泰勒展开,那么优化拟拉普拉斯算子可改写为:

|
(11) |
将(11) 替换(8) 中F(k),相应地,频率-空间域优化拟解析法可改写为:
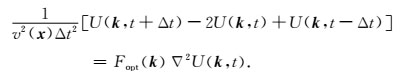
|
(12) |
在时间-空间域,式(12) 可写为任意阶Lax-Wendroff格式(Chen, 2007, 2009, 2011),公式为:
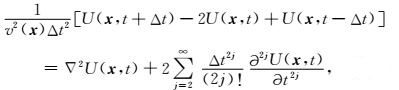
|
(13) |
其中:
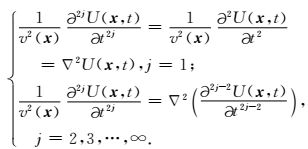
|
很明显,Lax-Wendroff格式利用空间导数项来近似补偿时间二阶导数的离散误差.
根据Chu和Stoffa(2010)提出的归一化拟拉普拉斯算子:
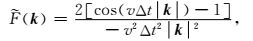
|
(14) |
将式(10) 优化拟拉普拉斯算子,改进为优化归一化拟拉普拉斯算子(Yan and Liu, 2016):
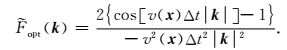
|
(15) |
由于式(15) 只能应用到标量声波方程,而本文用到的地震波方程为弹性波方程,那么弹性波优化归一化拟拉普拉斯算子可表示为:
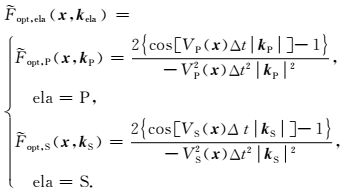
|
(16) |
其中,kP、kS分别为P波、S波空间波数矢量,ela=P, S表示P波和S波.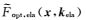
拟微分算子可以看作是微分算子的推广和一般形式,可以用傅里叶积分形式表示为(Wong, 1991):

|
(17) |
其中,α(x, kela)称为拟微分算子A的象征,E(kela, t)为位移矢量E(x, t)的空间傅里叶变换.
对于二阶微分算子和拟微分算子,本文将象征α(x, kela)改写为:
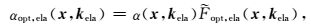
|
(18) |
其中,

|
(19) |
该算子不仅包括原始拟微分算子的谱估计,而且还包含一个时间补偿项.该时间补偿项可在波数-空间域精确地补偿二阶时间差分引起的误差.补偿速度在方程(16) 中为介质实际速度,因此,弹性波优化拟微分算子可以在空间每个网格点上,精确地补偿二阶时间差分引起的误差.
我们将Aopt, ela[E(x, t)]简记为:

|
(20) |
其中,FT-1表示空间傅里叶反变换.
那么,在式(2)(ela=P时)与式(3)(ela=S时)中,二阶微分算子

|
(21) |
由于弹性波优化拟微分算子中包含随空间坐标变化的P波、S波补偿速度vP (x)、vS(x),所以方程(20) 不能直接应用空间快速傅里叶变换进行计算.若直接计算方程(20),其计算量为O(Nx2)×2,其中Nx为3维网格总数.为了减少计算量,本文对优化拟微分算子中的象征,采用低秩分解近似方法.
可分低秩分解近似主要思想是:选取N个代表性的空间位置和M个代表性的波数,近似原始波数-空间混合域算子(Fomel, 2010, 2012).本文将象征近似分解为:
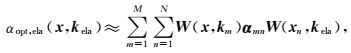
|
(22) |
其中,W(x, km)是象征αopt, ela(x, kela)的子矩阵, 其由与km有关的特定的列元素组成;W(xn, kela)是象征αopt, ela(x, kela)的另一个子矩阵,其由与xn有关的特定行元素组成;αmn代表中间的系数矩阵.
重新组合式(22) 可以加速计算Aopt, ela[E(x, t)],那么Aopt, ela[E(x, t)]可改写为:
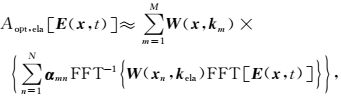
|
(23) |
式(23) 的计算量相当于应用N×2次空间快速傅里叶变换,其计算量为O(NNxlogNx)×2.N一般为一个很小的整数,其大小与式(23) 矩阵分解的秩有关.
3 模型试验 3.1 简单模型 3.1.1 均匀模型点源响应本文采用2-D均匀模型,其在X方向和Z方向采样间隔均为15 m.横波和纵波速度分别为1500 m·s-1、2500 m·s-1.Ricker子波的主频为20 Hz, 最大频率为50 Hz.震源位于模型中心,并同时产生纵波和横波.每个波场占最小网格点数为:1500/15/50=2个,这已达到Nyquist采样定理极限.为了观察到由于边界反射造成的转换波,所以本次模型试算不采用吸收边界条件.
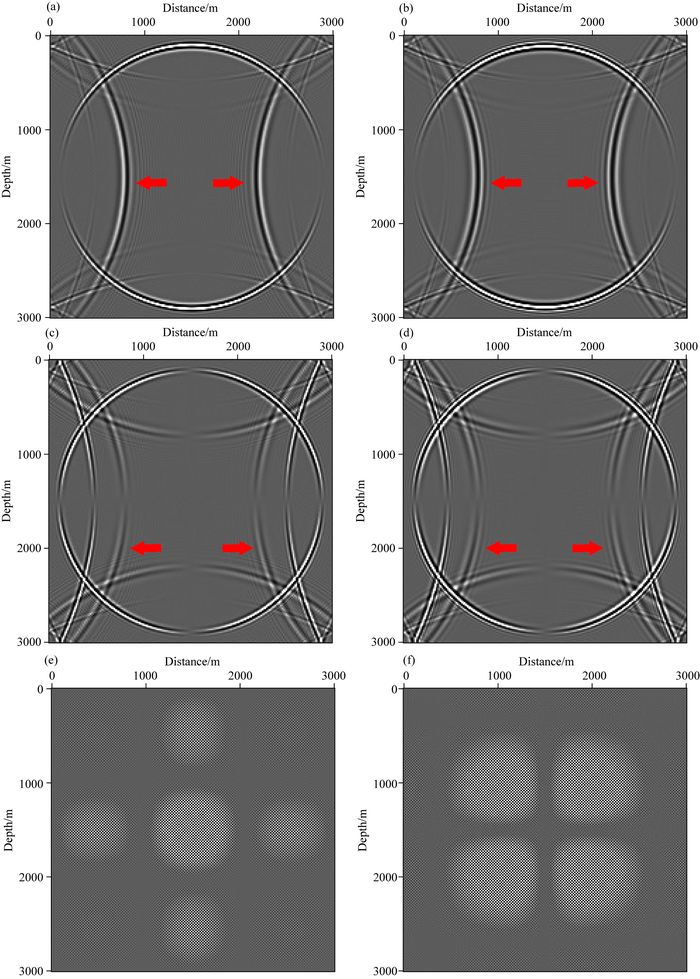
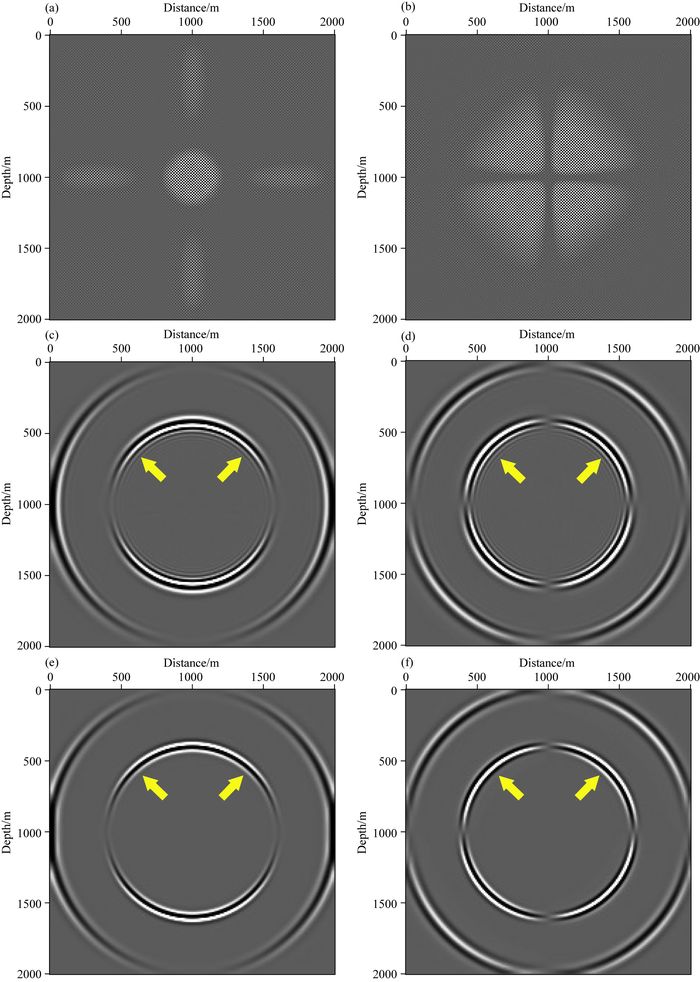
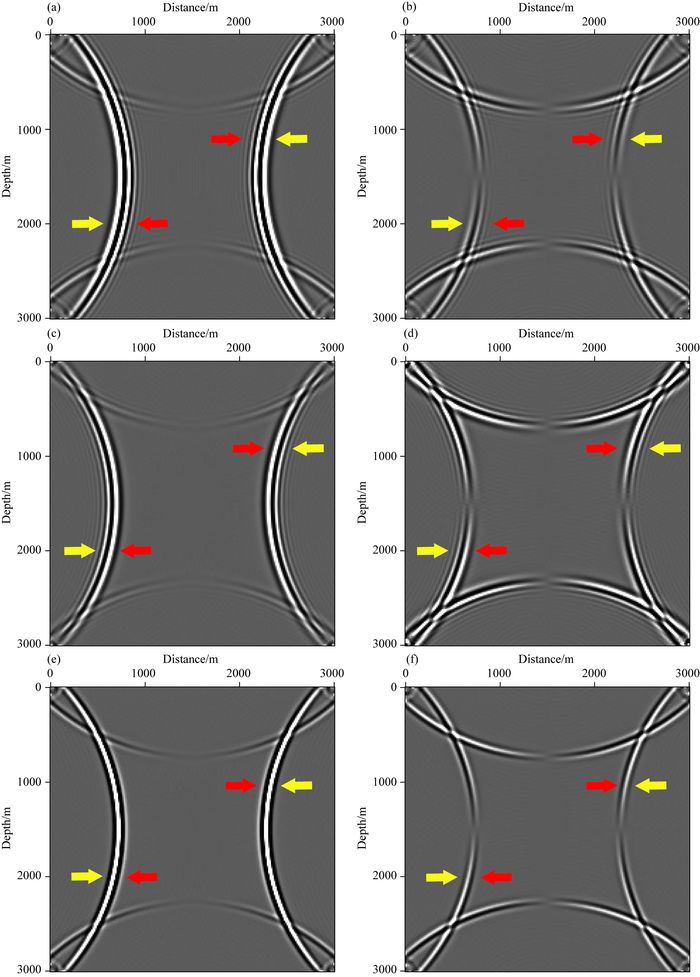
为测试本文提出的优化拟解析法,并与常规伪谱法和拟解析法进行对比.将这三种方法应用到上述2-D模型.图 1a—f分别显示了伪谱法不同时刻X方向和Z方向波场快照,其中图 1a和图 1c采样时间间隔为1.5 ms;图 1b和图 1d采样时间间隔为2.5 ms;图 1e和图 1f时间采样间隔为3 ms.图 2a和b为拟解析法得到的X方向和Z方向波场快照,采样时间间隔为2.5 ms.其中,纵波和横波补偿速度分别为3500 m·s-1和2500 m·s-1.图 3a—d为优化拟解析法得到的X方向和Z方向波场快照,除了采样时间间隔,采用的正演模拟参数与伪谱法一致;其中图 3a和b时间采样间隔为2.5 ms;图 3c和d时间采样间隔为4 ms.图 4a—d为优化拟解析法分离出的纯纵波和纯横波波场快照.
|
图 1 二维均匀弹性介质(VP =2500 m·s-1,VS=1500 m·s-1)伪谱法计算得到的波场快照 (a) X分量(Δt=1.5 ms);(b) X分量(Δt=2.5 ms);(c) Z分量(Δt=1.5 ms);(d) Z分量(Δt=2.5 ms);(e) X分量(Δt=3 ms);(f) Z分量(Δt=3 ms). Fig. 1 Wavefield snapshots in a 2-D homogeneous elastic medium (VP=2500 m·s-1, VS=1500 m·s-1) computed using the pseudo-spectral method (a) X component (Δt=1.5 ms); (b) X component (Δt=2.5 ms); (c) Z component (Δt=1.5 ms); (d) Z component (Δt=2.5 ms); (e) X component (Δt=3 ms); (f) Z component (Δt=3 ms). |

|
图 2 二维均匀弹性介质(VP =2500 m·s-1,VS=1500 m·s-1),拟解析法计算得到的波场快照 (a) X分量(Δt=2.5 ms);(b) Z分量(Δt=2.5 ms). Fig. 2 Wavefield snapshots in a 2-D homogeneous elastic medium (VP=2500 m·s-1, VS=1500 m·s-1) computed using the pseudo-analytical method (a) X component (Δt=2.5 ms); (b) Z component (Δt=2.5 ms). |

|
图 3 二维均匀弹性介质(VP=2500 m·s-1,VS=1500 m·s-1),优化拟解析法计算得到的波场快照 (a) X分量(Δt=2.5 ms);(b) Z分量(Δt=2.5 ms);(c) X分量(Δt=4 ms);(d) Z分量(Δt=4 ms). Fig. 3 Wavefield snapshots in a 2-D homogeneous elastic medium (VP=2500 m·s-1, VS=1500 m·s-1) computed using the optimized pseudo-analytical method (a) X component (Δt=2.5 ms); (b) Z component (Δt=2.5 ms); (c) X component (Δt=4 ms); (d) Z component (Δt=4 ms). |
|
图 4 二维均匀弹性介质(VP=2500 m·s-1,VS=1500 m·s-1)三种方法得到的波场快照(Δx=Δy=10 m,Δt=2.5 ms) (a) X分量(伪谱法);(b) Z分量(伪谱法);(c) X分量(拟解析法);(d) Z分量(拟解析法);(e) X分量(优化拟解析法);(f) Z分量(优化拟解析法). Fig. 4 Wavefield snapshots in a 2-D homogeneous elastic medium (VP=2500 m·s-1, VS=1500 m·s-1) computed using three methods (dx=dy=10 m, Δt=2.5 ms) (a) X component (pseudo-spectral method); (b) Z component (pseudo-spectral method); (c) X component (pseudo-analytical method); (d) Z component (pseudo-analytical method); (e) X component (optimized pseudo-analytical method); (f) Z component (optimizedpseudo-analytical method). |
在时间采样间隔较小的情况下(Δt=1.5 ms),图 1a和c均未出现时间频散(红色箭头所示),但是,当时间采样间隔由1.5 ms增加为2.5 ms时,尽管伪谱法仍然具有很高的空间精度,但有明显的时间频散.当时间采样间隔由2.5 ms增加为3.0 ms时,伪谱法已经不稳定,因为采样时间间隔超过了CFL(收敛条件)数2.7.因此可得出:在时间采样间隔变大时,虽然伪谱法的空间精度很高,但是容易出现时间频散和不稳定现象.
从图 2中可看出,尽管拟解析法可以有效地补偿时间误差,但由于补偿速度大于实际介质速度,空间误差(黄色箭头所示),明显增加.在速度变化剧烈的情况下,即使级联多个恒速补偿拟拉普拉斯算子,拟解析法也会产生空间误差.
将图 3分别与图 1、图 2对比分析可知:优化拟解析法所得到的波场快照(Δt=2.5 ms)比常规伪谱法(Δt=1.5 ms)频散更小;在相同采样时间间隔(Δt=2.5 ms)下,优化拟解析法比拟解析法频散更小.优化拟解析法的另一个优点是稳定性条件比较宽松,这由图 3c和d可知.图 3c和d为优化拟解析法得到的波场快照,其中时间采样间隔为4 ms, 其大于CFL数0.27,但是优化拟解析法仍然稳定.
当空间采样间隔15 m时,理论上最高频率50 Hz处的空间频散已经比较严重,为了进一步证明本文方法的有效性,我们将X方向和Z方向的空间采样间隔由15 m降低为10 m,分别使用伪谱法、拟解析法以及优化拟解析法进行正演模拟,时间采样间隔Δt=2.5 ms,波场快照如图 4所示.图 4a和b为伪谱法得到的X分量和Z分量,图 4c和d为拟解析法得到的X分量和Z分量,图 4e和f为优化拟解析法得到的X分量和Z分量.
分别对比三种测试方法得到的X分量以及Z分量,观测结果表明:当空间采样间隔为10 m,时间采样间隔为2.5 ms时,伪谱法已经不稳定;虽然拟解析法、优化拟解析法仍然稳定,但优化拟解析法的空间频散比拟解析法更少.
对于计算效率,在均匀介质情况下,每一个归一化的拟拉普拉斯算子通过低秩分解近似,其秩为2.这意味着相比较于常规的伪谱法,计算归一化的拟拉普拉斯算子需要额外2次快速傅里叶变换.但是,优化拟解析法能够适用于比较大的时间采样间隔,这将节约不少计算时间.表 1为不同方法在不同采样时间间隔条件下的计算时间(不同硬件条件下会有所有差别).其中,正演模拟时间长度为975 ms,空间间隔Δx=15 m.在Δt=3.0 ms和Δt=4.0 ms时:伪谱法已经不稳定,拟解析法虽然稳定,但是空间频散严重;优化拟解析法无论时间频散还是空间频散,均优于传统的伪谱法和拟解析法;且此情况下,优化拟解析法正演所需要的时间已经低于伪谱法.
|
|
表 1 三种正演方法计算时间对比 Table 1 Comparison of calculation time of three forward modeling methods |
此外,基于解耦的弹性波方程,我们可以在延拓矢量波场的同时,也可将矢量波场分解为纯纵波和纯横波,这在弹性波成像(如逆时偏移)时显得非常重要.图 5与图 6分别为时间采样间隔为2.5 ms时,从图 1、图 2、图 3中分离出的纯P波和纯S波分量.图 7为时间采样间隔为4 ms时,从图 3c和d中分离出的纯P波和纯S波.
|
图 5 P波X、Z分量对比图 (a) P波X分量(伪谱法);(b) P波Z分量(伪谱法);(c) P波X分量(拟解析法);(d) P波Z分量(拟解析法);(e) P波X分量(优化拟解析法);(f) P波Z分量(优化拟解析法). Fig. 5 Comparison of X and Z components of P waves for different methods (a) P-wave model of X component (pseudo-spectral method); (b) P-wave model of Z component (pseudo-spectral method); (c) P-wave model of X component (pseudo-analytical method); (d) P-wave model of Z component (pseudo-analytical method); (e) P-wave model of X component (optimized pseudo-analytical method); (f) P-wave model of Z component (optimized pseudo-analytical method). |
|
图 6 S波X、Z分量对比图 (a) S波X分量(伪谱法);(b) S波Z分量(伪谱法);(c) S波X分量(拟解析法);(d) S波Z分量(拟解析法);(e) S波X分量(优化拟解析法);(f) S波Z分量(优化拟解析法). Fig. 6 Comparison of X and Z components of S wave for different methods (a) S-wave model of X component (pseudo-spectral method); (b) S-wave model of Z component (pseudo-spectral method); (c) S-wave model of X component (pseudo-analytical method); (d) S-wave model of Z component (pseudo-analytical method); (e) S-wave model of X component (optimized pseudo-analytical method); (f) S-wave model of Z component (optimized pseudo-analytical method). |
|
图 7 从图 3(c)和图 3(d)中分离出的波场快照 (a)纵波X分量;(b)纵波Z分量;(c)横波X分量;(d)横波Z分量. Fig. 7 Separated wavefield snapshots from Fig. 3 (c) and Fig. 3 (d) (a) P-wave model of X component; (b) S-wave model of X component; (c) P-wave model of Z component; (d) S-wave model of Z component. |
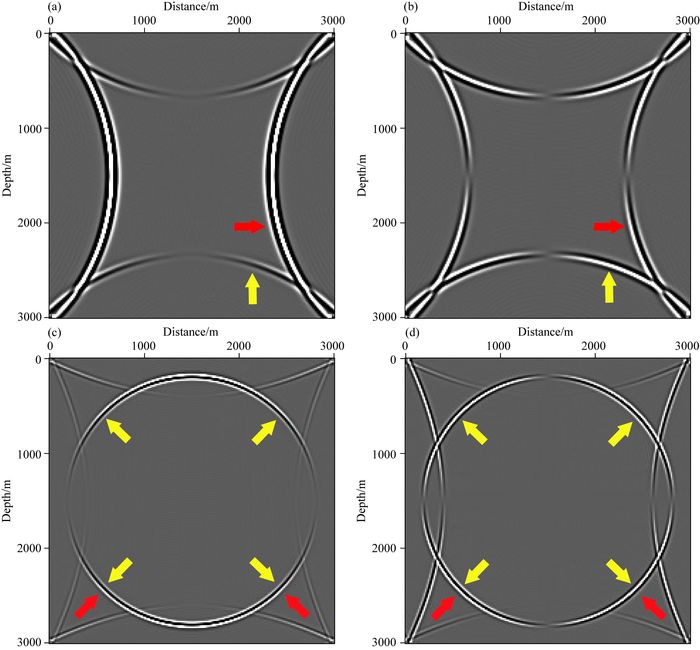
在采样时间间隔2.5 ms情况下,分别对比图 5、图 6、图 7中的伪谱法、拟解析法和优化拟解析法纵横波的X分量和Z分量,也说明:拟解析法相较于伪谱法在减少时间频散的同时,产生了空间频散;且在时间间隔4 ms情况下,图 7优化拟解析法得到的纵横波的X分量和Z分量,无论是时间频散还是空间频散的精度,都优于伪谱法和拟解析法,且时间采样间隔更大,将节省计算时间.
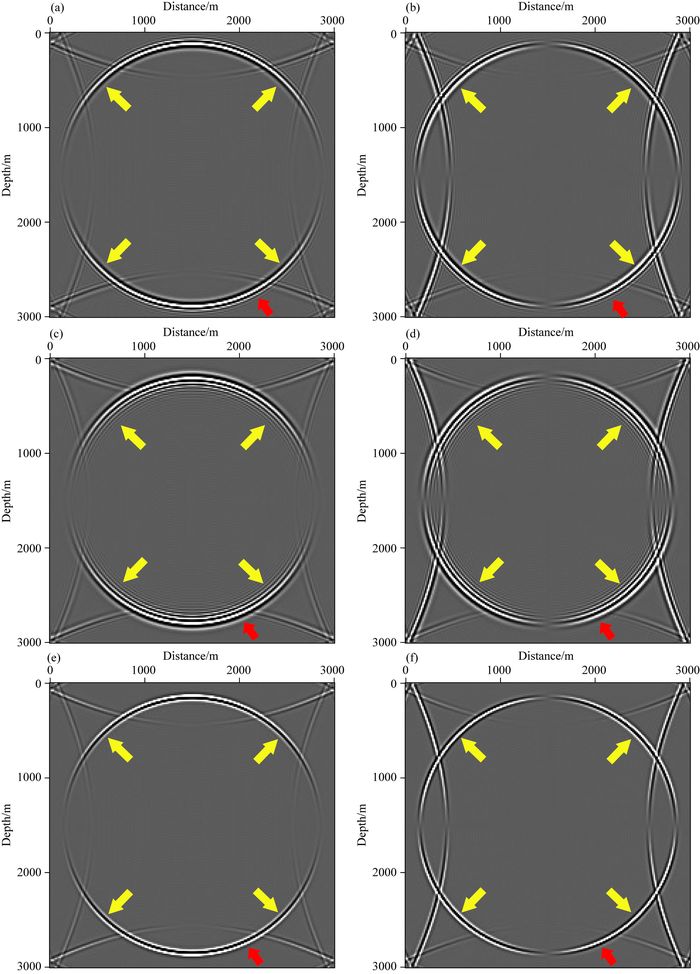
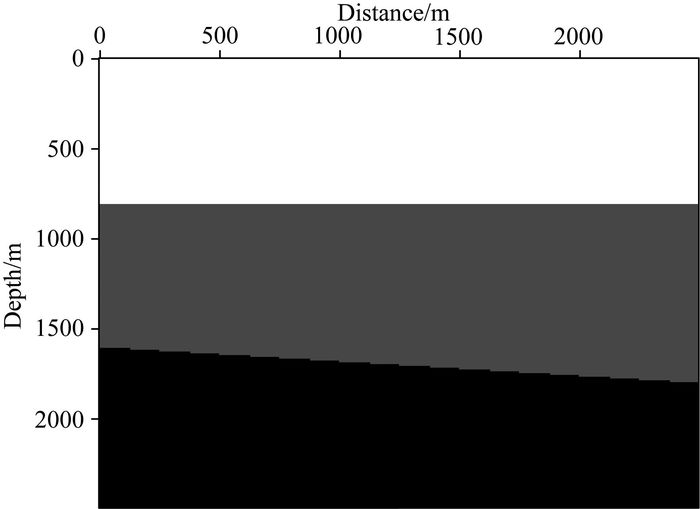
3.1.2 二维层状模型测试下面对二维层状模型应用本文提出的优化拟解析法,并与伪谱法以及拟解析法进行对比.二维层状模型包括上部一个水平反射层和下部一个倾斜反射层,倾斜反射层为阶梯界面.从上到下,每层的纵波速度为:2000 m·s-1、2350 m·s-1、2500 m·s-1,横波速度为:1500 m·s-1、1800 m·s-1、2300 m·s-1.模型区域大小为250×250,水平方向和垂直方向网格间距均为10 m,如图 8所示(纵波速度模型).正演模拟采用Richer子波,主频为30 Hz,可同时产生纵波和横波.波场模拟的时间采样间隔为1.5 ms,地震记录总的时间采样点数为1501个.炮点位于模型网格点(125, 5) 处,检波器均匀分布于模型整个表面.图 9为t=1.2 s时刻的X分量和Z分量波场快照,图 9a和b、图 9c和d、图 9e和f分别为优化拟解析法、拟解析法、伪谱法得到的X分量和Z分量.图 10为X分量单炮记录,图 11为图 10中X分量单炮记录局部放大.
|
图 8 倾斜层状模型 Fig. 8 Inclined layered model |

|
图 9 二维倾斜层状模型,三种方法得到的波场快照(Δt=1.5 ms) (a) X分量(伪谱法);(b) Z分量(伪谱法);(c) X分量(拟解析法);(d) Z分量(拟解析法);(e) X分量(优化拟解析法);(f) Z分量(优化拟解析法). Fig. 9 Wavefield snapshots in a 2-D inclined layered elastic model computed using three methods (Δt=1.5 ms) (a) X component (pseudo-spectral method); (b) Z component (pseudo-spectral method); (c) X component (pseudo-analytical method); (d) Z component (pseudo-analytical method); (e) X component (optimized pseudo-analytical method); (f) Z component optimized pseudo-analytical method). |
|
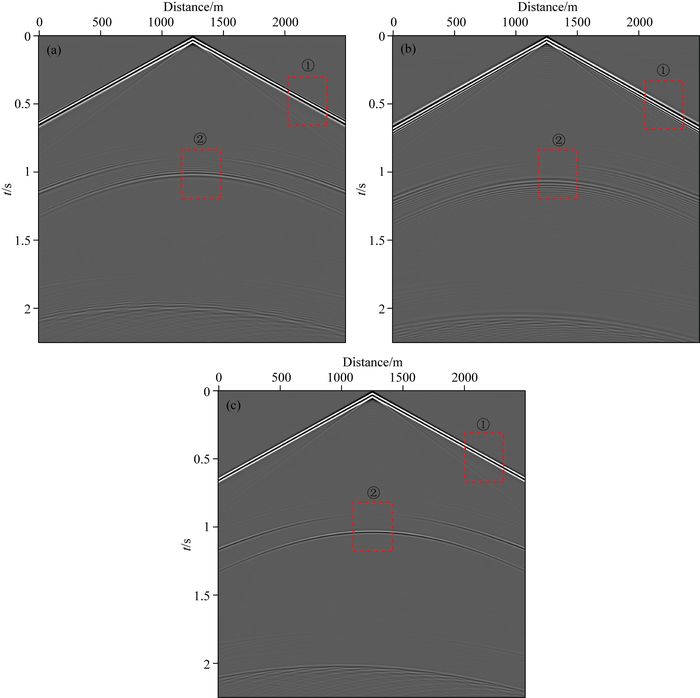
图 10 水平分量单炮记录 (a)伪谱法;(b)拟解析法;(c)优化拟解析法. Fig. 10 Horizontal component of single-shot seismogram (a) Psudo-spectral method; (b) Psudo-analytical method; (c) Optimized psudo-analytical method. |
对图 9中三种方法得到的波场快照进行对比分析得出:在时间采样间隔1.5 ms时,伪谱法具有明显的时间频散;拟解析法虽然压制了时间频散,但是由于补偿速度大于实际速度,会产生空间频散;优化拟解析法,在压制时间和空间频散上,优于伪谱法和拟解析法.
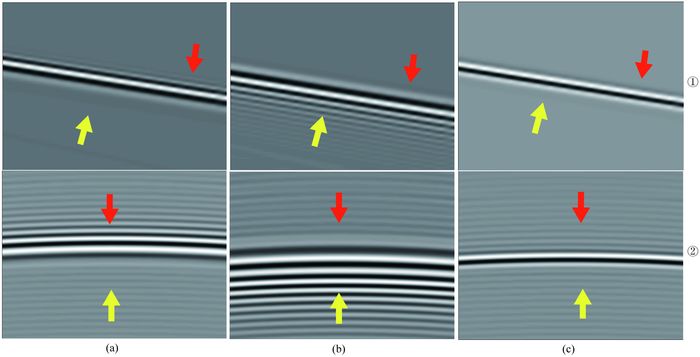
将图 10a—c中红色方框①② 部分局部放大,分别对应图 11a—c中① 和②.可以观察到方块① 中:图 11a伪谱法,直达波有明显的时间频散,图 11b拟解析法,很好的压制了时间频散,但是有较严重的空间频散,图 11c优化拟解析法,在压制时间频散的同时,也消除了拟解析法由于补偿速度选取过大产生的空间频散;方块② 中同样如此.
|
图 11 水平分量单炮记录局部放大 (a)伪谱法;(b)拟解析法;(c)优化拟解析法. Fig. 11 Zoom of horizontal component in single-shot seismogram (a) Psudo-spectral method; (b) Psudo-analytical method; (c) Optimized-psudo-analytical method. |
倾斜层状模型的数值模拟也证明:优化拟解析法在压制时间频散和空间频散上,相较于传统的伪谱法和拟解析法,更有优势.
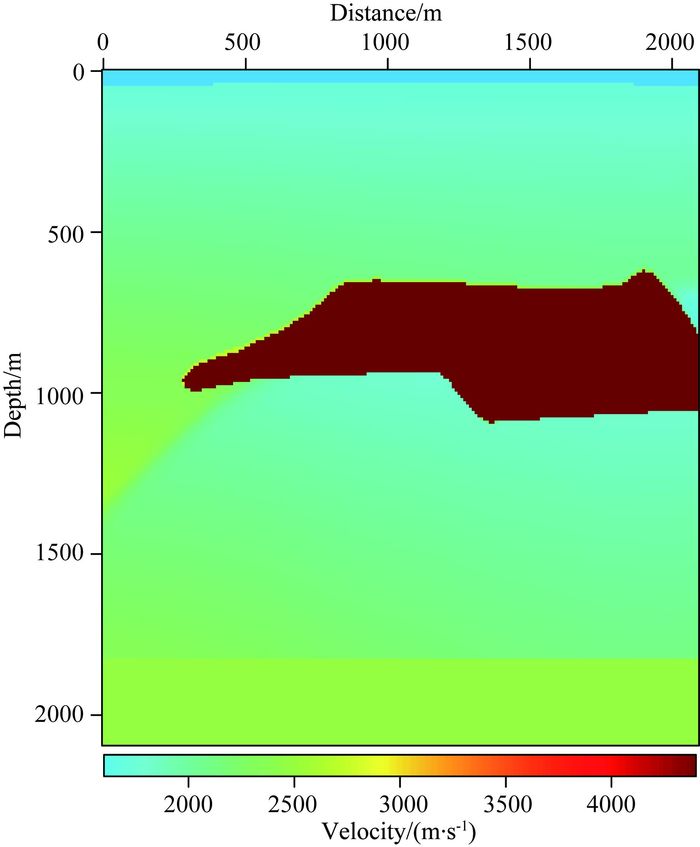
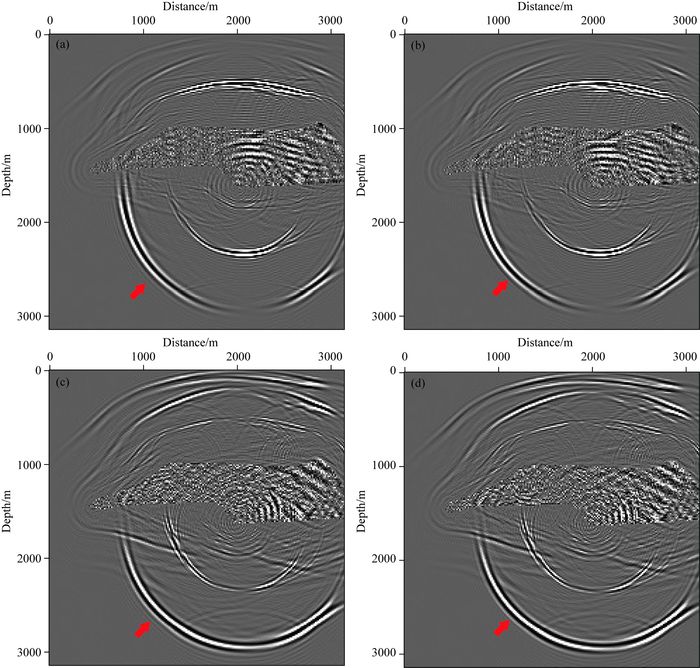
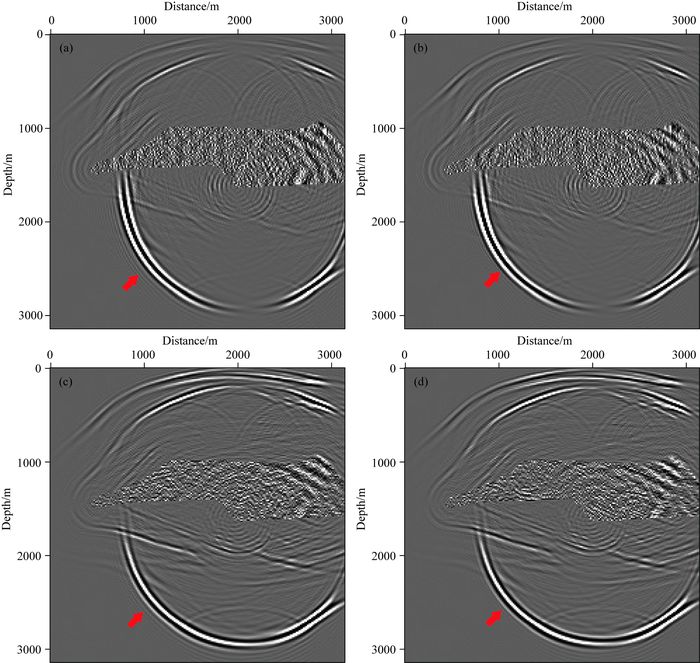
3.2 二维部分盐丘模型测试下面将本文提出的优化拟解析法,应用到2-D非均匀模型,并将所得的结果与常规伪谱法进行比较.该2-D非均匀模型来源于SEG/EAGE盐丘模型一部分,模型区域大小为210×210,水平方向和垂直方向网格间距均为15 m,模型如图 12所示.本文只显示了纵波速度,纵横波速度比为VP/VS=1.732.Ricker子波的主频为20 Hz, 震源位于模型网格点(139, 105) 处,并可同时产生纵波和横波.波场模拟的时间采样间隔为1.5 ms.图 13显示了由伪谱法和优化拟解析法得到的X分量和Z分量波场快照.从图 13b和d中可以看出优化拟解析法没有时间频散,因优化拟解析法可在速度强烈变换情况下补偿时间误差.不过,我们依然可以看到一些空间频散,特别是横波,因最小波长采样网格数小于2个,不满足Nyquist采样定理要求.图 14显示了从图 13中分离出的纯纵波分量.当时间采样间隔由1.5 ms增加为2 ms时,伪谱法不稳定,如图 15a所示.但是,优化拟解析法仍然稳定,如图 15b所示.
|
图 12 部分二维盐丘纵波速度模型 Fig. 12 P wave velocity model of partial 2D SEG/EAGE salt |
|
图 13 非均匀弹性波介质由伪谱法和优化拟解析法计算得到的波场快照(时间采样步长为1.5 ms) (a) X分量(伪谱法);(b) X分量(优化拟解析法);(c) Z分量(伪谱法);(d) Z分量(优化拟解析法). Fig. 13 Wavefield snapshots in a inhomogeneous elastic medium computed using pseudo-spectral and optimized psuedo-analytical methods (time sampling interval is 1.5 ms) (a) X component (pseudo-spectral method); (b) X component (optimized psuedo-analytical method); (c) Z component (pseudo-spectral method); (d) Z component (optimized psuedo-analytical method). |
|
图 14 从图 13中分离出的波场分量快照 (a)纵波X分量(伪谱法);(b)纵波X分量(优化拟解析法);(c)纵波Z分量(伪谱法);(d)纵波Z分量(优化拟解析法). Fig. 14 Separated wavefield snapshots from Fig. 13 (a) P-wave model of X component (pseudo-spectral method); (b) P-wave model of X component (optimized psuedo-analytical method); (c) P-wave model of Z component (pseudo-spectral method); (d) P-wave model of Z component (optimized psuedo-analytical method). |

|
图 15 伪谱法和优化拟解析法计算得到的波场快照(时间采样步长为2 ms) (a) X分量(伪谱法);(b) X分量(优化拟解析法). Fig. 15 Wavefield snapshots computed using pseudo-spectral and optimized psuedo-analytical methods (time sampling interval is 2 ms) (a) X component (pseudo-spectral method); (b) X component (optimized pseudo-analytical method). |
本文分析了伪谱法以及拟解析法的优缺点,在此基础上,首先对拟拉普拉斯算子进行了改进,进而对归一化拟拉普拉斯算子进行改进,提出了弹性波优化归一化拟拉普拉斯算子.然后,利用拟微分算子对弹性波优化归一化的拟拉普拉斯算子进行表示,得到弹性波优化拟微分算子表达式,由于弹性波优化拟微分算子中包含随空间变化的补偿速度,不能直接应用空间快速傅里叶变换进行计算,所以我们采用低秩分解近似来进行计算.
本文采用该优化拟解析方法对弹性波波场进行数值模拟和分析,并与传统的伪谱方法和拟解析法在稳定性和数值频散方面进行了对比.在对简单模型(均匀模型、倾斜层状模型)正演模拟中,利用传统的伪谱法、拟解析法以及优化拟解析法进行数值模拟,通过波场快照、计算效率、单炮记录等分析可以看出:在相同模拟参数的条件下,伪谱法具有较大的时间频散,拟解析法的时间频散要优于伪谱法,但是由于补偿速度取得过大,会产生较严重的空间频散,而优化拟解析法在时间和空间频散方面均要优于传统的伪谱法和拟解析法;在相同的时间采样间隔下,若时间采样间隔较大,伪谱法更容易产生不稳定,而拟解析法和优化拟解析法没有这种现象.当时间采样步长取得较大时,优化拟解析法仍具有较高的精度,若三种方法采样时长相同,那么优化拟解析方法计算效率要高于伪谱法和拟解析法.在对复杂模型(部分盐丘模型)正演模拟中,利用传统的伪谱法和优化拟解析法进行数值模拟,仅仅通过波场快照便可以看出:当时间采样间隔较小时,伪谱法模拟结果稳定,但时间频散比较明显,优化拟解析法有效地压制了数值频散;当时间采样间隔较大时,伪谱法模拟结果不稳定,但是优化拟解析法仍然能得出稳定的高精度模拟结果.因此,本文提出的优化拟解析法具有更高的模拟精度和计算效率,为弹性波正演模拟提供了一种新的算法.
| Alterman Z, Karal F C. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of Seismological Society of America, 58(2): 367-398. | |
| Bayliss A, Jordan K E, Lemesurier B J., et al. 1986. A fourth-order accurate finite-difference scheme for the computation of elastic waves. Bull. Seismol. Soc. Am., 76(4): 1115-1132. | |
| Carcione J M, Herman G C, Ten Kroode A P E. 2002. Seismic modeling. Geophysics, 67(4): 1304-1325. DOI:10.1190/1.1500393 | |
| Chen J. 2007. High-order time discretizations in seismic modeling. Geophysics, 72(5): SM115-SM122. DOI:10.1190/1.2750424 | |
| Chen J. 2009. Lax-Wendroff and Nystr m methods for seismic modeling. Geophysical Prospecting, 57(6): 931-941. DOI:10.1111/gpr.2009.57.issue-6 | |
| Chen J. 2011. A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation. Geophysics, 76(2): T37-T42. DOI:10.1190/1.3554626 | |
| Chu C L, Stoffa P L. 2010. Acoustic anisotropic wave modeling using normalized pseudo-Laplacian.//80th Annual International Meeting, Soc. Exp. Geophys. Expanded Abstracts, 2972-2976. | |
| Chu C L, Stoffa P L, Seif R. 2009. 3D elastic wave modeling using modified high-order time stepping schemes with improved stability conditions.//79th Annual International Meeting, Soc. Exp. Geophys. Expanded Abstracts. | |
| Crase E. 1990. High-order (space and time) finite-difference modeling of the elastic wave equation.//60th Annual International Meeting, Soc. Exp. Geophys. Expanded Abstracts, 987-991. | |
| Crawley S, Brandsberg-Dahl S, McClean J. 2010a. 3D TTI RTM using the pseudo-analytic method.//80th Annual International Meeting, Soc. Exp. Geophys. Expanded Abstracts, 3216-3220. | |
| Crawley S, Brandsberg-Dahl S, McClean J, et al. 2010b. TTI reverse time migration using the pseudo-analytic method. The Leading Edge, 29(11): 1378-1384. DOI:10.1190/1.3517310 | |
| Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 | |
| Dong K L, Ma Z T, Cao J Z. 2000. A study on stability of the staggered-grid high-order diffe rence method of first-order elastic wave equation. Chinese Journal of Geophysics (in Chinese), 43(6): 856-864. DOI:10.3321/j.issn:0001-5733.2000.06.015 | |
| Du Q Z, Bai Q Y, Li B. 2010. Optimized difference coefficient method seismic wave field numerical simulation in vertical transverse isotropic medium. Oil Geophysical Prospecting (in Chinese), 45(2): 170-176. | |
| Etgen J T, Brandsberg-Dahl S. 2009. The pseudo-analytical method:Application of pseudo-Laplacians to acoustic and acoustic anisotropic wave propagation.//79th Annual International Meeting, Soc. Exp. Geophys. Expanded Abstracts, 2552-2556. | |
| Fomel S, Ying L, Song X. 2010. Seismic wave extrapolation using lowrank symbol approximation.//80th Annual International Meeting, Soc. Exp. Geophys. Expanded Abstracts, 3092-3096. | |
| Fomel S, Ying L X, Song X L. 2012. Seismic wave extrapolation using lowrank symbol approximation. Geophysical Prospecting, 61(3): 526-536. | |
| Fornberg B. 1987. The pseudospectral method:Comparisons with finite differences for the elastic wave equation. Geophysics, 52(4): 483-501. DOI:10.1190/1.1442319 | |
| Gazdag J. 1981. Modeling of the acoustic wave equation with transform methods. Geophysics, 46(6): 854-859. DOI:10.1190/1.1441223 | |
| Graves R W. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bull. Seismol. Soc. Am., 86(4): 1091-1106. | |
| Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. DOI:10.1190/1.1441288 | |
| Lax P, Wendroff B. 1960. Systems of conservation laws. Communications on Pure and Applied Mathematics, 13(2): 217-237. DOI:10.1002/(ISSN)1097-0312 | |
| Levander A R. 1988. Fouth-order finite-difference P-SV seismograms. Geophysics, 53(11): 1425-1436. DOI:10.1190/1.1442422 | |
| Liu Y, Sen M K. 2009. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 | |
| Liu Y, Sen M K. 2011. Finite-difference modeling with adaptive variable-length spatial operators. Geophysics, 76(4): T79-T89. DOI:10.1190/1.3587223 | |
| Ma D T, Zhu G M. 2003. Numerical modeling of P-wave and S-wave separation in elastic wavefield. Oil Geophysical Prospecting (in Chinese), 38(5): 482-486. | |
| Pei Z L, Mu Y G. 2003. A staggered-gird high-order difference method for modeling seismic wave propagation in inhomogeneous media. Journal of the University of Petroleum, China(Edition of Natural Science)(in Chinese), 27(6): 17-21. | |
| Robertsson J O, Blanch J O, Symes W W. 1994. Viscoelastic finite-difference modeling. Geophysics, 59(9): 1444-1456. DOI:10.1190/1.1443701 | |
| Takeuchi N, Geller R J. 2000. Optimally accurate second order time-domain finite difference scheme for computing synthetic seismograms in 2-D and 3-D media. Physics of the Earth and Planetary Interiors, 119(1-2): 99-131. DOI:10.1016/S0031-9201(99)00155-7 | |
| Tessmer E, Kosloff D, Behle A. 1992. Elastic wave propagation simulation in the presence of surface topography. Geophysical Journal International, 108(2): 621-632. DOI:10.1111/gji.1992.108.issue-2 | |
| Virieux J. 1984. SH-wave propagation in heterogeneous media:Velocity-stress finite difference method. Geophysics, 49(11): 1933-1957. DOI:10.1190/1.1441605 | |
| Wong M W. 1991. An Introduction to Pseudo-Differential Operators. 2nd ed. Singapore: World Scientific Publishing. | |
| Yan J, Liu H. 2016. Modeling of pure acoustic wave in tilted transversely isotropic media using optimized pseudo-differential operators. Geophysics, 81(3): T91-T106. DOI:10.1190/geo2015-0111.1 | |
| 董良国, 马在田, 曹景忠. 2000. 一阶弹性波方程交错网格高阶差分解法稳定性研究. 地球物理学报, 43(6): 856–864. DOI:10.3321/j.issn:0001-5733.2000.06.015 | |
| 杜启振, 白清云, 李宾. 2010. 横向各向同性介质优化差分系数法地震波场数值模拟. 石油地球物理勘探, 45(2): 170–176. | |
| 马德堂, 朱光明. 2003. 弹性波波场P波和S波分解的数值模拟. 石油地球物理勘探, 38(5): 482–486. | |
| 裴正林, 牟永光. 2003. 非均匀介质地震波传播交错网格高阶有限差分法模拟. 石油大学学报(自然科学版), 27(6): 17–21. | |
 2017, Vol. 60
2017, Vol. 60


