2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95064, U. S. A;
3. 西安交通大学电子与信息工程学院波动与信息研究所, 西安 710049;
4. 海洋石油勘探国家工程实验室, 西安 710049
2. Modeling and Imaging Laboratory, University of California, Santa Cruz, CA 95064, U. S. A;
3. Institute of Wave and Information, School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
4. National Engineering Laboratory for Offshore Oil Exploration, Xi'an 710049, China
各种局域化分解方法的提出是现代信号处理领域的一个革命性突破,最开始主要应用于分析非平稳时间信号的时频分析技术,用于描述信号在时间和频率上的局域化性质.当涉及到地震波的传播与成像时,局域化具有不同的物理意义,主要指空间和传播方向上的局域化.局域化分解可以独立于波的传播过程,仅对波场进行分解,用以提取波场的局部角度信息,如基于双程波的照明分析及孔径补偿技术(Cao and Wu, 2009; Yan et al., 2014),或者反射角道集提取技术(Yan and Xie, 2012; Xu et al., 2011).空间局域化的另一个极具吸引的应用是用于波的传播,实现地震波在横向快速强变化介质中的高精度传播与成像,如小波束偏移(Beamlet migration)技术(Wu and Chen, 2002).可以预见, 以波动理论和信号分析为基础的波场分解、传播、成像以及反演的理论和方法在现代地震勘探中将越来越趋向于核心和关键地位.
小波束偏移是一类基于单程波波动方程的双域偏移方法,传播过程包括局部波数域背景传播和空间域局部扰动校正,其中主要发展了基于Gabor-Daubechies标架(Wu and Chen, 2002; Chen et al., 2006)、局部余弦基(Local Cosine Basis)(Wu et al., 2008a, 2008b)和局部谐和基(Local Harmonic Basis)(Wu and Mao, 2007; 毛剑等,2010)的小波束偏移算法.空间局域化的小波束传播算子能够适应速度的横向剧烈变化,使局部速度扰动显著减弱,通过简单的局部相移校正就可以保持很好的地震波传播精度.在涉及复杂速度介质成像时,如存在高速盐体情况下,能够得到很好的精度.然而,小波束偏移把时间空间域波场变换到频率域后,仅沿空间维做局域化分解,缺乏时间上的局域化,不能灵活适应地震数据在时间和空间上的非平稳变化,因此对波场稀疏表示的效果不理想.
Dreamlet偏移方法(Wu et al., 2008a, 2008b)在小波束空间局域分解的基础上增加了时间-频率局域化,是时间和空间完全局域化的偏移方法.Dreamlet原子由时间和空间局域化原子的张量积构成,可以灵活运用不同的局部分解方法分别实现,目前主要实现了冗余度为2的局部指数标架(时间)-局部余弦基(空间)(Wu et al., 2009)和正交的局部余弦基(时间)-局部余弦基(空间)(Wu B Y and Wu R S, 2010)dreamlet偏移方法.对于波场分解,正交dreamlet分解等价于多维局部余弦变换,如Wang和Wu(2000)将半自适应多维局部余弦变换(时间自适应或者空间自适应)应用于二维叠后地震数据压缩并测试不同压缩率下的偏移效果.结果表明二维局部余弦变换在高压缩率下仍能保持地震信号的有效成分,但其压缩相对于传播是透明的,也即将压缩后的数据重建后再偏移成像.Dreamlet偏移对波场和单程波传播算子同时实现时空局域分解变换,直接传播地震波场的时空局域化分解系数,不仅可以有效表示地震数据,而且时空局域化的单程波dreamlet传播算子在偏移过程中能够对波场进行灵活多样的与时间相关的操作.Wang等(2015)实现了基于dreamlet变换和凸集映射(Projection Onto Convex Sets)的地震数据插值及噪声消除.
单程波偏移方法是前向算法,波场总是沿一个特定方向(如深度方向)步进延拓,波场中的能量也相应地沿时间轴固定方向(如向零时刻点)流动.在每个深度,对延拓得到的波场应用成像条件来得到反射强度信息,使反射能量回归至其空间位置.在单程波偏移方法中,这些已经“归位”后的能量已经不再携带更深层结构的反射信息,没有必要再继续向下传播.然而,在所有频率域偏移算法中,由于在频率域连续的相移操作和傅里叶变换的周期性,即使能量到达地震波场的零时刻后,又会折叠回时间轴的另一端存在于波场中继续向下传播.Dreamlet传播算子利用时间上的局域化,在延拓波场时,如果dreamlet系数经传播后越过零时刻到达负时间,则被舍去不计.因此随着深度增加,流出波场的信号越来越多,时间轴的有效长度也越来越短,需要延拓的波场系数也相应减少,可使偏移效率提高.在炮域dreamlet偏移中,源波场和检波器波场分别延拓至空间所有位置,每点的反射值由源和检波器波场相关得到.一般情况下,反射能量到达其反射位置时并不会出现在零时刻,即使dreamlet算子丢掉所有到达负时间的信号,仍有大量的无用数据停留在波场中.虽然可以通过计算地震波走时来进一步丢弃无用数据(吴帮玉等,2012),但粗略估算走时不能完全丢弃无用数据,而精确地计算走时会增加额外计算量.
观测系统沉降成像与dreamlet传播算子是很好的结合.观测系统沉降法偏移(Claerbout, 1985)把地表接收到的所有炮数据同时向下延拓,延拓后的波场可以看作是在地下布置一个虚拟的观测平面所能接收到的数据.当观测系统“沉降”到某反射层所在的深度时,对应该反射层的地表接收到的反射信号会出现在零偏移距的零时刻.在波场延拓时dreamlet偏移操作自动舍弃越过零时刻的波场dreamlet系数,因此利用dreamlet实现观测系统沉降时,所有抵达零时刻后的波场值被提取出作为反射能量后都不会继续传播,延拓后的波场只包含观测系统下部结构的反射信息,而无需作额外处理.
传统观测系统沉降法每一步的波场延拓分两部分:首先,对每个点源道集,向下延拓所有的检波器波场;其次,对每个检波器道集,向下延拓所有的源波场.对于波场,dreamlet分解沿源、检波器和时间记录连续进行分解,是对波场的完全局域化分解.源被分解为小波束源,检波器被分解为小波束检波器.分解后,波场传播也从共点源、共点检波器变为以共小波束源和共小波束检波器道集延拓.
本文首先引入正交dreamlet变换及其对叠前地震数据的分解,接着推导了dreamlet传播算子应用于观测系统沉降法的传播公式和算法.数值计算部分以二维SEG/EAGE模型叠后数据和Marmousi模型叠前数据为例展示dreamlet传播算子观测系统沉降法偏移特点及结果.最后是讨论和结论.
2 正交dreamlet变换及其对叠前地震数据的分解二维空间,地表接收到的叠前地震数据是一个三维数据体u(t, xs, xr),其中xs和xr分别代表产生该条记录的源和检波器所在位置,t表示记录时间.该三维数据体经过偏移后,得到地下反射层的二维图像.从三维输入得到二维输出,地表记录到的数据用来多次成像地下同一反射结构,因此地表各条记录之间,尤其是相邻炮的邻近记录有一定的冗余度.局部余弦基是一组正交基(Wickerhauser, 1994),对平滑和相关性较好的数据有很好的压缩能力,可以有效表示地震数据.局部余弦变换的另一个特点是不改变信号的数据类型.因此,经过局部余弦变换后,地震数据的正交dreamlet系数仍为实数.
2.1 局部余弦正交dreamlet基函数局部余弦变换是局域化了的离散余弦变换,其基函数是由平滑、紧支撑的钟函数与一个余弦函数的乘积构成.局部余弦变换具有很多与加窗傅里叶变换相似的性质,可以利用快速傅里叶变换实现快速算法.
在空间域,起始位置在xn,空间宽度为Ln=xn+1-xn及局部波数指数为m(m=0, …, M-1, M表示局部余弦基的空间点数)的局部余弦基表达式如下:

|
(1) |
式中Bn(x)表示在区间[xn, xn+1]上光滑紧支撑的钟型函数.局部余弦基在波数域的表达式如下:
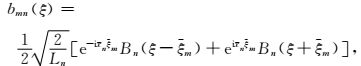
|
(2) |
其中Bn(ξ)为钟函数Bn(x)的傅里叶变换,且ξm=
与在时间域类似,局部余弦基可由时间起始位置tj,时间长度Tj=tj+1-tj和局部频率ωi表示,其时间和频率域表达式分别为:
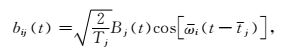
|
(3) |

|
(4) |
其中Bj(ω)是Bj(t)的傅里叶变换,且有ωi=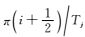
二维炮域偏移时,对源和检波器波场分别分解,dreamlet原子由时间和空间域局部余弦基的张量积构成(吴帮玉等,2012):

|
(5) |
Dreamlet原子的支集为时间和空间钟型函数的笛卡尔乘积(Cartesian product).本文中字母上的横线表示关于时空窗的局部变量,如(tj, ωi, xn, ξm)分别表示了局部时间、局部频率、局部位置以及局部波数.可以证明dreamlet原子是一种定义在观测平面上的物理小波(Wu et al., 2011),其本身以及其传播算子满足因果律(频散关系),这些特点在本质上区别于一般的物理小波,使其在波场表示、波传播以及成像方面具有一定优势.
2.2 多维叠前地震数据dreamlet分解炮域叠前深度偏移对单炮分别成像,把各炮偏移结果叠加形成最终偏移剖面,各个炮的数据单独处理.但地震波传播以及偏移成像是一个线性过程,也可以把接收到的所有炮数据同时延拓传播,即观测系统沉降法偏移.由于多炮、多偏移距对地表的多次覆盖,二维空间地表叠前地震记录为三维连续数据体.在观测系统沉降法偏移开始前,要将接收到的所有数据读入内存,并按共源点xs和共检波点xr排列,表示为u(t, xs, xr).
图 1是二维Marmousi叠前地震道数据排列示意图.该模型水平采样间隔为12.5 m,一共240炮,炮间距为25 m.时间采样间隔为0.004 s,记录长度3 s.图中时间轴垂直于源-检波器坐标平面,与炮域计算类似,对接收数据以零值扩边以扩大计算孔径.
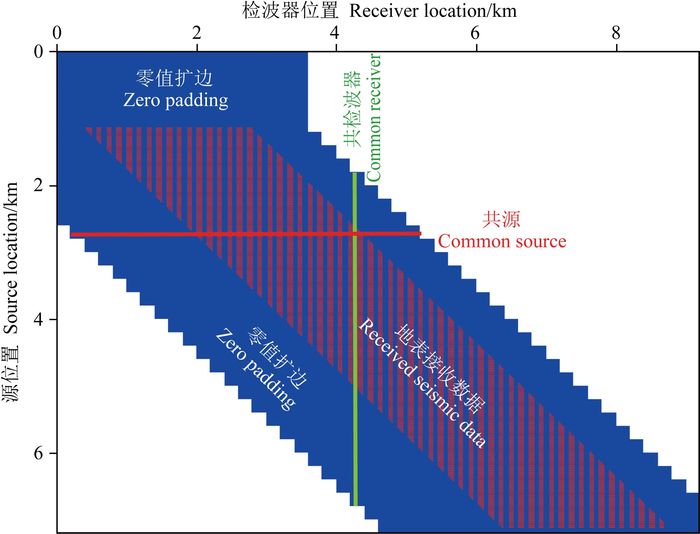
|
图 1 二维Marmousi模型观测系统沉降法叠前数据排列示意图 以零值扩边加宽计算孔径,中间是地表接收地震数据位置处. Fig. 1 Schematic illustration of the survey sinking prestack recording trace distribution for the 2D Marmousi model acquisition system Zero edge extension is applied to the calculation apertures.The surface seismic data receiving location is at the middle of the plane. |
在二维情况下,源-检波器坐标系下的观测系统沉降法偏移中,实现完全局域化分解三维数据体u(t, xs, xr)的dreamlet原子由bmn(xs),bpq(xr)和bij(t)的张量积构成:

|
(6) |
其中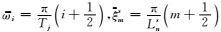
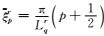
每一层的波场u(t, xs, xr)可以由dreamlet原子表示如下:

|
(7) |

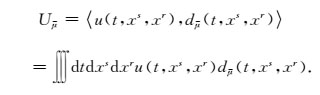
|
(8) |
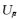
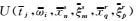

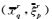
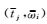
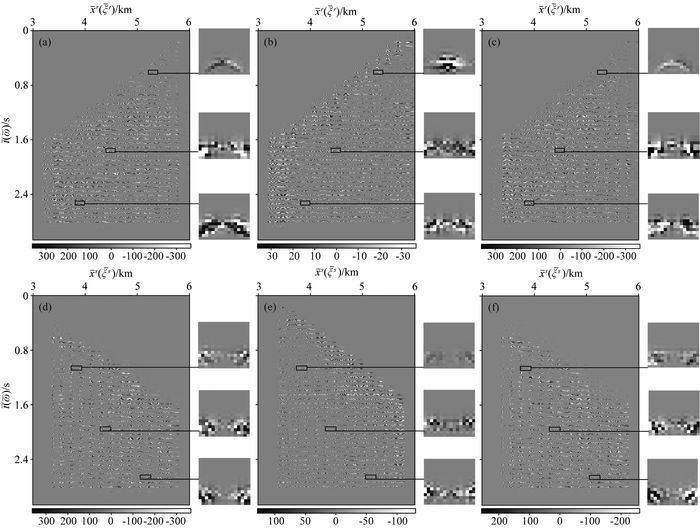
图 2显示二维Marmousi模型地表接收数据的共beamlet源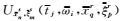

|
图 2 二维Marmousi模型源-检波器坐标下地表接收数据dreamlet分解系数 (a, b, c)和(d, e, f)分别为共小波束源和共小波束检波器道集dreamlet系数.其中(a, d),(b, e)和(c, f)分别为低小波束波数、中间小波束波数和高小波束波数dreamlet系数. Fig. 2 Source-receiver coordinate dreamlet coefficients for the 2D Marmousi model surface received data (a, b, c) Common beamlet sources; (d, e, f) Common beamlet receivers. The panels from left to right are for coefficients at low (a, d), middle (b, e) and high (c, f) beamlet wavenumbers. |
偏移时,只有高于某一阈值的系数值被传播,而小的dreamlet系数被舍弃,也即实现压缩传播过程.何种压缩策略直接影响本算法的效率和精度,例如可以设置全局阈值或者源/检波器小波束域分别设置阈值,或设置随深度变化的阈值等等,鉴于该问题的复杂性,本文暂不讨论.在后文的应用中,每个深度的阈值设置为该层深度dreamlet系数绝对值最大值的10-4倍.
3 Dreamlet域观测系统沉降法偏移成像大多数观测系统沉降偏移都用单程波算子延拓.最近,Sandberg和Beylkin(2009)以及Alkhalifah和Fomel(2010)分别发展了基于全波波动方程延拓的观测系统沉降算法.Wu等(2012)探索了基于双程波向下延拓的小波束偏移算子.
观测系统偏移过程可以在源-检波器坐标下完成也可以通过线性坐标变换在中心点-偏移距坐标系进行(Popovici, 1996; Jin et al., 2002; 程玖兵,2003; Claerbout, 2009).但中心点-偏移距域观测沉降算子不能分裂成分别仅含中心点或者偏移距项,其泰勒展开式中包含中心点与偏移距交叉相乘项,这表明对源和检波器的偏移和叠加必须同时进行,不能分开依次按顺序完成(Claerbout, 2009),而且当横向速度有变化时,忽略这些交叉项使成像结果变差(Hua et al., 2007).另外,通过后文推导可知,源-检波器坐标系下dreamlet观测系统沉降算子与炮域相同,该偏移过程只是对不同的道集(小波束源或者小波束检波器)连续作用.因此,本文选择在源-检波器坐标系下完成观测系统沉降过程.
3.1 源-检波器坐标dreamlet观测系统沉降算子时空域中,源-检波器域双平方根算子(DSR)(Claerbout, 1985)表达式为
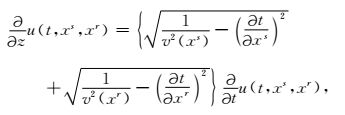
|
(9) |
其中v(xs)和v(xr)分别为源和检波器位置处的速度.双平方根算子把源和检波器同时向下延拓,但二者也可以分别依次向下传播,则(9) 式可以等价分裂为两个单平方根(SSR)等式:
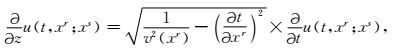
|
(10) |
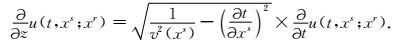
|
(11) |
公式(10) 和(11) 具有相同的形式,对地震数据u(t, xr; xs)分别向下延拓检波器波场(共源)和源波场(共检波器).后文中以(10) 式为例推导dreamlet观测系统传播算子.
式(10) 的解为
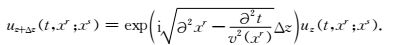
|
(12) |
令
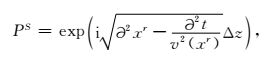
|
(13) |
为形式上的单平方根单程波算子,并不能直接在时空域求解,v(xs)在横向有变化时也不能变换到波数域求解.
根据局部扰动理论,单平方根传播算子(13) 可以分离为局部均匀速度下传播算子PS0和局部相位屏校正PS1:

|
(14) |
且有
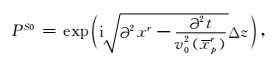
|
(15) |
其中

通过介质后,dreamlet原子的演化必须遵循波动方程.经过传播后,单个dreamlet原子会扩散到相空间的其他时空窗口中.对传播畸变后的dreamlet原子的重新分解,构成了dreamlet传播矩阵:
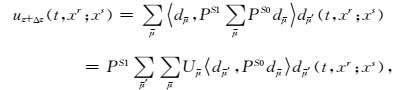
|
(16) |
其中带撇的下标都是传播到新一层深度上的dreamlet系数参数.
因此对应于观测系统沉降偏移成像中的dreamlet传播矩阵原子为
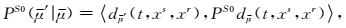
|
(17) |
它表示传播前和后不同dreamlet原子之间的耦合系数权重.
把dreamlet表达式(6) 代入(17) 式后,有
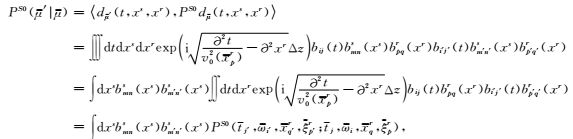
|
(18) |
其中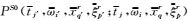
由于局部余弦基的正交性,公式(18) 等价于
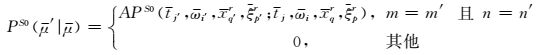
|
(19) |
其中A=∫dxs|bmns(xs)|2.
由式(19) 可以看出,其实观测系统沉降的dreamlet延拓算子与炮域dreamlet算子完全相同(吴帮玉等,2012),且共小波束源波场经过传播后只是在检波器dreamlet系数间扩散,并不会传播到其他小波束源.
把波动方程在频率波数域的解析解以及频率和波数域的局部余弦基表达式代入公式(19) 后得
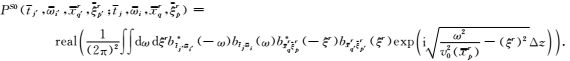
|
(20) |
虽然dreamlet传播算子由复数域频率波数域单程波波动方程解析解推导得出,最后只需保存实数部分.如前文提到的,正交dreamlet波场分解系数为实数,这说明待传播的和已传播的dreamlet系数均为实数,那么传播矩阵也应该为实数,因此即使虚部存在也将不起作用.
局部扰动相位校正在空间频率域u(ω, xs, xr)完成,详细过程参见吴帮玉等(2013).
3.2 Dreamlet观测系统沉降算法Dreamlet观测系统沉降偏移算法步骤总结如下:
(a)将地震数据u(t, xs, xr)进行dreamlet分解,得到波场的dreamlet系数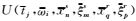
(b)在每个深度,首先应用dreamlet算子延拓共小波束源
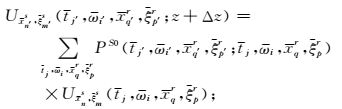
|
(c)把经步骤(b)延拓后的波场再次应用dreamlet算子沉降共小波束检波器
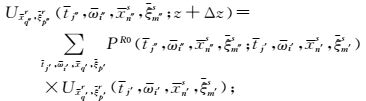
|
(d)将波场变换到频率域进行局部扰动校正;
(e)应用成像条件,提取零偏移距零时刻波场振幅作为像值.
步骤(b)和步骤(c)dreamlet传播过程完全相同,只是以不同参考速度算子作用于不同的道集而已.
4 数值算例 4.1 二维SEG/EAGE叠后深度偏移叠后地震数据偏移是观测系统沉降法偏移的一种特例.叠后地震数据是叠前数据经过叠加处理得到的结果,可视为源和检波器在相同位置时采集到的地震记录,因此又称为零偏移距剖面.叠后数据维数较低,更容易用来展示dreamlet偏移的特点.
叠后记录剖面也可以另外一种理论模型来理解,即爆炸反射面模型(Claerbout, 1985).模型假设所有的检波器仍在地表,但源分布在地下各个反射面上,并在零时刻以与反射层反射系数成正比的强度激发,传播过程忽略所有界面多次反射与透射效应,记录从反射面传播到地表的能量.实际地表接收到的反射记录是双程走时,从地表到反射层再从反射层返回地表.因此,爆炸反射面模型中,需要将双程走时剖面转换为单程走时,但也可以简单地把相应叠后偏移速度取为实际速度的一半进行偏移.
图 3a是二维SEG/EAGE合成叠后地震记录,该记录空间采样点数为1408,采样间隔为12.5 m(40 ft),每条记录时间长度为5 s,采样率8 ms.图 3b显示的网格是dreamlet变换对该数据的时空窗划分,时间和空间窗的长度同样均为16个采样点.图 3c是对输入数据(图 3a)的dreamlet分解系数,水平轴代表空间-波数坐标,垂直坐标表示时间-频率,该图直观地显示波场在dreamlet域的稀疏性.同样为了显示细节,相邻窗口的地震图(图 3d)及其对应的dreamlet系数(图 3e)被放大显示.

|
图 3 二维SEG/EAGE叠后地震数据及其dreamlet分解 (a)地表叠后数据;(b) Dreamlet变换对地震数据的时空窗划分;(c) Dreamlet变换系数;(d)放大显示邻近窗口的地震信号;(e)放大显示邻近窗口的dreamlet系数. Fig. 3 2D SEG/EAGE poststack seismic data and its dreamlet decomposition (a) Surface poststack seismic data; (b) Time-space window division for seismic data by dreamlet transform; (c) Dreamlet transform coefficients; (d) Enlarged seismic signal of adjacent window; (e) Enlarged dreamlet coefficients of adjacent window. |
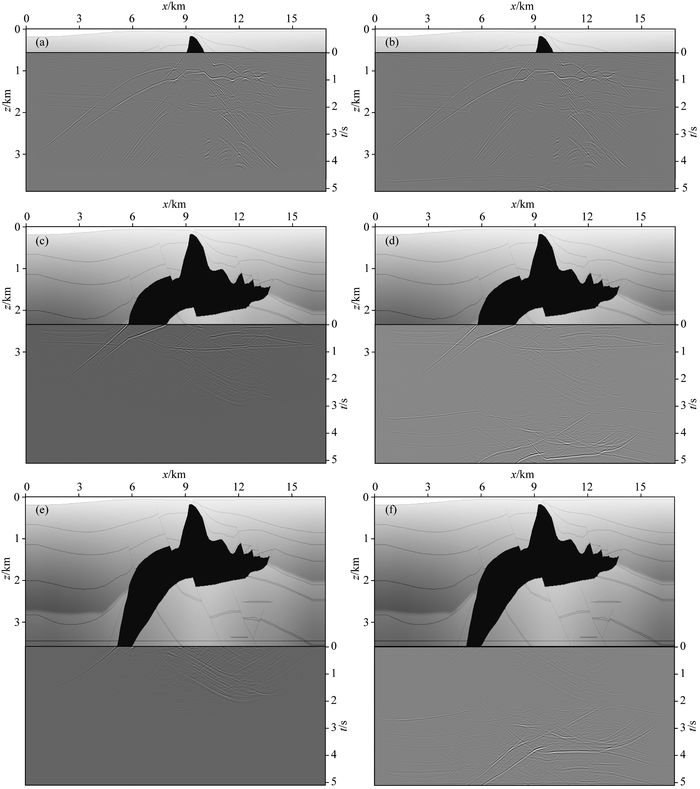
地震偏移成像过程分两个步骤:波场重建和应用成像条件.波场重建由地表接收到的数据得到地下目标区域的波场,然后再应用成像条件得到反射信息.图 4显示的是由dreamlet和beamlet传播算子深度延拓得到的波场,并将零时刻波场值放置在速度模型上的对应深度上.从地震图上可以清楚地看到地表接收到的反射能量经过波场延拓后出现在反射空间位置波场的零时刻处.因此,基于爆炸反射面模型的叠后数据成像条件即抽取延拓后波场的零时刻幅度即可得到地层的反射信息.这些被归位至空间位置处的能量不再携带更深处地层的反射信息,在应用完成像条件后不应再被继续传播.然而,在频率域延拓波场中,由于有限时间长度傅里叶变换的周期性以及偏移持续的相移操作,这些抵达零时刻后的能量等效于在时空域又周期卷绕到波场时间轴的另一端,停留在波场中被继续向下传播(图 4b, 4d, 4f).Dreamlet传播算子在空间和时间上都具有局域化,通过传播每一个时空窗里的dreamlet系数来延拓波场.对每一个时空窗口,dreamlet传播算子只将每个系数向相对小于该系数所在时间窗中传播,当dreamlet系数经过传播后越过零时刻到达负时间,dreamlet算子即将该原子舍弃.因此,抵达零时刻后的波场能量经继续传播后会被丢弃,波场中仅会保留用于成像更深层结构的有用信号.随着深度的增加,有效信号长度也会不断缩短(图 4a, 4c, 4e).对比最深层dreamlet和beamlet延拓波场(图 4e, 4f), 可以清楚直观地看出频率域方法延拓过程中传播了大量能量强但对成像没有贡献的信号.
|
图 4 二维SEG/EAGE叠后偏移不同深度的波场 地震图与速度模型重叠放置,地震图的零时刻位于相应深度位置.(a, c, e) Dreamlet算子延拓波场;(b, d, f) Beamlet算子延拓波场. Fig. 4 2D SEG/EAGE poststack data downward continuation wavefield at different depths The seismograms are overlaid on the velocity model and the zero time is located at the corresponding depth. (a, c, e) Continued wave field by dreamlet propagaotor; (b, d, f) Continued wavefield by beamlet propagator. |
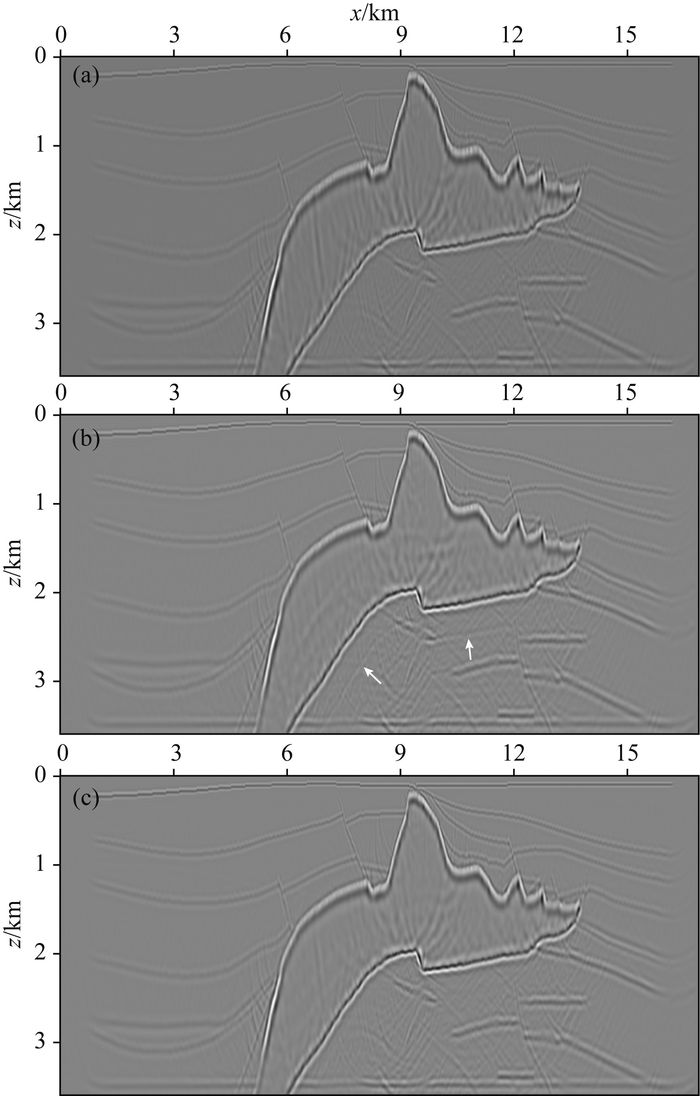
叠后数据偏移中,把每一层深度延拓得到波场的零时刻抽取出来即可构成最终成像结果,在频率域等效于把各个频率波场加和.图 5a为dreamlet成像结果,图 5b为频率域beamlet成像结果.仔细对比二者盐下结构成像发现,dreamlet成像结果噪声更少,而由于受到折叠信号的影响,在频率域beamlet偏移结果中甚至出现了一些假的反射结构,如图 5b中白色箭头所示.当然,也可以通过在每条地震记录的末尾补零增加时间轴长度来减少周期折叠信号的影响(Yilmaz and Doherty, 2001),如图 5c所示.但补零会使频率域采样加密,增加需要传播的频率个数,从而增加计算量.
|
图 5 二维SEG/EAGE叠后偏移成像结果 (a) Dreamlet成像结果;(b) Beamlet偏移成像结果, 时间轴长度为5 s;(c) Beamlet偏移成像结果,时间轴长度补零延长至8.192 s. Fig. 5 2D SEG/EAGE poststack migration results (a) Image by dreamlet method; (b) Image by beamlet method with time axis length 5 seconds; (c) Image by beamlet method with time axis length zero padding to 8.192 seconds. |
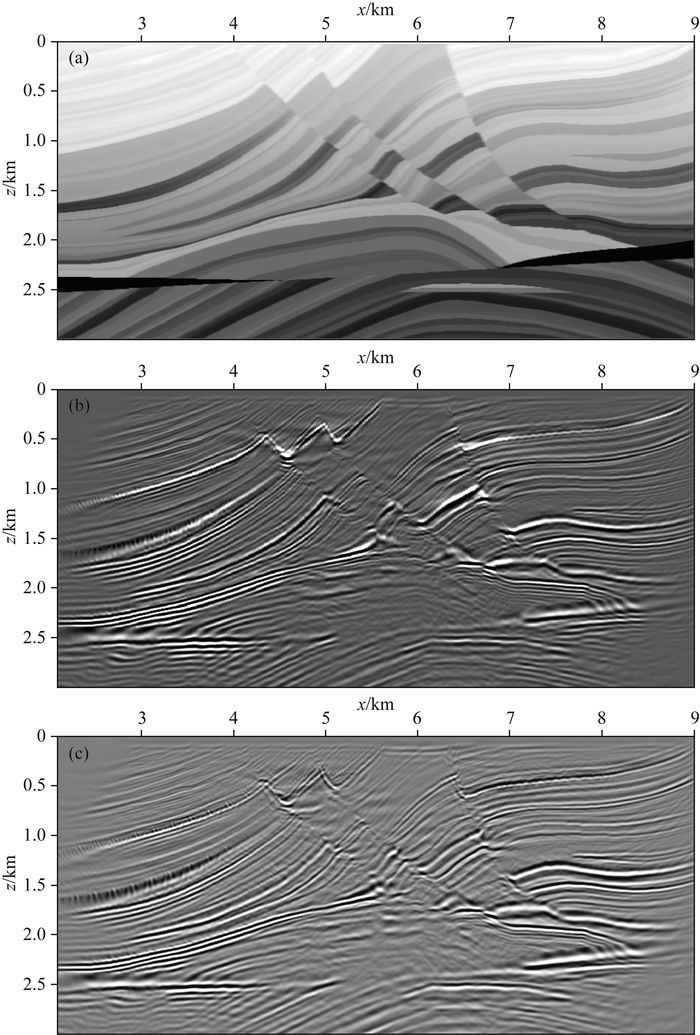
本次测试中,二维Marmousi叠前偏移速度模型横向和深度方向各有737和750个采样点,采样间隔分别为12.5 m和4 m.最大和最小速度分别为1500 m·s-1和5500 m·s-1,选择50个速度作为背景传播的参考速度,从最小速度到最大速度均匀采样.图 6a为Marmousi偏移速度模型.图 6b展示了dreamlet观测系统沉降法成像结果.作为对比,图 6c展示了炮域dreamlet偏移成像结果.对比图 6中偏移结果可以看出,dreamlet观测系统沉降法成像结果与炮域dreamlet成像结果质量相同,尤其是模型深部结构均具有较高分辨率.
|
图 6 二维Marmousi模型叠前深度成像结果 (a) Marmousi偏移速度模型;(b) Dreamlet炮域偏移;(c) Dreamlet观测系统沉降法偏移. Fig. 6 2D Marmousi model prestack depth imaging results (a) Marmousi migration velocity model; (b) Dreamlet shot domain migration; (c) Dreamlet survey sinking migration. |
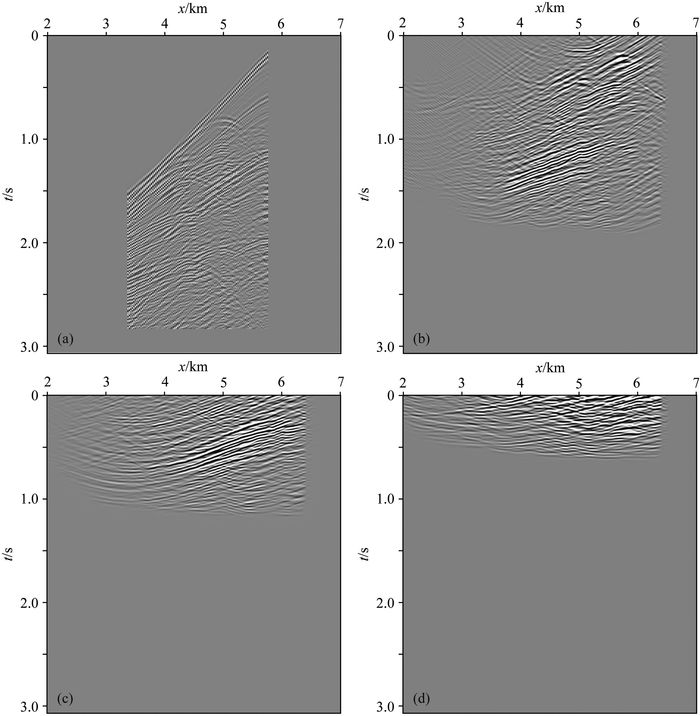
图 7是dreamlet观测系统沉降法偏移中不同深度的共点源波场.在炮域偏移中,延拓后的检波器波场与地表放置的虚拟源向下传播的源波场做相关来得到反射信息.一般情况下,当反射能量到达其深度时不会出现在零时刻.为了提高计算效率,我们通过模型中的最大速度和最小速度估算走时来切除一些已经用于成像浅部结构的时间窗能量(吴帮玉等,2012).而观测系统沉降法偏移成像条件为零时刻零偏移距波场值,用于成像后的零时刻波场能量在后续传播时会被自动丢弃,无需做额外处理.
|
图 7 Dreamlet观测系统沉降法偏移某共点源道集波场 (a)地表;(b) 1.0 km深度;(c) 2.0 km深度;(d) 3.0 km深度. Fig. 7 Dreamlet survey sinking migration common point source seismograms (a) Surface; (b) Depth 1.0 km; (c) Depth 2.0 km; (d) Depth 3.0 km. |
图 8表示二维Marmousi模型dreamlet系数个数在偏移时随深度变化情况,总体来说随着深度的增加dreamlet系数呈下降趋势.对于此次测试的Marmousi模型的观测系统,源和检波器之间有间隙,因此在传播初期,波场传播后会扩散产生布满整个观测系统的等效源,但在沉降一定深度后,dreamlet系数快速下降.在本次测试中,地表的dreamlet系数个数是最深层系数个数的14倍,最深一层的偏移效率高于第一层效率一个数量级.

|
图 8 二维Marmousi模型观测系统沉降法偏移dreamlet系数随深度变化示意图 Fig. 8 Dreamlet survey sinking coefficients changing with depth on 2D Marmousi model |
本文将dreamlet偏移与观测系统沉降法成像相结合.观测系统沉降法中dreamlet变换是对波场的完全局域化分解,而且在波场延拓过程中仅保留用于成像观测系统下部有物理贡献的信号,已经用于成像的信号不会折叠回时间轴的另一端.二维SEG/EAGE叠后和Marmousi叠前数据算例表明,dreamlet偏移随着深度的增加需要传播的系数不断减少而能保证成像质量不受影响,在有些情况下甚至减少由于信号折叠在最终成像结果出现的噪声和假的反射结构.Dreamlet偏移时间-空间局域化分解的引入对地震波场和传播算子二者稀疏表示效果明显,但在波的延拓过程中,dreamlet原子会向别的时空域耦合,增加了波传播的复杂度.另外,基于计算精度因素考虑,目前该方法中局部速度扰动校正仍然在频率域完成,正反傅里叶变换耗费大量计算时间,因此整个方法计算效率不高.偏移过程中待传dreamlet系数的选择对整个偏移效率和成像质量都有较大影响,因此选择何种适合dreamlet偏移的压缩算法是值得进一步研究的问题.本文通过波场延拓过程中地震图以及波场dreamlet系数变化反映时空域波场延拓的一些特点,即有效波场图随深度增加而缩短,dreamlet系数个数随深度增加而减少.现存各类方法中均没有利用/反映波场延拓过程中的这些特点.基于dreamlet算子的观测系统沉降法偏移成像,更突出了dreamlet偏移的这些特点,希望可以为发展高效率高精度的偏移成像提供新的思路.
致谢非常感谢谢小碧、耿瑜、闫蕊等在本项工作进行中的讨论与帮助,感谢张国伟对论文提出的宝贵修改意见.
| Alkhalifah T, Fomel S, Wu Z D. 2010. Source-receiver two-way wave extrapolation for prestack exploding-reflector modeling and migration. Geophysical Prospecting, 63(1): 23-24. | |
| Cao J, Wu R S. 2009. Full-wave directional illumination analysis in the frequency domain. Geophysics, 74(4): S85-S93. DOI:10.1190/1.3131383 | |
| Chen L, Wu R S, Chen Y. 2006. Target-oriented beamlet migration based on Gabor-Daubechies frame decomposition. Geophysics, 71(2): S37-S52. DOI:10.1190/1.2187781 | |
| Cheng J B. 2003. Double square root equation 3D prestack depth migration. Chinese Journal of Geophysics (in Chinese), 46(5): 676-683. DOI:10.3321/j.issn:0001-5733.2003.05.015 | |
| Claerbout J F. 1985. Imaging the Earth's Interior. Oxford:Blackwell Scientific Publications. | |
| Claerbout J F. 2009. Imaging in shot-geophone space. http://www.reproducibility.org. | |
| Hua B L, Williamson P, Zhang L B, et al. 2007. 3-D prestack depth migration with survey sinking operator in shot-geophone and midpoint-offset hybrid domain.//77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts. | |
| Jin S W, Mosher C C, Wu R S. 2002. Offset-domain pseudoscreen prestack depth migration. Geophysics, 67(6): 1985-1902. | |
| Mao J, Wu R S, Gao J H. 2010. High-accuracy prestack depth migration and imaging using local harmonic basis beamlet. Chinese Journal of Geophysics (in Chinese), 53(10): 2442-2451. DOI:10.3969/j.issn.0001-5733.2010.10.018 | |
| Popovici A M. 1996. Prestack migration by split-step DSR. Geophysics, 61(5): 1412-1416. DOI:10.1190/1.1444065 | |
| Sandberg K, Beylkin G. 2009. Full-wave-equation depth extrapolation for migration. Geophysics, 74(6): WCA121-WCA128. DOI:10.1190/1.3202535 | |
| Wang B F, Wu R S, Chen X H, et al. 2015. Simultaneous seismic data interpolation and denoising with a new adaptive method based on dreamlet transform. Geophysical Journal International, 201(2): 1182-1194. DOI:10.1093/gji/ggv072 | |
| Wang Y Z, Wu R S. 2000. Seismic data compression by an adaptive local cosine/sine transform and its effects on migration. Geophysical Prospecting, 48(6): 1009-1031. DOI:10.1046/j.1365-2478.2000.00224.x | |
| Wickerhauser M V. 1994. Adapted Wavelet Analysis:from Theory to Software. Boca Raton: A K Peters. | |
| Wu B Y, Wu R S. 2010. Orthogonal dreamlet decomposition and its application to seismic imaging.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts. | |
| Wu B Y, Wu R S, Gao J H. 2009. Dreamlet prestack depth migration using local cosine basis and local exponential frames.//79th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts. | |
| Wu B Y, Wu R S, Gao J H. 2012. Preliminary investigation of wavefield depth extrapolation by two-way wave equations. International Journal of Geophysics, 2012: 968090. | |
| Wu B Y, Wu R S, Gao J H. 2012. Time-space localized seismic wave propagation:Dreamlet prestack depth migration. Chinese Journal of Geophysics (in Chinese), 55(9): 3105-3114. DOI:10.6038/j.issn.0001-5733.2012.09.028 | |
| Wu B Y, Wu R S, Gao J H. 2013. Survey sinking prestack depth migration using local cosine basis beamlets. Chinese Journal of Geophysics (in Chinese), 56(2): 635-643. DOI:10.6038/cjg20130227 | |
| Wu R S, Chen L. 2002. Wave propagation and imaging using Gabor-Daubechies beamlets.//Shang E C, Li Q, Goo T F eds. Theoretical and Computational Acoustics:World Scientific. 661-670. | |
| Wu R S, Geng Y, Wu B Y. 2011. Physical wavelet defined on an observation plane and the dreamlet.//81th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts. | |
| Wu R S, Mao J. 2007. Beamlet migration using local harmonic bases.//77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts. | |
| Wu R S, Wang Y Z, Luo M Q. 2008a. Beamlet migration using local cosine basis. Geophysics, 73(5): S207-S217. DOI:10.1190/1.2969776 | |
| Wu R S, Wu B Y, Geng Y. 2008b. Seismic wave propagation and imaging using time-space wavelets.//78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts. | |
| Xu S, Zhang Y, Tang B. 2011. 3D angle gathers from reverse time migration. Geophysics, 76(2): S77-S92. DOI:10.1190/1.3536527 | |
| Yan R, Guan H M, Xie X B, et al. 2014. Acquisition aperture correction in the angle domain toward true-reflection reverse time migration. Geophysics, 79(6): S241-S250. DOI:10.1190/geo2013-0324.1 | |
| Yan R, Xie X B. 2012. An angle-domain imaging condition for elastic reverse time migration and its application to angle gather extraction. Geophysics, 77(5): S105-S115. DOI:10.1190/geo2011-0455.1 | |
| Yilmaz Ö, Doherty S. 2001. Seismic data analysis:processing, inversion, and interpretation of seismic data. SEG, Volume (Ⅰ)(I). DOI:10.1190/1.9781560801580 | |
| 程玖兵. 2003. 双平方根方程三维叠前深度偏移. 地球物理学报, 46(5): 676–683. DOI:10.3321/j.issn:0001-5733.2003.05.015 | |
| 毛剑, 吴如山, 高静怀. 2010. 利用局部谐和基小波束的高精度叠前深度域偏移成像方法研究. 地球物理学报, 53(10): 2442–2451. DOI:10.3969/j.issn.0001-5733.2010.10.018 | |
| 吴帮玉, 吴如山, 高静怀. 2012. 时空局域化地震波传播方法:Dreamlet叠前深度偏移. 地球物理学报, 55(9): 3105–3114. DOI:10.6038/j.issn.0001-5733.2012.09.028 | |
| 吴帮玉, 吴如山, 高静怀. 2013. 基于局部余弦基小波束的观测系统沉降法叠前深度偏移. 地球物理学报, 56(2): 635–643. DOI:10.6038/cjg20130227 | |
 2017, Vol. 60
2017, Vol. 60

