2. 中南大学有色资源与地质灾害探查湖南省重点实验室, 长沙 410083;
3. 中南大学教育部有色金属成矿预测重点实验室, 长沙 410083
2. Hunan Key Laboratory of Non-ferrous Resources and Geological Hazard Detection, Changsha 410083, China;
3. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Changsha 410083, China
自然电场法由于其快速高效、对污染物及地下水活动敏感等特点,在环境与工程地球物理中被广泛采用(Gallas et al., 2011; Gasperikova et al., 2012; De Carlo et al., 2013; 李虎等, 2013; Cui et al., 2016).其作为一种被动源方法,野外观测比较简便,特别适合污染物及地下水等动态目标的长期监测作业(Martínez-Pagán et al., 2010; Rittgers et al., 2013).对于监测数据的反演,常规的做法就是对监测过程中各时刻的观测数据进行独立的反演成像(Tsourlos et al., 2003).Kim(2009)指出这种各时刻数据独立地静态反演,其解释效果受观测误差和反演方法的影响巨大.LaBrecque和Yang(2001)提出了差分反演的方法,通过反演时序数据与背景的差异来处理电阻率监测数据.Daily等(2004)提出了另外一种差分的方法,即反演时序数据间的比值.但是,这类方法对初始模型的依赖严重.怎样充分利用时序数据间的关联信息来增加约束提高反演的可靠性亟待研究.Oldenborger等(2007)和Miller等(2008)在时序数据的反演中,利用前一时刻数据的反演结果作为下一时刻数据反演的初始参考模型,发现这种方法具有较好的反演效果.最近,Kim等(2009, 2013)把时间维加入时序数据的反演中.在这种被称为4维反演的方法中,同时采用了时间域与空间域的正则化手段来减少反演偏差并提高反演算法的稳定性.但由于在所有时刻都采用统一的时间正则化,增加的时间正则化虽然减少了反演偏差但同时也在某种程度上抑制了真实模型参数的变化.相反地,如果降低时间正则化的权重来凸显这种模型参数的变化,则又会增加反演的偏差.因此,Karaoulis等(2011)提出了一种改进的4维算法,称为4维主动时间约束反演,来试图克服这个缺点.但其巨大的计算开销在解决实际问题时又是一个挑战.
卡尔曼滤波作为一种优化估计技术,在许多动态系统参数估计中广泛运用.王玉斗等(2011)采用集合Kalman滤波方法对河流相油藏渗透率场进行反演估计,赵运超等(2014)将卡尔曼滤波运用到电离层TEC成像的研究中,郑崴和张贵宾(2016)则利用自适应卡尔曼滤波技术来对航空重力异常进行解算估计.Lehikoinen等(2009, 2010)运用卡尔曼滤波技术来处理直流电法电阻率监测数据,实现了对地电模型参数的动态估计.Nenna等(2011)同样也尝试了采用卡尔曼滤波来反演时序电阻率数据获得动态地电模型.在对时序数据反演进行模型估计中,卡尔曼滤波技术表现出良好的时间正则化效果.因此,本文尝试构建卡尔曼滤波递归来处理自然电场监测数据,融合动态地电模型的演化信息和自然电场观测数据,实现监测数据的时序反演.
2 动态地电模型 2.1 状态模型
在污染物或地下水活动的过程中,考虑地电模型随时间连续变化,即电导率分布等地电参数在数据采集过程中会发生变化.对连续变化模型进行监测,用所有监测时间点对应的离散模型集合来表示动态模型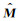
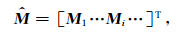
|
(1) |
式中Mi为时刻i对应的模型.
液体在饱和孔隙介质中的运动可以用达西公式来描述(Martínez-Pagán et al., 2010):
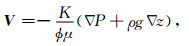
|
(2) |
式中V为达西速度,K为渗透率,ϕ为介质孔隙度,μ为动黏度,P为压差,ρ为流体密度,g为重力加速度,z为高差.
如用若干粒子来标示污染物或地下水的活动,则其活动可以看成是这些粒子各自运动的宏观体现.在时刻k,粒子i的位置可以表示为
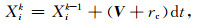
|
(3) |
式中Xik-1是粒子在时刻k-1的位置,V为达西速度,dt是时间步间隔,rc是粒子的随机运动速度,用来反映介质的各向异性以及运动噪声.
所有粒子的位置确定后,可计算相对粒子浓度S:
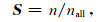
|
(4) |
式中n是单元网格内的粒子数量,nall是全部空间内的粒子数量.
在饱和孔隙介质中,由于介质孔隙度ϕ、固结指数b、水饱和度sw及饱和系数n均为常数,计算孔隙介质电导的阿尔奇公式(Lehikoinen et al., 2010)可以简化为
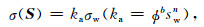
|
(5) |
即介质的电导率分布主要由孔隙水的电导率分布决定,简便起见,设孔隙水的电导率与与粒子浓度呈线性关系,线性系数为kc,(5) 式可改写为
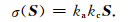
|
(6) |
这样就可以把相对粒子浓度分布转换成模型介质电导率分布.把孔隙介质中污染物或地下水的活动看成动态系统,考察系统的电导分布变化,则当前时刻k的模型状态与前一时刻k-1的模型状态满足
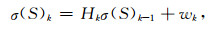
|
(7) |
简写为
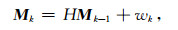
|
(8) |
式中H是由公式(3)、(4)、(5) 和(6) 表述的状态演化算子,Mk为用相对粒子浓度表征的模型状态,wk是由各种原因引起的过程噪声,服从协方差为Qk的零均值正态分布:
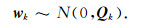
|
(9) |
观测模型主要由正演模型组成,由给定介质电导率分布和观测方法的情况下获得电势差分布.自然电场法的正演服从泊松方程:
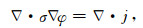
|
(10) |
式中σ是地下介质的电导率,φ是自然电位,j是各种自然电位引起的电流密度.简便起见,只考虑占主导地位的流动电位.孔隙介质中的流动电位电流密度可表示为

|
(11) |
式中Qv是孔隙间的剩余电荷密度,ϕ是孔隙度,v是孔隙水的平均流速.Linde等(2007)证明了公式(11) 能够提供比较准确的流动电位电流密度估计.因此,在获得模型的电导率分布的基础上,相应的正演计算即观测模型可以通过求解方程(12) 得到,即
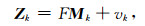
|
(12) |
Zk为当前时刻k对模型Mk的观测,F是正演算子或称状态观测算子,把状态模型空间映射到观测数据空间,v k是观测噪声,服从协方差为Rk零均值正态分布:

|
(13) |
动态模型

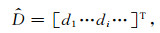
|
(14) |
式中di为时刻i对应的观测数据.常规静态反演方法被用来求解满足目标函数最小值的模型:

|
(15) |
式中G为正演算子.常规反演方法毫无疑问属于静态重构(Lehikoinen et al., 2010),而动态时序重构方法应该更加适合解决动态问题.
如果系统的初始状态、以及各时刻的过程噪声与观测噪声{x0, w1, …, wk, v1 … vk}都相互独立不相关,模型状态过程方程(8) 和模型观测方程(12) 就可以用来构建起动态过程的卡尔曼滤波.与传统反演不同,卡尔曼滤波通过基于状态模型的状态预测与基于观测数据的滤波校正,能够提供动态系统的一系列状态估计来重构动态过程.作为一种递归估计方法,卡尔曼滤波只需要前一时刻的状态估计和当前的观测数据就可以计算出当前的状态估计.滤波过程中不需要系统的历史观测数据和估计数据,系统的状态估计由后验估计状态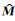
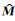
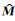
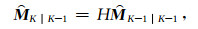
|
(16) |
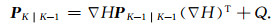
|
(17) |
在滤波校正阶段,用当前时刻的观测数据对先验状态估计进行修正,优化后的先验估计被称为后验状态估计,用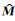
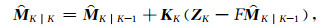
|
(18) |
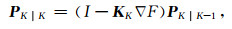
|
(19) |
式中
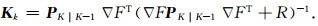
|
(20) |
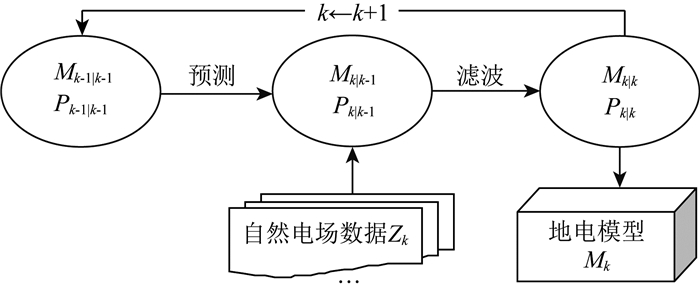
如图 1所示,将监测的时序自然电场观测数据不断融合到动态地电模型中,构建卡尔曼滤波递归,实现对自然电场数据的时序反演.与需要求解的模型状态参数相比,观测数据往往比较有限,这就导致地球物理反演的多解性难题难以解决.在自然电场监测中,仅凭单次有限的自然电场观测数据同样也难以确定模型的状态.而利用卡尔曼滤波框架,可将历史的多次观测信息传递到当前时刻来增加观测数据的信息量.随着新的监测数据不断地加入系统,待求解的模型状态便可以不断得到修正完善,不断逼近真实模型,从而实现观测数据的时序反演.
|
图 1 基于卡尔曼滤波的时序反演框图 Fig. 1 The Kalman filter cycle of time-lapse inversion |
首先采用数值模拟合成数据对卡尔曼滤波时序反演算法进行了测试.设二维数值模型网格数为30×30,网格大小0.1 m×0.1 m.
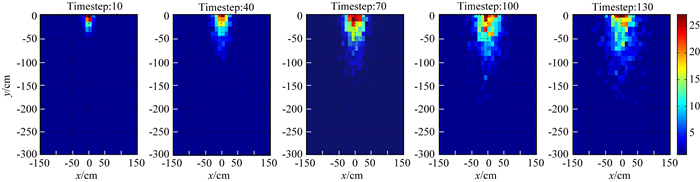
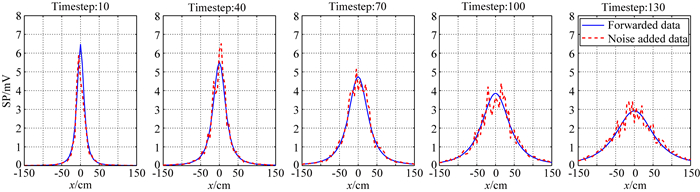
聚集在断面顶层中心的高浓度溶液随时钟节拍按公式(3) 在断面内扩散,来模拟污染物在地下介质中的迁徙运动.高浓度溶液用3000个粒子表示,介质渗透率、孔隙度、溶液的动黏度、密度等均设为常数,则粒子的达西速度与高差z呈线性关系.随着模型的演化,可以得到各时刻的系列地电断面.图 2为截取的5个电导率分布模型,从左至右分别为10、40、70、100以及130timestep对应的地电断面.为获得模拟地表自然电场观测数据,对各时刻的地电模型进行自然电场正演计算,得到相应的自然电场时序数据.图 2中各时刻模型计算出对应的模拟地表自然电场观测数据如图 3所示,图中蓝实线为直接正演计算数据曲线.由于实际观测中,自然电场数据比较容易受各种干扰影响,为模拟实际观测各种误差,在直接正演计算数据中加入了幅值30%随机噪声,加入噪声的模拟数据曲线如图 3中的红虚线所示.
|
图 2 数值地电模型 Fig. 2 The numerical geoelectric models |
|
图 3 模拟时序自然电场数据曲线 Fig. 3 The synthetic time-lapse self-potential data |
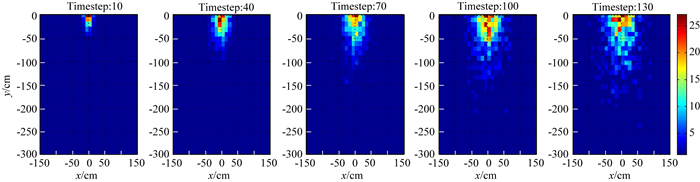
将加入了噪声的模拟时序自然电场数据对卡尔曼滤波时序反演算法进行测试.在设置合理初始模型的情况下,反演获得各时刻的系列地电模型,为便于比对,选取与图 2相同时刻的各反演结果模型如图 4所示.反演的各时刻结果模型比较精确地重现了原数值模型,表明时序反演算法能克服一定程度的噪音干扰,有效地重构地电模型的演化过程.
|
图 4 模拟数据反演结果 Fig. 4 The geoelectric models inverted from synthetic time-lapse self-potential data |
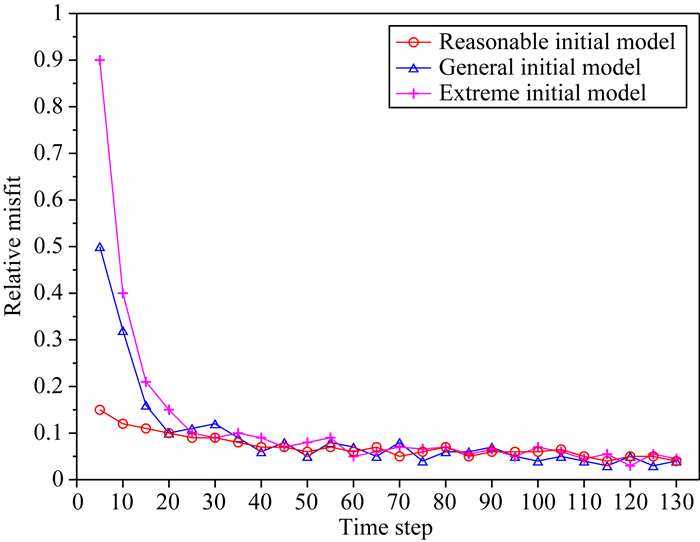
为定量分析评价反演效果,对各时刻反演结果模型进行正演,进而计算出与模拟数据的拟合差.在不同初始模型设置情况下,反演过程中的拟合差变化情况如图 5所示.不同初始模型测试表明,时序反演算法对初始模型依赖性低,无论是合理的初始模型(misfit 16%)、一般的初始模型(misfit 50%)还是极端的初始模型(misfit 90%),在经过2~3次数据同化后,均能达到并保持在较低的拟合差的水平.
|
图 5 不同初始模型的反演拟合差曲线 Fig. 5 The variation of relative misfit from different initial model |
为进一步验证时序反演方法的有效性,利用物理模拟实验获得的实测时序自然电场数据对算法进行了测试.实验数据来自对沙槽实验箱的自然电场监测.在沙槽中注入高浓度的盐水来模拟污染物在地下介质中的动态扩散过程,并对过程中的自然电场变化进行监测记录.实验装置如图 6所示,沙箱长1.0 m,宽0.5 m,高0.5 m,顶面敞开,填充有平均粒径约为0.25 mm的细砂.细砂顶部放置装有饱和盐水的容器.容器底部开有小孔,盐水可以通过开孔渗漏到沙箱中,受盐水影响范围内的饱和沙电导率发生相应变化,同时也引发自然电位变化.沿沙箱顶面中心线设置了一排不极化电极,盐水容器两侧各9个电极,共18个电极,电极距为5 cm(其中9#和10#电极之间由于有盐水容器,距离为10 cm).采用多通道电法仪器测量这些电极与放置在沙箱底部的公共参考电极之间的电位差,来监测沙面的自然电场变化.

|
图 6 沙槽自然电场监测实验装置 (a)观测电极布置平面图;(b)沙槽实验装置照片. Fig. 6 The experimental setup (a) Sketch of the electrode system; (b) The photo of the setup. |
在渗漏开始前,对各电极的自然电位背景场进行了观测,各电极点的背景电位从-0.3 mV到0.9 mV变化.渗漏开始后即开始正式监测,观测时间间隔为60 s,所有电极的自然电位值在渗漏过程中都发生一定的变化.如图 7所示,随着渗漏的发生,盐水扩散范围内的电极有明显迅速升高的正电位,而远离扩散中心的电极电位变化幅度要小得多.在120 s时,电极自然电位值达到峰值,然后开始缓慢下降,360 s后开始保持基本稳定.

|
图 7 部分电极自然电位变化曲线 Fig. 7 Time sequences of the recorded data at some selected electrodes |
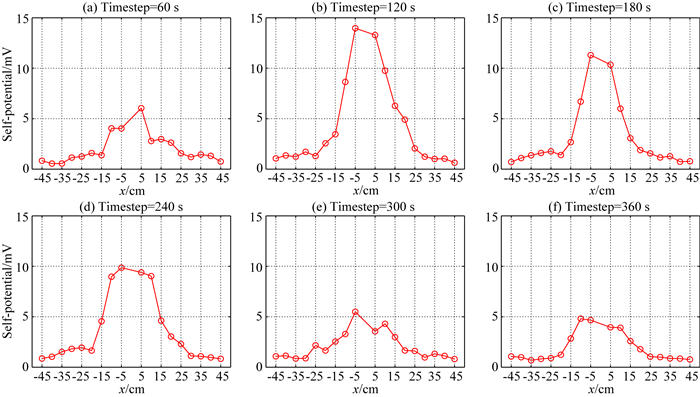
按电极排列绘制的自然电场曲线如图 8所示,图中(a)、(b)、(c)、(d)、(e)和(f)分别对应从60 s到360 s间隔60 s的各时刻自然电场数据曲线.
|
图 8 沙槽自然电场监测数据曲线 Fig. 8 The monitoring self-potential data recorded on the electrodes in sandbox |
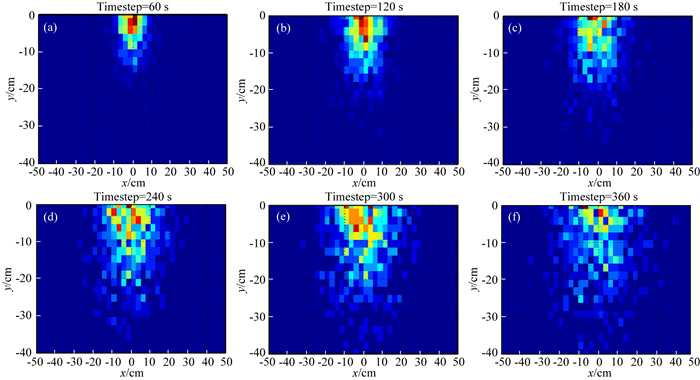
将观测到的时序自然电场数据进行时序反演,反演结果如图 9所示.图 9中(a)、(b)、(c)、(d)、(e)、(f)、(g)分别对应60 s、120 s、180 s、240 s、300 s、360 s时刻的反演结果模型.各时刻反演模型对应的拟合差分别为19.2%、16.7%、14.5%、15.3%、12.8%和13.6%,随着观测数据的不断输入,时序反演结果拟合差呈现明显逐渐减小的趋势.
|
图 9 沙槽监测数据反演结果 Fig. 9 The results of time-lapse inversion of the monitoring data |
从沙槽自然电场监测数据反演结果来看,盐水在沙槽中垂向扩散速度明显大于水平方向的速度,表明其运动主要受达西速度控制,同时也伴随随机扩散运动.事先在盐水中加入的红色染色示踪剂扩散轨迹表明反演结果与实际情况基本相符,时序反演方法可以有效对自然电场实测数据进行反演,实现了对实际动态过程的重构.
5 结语根据监测时序数据的特点,通过采用卡尔曼滤波技术替代常规直接求解反问题的反演方法,对自然电场监测数据进行卡尔曼滤波递归处理.通过递归过程中将地电模型演化信息与自然电场观测数据信息进行融合,实现对监测数据的时序反演,进而实现对动态地电模型的过程重构.数值模拟计算实验表明该时序反演方法能有效反演时序自然电场数据,即使在每个观测时刻的数据都非常有限的条件下,仍能比较准确地反演重构地电模型.这说明时序反演在反演动态模型时可以提供较好时间正则化,有效减少直接求解反问题的反演误差.加入噪声的自然电场模拟数据测试表明基于卡尔曼滤波的时序反演算法具有较好的鲁棒性,对噪声不敏感.沙槽物理模拟实验监测数据的计算测试也同样证明了时序反演算法对监测数据的反演处理具有良好的效果.这些优点使得时序反演方法不仅可以用于自然电场监测数据的反演解释,同样可以用于其他地球物理监测数据的解释处理.
致谢感谢康涅狄格大学刘澜波教授在数值模拟和物理实验过程的指导和建议,感谢审稿专家和编辑部的大力支持.
| Cui Y A, Zhu X X, Chen Z X, et al. 2016. Performance evaluation for intelligent optimization algorithms in self-potential data inversion. Journal of Central South University, 23(10): 2659-2668. DOI:10.1007/s11771-016-3327-2 | |
| Daily W, Ramirez A L, Binley A, et al. 2004. Electrical resistance tomography. The Leading Edge, 23(5): 438-442. DOI:10.1190/1.1729225 | |
| De Carlo L, Perri M T, Caputo M C, et al. 2013. Characterization of a dismissed landfill via electrical resistivity tomography and mise-à-la-masse method. Journal of Applied Geophysics, 98: 1-10. DOI:10.1016/j.jappgeo.2013.07.010 | |
| Gallas J D F, Taioli F, Filho W M. 2011. Induced polarization, resistivity, and self-potential: a case history of contamination evaluation due to landfill leakage. Environmental Earth Sciences, 63(2): 251-261. DOI:10.1007/s12665-010-0696-y | |
| Gasperikova E, Hubbard S S, Watson D B, et al. 2012. Long-term electrical resistivity monitoring of recharge-induced contaminant plume behavior. Journal of Contaminant Hydrology, 142-143: 33-49. DOI:10.1016/j.jconhyd.2012.09.007 | |
| Karaoulis M C, Kim J H, Tsourlos P I. 2011. 4D active time constrained resistivity inversion. Journal of Applied Geophysics, 73(1): 25-34. DOI:10.1016/j.jappgeo.2010.11.002 | |
| Kim J H, Yi M J, Park S G, et al. 2009. 4-D inversion of DC resistivity monitoring data acquired over a dynamically changing earth model. Journal of Applied Geophysics, 68(4): 522-532. DOI:10.1016/j.jappgeo.2009.03.002 | |
| Kim J H, Supper R, Tsourlos P, et al. 2013. Four-dimensional inversion of resistivity monitoring data through Lp norm minimizations. Geophysical Journal International, 195(3): 1640-1656. DOI:10.1093/gji/ggt324 | |
| LaBrecque D J, Yang X P. 2001. Difference inversion of ERT data: a fast inversion method for 3-D in situ monitoring. Journal of Environmental and Engineering Geophysics, 6(2): 83-90. DOI:10.4133/JEEG6.2.83 | |
| Lehikoinen A, Finsterle A, Voutilainen M B., et al. 2009. Dynamical inversion of geophysical ERT data: state estimation in the vadose zone. Inverse Problems in Science and Engineering, 17(6): 715-736. DOI:10.1080/17415970802475951 | |
| Lehikoinen A, Huttunen J M J, Finsterle S, et al. 2010. Dynamic inversion for hydrological process monitoring with electrical resistance tomography under model uncertainties. Water Resources Research, 46(4): W04513. | |
| Li H, Fan Y R, Hu Y Y, et al. 2013. Joint inversion of HDIL and SP with a five-parameter model for estimation of connate water resistivity. Chinese Journal of Geophysics (in Chinese), 56(2): 688-695. DOI:10.6038/cjg20130233 | |
| Linde N, Jougnot D, Revil A, et al. 2007. Streaming current generation in two-phase flow conditions. Geophysical Research Letters, 34(3): L03306. DOI:10.1029/2006GL028878 | |
| Martínez-Pagán P, Jardani A, Revil A, et al. 2010. Self-potential monitoring of a salt plume. Geophysics, 75(4): WA17-WA25. DOI:10.1190/1.3475533 | |
| Miller C R, Routh P S, Brosten T R, et al. 2008. Application of time-lapse ERT imaging to watershed characterization. Geophysics, 73(3): G7-G17. DOI:10.1190/1.2907156 | |
| Nenna V, Pidlisecky A, Knight R. 2011. Application of an extended Kalman filter approach to inversion of time-lapse electrical resistivity imaging data for monitoring recharge. Water Resources Research, 47(10): W10525. | |
| Oldenborger G A, Knoll M D, Routh P S, et al. 2007. Time-lapse ERT monitoring of an injection/withdrawal experiment in a shallow unconfined aquifer. Geophysics, 72(4): F177-F187. DOI:10.1190/1.2734365 | |
| Rittgers J B, Revil A, Karaoulis M, et al. 2013. Self-potential signals generated by the corrosion of buried metallic objects with application to contaminant plumes. Geophysics,, 78(5): EN65-EN82. DOI:10.1190/geo2013-0033.1 | |
| Tsourlos P, Ogilvy R D, Meldrum P I, et al. 2003. Time-lapse monitoring in single boreholes using electrical resistivity tomography. Journal of Environmental and Engineering Geophysics, 8(1): 1-14. DOI:10.4133/JEEG8.1.1 | |
| Wang Y D, He J, Li G M. 2011. Inverse of the fluvial channel reservoir permeability field using ensemble Kalman filter based on discrete cosine transform. Chinese Journal of Geophysics (in Chinese), 54(7): 1900-1911. DOI:10.3969/j.issn.0001-5733.2011.07.024 | |
| Zhao Y C, Gui X C, Hong Z J, et al. 2014. The Kalman Filter imaging studies of ionosphere TEC. Chinese Journal of Geophysics (in Chinese), 57(11): 3617-3624. DOI:10.6038/cjg20141115 | |
| Zheng W, Zhang G B. 2016. Application research on adaptive Kalman filtering for airborne gravity anomaly determination. Chinese Journal of Geophysics (in Chinese), 59(4): 1275-1283. DOI:10.6038/cjg20160410 | |
| 李虎, 范宜仁, 胡云云, 等. 2013. 基于阵列感应与自然电位联合反演地层水电阻率. 地球物理学报, 56(2): 688–695. DOI:10.6038/cjg20130233 | |
| 王玉斗, 何健, 李高明. 2011. 基于离散余弦变换的集合Kalman滤波方法对河流相油藏渗透率场的反演. 地球物理学报, 54(7): 1900–1911. DOI:10.3969/j.issn.0001-5733.2011.07.024 | |
| 赵运超, 桂晓纯, 洪振杰, 等. 2014. 电离层TEC卡尔曼滤波成像研究. 地球物理学报, 57(11): 3617–3624. DOI:10.6038/cjg20141115 | |
| 郑崴, 张贵宾. 2016. 自适应卡尔曼滤波在航空重力异常解算的应用研究. 地球物理学报, 59(4): 1275–1283. DOI:10.6038/cjg20160410 | |
 2017, Vol. 60
2017, Vol. 60

