2. 北京工业大学建筑工程学院, 北京 100124
2. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China
在地震记录稀疏或缺乏的地区,模拟地震动的随机性方法(随机点源法和随机有限断层法)在建立地震动预测方程(Ground Motion Prediction Equations,GMPEs)和估计地震动场中得到了广泛且成功的应用(Campbell,2003;王海云,2010;Drouet and Cotton, 2015;Stewart et al., 2015),证明了该方法具有很高的可信度和发展前景.
对于给定震级和断层几何产状的地震,对随机有限断层法模拟结果影响最大的参数有三个:一是控制大于拐角频率的傅里叶谱振幅大小的应力降(Δσ),二是控制每个子断层滑动量的有限断层震源模型(Finite-Fault Source Model,FFSM),三是控制傅里叶谱高频部分衰减速率和大小的高频衰减参数(κ0)(Boore et al., 1992).
基于剪切位错模型的地震波辐射理论,Brune(1970)提出了经典的ω-2加速度震源谱模型,即
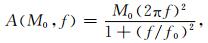
|
(1) |
式中,震源拐角频率(f0)与震源持时(T)成反比,即f0~1/T.当f≫f0时,傅里叶谱高频部分的大小(ahf)与地震矩(M0)和震源拐角频率的标度关系为ahf~M0f02.如果用Δσ和震源破裂半径(r)表示地震矩的大小,即M0~r3Δσ,那么高频谱的大小就可以表示为ahf~M01/3Δσ2/3.所以,应力降的标度为Δσ~M0f03(Brune,1970;Boore,2003).在随机有限断层法中,Δσ的物理意义接近于Kanamori和Anderson(1975)提出的静态应力降,他们通过研究41个MS为5.8~8.5的强震得到静态应力降范围集中在1~10 MPa之间,并且与震级大小无关.所以在随机有限断层法中,通常把Δσ取为5 MPa的平均值.
计算FFSM的方法主要有两种:一种是根据远震记录、近震记录和测地资料等数据进行单一或多种数据(包括近场强震动记录)的联合反演,另一种是经验方法.使用不同数据反演得到的FFSM之间虽然存在某些差异(比如破裂面上凹凸体的位置和面积),但是均能够较为准确地反映破裂断层的基本宏观特性.可是在模拟未来可能发生的地震时,无法事前获取数据来进行反演.所以,通过假设相似地质构造的活动断层发生的地震有相似的震源过程,人们还发展了矩震级与震源全局参数和局部参数的经验关系来预测未来强震的FFSM(Wells and Coppersmith, 1994;王海云,2004).Ghasemi等(2010)分别用反演得到的FFSM和随机生成的FFSM模拟了汶川地震54个断层距小于150 km的台站的地震动.结果表明,两类FFSM模拟的反应谱,在短周期段内( < 0.7 s)有相似的精度,但是在长周期段则有较大的差异.因而在随机有限断层法中,反演得到的FFSM对结果的影响主要集中在长周期段,对高频段的影响相对较小.另外,因为随机有限断层法中采用点源法计算每个子断层的时程,然后在时域中叠加得到目标场点的总时程,FFSM通过控制每个子断层能量的大小控制了模拟时程的形状和振幅.
Anderson和Hough(1984)提出了高频衰减参数κ来描述加速度傅里叶谱中高频部分的衰减现象.经过30多年的发展,κ逐渐被地震学家和工程地震学家所接受和采用,并发展为地震动模拟中的一个重要参数.但是,κ的物理意义至今仍然是个有争议的问题.一些研究者认为地震动谱的高频衰减特性主要受震源效应的影响(Papageorgiou and Aki, 1983),另一些研究者则认为近地表地质条件与震源效应对高频衰减特性的影响同样重要(Purvance and Anderson, 2003),但是大部分研究者认为κ主要是与近地表地质条件中与频率无关的品质因子、介质密度和剪切波速有关(Anderson and Hough, 1984;Hough and Anderson, 1988;Campbell,2009;Gentili and Franceschina, 2011).在随机性方法中,κ0是描述场地衰减效应的唯一参数(Boore,2003).在地震危险性分析中,κ0较小的地区被认为会得到更大的地震动(Kilb et al., 2012).Mena等(2010)的研究表明,当κ0从0.01 s增大到0.1 s时,阿里亚斯烈度大约减小了87%,峰值加速度(PGA)大约减小了67%.Boore和Joyner(1997)的研究表明,当κ0从0.02 s增大到0.04 s时,高频部分的场地放大因子从1.8减小到1.5.Anderson等(1996)模拟了S波在5 km中间层和地表30 m土层的传播,结果表明κ0对地震动峰值振幅的影响与地表以下30 m的平均剪切波速(VS30)有相同的量级,并建议完备的场地分类应该同时考虑VS30、κ0和场地共振频率的影响.因此,考虑到κ0在工程地震学研究中的重要性,许多研究者专门研究了不同国家和地区的κ模型(Atkinson,1996;Fernández et al., 2010;Douglas et al., 2010;Van Houtte et al., 2011;Kilb et al., 2012;Fu and Li, 2016).
近些年,随着观测技术的发展和强震动观测数据的积累,对地震动谱的研究逐渐向更高频的部分推进,作为表征地震动高频谱特性的重要参数,κ的物理意义和计算方法逐渐成为了工程地震学领域的研究热点.但是在国内,针对κ的专门研究还很少.本文利用1671个汶川地震和芦山地震的强地震动记录计算了龙门山断裂带及其邻区50个强震动台站的κ0,分析了κ0与高程之间的相关性,并建立了该地区的κ0经验模型.以汶川地震为例,对比研究了本文计算的κ0与Sun等(2013)根据汶川主震的强地震动记录计算的κ0对随机有限断层法的模拟结果的影响.采用考虑高程的κ0模型计算了汶川主震的峰值加速度分布场,与采用Ghasemi等(2010)计算的该地区的平均κ0=0.04 s的模拟结果和所选台站的实际观测PGA进行了比较.目的是强调κ0在强地震动模拟中的重要性,并验证与高程相关的κ0模型在模拟四川地区的地震动中的适用性,为进一步研究κ的物理机制和建立更完备的κ0模型打下基础.
2 数据本文根据Nakamura等(2010)提供的断层面位置计算断层距,选择了50个断层距小于150 km的强震动台站分别计算κ0.台站的位置、场地类型、断层距和κ值见表 1.其中,台站的位置来自于建台报告,场地类型来自于Yu等(2016)的研究结果(见原文表7).根据NEHRP(National Earthquake Hazard Reduction Program)的场地分类标准(Chiou et al., 2008),有钻孔数据的41个强震动台站中共有4个A类场地、18个B类场地和19个C类场地.没有钻孔数据的9个强震动台站中,4个为基岩场地,5个为土层场地.图 1给出了台站地理位置、汶川地震震中和FFSM的地表投影.
|
|
表 1 50个强震动台站的地理位置、高程、场地类型、断层距和κ0 Table 1 Geographical location, elevation, site type, fault distance and κ0 of 50 strong motion stations |

|
图 1 强震动台站分布 三角形表示台站位置, 五角星表示汶川主震震中, 圆点表示FFSM中子断层的地表投影.西南段和东北段分别划分为11×4和18×4个子断层. Fig. 1 Geographical distribution of strong motion stations Triangles represent the location of stations. Star represents the epicenter of mainshock of the Wenchuan earthquake. Solid circles represent surface projection of sub-faults of FFSM, in which the fault plane is divided into southwest and northeast segments, and the sub-fault numbers of segments are 11×4 and 18×4, respectively. |
地震动的傅里叶谱Y(f, R)可以表示为
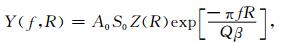
|
(2) |
式中,R为震中距,Q为品质因子,β为地壳的平均剪切波速,A0为震源项,S0为不考虑衰减的场地放大效应,Z(R)为几何扩散衰减.Cormier(1982)提出,不考虑物理机制,Q可以分为与频率有关的部分(Qf)和与频率无关的部分(QI),
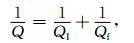
|
(3) |
所以(2) 式中与Q有关的部分可以写为
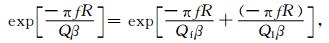
|
(4) |
R实际上是远场点源假设中对震源距的近似,更准确的表达中应该包括一个接收台站下方等于震源深度的距离H,所以(4) 式右边第二项可以改为
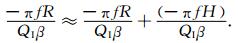
|
(5) |
定义
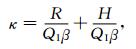
|
(6) |
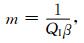
|
(7) |
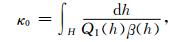
|
(8) |
式中,h,QI(h)和β(h)分别为地壳内水平层状介质的厚度、与频率无关的品质因子和层间剪切波速.从(6)—(8) 式容易得到
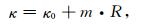
|
(9) |
式中,κ为高频衰减参数,κ0为与台站下方地质条件有关的分量,m为与地壳中QI和β有关的分量.Anderson和Hough(1984)发现,κ可以通过拟合半对数坐标中傅里叶谱的高频成分得到

|
(10) |
式中,A(f)为加速度傅里叶谱振幅,fE为高频衰减开始频率,fX为高频衰减结束频率.
计算单个记录的κ前,首先对每条加速度记录进行基线校正和滤波.然后选择噪声时程和S波时程.其中,噪声时程在事前部分选取,S波时程选为S波到时至80%能量持时的部分.用汉宁(Hanning)窗分别对以上两个时程两端的2.5%持时进行尖灭处理.计算S波时程与噪声时程的信噪比,舍弃信噪比大于3的记录.然后通过FFT得到加速度傅里叶振幅谱.
在计算过程中,fE和fX通过目测选取.fE必须大于f0以减小震源效应对κ的影响,并且fE的物理意义与高频截止频率(fmax)相似,所以取值应该在fmax附近.fX的选择考虑了两个因素,一是高频衰减终止,二是S波谱与噪声谱的信噪比大于3.在计算过程中为了尽量减小傅里叶谱的局部异常对结果的影响,fE到fX之间的频带宽度不能小于10 Hz(Ktenidou et al., 2013).图 2为一个算例.

|
图 2 κ的计算过程 (a)加速度时程, 黑色部分分别为所选择的噪声时程和S波时程; (b)半对数坐标中的加速度傅里叶谱, 在fE和fX之间的频段可以看到明显的高频衰减, 黑色实线表示高频衰减趋势, 计算得到κ=0.0528 s. Fig. 2 Process of calculating κ value (a) shows the acceleration time-history and the intervals used to calculate noise and S-wave spectra; (b) shows the Fourier amplitude spectra of noise and S-wave windows plotted in log-linear space, the frequency band ranging from fE to fX is used to estimate κ value. Solid line represents the high-frequency linear trend. In this case, κ=0.0528 s. |
在计算得到每个强地震动记录的κ之后,用(3) 式拟合得到每个台站的κ0,并得到山区和盆地的平均m分别为0.0001427 s·km-1和0.0001031 s·km-1.对于只有近断层记录的台站,我们用山区和盆地的平均m分别拟合得到每个台站的κ0(表 1中的κ0(1)).表 1中κ(2)为Sun等(2013)用汶川主震记录计算得到的52个震中距为19~311 km强震动台站的水平分量和竖向分量的平均κ.比较κ0(1)和κ(2),可以看到两者之间存在显著的差异.造成这种差异的原因主要有两点:首先,从(9) 式可以看到,κ0实际上是κ校正了m·R之后的结果.当震中距达到300 km时,m·R引起的山区和盆地地区κ的平均差异分别达到了0.04 s和0.03 s;其次,本文采用了大量的强地震动记录来计算κ0,而Sun等(2013)只用了汶川主震的一个记录.Douglas等(2010)指出,用单个记录计算的κ的最大偏差可能达到50%以上,只有通过丰富的数据计算得到的κ拟合的κ0才真实可信.
4 模型参数设定为了方便与Sun等(2013)的模拟结果比较,本文采用FINSIM程序进行随机有限断层法模拟(Beresnev and Atkinson, 1998).表 2给出了选用的参数.Δσ是控制震源谱能量大小的参数,通常设为5 MPa.辐射强度因子通过改变破裂面上最大滑动速率来控制子断层辐射能量的大小,通常设为1.0.几何扩散方程选用Atkinson和Boore(1995)根据北美东部强震动记录建立的三段式模型.有效品质因子采用Pei等(2006)得到的Q(f)=415f0.5.场地放大系数采用喻畑和李小军(2012)的结果,他们对四川和甘肃地区147个强震动台站的场地进行了分类,把A类和B类场地划分为“浅硬场地”,把C类和D类场地划分为“深厚土层场地”,并用四分之一波长法(Boore and Joyner, 1997)分别计算了浅硬场地和深厚土层场地的平均场地放大系数(见其原文中表4).
|
|
表 2 随机有限断层法模拟汶川地震所用的参数 Table 2 Parameters in the stochastic finite-fault method used in simulation of the Wenchuan earthquake |
采用Nakamura等(2010)用远震数据反演得到的FFSM.该模型中,汶川地震的破裂断层面被分为西南段和东北段.西南段为小倾角逆冲破裂,倾角为33°,最大滑动量为11.0 m,破裂面沿走向和倾向离散为11×4个子断层;东北段为大倾角右旋走滑破裂,倾角为60°,最大滑动量为4.8 m,破裂面沿走向和倾向离散为18×4个子断层(图 3).
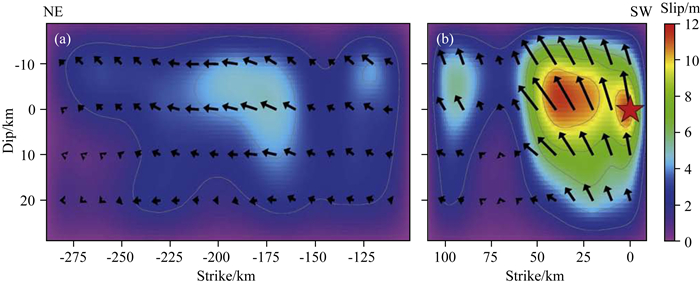
|
图 3 汶川地震的有限断层模型 (a)东北段, 倾角为60°, 最大滑动量为4.8 m;(b)西南段, 倾角为33°, 最大滑动量为11.0 m (来自Nakamura et al., 2010;图 2). Fig. 3 Finite-fault source model for the Wenchuan earthquake (a) Northeastern segment, dip angle is 60° and maximum slip is 4.8 m; (b) Southwestern segment, dip angle is 33° and maximum slip is 11.0 m (after Nakamura et al., 2010; Fig. 2). |
我们把采用κ0(1)和κ(2)的模拟分别称为模型A(model A)和模型B(model B).图 4中展示了部分台站的模拟和观测加速度时程、傅里叶谱和反应谱(阻尼比为5%).两个模型的模拟结果在频率小于1 Hz的部分非常接近.但是在频率大于1 Hz的部分,模型A的模拟结果与观测反应谱和傅里叶谱较为符合,模型B的符合度相对较差.以上结果表明,κ0主要影响的是加速度傅里叶谱和反应谱中大于1 Hz的高频部分.通常,高频部分与加速度时程的振幅有关,但是对加速度时程的形状影响很小.从时程上看,大部分台站模拟结果的持时与观测结果较为相似,但是部分台站的时程形状与观测结果有较大偏差(比如图 4中CDZ、WCW和BXD台站).这是因为在随机有限断层法中,震源破裂过程假设为从破裂起始子断层开始,以破裂传播速度向周围的子断层扩散;而实际的震源破裂过程中,子断层的破裂顺序、破裂时间和破裂传播速度等因素与本文假设模型存在一定的差异.但是对于未来可能发生的地震,这些因素很难确定.另一方面,κ0对PGA的影响非常显著,比如MZQ台站(图 4a),κ0(2)比κ(2)小0.014 s,但是PGA增大了2倍以上.

|
图 4 部分台站的加速度模拟结果与观测结果的比较 每个台站的左上图为反应谱, 右上图为傅里叶谱.其中红色实线和蓝色虚线分别表示模型A和模型B的模拟结果;灰色实线和灰色虚线分别表示东西向(EW)和南北向(NS)的观测结果.左下图为观测时程, 右下图为模拟时程. Fig. 4 Comparison between simulation and recording for several stations For each station, the upper left panel represents response spectra, and the upper right panel represents the Fourier amplitude spectra. Red solid line and blue dashed line represent the results of models A and B, respectively. The gray solid line and gray dash line represent the EW and NS components of recordings, respectively. Lower left panel represents the recorded acceleration time-history. Lower right panel represents the simulated time-history. |
图 5a和5b分别给出了模型A和模型B在0.01~10.0 s周期段的加速度反应谱的模型偏差.模型偏差定义为所有台站的模拟和观测反应谱之间的对数差,其中阴影部分表示95%置信区间,虚线表示模型的标准差.模型A和模型B的标准差分别为0.34和0.38.在短周期部分( < 1 s),模型A与观测结果非常相符,模型B则明显大于观测反应谱;在长周期部分(>5 s),模型A与模型B的反应谱模拟结果一致且均有较大的误差.综合图 4和图 5的结果可以看到,合理地估计台站的κ0,可以有效地改善高频反应谱、高频加速度傅里叶谱和PGA的模拟结果.如果κ0的取值过大或过小,模拟结果可能出现较大的偏差.

|
图 5 模型A和模型B与观测反应谱在0.01~10 s周期段的模型偏差 阴影部分表示95%置信区间, 虚线表示± 1倍的标准差. Fig. 5 Model deviations of model A and model B versus recorded spectra acceleration in the period band from 0.01~10 s Shaded areas represent 95% confidence limits. Dashed lines represent ±1 standard deviations. |
本文选用的50个强震动台站的断层距范围为8.8~148.1 km,南北向和东西向分量强地震动记录的PGA范围分别为23.74~802.48 cm·s-2和27.64~957.43 cm·s-2.为了更好地与模拟结果比较,对每个台站两个水平分量的PGA求算数平均,得到的平均PGA范围为25.69~813.41 cm·s-2.采用简化的衰减模型拟合PGA和不同周期反应谱幅值与断层距的经验衰减关系(于海英等,2009):
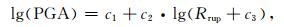
|
(11) |
标准差定义为:

|
(12) |
图 6比较了模拟PGA与观测PGA随断层距的衰减曲线.其中,观测PGA和模拟PGA的标准差分别为0.20和0.11.如图 6所示,随着断层距的增大,观测PGA的离散性增大,而模拟PGA的离散性较小.这可能由三个原因造成:一是传播路径的复杂性随着距离的增大而增大;二是本文采用平均的场地放大系数,没有完全考虑到台站间局部场地效应的差异;三是随机有限断层法对震源过程、路径效应和场地效应做了较多的简化.总体上,模拟与观测的PGA的衰减曲线在10~200 km距离范围内非常接近,表明通过合理的参数选择,随机有限断层法在模拟近场强震动的PGA时表现良好.
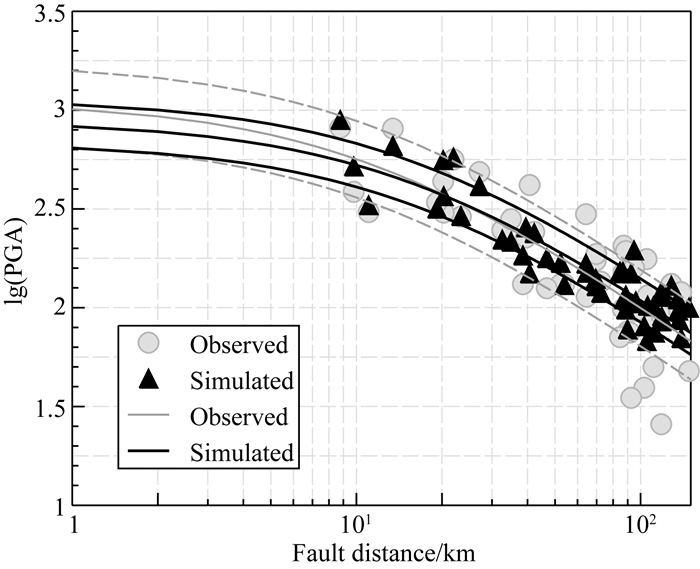
|
图 6 峰值加速度随断层距的衰减曲线 黑色三角表示模型A的模拟结果, 灰色圆形表示观测结果.灰色实线表示观测峰值加速度的衰减曲线, 灰色虚线表示±1倍的标准差;黑色实线表示模拟峰值加速度的衰减曲线, 黑色虚线表示±1倍的标准差. Fig. 6 Attenuation curves of PGA versus fault distance Black triangles represent the simulation of model A, gray circles represent the recorded PGA. Gray solid line and dash lines represent the attenuation curves of recorded PGA and the ±1 standard derivation, respectively. Black solid line and dash lines represent the attenuation curves of simulated PGA and the ±1 standard derivation, respectively. |
图 7比较了模型A的模拟结果与观测记录在不同周期(T=0.04,0.05,0.1,0.2,0.5和1.0 s)的反应谱幅值.因为κ0主要影响的是小于1 s的短周期段,我们只给出了这个周期段的结果.T=0.04 s时,模拟结果相对于观测结果整体偏低;在0.05~0.5 s之间,模拟结果与观测结果符合很好;T=1.0 s时,断层距小于100 km时模拟结果较好,断层距大于100 km时模拟结果偏大.另外,我们也对周期为2.0和5.0 s的反应谱幅值进行了比较,发现模拟结果较观测结果在不同距离范围出现了不同程度的偏差.Boore和Joyner(1997)、Campbell(2009)的研究表明,小于1 s的周期段主要受到近地表地质条件的影响.本文的模拟结果在这一周期段与观测结果符合较好,表明所采用的κ0和场地放大系数较好地反映了场地效应,从而改善了高频部分的模拟结果.因此,研究κ0的物理机制,可以尝试围绕几十到几百米的深钻孔的岩土参数来展开.

|
图 7 本文结果与观测反应谱在不同周期的衰减关系的比较 黑色三角形表示模拟反应谱幅值, 灰色圆形表示观测反应谱幅值.黑色实线表示模拟结果的衰减曲线.灰色实线和虚线分别表示观测结果的衰减曲线和±1倍标准差. Fig. 7 Comparison of attenuation between simulated and recorded response spectra at different periods Black triangles and gray circles represent the simulated and recorded spectral amplitudes, respectively. Black solid line represents the attenuation curve of simulated spectra. Gray solid line and dash lines represent the attenuation curve of recorded spectra and the ±1 standard deviation, respectively. |
综上,本文计算的κ0可以有效地改善模拟的PGA和0.05~1.0 s周期范围的反应谱幅值.随机有限断层法相对于确定性方法的优势之一在于高频部分模拟结果较好,选择适当的κ0可以使模拟结果更为可靠,从而更加突出该方法模拟PGA和高频谱的优势.
6 考虑κ0模型的峰值加速度分布如引言中所介绍,随机法被广泛应用于估计近断层强地震动场和建立地震记录缺乏地区的GMPEs.如图 4和图 7所示,κ0对模拟得到的PGA和0.05~1.0 s周期段的反应谱幅值影响显著.但是,对于地震记录稀疏或缺少的地区,κ0并不总能用地震记录来计算.因此,需要建立κ0的经验模型.笔者发现本文所研究的50个台站的κ0随着高程的增加而减小,这可能是因为κ0主要受区域近地表地质条件的影响.通常在同一区域,高程越高几十到几百米的近地表地质条件越坚硬,所以κ0越小(Fu and Li, 2016).采用简单的对数模型,我们拟合得到的四川地区κ0

|
(13) |
式中,he为高程(m).另外,我们还计算了每个台站竖向分量的κ0,结果表明竖向分量的κ0整体上小于水平分量.Motazedian(2006)和Ktenidou等(2013)的研究也得到了类似的结论.Ktenidou等(2013)计算了一个竖向台阵中地表记录和井下记录(深178 m)的κ0,发现地表和178 m深度处的水平向与竖向κ0的比值分别为1.4和1.0.所以,通过假设竖向分量的高频衰减受场地条件的影响较小,我们把水平分量的最小κ0经验地取为研究区内竖向分量κ0的最小值0.0112 s.图 8为κ0随高程增大而减小的经验关系,标准差为0.00853 s.在模拟地震动加速度场时,为了用(6) 式计算每个节点的κ0,以数字高程模型(Smith and Sandwell, 1997)为基础进行二维线性插值来估算每个节点的平均高程.

|
图 8 四川地区高程与κ0的经验相关性 灰色圆形表示单个台站的κ0.黑色实线为κ0与高程的经验关系, 黑色虚线为±1倍标准差. Fig. 8 Correlation between κ0 and elevation in Sichuan province Gray circles represent κ0 of individual stations. Black solid line represents the attenuation trend of κ0 with respect to elevation. Black dash lines represent ±1 standard deviation. |
模拟的区域范围为东经101°—107°和北纬29°—34°,该区域包括了汶川地震的整个破裂面和表 1中所有台站.沿经度和纬度的节点间隔取为0.1°×0.1°.模拟参数见表 2,场地放大系数取为浅硬土层场地的平均放大系数.计算节点的高程在283~4616 m之间,根据(13) 式估算的κ0的变化范围为0.0186~0.0536 s.取Ghasemi等(2010)计算的四川地区的平均κ0=0.04 s的模拟结果作为对照,与高程相关的κ0模型的模拟结果进行比较.然后与50个台站的实际观测PGA比较,研究两种模拟结果的差异.因为就整个区域的PGA分布而言,东西向和南北向分量的大小没有明显差异,采用两个水平分量的平均PGA进行比较.
图 9a和9b分别给出了与高程相关的κ0模型(简称为模型C)和κ0=0.04s(简称为模型D)的模拟结果,从外到内的黑色实线分别是PGA为50 cm·s-2、150 cm·s-2、300 cm·s-2、500 cm·s-2和800 cm·s-2的等值线.强震动台站的颜色表示该台站两个水平向分量观测PGA的平均值大小.模型C和模型D的最大PGA分别为1028.93 cm·s-2和707.45 cm·s-2,观测的最大平均PGA为MZQ台站的813.64 cm·s-2.
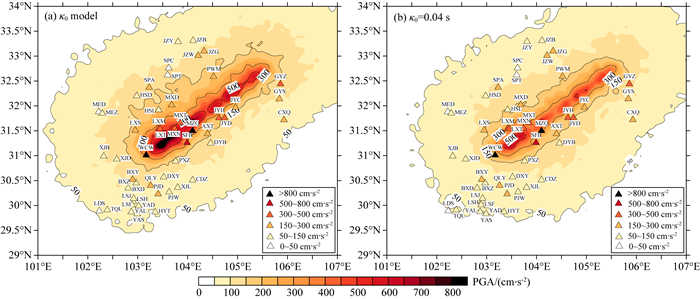
|
图 9 模拟PGA分布与台站观测PGA的比较 (a)模型C的结果;(b)模型D的结果. Fig. 9 Comparison of simulated PGA and observed PGA distributions (a) Model C; (b) Model D. |
从模拟结果可以看到,观测PGA小于50 cm·s-2的4个台站中,模型C和模型D的结果都大于观测值.对于观测PGA在50~150 cm·s-2范围内的23个台站,两个模型中HSL台站的结果都大于观测值,模型D中HYT、LSH、LSJ、LSF、YAD和YAS等6个台站的PGA都接近于50 cm·s-2,远小于观测的88.22~131.25 cm·s-2,模型C的结果与观测值更为接近.对于观测PGA在150~300 cm·s-2范围内的13个台站,模型C中山区的模拟结果明显好于模型D,盆地地区的模拟结果则与模型D相似.对于观测PGA在300~500 cm·s-2范围内的7个台站,模型C中MXN台站的结果大于观测值.对于观测PGA大于500 cm·s-2的3个台站,模型C的结果比模型D更接近于观测值.另外,模型C中靠近3个最大凹凸体地表投影区的范围内有PGA明显大于600 cm·s-2的区域,相对于最大PGA为707.45 cm·s-2的模型D,这与靠近极震区的WCW和MZQ台站的结果更为接近.综上,模型C的PGA空间分布与观测结果更为相符,特别是在破裂传播方向的反方向区域和山区.另外,在相同的断层距,模型C中山区的PGA明显高于盆地地区,而模型D中的PGA近似为对称分布.
以上结果表明,采用与高程相关的κ0模型,可以有效地改善汶川地震中PGA的模拟结果.汶川地震中山区的PGA明显大于盆地地区的现象,不仅与上盘效应有关,而且还与山区的κ0明显小于下盘有关.所以在采用随机有限断层法进行模拟时,κ0对PGA和高频谱的影响不能忽视,特别是对于近断层的强地震动.比如前文中,κ(2)平均比κ0(1)小0.012 s,但是使用前者模拟的PGA与观测PGA之间的平均相对误差比后者大40%左右.所以,建立合理的区域性κ0模型对随机有限断层法的应用和推广具有重要的实际意义.另一方面,因为κ0强烈地受到近地表地质条件的影响,根据单个参数建立的经验κ0模型必然存在一定的误差.比如图 8中,高程为900 m左右的台站的κ0之间的最大差异达到了0.03 s,κ0模型的相关系数为41%,离散性较大.然而Ktenidou等(2014)指出,根据VS30建立的κ0模型的相关系数通常小于30%.我们对四川地区κ0和VS30的相关性也做了研究,结果表明κ0与VS30并没有明显的相关性.所以,VS30虽然能较好地表征地表土层的性质,但是可能并不能很好地表征κ0.因为κ0不仅与地表场地条件(控制VS30大小)有关,还受到了更深部的介质性质的影响.所以,对于龙门山地区或者其他地质条件相似的地区,根据区域的相对高程来建立κ0的经验模型是较好的选择.本文所建立的与高程相关的κ0模型,不仅为龙门山地区的强地震动模拟中κ0的选择提供依据,而且为其他相关的研究提供了思路.
7 结论本文计算了龙门山地区50个强震动台站的κ0,用随机有限断层法模拟了汶川地震中这50个台站的地震动加速度时程、反应谱和傅里叶谱.通过与实际强震动观测记录及前人研究成果的比较,研究了κ0对PGA、加速度傅里叶谱和加速度反应谱的影响.分别采用与高程相关的κ0模型和κ0= 0.04 s计算了汶川地震的峰值加速度场,并与观测PGA进行了比较.得到以下主要结论:
(1) 与Sun等(2013)的模拟结果比较,本文计算的κ0平均比前者大0.012 s,模拟得到的PGA与观测结果的相对误差平均小40%.表明用单个或少量强地震动记录计算的κ0不一定可靠.并且,在用随机有限断层法模拟四川地区的近断层强地震动时,本文计算的κ0可以有效地改善加速度时程的振幅大小以及高频谱的模拟结果.
(2) 通过比较0.04~1.0 s周期范围内模拟与观测反应谱幅值随断层距的衰减关系,确定了κ0主要影响的周期范围为0.05~1.0 s.因为这一周期范围的地震动显著受到近地表地质条件的影响,认为针对κ0的物理机制的研究,可以围绕着与几十到几百米的深钻孔的岩土参数的相关性来展开.
(3) 本文建立了龙门山地区与高程相关的κ0模型,并模拟了汶川地震的PGA分布.与采用κ0=0.04 s的模拟结果比较,采用与高程相关的κ0模型的模拟结果与观测PGA更为符合,特别是在山区和破裂传播方向的反方向区域.表明在地震动模拟中,根据与高程相关的κ0模型来确定目标场点的κ0是一种合理的选择.另外,我们还发现在汶川地震中观测到的山区PGA明显大于盆地地区的现象,不仅与上盘效应有关,还与山区的κ0明显小于盆地地区有关.
(4) 本文在模拟中采用了喻畑和李小军(2012)建立的四川、甘肃地区浅硬土层场地和深厚土层场地的平均场地放大系数,结合适当的κ0模型,模拟结果与观测记录符合良好.表明相对于Boore和Joyner(1997)根据北美西部地区建立的平均场地放大系数,喻畑和李小军(2012)的结果与中国西南地区的实际情况更为接近.
致谢感谢中国强震动台网中心提供汶川和芦山地震的强震数据.感谢两位审稿专家提出的宝贵意见,与他们的讨论让我们受益匪浅.感谢本文编辑的仔细校对.还要感谢南京工业大学周正华教授为本文研究内容的改进提出的宝贵意见.感谢Nakamura T.提供FFSM模型.
| Anderson J G, Hough S E. 1984. A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies. Bulletin of the Seismological Society of America, 74(5): 1969-1993. | |
| Anderson J G, Lee Y J, Zeng Y H, et al. 1996. Control of strong motion by the upper 30 meters. Bulletin of the Seismological Society of America, 86(6): 1749-1759. | |
| Atkinson G M. 1996. The high-frequency shape of the source spectrum for earthquakes in eastern and western Canada. Bulletin of the Seismological Society of America, 86(1A): 106-112. | |
| Atkinson G M, Boore D M. 1995. Ground-motion relations for eastern North America. Bulletin of the Seismological Society of America, 85(1): 17-30. | |
| Beresnev I A, Atkinson G M. 1998. FINSIM-A FORTRAN program for simulating stochastic acceleration time histories from finite faults. Seismological Research Letters, 69(1): 27-32. DOI:10.1785/gssrl.69.1.27 | |
| Boore D M. 2003. Simulation of ground motion using the stochastic method. Pure and Applied Geophysics, 160(3): 635-676. DOI:10.1007/PL00012553 | |
| Boore D M, Joyner W B. 1997. Site amplifications for generic rock sites. Bulletin of the Seismological Society of America, 87(2): 327-341. | |
| Boore D M, Joyner W B, Wennerberg L. 1992. Fitting the stochastic ω-2 source model to observed response spectra in western North America: trade-offs between Δσ and κ. Bulletin of the Seismological Society of America, 82(4): 1956-1963. | |
| Brune J N. 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes. Journal of Geophysical Research, 75(26): 4997-5009. DOI:10.1029/JB075i026p04997 | |
| Campbell K W. 2003. Prediction of strong ground motion using the hybrid empirical method and its use in the development of ground-motion (attenuation) relations in eastern North America. Bulletin of the Seismological Society of America, 93(3): 1012-1033. DOI:10.1785/0120020002 | |
| Campbell K W. 2009. Estimates of shear-wave Q and κ0 for unconsolidated and semiconsolidated sediments in eastern North America. Bulletin of the Seismological Society of America, 99(4): 2365-2392. DOI:10.1785/0120080116 | |
| Chiou B, Darragh R, Siva W, et al. 2008. NGA project strong-motion database. Earthquake Spectra, 24(1): 23-44. DOI:10.1193/1.2894831 | |
| Cormier V F. 1982. The effect of attenuation on seismic body waves. Bulletin of the Seismological Society of America, 72(6B): S169-S200. | |
| Douglas J, Gehl P, Bonilla L F, et al. 2010. A κ model for mainland France. Pure and Applied Geophysics, 167(11): 1303-1315. DOI:10.1007/s00024-010-0146-5 | |
| Drouet S, Cotton F. 2015. Regional stochastic GMPEs in low-seismicity areas: scaling and aleatory variability analysis-Application to the French Apls. Bulletin of the Seismological Society of America, 105(4): 1883-1902. DOI:10.1785/0120140240 | |
| Fernández A I, Castro R R, Huerta C I. 2010. The spectral decay parameter kappa in northeastern Sonora, Mexico. Bulletin of the Seismological Society of America, 100(1): 196-206. DOI:10.1785/0120090049 | |
| Fu L, Li X J. 2016. The characteristics of high-frequency attenuation of shear waves in the Longmen Shan and adjacent regions. Bulletin of the Seismological Society of America, 106(5): 1979-1990. DOI:10.1785/0120160002 | |
| Gentili S, Franceschina G. 2011. High frequency attenuation of shear waves in the southeastern Alps and northern Dinarides. Geophysical Journal International, 185(3): 1393-1416. DOI:10.1111/gji.2011.185.issue-3 | |
| Ghasemi H, Fukushima Y, Koketsu K, et al. 2010. Ground-motion simulation for the 2008 Wenchuan, China, earthquake using the stochastic finite-fault method. Bulletin of the Seismological Society of America, 100(5B): 2476-2490. DOI:10.1785/0120090258 | |
| Hough S J, Anderson J G. 1988. High-frequency spectra observed at Anza, California: implications for Q structure. Bulletin of the Seismological Society of America, 78(2): 672-691. | |
| Kanamori H, Anderson D L. 1975. Theoretical basis of some empirical relations in seismology. Bulletin of the Seismological Society of America, 65(5): 1073-1095. | |
| Kilb D, Biasi G, Anderson J, et al. 2012. A comparison of spectral parameter kappa from small and moderate earthquakes using southern California ANZA Seismic Network Data. Bulletin of the Seismological Society of America, 102(1): 284-300. DOI:10.1785/0120100309 | |
| Ktenidou O J, Cotton F, Abrahamson N A, et al. 2014. Taxonomy of κ: a review of definitions and estimation approaches targeted to applications. Seismological Research Letters, 85(1): 135-146. DOI:10.1785/0220130027 | |
| Ktenidou O J, Gélis C, Bonilla L F. 2013. A study on the variability of kappa (κ) in a borehole: Implications of the computation process. Bulletin of the Seismological Society of America, 103(2A): 1048-1068. DOI:10.1785/0120120093 | |
| Mena B, Mai P M, Olsen K B, et al. 2010. Hybrid broadband ground-motion simulation using scattering Green's functions: Application to large-magnitude events. Bulletin of the Seismological Society of America, 100(5A): 2143-2162. DOI:10.1785/0120080318 | |
| Motazedian D. 2006. Region-specific key seismic parameters for earthquakes in northern Iran. Bulletin of the Seismological Society of America, 96(4A): 1383-1395. DOI:10.1785/0120050162 | |
| Nakamura T, Tsuboi S, Kaneda Y, et al. 2010. Rupture process of the 2008 Wenchuan, China earthquake inferred from teleseismic waveform inversion and forward modeling of broadband seismic waves. Tectonophysics, 491(1-4): 72-84. DOI:10.1016/j.tecto.2009.09.020 | |
| Papageorgiou A S, Aki K. 1983. A specific barrier model for the quantitative description of inhomogeneous faulting and the prediction of strong ground motion. I. Description of the model. Bulletin of the Seismological Society of America, 73(3): 693-722. | |
| Pei S, Zhao J, Rowe C A, et al. 2006. ML amplitude tomography in North China. Bulletin of the Seismological Society of America, 96(4A): 1560-1566. DOI:10.1785/0120060021 | |
| Purvance M D, Anderson J G. 2003. A comprehensive study of the observed spectral decay in strong-motion accelerations recorded in Guerrero, Mexico. Bulletin of the Seismological Society of America, 93(2): 600-611. DOI:10.1785/0120020065 | |
| Smith W H F, Sandwell D T. 1997. Global sea floor topography from satellite altimetry and ship depth soundings. Science, 277(5334): 1957-1962. | |
| Sun X D, Tao X X, Duan S S, et al. 2013. Kappa (κ) derived from accelerograms recorded in the 2008 Wenchuan mainshock, Sichuan, China. Journal of Asian Earth Sciences, 73: 306-316. DOI:10.1016/j.jseaes.2013.05.008 | |
| Stewart J P, Douglas J, Javanbarg M, et al. 2015. Selection of ground motion prediction equations for the global earthquake model. Earthquake Spectra, 31(1): 19-45. DOI:10.1193/013013EQS017M | |
| Van Houtte C S, Drouet S, Cotton F. 2011. Analysis of the origins of κ (kappa) to compute hard rock to rock adjustment factors for GMPEs. Bulletin of the Seismological Society of America, 101(6): 2926-2941. DOI:10.1785/0120100345 | |
| Wang H Y. 2004. Finite fault source model for predicting near-field strong ground motion [Ph. D. thesis] (in Chinese). Harbin: Institute of Engineering Mechanics, China Earthquake Administration. | |
| Wang H Y. 2010. Prediction of acceleration field of the 14 April 2010 Yushu earthquake. Chinese Journal of Geophysics, 53(10): 2345-2354. DOI:10.3969/j.issn.0001-5733.2010.10.008 | |
| Wells D L, Coppersmith K J. 1994. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bulletin of the Seismological Society of America, 84(4): 974-1002. | |
| Yu H Y, Wang D, Yang Y F, et al. 2009. The preliminary analysis of strong ground motion records form the MS8.0 Wenchuan earthquake. Journal of Earthquake Engineering and Engineering Vibration, 29(1): 1-13. | |
| Yu T, Li X J. 2012. Inversion of strong motion data for source parameters of Wenchuan aftershocks, attenuation function and average site effect. Acta Seismologica Sinica, 34(5): 621-632. | |
| Yu Y, Silva W J, Darragh B, et al. 2016. VS30 estimate for southwest China. International Journal of Geophysics. DOI:10.1155/2016/9305095 | |
| 王海云. 2004. 近场强地震动预测的有限断层震源模型[博士论文]. 哈尔滨: 中国地震局工程力学研究所. http://cdmd.cnki.com.cn/Article/CDMD-85406-2004102032.htm | |
| 王海云. 2010. 2010年4月14日玉树Ms7.1地震加速度场预测. 地球物理学报, 53(10): 2345–2354. DOI:10.3969/j.issn.0001-5733.2010.10.008 | |
| 于海英, 王栋, 杨永强, 等. 2009. 汶川8.0级地震强震动加速度记录的初步分析. 地震工程与工程振动, 29(1): 1–13. | |
| 喻畑, 李小军. 2012. 汶川地震余震震源参数及地震动衰减与场地影响参数反演分析. 地震学报, 34(5): 621–632. | |
 2017, Vol. 60
2017, Vol. 60




