2. 青岛海洋科学与技术国家实验室, 海洋矿产资源评价与探测技术功能实验室, 青岛 266061
2. Functional Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266061, China
时频变换方法在过去的30年中不断发展,并在地球物理中得到成功应用(Huang and Zhang, 2014;林红波等, 2015;王鹏等, 2014),其中最重要的应用之一,是用于油气地震勘探的谱分解方法(Partyka et al., 1999).谱分解将地震信号分解为三维时频能量体,刻画地下岩石和储层与时间相关的频率响应.时频变换是谱分解中至关重要的一环.谱分解中使用的时频变换方法包括短时傅立叶变换(Short-Time Fourier Transform, STFT)、连续小波变换(Continuous Wavelet Transform, CWT)和S变换(S-Transform, ST).但是这些常用的时频变换方法得到的瞬时频率能量在时频谱上呈带状分布,其几何形态取决于信号和分析窗口的属性(Auger et al., 2013),使得在时频谱上会出现虚假时频能量.这些虚假能量的存在会导致对谱分解的结果做出错误的解释.消除这些虚假时频能量的一种解决方法是提高谱分解的时频分辨率.
同步挤压变换(Synchrosqueezing Transform, SST)是Daubechies等提出的一种替代经验模态分解(Empirical Mode Decomposition, EMD)方法的新方法(Daubechies and Maes, 1996; Daubechies et al., 2011).SST的思路和时频重排算法(Reassignment Method, RM)(Kodera et al., 1978) 类似,但是相比之下,SST支持非平稳信号的重构.SST不仅拥有与EMD相当的时频分辨率,而且具有坚实的数学基础,这使得我们可以在SST的基础上根据要处理信号的特点对其进行修改.近年来,很多学者都致力于改进EMD,RM以及SST的效果.例如,Chui和Van Der Walt(2015) 提出一种EMD-SST混合的计算策略来估计瞬时频率;Auger等(2012) 给出了一种新的Levenberg-Marquardt方法来使得RM具有更好的适应性;Li和Liang(2012) 引入了一种广义挤压变换来进行齿轮箱故障检测.目前,SST已经被成功应用在诸多领域,例如齿轮故障检测(Feng et al., 2015)、古气候研究(Thakur et al., 2013)、信号识别和恢复(Wu et al., 2014; Wang et al., 2013, 2015; Ahrabian et al., 2015) 以及信号消噪(Meignen et al., 2012; Ahrabian and Mandic, 2015)等.在地球物理应用方面,Wang等(2014) 应用SST处理沉积盆地地震资料以寻找地下古河道;Herrera等(2014, 2015) 将SST应用于在瞬时频率切片上寻找河道和断裂,还从微震信号中分离了体波,从时频谱上重构了相位;我们应用SST压制地震勘探资料中的面波(刘晗等, 2016),从低信噪比地面微震监测数据中检测了有效微震波(刘晗等, 2015).
SST既可以利用STFT实现,也可以利用CWT实现,相应的挤压效果与所用的时频变换密切相关.因此,对于非平稳信号来说,SST利用CWT能够取得比利用STFT时更好的时频分辨效果.但是,在利用CWT进行挤压时,必须考虑选择合适的母小波,因为基于不同母小波CWT的时频变换效果可能会相差很大.ST不但可以实现无损逆变换,还保留了信号原相位信息(Tary et al., 2014; Stockwell, 1999).此外,ST的结果是时间-频率谱,比CWT的时间-尺度谱更加直观.在地震勘探中,薄目标储层的反射波信号经常具有高频和低幅度的特征(Liu, 2006),通常很难在时频谱中辨别这些薄储层.由于ST对薄储层时频能量的刻画效果较好,其单频率切片的时频分辨高,从而能反映出薄储层的位置.
为了提高ST的分辨率,我们提出了一种基于ST的同步挤压变换方法,称之为同步挤压S变换(Synchrosqueezing S-transform, SSST)(黄忠来和张建中, 2016),并应用该方法提高天然气水合物地震信号谱分解的时频分辨率,取得了较好的效果(Huang et al., 2016).但是,当信号的瞬时频率随时间呈现非线性变化时,SSST所计算出的候选瞬时频率与信号的真实瞬时频率有误差,并在真实值附近出现伪频率点,这导致在挤压时,信号的时频能量不能正确集中到真实的时频位置,降低了SSST的时频分辨率.为了进一步改善SSST的时频分解效果,在本文中我们利用时频谱对时间和频率的二阶导数,对SSST的瞬时频率计算式进行修正,提高了计算瞬时频率的精度,并提出二阶同步挤压S变换(second-order Synchrosqueezing S-transform, SSST2nd).该方法对于瞬时频率随时间呈现非线性变化的非平稳信号能获得高时频分辨率.在接下来的章节中,我们将首先回顾SSST的基本原理,再进一步推导SSST2nd的公式.之后,我们利用合成信号分析和比较了SSST2nd和其他常用时频变换方法的时频特征刻画效果,最后,将SSST2nd应用到实际地震信号的谱分解中.
2 方法 2.1 同步挤压S变换
首先简要介绍SSST的原理.挤压类时频变换的基本思想是:为了提高STFT、CWT等时频变换的分辨率,要先计算出时频谱上能量的“重心”位置,再将此位置周围的能量重新排列到该“重心”处,从而完成对能量的挤压.例如,设argTFs(f, t)为信号s(t)的时频变换结果TFs(f, t)的幅角,则时频重心的时间坐标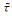
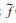
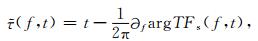
|
(1) |
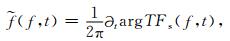
|
(2) |
显然,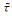
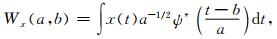
|
(3) |
这里ψ*为母小波的复共轭,a为尺度变量,b为时间变量.对于小波变换的时间-尺度谱上任意一点(a, b),如果Wx(a, b)≠0,那么此点所对应的瞬时频率为(Daubechies et al., 2011)

|
(4) |
给定了时间-尺度谱上每一点(a, b)的瞬时频率后,时间-尺度谱就变成了时间-频率谱,即(a, b)被投影到了(ω(a, b), b),再对时频谱进行重新排列(挤压).如果信号的采样频率为sf,小波变换中使用的尺度个数为N,由于Wx(a, b)只在离散的尺度值ak计算,在挤压后的时频谱上,频率为ωl=l·sf/N, l∈[1, N].这样,每个瞬时频率的小波系数在频率范围Δω= ωl-1, ωl内,被叠加到频率ωl处.据此,SST被定义为(Daubechies et al., 2011)

|
(5) |
其中ak为第k个离散尺度,且Δa=ak-ak-1.在每一个时间点沿着频率轴挤压,SST将时频能量变得更加集中.
为了利用ST的时频谱在刻画薄储层方面的优势,我们提出了同步挤压S变换.设信号x(t)的ST表达式为
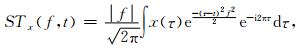
|
(6) |
其中f是频率.令

|
(7) |
比较(7)和小波变换的表达式(3),如果令f =1/a,t =b,则ST和CWT具有下面的关系:

|
(8) |
这里
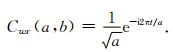
|
(9) |
可见,ST可以表示成CWT与函数Cwx(a, b)的乘积.函数Cwx(a, b)从两个方面影响CWT的结果,首先,e-i2πt/a项保持了原信号的相位;其次,系数
SSST的瞬时频率定义为(黄忠来和张建中, 2016a)
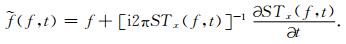
|
(10) |
根据瞬时频率的表达式,信号x(t)的SSST被定义为
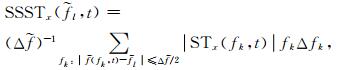
|
(11) |
这里,fk是计算ST时的离散频率,且Δfk=fk-fk-1.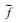
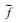
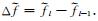
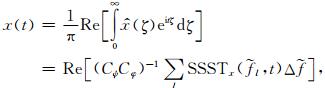
|
(12) |
这里Cφ=e-i[2πft+φ(f, t)]f2.
SSST时频谱的频率轴是线性分布的.但是,如果SST中小波的尺度a选取的是2的指数倍(aj=2j/nv, 这里nv是自定义的整数,用来控制尺度的个数),那么根据尺度和频率的关系ω=sf·Fc/a(这里Fc是母小波的中心频率),从这样的尺度得到的频率并不是线性分布的.由于线性频率的结果更加直观,同时也为了方便比较SST和SSST的结果,我们选取一组特殊的尺度序列来得到线性频率的SST结果.如果尺度的个数为N,那么我们在SST中使用的尺度序列为
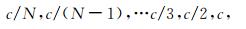
|
其中c=2FcN.
2.2 二阶同步挤压S变换
从上可以看到,针对形如x(t)=Acos(ωt)的信号,基于小波的SST和SSST所推导出的瞬时频率计算式(4)和(10) 与式(2) 不同,两个算式(4)和(10) 成立的前提是信号的相位随时间呈线性变化.若不满足这个前提条件,计算出的瞬时频率将与真实瞬时频率存在误差.例如,对于形如h(t)=Aej2πϕ(t)的信号,设相位ϕ(t)和时间t是二次方的关系,即设
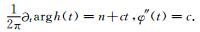
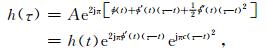
|
(13) |
信号h(t)的ST表达式为
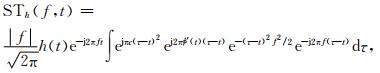
|
(14) |
令(τ-t)=x,
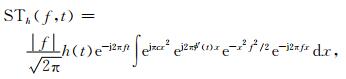
|
(15) |
这时STh(f, t)的幅角为
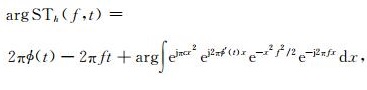
|
(16) |
(16) 中的积分项可以写成下面的形式

|
(17) |
为方便后面对于瞬时频率计算公式的讨论,避免直接计算(16) 中的积分项,这里引入辅助函数u来代表积分项.令

|
这时,频率坐标

|
接下来,利用函数u来表示积分项对时间t的偏导数,令函数u(ξ)中的自变量ξ=f-ϕ′(t),则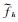
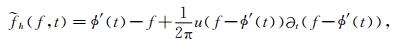
|
(18) |
因为ϕ″(t)=c,所以
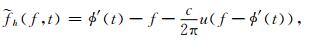
|
(19) |
类似地,对于时间位置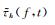
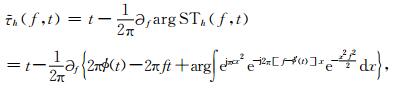
|
利用函数u,可以得到
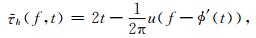
|
(20) |
从式(19) 可以看到,当c不等于0时,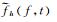
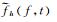
由于ϕ′(t)=b+ct,所以
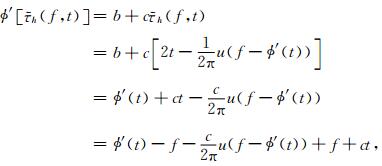
|
代入式(19)和ϕ″(t)=c可以得到
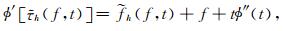
|
(21) |
另一方面,
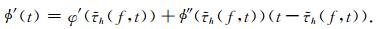
|
(22) |
式(22) 说明,为了准确估计ϕ′(t)的值,我们需要相位的二阶导数ϕ″(t).Oberlin等(2015) 提出一种调制算子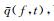

|
(23) |
这里V(f, t)是信号的短时傅里叶变换.由于该调制算子中包含对时间和频率的二阶偏导数,因此我们将提出的方法称为二阶同步挤压S变换.根据(21)和(22) 式,可以得到
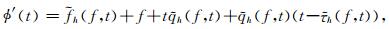
|
(24) |
由于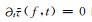
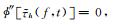

|
(25) |
从式(25) 可以看到,通过在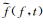
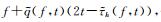
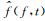
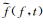
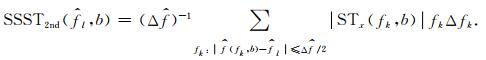
|
(26) |
为了对比SSST2nd和CWT、ST、SST以及SSST的时频刻画效果,我们合成了两个信号.第一个合成信号为调幅-调频信号,包含四个正弦波分量,表达式如下:
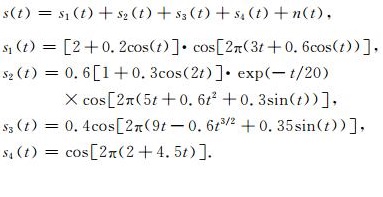
|
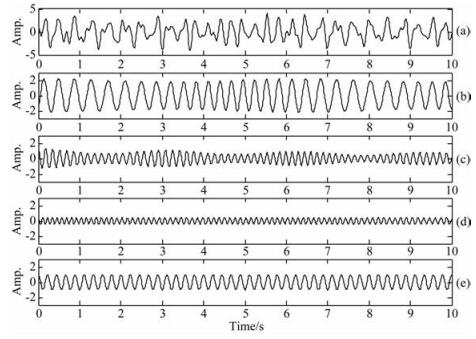
这里,n(t)是高斯白噪声,采样频率为1000 Hz,信号的信噪比为10 dB,t的范围是0~10 s.合成信号及其四个分量分别如图 1a—1e所示.其中s1的频率是四个分量中最低的,但是它的幅度是最高的.s2的频率随着时间的增加而增加,且它的幅度随着频率的增大而减小.s3的幅度是最小的,并且它的频率是常数.这些分量是特别设计的,使分量的幅度越大分量的频率越低.这样一来,合成信号就包含了高频低幅成分.此外,为了展示同步挤压变换和二阶同步挤压变换的区别,s1、s2和s3这三个分量的相位随时间都不是线性变化,而是按照正弦或者二次方变化,s4的相位则随时间线性变化.图 2a—2f分别是合成信号的小波变换、S变换、基于gauss小波的SST、基于morlet小波的SST、SSST以及SSST2nd的时频谱.本文所使用的gauss小波和morlet小波的表达式如下:
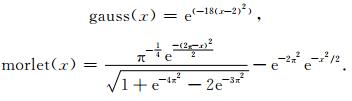
|
|
图 1 合成调幅-调频信号以及它的四个分量时域图形 (a)合成信号s(t);(b) s1(t)分量;(c) s2(t)分量;(d) s3(t)分量;(e) s4(t)分量. Fig. 1 The synthetic amplitude modulation-frequency modulation signal s(t) in (a), and its three components s1(t), s2(t), s3(t), and s4(t), respectively, in (b), (c), (d), and (e) |
CWT和SST的纵轴已经被转换为了线性频率,使用的尺度序列如前所述.
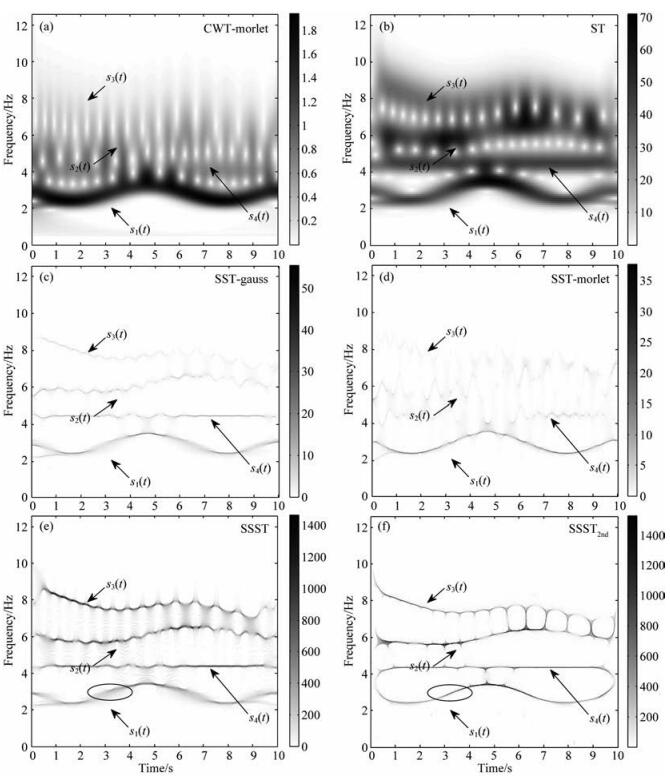
从图 2a和2b中看到,CWT和ST的时频谱都被“模糊”化,即信号的能量分布在真实瞬时频率周围分布.由于将信号的时频能量“挤压”到了真实瞬时频率处,SST、SSST以及SSST2nd的时频谱的分辨率改善了很多,如图 2c—2f所示.其次,由于s3的幅度相对较小,在CWT的结果中很难被辨识出来,而在ST的时频谱中可以被分辨,这展示了ST在刻画此类信号成分时的优势.SST的结果则与所使用的小波有关,如图 2c和2d所示,当使用gauss小波进行变换时,s3的成像效果比使用morlet小波的结果更好,这说明SST的效果极大取决于所选择的母小波类型.相比之下,这4个分量在SSST和SSST2nd的结果中都能被明显表示出来,这都是得益于ST对于此类信号的增强作用.此外,由于将能量进行了“挤压”,与小波变换和S变换相比,挤压类变换的能量要比前两者高得多.
|
图 2 合成信号的时频谱 (a)小波变换;(b) S变换;(c)使用“gauss”小波的同步挤压变换;(d)使用“morlet”小波同步挤压变换;(e)同步挤压S变换;(f)二阶同步挤压S变换. Fig. 2 T-F spectra of the synthetic signal using (a) CWT, (b) ST, (c) SST with "gauss" wavelet (d) SST, with "morlet" wavelet (e) SSST, (f) SSST2nd |
再来比较SSST和SSST2nd的结果.从信号能量刻画效果来看,对于相位线性变化的信号s4,SSST2nd和SSST都能正确地给出瞬时频率分布,两者的效果基本相同.当信号的瞬时频率随着时间不是线性变化时,按照SSST瞬时频率计算公式所得到的瞬时频率与真实的频率存在误差,而SSST2nd计算的瞬时频率更加接近真实值.比较图 2e和图 2f中椭圆区域的时频分布就能明显看出两者的区别.这说明当瞬时频率的变化呈现非线性变化时,SSST2nd的挤压效果比SSST的更好.
最后,在信号采样频率一定,且没有噪声的前提下,SSST2nd时频谱在时间方向上的分辨程度取决于信号的采样间隔,而频率方向的分辨率与变换时所设置的频率数量和采样频率有关.就本例中的信号而言,采样频率为1000 Hz,我们在时频结果的输出范围0~500 Hz内设置了2000个点,因此,时频谱上频率方向的分辨率为0.25 Hz.此外,从挤压类变换的时频能量分布来看,由于将时频能量进行了集中,挤压变换后的时频能量集中区域的幅度比原时频变换有了很大提高.
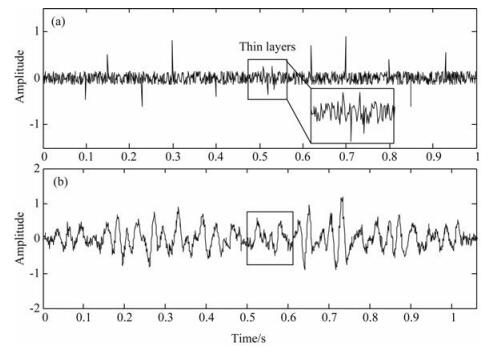
3.2 仿真地震信号第二个仿真信号是利用雷克子波褶积反射系数序列而合成的地震信号,仿真所用雷克子波的峰值频率为30 Hz,采样频率1000 Hz.为了分析噪声对于时频结果的影响,在反射系数序列以及合成记录中都添加了高斯白噪声.在反射系数序列的0.5 s附近,我们设置了由4个幅度较小的反射系数所组成的3个薄层,如图 3中方框所示.根据谱分解原理,薄层的存在会导致反射波中心频率升高.又由于薄层处设置的反射系数较小,因此薄层的合成地震信号具有高频、低振幅的特点.
|
图 3 仿真地震信号 (a)反射系数序列;(b)信号时域波形. Fig. 3 The synthetic seismic signal (a) reflection coefficient sequence (b) time-domain waveform of the signal |
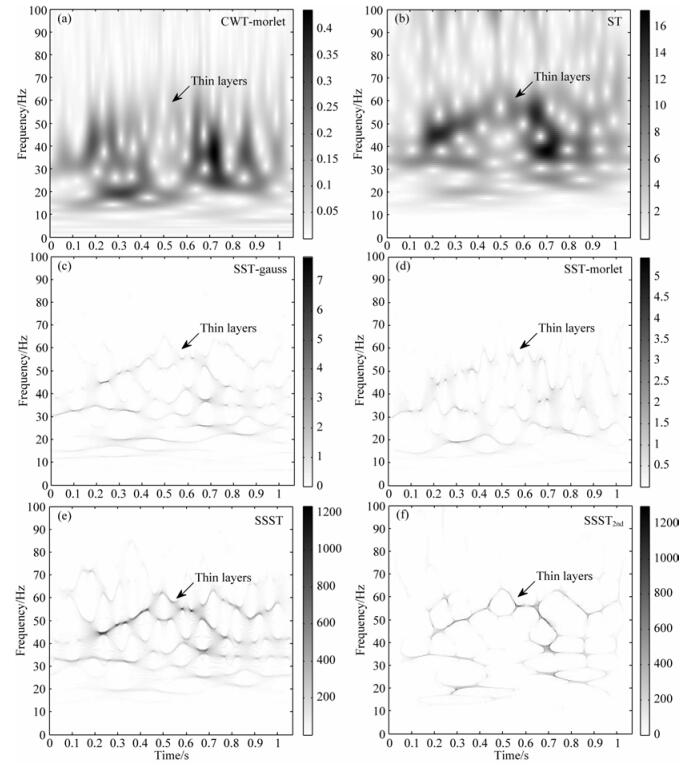
我们分别利用CWT、ST、基于gauss小波的SST、基于morlet小波的SST、SSST以及SSST2nd对仿真地震信号进行处理,结果依次显示在图 4a—4f.比较得到的时频结果可以发现,与调幅-调频信号的情况类似,对于地震信号,SSST和SSST2nd同样可以得到比CWT、ST和SST分辨率更高的时频谱.此外,相比于CWT和SST时频谱,薄层反射波信号的能量在SSST和SSST2nd的时频谱上能得到更清楚的显示.虽然薄层在ST时频谱上的能量也很明显,但是时频分辨率没有挤压类变换的结果高.最后,SSST2nd的时频能量分布比SSST更加集中,因此时频分辨效果更好,这对于提高谱分解单频切片的分辨率是有利的.
|
图 4 仿真地震信号的时频谱 a)小波变换;(b) S变换;(c)使用“gauss”小波的SST同步挤压变换;(d)使用“morlet”小波的SST同步挤压变换;(e)同步挤压S变换;(f)二阶同步挤压S变换. Fig. 4 T-F spectra of the synthetic seismic signal using (a) CWT, (b) ST, (c) SST with "gauss" wavelet, (d) SST with "morlet" wavelet, (e) SSST, (f) SSST2nd |
为了说明使用二阶同步挤压S变换的谱分解效果,我们用其对实际地震数据进行谱分解处理.实测数据是在我国西南某工区采集到的一条地震剖面,地震数据的采样率为500 Hz,在380道附近进行了钻探,证实该处存在二层含天然气藏.我们分别利用不同的时频变换方法对该地震剖面进行谱分解处理,并比较和分析这些结果的优劣.图 5是该地震剖面包含气层的一部分,图中标注出了气层以及测井的位置,并给出了速度测井(左)和密度测井曲线(右).测井曲线表明,在1950~1980 ms和2150~2200 ms附近,速度和密度都明显变小.图 6a—6j分别是利用CWT、ST、SST、SSST和SSST2nd对该区域进行谱分解处理后提取的30 Hz和60 Hz单频切片.其中CWT和SST所使用的母小波是morlet小波.

|
图 5 地震剖面以及测井曲线 Fig. 5 Seismic profile and well logs |

|
图 6 不同时频变换的谱分解结果比较 (a) CWT 30 Hz单频切片; (b) CWT 60 Hz单频切片; (c) ST 30 Hz单频切片;(d) ST 60 Hz单频切片; (e) 使用morlet小波的 SST 30 Hz单频切片; (f) 使用morlet小波的SST 60 Hz单频切片; (g) SSST 30 Hz单频切片; (h) SSST 60 Hz单频切片; Fig. 6 Comparison of the spectral decomposition results using different time-frequency transforms (a) 30 Hz constant frequency slice of CWT; (b) 60 Hz constant frequency slice of CWT; (c) 30 Hz constant frequency slice of ST; (d) 60 Hz constant frequency slice of ST; (e) 30 Hz constant frequency slice of morlet-based SST; (f) 60 Hz constant frequency slice of morlet-based SST; (g) 30 Hz constant frequency slice of SSST; (h) 60 Hz constant frequency slice of SSST; |
|
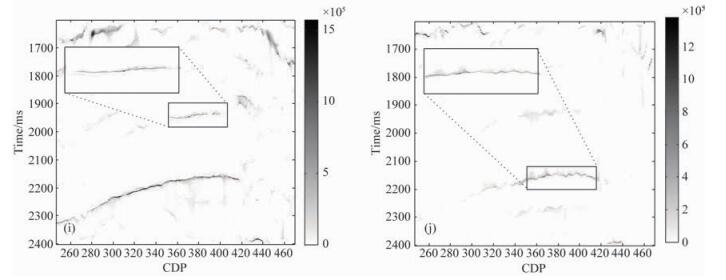
图 6 不同时频变换的谱分解结果比较 (i) SSST2nd 30 Hz单频切片; (j) SSST2nd 60 Hz单频切片. Fig. 6 Comparison of the spectral decomposition results using different time-frequency transforms (i) 30 Hz constant frequency slice of SSST2nd; (j) 60 Hz constant frequency slice of SSST2nd. |
对比不同时频变换的时频谱可以看出:
(1) 在图 6a小波变换的30 Hz切片上,在圆圈处可以明显看到储层反射波的能量,但是较弱,在同一位置的60 Hz高频切片上,能量则减弱很多,这是气层对于地震波的衰减所造成的结果.相比之下,在图 6b的S变换30 Hz切片上,同样位置储层的能量强的多.在S变换的60 Hz切片上,气层A处的能量也显示明显地衰减,但是能量比小波变换切片中的要强,因此,对于本数据中的气层,使用S变换的谱分解能更加准确地给出气层的深度和展布情况.
(2) 与小波变换和S变换相比,在SST谱分解的30 Hz切片上,不但可以清晰地识别出气层A所对应的时频能量,且其分辨率比前两者都要高得多.而在60 Hz切片上,气层A处的能量同样衰减明显.另外,SST切片的能量比CWT和ST切片都要高得多,在有的区域,能量幅度达到了挤压前的10倍.
(3) 在SSST谱分解的30 Hz切片上,气层A所对应的时频能量与CWT、ST的结果相比,时频分辨率明显变高.与SST的结果相比,其能量则更强,且时频聚集效果更好,从而能更清楚地对气层位置进行成像.在60 Hz切片上,SSST在方框所示区域的时频压缩效果也明显好于SST.
(4) 在SSST2nd谱分解的30 Hz切片上,气层A和B的深度和空间展布非常清晰.在框体所标记的位置,其时频聚集效果比SSST和SST都要更好.同样,在60 Hz切片上,对于气层B的成像效果也比前两者更清晰,因此对储层的深度和空间展布的成像也更准确.
(5) 实际数据中不可避免地含有各类噪声,除了广泛存在的白噪声外,还可能包含特定频率的干扰信号,这些噪声的时频能量在处理过程中同样会被挤压.噪声的能量被挤压后,它们在时频谱的分布区域会被压缩,这对于谱分解来说是有利的,因为谱分解在提取单频切片的过程中,对于某一道数据的时频谱,只提取单一频率的数据,噪声频率分布的越广,提取切片时就越容易将噪声能量一同提取出来.相比之下,从挤压后的时频谱上提取数据,能更好地避开噪声能量出现的区域.
由此可见,利用上述几种方法的谱分解虽然都可以判断出气层的存在,但是对于气层的具体位置和展布,SSST2nd的效果是最好的.
5 结论为了改善同步挤压S变换对于瞬时频率随时间呈非线性变化信号的时频聚焦效果,本文提出了二阶同步挤压S变换.与基于短时傅里叶变换或小波变换的同步挤压变换相比,二阶同步挤压S变换对于高频-低振幅信号的时频特征刻画效果更好.另一方面,与同步挤压S变换相比,当相位随时间非线性变化时,二阶同步挤压S变换能够更准确地计算出信号的瞬时频率,从而进一步提高了时频挤压时的能量聚焦能力.利用不同的时频变换方法对含气层的地震资料进行了谱分解处理.结果表明,二阶同步挤压S变换改善了地震资料时频谱的聚焦程度和分辨率,提高了对储层地震信号时频能量异常的检测能力,能更精细地刻画气层的深度和空间展布.
| Ahrabian A, Looney D, Stanković L, et al. 2015. Synchrosqueezing-based time-frequency analysis of multivariate data. Signal Processing, 106: 331-341. DOI:10.1016/j.sigpro.2014.08.010 | |
| Ahrabian A, Mandic D P. 2015. A class of multivariate denoising algorithms based on synchrosqueezing. IEEE Transactions on Signal Processing, 63(9): 2196-2208. | |
| Auger F, Chassande-Mottin E, Flandrin P. 2012. Making reassignment adjustable:The levenberg-marquardt approach.//2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Kyoto:IEEE, 3889-3892. | |
| Auger F, Flandrin P, Lin Y T, et al. 2013. Time-frequency reassignment and synchrosqueezing:An overview. IEEE Signal Processing Magazine, 30(6): 32-41. DOI:10.1109/MSP.2013.2265316 | |
| Chui C K, Van Der Walt M D. 2015. Signal analysis via instantaneous frequency estimation of signal components. GEM-International Journal on Geomathematics, 6(1): 1-42. DOI:10.1007/s13137-015-0070-z | |
| Daubechies I, Lu J F, Wu H T. 2011. Synchrosqueezed wavelet transforms:An empirical mode decomposition-like tool. Applied and Computational Harmonic Analysis, 30(2):243-261. | |
| Daubechies S, Maes I. 1996. A nonlinear squeezing of the continuous wavelet transform based on auditory nerve models.//Aldroubi A, Unser M, eds. Wavelets in Medicine and Biology. Boca Raton, FL, USA:CRC Press, 527-546. | |
| Feng Z P, Chen X W, Liang M. 2015. Iterative generalized synchrosqueezing transform for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Mechanical Systems and Signal Processing, 52-53: 360-375. DOI:10.1016/j.ymssp.2014.07.009 | |
| Herrera R H, Han J J, Van Der Baan M. 2014. Applications of the synchrosqueezing transform in seismic time-frequency analysis. Geophysics, 79(3): V55-V64. DOI:10.1190/geo2013-0204.1 | |
| Herrera R H, Tary J B, Van Der Baan M, et al. 2015. Body wave separation in the time-frequency domain. IEEE Geoscience and Remote Sensing Letters, 12(2): 364-368. DOI:10.1109/LGRS.2014.2342033 | |
| Huang Z L, Zhang J Z. 2014. Determination of parameters of subsurface layers using GPR spectral inversion method. IEEE Transactions on Geoscience and Remote Sensing, 52(12): 7527-7532. DOI:10.1109/TGRS.2014.2313603 | |
| Huang Z L, Zhang J Z. 2016. Synchrosqueezing S-transform. Science China (Information Sciences), 46(5): 643-650. | |
| Huang Z L, Zhang J Z, Zhao T H, et al. 2016b. Synchrosqueezing S-Transform and its application in seismic spectral decomposition. IEEE Transactions on Geoscience and Remote Sensing, 54(2): 817-825. DOI:10.1109/TGRS.2015.2466660 | |
| Kodera K, Gendrin R, Villedary C. 1978. Analysis of time-varying signals with small BT values. IEEE Transactions on Acoustics, Speech, and Signal Processing, 26(1): 64-76. DOI:10.1109/TASSP.1978.1163047 | |
| Li C, Liang M. 2012. Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform. Mechanical Systems and Signal Processing, 26: 205-217. DOI:10.1016/j.ymssp.2011.07.001 | |
| Lin H B, Ma H T, Xu L P. 2015. A radial time-frequency peak filtering based on ROAD for suppressing spatially nonstationary random noise in seismic data. Chinese Journal of Geophysics, 58(7): 2546-2555. DOI:10.6038/cjg20150729 | |
| Liu H, Zhang J Z, Huang Z L. 2015. Microseismic event detection based on synchrosqueezing wavelet transform. China Science Paper, 10(21): 2472-2476. | |
| Liu H, Zhang J Z, Huang Z L. 2016. Surface wave removal with synchrosqueezing wavelet transform. Oil Geophysical Prospecting, 51(1): 71-79. | |
| Liu J L. 2006. Spectral decomposition and its application in mapping stratigraphy and hydrocarbons[Ph.D. thesis]. Houston, TX, USA:University of Houston. | |
| Meignen S, Oberlin T, McLaughlin S. 2012. A new algorithm for multicomponent signals analysis based on synchrosqueezing:With an application to signal sampling and denoising. IEEE Transactions on Signal Processing, 60(11): 5787-5798. DOI:10.1109/TSP.2012.2212891 | |
| Oberlin T, Meignen S, Perrier V. 2015. Second-order synchrosqueezing transform or invertible reassignment? Towards ideal time-frequency representations. IEEE Transactions on Signal Processing, 63(5): 1335-1344. DOI:10.1109/TSP.2015.2391077 | |
| Partyka G, Gridley J, Lopez J. 1999. Interpretational applications of spectral decomposition in reservoir characterization. The Leading Edge, 18(3): 353-360. DOI:10.1190/1.1438295 | |
| Stockwell R G. 1999. S-transform analysis of gravity wave activity from a small scale network of airglow imagers[Ph.D. thesis]. London, ON, Canada:The University of Western Ontario (Canada). | |
| Tary J B, Herrera R H, Han J J, et al. 2014. Spectral estimation-What is new? What is next?. Reviews of Geophysics, 52(4): 723-749. DOI:10.1002/2014RG000461 | |
| Thakur G, Brevdo E, Fǔckar N S, et al. 2013. The synchrosqueezing algorithm for time-varying spectral analysis:Robustness properties and new paleoclimate applications. Signal Processing, 93(5): 1079-1094. DOI:10.1016/j.sigpro.2012.11.029 | |
| Wang P, Chang X, Wang Y B, et al. 2014. Automatic event detection and event recovery in low SNR microseismic signals based on time-frequency sparseness. Chinese Journal of Geophysics (in Chinese), 57(8): 2656-2665. DOI:10.6038/cjg20140824 | |
| Wang P, Gao J H, Wang Z G. 2014. Time-frequency analysis of seismic data using synchrosqueezing transform. IEEE Geoscience and Remote Sensing Letters, 11(12): 2042-2044. DOI:10.1109/LGRS.2014.2317578 | |
| Wang S B, Chen X F, Wang Y, et al. 2015. Nonlinear squeezing time-frequency transform for weak signal detection. Signal Processing Archive, 113: 195-210. DOI:10.1016/j.sigpro.2015.01.022 | |
| Wang Z C, Ren W X, Liu J L. 2013. A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction. Journal of Sound and Vibration, 332(22): 6016-6028. DOI:10.1016/j.jsv.2013.04.026 | |
| Wu H T, Chan Y H, Lin Y T, et al. 2014. Using synchrosqueezing transform to discover breathing dynamics from ECG signals. Applied and Computational Harmonic Analysis, 36(2): 354-359. DOI:10.1016/j.acha.2013.07.003 | |
| 黄忠来, 张建中. 2016. 同步挤压S变换. 中国科学:信息科学, 46(5): 643–650. | |
| 林红波, 马海涛, 许丽萍. 2015. 压制空间非平稳地震勘探随机噪声的ROAD径向时频峰值滤波算法. 地球物理学报, 58(7): 2546–2555. DOI:10.6038/cjg20150729 | |
| 刘晗, 张建中, 黄忠来. 2015. 利用同步挤压变换检测微地震信号. 中国科技论文, 10(21): 2472–2476. DOI:10.3969/j.issn.2095-2783.2015.21.002 | |
| 刘晗, 张建中, 黄忠来. 2016. 应用同步挤压小波变换去除面波. 石油地球物理勘探, 2016. | |
| 王鹏, 常旭, 王一博, 等. 2014. 基于时频稀疏性分析法的低信噪比微震事件识别与恢复. 地球物理学报, 57(8): 2656–2665. DOI:10.6038/cjg20140824 | |
 2017, Vol. 60
2017, Vol. 60


