2. 河南理工大学物理与电子信息学院, 河南焦作 454000
2. Department of Physics and Electronic Information, Henan Polytechnic University, Henan Jiaozuo 454000, China
大地电磁测深法(Magnetotelluric,MT)是一种频率域电磁方法,通过观测天然电磁场的电、磁场分量并利用一定的手段定性或定量的获得符合地质规律的电阻率模型,得到地下电性结构.随着计算机技术的发展及理论方法的进步,大地电磁三维正反演技术得到了快速发展,并已在实际工作中取得应用.
近20年来,国内外大量学者对大地电磁法的三维正演方法展开了大量研究.目前,三维正演常用的方法有有限差分法、有限单元方法等,其中有限差分法以其实现简单、计算量较小的优点,成为三维反演中使用最为广泛的方法.Mackie等(1993)采用交错网格有限差分法实现了三维大地电磁法的正演.Smith(1996a, b)详细阐述了交错网格有限差分法的的性质、误差分析及散度校正方法.谭捍东等(2003)实现了三维大地电磁法的有限差分正演算法,陈辉等(2012)详细比较了交错网格有限差分法中求解线性方程组过程时不同散度校正方法的效率.Siripunvaraporn等(2002)比较了求解电场方程和求解磁场方程的精度,认为直接求解电场的方法的精度较高.
大地电磁的三维反演方法也发展迅速,Newman等(2000)实现了三维大地电磁法的非线性共轭梯度反演,Sasaki(2001)实现了高斯-牛顿反演,由于方法的限制,只能使用很小的网格进行反演,Siripunvaraporn等(2005)将数据空间Occam反演应用到三维大地电磁反演中,取得了比较好的效果,胡祖志等(2006)研究了大地电磁法的非线性共轭梯度拟三维反演,Avdeev等(2009)实现了三维大地电磁法的拟牛顿法反演,胡祥云等(2012)研究了数据空间算法的并行化,董浩等(2014)研究了带地形的三维反演.到目前为止,大地电磁法三维反演研究均主要针对比较简单的理论模型.在地形及地下电性结构比较复杂,特别是海洋和陆地同时存在时,现有正反演算法的表现如何,还未见到相关文献报道.
在可控源电磁法的正演模拟中,其场源为电偶源或磁偶源,由于场源的奇异性,直接求取总场精度较低,因此多采用二次场方法(Newman等,2002).在大地电磁法的正演模拟中,可以采用总场方法或二次场方法.由于大地电磁法的场源为平面电磁波,不存在奇异性,因此多使用总场方法.但是,在电性分界面处,若介质的电阻率差异过大(空气和大地的电阻率通常相差6~8个数量级),也会带来奇异性,此时二次场方法具有优势.Key等(2006)将二次场方法应用到大地电磁法的二维自适应有限元模拟中,取得了较好的效果.
本文提出了一种基于二次场的三维大地电磁正演方法,引入一维层状背景模型,以平面波场源在层状模型中的响应作为一次场,使用交错网格有限差分法求取二次场,最终获得总场.采用C++编程语言实现了二次场正演算法,通过对国际标准模型的模拟并与其他学者的结果做对比验证了本文所用方法的正确性及效率.为提高计算效率,使用MPI实现了正演的并行化.在正演的基础上实现了基于L-BFGS方法的三维反演算法,并对公开的复杂反演数据集进行了试算.
2 基于二次场的三维正演算法 2.1 控制方程大地电磁法是频率域电磁方法,满足频率域的Maxwell方程组.取时谐因子为e-iωt,介质中电磁场应满足的方程为
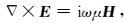
|
(1) |
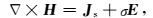
|
(2) |
其中,ω是角频率,μ是真空中的磁导率,σ是地下介质的电导率,Js为场源项.实际勘探中的信号发射频率一般不超过10000 Hz,因此,应用似稳场假设,在式(2) 中忽略位移电流.对(1) 式两边求旋度,并将(2) 式代入可得:

|
(3) |
(3) 式是介质中电场总场所满足的二阶偏微分方程.对于大地电磁法,其场源为平面电磁波,目前的常用方法是令场源项为0,并并令边界上的电场值等于二维介质中的场值.即
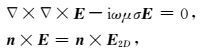
|
(4) |
其中n是边界网格的外法向向量.这种方法直接求解电场总场,比较直观,但是施加边界条件时较为复杂.
本文采用求电场二次场的方法,通过引入一个层状的背景模型σ0,并以平面波场源在该背景模型中的响应Ep为场源,求解异常模型的二次电场(Newman et al., 2002).二次场Es满足的方程为

|
(5) |
若计算区域足够大,可认为二次电磁场已充分衰减,可以在边界上应用Dirichlet边界条件,将边界上电场二次场的切向分量设置为0,即

|
(6) |
式(5) 和式(6) 构成了电场二次场所满足的边值问题.
2.2 数值离散采用交错网格有限差分方法求解式(5) 和边界条件式(6) 所构成的方程的数值解.将计算区域剖分成正交的笛卡尔网格,为满足电磁场的连续条件,在交错网格上对电磁场进行离散化,将电场分量定义在网格边的中点,磁场分量定义在网格面的中心处.这样电场和磁场的分量在空间中被交叉地放置,从而使得每个坐标平面上的每个电场分量四周由磁场分量环绕,同时每个磁场分量四周由电场分量环绕,如图 1所示.

|
图 1 Yee交错网格 Fig. 1 Yee staggered grid |
将式(5) 写为分量形式,其x方向上的方程为
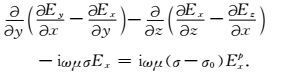
|
(7) |
为表述方便,将定义在网格各棱边上的电场分量进行编号,如图 2所示,与节点(i, j, k)处x分量有关的各分量的编号.按照图 2中定义的各分量编号及其位置关系,用差分近似微分,得到
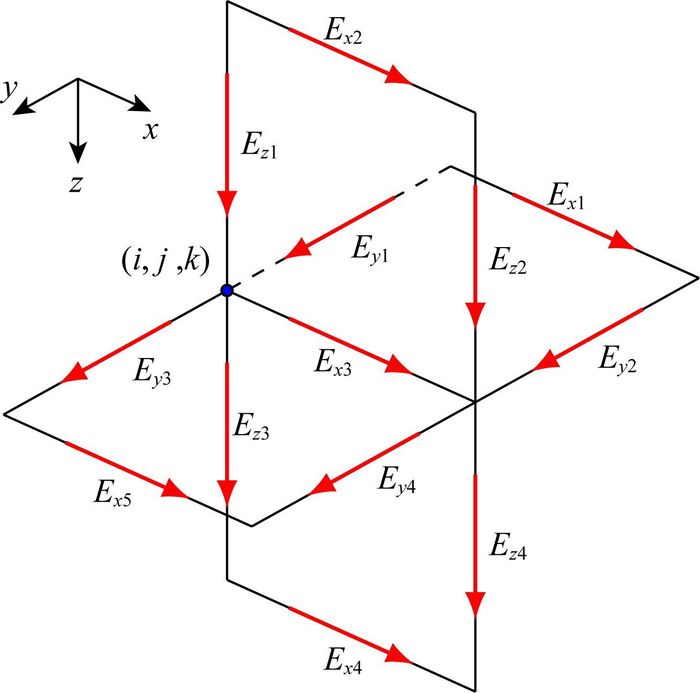
|
图 2 与x方向电场分量有关的各分量示意图(Weiss et al., 2006) Fig. 2 Position of each electrical component coupled with x-direction edge (Weiss et al., 2006) |
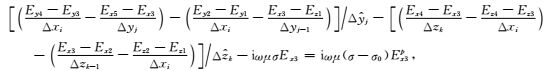
|
(8) |
其中,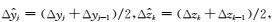
计算区域内的每一个棱边上均可写出类似式(8) 的差分方程,联立所有的方程, 并施加边界条件,就可以形成一个稀疏的复线性方程组.需要注意的是,在非均匀网格剖分的情况下,线性方程组并不对称,需要对其进行变换.将线性方程组的每一行乘以该行所对应棱边的包围体积,得到一个复对称线性方程组
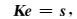
|
(9) |
K为系数矩阵, e为待求的电场二次场值,s为右端项.
2.3 线性方程组求解方法线性方程组式(9) 是复系数对称方程,仅在矩阵对角元的虚部包含介质电阻率及频率信息.当频率较低时,方程的定解条件变弱.同时,不均匀网格剖分及介质电阻率的巨大差异(空气电阻率与地下介质电阻率通常相差几个数量级),对方程的条件数影响非常大(Weiss et al., 2003),采用迭代方法求解时较难收敛.本文通过以下几个方法解决这个问题:(1) 选用合适的迭代方法;(2) 采用带填充的不完全LU分解作为预条件;(3) 迭代过程中施加静态散度校正.
常用的求解非正定方程的迭代方法主要有GMRES(Saad et al., 1986)、稳定双共轭梯度法BICGStab(Sleijpen et al., 1993)及拟最小残差法QMR (Freund et al., 1991)等.其中QMR方法对于式(9) 具有较快的收敛速度和较高的稳定性.因为式(9) 是对称的,所以本文选用QMR方法的对称变种对称拟最小残差法SQMR(Freund et al., 1994)求解线性方程组,该方法每次迭代只需要计算一次矩阵向量乘法和求解一次预条件矩阵, 计算开销相对较小.
合适的预条件可大大加快迭代方法的收敛速度.本文采用矩阵K的对角块矩阵构造预条件.根据式(8) 中各分量的耦合关系,矩阵K可以写为

|
(10) |
其中Kxx是网格中x方向的棱边与x方向的棱边耦合形成的矩阵,Kyy是网格中y方向的棱边与y方向的棱边耦合形成的矩阵,依次类推.由K的对角块所构成的矩阵是对称正定的,并且K具有分块对角占优的性质,因此使用K的对角块矩阵作为预条件.令预条件矩阵为M,则

|
(11) |
实际上不需要计算矩阵Kxx, Kyy, Kzz的逆矩阵,使用不完全LU分解(Saad, 1994)已经可以取得足够好的收敛效果.不完全LU分解是对LU分解的近似,丢弃分解结果中的一些非零元来节省内存和计算时间.在构造矩阵的不完全LU分解时, 可以通过两个参数控制分解的近似程度:(1) 填充数量,即分解结果中非零元数量与原矩阵非零元数量的比值;(2) 丢弃阈值,用来控制分解结果中的哪些元素应被丢弃.使用大的填充数量和小的丢弃阈值将得到更精确的近似,但同时分解结果中的非零元也更多,需要更多的内存空间和计算时间.在此取填充数量为5,丢弃阈值为10-4,在占用较少内存空间和较短计算时间的同时保证了较好的效果.
交错网格本身可以满足电流密度散度为0的连续性条件,即在无源区域应满足
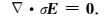
|
(12) |
但是,在使用迭代法求解方程时,由于计算机的字长有限,不可避免地存在截断误差,中间解不再满足散度条件.散度条件得不到满足不仅导致迭代方法收敛慢,而且得到的解可能是不满足物理条件的伪解,因此必须加以校正.
假定当前解为Ec,首先计算其对应的电流密度的散度
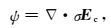
|
(13) |
若其不为0,通过求解下面方程得到具有负散度的标量φ,φ满足
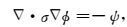
|
(14) |
(14) 式是泊松方程,在交错网格上利用七点差分公式对其进行离散,并利用迭代方法进行求解.在求得φ后,使用φ的梯度对当前解Ec进行矫正,得到满足散度条件的解,即
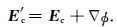
|
(15) |
需要注意的是,上述的散度校正方法是针对无源问题的,本文采用的是二次场方法,方程的右端是一次场源项,其散度不为0,所以在校正的过程中应消去其影响,式(13) 变为

|
(16) |
另外,式(14) 左端只与介质电导率及网格剖分有关,由其离散得到的线性方程组是实数的,而右端项是复数的.将方程组存储为实矩阵,分别针对右端项的实部和虚部求解两次方程.引入散度校正后,方程组求解过程中速度和精度都得到了显著提高.
在得到电场二次场之后,电磁场总场可通过如下方式进行计算:
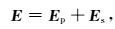
|
(17) |
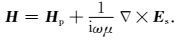
|
(18) |
阻抗张量的计算公式为
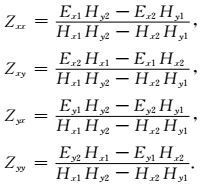
|
(19) |
目前,绝大多数的计算机都有多个计算核心,串行的程序并不能全部发挥多核计算机的计算能力.大地电磁的正演和反演问题,特别是三维正演和反演,需要消耗大量的计算时间,因此适当应用并行策略对算法进行加速非常必要.大地电磁法的正演和反演包含对多个频率的计算,不同频率之间的计算是独立的,因此可以将不同频率的计算任务分配到不同的计算单元上,以此实现并行计算.
常用的并行策略有多线程并行和多进程并行(Newman, 2014).多线程并行(OpenMP或使用操作系统提供的线程接口)是轻量级的并行方式,实现较为简单,多个线程共享内存,内存占用较少,但是只能运行在单个结点内,不能使用在集群环境中.多进程并行目前的事实标准是消息传递接口(Message Passing Interface, MPI),每个进程有自己独立的内存空间,各进程之间通过网络来传递消息,这种并行策略实现较为复杂,但扩展性强,可以使用在集群环境中,理论上可以运行在任意数量的结点上.
经综合考虑,本文选用基于MPI的多进程并行策略.在计算过程中,将不同频率的计算任务尽量平均的分配到各个计算单元上,计算过程中,通过MPI提供的函数交换数据并保持同步.
2.5 正确性验证及效率分析为了比较二次场算法和总场算法的计算精度,我们也实现了式(4) 中的总场算法.选取一个三层地电模型进行对比,模型第一层的电阻率为100 Ωm,厚度为1000 m,第二层电阻率为1 Ωm,厚度为1000 m,第三层电阻率为100 Ωm.对于一维模型,可以利用递推公式计算视电阻率和阻抗相位的解析解.计算过程中二次场算法和总场算法使用相同的网格,使用的网格是24×24×33,二次场算法使用的背景模型是100 Ωm均匀半空间.我们分别计算了从1000 Hz到0.0001 Hz共7个频率的视电阻率和相位响应.表 1是二次场算法和总场算法的解与解析解的对比结果,二次场解和总场解均与解析解吻合良好,视电阻率的相对误差不超过2%,相位误差不超过1°.另外,高频时电磁波衰减较快,式(6) 中的零边界条件满足的更好,二次场解的精度要高于总场解.低频时,二次场解的精度与总场解相当,部分频点要差一些.本例中,如果我们选择的背景模型与真实模型一致,则二次场解与解析解完全相同.这也是二次场算法的优势所在,即可以通过选取尽量准确的背景模型得到比较精确的解.
|
|
表 1 三层模型二次场解与总场解与解析解的对比 Table 1 Compasion of secondary-field solution and total-field solution and analytical solution of 3-layer model |
通过DTM1(Dublin Test Model 1) 模型(https://www.dias.ie/mt3dinv/3D_forward_model.html)分析程序的效率并与其他学者的结果做对比.DTM1是在2008年召开的第一届三维大地电磁反演讨论会上提出的三维正演模型,主要用来比较不同三维正演程序在模型电阻率差异巨大时的正演结果.该模型包含了100 Ωm均匀半空间中的三个块状异常体,三个异常体的电阻率分别是10 Ωm, 1 Ωm, 10000 Ωm,如图 3所示.
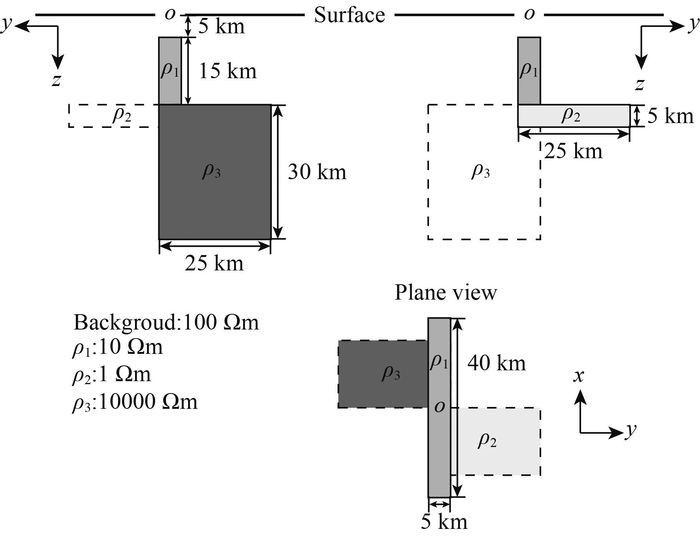
|
图 3 DTM1模型示意图 Fig. 3 Sketch of DTM1 model |
使用本文的三维正演程序对该模型进行了模拟,计算了从10 Hz到0.0001 Hz共21个频率的响应.使用的网格为56×60×50,根据频率不同,两个模式的计算时间大约为10~60 s,计算环境为笔者的Linux工作站,CPU主频2.8 GHz,内存16 GB.
国际上很多学者已对该模型做过模拟,并有公开的数据可做比较.(0 km, 0 km)是这个模型中响应最奇异的点,这个点可以作为代表来比较不同程序正演响应.图 4是本文的结果与Mackie(Mackie,1993)的有限差分结果、Ham(Nam et al., 2007)的有限元结果的响应结果对比.从图中可以看出,阻抗张量副对角元的响应及频率小于1 Hz的主对角元响应吻合的很好.大于1 Hz的主对角元视电阻率已小于10-5Ωm,相位波动严重,可以认为已不包含模型结构信息,是由不同方法所采用的网格不同及数值误差造成的.证明了本文所采用的方法是正确的.

|
图 4 DTM1模型(0, 0) 点处的响应对比 Fig. 4 Comparison of the obtained DTM1 responses at site (0, 0) |
另外,为分析本文所用散度校正方法的效率,比较了有无散度校正两种情况下线性方程组迭代解法的收敛速度.图 5是三个频率的SQMR收敛曲线以及不进行散度校正时的收敛曲线.从图中可以看出, 频率为10 Hz时收敛最快,且散度校正在迭代早期所起的作用并不明显,但在迭代晚期可以使迭代法迅速收敛到更低的残差水平;这是因为频率较高时方程的定解条件较强,舍入误差对散度条件影响不大.频率为0.0001 Hz时散度校正所起的作用最大,影响迭代算法收敛性的主要原因在于不满足散度条件.若无散度校正,迭代解法几乎不收敛.频率为0.1 Hz时散度校正也起到很大作用,但收敛最慢,此时方程的条件数对迭代法的影响大于不满足散度条件的影响.
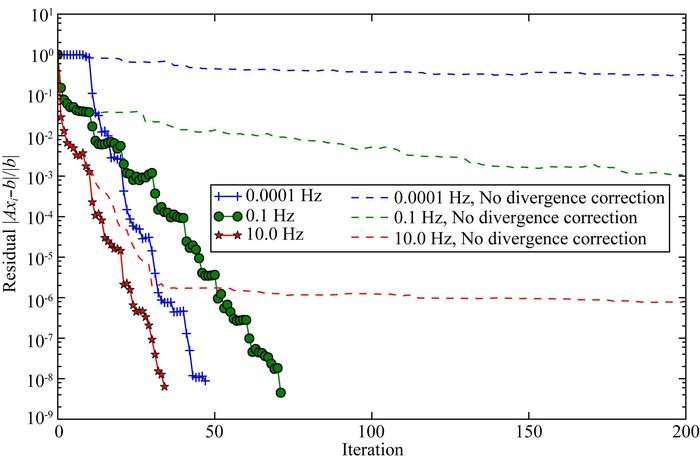
|
图 5 DTM1模型不同频率的SQMR收敛曲线:与无散度校正的对比 Fig. 5 Convergence procedure of SQMR of DTM1 model, compared to the result without divergence correction |
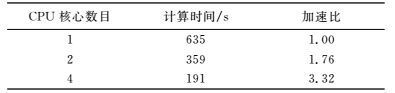
分别用1、2和4个CPU核心对该模型进行模拟,以比较本文使用并行策略的效率, 计算时间如表 2所示.可以看出,我们获得了接近线性的加速比.经过分析,没有达到线性加速比的原因有三个方面:(1) 计算过程中需要在多个进程间传递数据,会占用一部分时间.(2) 计算任务没有平均分配到各个计算单元上,而总的计算时间取决于任务最多的CPU核心的计算时间.在本文的模拟中,频率总数不能被CPU核心数整除,部分计算核心的任务多于其他核心.另外,由图 5可以看出,求解线性方程组的过程中,不同频率所需的迭代次数不同,需要的计算时间不同,导致任务分配不平均. (3) 计算过程中主要的计算量集中在求解线性方程组上,求解线性方程组过程中最耗时的部分是计算稀疏矩阵与向量乘积,在现代计算机系统中, 稀疏矩阵向量乘法的主要瓶颈是内存带宽.由于使用的是单个结点内的计算核心,结点的内存带宽是一定的,因此没有完全将多个核心计算能力发挥出来.
|
|
表 2 使用不同数量CPU核心时DTM1模型的计算时间 Table 2 Total computing time of DTM1 using different number of CPU cores |
反演的目标是为了获取一个既能在一定程度上拟合观测数据又符合地质规律的模型.根据吉洪诺夫的正则化理论(Tikhonov, 1977),反演问题等价于求如下目标函数的极小值:

|
(20) |
其中,d为观测数据向量,m为待反演模型向量,F为模型的正演响应向量,V为数据方差矩阵,L为模型约束矩阵,一般为拉普拉斯算子的离散形式,λ为正则化因子.
由于上述函数是非线性的,通常采用迭代法求其极小值.迭代形式为
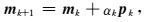
|
(21) |
其中pk为搜索方向,αk为步长.目前常用的反演方法,如高斯牛顿法(GN)、高斯牛顿共轭梯度法(GN-CG)、非线性共轭梯度法(NLCG)及拟牛顿法(QN)等的主要区别在于如何确定pk及αk.
3.1 L-BFGS方法本文采用有限内存拟牛顿法(L-BFGS)求解上述极小值问题.搜索方向pk通过下式确定:

|
(22) |
Hk是采用L-BFGS方法近似的Hessian矩阵的逆,gk是mk处的梯度.步长αk通过线搜索获得.
类似BFGS方法,L-BFGS使用近似方法求取Hessian矩阵的逆.它只存储最近l次迭代的中间信息:每次迭代模型的修正量
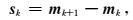
|
(23) |
和梯度的改变量

|
(24) |
因此需要的内存空间较少.L-BFGS计算搜索方向pk=-Hkgk的方法如下所示(Nocedal et al., 2006):
q=gk
for i=k-1, …, k-l do
ηi=ρisiq
q=q-ηiyi
end for
pk=Hk0q
for i=k-l, …, k-1 do
β=ρiyiTpk
pk=pk+si(ηi-β)
end for
3.2 步长搜索方法确定步长的线搜索方法在反演过程中扮演很重要的角色.对于L-BFGS方法,步长αk需要满Wolfe条件(Nocedal et al., 2006),
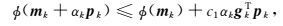
|
(25) |

|
(26) |
其中c1、c2为常数,且0<c1<c2<1.式(25) 也称为充分下降条件,为了保证目标函数在搜索方向上减小足够的量;式(26) 被称为曲率条件,是为了排除满足充分下降条件但步长非常小的情况.
本文使用Moré等(1994) 提出的线搜索方案,具体思路:从初始步长1.0开始,根据当前步长的特性确定插值区间,综合使用二次、三次插值方法得到新的步长.该线搜索策略稳定可靠,在初始步长不满足Wolfe条件时,通常只需要2~3次迭代即可获得满足条件的步长.
3.3 反演流程综合前面描述的计算搜索方向和搜索步长的方法,L-BFGS方法的流程如下所示:
选择初始模型m0, 确定l, Nmax
for k=0, …, Nmax do
计算梯度gk
计算搜索方向pk=-Hkgk
计算满足Wolfe条件的步长αk
计算新的模型mk+1=mk+αkpk
if k>l then
丢弃sk-l, yk-l
end if
计算并保存sk=mk+1-mk, yk=gk+1-gk
if拟合差小于给定值then
退出
end if
end for
在上述流程中,gk可以通过互易定理求取(Newman et al., 2000; Rodi et al., 2001),对每个频率只需求解两次线性方程组,一次在正演中计算模型响应,另一次在拟正演中计算数据拟合项的梯度,这也是整个反演过程中最耗时的部分.另外线搜索的每次迭代也需要计算目标函数及其梯度,由于由L-BFGS方法获得搜索方向在大多数情况下都很接近牛顿方向,初始步长1.0已满足Wolfe条件,所以反演过程中大多数迭代中只需要计算一次梯度,大大加快了反演速度.
4 理论数据反演 4.1 DSM2数据集DSM2(Dublin Secret Model 2) 数据集(https://www.dias.ie/mt3dinv2/3D_inversion_test_data_set.html)包含12条测线,每条测线12个测点,总共144个测点,覆盖了大约80 km×80 km的范围.共30个频率,从0.0001 Hz到62.5 Hz.
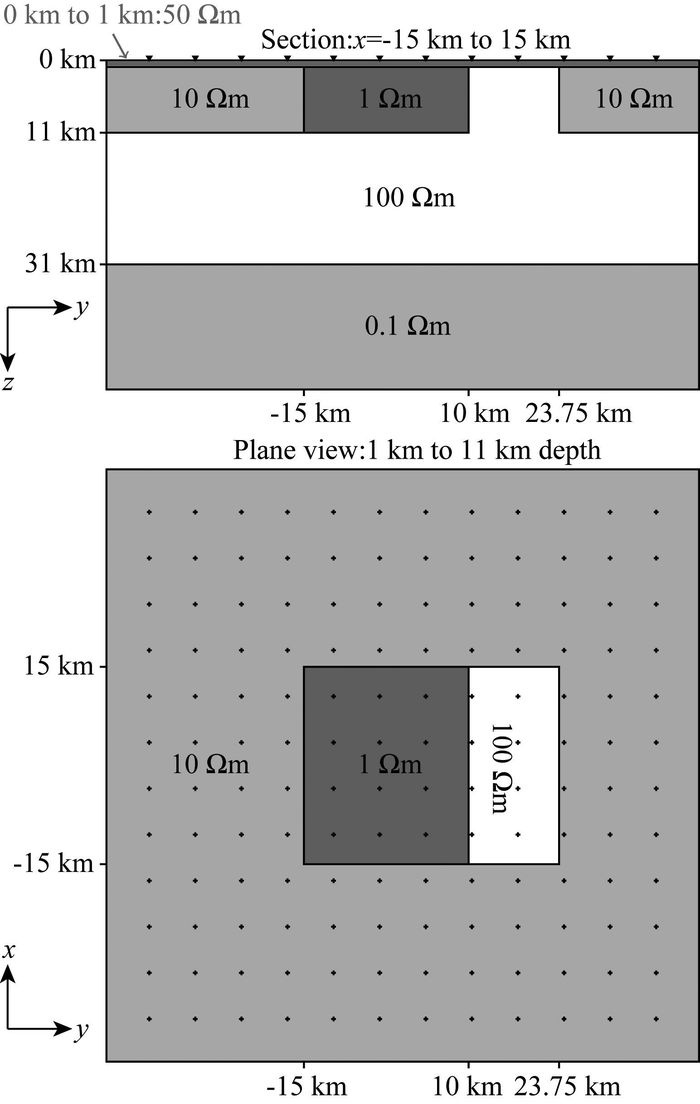
生成该数据集的真实模型是在COMMEMI 3D-2A (Zhdanov, 1997)模型的基础上增加了一个电阻率为50 Ωm的1 km厚的覆盖层,并对两个块状的异常体尺寸做了一些修改,如图 6所示.另外,数据中还加入了随机的电性畸变和5%的高斯噪声.
|
图 6 DSM2真实模型示意图 Fig. 6 Sketch of Dublin Secret Model 2 (DSM2) |
首先使用50 Ωm的均匀半空间作初始模型对该数据集进行反演.反演使用的网格为42×42×58,使用了所有测点所有频率的Zxy和Zyx数据,正则化因子为1.0.反演累计迭代24次,用时11 h,拟合差从13.121下降至3.703.结果如图 7所示.

|
图 7 均匀半空间初始模型时DSM2数据反演结果 Fig. 7 Inversion result of DSM2 data set using half space as prior model |
反演结果对浅部的两个异常体恢复的较好,位置和电阻率都相对准确.中间的高阻层基本没有反映出来,推测原因可能是一方面大地电磁法对深部高阻不灵敏,另一方面基底是低阻,对观测数据的影响较大,将数据中高阻层的信息掩盖掉了.另外,深部的低阻层有所反映,但位置不准确.
经过对数据的分析发现,数据中低频部分的响应比较接近,并且大部分数据点的一维反演结果很相似.对所有测点的视电阻率和相位数据取平均,并对其进行一维反演,利用一维反演结果做初始模型,对该数据集进行了第二次反演,反演使用的网格为42×42×58,迭代50次,用时33 h,拟合差从6.499下降至1.434,结果如图 8所示.反演结果得到明显改善,中间的高阻层和深部的低阻基底都反映的比较好,电阻率和位置比较准确.

|
图 8 一维反演结果做初始模型时DSM2数据反演结果 Fig. 8 Inversion result of DSM2 data set using 1D inversion result as prior model |
对DSM3(Dublin Secret Model 3) 数据集(https://www.dias.ie/mt3dinv3/3D_inversion_test_data_set.html)进行了反演.该数据集包含14条测线,每条测线30个测点,总共420个测点,覆盖了大约800 km×800 km的范围.共24个频率,从0.000025 Hz到14 Hz.图 9是测点的位置及高程示意图,图中黑线为海洋和陆地的分界线.模拟区域的地形是由美国西海岸部分地区的地形经缩放得到,观测区域包含了海洋和陆地,地形起伏剧烈,海拔最高点为2 km,海底最深处为2.9 km.

|
图 9 DSM3测点位置及地形 Fig. 9 Site location and topography of DSM3 |
真实模型如图 10所示,除海水以外,最上层是一个电阻率为100 Ωm、厚度为3.7 km的薄层,下方是电阻率为200 Ωm的岩石圈,岩石圈之下是电阻率为10 Ωm的软流层,其深度由海水下方100 km变化至陆地下方200 km,软流层下是电阻率为100 Ωm,深度延伸至400 km的地幔结构,再往下是电阻率为10 Ωm的半空间.另外,岩石圈中嵌有三个形状为M的和三个形状为T的电阻率为30 Ωm的低阻异常体,分别位于陆地、近海岸及海洋下方,它们是反演的主要目标.
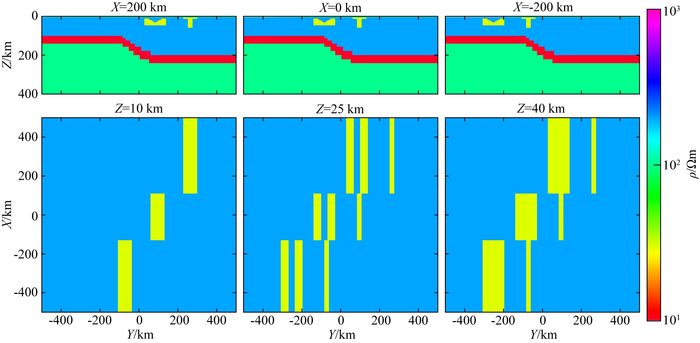
|
图 10 DSM3真实模型示意图 Fig. 10 Sketch of DSM3 true model |
该数据集采用三维有限元方法和有限差分法模拟得到,其中有限元方法用来计算地形影响,数据中加入了3%的高斯噪声.部分测点位于海底,部分测点位于陆地,海岸线贯穿整个观测区域(图 9中黑线),受海岸效应的影响(Key et al., 2011; Constable et al., 2009),海岸线附近的测点响应产生了严重的畸变.图 11是测点A01、F07和N15(位置在图 9中以红点标出)的视电阻率和相位曲线,可以看出,在中间频率段视电阻发生突变,个别频率的视电阻率变化达到两个数量级,相位响应的畸变也比较严重.另外,陆地上和海底的地形起伏也非常剧烈,对观测数据产生了严重影响.这是DSM3数据集最具挑战性的地方,若无法消除海岸效应和地形的影响,则不可能得到理想的结果.
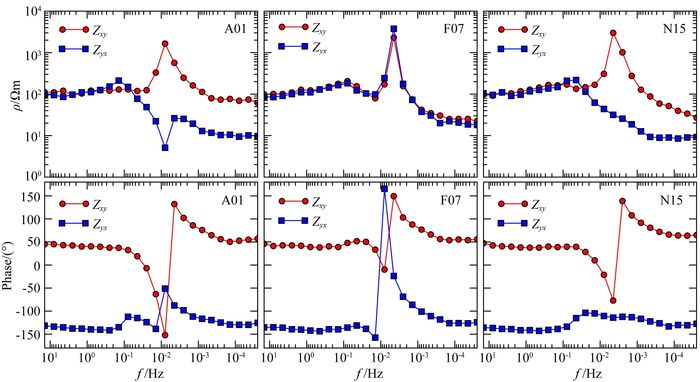
|
图 11 部分受海岸效应影响的测点响应 Fig. 11 Response of some selected sites that influenced by coastal effect |
对于海岸效应和地形影响,还没有比较有效的校正方法.为最大程度上消除海岸效应及地形的影响,我们将海洋及地形包含在初始模型中.在地形变化的范围内,采用均匀的纵向网格,间距200 m,其余部分网格以比例因子1.3等比增大.观测区域内,东西向的网格间距为12 km,南北向的网格间距为30km,两边各加入7个扩展网格.最终的网格为41×75×64.初始模型中海水的电阻率设置为0.3 Ωm,地下为100 Ωm的半空间.
我们使用数据中频率小于2 Hz的副对角元阻抗数据进行反演,共迭代50次,用时31 h,拟合差从10.253下降至3.337,反演结果如图 12所示.从反演结果中看出,模型的总体结构如高阻的岩石圈,低阻的软流层以及地幔结构等得到了比较好的反应,特别是软流层由海洋下方向陆地下方过渡的区域.另外,岩石圈中的低阻异常体的电阻率值及形态也很好的恢复出来.图 13是测点A01、F07和N15的数据拟合结果.测点A01位于反演区域的边界,由于网格设置的原因,视电阻率及相位突变最严重的中间频段数据没有完全拟合上,这在图 12中X=400 km处的切片图中得到了体现:左侧的高阻岩石圈结构和电阻的软流层结构未反演出来.测点F07和N15的数据拟合很好,海岸效应的影响基本被消除.

|
图 12 DSM3数据集反演结果切片图 Fig. 12 Slices of inversion result of DSM3 dataset |

|
图 13 DSM3数据集部分测点反演数据拟合结果 Fig. 13 Data fit of some selected sites of DSM3 dataset |
需要指出的是,DSM3的反演结果是在笔者在真实模型公布之前完成的,模型较为复杂且加入了随机噪声,对该数据集的反演在某种程度上可看作对实测数据的处理.
5 结论本文提出了一种基于二次场的并行三维大地电磁正演方法,通过对国际标准模型的模拟并与其他学者的结果进行对比,验证了本文所提出的基于二次场的算法的正确性.另外,本文使用的带填充的不完全LU分解作为预条件和迭代过程中施加散度校正等方法能有效加快正演过程中线性方程组迭代解法的收敛速度,通常经过数10次迭代即可收敛,具有较高的效率.基于MPI的分频并行策略能获得接近线性的加速比,可更好的利用日益普遍的多核计算机和集群的计算能力,加快反演速度.在根据频率分配计算任务时,要考虑到计算核心数目和频率个数的关系及不同频率计算时间上的差异,平均分配计算量,才能得到更好的加速效果.
在正演的基础上,实现了基于L-BFGS的反演方法,并对DSM2及DSM3两个公开的数据集进行了反演.DSM3的反演结果表明,考虑地形及海洋的三维反演能有效消除海岸效应及起伏地形的影响.然而,由于有限差分法采用阶梯状的网格模拟地形以及网格设置的关系,地形及海岸效应的影响并没有完全消除,反演结果中的细微构造较多,这也是下一步研究的重点.另外,虽然DSM3数据集较为复杂且包含噪声,但它在复杂性上与实际中的观测得到的数据仍有差距,本文的算法还未得到实测数据的检验.
致谢感谢国家自然科学基金对本研究的资助.另外,感谢意大利巴里大学对笔者前往参加第三届三维大地电磁反演讨论会提供的经费支持,与Alan Jones的交流大大提高了本文草稿的质量.感谢审稿专家提出的宝贵意见.
| Avdeev D, Avdeeva A. 2009. 3D magnetotelluric inversion using a limited-memory quasi-newton optimization. Geophysics, 74(3): F45-F57. DOI:10.1190/1.3114023 | |
| Chen H, Deng J Z, Tan H D, et al. 2011. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method. Chinese J. Geophys. , 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 | |
| Constable S, Key K, Lewis L. 2009. Mapping offshore sedimentary structure using electromagnetic methods and terrain effects in marine magnetotelluric data. Geophys. J. Int., 176(2): 431-442. DOI:10.1111/j.1365-246X.2008.03975.x | |
| Dong H, Wei W B, Ye G F, et al. 2014. Study of Three-dimensional magnetotelluric inversion including surface topography based on Finite-difference method. Chinese J. Geophys. , 57(3): 939-952. DOI:10.6038/cjg20140323 | |
| Freund R W, Nachtigal N M. 1991. Qmr: a quasi-minimal residual method for non-hermitian linear systems. Numer. Mathem., 60(1): 315-339. DOI:10.1007/BF01385726 | |
| Freund R W, Nachtigal N M. 1994. An implementation of the QMR method based on coupled two-term recurrences. SIAM J. Sci. Comput., 15(2): 313-337. DOI:10.1137/0915022 | |
| Hu X Y, Li Y, Yang W C, et al. 2012. Three-dimensional magnetotelluic parallel inversion algorithm using data space method. Chinese J. Geophys. , 55(12): 3969-3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 | |
| Hu Z Z, Hu X Y, He Z X. 2006. Pseudo-Three-Dimensional magnetotelluric inversion using nonlinear conjugate gradients. Chinese J. Geophys. , 49(4): 1226-1234. DOI:10.3321/j.issn:0001-5733.2006.04.039 | |
| Key K, Constable S. 2011. Coast effect distortion of marine magnetotelluric data: insights from a pilot study offshore northeastern japan. Phys Earth Planet Inter, 184(3-4): 194-207. DOI:10.1016/j.pepi.2010.11.008 | |
| Mackie R L. 1993. Three-dimensional magnetotelluric modeling using difference equations-theory and comparisons to integral equation solutions. Geophysics, 58(2): 215-226. DOI:10.1190/1.1443407 | |
| Moré J J, Thuente D J. 1994. Line search algorithms with guaranteed sufficient decrease. ACM Trans. Mathemat. Softw. (TOMS), 20(3): 286-307. DOI:10.1145/192115.192132 | |
| Nam M J, Kim H J, Song Y, et al. 2007. 3d magnetotelluric modelling including surface topography. Geophys. Prospect., 55(2): 277-287. DOI:10.1111/j.1365-2478.2007.00614.x | |
| Newman G A, Alumbaugh D L. 2000. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int., 140(2): 410-424. DOI:10.1046/j.1365-246x.2000.00007.x | |
| Newman G A, Alumbaugh D L. 2002. Three-dimensional induction logging problems, part 2: A finite-difference solution. Geophysics, 67(2): 484-491. DOI:10.1190/1.1468608 | |
| Newman G A. 2014. A review of high-performance computational strategies for modeling and imaging of electromagnetic induction data. Surv. Geophys, 35(1): 85-100. DOI:10.1007/s10712-013-9260-0 | |
| Nocedal J, Wright S. 2006. Numerical Optimization. New York: Springer Science & Business Media. | |
| Rodi W, Mackie R L. 2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics, 66(1): 174-187. DOI:10.1190/1.1444893 | |
| Saad Y, Schultz M H. 1986. Gmres: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput., 7(3): 856-869. DOI:10.1137/0907058 | |
| Saad Y. 1994. ILUT: A dual threshold incomplete LU factorization. Numer. Lin. Algebra Applicat, 1(4): 387-402. DOI:10.1002/nla.1680010405 | |
| Sasaki Y. 2001. Full 3-D inversion of electromagnetic data on PC. J. Appl. Geophys., 46(1): 45-54. DOI:10.1016/S0926-9851(00)00038-0 | |
| Siripunvaraporn W, Egbert G, Lenbury Y. 2002. Numerical accuracy of magnetotelluric modeling: a comparison of finite difference approximations. Earth, Plan. Space, 54(6): 721-725. DOI:10.1186/BF03351724 | |
| Siripunvaraporn W, Egbert G, Lenbury Y, et al. 2005. Three-dimensional magnetotelluric inversion: data-space method. Phys. Earth Planet, Inter., 150(1-3): 3-14. DOI:10.1016/j.pepi.2004.08.023 | |
| Sleijpen G L G, Fokkema D R. 1993. Bicgstab (l) for linear equations involving unsymmetric matrices with complex spectrum. Electron.Trans. Numer. Anal., 1: 11-32. | |
| Smith J T. 1996a. Conservative modeling of 3-D electromagnetic fields, part Ⅰ: Properties and error analysis. Geophysics, 61(5): 1308-1318. DOI:10.1190/1.1444054 | |
| Smith J T. 1996b. Conservative modeling of 3-D electromagnetic fields, part Ⅱ: Biconjugate gradient solution and an accelerator. Geophysics, 61(5): 1319-1324. DOI:10.1190/1.144405 | |
| Tan H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method. Chinese J. Geophys. , 46(5): 705-711. DOI:10.3321/j.issn:0001-5733.2003.05.019 | |
| Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-Posed Problems. Washington: Winston and Sons. | |
| Weiss C J, Newman G A. 2003. Electromagnetic induction in a generalized 3d anisotropic earth, part 2: The LIN preconditioner. Geophysics, 68(3): 922-930. DOI:10.1190/1.1581044 | |
| Weiss C J, Constable S. 2006. Mapping thin resistors and hydrocarbons with marine em methods, part Ⅱ-modeling and analysis in 3D. Geophysics, 71(6): G321-G332. DOI:10.1190/1.2356908 | |
| Zhdanov M, Varentsov I, Weaver J T, et al. 1997. Methods for modelling electromagnetic fields: results from COMMEMI-the international project on the comparison of modelling methods for electromagnetic induction. J. Appl. Geophys., 37(3-4): 133-271. DOI:10.1016/S0926-9851(97)00013-X | |
| 陈辉, 邓居智, 谭捍东, 等. 2011. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究. 地球物理学报, 54(6): 1649–1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 | |
| 董浩, 魏文博, 叶高峰, 等. 2014. 基于有限差分正演的带地形三维大地电磁反演方法. 地球物理学报, 57(3): 939–952. DOI:10.6038/cjg20140323 | |
| 胡祥云, 李焱, 杨文采, 等. 2012. 大地电磁三维数据空间反演并行算法研究. 地球物理学报, 55(12): 3969–3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 | |
| 胡祖志, 胡祥云, 何展翔. 2006. 大地电磁非线性共轭梯度拟三维反演. 地球物理学报, 49(4): 1226–1234. DOI:10.3321/j.issn:0001-5733.2006.04.039 | |
| 谭捍东, 余钦范, BookerJ, 等. 2003. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 46(5): 705–711. DOI:10.3321/j.issn:0001-5733.2003.05.019 | |
 2017, Vol. 60
2017, Vol. 60