2. 国家海洋局第二海洋研究所, 海底科学重点实验室, 杭州 310012
2. Key Laboratory of Submarine Geosciences, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China
规则形体重、磁正演问题是一个重要的课题,尤其是在反演成像中,正演结果的精度和计算速度直接影响到反演结果的精度和速度.国外学者对于规则形体的重、磁异常正演已有很多研究,比如Talwani等 (1959)推导了截面为任意多边形的二度体的重力异常表达式,并将其应用于海底断裂带的模拟;Cady (1980)对其进行了发展,推导出了有限延伸的二度半体的重、磁异常计算公式;Plouff (1976)给出了截面为多边形的棱柱体的重力和磁异常正演计算方法,并将其应用于地形改正.国内学者对于三度体的重、磁异常正演研究也取得了很大进展,王邦华等 (1980)建立了均匀磁化多面体总磁异常 (ΔT) 及其各分量 (Hax、Hay、Za) 的规格化解析表达式,由各角点坐标和磁参数值表示;吴宣志 (1981)针对均质三度体位场的波谱正演计算进行了研究,得到了均质直线段、多边形面和多面体的重磁异常谱的解析表达式,并将其推广到变密度、变磁化强度的更一般情形 (吴宣志, 1983);郭志宏等 (2004)对长方体的ΔT场及其梯度场的解析“奇点”进行了分析,推导出了长方体ΔT场及其梯度场在上半空间无解析“奇点”的理论表达式;骆遥和姚长利 (2007)在此基础上引入欧拉方程对长方体磁场理论表达式进行重新推导,得到了新的长方体ΔT场及其梯度在上半空间的无解析“奇点”表达式,对二度体的重、磁异常正演计算也进行了类似的研究 (骆遥等, 2009).为了更快速更精确地计算模型体的重、磁异常及其导数,有学者对于模型体正演计算的效率和加速策略进行研究,比如几何格架等效压缩存储技术 (姚长利等, 2003) 和基于GPU的并行计算方法 (陈召曦等, 2012a, 2012b).
在重、磁异常反演中,有限长圆柱体也是一类很重要的三维理论模型体,可应用于模拟圆柱状地质体 (如矿化岩脉和岩管),以及圆柱形外壳的非地质体.圆柱体轴线上的重力异常和磁异常较容易求得,例如地形改正中的扇形公式就是基于圆柱体在轴线上的重力场公式得到的.但是由于求解柱体轴线以外空间的重、磁异常为椭圆积分,计算较为困难.前人的做法都是将其近似为物质线 (Telford et al., 1990) 或者磁偶极子 (Jain, 1991),但是当柱体的顶部埋深较小时,这种近似将会存在很大误差.Singh和Sabina (1978)给出了均匀磁化的下底无限延伸直立圆柱体的磁异常正演公式,这是一个针对均匀磁化的半无限延伸柱体磁场的封闭解.Pedersen (1978)给出了直立圆柱体重、磁场的频率域表达式.Soto等 (1983)利用傅里叶频谱分析理论研究了有限长直立圆柱体的重力和磁异常特征,有限长直立圆柱体的频谱可以用贝塞尔函数表示,利用几个频率的频谱比值可以估计圆柱体的半径、上下顶埋深以及其他参数,Keating和Sailhac (2004)将其与解析信号振幅相结合应用于金伯利岩管的识别.Van Baak (1989)推导了有限长直立圆柱体重力异常的一维线积分形式,也将类似的方法推广到了截面为多边形的柱体.国内学者对于实心圆柱体模型的引力场正演研究主要有两方面应用:引力常数G的测量实验验证问题 (陈应天和王勤, 1983; 胡延昌, 1987);地球物理中的密度结构的模拟问题.罗俊等 (1990)给出了有限长圆柱体的径向牛顿引力场的一个新的解析表达式,得到与前人研究完全相同的结果而且在形式上较之更为简洁.杜劲松等 (2010)采用一种新的积分方法得到了圆柱体的重力异常的一维积分公式,并将其应用于月球“质量瘤”模拟计算中.前人对于圆柱体的重、磁正演做了很多详细的研究,但大多是针对轴向的引力场公式,并没有给出全空间的计算方法,而且公式较为复杂,不易推广计算其高阶导数.Kwok (1989)将共轭复数变量方法用于重力异常及其高阶导数的计算中,将面积分转换为一个复变函数的环路积分,最后用一个定积分表示.
本文基于共轭复数变量替换方法求解有限长圆柱体在其外部空间的引力位及其梯度张量,由引力位的二阶导数和重力、磁位之间的Poisson关系 (Hinze et al., 2013) 求得其磁场分布.公式推导是基于直立圆柱体,因此只需要进行简单的坐标旋转变换就可求得任意方向延伸 (倾斜) 的圆柱体在其外部空间的磁场分布.在推导圆柱体磁场正演公式之前,首先推导了线模型 (细柱体近似为物质线或磁偶极子模型) 的正演公式,并在最后通过计算得到二者近似转换的条件;并求解圆柱体磁异常正演公式在中心轴线上的解析解,得到了与前人 (Telford et al., 1990) 相同的结果.通过数值计算给出了单个管状模型和组合管线模型的磁异常ΔT分布图,说明正演方法的有效性及其磁异常分布的基本特征,这对实际管线探测及等轴状地质体磁异常模拟计算工作具有指导意义.
2 有限长线模型当圆柱体的长度及上顶埋深相对于半径很大时,通常将其近似为物质线 (细圆柱体) 模型,为了对比其和圆柱体的异同点,首先推导细圆柱体的引力位计算公式.计算一个三维模型重力场的数学模型为计算一个三重积分 (Telford et al., 1990)(下文所讨论的所有模型体都是均质模型):
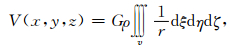
|
(1) |
其中V(x, y, z) 表示体积为v的物体引起的引力位;ρ表示物体的密度;G表示万有引力常数;r表示观测点P(x, y, z) 到质量元dm(ξ, η, ζ) 的距离:
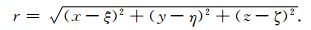
|
(2) |
为了方便,从直立圆柱体出发进行推导,对于任意方向模型只需对其乘以坐标旋转矩阵即可.
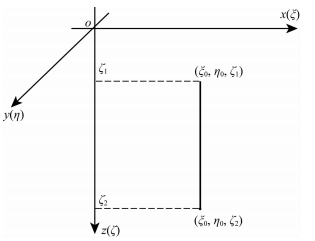
2.1 有限长直立线模型直立线模型示意如图 1所示,在z方向的延伸范围:ζ1~ζ2;水平方向中心坐标为 (ξ0, η0),半径为R.
|
图 1 直立有限长线模型示意图.中心坐标为 (ξ0, η0),延伸方向从ζ=ζ1到ζ=ζ2 Fig. 1 Sketch of a finite vertical line model with longitudinal extent from ζ=ζ1 to ζ=ζ2. Its cross-sectional point is centered at (ξ0, η0) |
对于线模型,忽略其半径对形态的影响,将横截面积与体密度之积看作线密度ρS,取其质量微元为dm=ρSdζ,则公式 (1) 转化为线积分:
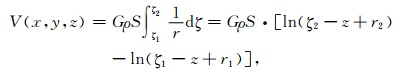
|
(3) |
其中,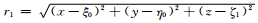
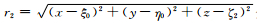
根据引力位和磁位之间的Poisson关系可以从引力位出发推导磁场三分量:
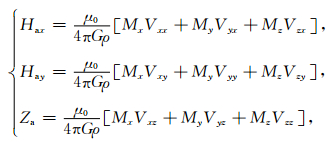
|
(4) |
其中Mx, My, Mz分别表示磁化强度M在x, y, z方向上的投影;μ0表示真空中的磁导率;Vij(i, j=x, y, z) 表示重力位的方向导数.
对公式 (3) 分别求x, y, z三个方向上的二阶梯度张量分量,根据对称性,只需求解公式 (5) 所示的六个二阶导数即可组合求得磁场分量,这个推导过程较简单,直接给出结果:
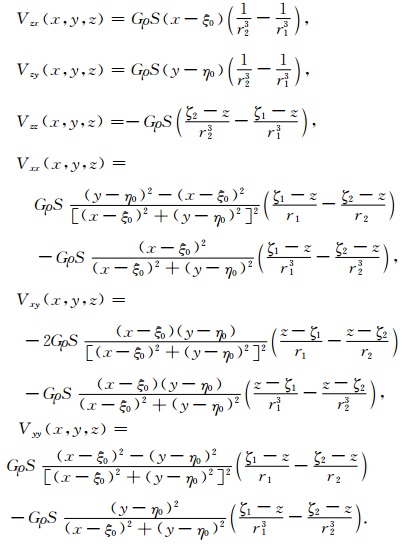
|
(5) |
直立圆柱体是特殊情况,更一般的情况是倾斜圆柱体.有限长倾斜线模型示意图如图 2所示.在观测坐标系oxy下,x轴指向磁北,倾斜物质线两个端点的坐标分别为P1(x1, y1, z1) 和P2(x2, y2, z2)(z1≤z2),倾角 (与水平投影之间的夹角) 为I(偏下为正,偏上为负),偏角 (水平投影与x轴的夹角) 为D(偏西为负,偏东为正).

|
图 2 倾斜线模型示意图 两端点坐标分别为P1(x1, y1, z1) 和P2(x2, y2, z2),倾角和偏角分别为I和D. Fig. 2 Sketch of a inclined line model with angle of inclination (I) and declination (D) Its two endpoints are P1(x1, y1, z1) and P2(x2, y2, z2), respectively. |
从观测坐标系oxyz旋转到模型局部坐标系oξηζ(oζ轴与线模型平行) 的操作可视为两步:绕z轴旋转角度D;再绕y轴旋转角度I′=90°-I.由坐标旋转理论可知,观测坐标系oxy与直立线模型坐标系oξηζ的关系为:
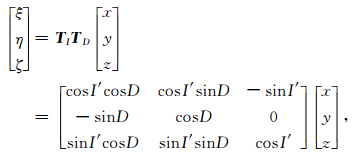
|
(6) |
其中,TI和TD分别表示绕y轴和绕z轴旋转的变换矩阵:

|
(7) |
首先由给定的倾斜线模型的两个端点坐标计算D和I,代入公式 (6) 和 (7) 计算坐标旋转矩阵.然后计算模型两个端点在oξηζ坐标系中的坐标:
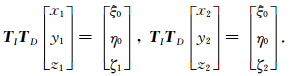
|
(8) |
对于观测点P(x, y, z) 同样利用公式 (6) 将其变换到直立线模型坐标系oξηζ中得到对应坐标P(ξ, η, ζ),并将其与公式 (8) 得到的ξ0, η0, ζ1, ζ2代入公式 (4)、(5) 即可得到倾斜线模型在其外空间任意一点的重力异常及其二阶导数、磁场值.
3 有限长圆柱体模型有限长线模型是有限长圆柱体的一种近似,当其半径相对于上顶埋深较大时,这种近似显然是不成立的,需要考虑其半径所带来的影响,不能将横截面看作是一个常系数直接从积分号里提出来,需要将其纳入到积分微元中.
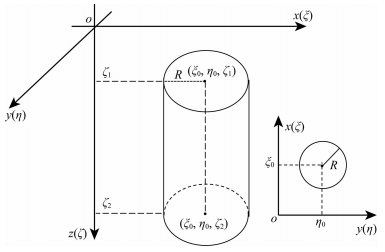
3.1 有限长直立圆柱体有限长直立圆柱体模型几何形状及坐标位置如图 3所示,z轴向下为正,x轴指向正北,y轴指向正东.圆柱体半径为R,中心轴线平行于z轴,在z轴方向的延伸为:ζ1~ζ2;其横截面在水平面ξ-η的投影中心坐标为 (ξ0, η0).为表述方便,引入两个坐标系:(x, y, z) 表示观测点坐标;(ξ, η, ζ)表示模型体局部坐标.
|
图 3 直立圆柱体示意图 延伸方向从ζ=ζ1到ζ=ζ2,横截面圆心位于 (ξ0, η0),半径为R. Fig. 3 Sketch of a vertical cylinder prism with longitudinal extent from ζ=ζ1 to ζ=ζ2 Its cross-sectional curve is a circle centered at (ξ0, η0) and the radius equals to R. |
为了计算三度体在空间中的引力位及其各阶导数和磁场分布,需要求解由公式 (1) 给出的体积分.对于有限长直立圆柱体而言,沿轴向的积分很容易得到.因此首先计算轴向从ζ1~ζ2积分可以将三重积分降为二重积分,然后利用格林公式将二重积分化为线积分.Kwok (1989)利用一对共轭复数变量成功计算了二度体的重力异常及其高阶导数.格林公式的复数形式方便地将二重积分化为一个复数域的环路积分 (其具体证明过程见Kwok (1989)附录A-1~A-3),复数格林公式可以表示为:

|
(9) |
其中,w=x+iy和w=x-iy是一对共轭复数;认为函数F(w, w) 在区域S和边界C上连续并且有连续的一阶偏导数.
3.1.1 方向导数Vz为了简便,现在从直立圆柱体的引力位的z方向导数开始推导,对公式 (1) 求z方向的导数可得直立圆柱体在观测点P(x, y, z) 处的Vz表达式:
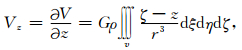
|
(10) |
先求公式 (10) 从ζ1~ζ2的积分,将三重积分化为二重积分:

|
(11) |
其中S是直立圆柱体的横截面在ξ-η面的投影.(11) 式积分仅在直立圆柱体之外成立,如果P点在圆柱体内部,则会存在奇异点,也就是公式 (2) 中的r=0.
针对积分式 (11),定义下面的共轭复数对:
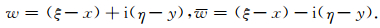
|
(12) |
利用公式 (12) 可以将公式 (11) 的第一项设置为:
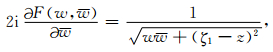
|
(13) |
对w积分可得:
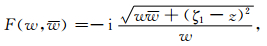
|
(14) |
将函数F(w, w) 代入复数格林公式 (9) 可将公式 (11) 的二重积分化为环路积分 (Kwok, 1991):
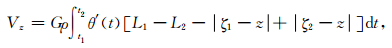
|
(15) |
其中u(t),v(t),L2,L1,θ(t) 和θ′(t) 可定义为:

|
(16) |
由于公式 (15) 表示的Vz最后两项含有绝对值,求z方向导数以后就会成为一个阶跃函数,用符号函数表示为:
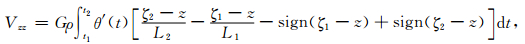
|
(17) |
用分段函数表示为:

|
(18) |
为方便推导Vzx计算公式,从Vz的积分式 (10) 出发,求其x方向的导数并求ζ从ζ1到ζ2的积分得:
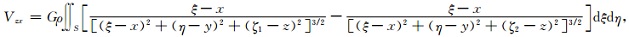
|
(19) |
(19) 式表示的是两项之和,现只考虑第一项 (同理可得第二项),可以将其表示为:
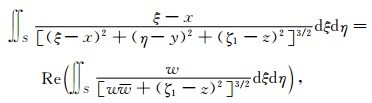
|
(20) |
对比公式 (20) 和格林公式的复数形式定义式 (9),可构造复数变量为:
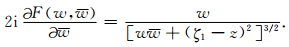
|
(21) |
综合公式 (9)、(20)—(21) 取实部可求得Vzx为:
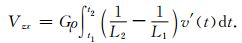
|
(22) |
Vzy求解思路与Vzx相似,不同点是将公式 (20) 改为取其虚部:
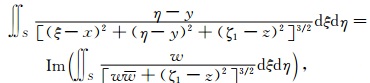
|
(23) |
同理利用格林公式并取虚部可得Vzy为:
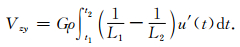
|
(24) |
对公式 (1) 求x方向导数并对ζ求积分 (此类积分见附录公式 (A1)) 有:
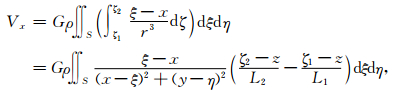
|
(25) |
以方程右边第一项为例进行推导:
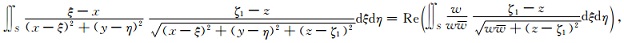
|
(26) |
对比公式 (26) 和格林公式的复数形式 (9) 定义:

|
(27) |
根据公式 (27) 容易求出F(w, w)(参考附录公式 (A2)):
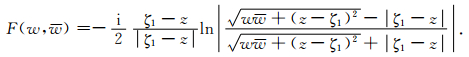
|
(28) |
由格林公式 (9) 及公式 (27), (28) 取其实部可求得Vx为:
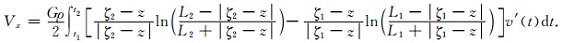
|
(29) |
由公式 (16) 可知:

|
(30) |
因此,对Vx求x方向导数并结合公式 (30) 可得Vxx:

|
(31) |
同理可得Vxy:
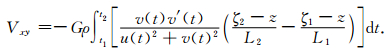
|
(32) |
Vy的求解方法与Vx类似,只需将公式 (26) 改为:
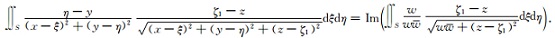
|
(33) |
由格林公式 (9) 及公式 (27)—(28) 取其虚部可求得Vy为:
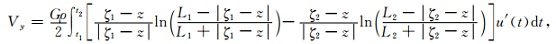
|
(34) |
与Vxx求解方法类似,可得Vyy为:
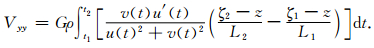
|
(35) |
对于圆柱体而言,可以定义如下变量:
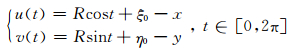
|
(36) |
将u(t) 和v(t) 的具体表达代入公式 (17)、(22)、(24)、(31)—(32)、(35) 可得到有限长直立圆柱体在模型体外空间的引力位及其偏导数,将偏导数代入Poisson关系 (4) 可得磁场分布:
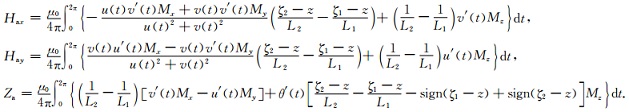
|
(37) |
对于椭圆形截面的柱体,假设其x和y方向的半轴长度分别为a和b,则u(t) 和v(t) 可以定义为:

|
(38) |
由于圆柱体的重力位及其高阶导数涉及到椭圆函数,无法求得其解析解,最后化简为[0, 2π]区间内的定积分.对于一个已知被积函数和积分限的定积分,有很多种积分方法解之,比如梯形求积公式、辛普森公式、牛顿-科茨求积公式、复化求积公式以及龙贝格公式和高斯型求积公式等 (李星,2014).不同方法具有不同的计算精度,其计算的核心思路都是将积分区间划分为n段,利用插值计算每个区间的积分结果然后累加.提高计算精度的一种策略就是加密计算节点,但是不能无限的增加节点,当插值节点增加时,拉格朗日插值会产生龙贝格现象,相应地,牛顿-科茨求积公式也会产生较大误差.本文选择高精度的自适应递归辛普森求积方法 (Gander and Gautschi, 2000),这种方法能够根据给定的误差容限自适应选择积分节点数,得到符合精度要求的解,Matlab已集成了这种方法的程序实现 (matlab对应的函数名为:quad),辛普森 (Simpson) 求积公式为:
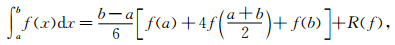
|
(39) |
其中,R(f) 为辛普森求积公式的截断误差:

|
(40) |
对于圆柱体磁异常正演公式 (37),求关于t的四阶导数过于复杂,因此采用Gander和Gautschi (2000)提出的自适应递归算法,可以借助Matlab进行积分计算.
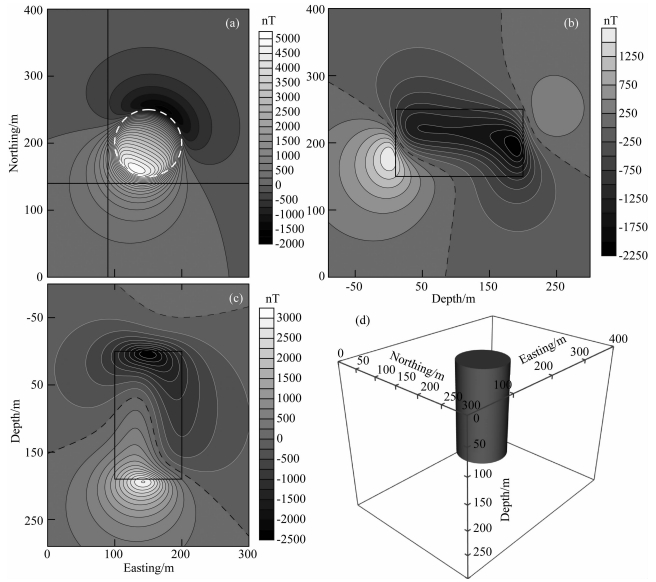
利用上面推导的圆柱体磁场计算公式进行正演计算,计算方法为自适应辛普森求积方法,绝对误差设置为10-6 nT (下同).为检验公式有效性,以一个斜磁化的直立圆柱体为例,不考虑剩磁,求解其磁异常ΔT在模型外部空间的分布.模型参数见表 1,x方向为磁北方向,y轴指向东,计算面为z=0平面以及两个纵向切片,切片位置分布如图 4a白色线所示,正演结果见图 4.
|
|
表 1 有限长直立圆柱体模型参数 Table 1 Model parameters of a finite vertical cylinder |
|
图 4 有限长直立圆柱体ΔT正演结果 (a) z=0平面上的ΔT分布,白色点划线表示切片位置;(b) 南北向纵向切片上的ΔT分布;(c) 东西向纵向切片上的ΔT分布;白色虚线表示圆柱体的投影位置;(d) 直立圆柱体三维视图. Fig. 4 Image of magnetic anomalies (ΔT) of a finite cylinder from forward modeling Three slice images represent the magnetic distribution on different planes: (a) horizontal plane at z=0, white dash dot lines show slice lateral position of image (b) and (c); vertical plane in the direction of (b) north-south and (c) east-west. White dashed lines represent projection position of the cylinder on each plane; (d) 3-D view of the cylinder model. |
对于有限长的倾斜圆柱体,与有限长倾斜线模型的正演类似,首先根据圆柱体的两个界面中心点的坐标计算观测坐标系和模型坐标系的变换矩阵 (见公式 (6)—(8)),然后将观测点 (正演计算点) 的坐标变换到模型体局部坐标系oξηζ中,然后代入公式 (37) 中计算磁场.
验证有限长倾斜圆柱体正演结果,做一个简单的模型试验,其模型参数见表 2,不考虑剩磁,计算面为z=0平面,其ΔT正演结果见图 5.
|
|
表 2 有限长倾斜圆柱体模型参数 Table 2 Model parameters of an inclined cylinder with finite length |

|
图 5 有限长倾斜圆柱体磁异常正演结果 (a) 白色虚线框是倾斜圆柱体在计算面上 (z=0) 的投影位置; (b) 倾斜圆柱体三维视图. Fig. 5 Image of the magnetic anomalies of a inclined cylinder with finite length from forward modeling (a) The white dashed rectangle represents projection position of the cylinder on the plane (z=0); (b) 3-D view of the inclined cylinder model. |
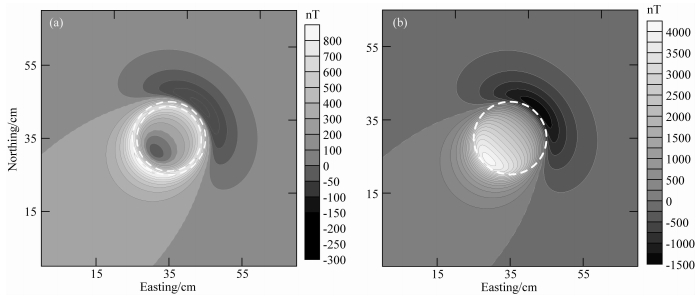
为了说明管状磁性体的磁场分布特征,分别计算单个直立管的磁异常和符合实际情况的管线分布所产生的磁异常.其中单个磁性管模型的参数见表 3,磁异常ΔT的正演结果见图 6,从正演结果发现实心圆柱体的磁异常分布范围较空心的磁性管更集中于中心,后者在中心表现出明显的低磁异常,高值对应于磁性管壁.
|
|
表 3 直立空心柱体的物性参数和几何参数 Table 3 Physical and geometric parameters of a vertical hollow cylinder |
|
图 6 有限长直立管 (a) 及实心圆柱体 (b) 磁异常ΔT正演结果 白色虚线表示直立管和实心圆柱体截面在正演平面上的投影. Fig. 6 Image of magnetic anomalies (ΔT) of (a) vertical hollow cylinder and (b) solid cylinder from forward modeling The white dashed circle represents projection position of cross-section of the hollow cylinder and solid cylinder. |
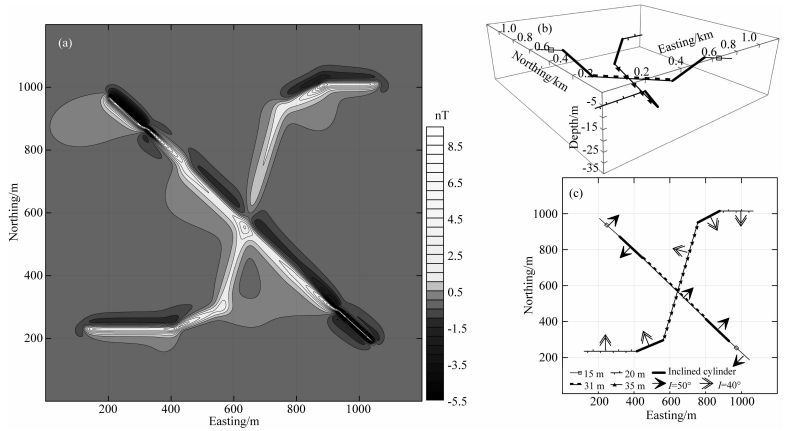
真实的管线一般都比较长,而且分布较复杂 (如拐弯的和倾斜的),且受到生产条件和安装环境的影响,每一段的磁化方向都是不同的,因此为了模拟多个管线组合在一起所产生的磁异常,设置几个长度、磁化方向和埋深不同的管线彼此对接,由于接头处的磁场计算较为复杂,不影响磁异常整体分布特征的情况下,这里只做了简单的叠加处理.管线分布图及计算结果见图 7,所有管线的半径都相同:r=0.8 m,厚度为0.2 m,磁化率为0.25 SI,地磁场大小为50000 nT.
|
图 7 组合管线模型ΔT正演 (a) ΔT正演计算结果;(b) 管线分布图,不同线型线段表示埋深不同的管线模型,黑色表示倾斜管,见图例;(c) 不同线型表示管线的深度,箭头方向表示磁化偏角方向,不同类型的箭头表示不同的磁化倾角,见图例. Fig. 7 Magnetic anomalies (ΔT) of a multi-pipeline model from forward modeling (a) Image of the magnetic anomaly; (b) Distribution map of the pipelines. Different types represent different depth and black lines show the inclined pipelines; (c) Different types of line represent the depth of each pipeline. The black arrows indicate the angle of magnetic declination of each segment, and the two different shapes of the arrow represent two different angle of magnetic inclination, respectively. The details are shown in legend. |
有限长圆柱体全空间磁场正演计算公式用一个[0, 2π]的定积分表示,这个定积分是一个椭圆积分,无法求得其原函数,但对于某些特殊位置,是可以求得其解析解,比如轴线上 (x=ξ0, y=η0):u(t)2+v(t)2=R2,θ(t)=t,θ′(t)=1代入公式 (15) 得:
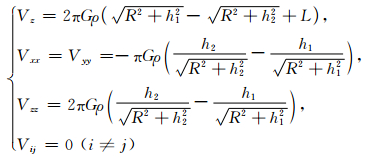
|
(41) |
其中h1和h2分别表示上顶埋深和下底埋深,且h2=h1+L,L为圆柱体的长度.
将公式 (41) 代入重磁位场的Poisson关系 (4) 中即可得到中心轴线上的磁场分量公式:
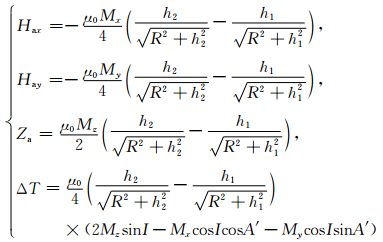
|
(42) |
其中I和A′分别表示磁化倾角和磁化偏角.
特别地,当h1=0时,h2=L,相当于圆柱体露头,则
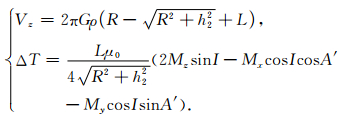
|
(43) |
有限长圆柱体与线模型的磁异常分布的一个主要的区别就是形态差异.当圆柱体的上顶埋深较浅时,其磁异常分布可以显示出明显的形态特征,但是线模型不论在什么情况下均是一个形态,半径不同只会影响其幅值.利用上文中推导的圆柱体磁异常计算公式计算不同情况下圆柱体与线模型的磁异常差异,用二者差值的相对误差 (Relative Error,RE) 来表示:
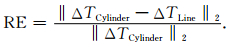
|
(44) |
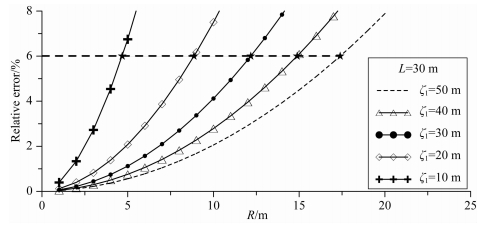
影响圆柱体磁异常大小的三个量:上顶埋深 (ζ1)、半径 (R) 和长度 (L).在长度固定的情况下,计算相同参数的直立圆柱体与直立线模型的磁异常ΔT的差异随半径的变化关系,如图 8所示.地磁场为50000 nT, 磁化率为0.25 SI,磁化偏角为0°,磁化倾角为90°,不考虑剩磁.由于两种模型的磁异常差异主要集中在中心点周围,因此选择计算范围为圆柱体在平面投影中心周围40 m×40 m,计算间隔为1 m×1 m.圆柱体长度为30 m,线模型参数与圆柱体一致.不同的埋深用不同线型的曲线表示,每条曲线上五角星表示相对误差为6%的点.
|
图 8 RE随半径 (R) 和上顶埋深 (ζ1) 的变化关系 Fig. 8 RE varying with the radius (R) and depth (ζ1) |
图 8中的曲线表明,当圆柱体长度一定时,上顶埋深越大,半径越小,其近似为线模型时误差更小;相反,上顶埋深越小,其近似误差随着半径增大而急剧增大.Telford等 (1990)指出,在相对误差小于6%的情况下,可以将圆柱体近似为线模型,提取图 8中相对误差为6%所对应的半径 (R) 和上顶埋深 (ζ1),并对不同长度的圆柱体使用同样的做法,其关系曲线见图 9.

|
图 9 RE为6%的情况下ζ1,L,R三者之间的关系 (a) 不同长度情况下,半径 (R) 与上顶埋深 (ζ1) 的关系;(b) L=30 m的R-ζ1直线拟合,直线斜率为3.2,拟合误差的二范数为4.06,黑色直线表示拟合直线,三角形表示散点;黑色条棒表示拟合误差;(c) ζ1/R随圆柱体长度L的变化曲线. Fig. 9 Relationship among ζ1, L, and R on the condition of RE equal to 6% (a) Relationship between R and ζ1 for different length (L); (b) Linear fitting of R-ζ1 when L=30 m, and the slope ζ1/R equal to 3.2, norm of residuals is 4.06. The black line shows the straight line, the triangles represent scatter data, and the black bars indicate fitting error; (c) ζ1/R varying with the length. |
图 9a表明,圆柱体长度一定,且满足近似为线模型的条件 (RE≤6%) 时,半径与上顶埋深近似呈线性关系.为了定量表示三个变量 (ζ1,L,R) 之间的关系,对图 9a曲线进行最小二乘直线拟合,L=30 m时的拟合结果和误差见图 9b,拟合直线的斜率为3.2,拟合误差为7.6%.为统计计算ζ1/R随圆柱体长度L的变化关系,对长度5~5000 m (间隔5 m) 的一系列圆柱体计算在近似条件下的ζ1/R,二者关系曲线如图 9c所示:ζ1/R变化并不大 (2.5~3.4),而且随着圆柱体长度的增大,ζ1/R变化很小,并趋于一个常值 (≈2.5).因此,当圆柱体上顶埋深ζ1小于2.5R时,需要考虑其形状带来的影响,将其近似为线模型将带来较大误差 (>6%).
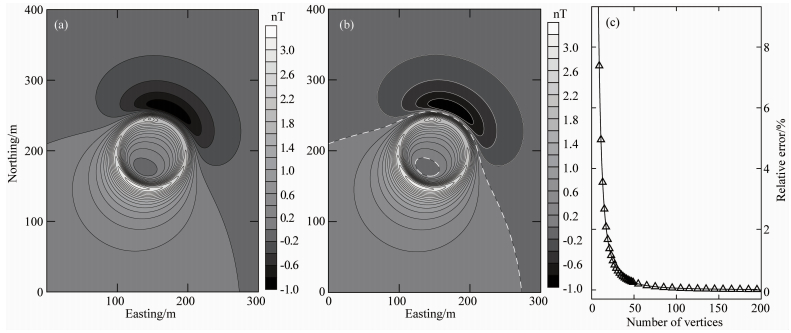
5.3 多边形截面棱柱体近似将圆柱体磁异常正演结果与棱柱体正演结果进行对比,一方面可以检验圆柱体正演公式的正确性;另一方面可以讨论棱柱体近似为圆柱体的精度.Uieda等 (2013)对Plouff (1976)的方法进行了程序实现,集成于fatiando (http://www.fatiando.org/) 程序包中.以fatiando软件中截面为多边形的棱柱体的磁异常正演程序为参考,与本文的结果进行对比.参与对比的圆柱体模型参数如表 1所示,磁异常正演结果如图 4a所示.直立棱柱体截面设置为正多边形,其中心与圆柱体截面圆心重合,外接圆与圆柱体截面圆重合,模型参数除多边形顶点个数之外与圆柱体模型相同.设置多边形顶点个数为100,本文的磁异常正演结果 (图 4a) 与顶点个数为100的多边形棱柱体的差值见图 10a,其相对误差最大值为0.06%,棱柱体对圆柱体的近似程度随着顶点个数的增加而增加.为了定量表示棱柱体对圆柱体的近似关系,计算一系列正多边形截面棱柱体与图 4a的相对误差,计算方法见公式 (44),多边形顶点个数从8增加到200,其关系曲线见图 10c.当多边形个数为200时,相对误差为0.01%.
|
图 10 圆柱体正演结果与多边形截面柱体比较 (a) 图 4a与多边形 (顶点个数=100) 截面棱柱体磁异常之差;(b) 顶点个数分别为1000和100的多边形截面柱体磁异常之差;(c) 相对误差与多边形顶点个数的变化关系. Fig. 10 Comparison of magnetic forward results of a cylinder and polygonal prism (a) Difference of ΔT between Fig. 4a and polygonal prism, of which vertices are 100; (b) Difference of ΔT between two polygonal prisms, which vertices are 1000 and 100, respectively; (c) RE changes with the number of vertices. |
利用共轭复数变量替换方法推导出了均匀有限长直立圆柱体的引力位及其一阶、二阶导数计算公式,将三重积分化为[0, 2π]的定积分,结合引力位和磁位之间的Poisson关系计算均匀磁化的有限长直立圆柱体的磁场分量.在前人的基础上进行了发展,不仅能计算轴线上的磁异常而且对于圆柱体外的全空间均适用.文中得到的正演计算公式均针对直立圆柱体,对于倾斜的情况还需要进行坐标旋转.
有限长圆柱体的磁异常正演公式涉及到椭圆积分,无法在全空间求得其解析解,但是在中心轴线上可以求得解析解.通过正演计算和统计得到了有限长圆柱体与有限长线模型的区别和联系.当长度一定时,圆柱体近似为线模型的条件与上顶埋深和半径有关,二者近似呈线性关系,二者比值与长度变化呈反比.当ζ1/R < 2.5时,用线模型近似表示圆柱体所带来的误差将超过6%;当ζ1/R > 3.4时,可以用线模型近似代替圆柱体.有限长圆柱体全空间正演公式不仅从理论上补充了圆柱体磁异常在全空间正演的空缺,也可将这种方法推广到截面是椭圆形以及多边形的柱体的引力位及其高阶导数和磁场正演计算,同时也解决了管状模型体的重、磁场正演问题.
用这种方式简化其表达式,更容易求取高阶导数.用数值积分的方法求解是一种很好的途径,而且对于一定的数值积分方法,可以方便讨论其计算误差或者代数精度或者给定计算精度,利用自适应递归辛普森方法直接计算最终结果.
致谢 中国地质大学 (武汉) 地球物理与空间信息学院梁青老师以及两位外审专家对于本文提出了宝贵意见;多边形截面棱柱体的磁异常正演是基于fatiando程序包,在此一并表示感谢.
附录
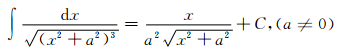
|
(A1) |
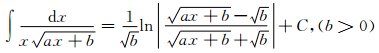
|
(A2) |
对Vz求z方向的积分,可得到重力位的表达式为:

|
(A3) |
公式 (22) 详细结果:
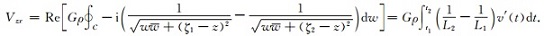
|
(A4) |
| Cady J W. 1980. Calculation of gravity and magnetic anomalies of finite-length right polygonal prisms. Geophysics, 45(10): 1507-1512. DOI:10.1190/1.1441045 | |
| Chen Z X, Meng X H, Guo L H, et al. 2012a. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU. Chinese Journal of Geophysics, 55(12): 4069-4077. DOI:10.6038/j.issn.0001-5733.2012.12.019 | |
| Chen Z X, Meng X H, Liu G H, et al. 2012b. The GPU-based parallel calculation of gravity and magnetic anomalies for 3D arbitrary bodies. Geophysical & Geochemical Exploration, 36(1): 117-121. | |
| Du J S, Liang Q, Chen C, et al. 2010. Deep structure and impact evolution of lunar mascon basins. Geological Science and Technology Information, 29(5): 135-142. | |
| Gander W, Gautschi W. 2000. Adaptive quadrature-revisited. BIT Numerical Mathematics, 40(1): 84-101. DOI:10.1023/A:1022318402393 | |
| Guo Z H, Guan Z N, Xiong S Q. 2004. Cuboid (T and its gradient forward theoretical expressions without analytic odd points. Geophysical & Geochemical Exploration, 47(6): 1131-1138. | |
| Hinze W J, Von Frese R R B, Saad A H. Gravity and Magnetic Exploration:Principles, Practices, and Applications. New York: Cambridge University Press, 2013. | |
| Hu Y C. 1987. Expressions for the axial gravitational field of the finite cylinder. Crustal Deformation and Earthquake, 7(1): 19-22. | |
| Jain B K. 1991. Magnetic effects of a finite, arbitrarily oriented line of dipoles. Geophysics, 56(9): 1474-1476. DOI:10.1190/1.1443167 | |
| Keating P, Sailhac P. 2004. Use of the analytic signal to identify magnetic anomalies due to kimberlite pipes. Geophysics, 69(1): 180-190. DOI:10.1190/1.1649386 | |
| Kwok Y K. 1989. Conjugate complex variables method for the computation of gravity anomalies. Geophysics, 54(12): 1629-1637. DOI:10.1190/1.1442631 | |
| Kwok Y K. 1991. Singularities in gravity computation for vertical cylinders and prisms. Geophysical Journal International, 104(1): 1-10. DOI:10.1111/gji.1991.104.issue-1 | |
| Luo Y, Yao C L, Xue D J, et al. 2009. Analytic singularity-free forward computation of gravity and magnetic anomaly for 2^5-D geologic body. Oil Geophysical Prospecting, 44(4): 487-493. | |
| Luo Y, Yao C L. 2007. Theoretical study on cuboid magnetic field and its gradient expression without analytic singular point. Oil Geophysical Prospecting, 42(6): 714-719. | |
| Pedersen L B. 1978. A statistical analysis of potential fields using a vertical circular cylinder and a dike. Geophysics, 43(5): 943-953. DOI:10.1190/1.1440875 | |
| Plouff D. 1976. Gravity and magnetic fields of polygonal prisms and application to magnetic terrain corrections. Geophysics, 41(4): 727-741. DOI:10.1190/1.1440645 | |
| Singh S K, Sabina F J. 1978. Magnetic anomaly due to a vertical right circular cylinder with arbitrary polarization. Geophysics, 43(1): 173-178. DOI:10.1190/1.1440818 | |
| Soto A, Singh S K, Flores C. 1983. Spectral analysis of gravity and magnetic anomalies due to a vertical circular cylinder. Geophysics, 48(2): 224-228. DOI:10.1190/1.1441461 | |
| Talwani M, Worzel J L, Landisman M. 1959. Rapid gravity computations for two (dimensional bodies with application to the Mendocino submarine fracture zone. Journal of Geophysical Research, 64(1): 49-59. DOI:10.1029/JZ064i001p00049 | |
| Telford W M, Geldart L P, Sheriff R E. Applied Geophysics. Cambridge: Cambridge University Press, 1990. | |
| Uieda L, Oliveira V C Jr, Barbosa V C F. 2013. Modeling the Earth with Fatiando a Terra.//Proceedings of the 12th Python in Science Conference. 91-98, http://www.fatiando.org/cite.html. | |
| Van Baak D A. 1989. Efficient computation of the gravitational field of a generalized cylindrical prism. Geophysics, 54(3): 402-405. DOI:10.1190/1.1442665 | |
| Wang B H, Lin S B, Deng Y Q. 1980. Magnetic fields of uniformly magnetized polyhedra. Chinese Journal of Geophysics (Acta Geophysica Sinica), 23(4): 415-426. | |
| Wu X Z. 1981. Computation of spectrum of potential field due to 3-dimensional bodies (homogeneous models). Chinese Journal of Geophysics (Acta Geophysica Sinica), 24(3): 336-348. | |
| Wu X Z. 1983. The computation of spectrum of potential field due to 3-D arbitrary bodies with physical parameters varying with depth. Chinese Journal of Geophysics (Acta Geophysica Sinica), 26(2): 177-187. | |
| Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese Journal of Geophysics, 46(2): 252-258. | |
| 陈应天, 王勤. 1983. 论有限圆柱体轴向牛顿引力场的意义. 中国科学 (A辑), 11(2): 166–171. | |
| 陈召曦, 孟小红, 郭良辉, 等. 2012a. 基于GPU并行的重力、重力梯度三维正演快速计算及反演策略. 地球物理学报, 55(12): 4069–4077. DOI:10.6038/j.issn.0001-5733.2012.12.019 | |
| 陈召曦, 孟小红, 刘国峰, 等. 2012b. 基于GPU的任意三维复杂形体重磁异常快速计算. 物探与化探, 36(1): 117–121. | |
| 杜劲松, 梁青, 陈超, 等. 2010. 月球"质量瘤"盆地的深部结构与撞击演化. 地质科技情报, 29(5): 135–142. | |
| 郭志宏, 管志宁, 熊盛青. 2004. 长方体ΔT场及其梯度场无解析奇点理论表达式. 地球物理学报, 47(6): 1131–1138. | |
| 胡延昌. 1987. 有限圆柱体轴向引力场的表达式. 地壳形变与地震, 7(1): 19–22. | |
| 李星. 数值分析. 北京: 科学出版社, 2014. | |
| 罗俊, 张学荣, 李建国, 等. 1990. 有限圆柱体的径向牛顿引力场. 中国科学 (A辑)(2): 163–168. | |
| 骆遥, 姚长利. 2007. 长方体磁场及其梯度无解析奇点表达式理论研究. 石油地球物理勘探, 42(6): 714–719. | |
| 骆遥, 姚长利, 薛典军, 等. 2009. 2^5D地质体重磁异常无解析奇点正演计算研究. 石油地球物理勘探, 44(4): 487–493. | |
| 王邦华, 林盛表, 邓一谦. 1980. 均匀磁化多面体的磁场. 地球物理学报, 23(4): 415–426. | |
| 吴宣志. 1981. 三度体 (均质模型) 位场波谱的正演计算. 地球物理学报, 24(3): 336–348. | |
| 吴宣志. 1983. 三度体 (物性随深度变化模型) 位场波谱的正演计算. 地球物理学报, 26(2): 177–187. | |
| 姚长利, 郝天珧, 管志宁, 等. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报, 46(2): 252–258. | |
 2017, Vol. 60
2017, Vol. 60


