2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
实际的地球介质不是完全弹性的,是黏声介质.传播过程中地震波发生频散,导致能量逐渐衰减,相位畸变.基于声波方程的常规地震模拟与成像方法忽略了黏声介质的这种吸收衰减作用.为了更准确描述波在实际介质中的传播规律,需要在波场模拟中考虑介质的吸收衰减作用 (傅旦丹等,1993;张智等,2005;Dvorkin and Mavko, 2006;单启铜和乐友喜,2007).长期以来,对黏声介质的吸收衰减机制进行了广泛的研究,相关衰减模型可以大致分为两类:(1) 在频域引入复速度 (Aki and Richards, 2002; Liao and McMechan, 1996; Štekl and Pratt, 1998); (2) 在时域波动方程中引入品质因子Q.其中,时域的方法通常用一系列黏性参数 (即标准线性体) 的组合来描述介质的黏性,其相关模型被称为近似的常Q模型 (Liu et al., 1976; Emmerich and Korn, 1987; Carcione, 2007; Zhu et al., 2013).Kjartansson (1979)提出的常Q模型,衰减因子是频率的线性函数,其Q在常规地震勘探的频带内与频率基本无关.基于常Q模型推导的波动方程含有分数阶时间导数 (Caputo and Mainardi, 1971; Mainardi and Tomirotti, 2010),Carcione采用Grünwald-Letnikov (GL) 逼近来近似求解分数阶时间导数,实现了黏声波方程和黏弹性波方程的波场模拟 (Carcione et al., 2002; Carcione, 2008).因为一个变量的分数阶时间导数依赖于该变量此前时刻的所有值,因此,直接数值求解黏声波方程需要保存每一时刻的应力-应变值,通常需要很大的内存,计算效率较低.可以对算子进行截断 (Podlubny, 1999; Carcione et al., 2002),适当降低精度来减少内存需求.即使如此,内存需求问题依然不能忽略,特别是黏声介质三维地震模拟.
为了解决内存需求问题,Lu和Hanyga (2004)采用一系列中间变量来求解分数阶导数,但是这种方法以增加计算量为代价.Chen和Holm (2004)采用分数阶拉普拉斯算子计算黏声介质中的波场,这种分数阶拉普拉斯算子可以通过一种改进的伪谱法在波数域中方便求取,该算子把分数阶时间导数转化为分数阶空间导数,提高了计算效率.Carcione (2010)直接采用改进的伪谱法进行黏声介质中的地震波场模拟,由于衰减项和频散项是耦合在一起的,数值求解需要大量内存.Treeby和Cox (2010)进一步将频散项和衰减项关联方程进行显式分解,极大地提高了数值求解的计算效率,有利于反问题的求解.特别是在地球物理领域,黏声介质地震偏移,实现了在波场延拓过程中同时进行频散校正和衰减补偿,提高成像质量 (Zhu, 2014; Zhu et al., 2014).
本文从Kjartansson常Q应力-应变关系出发,结合声波介质的运动方程和动力学方程,推导了含分数阶时间导数的时间域常Q黏声波方程.该方程的求解由于内存需求大,不利于逆时偏移的实施.本文基于Treeby-Cox分解方法 (Treeby and Cox, 2010),通过一系列近似,推导了频散项和衰减项解耦的分数阶拉普拉斯算子黏声波方程.通过交错网格有限差分逼近时间导数,改进的伪谱法求解分数阶拉普拉斯算子,本文采用PML边界条件,利用含分数阶拉普拉斯算子黏声波方程进行黏声介质一维和二维地震波场正演模拟.由于具有较高的计算效率,该方程主要用于黏声介质的地震数据逆时偏移,改善深层构造的成像精度.黏声介质逆时偏移需要解决的问题是波场衰减补偿后延拓过程的稳定性.在延拓过程中,波场衰减补偿的同时,高频噪声能量得到过度放大,导致数值延拓发散.因此,需要在每步波场延拓后进行带通滤波,消除高频噪声.模型试算的结果表明本文方法可以进行较高精度的波场正演模拟,逆时偏移可以有效地进行频散校正和衰减补偿,显著提高成像质量.
2 常Q模型和分数阶拉普拉斯算子 2.1 常Q模型 2.1.1 应力-应变关系尽管有实验数据表明在超声频段Q与频率密切相关 (Kan et al., 1983; Sams et al., 1997; Batzle et al., 2006),但对于低频段的地震勘探而言,常Q模型是对实际衰减介质的一个很好近似 (McDonal et al., 1958; Aki and Richards, 2002).Kjartansson (1979)给出了如下的松弛函数来模拟常Q介质的线性衰减特性:
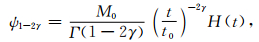
|
(1) |
其中M0=ρ0c02cos (πγ/2) 是体积模量, ρ0是介质密度, c0是参考频率ω0处的相速度, t0是参考时间, H(t) 是赫维赛德阶跃函数, Γ是伽马函数.参数γ=arctan (1/Q)/π是一个无量纲量,因为Q>0, 所以0 < γ < 0.5
黏弹性介质的应力-应变关系可以表示为松弛函数的卷积:
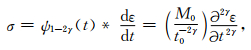
|
(2) |
其中*表示卷积,公式 (2) 包含关于时间的分数阶导数.当Q→∞, γ→0, 公式 (2) 退化为完全弹性介质的本构方程σ=M0ε.当0 < Q < ∞, 分数阶时间导数项 (∂2γε/∂t2γ) 的求解需要知道以前时刻的应变,即当下时刻的应力与之前的应变历史有关.因此,数值求解公式 (2),内存需求量大,计算效率低.
2.1.2 相速度与衰减因子对公式 (2) 进行傅里叶变换,可以得到:

|
(3) |
其中复模量

|
(4) |
其中
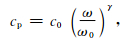
|
(5) |
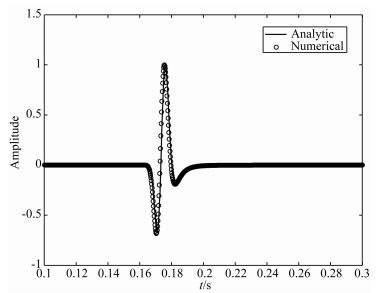
其中
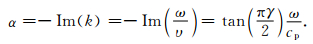
|
(6) |
可见,衰减因子α与角频率满足线性关系.据此,定义黏声介质的品质因子为:
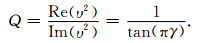
|
(7) |
根据声波介质的动力学方程:

|
(8) |
和运动方程:

|
(9) |
其中σ是压力场,ε是应变场,v=(vx, vy, vz) 是质点的振动速度,代入公式 (2) 可得黏声波方程:
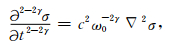
|
(10) |
其中∇ 2是拉普拉斯算子,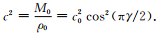
把平面波exp (iωt-ik · r) 代入 (10) 式,得到相应的频散方程:
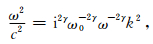
|
(11) |
其中复波数k=kR+ikI.把i2γ=cos (πγ)+isin (πγ) 代入 (11) 式,

|
(12) |
在 (12) 式右边乘以c02γ/c02γ,当γ很小,可采用近似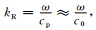
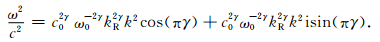
|
(13) |
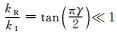
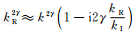

|
(14) |
其中的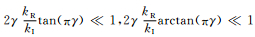
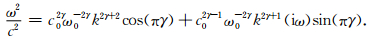
|
(15) |
(15) 式为新得到的频散关系.
在均匀介质中,c0和Q都为常数,对式 (15) 进行空间二维傅里叶逆变换和时间一维傅里叶逆变换,并考虑到如下的对应关系:k2γ+2→(-Δ 2)γ+1, k2γ+1→(-∇2)γ+1/2, (iω)2→ ∂2 ∂t2, 可得
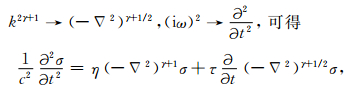
|
(16) |
其中η=c02γω0-2γcos (πγ),τ=c02γ-1ω0-2γ(iω) sin (πγ).
方程 (16) 是新得到的黏声波方程,含有分数阶拉普拉斯算子,和方程 (10) 相比,把时间分数阶导数转移到对空间求分数阶导数.空间分数阶导数可以在波数域方便求取.数值求解方程 (16) 只需保存前一时刻的波场 (一阶时间导数项),不需要把每一步的波场都保存下来,节省了内存,也提高了计算效率.方程 (16) 还有一个优越的特性是把介质的频散效应和衰减效应显式的区分开来.方程右边第一项主要和频散有关,而第二项主要与衰减有关,这两项的不同作用将在后续的数值试验中得到解释.
2.3 分数阶拉普拉斯算子计算直接采用差分计算分数阶拉普拉斯算子比较复杂,如果把波场变换到波数域,在波数域求解分数阶拉普拉斯算子将变得非常方便.根据空间微分算子的波数域表示∂x→ikx,Carcione (2010)将空间微分算子从整数阶扩展到分数阶,通过如下的傅里叶变换过程:u(xj)→FFT→ ur→(ik)βur→FFT-1→∂xβu(xj),波数域的分数阶拉普拉斯算子可表示为:
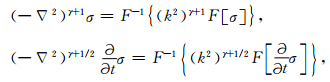
|
(17) |
其中F表示傅里叶变换.
3 正演模拟和逆时偏移 3.1 正演模拟为了应用PML吸收边界,需要将方程 (16) 转化为如下的一阶方程组:
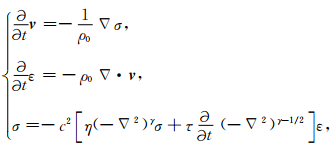
|
(18) |
式中的一阶空间导数采用伪谱法在波数域计算,一阶时间导数采用有限差分计算,分数阶拉普拉斯算子按2.3节的方法进行计算.数值离散后的方程为:

|
(19) |
逆时偏移和正演模拟依据的方程是相同的,不同的是正演模拟是已知时刻n的波场σn,求时刻n+1的波场σn+1,逆时偏移刚好反过来,所以离散方程为:
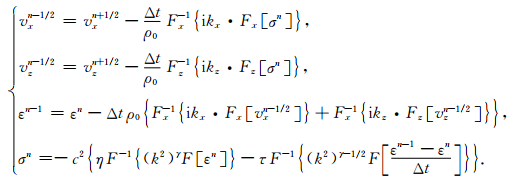
|
(20) |
逆时偏移的主要问题是保持波场延拓的稳定性.完全弹性介质中,正演模拟和逆时偏移在参数选取恰当的情况下都是稳定的.在黏性介质中,波场正向传播能量是逐渐衰减的,所以是稳定的.但在逆时延拓的过程中,延拓波场逐层得到补偿,能量逐渐增大,需要数值稳定性特殊处理.波场延拓过程中,能量补偿项是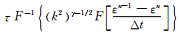
为了说明本文正演方法的可行性和准确性,首先进行一维情况下的数值解和解析解的对比.一维声波方程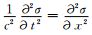
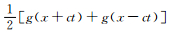
|
图 1 1D数值解 (圆圈) 与解析解 (实线) 的对比 Fig. 1 Comparison of numerical solution (circle) with the analytical solution (solid line) |

|
(21) |
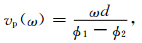
|
(22) |
其中A1,A2是两个不同位置的接收器接收波场的振幅谱,ϕ1,ϕ2是对应的相位谱,d是两个接收器之间的距离.波场模拟参数同上例,d=50 m.计算的衰减因子和相速度见图 2, 图中实线是相应的理论值,根据公式 (5) 和 (6) 计算得到.从图 2可以看出,理论值和数值模拟的结果吻合很好,只是相速度在低频和高频端出现一些偏差.高频端偏差是因为高频衰减比较严重,被数值噪声污染,影响相位谱计算的精度,后续的例子分析进一步印证此结论.低频端偏差是因为本文算法对低频的频散衰减存在低估.

|
图 2 黏弹性介质的衰减因子 (a) 和相速度 (b):数值解 (圆圈) 与解析解 (实线) 比较 Fig. 2 Attenuation factor (a) and phase velocity (b) in viscoacoustic modeling:numerical solution (circle) and analytical solution (solid line) |
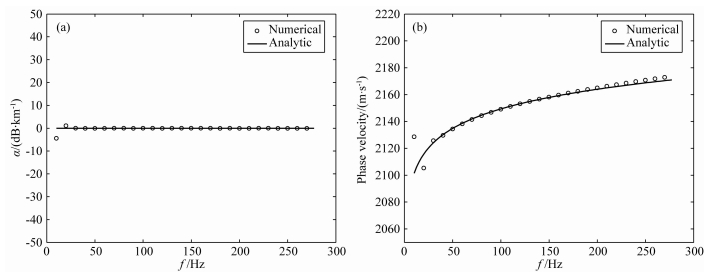
本文黏声介质正演模拟算法的一个显著特点是将频散效应和衰减效应显式分开来处理.为了研究两种效应的不同作用,我们对频散效应和衰减效应分别进行了数值模拟.图 3是仅考虑频散项得到的衰减因子和相速度, 因为没有考虑衰减项,所以衰减因子为0.值得注意的是,由于没有考虑衰减,相速度的数值解与理论值吻合较好 (特别是高频端).图 4是仅考虑衰减项的情形,从相速度上可以看出几乎没有频散.
|
图 3 只考虑频散效应的衰减因子 (a) 和相速度 (b):数值解 (圆圈) 与解析解 (实线) 比较 Fig. 3 Attenuation factor (a) and phase velocity (b) in only dispersion modeling:numerical solution (circle) and analytical solution (solid line) |
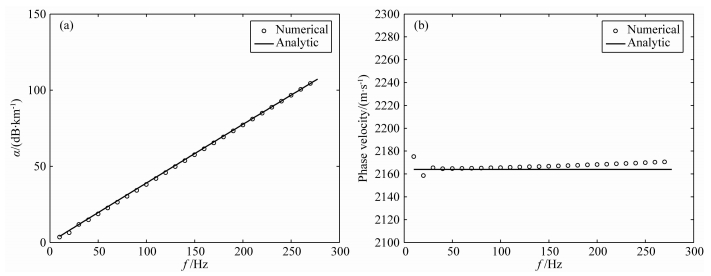
|
图 4 只考虑衰减效应的衰减因子 (a) 和相速度 (b):数值解 (圆圈) 与解析解 (实线) 比较 Fig. 4 Attenuation factor (a) and phase velocity (b) in only loss modeling:numerical solution (circle) and analytical solution (solid line) |
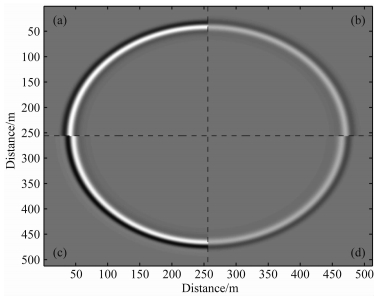
为了验证本文正演方法在二维情况下的可行性和精度,图 5是四种介质二维数值模拟110 ms的波场快照.数值模拟的参数为:黏声介质Q=32.5,网格大小为512×512,网格尺寸为1 m×1 m, 震源位于模型中心,主频为100 Hz, 其他参数同上例.从图 5可见,四种介质的波场特征与理论解释基本吻合.图 5b为黏声介质仅考虑衰减,其波场能量比图 5a的声波介质明显衰减,但二者波前面走时一致,表明波速没有发生频散.图 5c为黏声介质仅考虑频散,其波场能量与图 5a的声波介质基本一致,没有衰减,但其波前面明显延后,表明存在波速频散.图 5d为黏声介质衰减与频散同时考虑,其波形既有能量衰减又有波速频散.
|
图 5 四种介质二维数值模拟110 ms的波场快照及其衰减效应和频散效应 (a) 声波介质:无衰减和频散;(b) 黏声介质:仅考虑衰减项;(c) 黏声介质:仅考虑频散项;(d) 黏声介质:考虑衰减和频散. Fig. 5 Fourwavefield snapshots of 110ms in 2D acoustic and viscoacousticmedia (a) Acoustic media; (b) Only loss term; (c) Only dispersion term; (d) Viscoacoustic media. |
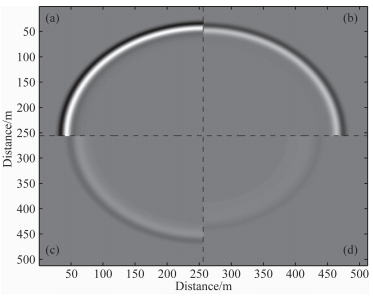
本文算法和直接求解分数阶黏声波方程 (10) 相比,把时间分数阶导数转移到对空间求分数阶导数.空间分数阶导数可以在波数域方便求取.数值求解方程 (16) 只需保存前一时刻的波场 (一阶时间导数项),不需要把每一步的波场都保存下来,节省了内存,也提高了计算效率.为了定量说明本文算法计算效率的提升,沿用图 5的模型,分别采用本文方法和直接求解方程 (10) 进行波场模拟.从图 6可以看出,两种方法得到的结果相似,表明两种方法都可以准确用于黏声介质的地震波模拟.直接数值求解方程 (10) 用了2334 s, 本文方法只用了276 s, 计算效率差不多提高了8.5倍.图 7比较了黏声介质Q=100, 30, 10, 4时二维数值模拟110 ms的波场快照.其他数值模拟参数与图 5相同.从图中可以看出,Q值越小,波前面越延后,波场能量越弱,表明衰减和频散越严重.

|
图 6 两种数值算法模拟110ms的波场快照 (a) 本文方法;(b) 直接求解方程 (10). Fig. 6 Wavefield snapshots of 110ms in 2D viscoacoustic media simulated by two methods (a) Our method; (b) Direct numerical solution of equation (10). |
|
图 7 黏声介质不同Q值二维数值模拟110 ms的波场快照 (a) Q=100;(b) Q=30;(c) Q=10;(d) Q=4. Fig. 7 Snapshots of 110 ms corresponding to different Q values |
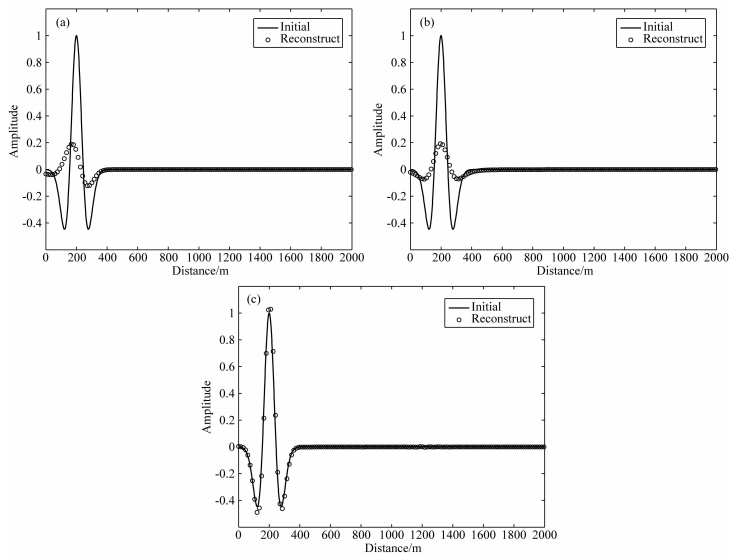
时间域常Q黏声波方程 (16),由于其频散和衰减解耦的特点,以及较高的计算效率,该方程最佳的应用在于黏声介质的地震数据逆时偏移,实现对波场进行频散校正和衰减补偿,有效改善深层构造的成像精度.由于波在黏声介质中传播高频衰减较快,因此,在波场逆时延拓过程中高频能量补偿较大,弱振幅的高频噪声同时也得到极大增强,破坏了波场逆时延拓的稳定性.为了解决这个问题,需要在波场延拓的每一步,进行滤波去除噪声,避免波场中高频噪声不断累积放大.为了了解黏声介质波场逆时延拓过程中频散校正和衰减补偿的直观效果,我们进行如下一维数值试验,首先将初始波场在黏声介质中正向延拓到一定深度,然后再采用不同的校正进行逆时延拓到零时刻来重建初始波场.数值模拟参数为nx=2000, d x=1 m, c0=2000 m·s-1, ρ0=2200 kg·m-3, Q=10, tmax=0.6 s, dt=2.5×10-4s.图 8a比较了既无频散校正又无衰减补偿的逆时延拓结果与初始波场,可见重建波场的相位和振幅与初始波场差距较远.图 8b考虑频散校正进行逆时延拓但无衰减补偿,可见重建波场的相位得到校正,但振幅与初始波场差距较远.图 8c同时考虑频散校正和衰减补偿的逆时延拓,重建波场的相位和振幅得到了精确恢复.
|
图 8 采用不同校正的逆时延拓重建的初始波场 (圆圈) 与实际初始波场 (实线) 对比 (a) 既无频散校正又无衰减补偿的逆时延拓结果;(b) 只考虑频散校正进行逆时延拓结果;(c) 同时考虑频散校正和衰减补偿的逆时延拓结果. Fig. 8 Comparison of reconstructed wave field (circle) and the actual initial wave field (solid line) (a) RTM without dispersion correction and amplitude compensation; (b) RTM with only dispersion correction; (c) RTM with dispersion correction and amplitude compensation. |
图 9是一个凹陷结构的速度和Q模型,网格点数为201×201,采样间隔为dx=dz=5 m.图 10是黏声波方程正演模拟得到的自激自收地震记录,可见深层的波场能量明显衰减,由于频散而频率降低,波形变宽.图 11是分别采用声波方程 (a) 和黏声波方程 (b) 对图 10地震记录进行逆时偏移成像结果.可见,声波方程偏移结果由于未考虑能量补偿和频散校正,深层波场振幅较弱,波形频散,模型界面的子波起跳点成像误差较大.这些问题通过黏声波方程偏移得到了很好的解决.

|
图 9 凹陷模型:(a) 速度模型;(b) Q模型 Fig. 9 Sag models: (a) velocity model; (b) Q model |

|
图 10 黏声波方程模拟的自激自收合成地震记录 Fig. 10 Zero offset synthetic seismic record in viscoacoustic media |
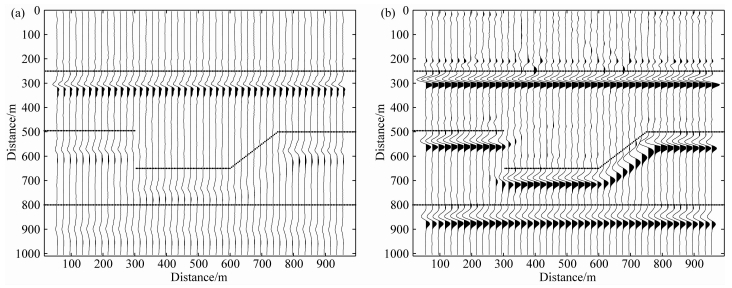
|
图 11 分别采用声波方程 (a) 和黏声波方程 (b) 对图 10地震记录进行逆时偏移成像结果 图中虚线表示对应模型的内部边界. Fig. 11 Migration profile of (a) acoustic RTM and (b) viscoacoustic RTM Dash line indicates the internal boundary in corresponding model. |
从Kjartansson常Q应力-应变关系出发,结合声波介质的运动方程和动力学方程,本文推导了含分数阶时间导数的时间域常Q黏声波方程.求解该方程需要保存所有时刻的波场值,内存需求大,计算效率低,不利于地震偏移的实施.基于Treeby和Cox的分解方法,通过一系列近似,本文推导了含分数阶拉普拉斯算子的时间域常Q黏声波方程.该方程的优点表现在两个方面:(1) 把分数阶时间导数转换到空间导数上,利用改进的伪谱法,分数阶空间导数可以在波数域方便快速求取;(2) 将频散效应和衰减效应显式解耦,实现分别模拟介质的频散效应和衰减效应.求解该方程仅需保存前一时刻的波场值,内存需求减小,提高了计算效率.
本文将含分数阶拉普拉斯算子的时间域常Q黏声波方程转为了一阶方程组,通过交错网格有限差分逼近时间导数,改进的伪谱法求解分数阶拉普拉斯算子,采用PML边界条件,进行黏声介质一维和二维地震波场正演模拟.模型试算的结果表明本文方法可以进行较高精度的波场正演模拟,模拟波场和理论波场吻合得较好,模拟得到的频散关系、衰减关系和理论值也吻合得较好.本文进而开展黏声介质的地震数据逆时偏移,通过偏移波场的频散校正和衰减补偿,改善深层构造的成像精度.由于波在黏声介质中传播高频衰减较快,因此,在波场逆时延拓过程中高频能量补偿较大,弱振幅的高频噪声同时也得到极大增强,破坏了波场逆时延拓的稳定性.因此,需要在每步波场延拓后进行带通滤波,消除高频噪声.模型试算结果表明:地震数据的黏声介质逆时偏移,可以实现偏移波场的频散校正和衰减补偿,显著提高成像质量,得到的偏移剖面明显优于常规声波偏移剖面.
| Aki K, Richards P G. Quantitative Seismology (Vol.1). Sansalito, CA: University Science Books, 2002. | |
| Batzle M L, Han D H, Hofmann R. 2006. Fluid mobility and frequency-dependent seismic velocity-Direct measurements. Geophysics, 71(1). | |
| Caputo M, Mainardi F. 1971. A new dissipation model based on memory mechanism. Pure and Applied Geophysics, 91(1): 134-147. DOI:10.1007/BF00879562 | |
| Carcione J M, Cavallini F, Mainardi F, et al. 2002. Time-domain modeling of constant-Q seismic wavesusing fractional derivatives. Pure and Applied Geophysics, 159(7-8): 1719-1736. DOI:10.1007/s00024-002-8705-z | |
| Carcione J M. Wave Fields in Real Media:Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media (Vol.38). Amsterdam: Elsevier, 2007. | |
| Carcione J M. 2008. Theory and modeling of constant-Q P-and S-waves using fractional time derivatives. Geophysics, 74(1): T1-T11. | |
| Carcione J M. 2010. A generalization of the Fourier pseudospectral method. Geophysics, 75(6): A53-A56. DOI:10.1190/1.3509472 | |
| Chen W, Holm S. 2004. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. The Journal of the Acoustical Society of America, 115(4): 1424-1430. DOI:10.1121/1.1646399 | |
| Dvorkin J P, Mavko G. 2006. Modeling attenuation in reservoir and nonreservoir rock. The Leading Edge, 25(2): 194-197. DOI:10.1190/1.2172312 | |
| Emmerich H, Korn M. 1987. Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics, 52(9): 1252-1264. DOI:10.1190/1.1442386 | |
| Fu D D, Liu Y, Chen Z D, et al. 1993. Acoustic wave modeling in viscoelastic media by pseudospectral method. Journal of Jianghan Petroleum Institute, 15(4): 32-39. | |
| Kan T K, Batzle M L, Gaiser J E. 1983. Attenuation measured from VSP:Evidence of frequency-dependent Q.//SEG Technical Program Expanded Abstracts 1983. Society of Exploration Geophysicists, 589-590. | |
| Kjartansson E. 1979. Constant Q-wave propagation and attenuation. Journal of Geophysical Research:Solid Earth, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 | |
| Liao Q B, McMechan G A. 1996. Multifrequency viscoacoustic modeling and inversion. Geophysics, 61(5): 1371-1378. DOI:10.1190/1.1444060 | |
| Liu H P, Anderson D L, Kanamori H. 1976. Velocity dispersion due to anelasticity; implications for seismology and mantle composition. Geophysical Journal International, 47(1): 41-58. DOI:10.1111/j.1365-246X.1976.tb01261.x | |
| Lu J F, Hanyga A. 2004. Numerical modelling method for wave propagation in a linear viscoelastic medium with singular memory. Geophysical Journal International, 159(2): 688-702. DOI:10.1111/gji.2004.159.issue-2 | |
| Mainardi F, Tomirotti M. 2010. Seismic pulse propagation with constant Q and stable probability distributions. arXiv preprint arXiv:1008.1341. | |
| McDonal F J, Angona F A, Mills R L, et al. 1958. Attenuation of shear and compressional waves in Pierre shale. Geophysics, 23(3): 421-439. DOI:10.1190/1.1438489 | |
| Podlubny I. 1998. Fractional Differential Equations:An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications (Vol.198). San Diego:Academic Press. | |
| Sams M S, Neep J P, Worthington M H, et al. 1997. The measurement of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 62(5): 1456-1464. DOI:10.1190/1.1444249 | |
| Shan Q T, Yue Y S. 2007. Wavefield simulation of 2-D viscoelastic medium in Perfectly Matched Layer boundary. Geophysical Prospecting for Petroleum, 46(2): 126-130. | |
| Štekl I, Pratt R G. 1998. Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators. Geophysics, 63(5): 1779-1794. DOI:10.1190/1.1444472 | |
| Treeby B E, Cox B T. 2010. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. The Journal of the Acoustical Society of America, 127(5): 2741-2748. DOI:10.1121/1.3377056 | |
| Zhang Z, Liu C, Shao Z G, et al. 2005. The application of pseudo spectral forward modeling of seismic wave field in constant Q viscoelastic medium. Progress in Geophysics, 20(4): 945-949. | |
| Zhu T Y, Carcione J M, Harris J M. 2013. Approximating constant-Q seismic propagation in the time domain. Geophysical Prospecting, 61(5): 931-940. DOI:10.1111/gpr.2013.61.issue-5 | |
| Zhu T. 2014. Time-reverse modelling of acoustic wave propagation in attenuating media. Geophysical Journal International, 197(1): 483-494. DOI:10.1093/gji/ggt519 | |
| Zhu T Y, Harris J M, Biondi B. 2014. Q-compensated reverse-time migration. Geophysics, 79(3): S77-S87. DOI:10.1190/geo2013-0344.1 | |
| 傅旦丹, 刘洋, 陈遵德, 等. 1993. 黏弹介质中声波的伪谱法模拟. 江汉石油学院学报, 15(4): 32–39. | |
| 单启铜, 乐友喜. 2007. PML边界条件下二维黏弹性介质波场模拟. 石油物探, 46(2): 126–130. | |
| 张智, 刘财, 邵志刚, 等. 2005. 伪谱法在常Q黏弹介质地震波场模拟中的应用效果. 地球物理学进展, 20(4): 945–949. | |
 2017, Vol. 60
2017, Vol. 60

