2. 中国地震局地壳应力研究所, 北京 100085
2. Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085, China
2010年2月27日,智利Maule地区近海发生MW8.8级特大地震,震源深度35 km, 震中位置 (35.85°S, 72.72°W) 位于康塞普西翁 (Concepcion) 东北89 km,距智利首都圣地亚哥西南339 km,此次地震发生在纳兹卡板块与南美板块的边界部.纳兹卡板块俯冲到南美板块之下,相对挤压速率约77 mm·a-1(Norabuena et al., 1998) 造成了安第斯山脉的隆起、火山的活动以及频繁地震的发生 (图 1).该俯冲带具有明显沿纬度方向火山、地震活动分节现象 (Chinn et al., 1980; 马宗晋, 1983),Barazangi和Isacks (1976)将该现象归结于南美板块之下的大洋板块具有不同俯冲角度,俯冲角度近水平的板块和上覆板块间只有很少的软流圈物质,无火山喷发物质基础,俯冲角度较陡板块上方则分布着密集火山.本次Maule地震俯冲角度约为18°,破裂从震中开始向南、北两个方向双侧扩展,北侧破裂明显强于南侧,破裂长度约650 km (Tong et al., 2010).20世纪以来, 南美大陆许多7.5级以上地震集中在纳兹卡板块和南美洲板块之间俯冲带上 (Bilek, 2010),其中最大一次为1960年MW9.5级地震,数次强震造成的破裂几乎贯穿智利近海两千公里.在秘鲁大陆边缘发生了1960年和1996年“海啸地震”.在该俯冲带还存在一些慢速地震过程,比如1995年MW8.1 Antofagasta地震的震后余滑 (Pritchard and Simons, 2006).

|
图 1 区域构造图 黑色震源球数据来源美国哈佛大学Global CMT (http://www.globalcmt.org[2015-10-20]);绿色震源球为2010年Maule地震;蓝色正方形表示历史地震,数据来源于 (Bilek, 2010),红色三角形代表第四季火山活动,数据来源 (http://www.ngdc.noaa.gov/hazard/volcano.shtml[2015-10-20]). Fig. 1 Regional tectonic map Black beach balls are the centroid moment tensor; Green beach ball indicates Maule earthquake; Blue squares are historical earthquakes (Bilek, 2010); Red triangles are Quaternary volcano. |
不同观测手段记录到了此次智利特大地震造成的影响.GPS观测结果 (尹志强等, 2011) 表明震中附近产生明显位移,康塞普西翁市整体向西移动达3 m, 智利首都圣地亚哥向西移动约30 cm.地震引发海啸,其中海啸受灾人数为124人 (Fritz et al., 2011),台湾周边海域的验潮站记录到明显的海啸信号,2月28日海啸最大波高达44 cm (谢燕双等, 2012).Peng等 (2010)在加州中部Coso地热区发现了此次智利地震远程触发的微地震和Tremor,在新西兰也发现了智利地震触发的高频Tremor信号 (Fry et al., 2011).该地震是人类有历史记载以来的第六大地震,那么除了观测手段之外,能否通过计算定量了解这样一个特大地震造成的同震影响,这是本文的研究目的.
目前广泛使用的计算地震同震形变、应力方法中,具有代表性的是Okada (1985, 1992) 弹性半无限空间位错表达式和Wang等 (2003)的EDGRN/EDCMP程序,但它们均采用平面坐标系.石耀霖和朱守彪 (2006)指出在由位移计算应变时,必须使用球坐标,特别当位移量较大或研究区面积大或在高纬度地区时,采用直角坐标带来的误差量级不可忽略.Sun和Okubo (2002)的研究也表明地球曲率对同震垂直位移的影响不可忽略.球型分层弹性地球模型的半解析方法 (Sun,1992) 可以考虑地球曲率,但无法考虑真实地球的介质强横向不均性和地表起伏.在同震形变和应力计算中,地表起伏和介质的不均匀性往往不可忽略,例如:Lin等 (2013)发现青藏高原东缘地形对汶川地震同震水平位移在近断层处最高影响为9%;2001年昆仑山MS8.1地震同震变形场在断裂带两侧的非对称分布必须考虑断层两侧弹性系数的不均匀 (邵志刚等,2008).真实地球横向不均匀性很大,半解析方法处理该类问题具有局限性,例如付广裕和孙文科 (2012)采用的“微小扰动方法”,该方法只适用于很小的三维构造变化的情况.目前未见公开发表文献在同震形变和应力计算中同时考虑球形地球、介质非均匀性和地表、Moho面地形起伏,本文采用数值方法,在同震应变应力计算中考虑椭球型地球、非均匀介质和界面起伏,更接近真实地球,对地震危险性的定量分析具有重要意义.
2010年智利Maule特大地震发生之后,不少学者计算了该地震引起的同震库仑应力变化 (缪淼和朱守彪,2012;Farías et al., 2011;Lorito et al., 2011),但这些研究在平面直角坐标系下计算应变和应力,也未能考虑安第斯地区剧烈的地表地形起伏和地壳结构的横向不均匀性.本文采用有限元方法,使用含地表地形起伏和横向不均匀地壳结构椭球地球模型,从力学角度定量计算2010年智利Maule特大地震的同震形变场和应力场,讨论地球曲率、分层结构对同震形变场的影响,并根据库仑应力变化分析周围断层的地震活动性和主震对余震的触发关系.
2 数值计算模型与方法半无限空间模型和球形地球模型计算的同震位移存在较大差异,Dong等 (2014)发现埋深100 km的走滑型点源位错在震中距约200 km处地球曲率对同震位移影响为5%.从位移计算应变以及应力时也需要在球坐标下进行 (石耀霖和朱守彪,2006),因此使用平面假设将带来位移、应力、应变计算不可忽略的误差,必须选用球形地球模型.Qu等 (2015)计算2004年苏门答腊地震发现,在断层破裂面所处近场、地形及三维横向不均匀地壳结构对同震水平、垂直位移的影响分别为23%和40%,这样的影响不可忽略.Sun和Okubo (2002)的半解析方法虽然可以考虑地球曲率和分层,却无法处理真实地球的介质强不均匀性和界面起伏,且该方法目前尚未计算同震应力变化,因此要研究真实地球,需要同时考虑地球曲率、介质的不均匀性和界面起伏,必须使用数值方法.
地震位错处理采用张贝等 (2015)提出的“有限元模拟弹性位错的等效体力方法”.该方法对位错处理体现在单元积分中将位错等效为体力添加到平衡方程右端项中.若单元包含位错,则在计算单元积分时,等效体力计算表达式为
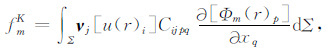
|
(1) |
其中,fmK为等效体力,Φm表示单元K中的第m个形函数,νj是位错面的法向矢量,[u (r)i]为位错,Cij pq为弹性系数,dΣ是单元内部位错面.
计算网格包含整个地球,上至地表,下至核幔边界.自然回避侧边界条件不确定性,只需给出上下边界条件,上边界为自由边界 (正应力、剪应力均为0),核幔边界为弹簧边界条件,其值由核幔密度差值决定.地表地形数据采用ETOPO1.0(Amante and Eakins, 2009),地壳采用Crust1.0(Laske et al., 2013) 模型,地幔采用GyPSuM模型 (Simmons et al., 2010),模型中使用的材料参数按照上述模型波速结构计算得到,地球椭球形状根据WGS-84参考椭球确定.采用根据误差识别自动调整网格疏密度的网格自适应技术,能够合理计算费用,提高复杂问题计算效率,改进结果精度.断层滑动模型使用Shao等 (2010)模型,对断层进行了加密处理,采用带悬点六面体单元,最终单元数目419万,计算网格见图 2.

|
图 2 计算网格地形放大30倍显示. Fig. 2 The computational grids The topography is vertically exaggerated by 30 times to highlight the elevation. |
大地震造成断层面及邻近区域的库仑应力变化被广泛用于研究地震对周围断层的应力触发作用,探讨大地震与后续地震关系.一般定义库仑应力变化 (Harris, 1998; 石耀霖和曹建玲, 2010) 为
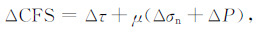
|
(2) |
式中,ΔCFS为库仑应力变化,Δτ为断层面上剪应力变化量 (与滑动方向同向为正),Δσn为断层面上正应力变化 (拉伸为正),ΔP为孔隙水压变化,μ为断层面摩擦系数.在实际应用中,常把孔隙水压的作用通过视摩擦系数μ′体现:
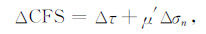
|
(3) |
本研究中,取视摩擦系数为典型值μ′=0.4.
3 计算结果和分析 3.1 地球曲率和分层结构对同震形变场影响分别用有限元方法计算球面分层模型同震位移,用EDGRN/EDCMP2.0程序 (Wang et al., 2003) 计算平面分层模型、平面半空间模型同震形变.这三个模型震源模型一样,介质参数都依据PREM模型,结果差别反映地球曲率和分层结构影响.
图 3a为球面分层模型计算同震位移和GPS观测比较,GPS数据来源于Vigny等 (2011)结果, 考虑Shao等 (2010)断层模型根据地震波反演,此处计算未考虑地形和横向不均匀性,结果虽与观测有一定差别但整体反映了同震位移特征,尤其在远场方向吻合较好,这也反映计算的合理性.由于Shao等 (2010)断层模型在反演中未使用大地测量数据约束,笔者还考察了Tong等 (2010)根据InSAR和近场GPS数据反演的滑动模型,计算发现Tong等模型虽然在近场破裂面附近与GPS吻合更好,在远场与实测位移方向偏离过大 (图 3d).目前公布的滑动模型里,使用远场GPS作为约束的仅有Sladen和Owen (2010)模型,根据Vigny等 (2011)文献,该模型和近场GPS吻合度极差,综合模型计算结果和远、近场GPS吻合程度高,本文选用Shao等 (2010)滑动模型计算Maule大地震同震效应.

|
图 3 同震位移比较 (a) 球面分层模型;(b) 平面分层模型;(c) 平面半空间模型;(d) 平面半空间模型. (a)-(c) 使用Shao等 (2010)模型,(d) 使用Tong等 (2010)模型.黑色、蓝色箭头为GPS观测值,红色、绿色箭头为计算值. Fig. 3 The comparison of co-seismic displacement between the calculation and observation (a) Spherical layered model; (b) Plane layered model; (c) Plane half-space model; (d) Plane half-space model. Model (a)-(c) based on slip distribution of Shao et al (2010), model (d) based on slip model of Tong et al (2010).The black and blue arrows indicate the GPS observation, while the red and green arrows indicate the calculated co-seismic displacement. |
根据图 3b和图 3c,平面分层模型和平面半空间模型计算所得水平位移方向和GPS实测位移方向吻合较好,但这2个模型远场位移均比观测值大,图 3a显示球面分层模型远场位移和观测值更为接近.付广裕和孙文科 (2008)计算2004年苏门答腊大地震同震水平位移发现在远场平面半空间模型计算结果约是球位错模型结果1.8倍,笔者结果与其类似.地球曲率、层状结构对远场位移影响不可忽略:球面分层模型远场位移小于平面分层模型远场位移;平面分层模型远场位移大于平面半空间模型远场位移.
地球曲率、层状结构对远场应变影响明显.Maule地震是一个低角度逆冲地震,应变积累/释放主要发生在水平面,考察低、高纬度两种极端情况,采用3种模型计算对比本次地震引起的赤道和南极洲水平位移、应变场.地震断层走向正交方向同震水平位移最大,因此选取位于断层西北方的近赤道区域 (150°W-120°W, 10°S-0°S) 和断层东南方的近南极洲区域 (0°E-30°E, 80°S-70°S) 作为研究区域,研究深度15 km,并采用墨卡托投影.
在赤道区域球面分层模型远场位移、应变量级均小于平面分层模型和平面半空间模型,而平面分层模型和平面半空间模型在赤道的远场位移和应变量级十分接近 (图 4),因此地球曲率对远场位移影响大于地球层状结构影响.对于2010年Maule地震,在低纬度远场,如果不采用球面分层模型,可能会造成位移和应变量值均被低估.
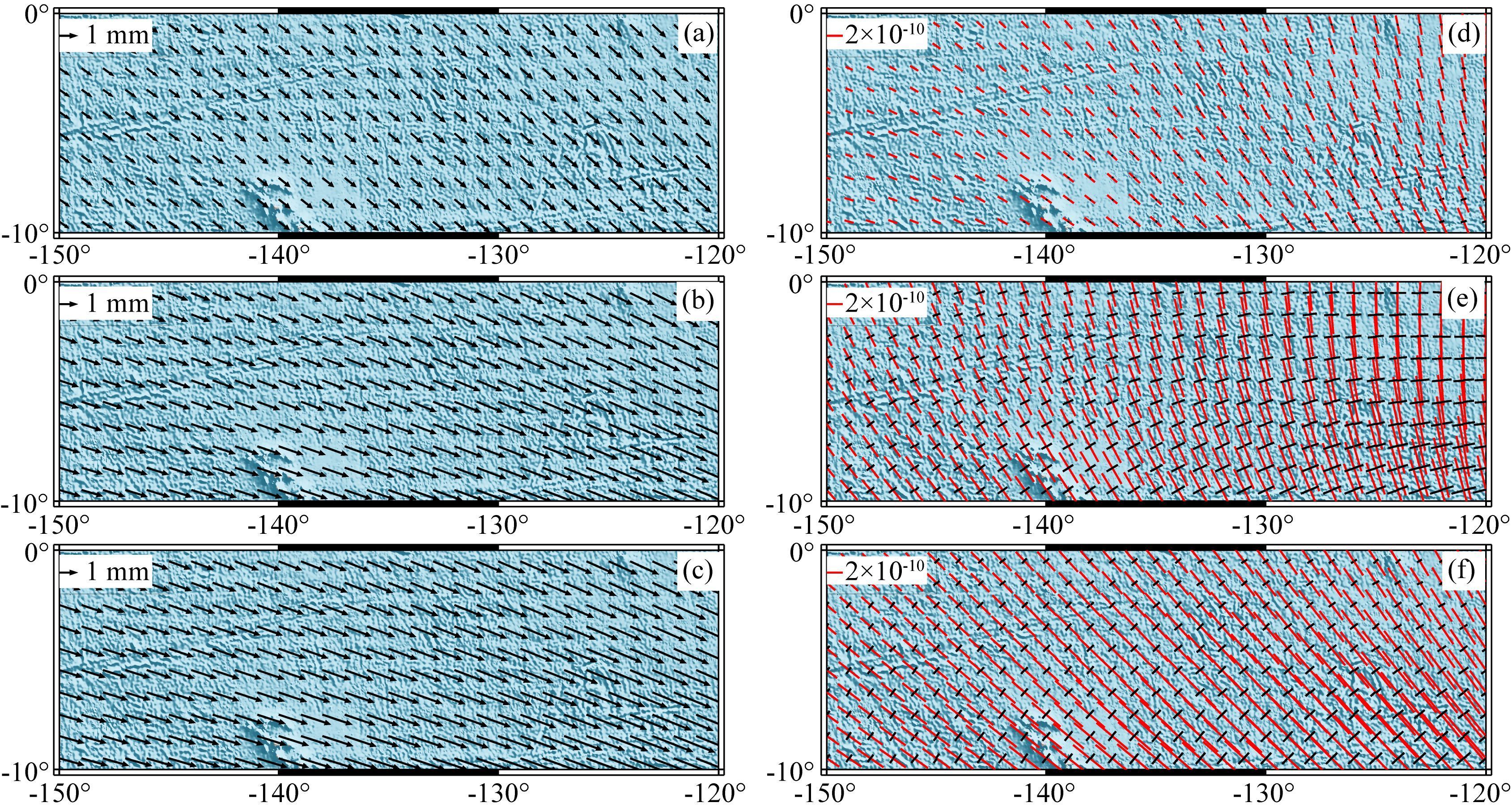
|
图 4 智利Maule地震引起的赤道区域形变场 (a)-(c) 水平位移场;(d)-(f) 水平主应变场 (红线为主拉应变,黑线为主压应变);(a)、(d) 球面分层模型结果;(b)、(e) 平面分层模型结果;(c)、(f) 平面半空间模型结果. Fig. 4 Deformation near the Equator (a)-(c) indicate displacement field and (d)-(f) indicate strain field (red lines are principal tensile strain, black lines are principal compression). (a) and (d) based on spherical layered model, (b) and (e) based on plane layered model, (c) and (f) based on plane half-space model. |
根据石耀霖和朱守彪 (2006)文献,在高纬度地区采用直角坐标计算应变将带来较大量级误差,因为球坐标应变公式里有一项与余纬的余切相关,纬度越高,该项值越大.在南极洲区域,虽然球面分层模型远场位移值小于平面分层模型和平面半空间模型,但其远场应变值大于平面分层模型和平面半空间模型 (图 5).对于2010年Maule地震,在高纬度远场,如果不采用球面分层模型,可能会造成位移被夸大而应变被低估.
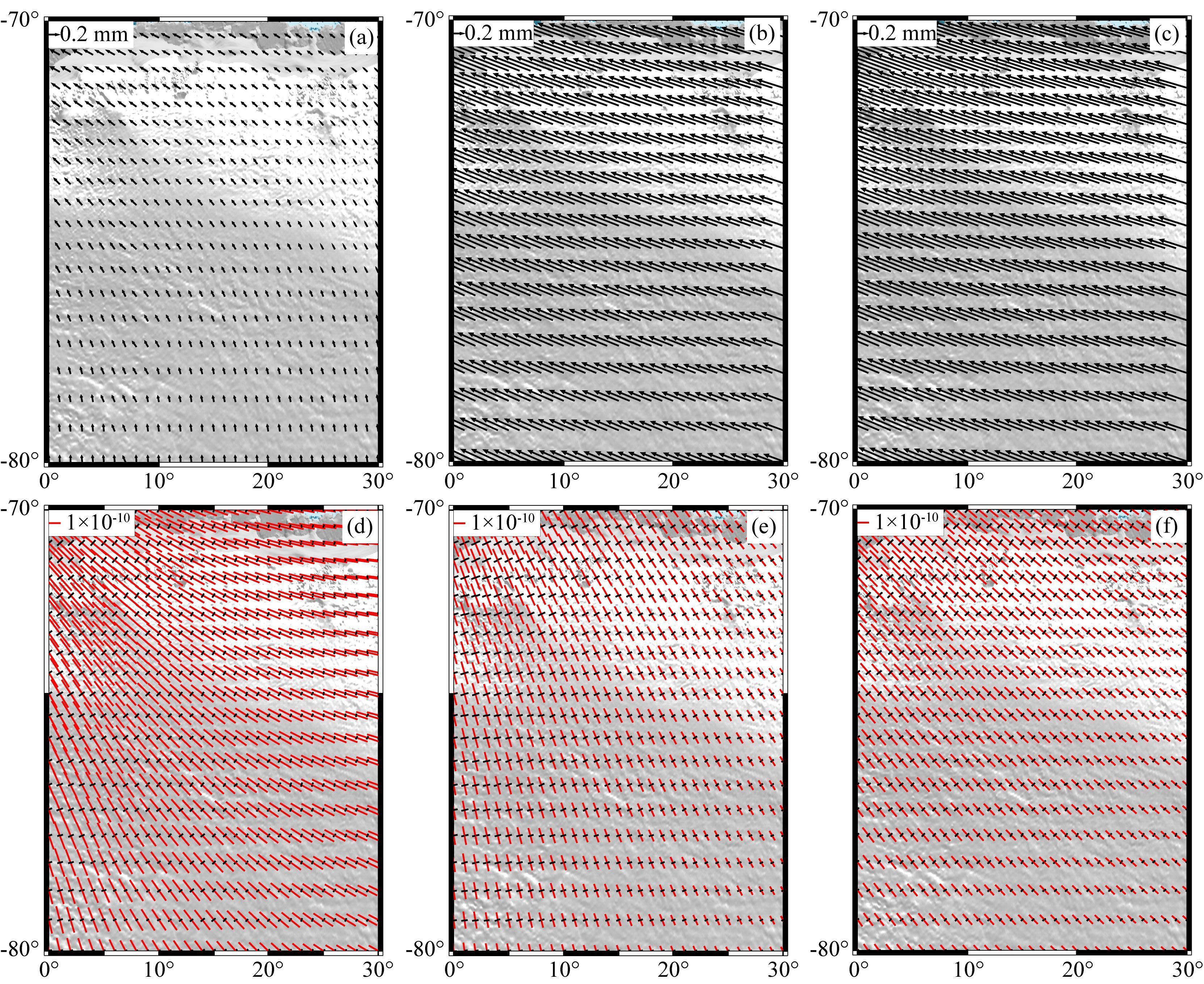
|
图 5 智利Maule地震引起的南极洲区域形变场 (a)-(c) 水平位移场;(d)-(f) 水平主应变场 (红线为主拉应变,黑线为主压应变);(a)、(d) 球面分层模型结果;(b)、(e) 平面分层模型结果;(c)、(f) 平面半空间模型结果. Fig. 5 Deformation near Antarctica (a)-(c) indicate displacement field and (d)-(f) indicate strain field (red lines are principal tensile strain, black lines are principal compression). (a) and (d) based on spherical layered model, (b) and (e) based on plane layered model, (c) and (f) based on plane half-space model. |
2010年Maule地震错动方向近似为西北-东南,相对较大水平位移主要发生在地震断层西北、东南部 (图 6).南美大陆接近一半面积水平位移量级达到0.5 mm,基本上可以被现代GPS观测技术捕捉到,但水平位移较大区域海洋居多,一定程度上影响本次地震同震位移观测.计算近场垂直最大隆升为2.9 m,与Farías等 (2010)根据海岸线上红石灰藻相对位置给出的最大同震垂向位移2.5 m结果较为接近.根据cGPS台站记录到位移 (Vigny et al., 2011),距离震中约3000 km的南美大陆东北部的法属圭亚那水平位移约为1 mm,南美大陆最南端南巴塔哥尼亚固定台站垂直位移小于1 mm,与计算吻合较好,也反映了本文选取滑动模型在远场具有合理性.总体上,远场垂直位移相对较小,约0.1 mm量级,并表现出正负相间的同心圆样式.

|
图 6 2010年智利地震引起的全球同震位移场等值线图 (单位mm) (a) 水平位移;(b) 垂直位移. Fig. 6 Contour lines of co-seismic displacements caused by the 2010 Maule earthquake (unit:mm) (a) Horizontal displacements; (b) Vertical displacements. |
地震发生时应变能释放,产生应力降,根据应力降可以了解区域的应力加/卸载状态.地震引起的15 km深度东西向正应力、南北向正应力和水平剪应力变化对智利和阿根廷中部影响均在10 kPa量级 (图 7a-7c).安第斯地区年应变率在10-8~10-7数量级 (Khazaradze and Klotz, 2003),上地壳的弹性模量估计为70 GPa (Wortel and Cloetingh, 1983), 根据弹性假设东西向压应力年增长量约为0.7~7 kPa,Allmendinger等 (2006)估计阿根廷的应变率约为智利高应变区0.2倍,近似取阿根廷东西向压应力年增长量为1 kPa,本次地震造成阿根廷中部约5~10年构造挤压应力释放、阿根廷北部和南部1~5年构造压应力积累.

|
图 7 同震应力变化 (a)、(d) 东西向正应力变化;(b)、(e) 南北向正应力变化;(c)、(f) 水平剪应力变化. (a)-(c) 考虑横向非均匀介质和地形;(d)-(f) 采用PREM分层介质、不考虑地形;(g)-(i) 为二者差值. Fig. 7 Co-seismic stress change (a), (d) E-W normal stress; (b), (e) S-N normal stress; (c), (f) Horizontal shear stress. Stress change (a)-(c) based on laterally heterogeneous earth model including topography; stress change (d)-(f) based on layered spherical earth model; (g)-(i) stress change difference between 2 models. |
安第斯俯冲带地区三维构造复杂,介质横向非均匀性、海陆地形差异对同震应力降的影响不可忽视.计算区域内地壳厚度变化剧烈,大陆地壳厚度最大70 km, 而洋壳厚度小于10 km,计算深度15 km在大洋已经深入到地幔,在安第斯大陆对应于上、中地壳,必然存在横向上介质性质的巨大差异,此外该区海陆地形起伏亦十分剧烈.作为对比,不考虑介质非均匀性和地形起伏,以球面分层模型 (以PREM模型给出分层介质参数) 计算得到相同深度应力降 (图 7d-7f),结果显示同震应力降被显著低估.在远场同震东西、南北向应力变化相对误差最高均超过100%,考虑到较远处绝对应力降很低的区域,由于绝对量很小,两种计算得到的相对差别可以非常大.在断层破裂面所处的近场,同震东西向应力变化相对误差最高95.4%,南北向应力变化误差最高90.8%,据图 7g-7i可以看出近场两种模型应力降的绝对差值可以达到10 kPa量级.
3.4 断层面库仑应力变化安第斯山脉西缘为地震多发的板块俯冲带,根据Bird (2003)板块边界数字模型,纳兹卡-南极洲转换断层历史上也发生过许多走滑型地震.Liu等 (2000)根据地质资料认为地壳缩短集中于安第斯山东缘褶皱冲断带,Brooks等 (2011)发现隐伏在玻利维亚安第斯山脉东缘之下一大段断层可能会在一次MW8.7~8.9地震中破裂.因此,本文选取上述地震多发的板块边界、活动断层及被预言将发生破裂断层作为研究对象.
库仑应力变化计算所需断层走向、倾角和可能滑动方向根据USGS工作报告 (Costa et al., 2000; Lavenu et al., 2000) 和文献 (Allmendinger and González, 2010; Veloza et al., 2012) 确定,对多数具有丰富地震资料的断层按照震源机制解平均确定其滑动角,少数没有地震资料断层根据区域主应力方向 (Assumpcao, 1992) 推测其可能滑动方向,表 1给出接收断层信息.
|
|
表 1 接收断层 Table 1 Receiver faults |
据表 1,将同震应力降投影到断层面滑动方向上得到库仑破裂应力变化 (图 8).虽然构造加载方向并不严格沿每条断层滑动方向,仍可粗略估计断层库仑应力变化的等效构造加载时间,安第斯西缘应变率较高构造应力积累率约7 kPa·a-1,安第斯东缘应变率较低构造应力积累率约1 kPa·a-1.Maule地震所在断层 (13号断层),库仑应力变化约为-100 kPa,相当于释放15年构造积累,板片俯冲造成应力积累在这次地震中得到释放,同一位置短期再发生强震可能性不大.与Maule地震紧邻断层 (12、14号断层) 库仑应力变化最大超过100 kPa,Maule北部Illapel地区 (12号断层) 发生了2015年智利MW8.3地震,Illapel地区上一次8级以上地震是1943MW8.2地震,该区8级以上地震复发周期约为80~90年 (Nishenko and Buland, 1987),Illapel地区库仑应力变化相当于15年构造积累,因此Maule地震显著加速了Illapel地震发生.在Maule南部,单侧破裂长度达1000 km的1960年Valdivia MW9.5地震破裂区已50余年未再次发生破裂,该破裂区对应14、15、16号断层,尤其14号断层库仑应力变化达到100 kPa,地震危险性增加.阿根廷境内褶皱冲断带La Dehesa断层 (6号) 和Sierra Chica断层 (7号) 库仑应力变化量级在0.4~1 kPa,相当于0.4~1年构造加载, 另一条走滑断层Liquiñe-Ofqui断层 (8号) 滑动方向和震源错动方向几乎正交,因此库仑应力变化的量级较小.转换断层 (17~21) 库仑应力变化以正值为主约0.4 kPa,约为0.1年构造积累.离震源较远的秘鲁、玻利维亚境内的断层库仑应力的加/卸载作用不明显.
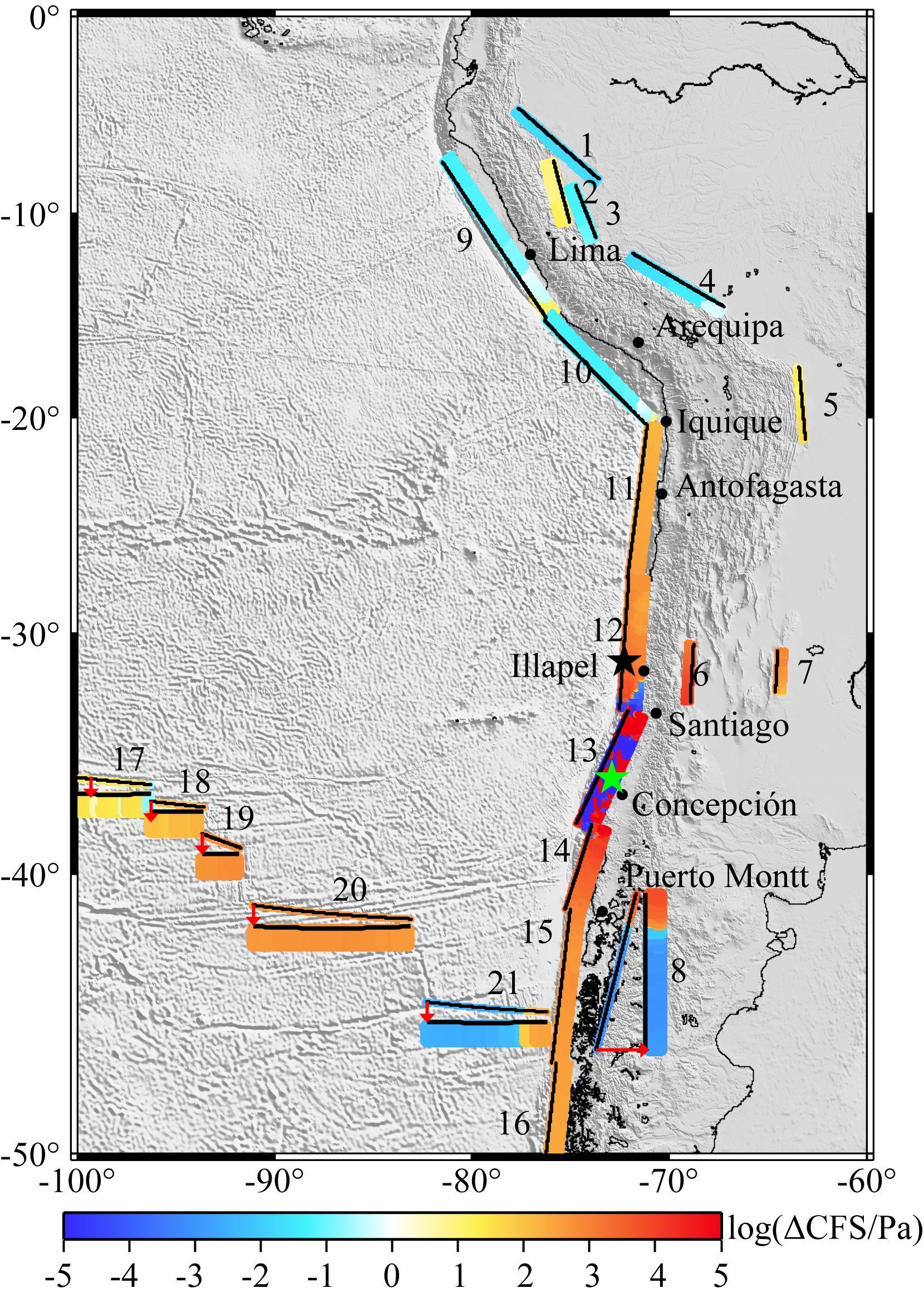
|
图 8 断层面上的库仑应力变化 黑线表示断层地表迹线,黑线上数字代表断层编号;绿色五角星代表 2010年Maule地震;黑色五角星代表 2015年Illapel地震. Fig. 8 Coulomb stress on faults Black line indicates surface trace of fault, number indicates fault number; Green star indicates 2010 Maule earthquake; Black star indicates 2015 Illapel earthquake. |
在破裂面未知情况下常以最优破裂方向投影库仑应力变化解释余震分布,预测后续地震活动 (King et al., 1994).最优破裂方向计算需知道区域应力场,本文区域应力场按照Luttrell等 (2011)反演的Maule地震破裂区偏应力场确定,即超过静岩压部分最大水平偏应力27 MPa (垂直于海沟方向NE)、最小水平偏应力15 MPa (平行于海沟方向NE),垂直偏应力0 MPa.为了形象表示计算得到的最优破裂方向,我们采取震源球方式表示,最优破裂方向基本上为逆冲型 (图 9a黑色震源球).最优破裂方向计算依赖于区域应力场和同震应力降叠加,应力降量级低于区域应力场,因此最优破裂方向表现为逆冲型较为合理.

|
图 9 库仑应力变化与余震空间分布 (a) 黑色沙滩球指示最优破裂方向,红色沙滩球指示余震的震源机制; (b) 投影到主震破裂面的库仑应力变化; (c) 投影到最优破裂方向的库仑应力变化. Fig. 9 Coulomb stress change and the spatial distribution of the aftershock (a) Black beach balls indicate the optimal planes, red beach balls indicate aftershocks; (b) Coulomb stress change on the actual fault planes; (c) Coulomb stress change on the optimal planes. |
由于后续陆续发生强余震会改变应力分布情况,在此仅讨论主震后一个月内面波震级大于4级的余震,数据来源于USGS (http://neic.usgs.gov/[2015-10-20]),其中181条数据 (图 9a红色震源球) 具有明确震源机制解,且多数为逆冲型,与代表最优破裂方向的黑色震源球吻合较好 (图 9a),说明本文采用区域应力场有一定合理性.部分余震为正断或走滑,和按照最优破裂方向给出的断层破裂类型不完全一致.原因如下:(1) 有些余震可能发生在隐伏的先存断层上,接收断层不能取为最优破裂方向;(2) 实际的区域应力场远比本文采用的均匀应力场复杂.
余震平均深度约30 km,因此计算深度取为30 km,投影到主震破裂面的库仑应力变化显示约63.4%余震落在库仑应力变化大于库仑应力触发阀值 (Harris, 1998)10 kPa区域 (图 9b),投影到最优破裂方向的库仑应力变化显示70.9%余震落在库仑应力变化大于10 kPa区域 (图 9c).如果介质参数采用PREM模型且不考虑地形,投影到主震破裂面和最优破裂方向的库仑应变变化显示,分别有52.9%和66.2%余震落在库仑应力变化大于10 kPa区域.然而,真实区域应力场并不是如此简单均匀应力场,余震震源机制也有很大不确定性,不同震源模型库仑应力差别也很大 (石耀霖和曹建玲, 2010),如何研究主震对余震序列触发还有很多问题需要解决.
3.5.2 对Pichilemu余震触发作用2010年3月11日在Pichilemu镇附近区域15 min内接连发生了MW6.9和MW7.0两次大的正断型地震,这两个大地震被认为是马乌拉特大地震的余震 (Ruiz et al., 2014),位于主震以北230 km处.这种大的板内地震在智利俯冲区十分罕见,在Pichilemu地区没有历史地壳浅表地震活动记载.Farías等 (2011)认为该区域发育有新生代伸展构造,存在隐伏的倾向SW的正断层,并根据高异常的Vp/Vs认为马乌拉地震产生的应力变化加强了该区流体流通,最终触发了这两个余震.
大地震发生后的大量余震会产生可以观测到的地表位移场,余震会对周围区域的应力场产生扰动 (万永革等,2005).因此对于发生时间相对较晚的MW7.0余震事件,在计算中需计入发生在它之前的MW6.9强余震影响,MW6.9强余震错动方向按照表 2给出,位错大小根据震级-位错经验公式 (Wells and Coppersmith, 1994) 给出.为了考虑流体活动异常造成的孔隙水压变化,分别计算视摩擦系数μ′=0、μ′=0.4和μ′=0.8情况下余震破裂面库仑应力变化.不同视摩擦系数下,两次余震破裂面上库仑应力变化均超过了库仑应力触发阀值0.01 MPa,由此可见本次俯冲带特大地震的应力释放触发了Pichilemu正断型MW6.9和MW7.0余震.
|
|
表 2 两次强余震破裂面上的库仑应力变化 Table 2 Coulomb stress change on 2 strong aftershocks |
本文应用高性能并行有限元方法,建立包含地表地形、Moho面起伏的大规模非均匀椭球地球模型,根据2010年智利Maule特大地震震源破裂分布计算了球坐标系下同震形变场、应力场,以库仑应力变化分析周围断层地震活动性和主震对余震的触发关系.主要得到以下结论.
(1) 地球曲率和层状结构对同震水平位移的影响不可忽略.对于2010年Maule地震,如果不采用球面分层模型,在低纬度远场可能会造成位移和应变量值均被低估,在高纬度远场可能会造成位移被夸大而应变被低估.
(2) 相对较大水平位移主要发生在地震断层的西北和东南部,近场垂直最大隆升为2.9 m,远场垂直位移相对较小,基本上在0.1 mm量级.
(3) 本次地震约造成了阿根廷中部5~10年构造挤压应力释放,阿根廷北部和南部1~5年构造应力积累.如果不考虑介质横向不均匀和地形, 同震应力降被显著低估,断层破裂面近场处同震东西向应力变化误差最高95.4%,南北向应力变化误差最高90.8%.Illapel地区库仑应力变化约10 kPa,相当于15年构造积累,Maule地震加速2015年Illapel地震发生.
(4) 以最优破裂方向投影得到库仑应力变化,经统计70.9%余震落在库仑应力变化大于10 kPa区域.本次特大地震应力释放触发了Pichilemu附近MW6.9和MW7.0两次大余震.
俯冲带地区构造加载强烈,构造运动对地震发生起主导作用,但特大地震引起的同震应力变化不容忽视,同震库仑应力变化使近场周边断层提前或延缓滑动时间约为1~10年量级,而俯冲带大地震的复发周期往往不足百年,因此俯冲带地区大地震引起的库仑应力变化仍然值得重视.
地震破裂过程的复杂性以及不同作者所采用数据、方法的不同,带来了滑动模型反演不确定性,造成同震应力应变计算不确定性.目前公开发表滑动模型差异集中如下:主要滑动区 (以5 m滑动量等值线定义的区域) 范围不一样,远震波形数据反演的模型 (Lay et al., 2010) 滑动区延伸到海沟处,大地测量数据反演的模型 (Tong et al., 2010; Vigny et al., 2011) 主要滑动区停止于5~10 km处,大地测量、地震波形数据联合反演的滑动模型主要滑动区停止于10~20 km (Delouis et al., 2010) 处;不同模型的南部滑动区中心和Arauco Peninsula的相对位置也有所区别,Delouis等 (2010)的模型中心在其北部,Tong等 (2010)的模型中心正好在Peninsula,Vigny等 (2011)的模型中心在其西部.Vigny对不同滑动模型的计算值和近场GPS的吻合程度做了对比,这样的对比具有一定片面性,并未比较远场GPS的吻合程度,例如,本文所选用的Shao等 (2010)的滑动模型与近场GPS的吻合程度虽然不如Tong等包含近场GPS约束给出的滑动模型高,但Shao等 (2010)模型与远场GPS的吻合程度较好且远高于Tong等 (2010)模型,这也是本文选用Shao滑动模型的重要原因.目前尚无模型在反演中同时纳入远、近场GPS约束,例如,根据Vigny等 (2011)文献,Sladen和Owen (2010)仅考虑远场GPS的模型与近场GPS吻合较差,据本文结果仅考虑近场GPS的模型 (Tong et al., 2010) 与远场GPS残差也很大,未来需要利用更详实的远、近场大地测量资料和地震波数据反演滑动模型,在此基础上的计算更趋可靠.
本文工作的意义在于同震应力、应变计算的模型更接近真实地球,考虑地表地形起伏、莫霍面起伏、地球介质横向不均匀性以及地球曲率,给出Maule特大地震同震响应.本文还计算了地表地形起伏和介质非均匀性对近场同震水平和垂直位移的影响,其百分比分别为41%和95%,林晓光和孙文科 (2014)计算日本东北大地震引起的同震位移,发现海山地形剧变处,介质非均匀性和地形效应对水平和垂直位移的影响分别为34%和92%,俯冲带地形起伏较大并具有强介质非均匀性,二者对同震形变的影响不能忽略.本文未定量讨论地球曲率和地球分层结构对库仑应力变化影响,未来还需要更多定量计算.值得注意的是,本文所得地球曲率和分层结构对同震位移场的影响是基于2010年智利Maule地震算例的结果,要得到更具普适意义结论需要做更多工作.此次研究采用线弹性本构,未考虑黏弹弹效应,但黏弹效应只在研究时间大于下地壳、地幔应力松弛的的特征时间时更加重要,本文仅探讨震后较短时间内对地震活动性的影响,黏弹效应可以近似忽略.此外,震源模型的不确定性、孔隙流体对视摩擦系数的影响等因素在未来的工作中需要做进一步考虑.
| Allmendinger R W, Yañez G, Cembrano J. 2006. Instantaneous deformation associated with flat subduction:insights from GPS strain rates and numerical modelling.//XI Congreso Geológico Chileno. Chile, 367-370. | |
| Allmendinger R W, González G. 2010. Invited review paper:Neogene to Quaternary tectonics of the coastal Cordillera, northern Chile. Tectonophysics, 495(1): 93-110. | |
| Amante C, Eakins B W. 2009. ETOPO1 1 arc-minute global relief model:procedures, data sources and analysis. National Geophysical Data Center Publish. | |
| Assumpcao M. 1992. The regional intraplate stress field in South America. J. Geophys. Res., 97(B8): 11889-11903. DOI:10.1029/91JB01590 | |
| Barazangi M, Isacks B L. 1976. Spatial distribution of earthquakes and subduction of the Nazca plate beneath South America. Geology, 4(11): 686-692. DOI:10.1130/0091-7613(1976)4<686:SDOEAS>2.0.CO;2 | |
| Bilek S L. 2010. Invited review paper:Seismicity along the South American subduction zone:Review of large earthquakes, tsunamis, and subduction zone complexity. Tectonophysics, 495(1): 2-14. | |
| Bird P. 2003. An updated digital model of plate boundaries. Geochem. Geophys. Geosyst., 4(3): 1027. DOI:10.1029/2001GC000252 | |
| Brooks B A, Bevis M, Whipple K, et al. 2011. Orogenic-wedge deformation and potential for great earthquakes in the central Andean backarc. Nat. Geosci., 4(6): 380-383. DOI:10.1038/ngeo1143 | |
| Chinn D S, Isacks B L, Barazangi M. 1980. High-frequency seismic wave propagation in western South America along the continental margin, in the Nazca plate and across the Altiplano. Geophys. J. Int., 60(2): 209-244. DOI:10.1111/j.1365-246X.1980.tb04290.x | |
| Costa C H, Dart R L, Ojeda G E, et al. 2000. Map of Quaternary faults and folds in Argentina. US Geological Survey. | |
| Delouis B, Nocquet J M, Vallée M. 2010. Slip distribution of the February 27, 2010 MW=8. 8 Maule earthquake, central Chile, from static and high-rate GPS, InSAR, and broadband teleseismic data. Geophysical Research Letters, 37(17): L17305. | |
| Dong J, Sun W K, Zhou X, et al. 2014. Effects of Earth's layered structure, gravity and curvature on coseismic deformation. Geophys. J. Int., 199(3): 1442-1451. DOI:10.1093/gji/ggu342 | |
| Farías M, Vargas G, Tassara A, et al. 2010. Land-level changes produced by the MW8. 8 2010 Chilean earthquake. Science, 329(5994): 916. DOI:10.1126/science.1192094 | |
| Farías M, Comte D, Roecker S, et al. 2011. Crustal extensional faulting triggered by the 2010 Chilean earthquake:The Pichilemu Seismic Sequence. Tectonics, 30: TC6010. DOI:10.1029/2011TC002888 | |
| Fritz H M, Petroff C M, Catalán P A, et al. 2011. Field survey of the 27 February 2010 Chile tsunami. Pure and Applied Geophysics, 168(11): 1989-2010. DOI:10.1007/s00024-011-0283-5 | |
| Fry B, Chao K, Bannister S, et al. 2011. Deep tremor in New Zealand triggered by the 2010 MW8. 8 Chile earthquake. Geophysical Research Letters, 38: L15306. DOI:10.1029/2011GL048319 | |
| Fu G Y, Sun W K. 2008. Far-field deformation caused by 2004 sumatra earthquake. Journal of Geodesy and Geodynamics (in Chinese), 28(2): 1-7. | |
| Fu G Y, Sun W K. 2012. Effects of earth's lateral heterogeneity on co-seismic gravity changes at deformed earth surface and space-fixed point. Chinese J. Geophys. (in Chinese), 55(8): 2728-2746. DOI:10.6038/j.issn.0001-5733.2012.08.025 | |
| Harris R A. 1998. Introduction to special section:Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res., 103(B10): 24347-24358. DOI:10.1029/98JB01576 | |
| Khazaradze G, Klotz J. 2003. Short-and long-term effects of GPS measured crustal deformation rates along the south central Andes. J. Geophys. Res., 108(B6): 2289. | |
| King G C P, Stein R S, Lin J. 1994. Static stress changes and the triggering of earthquakes. Bull Seismol. Soc. Am., 84(3): 935-953. | |
| Laske G, Masters G, Ma Z T, et al. 2013. Update on CRUST1.0:A 1-degree global model of Earth's crust.//EGU General Assembly Conference Abstracts. Vienna, Austria. | |
| Lavenu A, Thiele R, Machette M N, et al. 2000. Map and database of Quaternary faults in Bolivia and Chile. US Geological Survey.. | |
| Lay T, Ammon C J, Kanamori H, et al. 2010. Teleseismic inversion for rupture process of the 27 February 2010 Chile (MW8.8) earthquake. Geophysical Research Letters, 37(13): L13301. | |
| Lin X G, Sun W K, Zhang H, et al. 2013. A feasibility study of an FEM simulation used in co-seismic deformations:A case study of a dip-slip fault. Terrestrial, Atmospheric and Oceanic Sciences, 24(4): 637-647. | |
| Lin X G, Sun W K. 2014. Effects of topography and local geological structure on computing co-seismic deformation-A case study of the 2011 Japan Tohoku earthquake (MW9.0). Chinese J. Geophys. (in Chinese), 57(8): 2530-2540. DOI:10.6038/cjg20140814 | |
| Liu M, Yang Y Q, Stein S, et al. 2000. Crustal shortening in the Andes:Why do GPS rates differ from geological rates?. Geophysical Research Letters, 27(18): 3005-3008. DOI:10.1029/2000GL008532 | |
| Lorito S, Romano F, Atzori S, et al. 2011. Limited overlap between the seismic gap and coseismic slip of the great 2010 Chile earthquake. Nat. Geosci., 4(3): 173-177. DOI:10.1038/NGEO1073 | |
| Luttrell K M, Tong X P, Sandwell D T, et al. 2011. Estimates of stress drop and crustal tectonic stress from the 27 February 2010 Maule, Chile, earthquake:Implications for fault strength. J. Geophys. Res., 116(B11): B11401. | |
| Ma Z J. 1983. The plate stripe tectonics disclosed by the South American underthrust zone. Journal of Seismological Research (in Chinese), 6(3): 319-325. | |
| Miao M, Zhu S B. 2012. A study of the impact of static Coulomb stress changes of megathrust earthquakes along subduction zone on the following aftershocks. Chinese J. Geophys. (in Chinese), 55(9): 2982-2993. DOI:10.6038/j.issn.0001-5733.2012.09.017 | |
| Nishenko S P, Buland R. 1987. A generic recurrence interval distribution for earthquake forecasting. Bull Seismol. Soc. Am., 77(4): 1382-1399. | |
| Norabuena E, Leffler-Griffin L, Mao A L, et al. 1998. Space geodetic observations of Nazca-South America convergence across the central Andes. Science, 279(5349): 358-362. DOI:10.1126/science.279.5349.358 | |
| Okada Y. 1985. Surface deformation due to shear and tensile faults in a half-space. Bull Seismol. Soc. Am., 75(4): 1135-1154. | |
| Okada Y. 1992. Internal deformation due to shear and tensile faults in a half-space. Bull Seismol. Soc. Am., 82(2): 1018-1040. | |
| Peng Z G, Hill D P, Shelly D R, et al. 2010. Remotely triggered microearthquakes and tremor in central California following the 2010 MW8. 8 Chile earthquake. Geophysical Research Letters, 37(24): L24312. | |
| Pritchard M E, Simons M. 2006. An aseismic slip pulse in northern Chile and along-strike variations in seismogenic behavior. J. Geophys. Res., 111(B8): B08405. | |
| Qu W, Chang H, Shi Y. 2015. Equivalent body force finite elements method and 3-D earth model applied in 2004 Sumatra earthquake.//AGU Fall Meeting.AGU. | |
| Ruiz J A, Hayes G P, Carrizo D, et al. 2014. Seismological analyses of the 2010 March 11, Pichilemu, Chile MW7. 0 and MW6.9 coastal intraplate earthquakes. Geophys. J. Int, 197(1): 414-434. | |
| Shao G F, Li X Y, Liu Q M, et al. 2010. Preliminary slip model of the Feb 27, 2010 MW8.9 Maule, Chile Earthquake. http://www.geol.ucsb.edu/faculty/ji/big_earthquakes/2010/02/27/chile_2_27.html. | |
| Shao Z G, Fu R S, Xue T X, et al. 2008. The numerical simulation and discussion on mechanism of postseismic deformation after Kunlun MS8. 1 earthquake. Chinese J. Geophys. (in Chinese), 51(3): 805-816. | |
| Shi Y L, Zhu S B. 2006. Discussion on method of calculating strain with GPS displacement data. Journal of Geodesy and Geodynamics (in Chinese), 26(1): 1-8. | |
| Shi Y L, Cao J L. 2010. Some aspects in static stress change calculation-Case study on Wenchuan earthquake. Chinese J. Geophys. (in Chinese), 53(1): 102-110. DOI:10.3969/j.issn.0001-5733.2010.01.011 | |
| Simmons N A, Forte A M, Boschi L, et al. 2010. GyPSuM:A joint tomographic model of mantle density and seismic wave speeds. J. Geophys. Res., 115: B12310. DOI:10.1029/2010JB007631 | |
| Sladen A, Owen S. 2010. Preliminary model combining teleseismic and GPS data 02/27/2010 (MW8.8), Chile. http://www.tectonics.caltech.edu/slip_history/2010_chile/prelim-GPS.html. | |
| Sun W K. 1992. Potential and gravity changes caused by dislocations in spherically symmetric Earth models. Bull. Earthquake Res. Inst. Univ.Tokyo, 67(2): 89-238. | |
| Sun W K, Okubo S. 2002. Effects of earth's spherical curvature and radial heterogeneity in dislocation studies-for a point dislocation. Geophysical Research Letters, 29(12): 461-464. | |
| Tong X P, Sandwell D, Luttrell K, et al. 2010. The 2010 Maule, Chile earthquake:Downdip rupture limit revealed by space geodesy. Geophys.Res. Lett., 37(24): L24311. | |
| Veloza G, Styron R, Taylor M, et al. 2012. Open-source archive of active faults for northwest South America. GSA Today, 22(10): 4-10. DOI:10.1130/GSAT-G156A.1 | |
| Vigny C, Socquet A, Peyrat S, et al. 2011. The 2010 MW8. 8 Maule megathrust earthquake of Central Chile, monitored by GPS. Science, 332(6036): 1417-1421. | |
| Wan Y G, Shen Z K, Lan C X. 2005. Study on displacement field generated by aftershocks in Landers seismic fault plane and its adjacent areas. Acta Seismologica Sinica (in Chinese), 27(2): 139-146. | |
| Wang R J, Martín F L, Roth F. 2003. Computation of deformation induced by earthquakes in a multi-layered elastic crust-FORTRAN programs EDGRN/EDCMP. Computers & Geosciences, 29(2): 195-207. | |
| Wells D L, Coppersmith K J. 1994. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull Seismol. Soc. Am., 84(4): 974-1002. | |
| Wortel M J R, Cloetingh S A P L. 1983. A mechanism for fragmentation of oceanic plates.//WatkinsI S, Drake C L. Continental Margin Geology. American Association Petroleum Geologists Memoir. 34:793-801. | |
| Xie Y S, Shang S P, Wei Y, et al. 2012. Effect of the 2010 Chile ocean tsunami on seas surrounding Taiwan. Journal of Xiamen University (Nature Science) (in Chinese), 51(5): 899-902. | |
| Yin Z Q, Han Y B, Podestá R, et al. 2011. South American SLR stations monitoring ground displacement caused by the M8. 8 Chilean earthquake of 2010. Chinese Sci. Bull., 56(8): 738-742. | |
| Zhang B, Zhang H, Shi Y L. 2015. Equivalent-body force approach on modeling elastic dislocation problem using finite element method. Chinese J. Geophys. (in Chinese), 58(5): 1666-1674. DOI:10.6038/cjg20150518 | |
| 付广裕, 孙文科. 2008. 2004年苏门答腊地震引起的远场形变. 大地测量与地球动力学, 28(2): 1–7. | |
| 付广裕, 孙文科. 2012. 地球横向不均匀结构对地表以及空间固定点同震重力变化的影响. 地球物理学报, 55(8): 2728–2746. DOI:10.6038/j.issn.0001-5733.2012.08.025 | |
| 林晓光, 孙文科. 2014. 地形效应和局部地质构造对计算同震形变的影响--以2011年日本东北大地震 (MW9.0) 为例. 地球物理学报, 57(8): 2530–2540. DOI:10.6038/cjg20140814 | |
| 马宗晋. 1983. 南美俯冲带显示的板条构造. 地震研究, 6(3): 319–325. | |
| 缪淼, 朱守彪. 2012. 俯冲带上特大地震静态库仑应力变化对后续余震触发效果的研究. 地球物理学报, 55(9): 2982–2993. DOI:10.6038/j.issn.0001-5733.2012.09.017 | |
| 邵志刚, 傅容珊, 薛霆虓, 等. 2008. 昆仑山MS8.1级地震震后变形场数值模拟与成因机理探讨. 地球物理学报, 51(3): 805–816. | |
| 石耀霖, 朱守彪. 2006. 用GPS位移资料计算应变方法的讨论. 大地测量与地球动力学, 26(1): 1–8. | |
| 石耀霖, 曹建玲. 2010. 库仑应力计算及应用过程中若干问题的讨论--以汶川地震为例. 地球物理学报, 53(1): 102–110. DOI:10.3969/j.issn.0001-5733.2010.01.011 | |
| 万永革, 沈正康, 兰从欣. 2005. 兰德斯地震断层面及其附近余震产生的位移场研究. 地震学报, 27(2): 139–146. | |
| 谢燕双, 商少平, 魏艳, 等. 2012. 2010年智利强震引发的海啸对台湾周边海域的影响. 厦门大学学报 (自然科学版), 51(5): 899–902. | |
| 尹志强, 韩延本, PodestáR, 等. 2011. 南美SLR监测的2010年智利8.8级大地震产生的地面位移. 科学通报, 56(2): 142–146. | |
| 张贝, 张怀, 石耀霖. 2015. 有限元模拟弹性位错的等效体力方法. 地球物理学报, 58(5): 1666–1674. DOI:10.6038/cjg20150518 | |
 2017, Vol. 60
2017, Vol. 60


