2. 海底科学与探测技术教育部重点实验室, 青岛 266100
2. Key Lab of Submarine Geosciences and Prospecting Techniques of Ministry of Education, Ocean University of China, Qingdao 266100, China
大地电磁测深法是一种重要的地球物理勘探方法,它利用地球上广泛分布的太阳风和全球闪电等天然电磁场作为场源,接收频率的电磁信号,以达到探测深部地质构造和地球内部电性结构的目的 (李金铭, 2005).随着大地电磁理论研究的不断深入,以及计算机和电子仪器的飞速发展,大地电磁测深法在仪器研制、正演模拟和反演解释等方面都取得了显著的成果,已经成为一种成熟的频率域测深方法 (魏文博, 2002).
过去几十年里,许多学者提出了多种大地电磁场数值模拟方法.Dmitriev (1969)和Weidelt (1975)用积分方程法模拟大地电磁场响应.Jones和Pascoe (1971)、Mackie等 (1993)用有限差分法求解大地电磁场边值问题.Coggon (1971)、Wannamaker等 (1986)和徐世浙 (1994)等将有限单元法引入到地电场数值模拟计算中.边界单元法是在有限单元法基础上发展起来的一种数值方法,对于地下单个异常体和起伏地形等简单模型,边界单元法的计算量明显小于有限单元法 (Xu and Zhao, 1987, 徐世浙, 1995).自适应非结构化有限元能够更好地模拟起伏地形和倾斜界面等复杂地电模型,近年来该方法在二维和三维电磁场数值模拟中取得了很好的应用效果 (Key and Weiss, 2006;Li and Key, 2007;Li and Pek, 2008;Li and Dai, 2011;Everett, 2012;赵慧等, 2014).由于受到单元和网格的制约,当模拟复杂地电构造时,有限差分法和有限元法暴露出了自身的一些不足,如网格单元有时会出现畸变, 从而影响数值解的精度等 (Liu and Gu, 2005; 刘欣, 2011).
无网格法 (Meshfree or Meshless Method,MM) 或无单元法 (Element Free Method,EFM),是在有限差分法和有限单元法基础上发展起来的针对网格制约问题而提出的一类新的数值方法.该类方法利用模拟问题域内所有节点的排列关系和权函数 (或核函数),构成场函数的近似表达式.其近似函数仅仅建立在一系列离散点的相对空间位置上,不需要网格信息,克服了有限差分法和有限单元法对网格的依赖性,使问题分析的前处理步骤变得简单 (Liu and Gu, 2005; 刘欣, 2011).
目前,已经发展出了十几种基于不同公式推导方法、不同函数近似方法和不同域表示法的无网格方法 (Lucy, 1977;Nayroles et al., 1992;Babuska and Melenk, 1995;Oñate et al., 1996),并且在很多领域得到了应用.在局部边界积分方程的基础上,Atluri和Zhu (1998)提出了无网格局部Petrov-Galerkin法 (Meshfree Local Petrov-Galerkin method,MLPG),MLPG不仅是一种方法,而且是一个概念和框架.在该框架下,可以使用不同的插值函数和试函数.该方法的基本思想是在局部域内满足平衡方程的Galerkin积分形式,且由于其数值积分只在子域上进行,不需要背景网格来辅助积分,是一种真正的无网格方法.
Wittke和Tezkan (2014)导出了二维大地电磁场MLPG局部积分域内的松弛弱式形式,实现了MLPG法二维大地电磁正演,他们指出MLPG方法和有限元方法的收敛速度一致,其计算效率和精度与节点总数及径向基函数的参数选择有关.他们采用节点赋予物性参数的方法进行正演模拟,要求节点严格位于模型内部物性分界面上.模拟计算结果表明,对于简单模型,MLPG无网格法模拟结果与结构有限元方法所得到的结果基本一致,相差很小;而对于电导率局部连续变化的复杂地电模型,MLPG无网格方法比采用高次插值的结构有限元方法更具优势.
本文利用复合2次径向基函数进行插值,推导出了模型空间内任意一点场值的形函数表达式,并给出了二维大地电磁场MLPG局部积分域内的松弛弱式形式及其离散形式.为了克服传统无网格方法节点必须严格位于物性分界面上的限制,本文提出了采用高斯点赋予物性参数的方法,极大地提高了MLPG无网格方法的适用性.本文模拟了二维海洋地电模型的大地电磁场响应,并与有限元结果进行了比较,验证了算法的正确性.我们模拟了含有弯曲物性分界面地电模型的大地电磁场响应,讨论了不同离散网格对MLPG无网格法模拟结果的影响,并与结构有限元法结果进行了对比, 结果表明MLPG无网格法模拟结果受离散网格影响较小.最后利用MLPG无网格法不受网格限制的特点,用非均匀网格模拟了起伏地形下海洋地电模型的大地电磁场,并详细分析了海洋地堑和地垒对大地电磁场响应的影响.
2 径向点插值 (RPIM) 形函数在求解大地电磁场边值问题的近似解时,通常用形 (试) 函数近似描述未知场函数,从而建立电磁场边值问题的离散方程.在有限元法和有限差分法中,形 (试) 函数是通过单元上固定节点的相对位置采用插值方法构造的,称为固定单元插值 (Liu and Gu, 2005).而在MLPG无网格方法中,通常使用不依赖于网格的插值方法.
点插值方法 (Point Interpolation Methods, PIM) 是一种利用级数形式表示近似函数的方法.根据基函数的类型,点插值方法的形函数可以分为两类,即多项式基函数和径向基函数.对于一组给定的节点,当多项式基函数选取不当时,多项式基点插值会产生奇异的力矩矩阵 (Liu and Gu, 2005).为了避免多项式基点插值所引起的奇异性问题,本文采用径向基点插值方法 (Radial Point Interpolation Methods, RPIM).
假设计算点A (x, y)处的场值为u (A),可以用添加了多项式的RPIM函数表示为
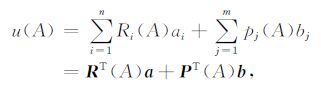
|
(1) |
式中,Ri(A)为径向基函数,pj(A)为空间坐标中的多项式,n和m分别为径向基函数和多项式基函数的个数,ai和bj为待定常数.在二维问题中,径向基函数Ri(A)仅是计算点A (x, y)和已知节点Ai(xi, yi)之间距离变量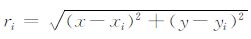
本文采用复合2次径向基函数Ri(x, y)=(ri2+(αcdc)2)q,这里αc和q为形状参数,且αc≥0.dc是与计算点A (x, y)的局部支持域内节点间距有关的特征长度,通常为局部支持域内节点的平均距离 (Liu and Gu, 2005;刘欣, 2011).多项式基函数pj(A)有一次或二次基函数,本文采用一次基函数.
为了确定常数ai和bj,需要形成以计算点A (x, y)为中心的支持域.假设支持域内n个节点的坐标和场值分别为Ai(xi, yi)和ui(i=1, …, n),支持域内所有节点处的场都满足方程 (1),可以得到由n个线性方程构成的方程组为
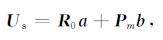
|
(2) |
式中,Us是由n个节点处的场值构成的场值向量,a和b为待定常数向量,R0和Pm分别为径向基函数矩阵和多项式矩阵.
方程 (2) 为n阶线性方程组,但它含有n+m个未知数,故而需利用以下约束条件添加m个方程,公式为

|
(3) |
联立方程 (1) 和 (3),可以得到矩阵方程为
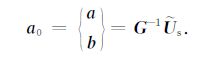
|
(4) |
其中:
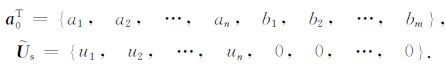
|
由方程式 (4),可得

|
(5) |
将式 (5) 代入式 (1),可得

|
(6) |
式中,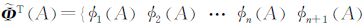
对应于支持域内n个节点的已知位移向量,RPIM形函数可以表示为
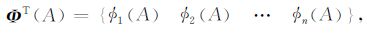
|
(7) |
则点A (x, y)处的场值可由下式得到
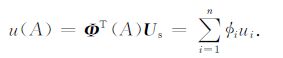
|
(8) |
由于径向基函数的特性,若式 (2) 中的R0表示关于x或y方向导数的矩阵,则可以利用同样的方法求得u (A)关于x或y方向的导数.
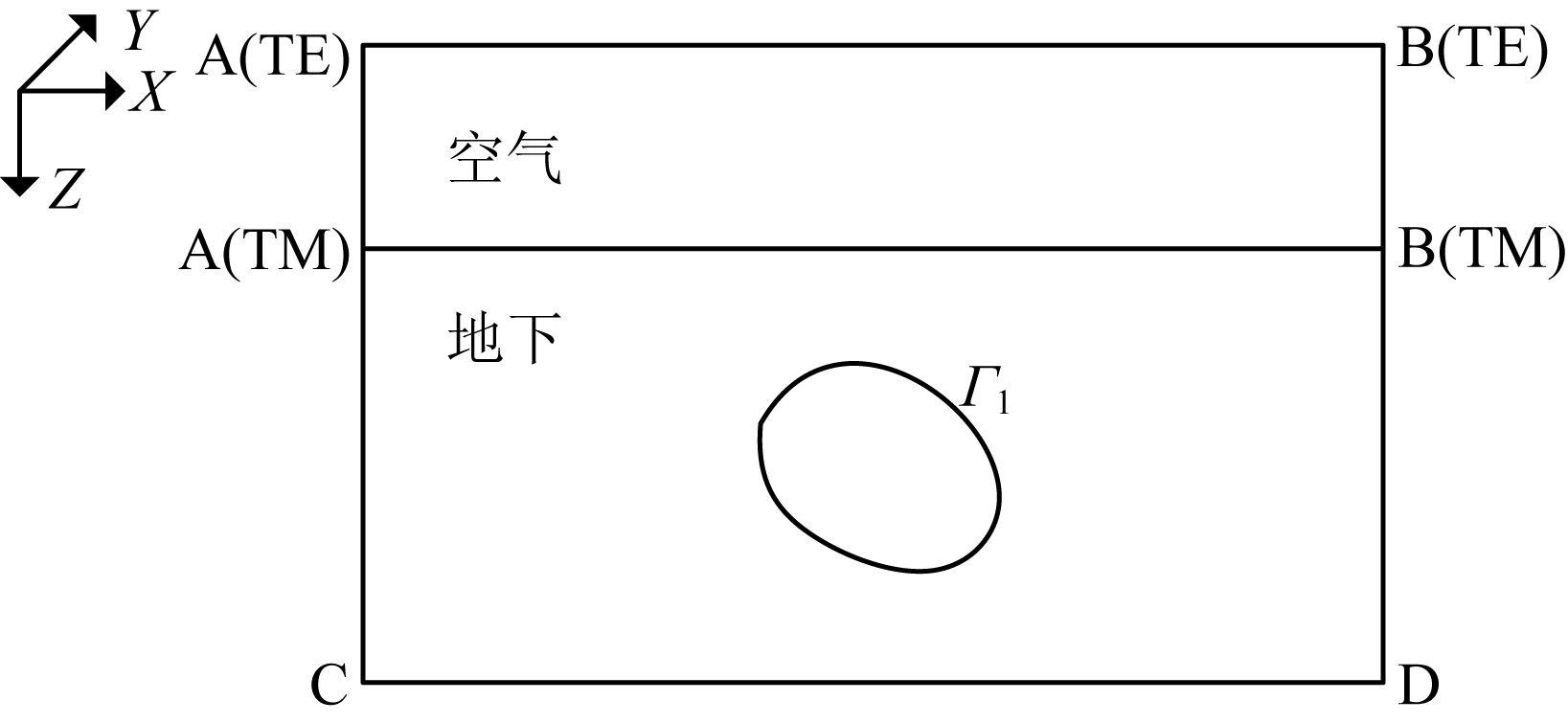
3 大地电磁场边值问题的局部弱式形式考虑二维大地电磁场地电模型 (图 1),假设y轴为地质体走向方向,x轴垂直于地质体走向方向,z轴垂直于地面指向地下.则二维大地电磁场的边值问题可以归纳为 (徐世浙, 1994):
|
图 1 二维大地电磁研究区域示意图 Fig. 1 Schematic illustration of 2-D magnetotelluric modeling domain |
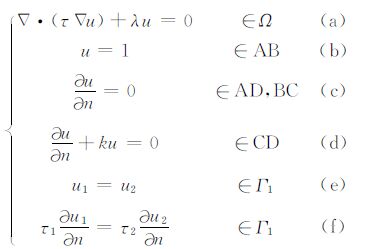
|
(9) |
其中,TE模式时,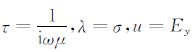
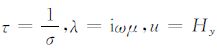
利用加权余量法,可以导出场函数u所满足的局部弱式形式为
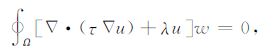
|
(10) |
式中,w为权函数.本文采用具有3阶连续性的四次样条插值权函数,公式为
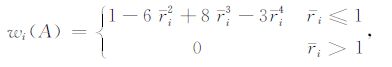
|
(11) |
其中,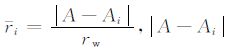
利用公式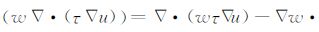
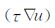
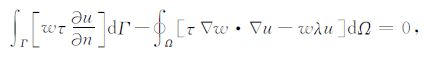
|
(12) |
式中,n表示边界Γ的外法向方向.
对于一个特定节点i,定义局部积分域Ωsi和权函数域Ωwi,Γsi为局部子域的边界 (图 2),则该节点上的场值ui满足:

|
(13) |

|
图 2 MLPG法的问题域、局部子域、权函数域、支持域示意图 Fig. 2 Schematic illustration of the problem domain, integral domain, weight function domain and support domain of MLPG |
由于每个节点的局部积分域范围都不得超过模型边界,于是对于某些节点来说,局部积分域的部分边界可能会落在模型外边界上,如图 2所示.结合如图 1所示二维大地电磁场模拟区域,式 (13) 可以改写成为
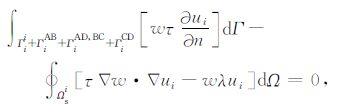
|
(14) |
其中,Γii表示未落在模型外边界上的局部积分域边界;ΓiAB, ΓiAD, BC, ΓiCD分别表示落在AB, AD, BC, CD模型外边界上的局部积分域边界.若局部积分域没有边界落在模型区域边界上,则ΓiAB, ΓiAD, BC, ΓiCD不存在.
将式9(c) 和 (d) 代入式 (14),可得
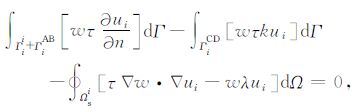
|
(15) |
上式中的线积分和面积分可以用高斯数值积分法计算求得.假设在面积分域内和线积分段上分别分布有gs和gl个高斯点,S和L分别为面积分域的面积和线积分段的长度.假定Aj为面积分域内高斯点所对应的积分系数 (j=1, …, gs),Bk为线积分段上高斯点所对应的积分系数 (k=1, …, gl),wjs和wkl分别表示面积分域内和线积分上高斯点所对应的权值,则式 (15) 可以离散成为
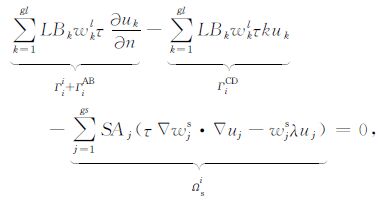
|
(16) |
其中,uj,uk分别为面积分域内和线积分段上高斯点处的场值.
类似地,每个高斯点处的场值及其偏导数的形函数可以用以它为中心的支持域内节点处的场值表示.假设每个高斯点的支持域含有m个节点 (每个高斯点所形成的支持域内节点个数不一定相同),则式 (16) 可以写为
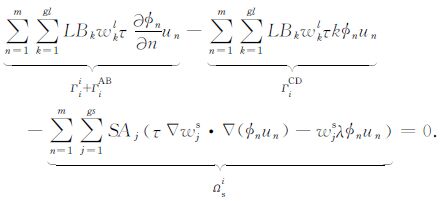
|
(17) |
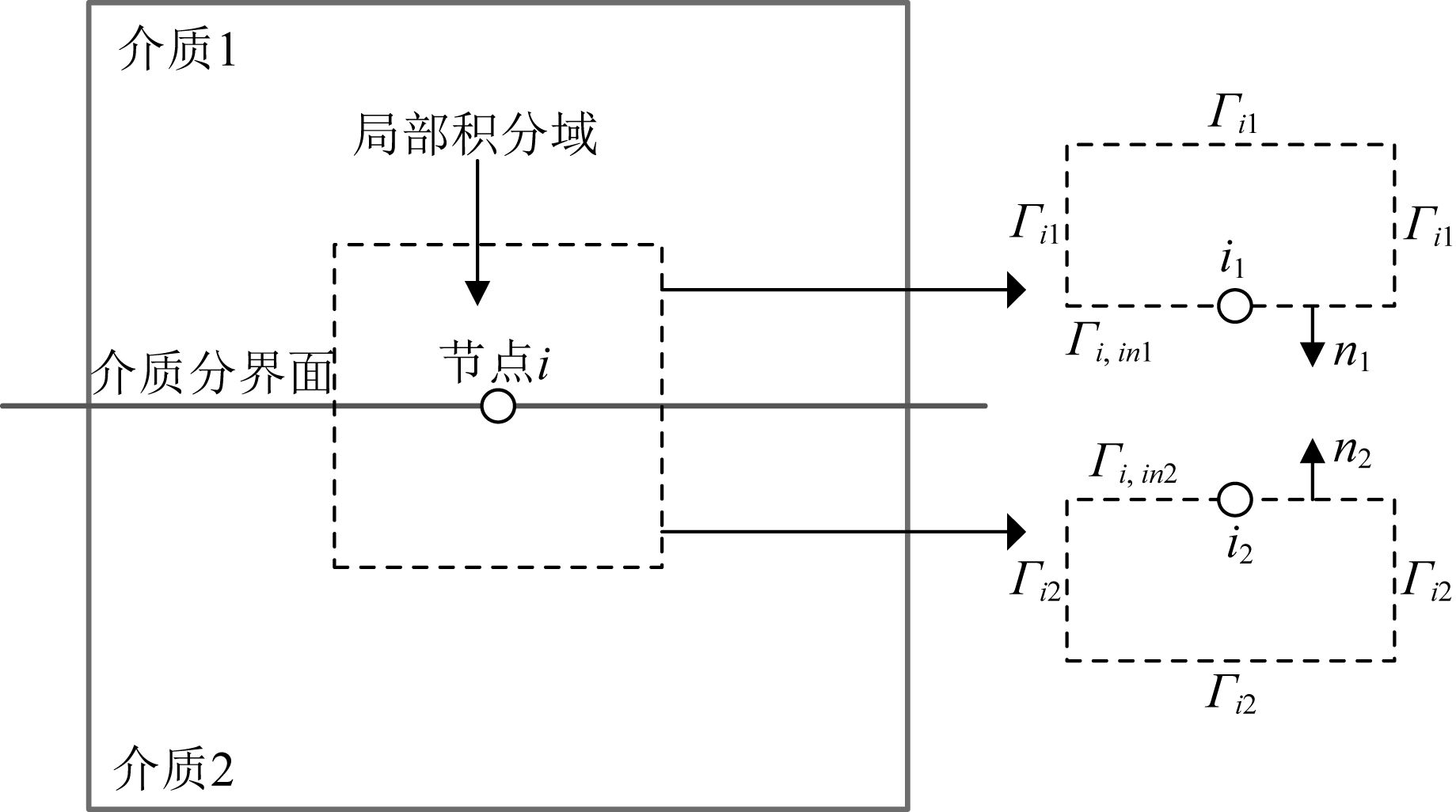
若当某个节点位于介质分界面处时 (图 3),需要将局部积分域沿着介质分界面剖分成两个小的积分域 (Wittke and Tezkan, 2014),每个小积分域都满足式 (15).于是可知,介质分界面上节点i处场值ui仍然满足式 (15).故大地电磁边值问题的MLPG局部弱式形式的内边界条件依然自动满足.若将式 (15) 离散成式 (17) 时,位于不同介质内高斯点应该采用其所处的介质内部的物性参数.
|
图 3 位于介质分界面上的节点局部积分域分解图 Fig. 3 Schematic illustration of the integral domain decomposition when a node is located on an material interface |
为了简化起见,取权函数域范围与局部积分域范围相同,则在局部积分域边界Γii上权函数w取值为零,则式 (15) 可以写成为

|
(18) |
或表示成向量形式为
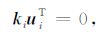
|
(19) |
式中,uiT=(u1u2…un) 为由节点i处局部积分域中所有高斯点局部支持域所包含的节点场值所构成的向量,ki为每个节点场值所对应的系数向量.
类似地,可以得到模型区域内每个节点与其周围节点场值间的关系向量,再经过向量扩展与重排,可以得到总体刚度矩阵k为
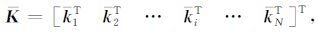
|
(20) |
其中,ki为ki的扩展向量.于是,得到方程组为
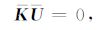
|
(21) |
代入边界条件,修正总体刚度矩阵和方程右端项,可得

|
(22) |
由于MLPG无网格法某些节点形成的局部积分域可能包含多个介质的信息,所以最终的总体刚度矩阵是非对称矩阵,它只能使用非零值全压缩存储方案贮存.用直接方法 (如MUMPS) 解线性方程组 (22),可以得到每个节点的场值.
因为传统MLPG无网格方法需要根据式 (6) 计算每一个高斯点处的场值,于是高斯点越多,形成总体刚度矩阵所耗费的时间越长.但是对于采用均匀结构网格的MLPG无网格方法,一旦确定了积分域大小和高斯点个数,除了边界上的节点之外,模型内部的节点与其积分域内高斯点的相对位置、每个高斯点的形函数和权函数都是相对确定的,故而并不需要对每个高斯点解方程求得形函数,这样可以极大地提高计算速度.总体刚度矩阵的大小只与节点个数有关,高斯点的个数与所需内存大小无关.
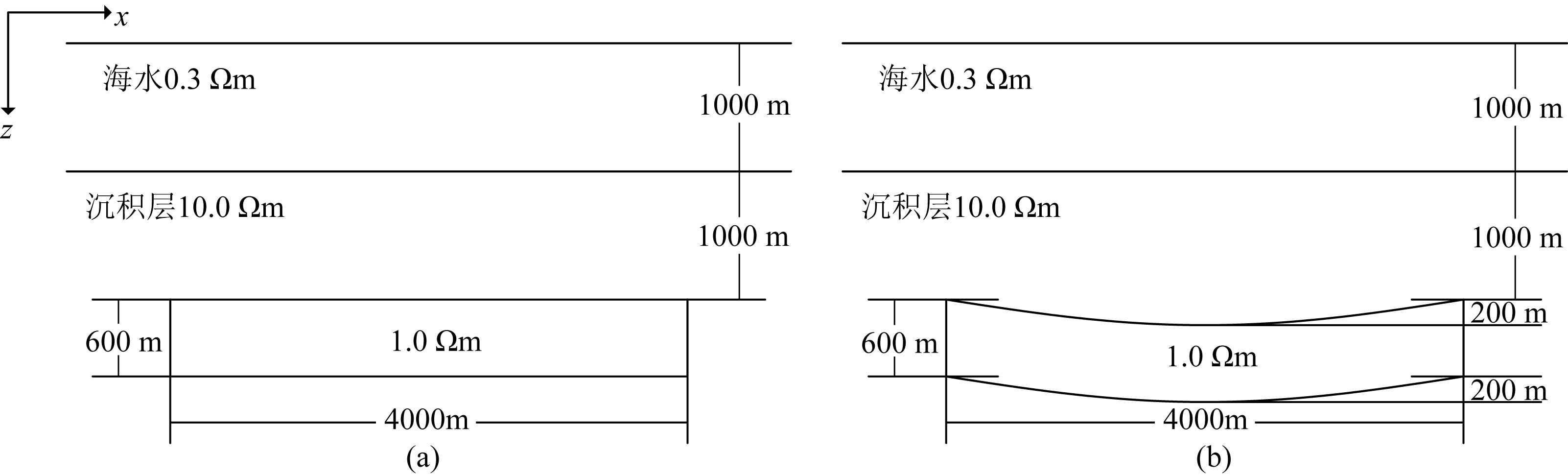
4 算法验证及模型计算为了验证前述数值方法和程序的正确性及有效性,构造如图 4a所示的二维海洋地电模型.假定海水厚度为1000 m,海水电阻率为0.3 Ωm.在电阻率为10.0 Ωm的海底地层中,嵌入一个厚度为600 m、长度为4000 m、电阻率为1.0 Ωm的矩形低阻异常体,其顶界面距离海底1000 m.大地电磁接收站位于海底,间距为1000 m.
|
图 4 二维海洋地电模型示意图 Fig. 4 Sketch showing two 2D conductivity models |
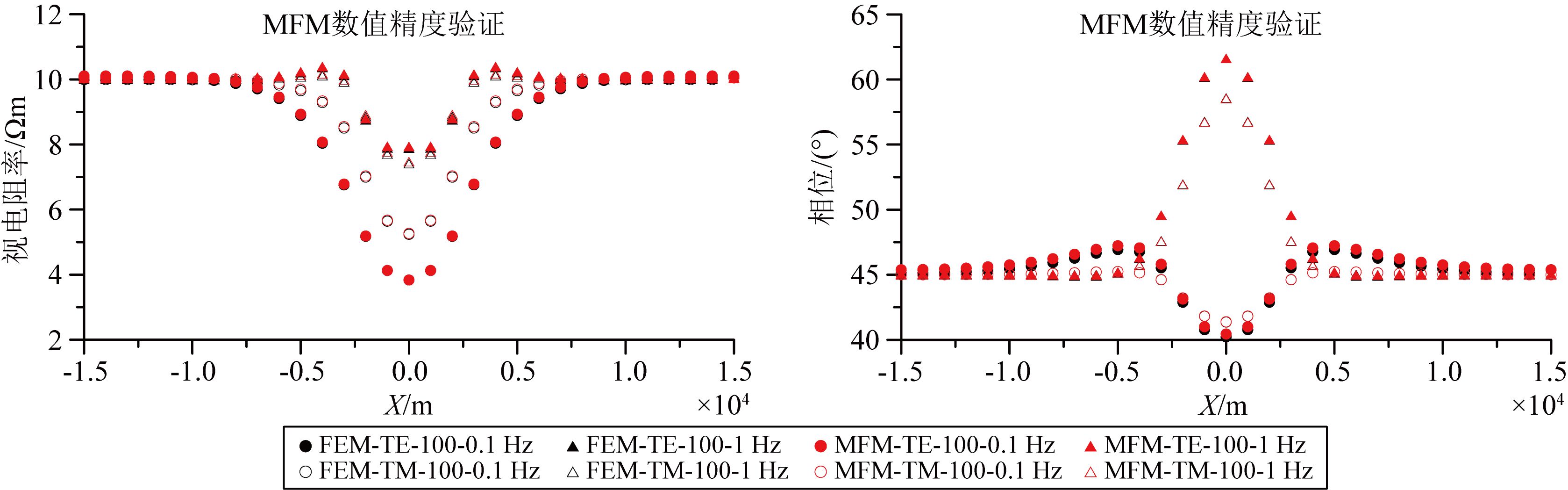
用本文提出的MLPG无网格法和结构化矩形网格有限元法 (徐世浙, 1994) 分别计算大地电磁场视电阻率和相位,并进行对比分析.两种方法均使用100 m×100 m的均匀网格.计算频率为1.0 Hz和0.1 Hz.由图 5可以看到,MLPG无网格法的数值解和矩形网格有限元法数值结果吻合得非常好.在x=0 m处,两种方法得到的视电阻率和相位均有最大相对误差,它们分别为0.5%和0.2%.
|
图 5 MLPG无网格法数值解与矩形网格有限元数值解的对比 Fig. 5 Comparison between the numerical solutions obtained by the MLPG and those by the FEM |
我们知道,数值模拟结果的精度取决于网格的离散情况.对于起伏地形、倾斜或弯曲物性分界面等复杂地电模型,构造合理可靠的离散网格通常是一个耗时的工作.依靠研究者的经验设计网格往往存在不确定性.而MLPG无网格法摆脱了网格的限制,不再利用预先设定的单元进行插值,故而较易于模拟复杂地电模型.
图 4b是含有弯曲物性分界面的二维海洋地电模型,它与前述二维模型 (图 4a) 类似,仅有的差别是二维低阻异常体的上下界面为向下弯曲的界面,曲面的最低点距离水平界面的高度为200 m.
利用MLPG无网格法和结构化矩形网格有限元法两种数值方法模拟图 4b所示模型的大地电磁场响应.MLPG无网格法和结构化矩形网格有限元法都使用相同的三套网格:100 m×100 m,200 m×200 m和250 m×250 m网格.计算频率仍为1.0 Hz和0.1 Hz.
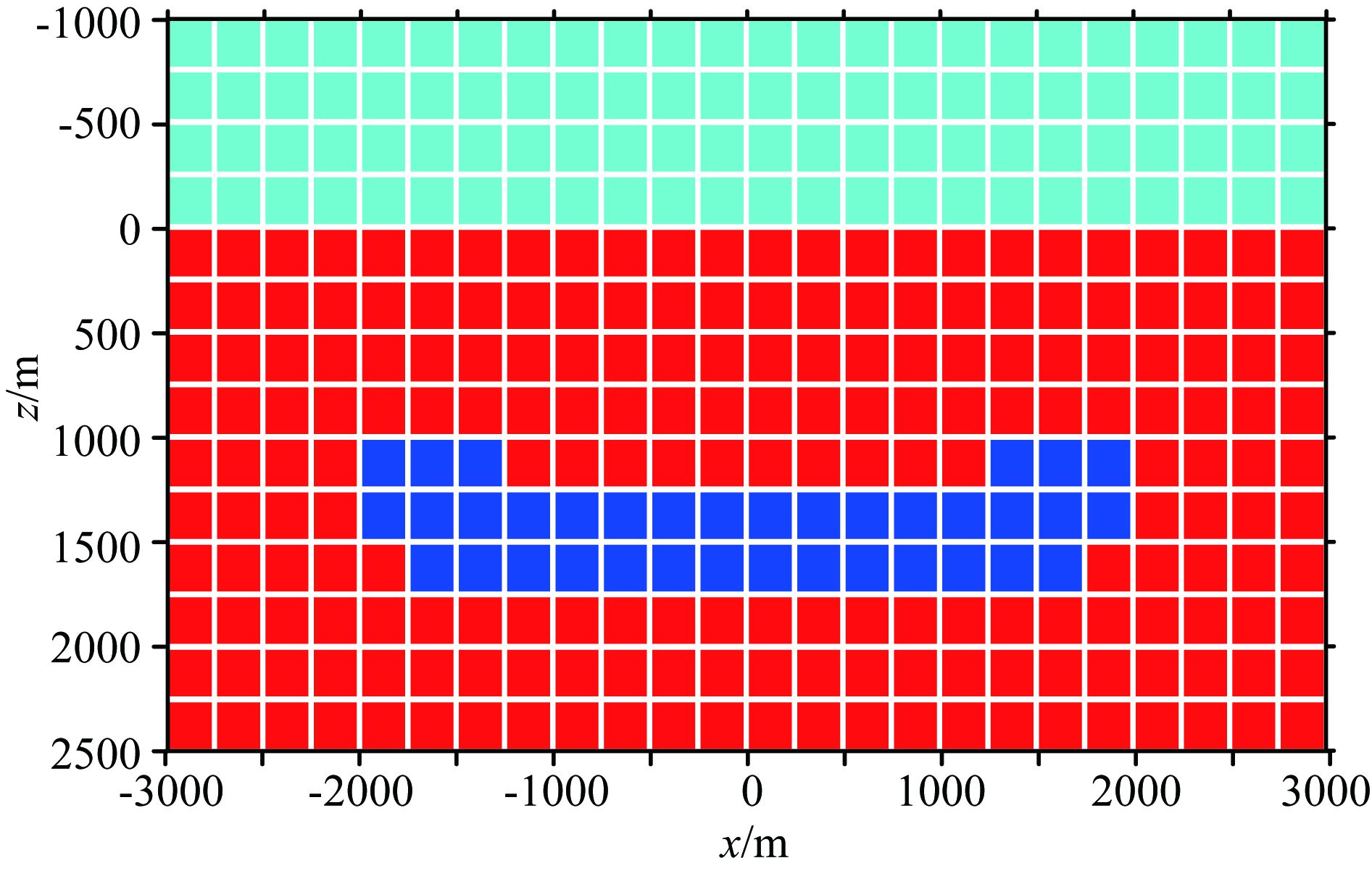
图 6-图 11分别为MLPG无网格方法和结构化网格有限元方法在100 m×100 m、200 m×200 m和250 m×250 m网格下对图 4b模型的剖分示意图.可以看到,网格越大,两种方法对模型的剖分就越粗糙.对于250 m×250 m网格,结构网格有限元方法对于异常体的顶边界和底边界的刻画都出现了偏差;而MLPG无网格方法,由于采用高斯点赋予物性参数,所以相对于结构网格有限元方法,在节点网格不合理的情况下,也能较好的刻画异常体边界.
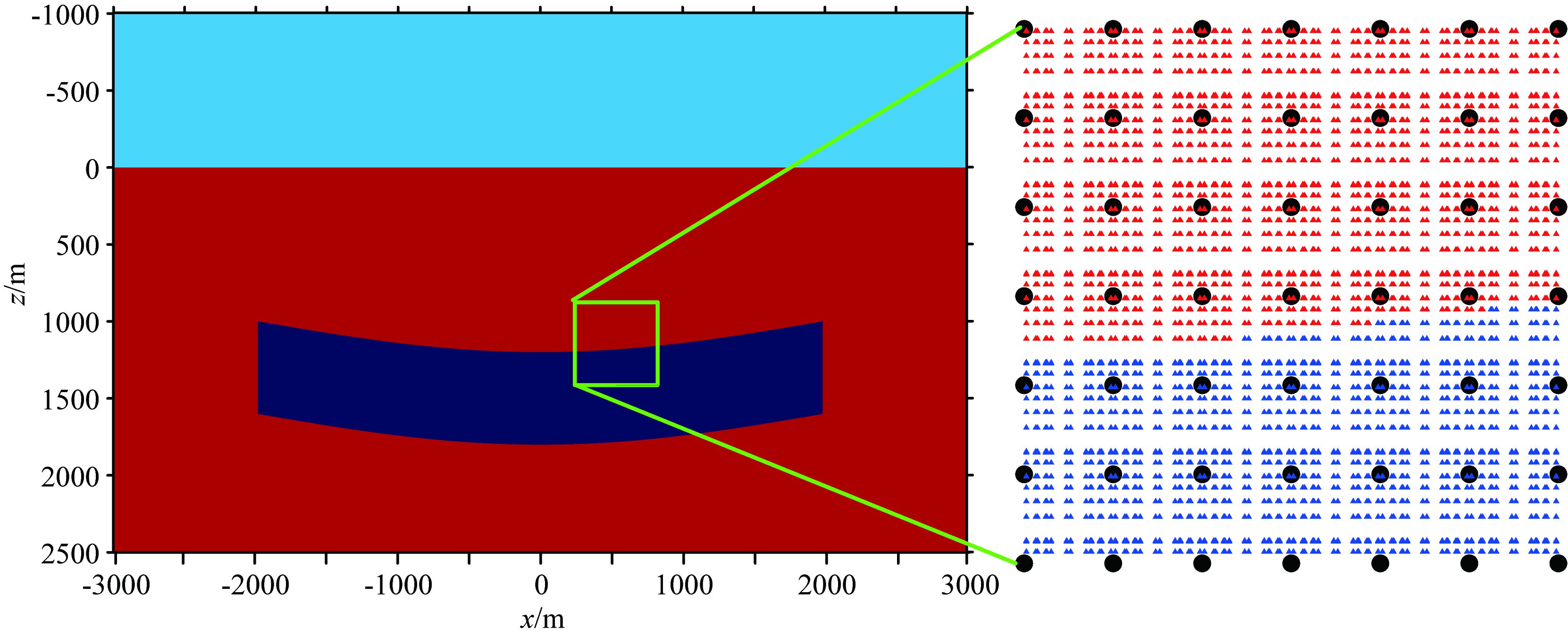
|
图 6 MLPG无网格法100m网格距时节点和高斯点的分布 ●表示节点,▲表示高斯点. Fig. 6 Distribution of nodes and Gauss points in MLPG grid with spacing100 m ●node, ▲Gauss point. |

|
图 7 结构化矩形网格有限元法100 m×100 m离散网格 Fig. 7 100 m×100 m structured rectangle FEM grid |
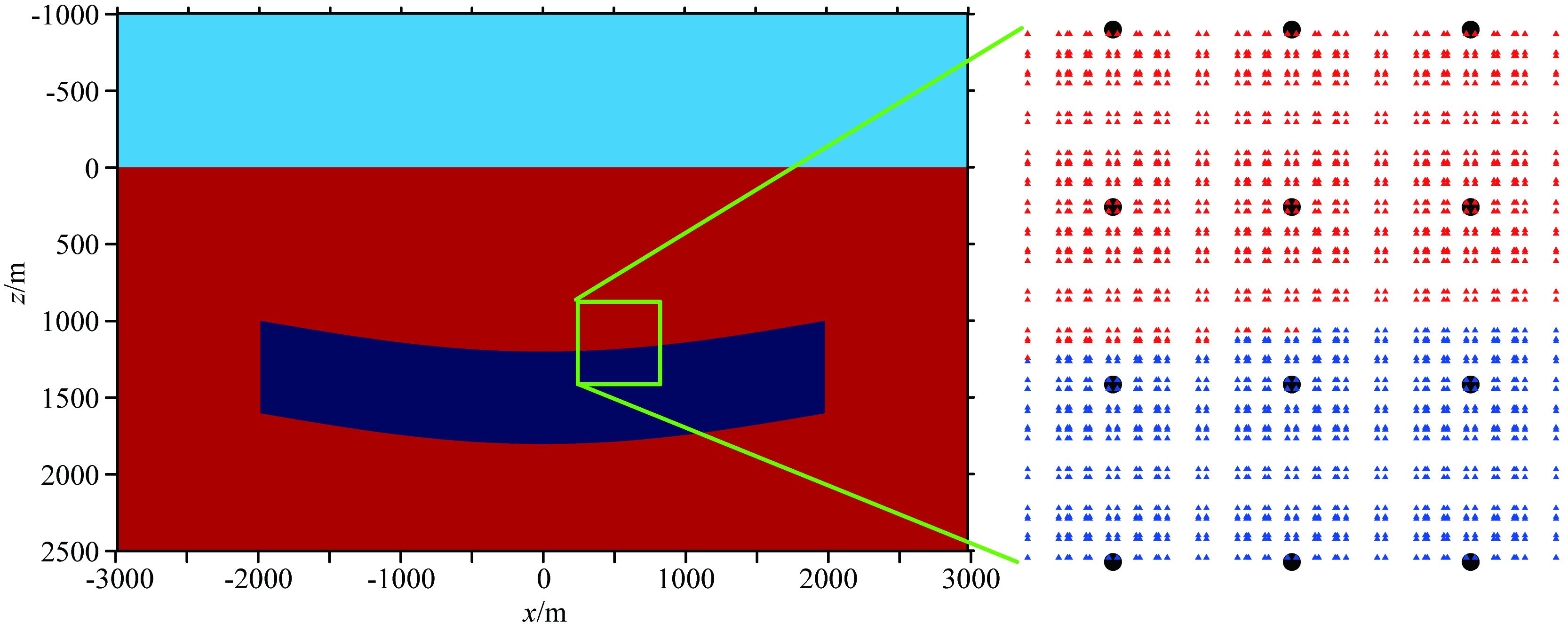
|
图 8 MLPG无网格法200 m网格距时节点和高斯点的分布 ●表示节点,▲表示高斯点. Fig. 8 Distribution of nodes and Gauss points in MLPG grid with spacing 200 m ●node, ▲Gauss point. |
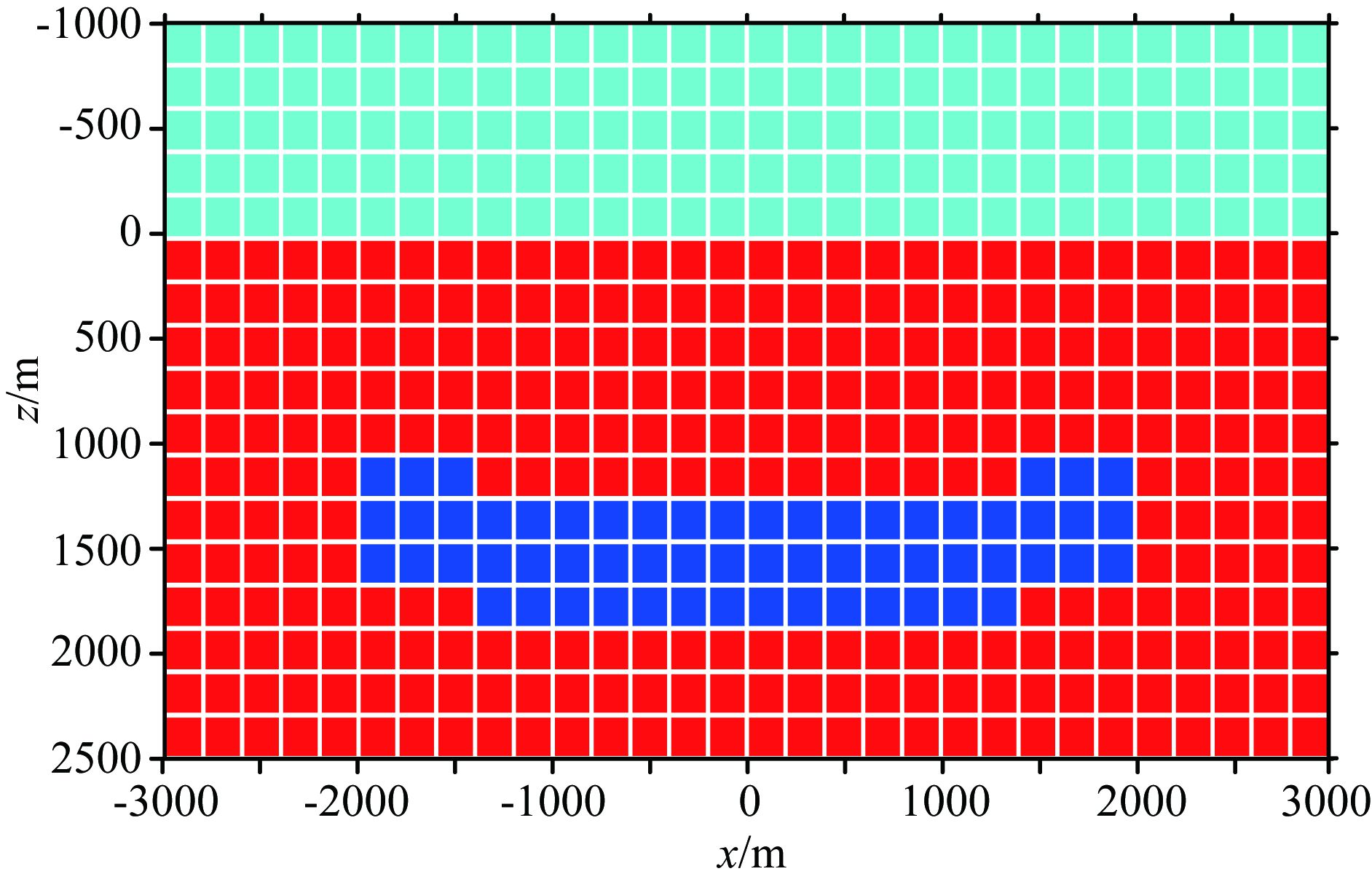
|
图 9 结构化矩形网格有限元法200 m×200 m离散网格 Fig. 9 200 m×200 m structured rectangle FEM grid |
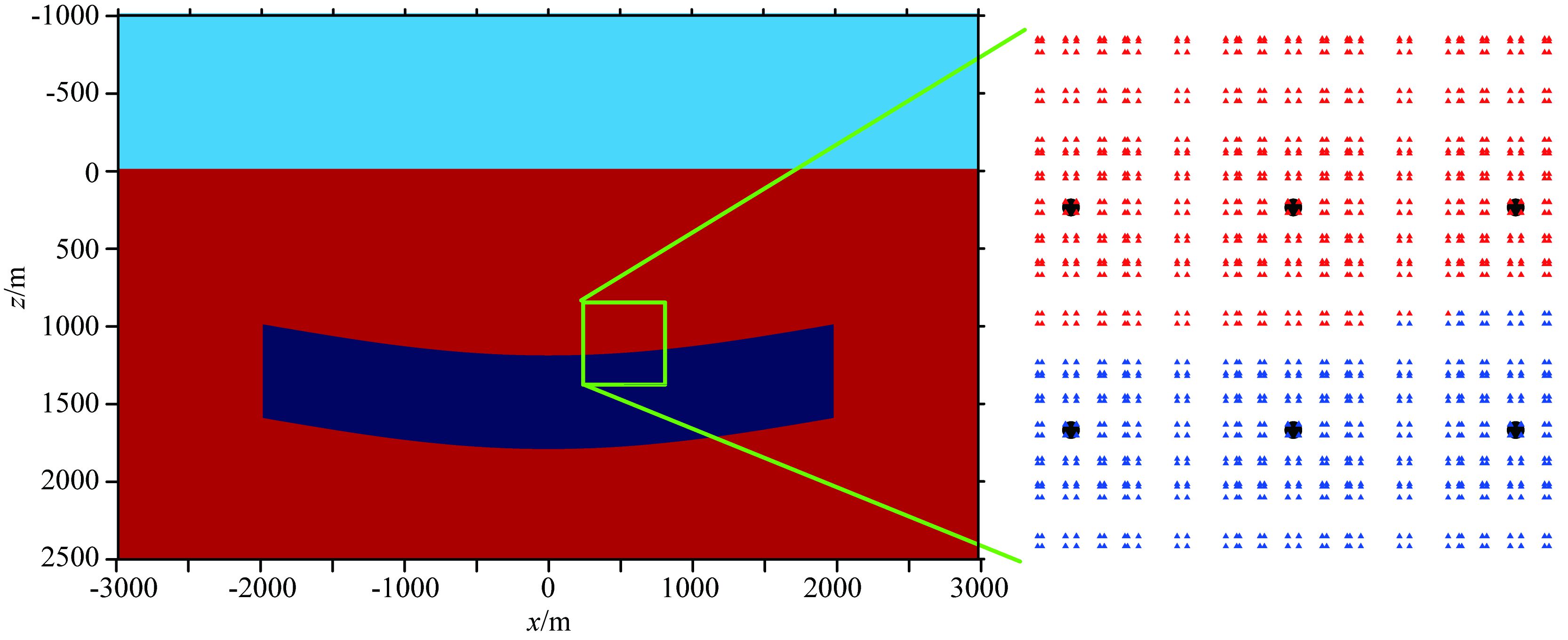
|
图 10 MLPG无网格法250 m网格距时节点和高斯点的分布 ●表示节点,▲表示高斯点. Fig. 10 Distribution of nodes and Gauss points in MLPG grid with spacing 250 m ●node, ▲Gauss point. |
|
图 11 结构化矩形网格有限元法250 m×250 m离散网格 Fig. 11 250 m×250 m structured rectangle FEM grid |
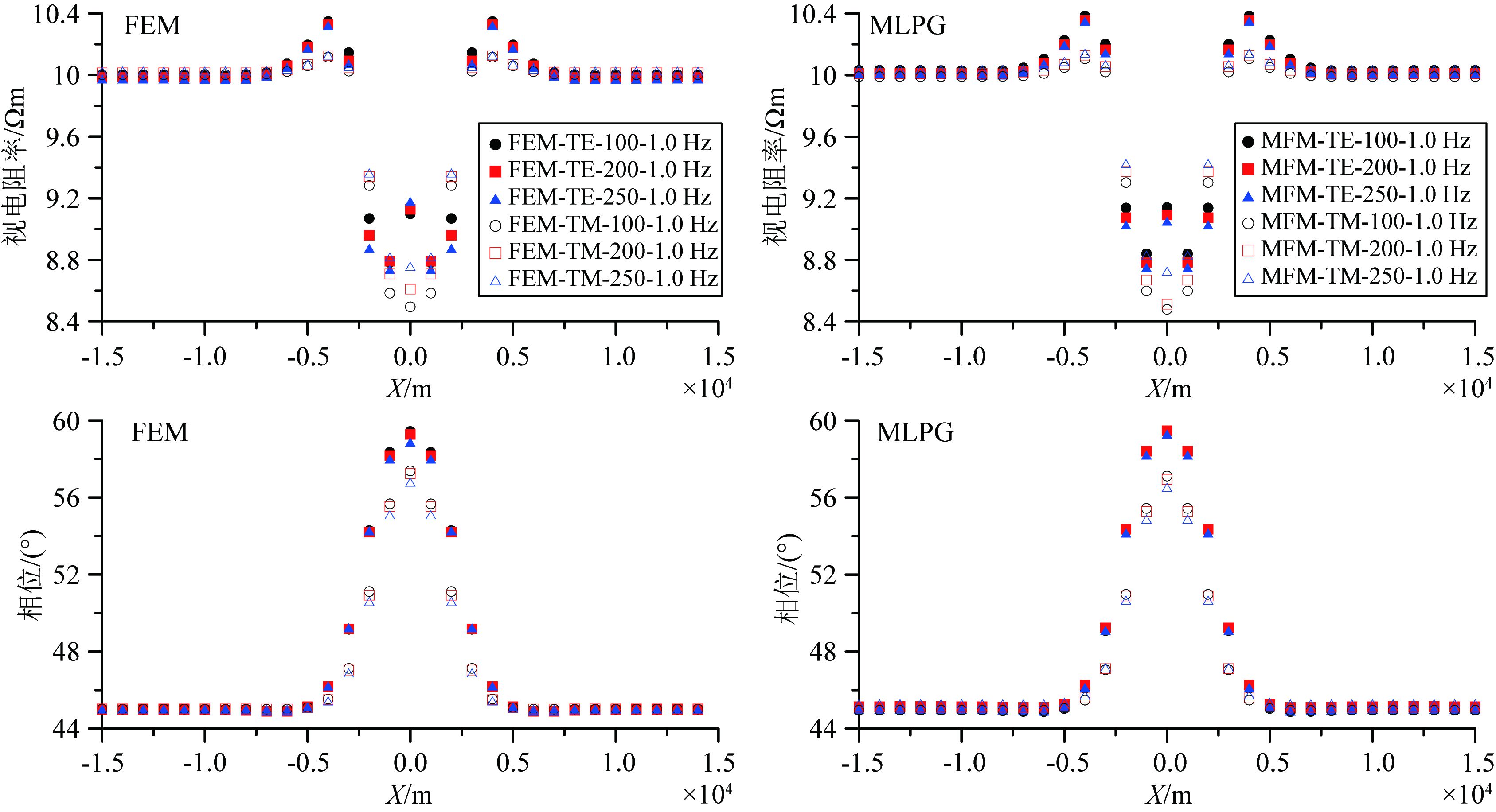
图 12为MLPG无网格法和结构网格有限元法采用3套不同离散网格得到的图 4b所示模型大地电磁场响应.计算频率为1.0 Hz.由图可见,当网格越来越粗糙时,两种数值方法的计算精度都有所损失,但程度不同.对于TE模式,结构网格有限元法当网格变大时,数值解的误差增加很快,尤其在±2.0 km处,相对误差增加到2.1%;而MLPG无网格法数值解的误差为1.2%.对于TM模式,从100 m×100 m网格变到200 m×200 m网格时,MLPG无网格法的视电阻率误差比结构有限元法的小,而从200 m×200 m变到250 m×250 m时,两种方法数值解的误差都较大.但MLPG无网格方法可以通过增加高斯点的方法更加细致的刻画模型边界,以提高计算精度.
|
图 12 MLPG无网格法和结构有限元法在1.0 Hz下3套不同离散网格模拟结果对比 Fig. 12 Comparison of MT responses (1.0 Hz) obtained by the MLPG andstructured FEmethodwith three different grids |
图 13为图 4b所示模型的大地电磁场响应,计算频率为0.1 Hz.由于此时趋肤深度已经远大于低阻异常体底界面的埋深,故而网格大小变化对模拟结果的精度影响不是很明显.但同样可以看到,MLPG无网格法的数值结果随网格的变化是小于结构有限元的.

|
图 13 MLPG无网格法和结构有限元法在0.1 Hz下3套不同离散网格模拟结果对比 Fig. 13 Comparison of MT responses (0.1 Hz) obtained by MLPG and structured FE method with three different grids |
综上所述,与结构网格有限元法相比,高斯点赋予物性参数的MLPG无网格法受网格影响小,其数值解相对稳定.当我们进行大地电磁资料反演时,常常不清楚地下地质体的大小、位置、形状等参数,传统数值模拟方法无法对模型空间进行合理剖分.由于离散网格对结构网格有限元解影响较大,于是可能会致使反演结果出现较大差异.而利用高斯点赋予物性参数值的MLPG无网格方法可以在一定程度上改善这一问题.
5 MLPG无网格法模拟海底起伏地形下的大地电磁场响应众所周知,起伏地形对大地电磁场响应有着很大的影响, 陆地起伏地形对TM模式大地电磁场响应的影响远大于对TE模式的影响 (Wannamaker et al., 1986, Chouteau and Bouchard, 1988),而海底起伏地形对大地电磁场的影响特征与陆地情况的大不相同.海底地形起伏对TE模式和TM模式的大地电磁响应都有很大的影响,且比陆地起伏地形的影响程度更加严重 (Schwalenberg and Edwards, 2004, 赵慧等, 2014).
利用足够小的规则矩形网格或者改变四边形网格形状都可以对复杂地形进行拟合,前者所模拟的地形部分呈现台阶状,但有时会加大网格单元的横纵比,使得线性方程组的收敛性变差;后者十分依赖于人工经验,并且会耗费大量形成网格的成本.自适应非结构有限单元法很好的解决了这些问题,通过自适应加密地形边缘部分的网格,以达到光滑地形,且不破坏线性方程组收敛性的目的.但自适应非结构有限单元法的误差估计算法及自适应策略相对复杂,并且由于受到网格的约束,无法通过自由调整节点的位置以达到优化网格的目的,导致节点个数增加过多,需要耗费更多的空间存储刚度矩阵.MLPG无网格法由于摆脱了网格对形函数限制的影响,对起伏地形的处理方法比结构有限元法更加灵活,于是可以先利用结构化网格剖分模型空间,再在仅有起伏地形存在的地方单独增加节点以光滑地形界面.而增加的节点个数相对于初始节点个数可以忽略不计,不会明显增加刚度矩阵的大小.
我们设计了两个海洋起伏地形模型.图 14为二维海洋梯形地堑模型.地堑的水平跨度为1200 m,在地堑底部海水深度为1500 m,在地堑两边水平海底上水深为1000 m.图 15为二维海洋梯形地垒模型.地垒的水平跨度为1200 m,在地垒顶部海水深度为500 m, 在地垒两边水平海底上水深为1000 m.设置空气层电阻率为1012 Ωm,海水电阻率为0.3 Ωm,海底地层为均匀介质,其电阻率为10.0 Ωm.大地电磁接收站位于海底,接收站间距为1000 m.计算频率为1.0 Hz和0.1 Hz.用MLPG无网格方法模拟地堑和地垒地形下的大地电磁场响应,采用100 m×100 m的结构网格剖分模拟区域,并在有地形起伏处加密节点.

|
图 14 二维海洋梯形地堑模型 Fig. 14 Sketch of a2D marine trapezoidal graben model |

|
图 15 二维海洋梯形地垒模型 Fig. 15 Sketch of a2D marine trapezoidal horstmodel |
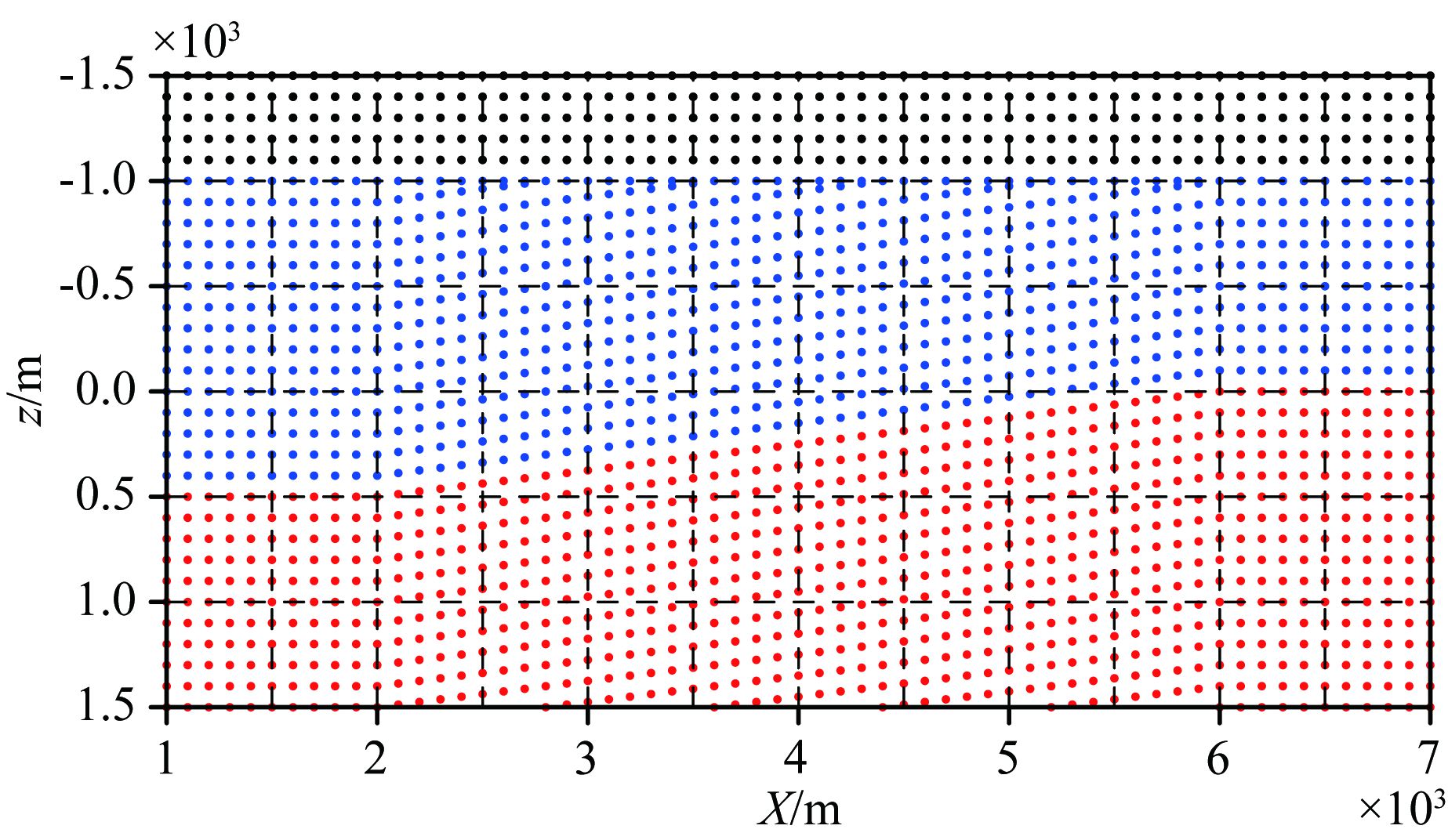
图 16和图 17分别为海洋地堑模型和海洋地垒模型的节点分布示意图,黑色、蓝色、红色点分别表示在空气、海水、海底的节点.首先利用结构网格剖分模型空间,然后仅在斜坡处增加了一个节点用于刻画起伏地形,避免了后期利用插值算法计算接收点处场值而引起的误差.为了减小地形上节点场值的计算误差,对节点间距进行重排,将不均匀的节点置于海水-空气分界面和模型的底界面处.相对于最初的结构网格节点个数,增加的节点数量占比例很小,几乎不影响最终总体刚度矩阵的大小,计算效率没有明显变化.
|
图 16 二维海洋梯形地堑模型节点分布 Fig. 16 Node distribution of 2-D marine trapezoidal grabenmodel |

|
图 17 二维海洋梯形地垒模型节点分布 Fig. 17 Node distribution of 2D marine trapezoidal horst model |
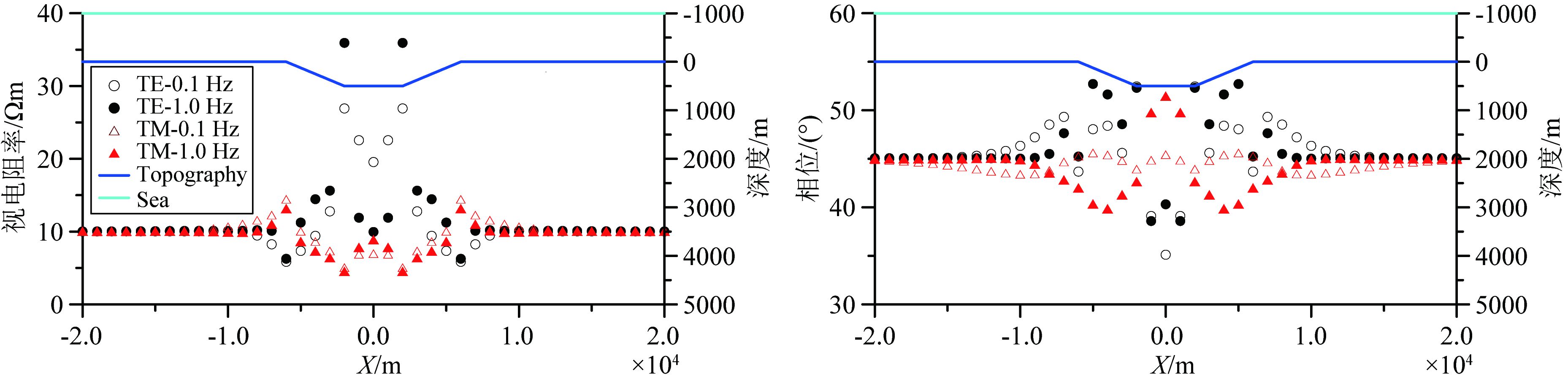
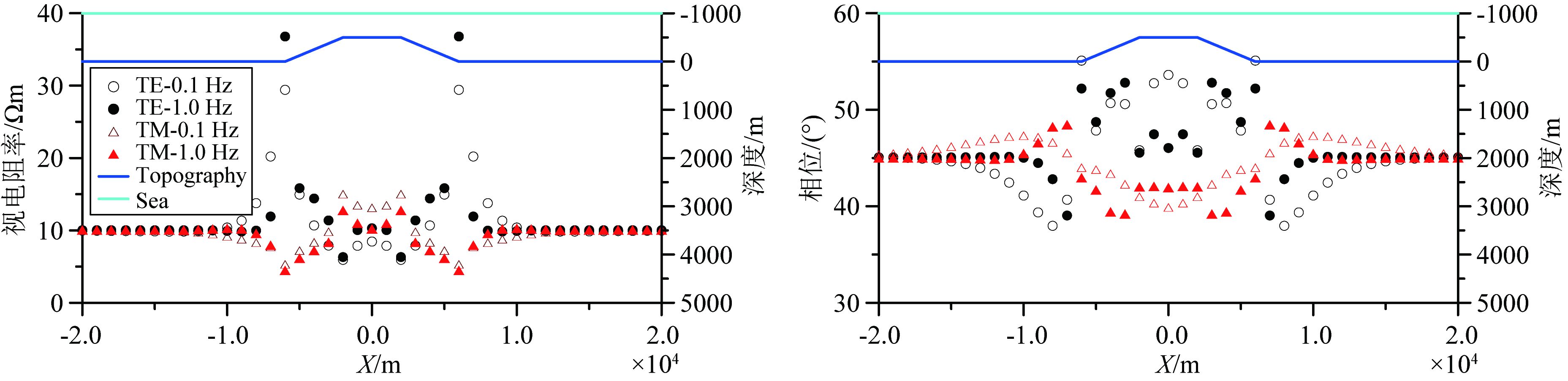
图 18和图 19分别为海洋地堑和地垒模型两个周期 (1.0 Hz和0.1 Hz) 的视电阻率和相位曲线.海洋地堑模型对TE模式视电阻率和相位的影响相对于TM模式的影响更大.地堑肩部 (斜坡处),TE模式下的视电阻率和相位为正异常,而TM模式下的视电阻率和相位都为负异常.1.0 Hz下地堑对大地电磁响应的影响比0.1 Hz下的影响要大,但0.1 Hz下地堑对大地电磁相应的影响范围比1.0 Hz下的要广,即0.1 Hz下距离地堑更远处的采集站收到的大地电磁信号依然受到地堑地形的影响.同样,海洋地垒模型对TE模式视电阻率和相位的影响比TM模式要大,且0.1 Hz下大地电磁响应极值受到地垒的的影响小于1.0 Hz下的影响,但影响范围要宽.在地垒肩部 (斜坡处),TE模式下视电阻率和相位为正异常,但相位在肩部外侧呈现负异常;TM模式下视电阻率和相位为负异常,但相位在肩部外侧呈现正异常.总体来说地垒模型对大地电磁响应的影响范围比地堑模型要广.
|
图 18 二维海洋梯形地堑模型在1.0 Hz和0.1 Hz下大地电磁响应 Fig. 18 MT responses of 2D marine trapezoidal graben model at 1.0 Hz and 0.1 Hz |
|
图 19 二维海洋梯形地垒模型在1.0 Hz和0.1 Hz下大地电磁响应 Fig. 19 MT responses of 2D marine trapezoidal horst model at 1.0 Hz and 0.1 Hz |
本文提出了MLPG无网格二维海洋大地电磁正演算法,推导了二维大地电磁场边值问题的MLPG局部弱式形式,讨论了总体刚度矩阵的特点.我们模拟二维地电模型的大地电磁场响应,并与结构化矩形网格有限元结果进行了对比,两者的相对误差小于1%.
由于MLPG无网格方法仅通过点与点之间的相对距离关系建立形函数,摆脱了网格的限制.采用高斯点赋予物性参数值的方法,克服了节点必须严格位于物性分界面上的局限性,增强了MLPG无网格方法的适用性,有利于模拟复杂地电模型的大地电磁响应.在模拟含有弯曲物性分界面地电模型的大地电磁场响应时,高斯点赋予物性参数值的MLPG无网格法仅利用高斯点就可以很好地刻画模型的内边界,当用粗糙的规则矩形网格进行离散化时,MLPG无网格法结果的总体稳定性优于结构化矩形网格有限元,为改善反演结果提供了另一种思路.
当海底存在起伏地形时,MLPG无网格方法仅需在结构网格剖分基础上,在地形起伏处增加少量加密节点便可以很好地刻画地形起伏,算法简单,几乎不改变总体刚度矩阵大小.海洋起伏地形对海洋大地电磁高频响应的影响比低频响应的影响要大,但对低频响应的影响范围比高频的响应要广.对于海洋地堑和地垒模型,TE模式下视电阻率和相位在地形肩部都呈现正异常,TM模式下视电阻率和相位呈现负异常,但地垒模型在肩部外侧的相位在TE模式下呈现负异常,TM模式下呈现正异常.总体来说,地垒模型对海洋大地电磁响应的影响比地堑模型的影响范围要大.
致谢感谢审稿专家的专业意见和编辑部老师的帮助和支持.
| Atluri S N, Zhu T. 1998. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech., 22(2): 117-127. DOI:10.1007/s004660050346 | |
| Babuska I, Melenk J M. 1995. The partition of unity finite element method. DTIC Document. | |
| Chouteau M, Bouchard K. 1988. Two-dimensional terrain correction in magnetotelluric surveys. Geophysics, 53(6): 854-862. DOI:10.1190/1.1442520 | |
| Coggon J H. 1971. Electromagnetic and electrical modeling by the finite element method. Geophysics, 36: 132-155. DOI:10.1190/1.1440151 | |
| Dmitriev V I. 1969. Electromagnetic fields in inhomogeneous media. Moscow State Univ. | |
| Everett M E. 2012. Theoretical developments in electromagnetic induction geophysics with selected applications in the near surface. Surv.Geophys., 33(1): 29-63. DOI:10.1007/s10712-011-9138-y | |
| Jones FW, Pascoe L J. 1971. A general computer program to determine the perturbation of alternating electric currents in a two-dimensional model of a region of uniform conductivity with an embedded inhomogeneity. Geophys J. Int, 24: 3-30. DOI:10.1111/gji.1971.24.issue-1 | |
| Key K, Weiss C. 2006. Adaptive finite-element modeling using unstructured grids:The 2D magnetotelluric example. Geophysics, 71(6): G291-G299. DOI:10.1190/1.2348091 | |
| Li J M. 2005. Geoelectric Field and Electrical Exploration (in Chinese). Beijing:China University of Geosciences. | |
| Li Y G, Dai S K. 2011. Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures. Geophys. J. Int., 185(2): 622-636. DOI:10.1111/gji.2011.185.issue-2 | |
| Li Y G, Key K. 2007. 2D marine controlled-source electromagnetic modeling:Part 1-An adaptive finite-element algorithm. Geophysics, 72(2): WA51-WA62. DOI:10.1190/1.2432262 | |
| Li Y G, Pek J. 2008. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media. Geophys. J. Int., 175(3): 942-954. DOI:10.1111/gji.2008.175.issue-3 | |
| Liu G R, Gu Y T. 2005. An Introduction to Meshfree Methods and Their Programming. Netherlands:Springer. | |
| Liu X. Meshfree Method (in Chinese).Beijing: Science Press, 2011. | |
| Lucy L B. 1977. A numerical approach to the testing of the fission hypothesis. The Astronomical Journal, 82: 1013-1024. DOI:10.1086/112164 | |
| Mackie R L, Madden T R, Wannamaker P E. 1993. Three-dimensional magnetotelluric modeling using difference equations-Theory and comparisons to integral equation solutions. Geophysics, 58(2): 215-226. DOI:10.1190/1.1443407 | |
| Nayroles B, Touzot G, Villon P. 1992. Generalizing the finite element method:diffuse approximation and diffuse elements. Comput. Mech., 10(5): 307-318. DOI:10.1007/BF00364252 | |
| Oñate E, Idelsohn S, Zienkiewicz O C, et al. 1996. A finite point method in computational mechanics. Applications to convective transport and fluid flow. Int. J.Numer. Meth. Eng, 39(22): 3839-3866. DOI:10.1002/(ISSN)1097-0207 | |
| Schwalenberg K, Edwards R N. 2004. The effect of seafloor topography on magnetotelluric fields:an analytical formulation confirmed with numerical results. Geophys. J. Int., 159(2): 607-621. DOI:10.1111/gji.2004.159.issue-2 | |
| Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements. Geophysics, 51(11): 2131-2144. DOI:10.1190/1.1442065 | |
| Weidelt P. 1975. Electromagnetic induction in three-dimensional structures. J. Geophys, 41: 85-109. | |
| Wei W B. 2002. New advance and prospect of Magnetotelluricsounding (MT) in China. Progress in Geophysics (in Chinese), 17(2): 245-254. | |
| Wittke J, Tezkan B. 2014. Meshfreemagnetotelluric modelling. Geophys. J. Int., 198(2): 1255-1268. DOI:10.1093/gji/ggu207 | |
| Xu S Z, Zhao S K. 1987. Two-dimensional magnetotelluric modelling by the boundary element method. Journal of Geomagnetism and Geoelectricity, 39(11): 677-698. DOI:10.5636/jgg.39.677 | |
| Xu S Z. Finite Element Methods in Geophysics (in Chinese).Beijing: Science Press, 1994. | |
| Xu S Z. Boundary Element Methods in Geophysics (in Chinese).Beijing: Science Press, 1995. | |
| Zhao H, Liu Y, Li Y G. 2014. Adaptive finite element forward modeling for two-dimensional marine magnetotelluric fields. Oil Geophysical Prospecting (in Chinese), 49(3): 578-585. | |
| 李金铭. 地电场与电法勘探.北京: 地质出版社, 2005. | |
| 刘欣. 无网格方法.北京: 科学出版社, 2011. | |
| 魏文博. 2002. 我国大地电磁测深新进展及瞻望. 地球物理学进展, 17(2): 245–254. | |
| 徐世浙. 地球物理中的有限单元法.北京: 科学出版社, 1994. | |
| 徐世浙. 地球物理中的边界单元法.北京: 科学出版社, 1995. | |
| 赵慧, 刘颖, 李予国. 2014. 自适应有限元海洋大地电磁场二维正演模拟. 石油地球物理勘探, 49(3): 578–585. | |
 2017, Vol. 60
2017, Vol. 60


