随着石油工业的发展和勘探开发的不断深入,从构造勘探阶段逐渐走向岩性勘探阶段,其勘探难度逐渐加大.为了顺应这种要求,全波形反演 (FWI) 迅速发展起来,并成为当今地球物理界的研究热点.20世纪80年代,Tarantola (1984)提出了时间域FWI方法,并通过伴随状态法求取目标函数的梯度,避免了Jacobian矩阵的求取,大大缩短了FWI梯度计算所需要的时间.20世纪90年代,Pratt将FWI推广到了频率域,提出只需要几个离散的频率就可以得到高精度的反演结果,且低频到高频的多尺度反演策略可以解决陷入局部极小值的问题.但FWI是一个强非线性问题,对低频成分、震源函数、噪声和初始模型非常敏感 (Virieux and Operto, 2009),这给FWI应用于实际数据处理带来了巨大的挑战.当地震数据中缺失低频成分,震源函数不准确或者伴随震源主频过高时,FWI结果都很容易出现周波跳跃现象.当前FWI的研究热点主要是如何缓解反演过程中的周波跳跃问题.导致FWI产生周波跳跃的主要因素有:(1) 地震数据为振荡的复频信号,且具有较高的主频,波形变化剧烈;(2) 地震数据中缺失低频成分;(3) 震源函数估计不准确;(4) 用于FWI的初始速度模型不准确.
在过去的几十年的时间里,为了克服FWI的周波跳跃问题,提出了许多解决方法.低频数据反演地下模型的宏观信息,高频信号体现构造的细节信息,利用低频到高频的多尺度反演策略能够有效缓解因地震数据主频过高产生周波跳跃问题.Bunks等 (1995)提出基于低通滤波的多尺度FWI,该方法能够有效缓解FWI的周波跳跃问题,但是当地震数据中缺失低频成分时,利用低通滤波滤除高频成分之后再进行FWI,并不能很好地恢复模型的宏观构造.Pratt等提出频率域多尺度FWI策略,然而当地震数据中缺失低频成分时,同样会出现周波跳跃问题.由于地震数据有限频带的特性以及去噪处理等原因导致地震数据中缺失可靠的低频信号,Zhang等 (2015)利用被动源重构数据中的低频信号来补偿主动源信号的低频成分,该方法得到的低频信号虽然可靠,但是地下噪声干扰严重,给波形反演带来了一定的困难.Wu等 (2013, 2014) 利用地震记录的Hilbert包络进行FWI,Hilbert包络中含有丰富的低频信号 (Chi et al., 2014;敖瑞德等, 2015; 董良国等, 2015; Luo et al., 2015),但Hilbert包络与原始信号波形存在较大的差异,同时会导致伴随震源的主频过高.Shin和Cha (2009)利用Laplace-Fourier域FWI能够在缺失低频的情况下获得一个好的初始模型,然后再利用常规FWI进行反演,但是该方法对地下深部成像时需要长偏移距的地震数据,而且对数据中的噪声特别敏感 (Chi et al., 2014).时间衰减FWI能够有效的减少每一步反演的参数 (Chen et al., 2015),由浅入深逐层进行反演,很好地缓解了周波跳跃现象.FWI还可以与其他的反演方法结合使用,例如:走时层析成像 (Dines and Lytle, 1979; Luo and Schuster, 1991) 和偏移速度分析 (Liu and Bleistein, 1995; Xie, 2008).
震源函数是FWI过程中的一个重要参数,微小的误差都会导致观测记录与模拟记录不匹配问题,甚至导致整个反演向错误的方向更新.但实际地震数据中,震源函数往往是未知的,这成为FWI的又一巨大挑战.其实最为直接的方法就是提取震源附近的直达波作为震源函数 (敖瑞德等, 2015),该方法存在一定的激发延时误差和振幅不准确等问题.在全波形反演过程中,提出了许多方法来消除震源函数的影响,例如:Rickett (2013)提出利用变量投影的方法可消除频率域FWI中震源函数的影响,得到较好的反演结果;Lee (2003)利用反褶积的方法成功消除了震源函数对频域FWI的影响;Choi (2011)利用交叉褶积方法消除震源函数对FWI的影响,并推导了相应的目标函数和梯度;Zhang等 (2016)利用褶积与反褶积的方法在重构低频的同时消除了震源函数的影响,有效缓解了低频缺失和震源函数不准确带来的周波跳跃问题.在FWI的过程中消除震源函数的影响固然是一种好的方法,但是在消除震源函数的同时必然会失去一些模型的有效信息.
本文提出解调包络方法重构地震数据中的低频信息,并结合低通滤波实现从低频到高频的多尺度FWI反演策略.该方法完全基于数据驱动,有效缓解FWI的非线性,解决了因缺失低频和观测记录主频过高所产生的周波跳跃问题.同时提出一种伴随状态震源函数反演方法,该方法只利用直达波的信息便可以精确地反演出震源函数,具有不依赖初始震源函数、不依赖地下背景速度模型,震源函数反演精度高等优点.在震源函数反演的过程中,利用一个短时窗,只截取震源附近直达波的信息,所以只需要正演截断时窗内的地震数据与观测记录进行匹配,计算效率得到了大大的改善.
本文首先介绍涉及的方法原理,包括:地震数据的解调包络提取方法;解调包络FWI目标函数的建立和梯度公式.然后推导伴随状态震源函数反演方法的梯度公式,并利用数值算例证明该震源函数反演方法具有反演精度高,计算速度快等优势.之后利用抽稀的Marmousi进行基于精确震源函数的解调包络多尺度FWI测试.最后通过与Hilbert包络FWI进行对比,证明了解调包络在重构低频和降低伴随震源主频方面均优于Hilbert包络.
2 方法原理 2.1 解调包络实际地震数据中低频部分信噪比 (SNR) 较低,例如海上数据中常含有低频涌浪等噪声的干扰,利用高通滤波等去噪方法处理之后,导致地震记录中缺失5Hz以下的低频信号,即使利用保护低频去噪策略,地震数据中仍然难以获得3Hz以下的低频信号 (Berkhout and Blacquière, 2011).为了解决采集方法引起的地震记录低频信号缺失的问题,本文利用解调包络方法来重构地震记录中缺失的低频信息.
|
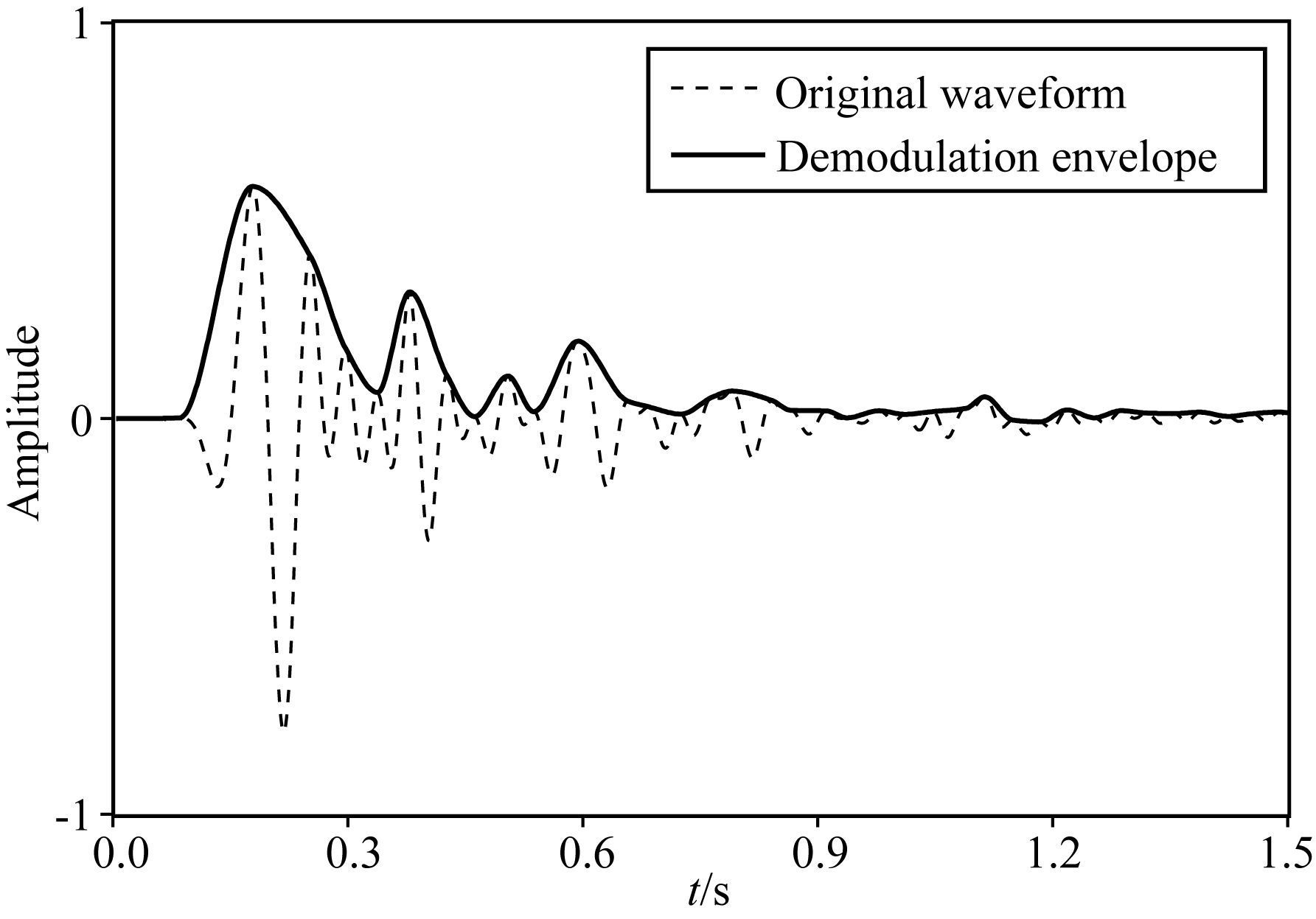
图 1 原始波形与解调包络 Fig. 1 Original waveform and demodulation envelope |
解调的目的是从已经调制的信号 (已调信号) 中提取反映被测量信号的测量值.对信号进行解调的方法有很多,本文利用三次样条曲线 (Interpolation, 1999) 来提取地震记录的解调包络.首先利用三次样条曲线平滑的连接单道地震数据的极大值点,形成的上包络线即为反映地震记录宏观信息的解调信号,本文将其称为解调包络.然后再逐道的对单炮地震记录进行处理,得到单炮解调包络记录.如图 1所示,解调包络很好地包裹着地震记录的有效信号,直观反映出地震记录的宏观信息.
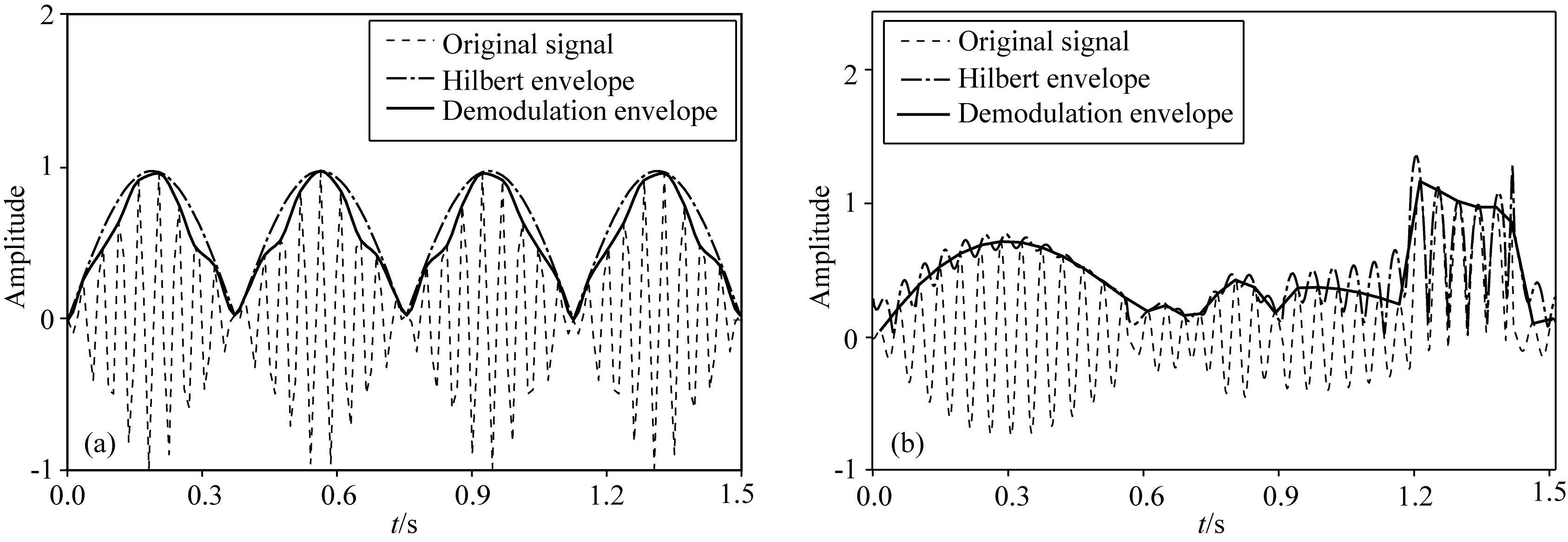
Wu等 (2014)利用Hilbert包络进行FWI,一定程度上解决了低频缺失问题,但Hilbert包络与地震记录波形存在着较大的差异.如图 2a当信号为正负对称信号时,Hilbert包络和解调包络都能很好地反映信号的宏观信息.但当存在非对称信号时,Hilbert包络不能很好地包裹有效信号,甚至出现剧烈的振荡现象 (图 2b),可见Hilbert包络在有些情况下并非时间域波形宏观信息的直观体现.两种信号包络的对比结果表明,解调包络能够较好地包裹有效信号,更直观反映信号的宏观信息.
|
图 2 原始信号、Hilbert包络和解调包络 (a) 对称信号;(b) 非对称信号. Fig. 2 Waveforms of original signal, Hilbert envelope and demodulation envelope (a) Symmetrical signal; (b) Non-symmetrical signal. |
从两层速度模型数值模拟得到的地震记录波形 (图 3a) 分析可见,解调包络能够恰好包裹有效信号,且波形变化较原始信号更平缓,能够很好地反映地震记录中的宏观信息.然而Hilbert包络与原始信号相比存在明显的假峰值现象 (图 3a虚线圆),其实Hilbert包络是地震信号绝对值的一种体现,并不完全是地震信号宏观信息的一种直观体现.同时从频谱 (图 3b) 可以看出,解调包络能够重构出更丰富的低频信息,这为缓解FWI周波跳跃问题提供了前提条件.

|
图 3 原始信号、Hilbert包络和解调包络的波形和频谱 (a) 波形;(b) 频谱. Fig. 3 Waveforms and spectrum of original signal, Hilbert envelope and demodulation envelope (a) Waveform; (b) Spectrum. |
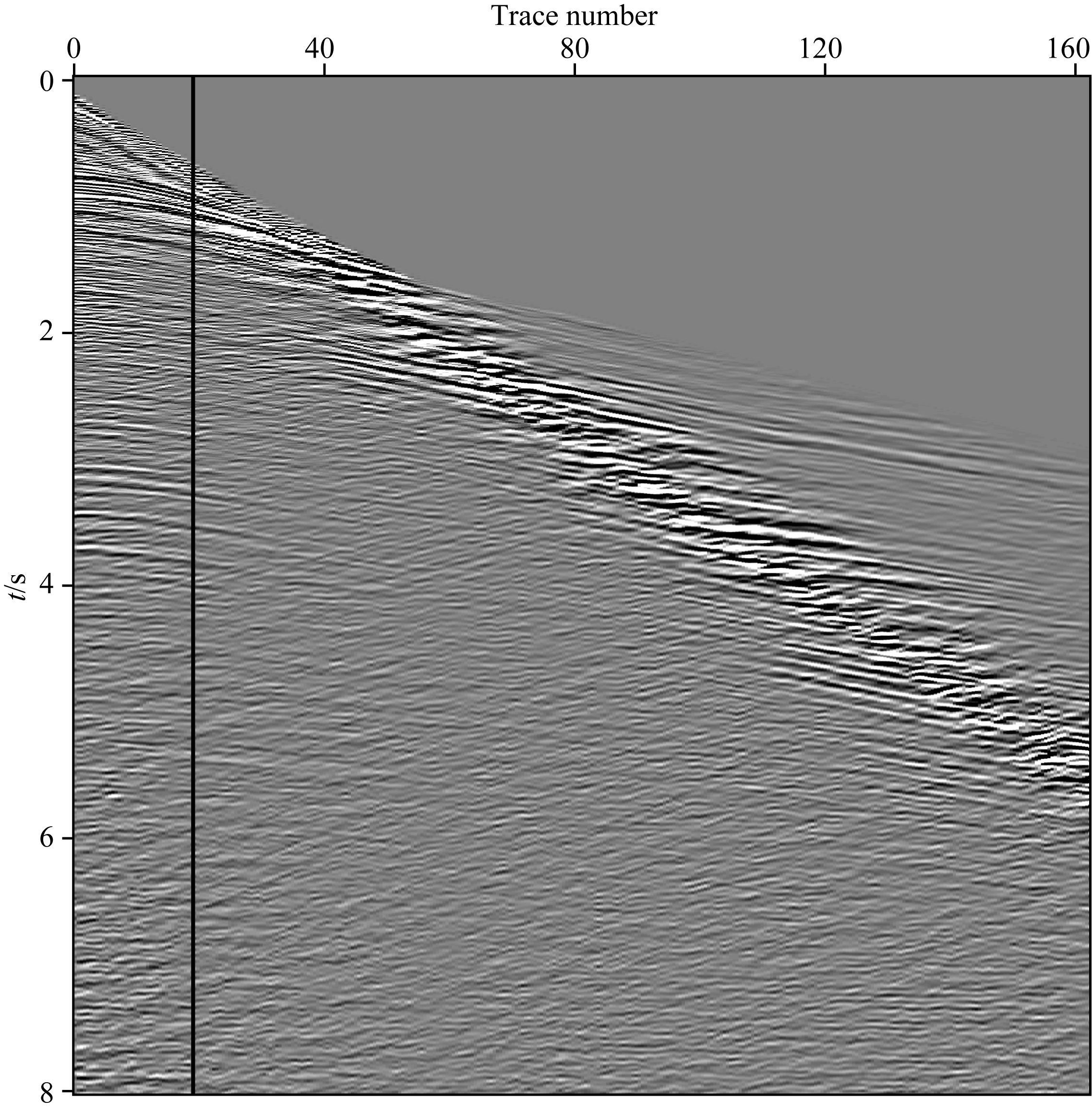
为了更好地体现解调包络在提取宏观信息方面的优势,本文利用某地区实际野外采集的拖缆单炮地震数据 (图 4) 来进行对比分析.该数据共162道,接收时长共8 s,取第20道数据波形信息 (图 4黑线) 来测试解调包络和Hilbert包络.该地区实际采集的地震信号信噪比较高,但是依然缺失5 Hz以下的低频信息.
|
图 4 野外实测地震数据 Fig. 4 Seismic data measured in field |
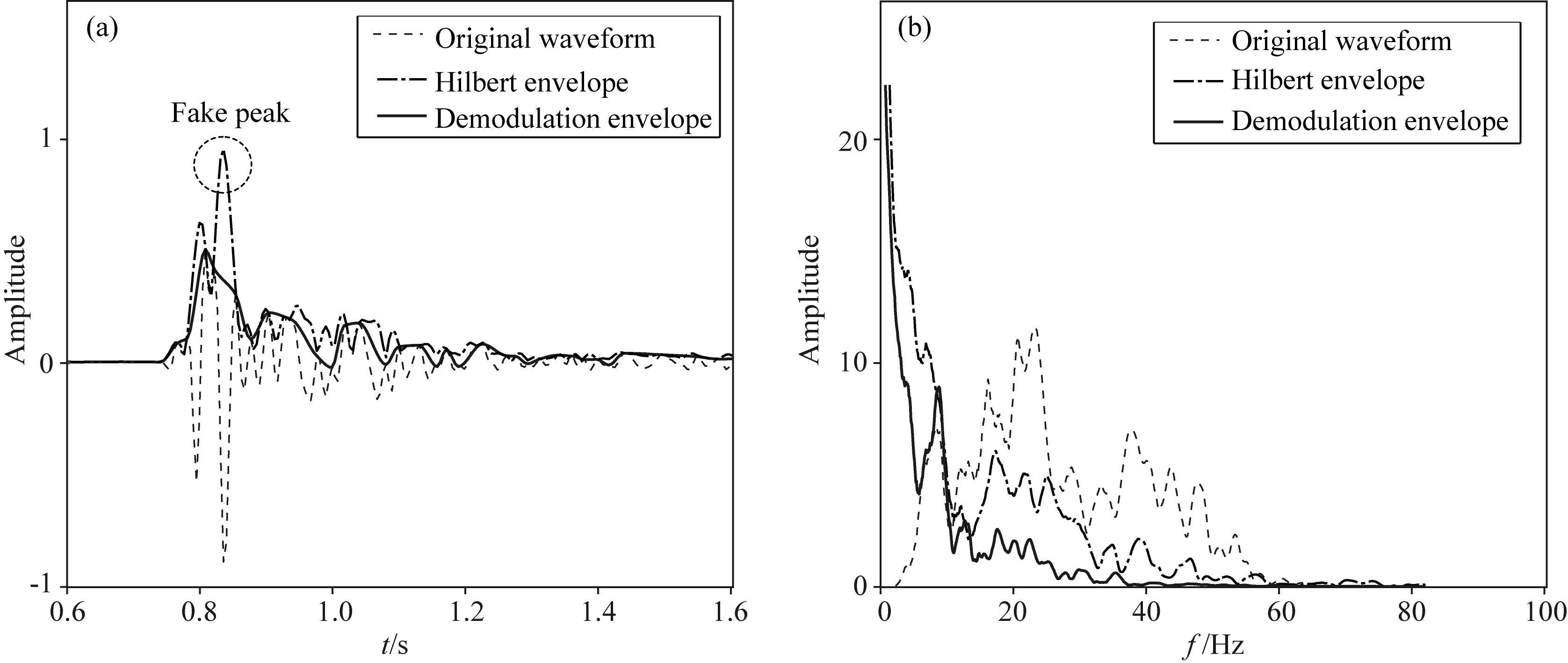
为了能够清晰看出波形的变化特征,只截取第20道波形变化剧烈的时段成图 (0.6~1.6 s),如图 5a所示.从图 5a中可以看出,解调包络较好包裹着有效信号,直观反映出了地震信号的宏观信息,然而Hilbert包络存在着多处假峰值现象,如果将这些虚假信息直接带入到FWI中可能会得到错误的反演结果,因此Hilbert包络FWI需要利用链式法则去推导伴随震源 (Chi et al., 2014),但是利用链式法则推导的伴随震源主频较高,相比于常规FWI伴随震源波形变化更剧烈,更容易出现周波跳跃问题 (详见下一节).
|
图 5 单道分析 (a) 波形; (b) 频谱. Fig. 5 Single trace analysis (a) Waveforms; (b) Spectrum. |
从频谱图 (图 5b) 可以看出,解调包络波形含有丰富的低频信息,利用含有丰富低频信息的解调包络进行FWI,可以得到一个较好的初始速度模型.同时结合低通滤波多尺度反演策略,能够有效缓解因缺失低频成分带来的周波跳跃问题.
2.2 目标函数、梯度和伴随震源FWI是一个不断用模拟数据去拟合实际数据的过程,最终找到一个速度模型使得数据残差平方最小.它具有成像精度高、反演模型参数准确、复杂构造成像效果好等优点.
2.2.1 常规FWI目标函数和梯度常规FWI目标函数定义为
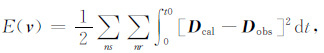
|
(1) |
其中v表示模型的速度参数,Dcal表示模拟记录,Dobs表示观测记录,ns表示震源的个数,nr表示检波器的个数,t0表示最大接收时间.
本文利用常密度声波方程进行数值模拟,则目标函数对模型速度参数v的导数为
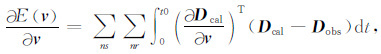
|
(2) |
其中Jacobian矩阵定义为:J=∂Dcal/∂v,T表示矩阵的转置.常规FWI伴随震源定义为:fsc=(Dcal-Dobs).在实际数据反演的过程中Jacobian矩阵的计算量巨大,本文采用伴随状态法 (Tarantola, 1984) 计算目标函数对速度参数的梯度,即正传波场与反传残差波场的零延迟互相关.则常规FWI目标函数的梯度可以表示为
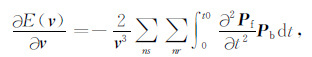
|
(3) |
其中Pb表示由伴随震源向地下传播得到的反传波场,Pf表示正演模拟波场.
2.2.2 解调包络FWI目标函数和梯度解调FWI是一个不断的用模拟数据解调包络去拟合实际数据解调包络的过程,最终找到一个宏观速度模型使得解调包络数据残差平方最小.因此可将解调包络FWI的目标函数定义为
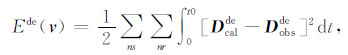
|
(4) |
其中Dcalde表示经过解调包络方法处理的模拟记录,Dobsde表示经过解调包络方法处理的观测记录.解调包络可以看成是一个地震数据预处理的方法,在解调包络FWI的过程中,利用Dcalde不断的去匹配Dobsde,这与常规FWI的原理一样,因此可以利用伴随状态法 (Tarantola, 1984) 计算目标函数对速度参数的梯度,公式为
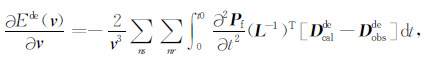
|
(5) |
其中L-1表示伴随算子,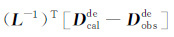

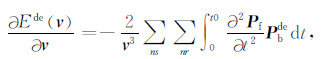
|
(6) |
其中Pbde表示由伴随震源fsde向地下传播得到的反传波场,Pf表示正演模拟波场.
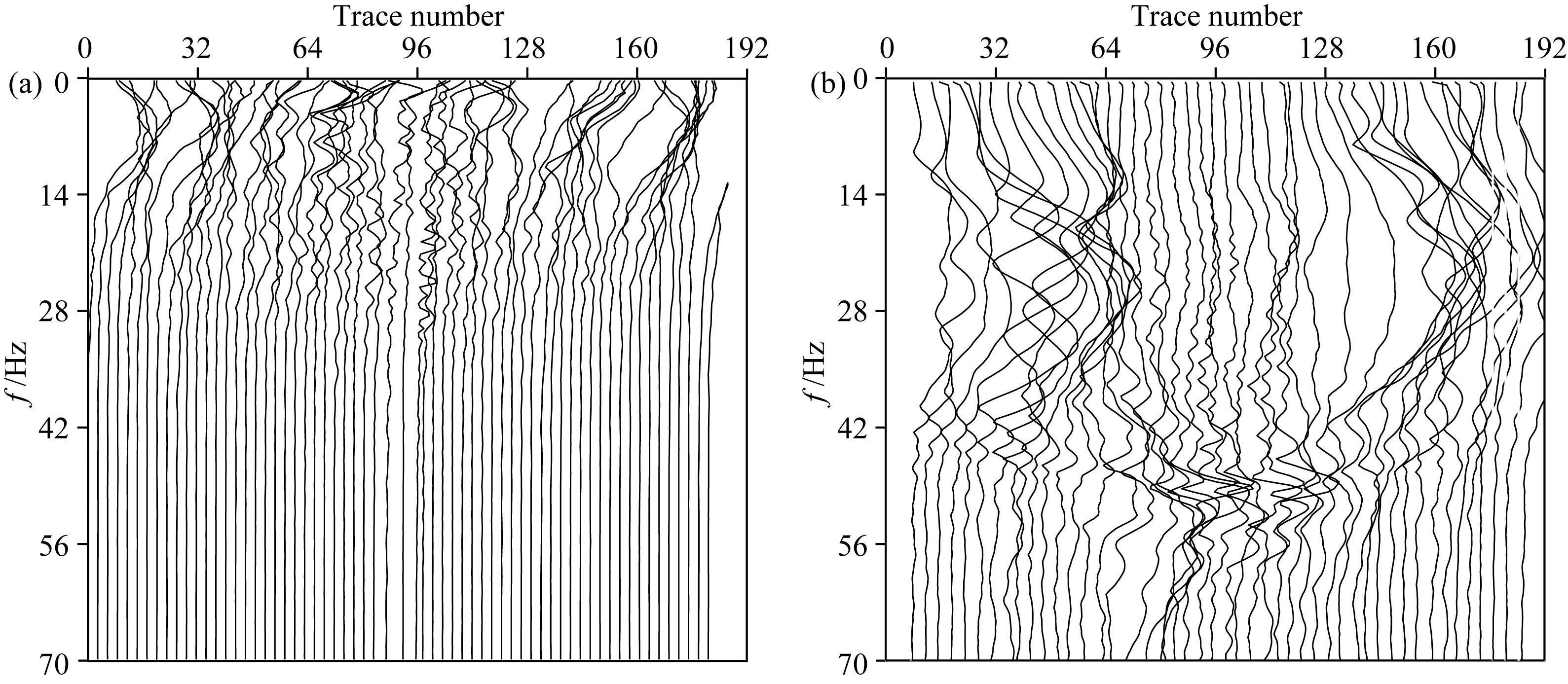
2.2.3 伴随震源频谱分析伴随震源主频和含有的低频成分决定着FWI是否会陷入局部极小值.伴随震源主频越高或者缺失低频成分越多,越容易出现周波跳跃问题,即反演结果精度越低.为了证明解调包络方法有较好的重构低频能力,本文利用Butterworth平滑高通滤波器滤除9 Hz以下的低频信息,震源函数主频22 Hz,震源位于96道.从图 6中可以看出,当地震数据缺失9 Hz低频信息的情况下,经解调包络方法处理之后,低频成分得到了恢复.解调包络FWI伴随震源频带范围为:0~25 Hz,然而相同条件下Hilbert包络FWI伴随震源频带范围为:0~70 Hz.震源附近主要为反射波信息,如图 6b(96道附近) 所示,Hilbert包络FWI伴随震源中的反射波低频成分并没有得到很好地恢复,反而具有很高的主频,使得整个反演过程容易产生周波跳跃问题.从图 6的对比结果中可以看出解调包络方法有效地重构出了地震数据中缺失的低频成分 (0~9 Hz),并且很好地降低了FWI伴随震源主频,能够缓解FWI的周波跳跃问题.
|
图 6 单炮伴随震源频谱 (a) 解调包络FWI伴随震源频谱;(b) Hilbert包络FWI伴随震源频谱. Fig. 6 Single shot spectra of adjoint source (a) Spectrum of DEFWI adjoint source; (b) Spectrum of HEFWI adjoint source. |
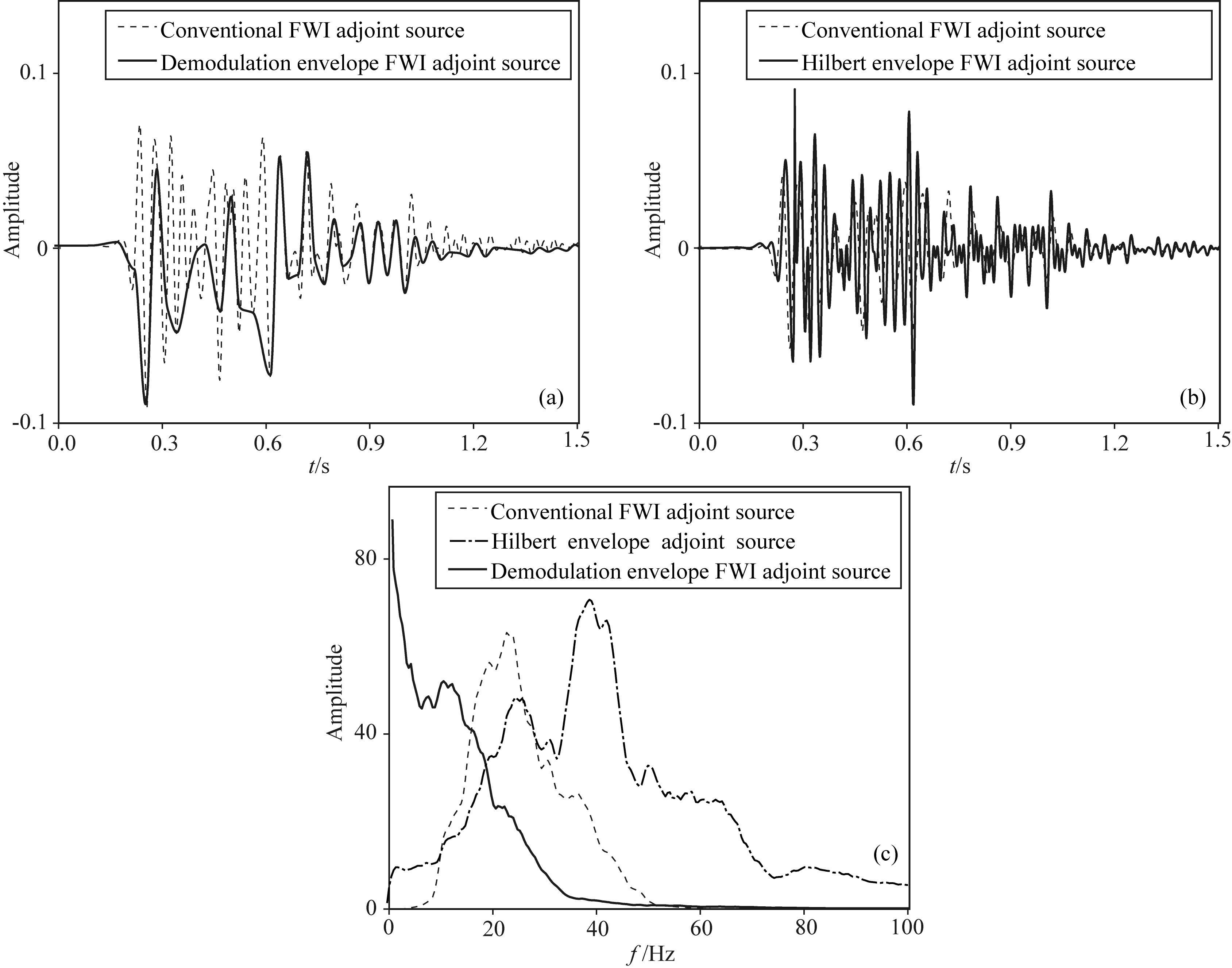
从单炮记录伴随震源中抽取一道进行分析,如图 7所示.从图 7中可以看出解调包络FWI伴随震源波形变化较常规FWI伴随震源更平缓 (图 7a),而Hilbert包络FWI伴随震源波形变化较常规伴随震源更剧烈 (图 7b).通过频谱分析 (图 7c) 可以看出,解调包络FWI伴随震源中含有丰富的低频信息,且伴随震源的主频较低.Hilbert包络虽然重构出了低频成分,但Hilbert包络FWI伴随震源主频相对于常规FWI伴随震源提高到了近42 Hz,较高主频的伴随震源极易让FWI陷入局部极小值,产生周波跳跃现象,影响FWI最终的反演精度.通过图 7的波形与频谱对比发现,无论从低频重构的角度还是伴随震源主频的角度,解调包络方法都优于Hilbert包络方法.
|
图 7 单道伴随震源 (a) 常规FWI伴随震源与解调包络FWI伴随震源波形;(b) 常规FWI伴随震源与Hilbert包络FWI伴随震源波形;(c) 频谱. Fig. 7 Single trace adjoint source (a) Adjoint source of conventional FWI and DEFWI; (b) Adjoint source conventional FWI and HEFWI; (c) Spectrum. |
震源函数是FWI过程中的重要参数,为了解决FWI过程中震源函数不准确的问题,本文提出伴随状态震源函数反演方法.该震源函数反演方法利用残差反传波场得到震源函数的更新梯度,避免求取Jacobian矩阵,大大节约了震源函数梯度计算所需要的时间.同时该震源函数反演方法只利用震源附近直达波信息,即只需要正演一小部分模拟波场,避免利用整个地震记录进行反演,大大缩短了正演模拟所需要的计算时间.震源附近直达波与地下模型信息无关,只利用震源附近直达波信息进行反演,有效避免了地下速度模型对震源函数反演的干扰.
伴随状态震源函数反演方法,是一个不断利用模拟数据直达波去拟合实际数据直达波的过程,最终找到一个震源函数使得数据残差平方最小.因此可将伴随状态震源函数反演方法的目标函数定义为
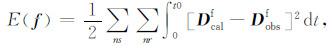
|
(7) |
其中Dcalf表示震源附近模拟记录的直达波,Dobsf表示震源附近观测记录直达波.目标函数对震源函数函数f的导数可表示为

|
(8) |
二维时间域常密度声波方程为
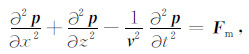
|
(9) |
其中p为声波波场,f为震源函数,一维时间序列.Fm表示震源函数对应着模型空间的一个矩阵,称为震源矩阵.将声波方程简化写成算子的形式为
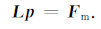
|
(10) |
将公式 (10) 两边同时对震源函数f求导得到 (Pratt et al., 1998):

|
(11) |
其中正演算子L与震源函数无关,有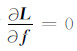
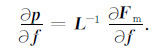
|
(12) |
将方程 (12) 代入方程 (8) 中,得到震源函数反演的更新梯度为
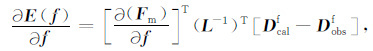
|
(13) |
其中伴随震源定义为: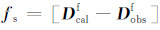
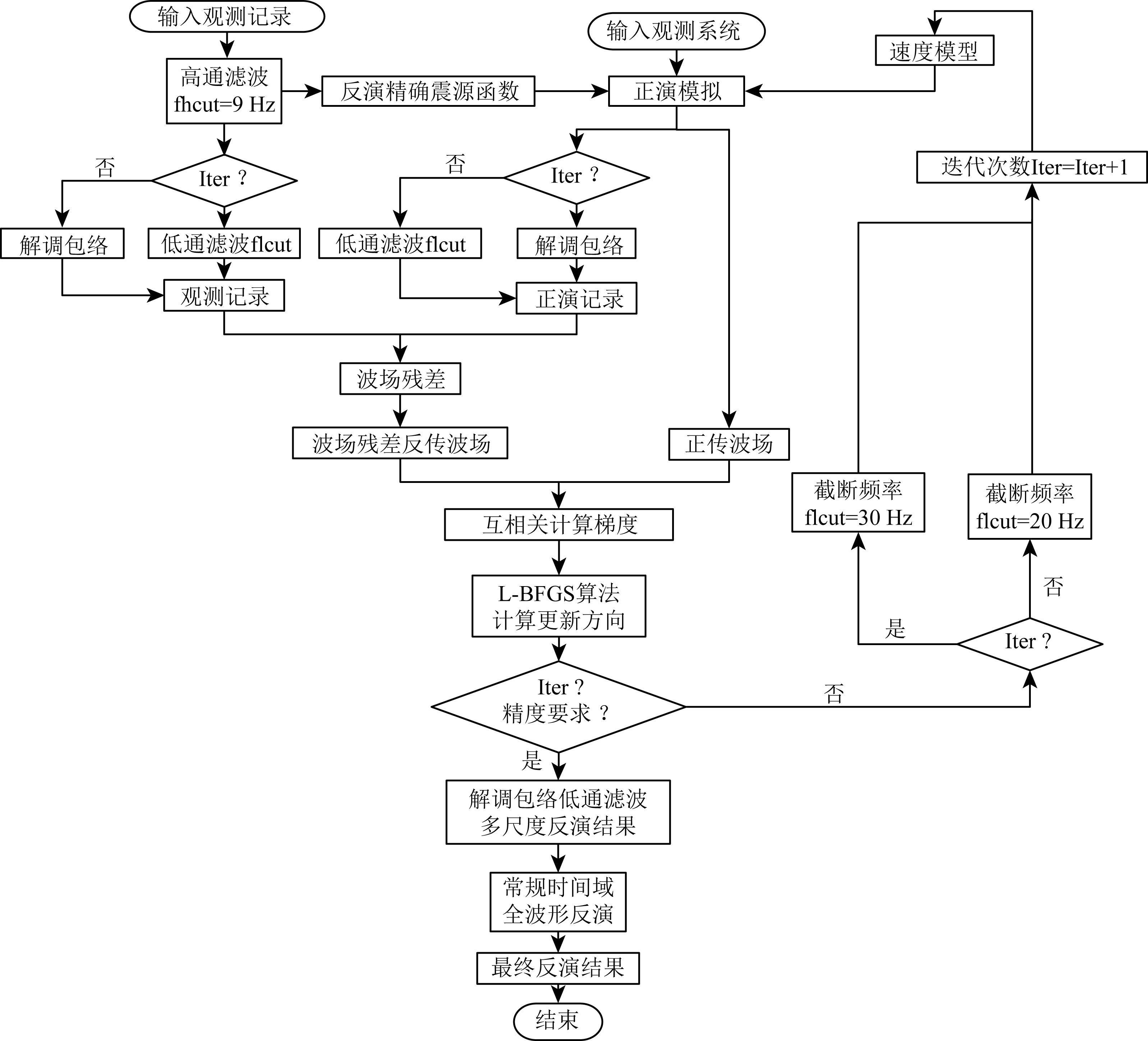
本文为了更好地模拟缺失低频的观测记录,利用Butterworth高通滤波滤除观测记录中9 Hz以下的低频信息,同时确保观测记录与模拟记录经历相同的处理过程,这样能有效避免因人为处理而导致数据不匹配问题.当地震数据中缺失低频信号时,低通滤波多尺度反演策略并不能根本上解决周波跳跃问题.针对地震数据低频缺失问题本文利用解调包络重构地震数据中的低频成分,利用重构出的低频数据进行FWI可以得到一个相对较好的初始速度模型 (宏观模型),再通过低通滤波多尺度FWI,得到最终的反演结果.同时利用伴随状态震源函数反演方法可以得到精确震源函,有效缓解了FWI周波跳跃问题.基于精确震源函数的解调包络多尺度FWI,有效解决了震源函数不准确、缺失低频成分、数据主频过高等因素导致的周波跳跃问题,详细流程如图 8所示.
|
图 8 基于精确震源函数的解调包络多尺度FWI Fig. 8 Demodulation envelope multi-scale full waveform inversion based on precise seismic source function |
如图 8所示,基于精确震源函数的解调包络多尺度FWI共分为4步:(1) 利用解调包络FWI得到较好的初始速度模型;(2) 利用低通滤波滤除地震数据中20 Hz以上的高频信息 (flcut=20 Hz),缓解地震数据因主频而过高而导致的周波跳跃问题;(3) 滤除地震数据中30 Hz以上的高频信息 (flcut=30 Hz),进一步获得模型的细节构造;(4) 利用第三步的反演结果作为初始速度模型进行常规时间域FWI,得到最终的反演结果.图 8其中Iter代表迭代次数,整个流程是根据迭代次数来判断进行哪一步FWI.
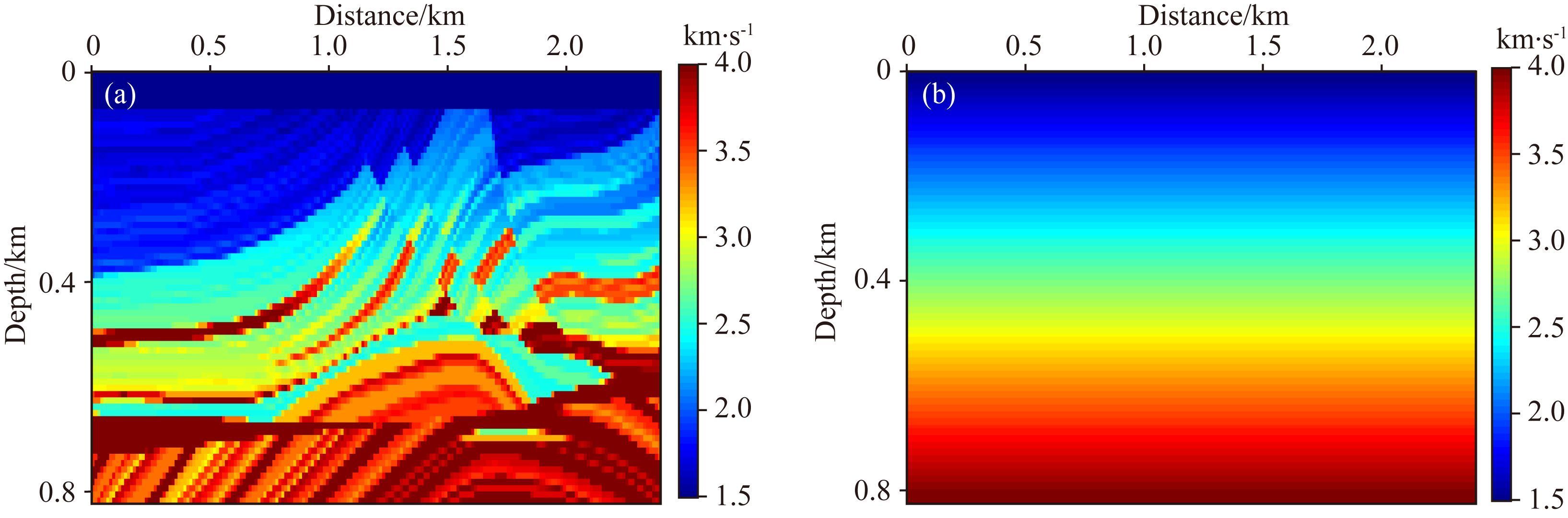
3 数值试验基于二维时间域常密度声波方程,对本文提出的新方法 (解调包络FWI和伴随状态震源函数反演方法) 进行测试.对Marmousi模型进行抽稀处理,测试模型网格横纵大小为192×69,模型网格间距为12.5 m,横向距离为2.4 km,纵向距离为0.8625 km.震源沉放深度为50 m,检波器沉放深度为12.5 m.震源选用22 Hz主频的雷克子波,采样间隔为0.001 s,时间采样总长度为2.5 s.本文利用水平线性模型作为FWI的初始速度模型,速度变化范围从1.5 km·s-1到4 km·s-1.从图 9b中可看出,线性初始速度模型与真实速度模型差距很大,不仅没有原始模型中深层的主要构造,甚至不满足速度变化的趋势.
|
图 9 速度模型 (a) 真实速度模型;(b) 线性初始速度模型. Fig. 9 Velocity models (a) True velocity model; (b) Linear initial velocity model. |

|
图 10 单炮观测记录 (a) 完整观测记录;(b) 截断观测记录. Fig. 10 Single shot recorded data (a) Complete recorded data; (b) Truncated recorded data. |
在震源函数反演的测试过程中选用图 9真实速度模型和水平线性速度模型作为震源函数反演的背景速度,利用线性初始震源函数作为震源函数反演的初始值,通过伴随状态法 (公式13) 求得震源函数反演的更新梯度,结合L-BFGS优化算法,对震源函数进行更新,使得线性初始震源函数不断向真实震源函数靠近,最终得到精确的震源函数反演结果.
本文只截取观测记录前0.15 s的波形进行震源函数反演,该截断时窗策略能有效减少正演模拟所需要的时间;避免地下速度扰动对震源函数反演结果的影响;减少了震源函数反演的未知数的个数,使得反演过程更加稳定;同时减少了反演结果的多解性.由于震源附近直达波未受到地下速度模型的影响,其波形与振幅最接近震源函数,最简单的方法是直接提取震源附近的直达波波形作为震源函数,从图 11可以发现,直达波 (距离震源水平距离50 m的检波器采集得到) 与真实震源函数存在明显的相位,振幅和延时不匹配等现象.FWI极度依赖震源函数,震源函数微小的错误都会使得FWI出现数据不匹配的问题.如果利用直达波作为震源函数直接进行FWI,将得不到预期的反演精度.

|
图 11 真实震源函数与直达波 Fig. 11 True source function and direct waves |
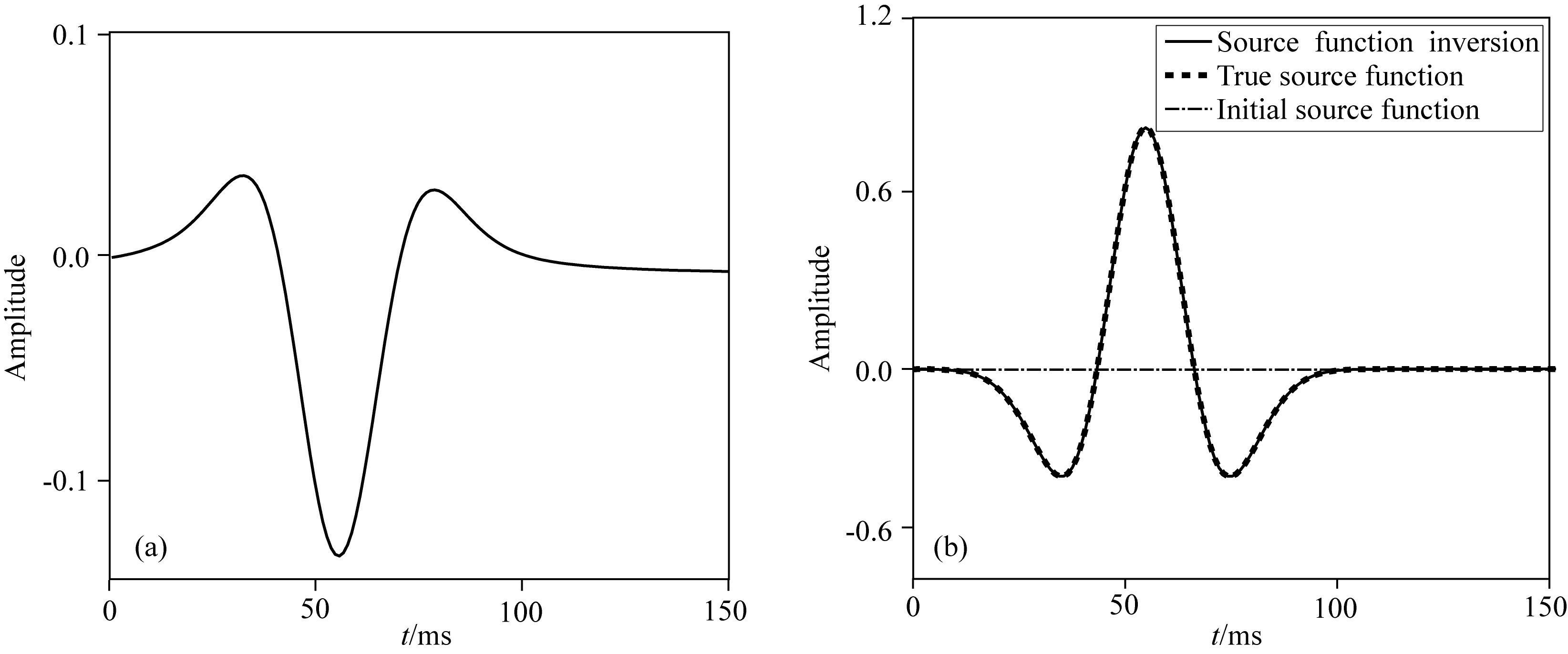
如图 12所示的真实震源函数和用于反演的线性初始震源函数,两者波形差距很大,线性初始震源函数不含有任何先验信息.从第一步反演的负梯度可以发现 (13a),其波形与真实震源函数相似,按照公式 (13) 求得的梯度,并利用L-BFGS优化算法不断对初始震源函数进行更新,最终到如图 13b所示的反演震源函数,其波形、相位、振幅等信息与真实震源函数完全一致.该反演结果证明了本文提出的伴随状态震源函数反演方法具有不依赖初始震源函数、不依赖初始速度模型、反演精度高等优点.

|
图 12 震源函数 (a) 真实震源函数;(b) 线性初始震源函数. Fig. 12 Source function (a) True source function; (b) Linear initial source function. |
|
图 13 震源函数反演 (a) 负梯度;(b) 最终反演结果. Fig. 13 Source function inversion (a) Negative gradient; (b) Final inversion result. |
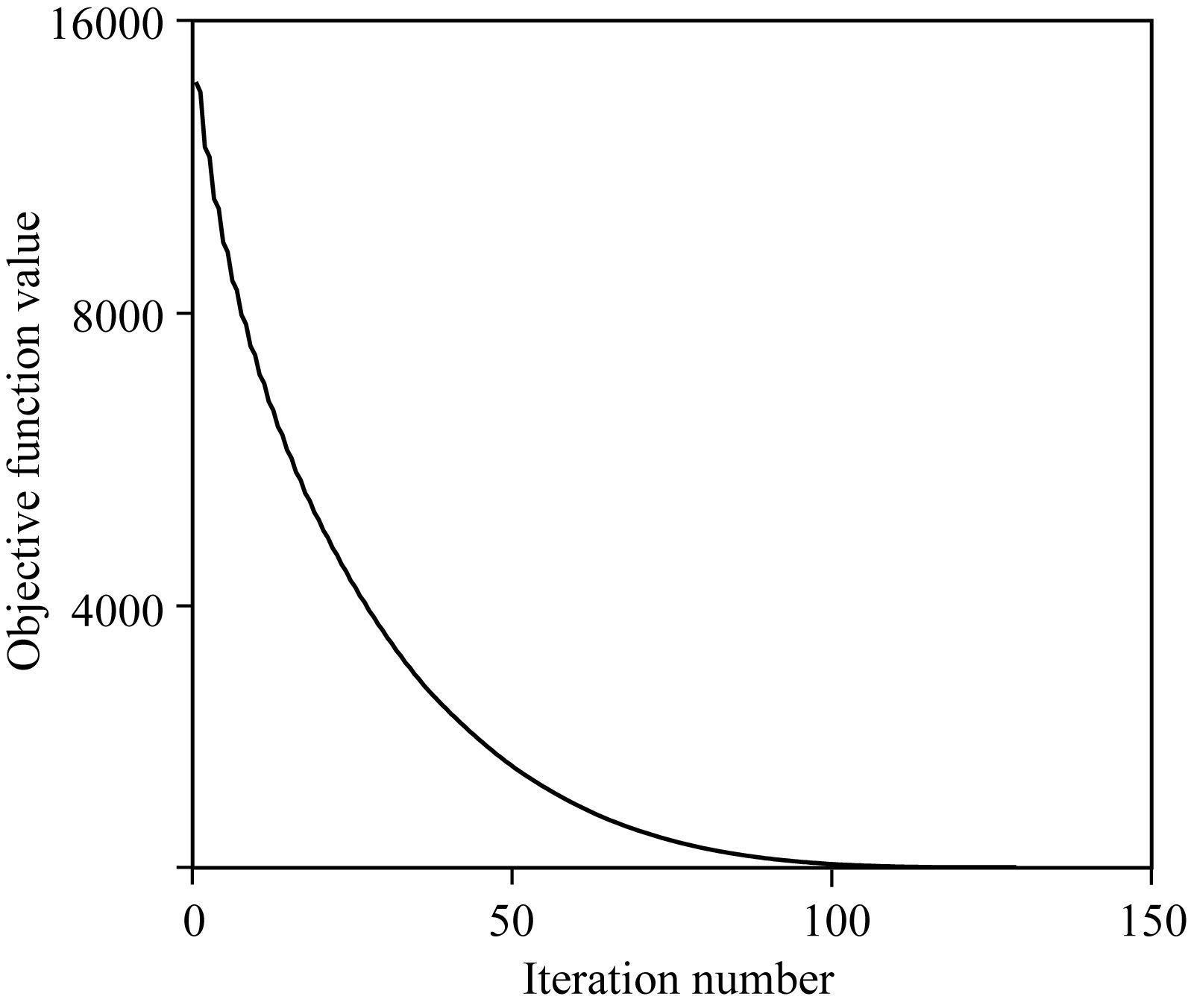
根据公式 (7) 所示的目标函数,当残差逐渐减小,即证明反演得到的震源函数越来越接近真实震源函数,最终目标函数的残差达到了0.001,停止更新迭代.目标函数的变化曲线如图 14所示,证明了伴随状态震源函数反演方法很好地解决了震源函数估计不准确的问题.该反演方法可为FWI,逆时偏移等波动方程成像方法提供精确的震源函数.
|
图 14 伴随状态震源函数反演目标函数 Fig. 14 Objective function of adjoint-state source function inversion |
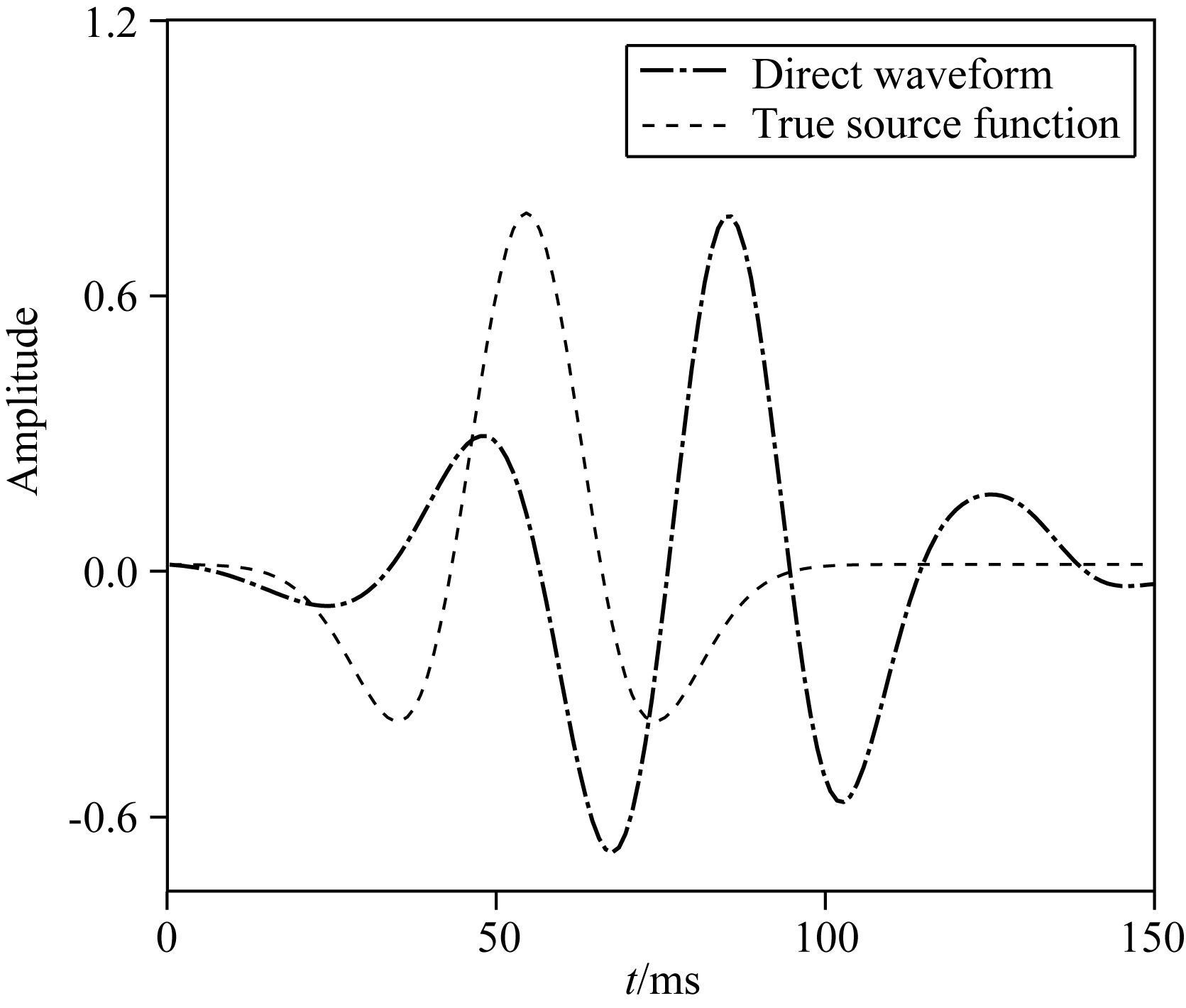
实际数据中常含有低频噪声,同时有效信号的低频能量较弱,需要利用高通滤波等去噪策略进行地震数据预处理,使得地震数据中的低频信号遭到破坏.通过缺失低频成分的地震记录估计得到的震源函数与真实震源函数相位和振幅相差更大.利用不准确的震源函数进行正演得到模拟记录与观测记录进行匹配,因震源函数不准,二者在匹配的过程中容易陷入局部极小值,产生周波跳跃问题.本文提出的伴随状态震源函数反演方法,可以在缺失低频的观测记录中反演得到精确的震源函数.为了测试该震源函数反演方法的精度,本文利用Buttreworth平滑高通滤波器,滤除观测记录9 Hz以下的低频信息.缺失低频信息的直达波波形变化更剧烈,如图 15所示.
|
图 15 真实震源函数与缺失低频成分的直达波 Fig. 15 True source function and direct waves without low-frequency information |
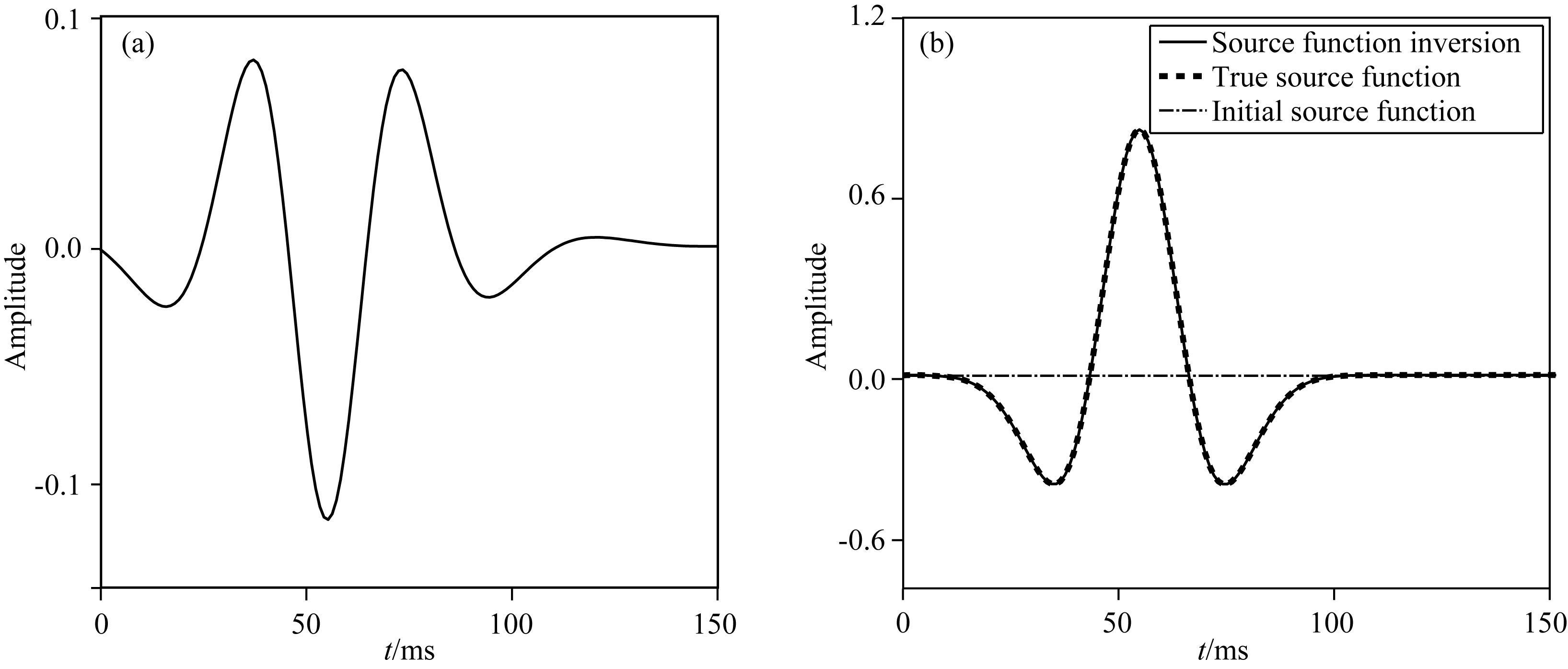
当地震数据缺失低频成分时,真实震源函数与直达波 (距离震源水平距离50 m检波器采集得到) 相位,振幅和延时等信息都存在明显的区别.不准确的震源函数直接用FWI,很容易出现正演记录与观测记录数据不匹配,使得FWI产生周波跳跃问题.利用图 9所示的真实速度模型和初始速度模型作为背景速度进行震源函数反演,同时利用线性初始震源函数 (图 12b) 作为反演的初始值.如图 16b所示的反演结果表明,即使在地震数据中缺失大量低频信号的前提下,伴随状态法反演得到的震源函数,波形的相位和振幅几乎与真实震源函数完全重合,证明了该震源函数反演方法,即使当观测记录信号不完整的情况下也可为地震数据处理提供一个精确的震源函数,但是观测记录和模拟记录必须经历相同的处理过程,避免人为因素导致的数据不匹配问题.
|
图 16 缺失低频震源函数反演 (a) 负梯度;(b) 最终反演结果. Fig. 16 Source function inversion without low-frequency information (a) Negative gradient; (b) Final inversion result. |
震源函数在FWI中占有重要的地位,若震源函数的相位和振幅不准则会导致反演结果中地质层位错动,甚至得不到正确的反演结果.敖瑞德等 (2015)利用交叉褶积的方法消除了震源函数对FWI的影响,该方法有效缓解了因震源函数不准而导致的周波跳跃现象,但是直接消除震源函数可能会损失一些可靠地质信号.最简单的方法是利用直达波作为震源函数,如图 11所示,直达波与真实震源函数不仅存在波形上的差别,还存在较大的延时差.本文分别用伴随状态震源函数反演方法得到的精确震源函数和直接从观测记录中提取的直达波作为震源函数进行FWI测试.并用图 9所示的真实模型和线性初始模型进行震源函数对FWI影响测试.
从图 17中可以看出,利用反演得到的精确震源函数进行FWI测试结果 (图 17a) 明显优于直达波作为震源函数的测试结果 (17b).图 17a虽然用精确的震源函数进行常规FWI测试,但是得到的反演结果并不理想,主要是因为初始模型较差且伴随震源主频较高,产生了明显的周波跳跃问题.从图 17b中可以看出,由于直达波与真实震源函数存在较大的延时差,在匹配的过程中极易出现周波跳跃现象,导致反演结果完全错乱.

|
图 17 常规FWI震源函数影响测试 (a) 反演得到的精确震源函数FWI测试结果;(b) 直达波作为震源函数FWI测试结果. Fig. 17 Influence tests of seismic source function in conventional FWI (a) FWI test with precise seismic source function obtained by inversion; (b) FWI test with initial seismic source function obtained from direct waves. |
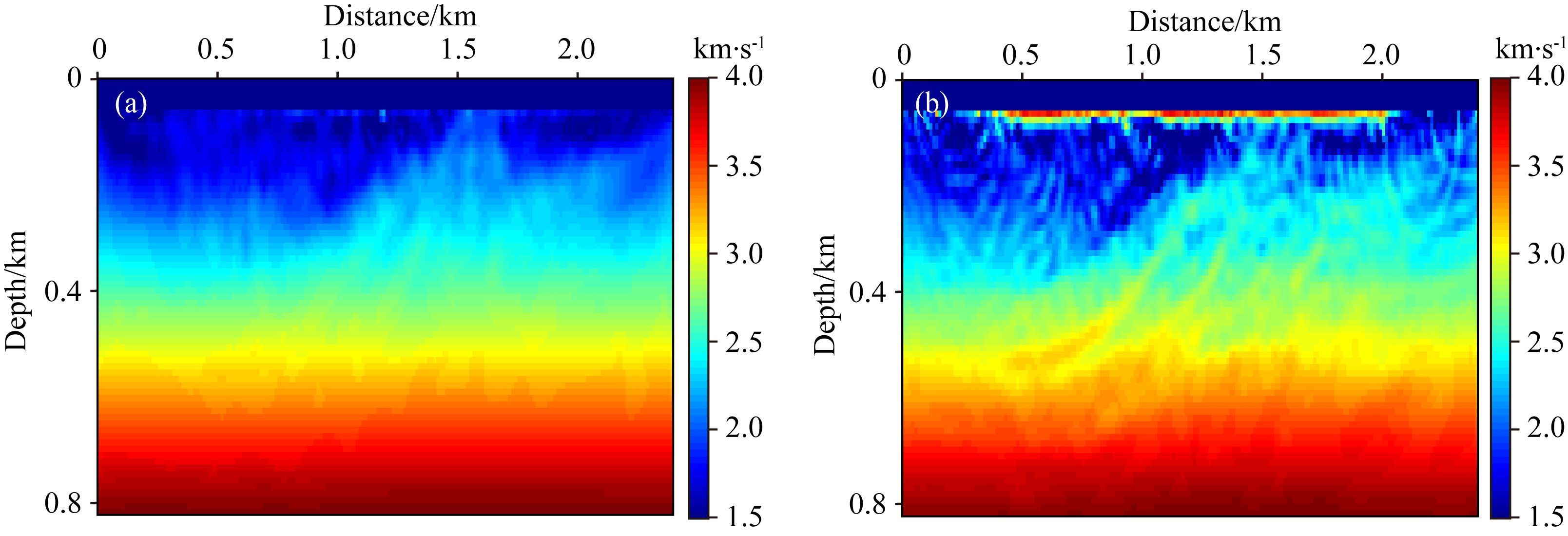
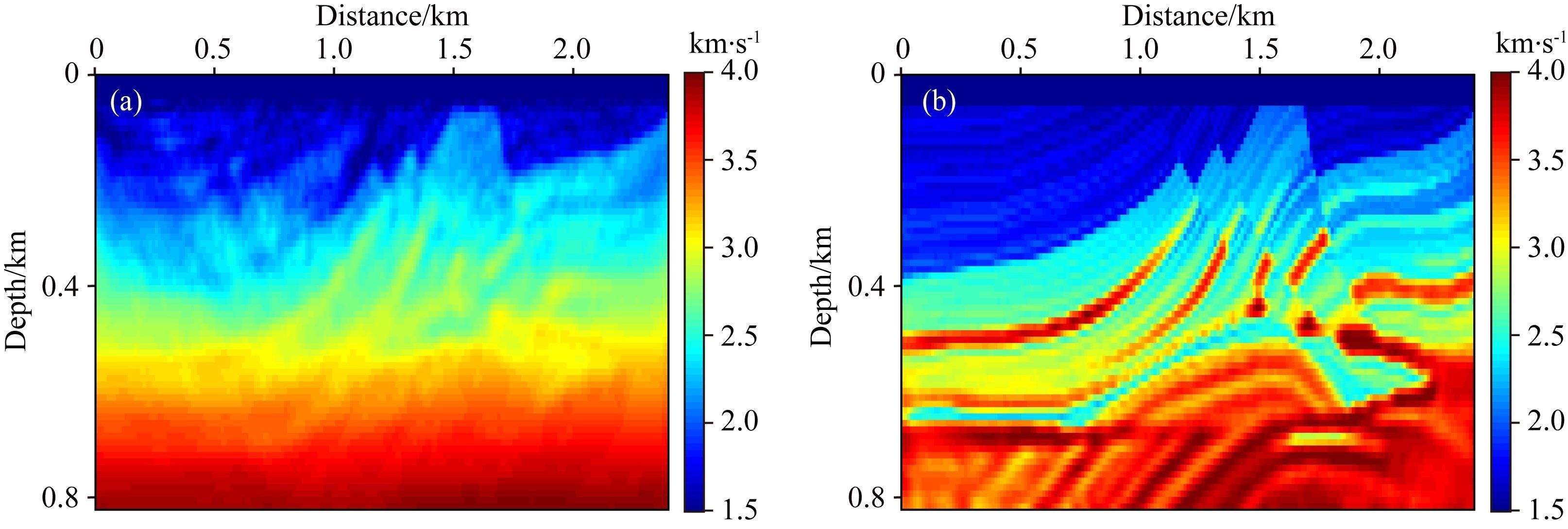
从图 18可以看出当震源函数不准确的情况下 (直达波作为震源函数),解调包络FWI基本能够恢复出Marmousi模型的宏观构造 (图 18a),证明了解调包络FWI对震源函数不敏感,但进一步利用解调包络多尺度FWI测试的过程中出现了明显的错误.如图 19,可以看出利用伴随状态法反演得到的精确震源函数有效压制了FWI过程中因震源函数不准带来的周波跳跃问题.对比图 18和图 19可以发现,震源函数在FWI中占有重要的地位,震源函数的准确与否直接关系到FWI的精度.同时从图 19与17a的对比结果可以看出,解调包络多尺度FWI能够有效缓解周波跳跃问题.本节测试结果证明了,伴随状态震源函数反演方法在FWI应用具有一定的价值,解决了FWI震源函数不准确的问题,同时可为逆时偏移等波动方程成像方法提供精确的震源函数.
|
图 18 直达波作为震源函数解调包络多尺度FWI测试 (a) 解调包络FWI反演结果;(b) 解调包络多尺度FWI反演结果. Fig. 18 Multi-scale DEFWI tests with initial seismic source function obtained from direct waves (a) DEFWI result; (b) Multi-scale DEFWI result. |
|
图 19 基于精确震源函数的解调包络多尺度FWI测试 (a) 解调包络FWI结果;(b) 解调包络多尺度FWI结果. Fig. 19 Multi-scale DEFWI test with precise seismic source function (a) DEFWI result; (b) Multi-scale DEFWI result. |
FWI是一个强非线性优化过程,当观测记录与模拟记录中对应的两个波峰相差大于半个周期时就会出现周波跳跃现象,尤其当观测记录缺失低频成分时,波形变化剧烈,很容易出现波形匹配错误的问题,即周波跳跃.常规采集方法得到的野外采集数据常常缺失低频成分,导致地震数据波形变化剧烈,波形匹配困难,这给FWI在实际数据应用中带来了巨大的挑战.
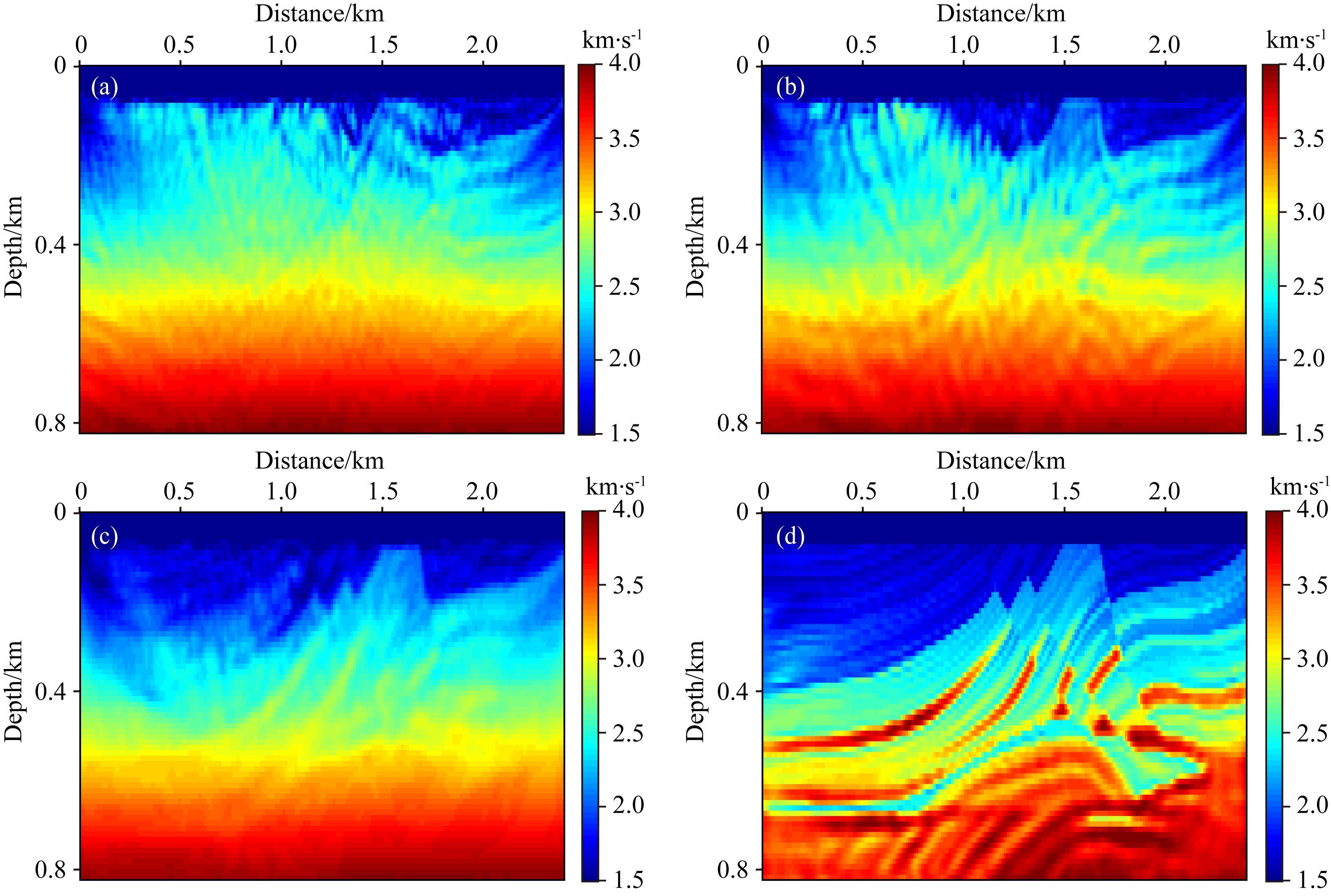
为了证明本文提出的解调包络能够有效重构低频成分,首先对地震记录利用Butterworth高通滤波器滤除9 Hz以下的低频信号,利用缺失低频信息的地震数据分别进行常规FWI、低通滤波多尺度FWI和解调包络多尺度FWI测试.真实模型和线性初始速度模型如图 9所示.图 20a与图 17a对比发现,虽然二者由于伴随震源主频过高的原因使得反演结果较差,但也可以明显看出,当常规FWI在低频缺失的情况下反演结果更差 (图 20a).如图 20a和20b对比可以看出,在缺失9 Hz以下的低频信息时,低通滤波多尺度FWI (20b) 相比于常规FWI结果 (20a) 得到了一定的改善,但当缺失9 Hz以下低频信息时,低通滤波多尺度FWI最终反演结果并不理想,出现了明显的周波跳跃现象.从图 20c和20d可以看出,低通滤波多尺度FWI方法,可在低频完好情况下得到较好的反演结果,反演结果明显优于常规FWI和缺失低频信息的低通滤波多尺度FWI反演结果.图 20的数值模拟测试结果表明,低通滤波多尺度FWI,只有在低频完整的情况下才能充分体现其缓解周波跳跃的优势,然而当缺失9 Hz以下的低频信息时,低通滤波多尺度FWI并不能得到理想的反演结果.
|
图 20 FWI测试 (a) 缺失低频常规FWI结果;(b) 缺失低频低通滤波多尺度FWI结果;(c) 含低频信息,低通滤波截断频率flcut=10 Hz FWI结果;(d) 含低频信息,低通滤波多尺度FWI结果. Fig. 20 FWI tests (a) Conventional FWI result without low frequency information; (b) Low-pass filtering multi-scale FWI result without low-frequency information; (c) Low-pass filtering multi-scale FWI result with low-frequency information and truncate frequency of flcut=10 Hz;(d) Low-pass filtering multi-scale FWI result. |
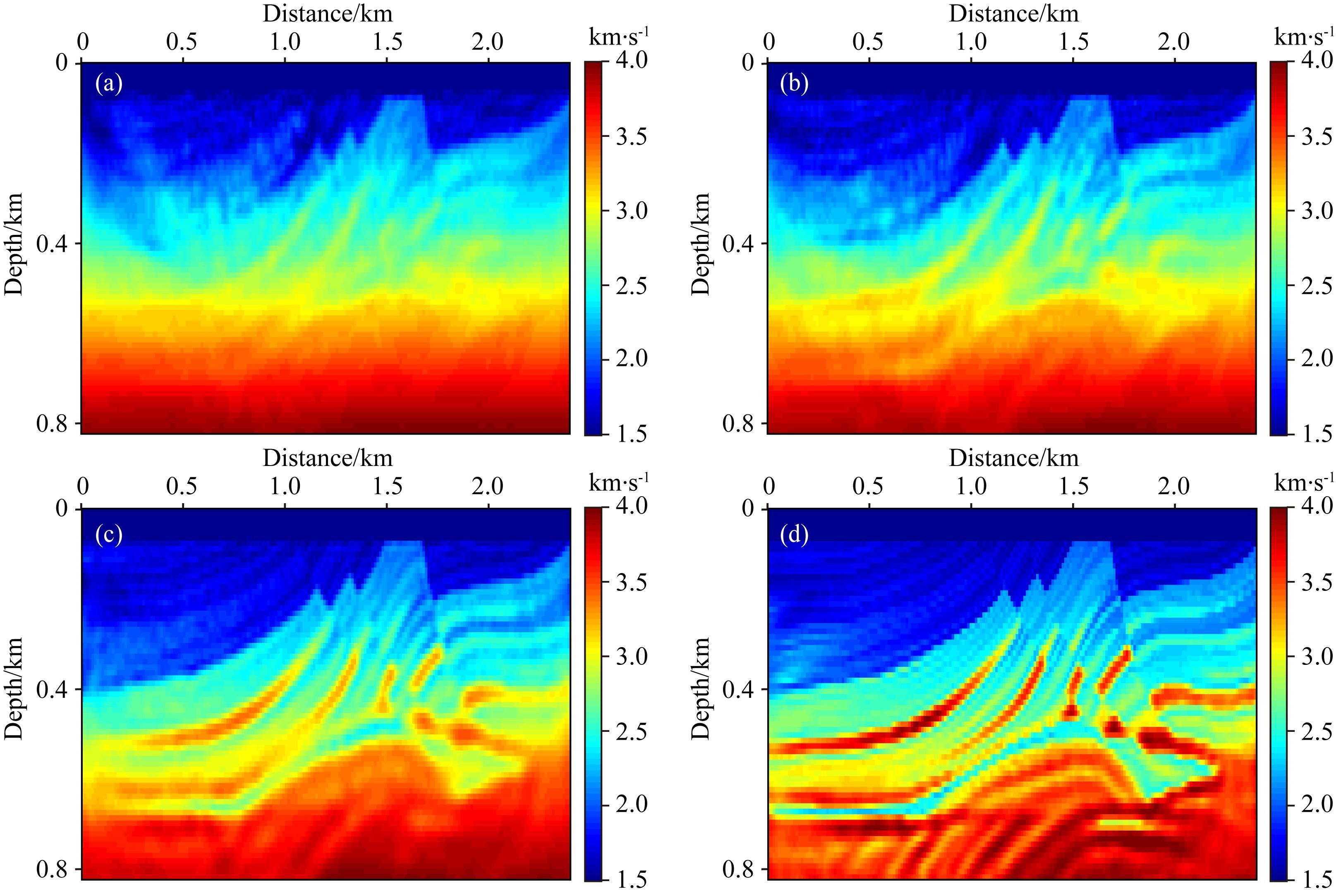
鉴于缺失低频信号导致低通滤波多尺度FWI测试结果较差 (图 20b) 的问题,本文利用解调包络方法根据原始地震记录波形信息重构出地震记录缺失的低频成分,用上述相同的参数测试解调包络+低通滤波多尺度FWI (解调包络多尺度FWI),反演结果如图 21所示.当地震数据缺失9 Hz以下低频信息时,利用解调包络FWI,可以得到一个较好的初始模型 (图 21a).如图 21b,21c可见,解调包络FWI得到的初始速度模型很好地缓解了周波跳跃现象,不断提高低通滤波的截断频率可以逐渐反演出Marmousi模型中的细节信息.如图 21d可以看出,当地震数据缺失低频信息且初始速度模型较差的情况下,利用解调包络尺度方法能够很好地缓解FWI的周波跳跃问题.模型测试结果证明了本文提出的解调包络多尺度FWI具有一定的实际应用价值,在低频成分严重缺失的地震数据中也可以得到高精度的反演结果.
|
图 21 缺失低频信息,解调包络多尺度FWI测试 (a) 解调包络FWI结果;(b) flcut=20 Hz的解调包络多尺度FWI结果;(c) flcut=30 Hz的解调包络多尺度FWI结果;(d) 解调包络多尺度FWI最终结果. Fig. 21 Multi-scale DEFWI tests without low-frequency information (a) DEFWI result; (b) Multi-scale DEFWI result with truncated frequency of flcut=20 Hz; (c) Multi-scale DEFWI result with truncated frequency of flcut=20 Hz; (d) Multi-scale DEFWI final result. |
野外采集的地震数据中存在严重的噪声干扰,然而常规FWI对噪声较为敏感,只有当地震记录信噪比较高的前提下FWI才能得到较好的结果,因此反演之前需对地震记录进行一系列的去噪处理.去噪过程是寻找有效信号与噪声区别的过程,例如对信号进行滤波处理,实际上滤波是以牺牲部分有效信号为代价来去除地震记录中的噪声.滤波去噪之后的地震记录与真实地震记录发生改变,导致了FWI数据匹配不准的问题.为了尽量减小去噪过程对地震记录破坏,本文利用解调包络多尺度FWI,可以在不去噪或者轻微去噪的情况下进行反演.本文通过讨论高斯噪声对地震记录的影响来分析FWI的抗噪能力,在含不同强度的高斯噪声环境中进行测试.如图 22所示,在单炮地震观测记录中加入不同强度的高斯噪声,使得整个地震记录信噪比逐渐降低,信噪比可以定义为
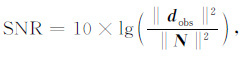
|
(14) |
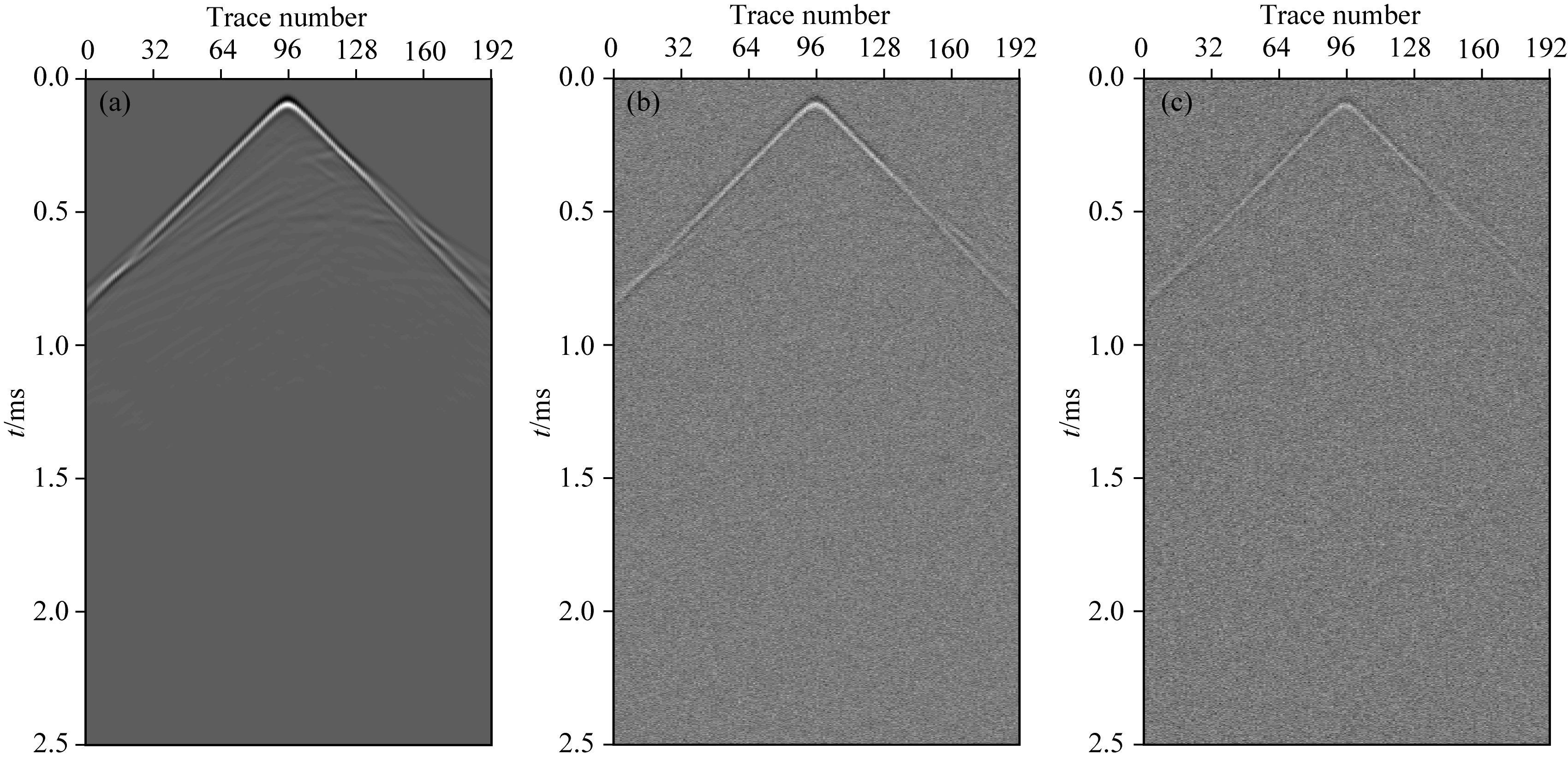
其中dobs表示观测记录,N表示加入的高斯噪声.从图 22可以看出高斯噪声对地震记录影响非常严重,当不加噪声时反射波相对明显 (图 22a),当信噪比SNR=-10.03时,地震记录只能看到部分直达波信号 (图 22c),其他有效信号完全淹没在噪声中.其中信噪比为负数,表示高斯噪声的功率谱大于有效信号的功率谱.
|
图 22 含不同强度的高斯噪声地震单炮观测记录 (a) 无噪观测记录;(b) 加入高斯噪声观测记录SNR=-3.92;(c) 加入高斯噪声观测记录SNR=-10.03. Fig. 22 Single shot recorded data with different intensities of Gaussian noise (a) Recorded data with no noise; (b) Recorded data with Gaussian noise SNR=-3.92;(c) Recorded data with Gaussian noise SNR=-10.03. |
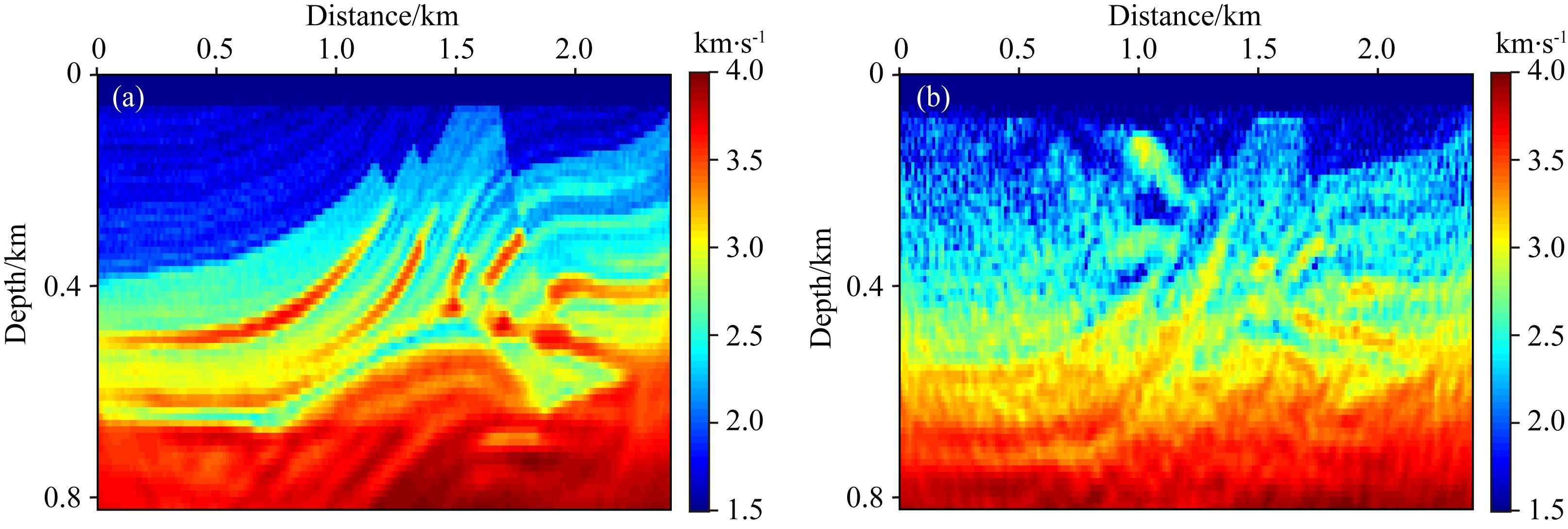
在地震数据含有较强高斯噪声的情况下,多尺度解调包络FWI与低通滤波多尺度FWI对比结果 (图 23) 可以看出,解调包络多尺度FWI方法能在较低信噪比的情况下也可以得到较好的反演结果,然而常规多尺度FWI出现明显的周波跳跃现象,证明了解调包络多尺度FWI具有较强的抗噪能力.
|
图 23 含高斯噪声多尺度FWI测试 (a) 多尺度解调包络FWI结果SNR=-3.92;(b) 多尺度FWI结果SNR=-3.92. Fig. 23 Multi-scale FWI tests with Gaussian noise (a) Multi-scale DEFWI with Gaussian noise SNR=-3.92;(b) Multi-scale FWI with Gaussian noise SNR=-3.92. |
解调包络FWI和Hilbert包络FWI都是通过重构地震数据中的低频成分来缓解FWI的周波跳跃问题.但是Hilbert包络与原始波形宏观信息存在着较大的差别 (图 2, 3, 5),因此必须利用链式法则来求得FWI的伴随震源,但是链式法则得到的伴随震源主频偏高.时间域FWI的梯度是通过正传波场与伴随震源反传波场互相关得到,如果伴随震源主频较高,互相关之后的波形能量集中在高频段,这样得到的梯度多为模型的细节信息,在没有得到速度模型宏观构造的前提下,过多的细节信息很容易导致FWI陷入局部极小值,出现严重的周波跳跃问题.
解调包络FWI相比于Hilbert包络FWI,不仅能够重构出更丰富的低频信息,更重要的是得到的伴随震源主频较低,较低的伴随震源主频互相关之后波形能量主要集中在低频段,这样得到的梯度多为模型的宏观信息,先利用解调包络FWI来更新模型的宏观构造,再利用低通滤波多尺度策略逐渐更新模型的细节信息.该解调包络多尺度FWI能够有效地缓解周波跳跃问题.
为了分析解调包络和Hilbert包络的优越性,本文都利用平方目标函数 (Chi et al., 2014) 进行对比分析,公式为
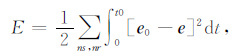
|
(15) |
其中ns, nr分别表示震源数目和检波器的数目.e0表示模拟数据的Hilbert包络,e表示实际数据的Hilbert包络.伴随震源利用链式法则可以求得:

|
(16) |
其中H表示Hilbert变换, u表示模拟数据,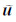
当震源函数利用22 Hz的雷克子波时,Hilbert包络FWI的伴随震源主频能达到42 Hz (图 7),如此高的主频很容易出现周波跳跃问题,因此Chi等 (2014)利用较低主频的雷克子波进行正演模拟 (雷克子波主频8 Hz,网格距为15 m).为了将解调包络FWI与Hilbert包络FWI结果进行对比,本文分别利用低主频和高主频的雷克子波进行测试 (主频8 Hz和主频20 Hz,虑除5 Hz以下低频信息).真实速度模型和初始速度模型如图 9所示.
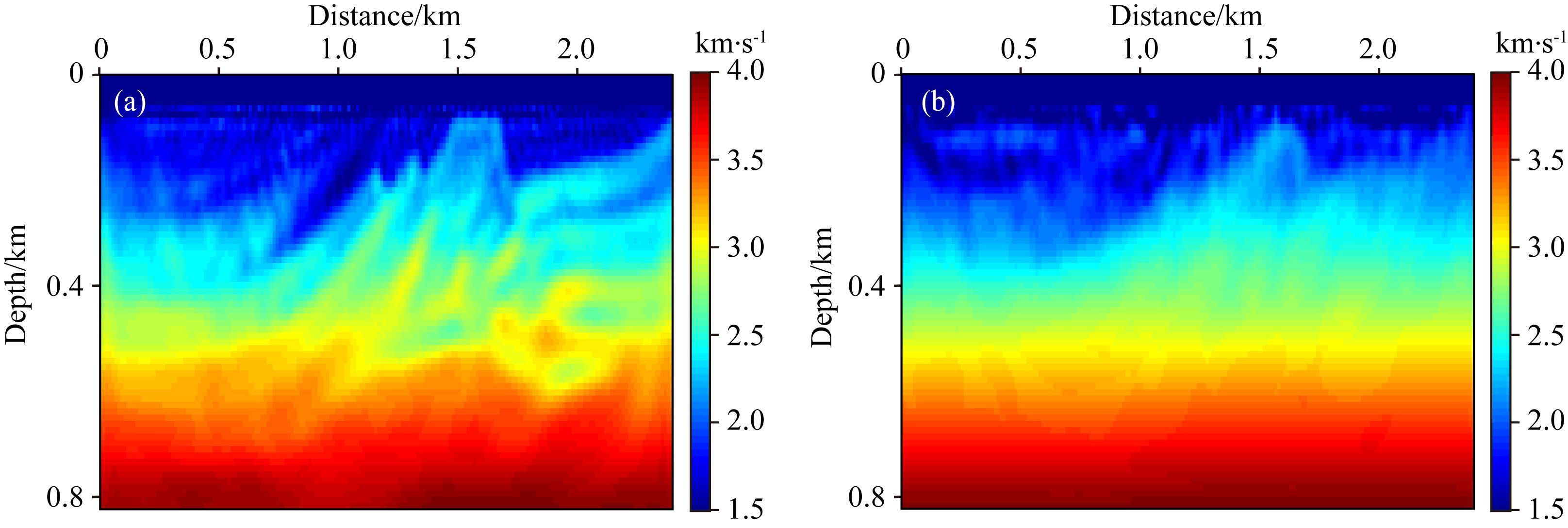
本文的主要目的是解决FWI的周波跳跃问题,所以只需要对比两种方法在缺失低频情况下,且不利用其他多尺度策略,恢复宏观速度模型的能力.从图 24中可以看Hilbert包络FWI的反演结果似乎比解调包络FWI的反演结果好,但是该测试结果是在雷克子波主频极低的情况下 (8 Hz) 得到的反演结果,而此时解调包络FWI的伴随震源主频远远低于8 Hz,这么低的主频只能得到更宏观的模型构造.从图 24中可以看出,解调包络FWI结果几乎不含有细节信息,完全是模型的宏观特征.低主频的雷克子波反演结果对比表明,在缺失低频情况下,解调包络FWI更适合反演模型的宏观构造.
|
图 24 FWI测试 (a) Hilbert包络FWI结果; (b) 解调包络FWI结果. Fig. 24 FWI tests (a) HEWI result; (b) DEFWI result. |
利用高主频的雷克子波进行测试 (主频20 Hz,网格距15 m,虑除5 Hz以下低频信息),结果如图 25所示,可以明显看出Hilbert包络FWI存在明显的周波跳跃问题,这主要是由于Hilbert包络FWI的伴随震源主频较高,不能很好地恢复模型的宏观信息.然而解调包络能够重构低频的同时,降低了伴随震源的主频.野外的实测地震数据有时主频能达到40 Hz,这么高主频的地震数据,如果不加任何处理手段,直接利用Hilbert包络方法来得到FWI的伴随震源,其伴随震源主频更高,极易出现周波跳跃问题,伴随震源这么高的主频甚至都没有办法进行有限差分数值模拟.利用解调包络的方法可以在重构低频的同时,降低伴随震源的主频,能够有效缓解FWI的周波跳跃问题.高主频的雷克子波测试结果表明,解调包络FWI方法在缺失低频,地震数据主频较高的情况下,能得到较好的初始速度模型.

|
图 25 FWI结果 (a) Hilbert包络FWI结果; (b) 解调包络FWI结果. Fig. 25 FWI tests (a) HEFWI result; (b) DEFWI result. |
从图 24和图 25对比结果证明了,解调包络方法在重构低频和降低伴随震源主频方面都优于传统Hilbert包络方法.在地震数据缺失低频和主频较高的情况下,利用解调包络FWI可以得到较好的初始速度模型.
4 结论(1) 为进一步推动FWI的发展,在前人的理论基础上,本文提出解调包络方法根据原始地震记录波形信息来重构低频信息.该方法计算效率高、重构低频信号强、重构的低频信息可靠,且完全基于数据驱动.利用重构出的含有丰富低频信息的解调包络进行FWI初始速度建模,可以得到一个高精度的初始速度模型,有效缓解低频缺失和初始速度模型不准确带来的周波跳跃问题.
(2) 伴随状态震源函数反演方法,利用震源附近直达波信息就可以反演得到精确的震源函数,解决了震源函数不准确的问题.该震源函数反演方法具有不依赖初始速度模型、不依赖初始震源函数、反演精度高、计算速度快等优点.可为FWI以及逆时偏移提供一个精确的震源函数,有效缓解了因震源函数不准确带来的周波跳跃问题.
(3) 解调包络FWI结合低通滤波多尺度反演策略 (解调包络多尺度FWI),可以从低频到高频逐渐反演模型中的细节信息.同时可以对缺失低频的地震观测记录,且在初始速度模型较差的情况下得到高精度的FWI反演结果.
(4) 高斯噪声测试结果可以看出,在较低信噪比的情况下,利用解调包络多尺度FWI能得到高精度的反演结果.证明了解调包络多尺度FWI方法具有较强的抗噪性.
陆上地震数据相比于海上震数据噪声干扰和低频缺失问题更为严重,这些问题使得陆上地震数据FWI难度更大.本文提出的解调包络多尺度FWI既能够重构出丰富的低频信号和降低伴随震源的主频,同时又具有较强的抗噪能力,在未来的研究发展中,该方法有可能很好地解决陆上地震数据FWI的相关难题.
| Ao R D, Dong L G, Chi B X. 2015. Source-independent envelope-based FWI to build an initial model. Chinese J. Geophys. (in Chinese), 58(6): 1998-2010. DOI:10.6038/cjg20150615 | |
| Berkhout A J, Blacquière G. 2011. Multi-bandwidth blending, the future of seismic acquisition.//73rd EAGE Conference and Exhibition Incorporating SPE EUROPEC 2011. SPE, EAGE. | |
| Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion. Geophysics, 60(5): 1457-1473. DOI:10.1190/1.1443880 | |
| Chen G X, Chen S C, Wu R S. 2015. Full waveform inversion in time domain using time-damping filters.//85th Annual International Meeting. SEG, 1451-1455. | |
| Chi B X, Dong L G, Liu Y Z. 2014. Full waveform inversion method using envelope objective function without low frequency data. Journal of Applied Geophysics, 109: 36-46. DOI:10.1016/j.jappgeo.2014.07.010 | |
| Choi Y, Alkhalifah T. 2011. Source-independent time-domain waveform inversion using convolved wavefields:Application to the encoded multisource waveform inversion. Geophysics, 76(5): R125-R134. DOI:10.1190/geo2010-0210.1 | |
| Dines K A, Lytle R J. 1979. Computerized geophysical tomography. Proceedings of the IEEE, 67(7): 1065-1073. DOI:10.1109/PROC.1979.11390 | |
| Dong L G, Huang C, Chi B X, et al. 2015. Strategy and application of waveform inversion based on seismic data subset. Chinese J. Geophys. (in Chinese), 58(10): 3735-3745. DOI:10.6038/cjg20151024 | |
| Interpolation C S. 1999. Cubic spline interpolation. Numer. Math. J. Chinese Univ., 64: 44-56. | |
| Ki Lee K H, Kim H J. 2003. Source-independent full waveform inversion of seismic data. Geophysics, 68(6): 2010-2015. DOI:10.1190/1.1635054 | |
| Li M K, Rickett J, Abubakar A. 2013. Application of the variable projection scheme for frequency-domain full-waveform inversion. . Geophysics, 78(6): R249-R257. DOI:10.1190/geo2012-0351.1 | |
| Liu Z Y, Bleistein N. 1995. Migration velocity analysis:Theory and an iterative algorithm. Geophysics, 60(1): 142-153. DOI:10.1190/1.1443741 | |
| Luo J R, Wu R S. 2015. Seismic envelope inversion:reduction of local minima and noise resistance. Geophysical Prospecting, 63(3): 597-614. DOI:10.1111/1365-2478.12208 | |
| Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion. Geophysics, 56(5): 645-653. DOI:10.1190/1.1443081 | |
| Pratt R G, Shin C, Hick G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x | |
| Shin C, Cha Y H. 2009. Waveform inversion in the Laplace-Fourier domain. Geophysical Journal International, 177(3): 1067-1079. DOI:10.1111/gji.2009.177.issue-3 | |
| Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 | |
| Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 | |
| Wu R S, Luo J R, Wu B Y. 2013. Ultra-low-frequency information in seismic data and envelope inversion.//2013 SEG Annual Meeting. Houston, Texas:Society of Exploration Geophysicists. | |
| Wu R S, Luo J R, Wu B Y. 2014. Seismic envelope inversion and modulation signal model. Geophysics, 79(3): WA13-WA24. DOI:10.1190/geo2013-0294.1 | |
| Xie X B, Yang H. 2008. A wave-equation migration velocity analysis approach based on the finite-frequency sensitivity kernel.//78th Annual International Meeting. SEG, 3093-3097. | |
| Zhang P, Han L G, Zhang F J, et al. 2016. Wavelet filter based low-frequency data reconstruction for time domain full waveform inversion.//78th EAGE Conference and Exhibition 2016. EAGE. | |
| Zhang P, Han L G, Zhou Y, et al. 2015. Passive-source multitaper-spectral method based low-frequency data reconstruction for active seismic sources. Applied Geophysics, 12(4): 585-597. DOI:10.1007/s11770-015-0520-2 | |
| 敖瑞德, 董良国, 迟本鑫. 2015. 不依赖子波、基于包络的FWI初始模型建立方法研究. 地球物理学报, 58(6): 1998–2010. DOI:10.6038/cjg20150615 | |
| 董良国, 黄超, 迟本鑫, 等. 2015. 基于地震数据子集的波形反演思路、方法与应用. 地球物理学报, 58(10): 3735–3745. DOI:10.6038/cjg20151024 | |
 2017, Vol. 60
2017, Vol. 60


