地球物理学报  2017, Vol. 60 Issue (2): 801-809   PDF    
引用本文
麻昌英, 柳建新, 刘海飞 等. 2017. 基于全局弱式无单元法直流电阻率正演模拟. 地球物理学报, 60(2): 801-809, doi: 10.6038/cjg20170230.  
Ma C Y, Liu J X, Liu H F, et al. 2017. A global weak form element free method for direct current resistivity forward simulation. Chinese J. Geophys. (in Chinese), 60(2): 801-809, doi: 10.6038/cjg20170230.  
基于全局弱式无单元法直流电阻率正演模拟
麻昌英1,2 , 柳建新1,2 , 刘海飞1,2 , 郭荣文1,2 , 曹创华3     
1. 中南大学 地球科学与信息物理学院, 长沙 410083;
2. 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083;
3. 湖南省地质调查院, 长沙 410083
收稿日期 2016-03-16, 2017-01-06 收修定稿
基金项目: 中南大学博士研究生自主探索创新项目（2016zzts088），国家自然科学基金项目（41674080，41674079，41574123）联合资助
作者简介: 麻昌英, 男, 1988年生, 博士研究生, 主要从事电磁法正反演和应用研究.E-mail:hktk-12@163.com
通讯作者: 柳建新, 男, 1962年生, 博士, 教授, 主要从事电磁法勘探理论与应用研究.E-mail:ljx6666@126.com
摘要: 全局弱式无单元法是在有限单元法基础上发展起来的一种数值模拟方法，它采用局部支持域内的节点信息来构造形函数实现局部精确逼近，摆脱了单元，仅依赖于节点信息，具有预处理简单、模拟精度高、灵活性强的特点，适用于复杂地电条件下直流电阻率正演模拟.本文采用RPIM构造直流电阻率全局弱式无单元法形函数，利用RPIM形函数推导了直流电阻率全局弱式无单元法方程.然后，编制了直流电阻率全局弱式无单元法正演模拟Fortran程序，利用该程序对典型的地电模型进行了正演模拟，并将正演结果与基于线性插值的FEM正演结果及解析解进行对比，结果表明采用RPIM形函数的全局弱式无单元法用于直流电阻率正演模拟的正确性及有效性，且在同等条件下，全局弱式无单元法模拟精度高于矩形剖分的FEM，更有利于指导电法勘探的数据解译；利用该程序对复杂地电模型进行了正演模拟，结果表明全局弱式无单元法对复杂地电模型模拟效果良好，适应性强，灵活性高，可任意加密节点提高模拟精度.
关键词: 无单元法      径向基点插值      直流电阻率      正演模拟     
A global weak form element free method for direct current resistivity forward simulation
MA Chang-Ying1,2, LIU Jian-Xin1,2, LIU Hai-Fei1,2, GUO Rong-Wen1,2, CAO Chuang-Hua3     
1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. Non-ferrous Resources and Geologic Disasters Prospecting Emphases Laboratory of Hunan, Changsha 410083, China;
3. Hunan Institute of Geology Survey, Changsha 410083, China
Abstract: We present a global weak form element free method (EFM) for simulation of direct current resistivity. EFM is a new numerical simulation method developed on the basis of finite element method (FEM). The key point of this method is the absence of elements and the nodes free from the elemental restraint, which makes it very flexible and the pre-processing simple. It utilizes the nodes of local support domain to construct shape functions to achieve the accurate approximations of the local domain. Approximations of EFM are of high order and boundary conditions are enforced simply, because the radial point interpolation method (RPIM) is used to construct shape function. Therefore, EFM is more suitable to simulate complex models than FEM. First, the boundary value problem and the corresponding variational problem of direct current resistivity forward simulation are derived starting from the partial differential equation of current field. Second, the construction of RPIM shape function is introduced in details. Third, equations of the global weak form EFM for direct current resistivity is derived in details based on RPIM shape function. Then, a Fortran program is written according to the equations. By forward simulation with this program, a homogeneous half-space model was used to verify our element free approach. At the same time, we compared the solutions of EFM and FEM in details which shows that the solutions of EFM are more accurate. Furthermore, the solutions indicate the correctness and effectiveness of the EFM for direct current resistivity forward simulation. Finally, we improve the simulation accuracy successfully by refining nodes arbitrarily, and the solutions of EFM forward simulation for complex geoelectric models show that EFM has a high degree of flexibility..
Key words: Element free method      Radial point interpolation method      Direct current resistivity      Forward simulation     
1 引言

目前，有限单元法(Finite element method, FEM)被广泛用于电法勘探二、三维正演模拟(徐世浙，1994；阮百尧等，2001；麻昌英等，2014)，是国内外电法勘探正演模拟中最主要的数值模拟方法.由于有限单元法使用预定义的固定单元进行模拟，使得它存在一些不足之处：首先，它对场变化剧烈的问题具有局限性；其次，对于物性参数分布或形状复杂的模型适应性较差；最后，当单元数很大时单元剖分成本较高，特别是非结构化单元的剖分十分复杂.

无单元法(Element free method, EFM)无需单元，仅依赖于节点信息，预处理简单，节点可根据需要任意布置，形函数具有高次近似的特点，可有效地解决有限单元法中存在的问题，且在同等条件下具有更高的模拟精度.20世纪80年代，滑动最小二乘(Moving Least Squares, MLS)被用于构造形函数(Lancaster and Salkauskas, 1981)，使得形函数的连续性问题得以解决；随后，在强加本质边界条件及数值积分处理等问题改进的基础上提出了无单元法(Belytschko et al., 1994)，自此开始无单元法引起了各个领域学者的浓厚兴趣.Cingoski等(1998)首次在电磁场计算领域中应用无单元法，成功解决电压互感器中的二维静电场问题；Viana等(1999)，Herault和Arechal (1999)对无单元法中基本边界和介质交界面问题进行了研究；刘素贞等(1999)利用无单元法计算了平行板电容器的电场、长直接地金属槽电场和载流导线的磁场；Cingoski等(2000)在分析电磁场问题中首次尝试无单元法和有限单元法相结合，取得了良好的效果；Liang等(2004)应用无单元法求解了稳态和似稳态电磁场问题；Brighenti (2005)应用无单元法求解了三维断裂力学中旳问题；Peng等(2011)利用复杂可变的无单元法模拟了在二维的弹塑性问题，对比常规无单元法得到了更高的模拟精度.在地球物理领域方面，无单元法的应用还不广泛，相关文献较少，贾晓峰等(2006)对地震波场应用无单元法进行了正演模拟研究；王月英(2007)探讨了无单元法应用于地震波正演模拟中的各种影响因素；冯德山等(2013)采用MLS构造形函数，实现了探地雷达二维无单元法正演模拟；严家斌和李俊杰(2014)也采用MLS构造形函数，将无单元法应用于大地电磁法二维模拟，计算了水平地形下大地电磁二维模型响应.

径向基点插值法(Radial point interpolation method, RPIM)以径向基函数(Radial base function, RBF)为基础，RBF具有的优良数学特性使得其成为当前众多计算领域的重要工具，如地球物理领域最新研究中将RBF用于局部重力场重建(吴怿昊等，2016).相比于MLS，RPIM为过点插值，具有Kronecker delta函数性质，使得本质边界条件可以使用直接法施加，简化边界处理；其次，RPIM形函数具有更高的稳定性，在支持域中节点的位置或数量稍微改变对构造的形函数影响不大，使得EFM对任意不规则分布的节点具有很强的适应性.以RPIM形函数为基础的无单元法在直流电阻率正演领域的研究，还未见报道.本文采用RPIM构造形函数，并基于全局弱式推导无单元法方程，利用背景单元积分，将无单元法应用于直流电阻率正演模拟.通过与有限单元法正演结果及解析解对比，表明了算法的正确性及有效性，为直流电阻率正演模拟提供了新的方法.

2 直流电阻率变分问题

假设地下介质电性二维分布，点电源供电产生的电场是三维分布的，这种条件下成为点源二维(2.5维)问题.对于传导类电法勘探，2.5维模型较符合勘探实际，相对于三维模型其计算成本低很多，被广泛应用.在直角坐标系中，2.5维稳定电流场情况电位满足偏微分方程：

(1)

式中, σ=(x, z)为介质电导率，U(λ, x, z)为波数域电位，λ为波数，I为电流，δ为狄拉克函数，A为场源点位置，二维哈密顿算子.

2.5维稳定电流场波数域总电位U满足第三类边界条件的边值问题可描述为(2)式：

(2)

式中, Ω为求解域，cos (r, n)为矢径r与外法向n的夹角余弦，K0、K1分别为第二类一阶、零阶修正贝塞尔函数.边值问题(2)式对应的变分问题为

(3)

3 构造RPIM形函数

求解域Ω中任意点的场值采用RPIM近似表示为

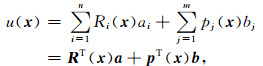
(4)

式中, Ri(x)为径向基函数，n为径向基函数的个数，pj(x)为空间坐标xT=[x, y]中的多项式，m为多项式基函数个数，ai和bj为待定系数.采用复合二次函数Ri(x, y)=(ri2+(αcdc))q作为径向基函数，包含两个形状参数：αc和q，通过实验αc取1.0左右，q取1.03左右，在直流电法勘探模拟中能取得良好的效果.dc为与计算点x的局部支持域中的节点间距有关的特征长度，该长度通常取为支持域中节点的平均间距.

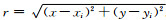
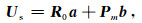
径向基函数Ri(x)中变量r为计算点x与节点xi之间的距离，2D情况下. (4)式中完备的p阶多项式pj(x)的一般形式为pT(x)=[1 x y x2 xy y2 … xp yp].为确定(4)式中的ai和bj，首先形成计算点x的支持域，获得支持域中的n个节点，令u(x)等于该n个节点上的场值，形成n个方程，这些方程可表示为

(5)

式中的场值向量Us=[u1 u2 … un]T.径向基函数对应的系数矩阵为

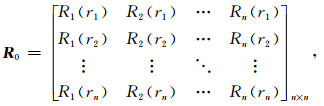
多项式基函数对应的系数矩阵为

径向基函数对应的系数向量a=[a1 a2 … an]T，多项式系数向量b=[b1 b2 … bm]T. (5)式中有n+m个变量，使用(6)式所示的m个约束条件添加m个方程：

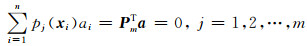
(6)

联立(5)和(6)式可得到矩阵方程(7)式：

(7)

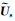
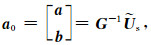
式中，a0=[a1 a2 … an b1 b2 … bm]T，=[u1 u2 … un 0 0 … 0]T.因为R0为对称矩阵，故矩阵G为对称矩阵，求解(7)式得到

(8)

将(8)式代入(4)式得到

(9)

式中的RPIM形函数为

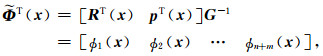
(10)

其中节点对应的RPIM形函数为

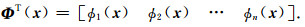
(11)

需要指出的是，当节点任意分布时可能存在局部节点分布极不合理的情况，这可能导致RPIM形函数中的G-1不存在，使得出现奇异性问题，因此布置节点时应避免.

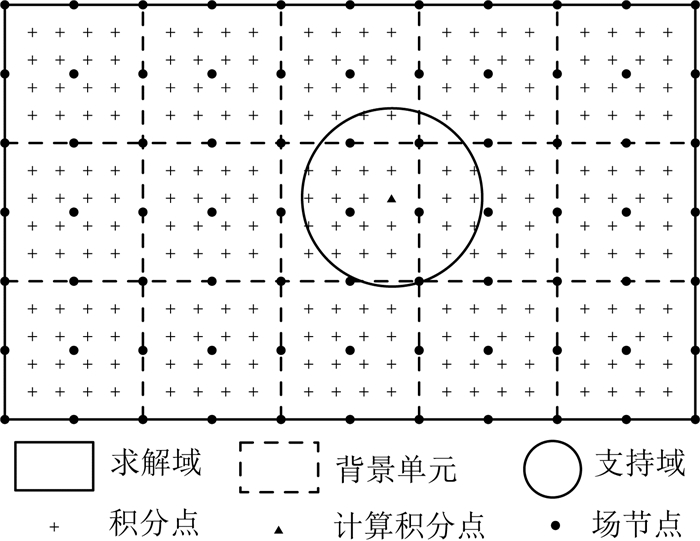
4 全局弱式无单元法

如图 1所示，全局弱式无单元法采用一组矩形背景单元将求解域Ω覆盖，然后在背景单元中布置高斯积分点，采用高斯积分计算单元上的积分.计算积分过程中对每一个计算点(高斯积分点)定义支持域(或影响域)，使用支持域内的节点构造RPIM形函数.将所有背景单元积分求和得到求解域Ω上的积分，从而求解2.5维稳定电流场满足的变分问题(3)式.

图 1 全局弱式无单元法求解示意图 Fig. 1 Sketch showing the solving process of global weak form EFM

将(3)式展开得到(12)式：

(12)

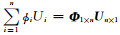
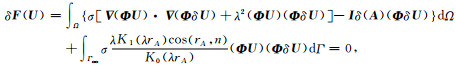
设在支持域Ωq中存在n个节点，采用RPIM形函数作为试函数近似任意点x=(x, z)的波数域电位U(x)=，代入(12)式得到：

(13)

将(13)式体积分项做变换得到：

(14)

将(13)式边界积分项做变换得到：

(15)

将(14)和(15)式代入(13)式并变换得到：

(16)

其中

由于δU是任意的，故(16)式成立的条件为(K1+K2)U=F.将求解域Ω用一组背景单元进行离散后，则在背景单元Ωe内(16)式成立的条件表示为(Ke1+Ke2)U=F，其中

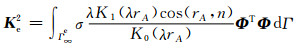
Ke1、Ke2)U=F为背景单元子刚度矩阵，它们各个元素的表达式分别为(17)和(18)式：

(17)

(18)

由于RPIM形函数具有Kronecker delta函数性质，右端项F的各个元素表达式为

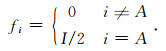
(19)

在求解域Ω内也采用RPIM形函数(或其他形函数)作为试函数近似任意点x=(x, z)的电导率，代入(17)和(18)式，得到：

(20)

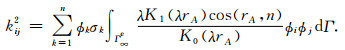
(21)

电导率的插值计算也可以使用其他方法，如找出距离计算点最近的几个节点，使用节点电阻率值对计算点电阻率值进行插值.(20)式对应背景单元Ωe与求解域Ω相交区域的积分，(21)式对应背景单元Ωe与求解域Ω边界相交的边界积分.采用高斯积分计算积分，在背景单元中设置N个高斯积分点xr=(xr, zr), r=1, 2, …, N，它们对应的高斯权重为wr, r=1, 2, …, N. 表 1给出了一组高斯积分点的坐标系数和权重系数，对应的局部积分域内面积积分雅克比值为Jr, r=1, 2, …, N.对(20)式采用高斯积分得到：

表 1 高斯积分点坐标系数与权重系数(Liu and Gu, 2007) Table 1 The coordinate and weighting coefficients of gauss integral points (Liu and Gu, 2007)

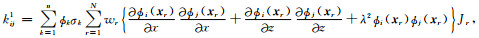
(22)

对边界积分(21)式使用高斯积分得到：

(23)

此时，Jr, r=1, 2, …, N为子边界在高斯积分点xr处进行曲线积分的雅克比值.

将计算得到的各个子元素组装到总体刚度矩阵K中得到方程组KU=F，解方程得到求解域Ω上节点的波数域电位U，反傅氏变换得到空间域电位u.

5 模型算例 5.1 均匀半空间模型

建立水平宽120 m、垂直深度60 m的均匀半空间模型，介质电阻率为100 Ωm，节点水平方向和垂直方向间隔均为2 m等间隔均匀分布，水平方向节点数61个，垂直方向节点数31个，总节点数1871个，在地面中间位置X=0 m处设置电流为1 A的点电源向地下供电.背景单元采用顶点与节点重合的矩形单元，水平方向单元数为60个，垂直方向单元数为30个，总单元数为1800个，每个单元内使用64个高斯积分点(即一维方向采用8个高斯积分点)计算积分，积分点坐标系数和权重系数见表 1.将背景单元内的每一个高斯积分点的支持域设为该背景单元，使用对应背景单元顶点的4个节点构造RPIM形函数，其中基函数选择线性基函数，即m=3.均匀半空间条件下，点电源向地下供电，除供电点外，地下和地表任意一点的电位解析解可由式u=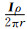计算，式中I为供电电流，ρ为均匀半空间介质电阻率，r为计算点到供电点的空间距离.无单元法正演得到地面节点的模拟电位值(由于对称，仅取供电点及其右边的节点模拟电位值)和根据解析式计算的电位解析解如图 2所示.图 2表明无单元法正演结果与解析解基本一致.

图 2 均匀半空间点电源电位计算 Fig. 2 The point source potentials in the homogeneous half-space model
5.2 无单元法与有限单元法对比

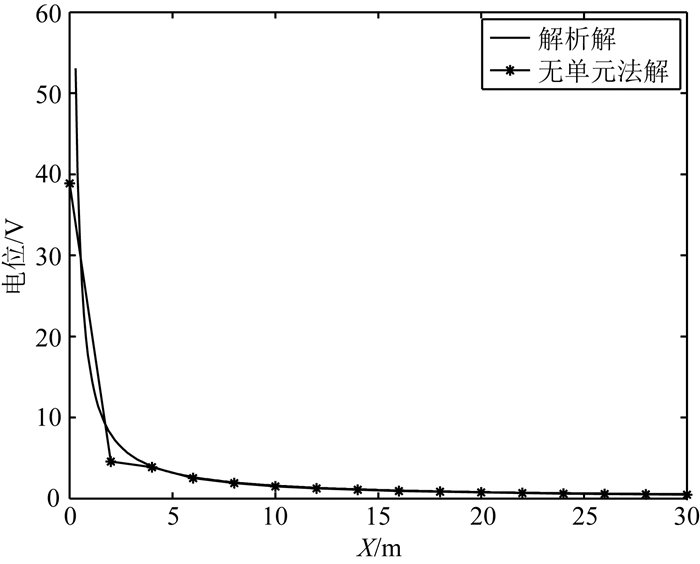
无单元法与有限单元法均采用上述均匀半空间模型进行正演模拟.无单元法使用的背景单元与有限单元法使用的单元相同，两种方法使用相同分布的节点，有限单元法在矩形单元中使用线性插值，对点电源供电模型进行电位正演模拟.两种方法正演模拟得到地面节点电位值，以及根据解析式计算的电位解析解，结果如图 3和表 2所示.

图 3 均匀半空间点电源电位模拟 Fig. 3 The point source potentials in the homogeneous half-space model
表 2 无单元法与有限单元法模拟电位对比 Table 2 The comparison of the point source potentials calculated by EFM and FEM respectively

由图 2、图 3及表 2分析，无单元法和有限单元法正演模拟的电位值与解析解基本一致，在点电源处附近两者都有一定的畸变，其余各个计算点电位值与解析解吻合很好，表明采用RPIM形函数的全局弱式无单元法对稳定电流场进行正演模拟是可靠的，验证了无单元法计算程序的正确性及有效性.由图 3和表 2分析，在点电源附近，虽然无单元法和有限单元法的正演结果都有一定的畸变，但无单元法的正演结果畸变程度较有限单元法低，表明了同等条件下在点电源处附近无单元法模拟精度较有限单元法高.由表 2分析，当计算点距离点电源相对较远时(r≥4 m，r为计算点与点电源的距离)，直至r≥30 m时，无单元法正演计算的电位值相对误差始终较有限单元法低，表明同等条件下在距离点电源相对较远处(r≥4 m)无单元法模拟精度较有限单元法高，随着计算点与点电源距离r的增大，无单元法与有限单元法模拟精度趋于一致.

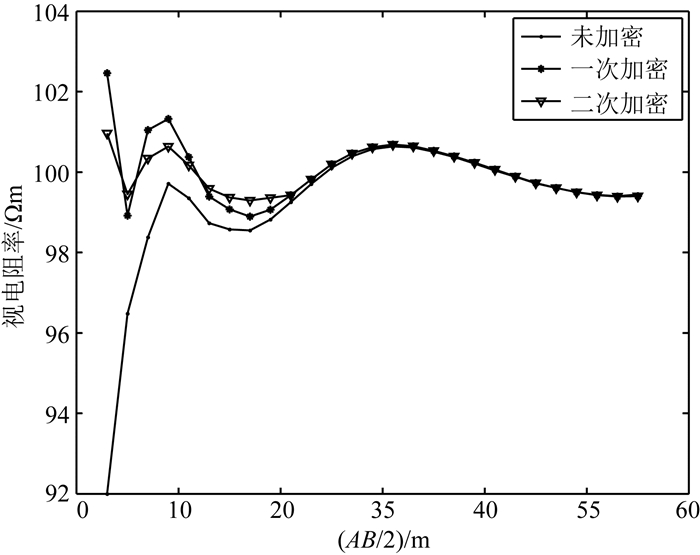
5.3 节点加密模拟结果对比

将上述模型表层节点加密.第一次加密：表层0~4 m水平方向和垂直方向均以1 m等间隔均匀分布，4 m以下为2 m等间隔均匀分布；第二次加密：表层0~4 m水平方向和垂直方向均以0.5 m等间隔均匀分布，4~8 m以下为1 m等间隔均匀分布，8 m以下为2 m等间隔均匀分布.以X=0 m为中心模拟对称四极测深视电阻率，未加密表层节点与加密表层节点模拟结果进行对比，如图 4所示.图 4表明通过浅层节点加密，小极距模拟精度明显提高，随着近场源节点的加密程度的提高，模拟精度也进一步提高.节点的加密是任意和独立的，无需改变其他参数，体现了在无单元法中节点加密的便捷性与灵活性，这使得无单元法在自适应模拟中将具有一定的优越性.

图 4 全局弱式无单元法模拟视电阻率 Fig. 4 The apparent resistivity simulated by the global weak form EFM
5.4 复杂地电模型

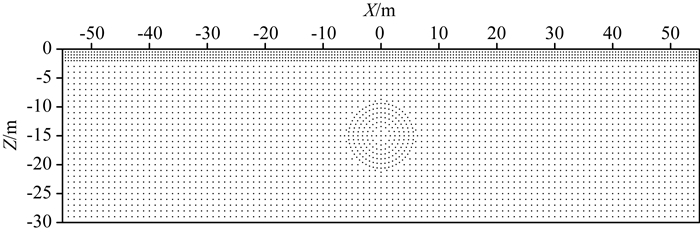
对低阻圆形异常体模型进行正演模拟，模型如图 5所示，在均匀半空间中存在一个二维圆形异常体，围岩电阻率为100 Ωm，异常体电阻率为10 Ωm，半径r=5 m，圆心点埋深15 m，异常体中心在水平坐标0 m处正下方.

图 5 低阻圆形异常体模型节点分布示意图 Fig. 5 Sketch showing the nodal distribution of the low resistivity circular anomaly model

求解域Ω水平方向-60~60 m，垂直方向0~-50 m，节点X和Z方向场节点间隔均为1 m均匀分布，为提高地表近场源及地形的模拟，在近地表加密节点；低阻圆形异常体区域节点呈圆形分布，圆心坐标(X=0 m, Z=-15 m)，如图 5所示.应用全局弱式无单元法进行对称四极电阻率测深模拟，以对称四极装置中心点为横坐标，AB/4为纵坐标绘制正演视电阻率等值线图，如图 6所示，异常体对应位置有明显的低阻异常.

图 6 低阻圆形异常体模型无单元法正演视电阻率拟断面图 Fig. 6 The apparent resistivity profile simulated by EFM of the low resistivity circular anomaly model

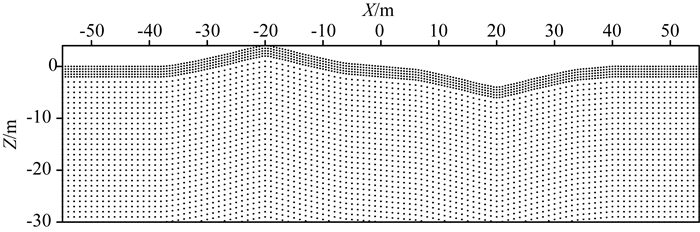
对山脊山谷起伏地形模型进行正演模拟，模型如图 7所示，左侧X=-20 m处为山脊最高点，右侧X=20 m处为山谷最低点，山脊和山谷以地面X=0 m为中心反对称分布，它们相对水平地面最高起伏均为4 m，地下介质电阻率为100 Ωm.

图 7 山脊山谷起伏地形模型节点分布示意图 Fig. 7 Sketch showing the nodal distribution of the ridge and valley undulating terrain model

求解域Ω和节点分布采用与低阻圆形异常体模型一致，采用平行四边形的背景单元模拟地形起伏，在近地表加密节点，如图 7所示.应用全局弱式无单元法进行对称四极电阻率测深模拟，以对称四极装置中心点为横坐标，AB/4为纵坐标绘制正演视电阻率等值线图，如图 8所示.图 8表明山脊山谷地形引起的视电阻率异常以地面X=0 m为中心反对称分布，山脊对应低阻异常，山谷对应高阻异常.

图 8 山脊山谷起伏地形模型无单元法正演视电阻率拟断面图 Fig. 8 The apparent resistivity profile simulated by EFM of the ridge and valley undulating terrain model
6 结论

(1)应用全局弱式无单元法对典型的地电模型进行了正演模拟，并与有限单元法模拟结果及解析解进行了对比，结果表明采用RPIM形函数的全局弱式无单元法用于直流电阻率正演模拟的正确性及有效性.

(2)在相同条件下，RPIM形函数高次近似使得无单元法具有更高的模拟精度.在有限单元法中单元仅有4个节点的情况下单元内只能进行线性插值，而无单元法由于其形函数具有高次近似的特点，使得无单元法具有更高的模拟精度，尤其是当场剧烈变化时，如场源附近，无单元法的模拟精度明显高于有限单元法.

(3)在节点合理分布的情况下，无单元法可任意加密节点提高模拟精度，且节点的加密是独立的，无需改变其他参数.对于基于结构化单元的有限单元法进行局部节点加密显然不易实行，对于基于非结构化单元的有限单元法进行局部节点加密虽然易于实行，但需要重新生成非结构化单元.无单元法展现出了较有限单元法更高的灵活性，使得其在自适应模拟将中具有一定的优越性，后续可研究直流电阻率自适应无单元法正演模拟.

(4)无单元法对每一个计算点(高斯积分点)需独立构造形函数，为了提高积分精度，往往采用较多的积分点，其计算时间与积分点数成正比，因此无单元法计算效率比有限单元法低.采用并行计算可大幅提高计算效率，后续可研究无单元法的并行计算.

参考文献
Herault, Marechal. 1999. Boundary and Interface conditions in meshless methods. IEEE Trans. On Magnetics, 35(3): 1450-1453. DOI:10.1109/20.767239
Viana, Aparecida, Mesquita, et al. 1999. Moving least square reproducing kernel method for electromagnetic field computation. IEEE Trans. On Magnetics, 35(3): 1372-1375. DOI:10.1109/20.767218
Feng D S, Wang H H, Dai Q W. 2013. Forward simulation of Ground Penetrating Radar based on the element-free Galerkin method. Chinese J. Geophys (in Chinese), 56(1): 298-307.
Jia X F, Hu T Y, Wang R Q. 2006. Wave equation modeling and imaging by using element-free method. Progress in Geophysics (in Chinese), 21(1): 11-17.
Jia X F, Hu T Y. 2006. Element-free precise integration method and its applications in seismic modelling and imaging. Geophysical Journal International, 166(1): 349-372. DOI:10.1111/gji.2006.166.issue-1
Li J J, Yan J B. 2014. Developments of meshless method and applications in geophysics. Progress in Geophysics (in Chinese), 29(1): 452-461.
Liu G R, Gu Y T. An Introduction to Meshfree Methods and Their Programming.Jinan: Shandong University Press, 2007.
Liu S Z, Yang Q X. 1999. Element free method applied to 2D electrical field numerical calculation. Journal of Hebei University of Technology, 28(2): 10-15.
Peng M J, Li D M, Cheng Y M. 2011. The complex variable element-free Galerkin (CVEFG) method for elasto-plasticity problems. Engineering Structures, 33(1): 127-135. DOI:10.1016/j.engstruct.2010.09.025
Ma C Y, Liu J X, Liu H F, et al. 2014. 2. 5 Dimensional numerical simulation of finite element method Of IP high density in complex terrain. Computing Techniques for Geophysical and Geochemical Exploration, 36(4): 405-409.
Lancaster P, Salkauskas K. 1981. Surface generated by moving least squares methods. Math. Comput, 37(155): 141-158. DOI:10.1090/S0025-5718-1981-0616367-1
Brighenti R. 2005. Application of the element-free Galerkin meshless method to 3-D fracture mechanics problems. Engineering Fracture Mechanics, 72(18): 2808-2820. DOI:10.1016/j.engfracmech.2005.06.002
Ruan B Y, Xiong B, Xu S Z. 2001. Finite element method for modeling resistivity sounding on 3-D Geoelectric section. Earth Science-Journal of China University of Geosciences, 26(1): 73-77.
Belytschko T, Lu Y Y, Gu L. 1994. Element-free Galerkin methods. Int. J. for Num. methods in Engrg, 37(1): 229-256.
Cingoski V, Miyamoto N, Yamashitaet H. 1998. Element-free Galerkin method for electromagnetic field computations. IEEE Trans. On Magnetics, 34(5): 3236-3239. DOI:10.1109/20.717759
Cingoski V, Miyamoto N, Yamashita Y. 2000. Hybrid element-free Galerkin-free Galerkin-finite element method for electromagnetic field computations. IEEE Trans. On Magnetics, 36(3): 1543-1547.
Wang Y Y. 2007. Study of element-free galerkin method in the seismic forward modeling. Progress in Geophysics (in Chinese), 22(5): 1539-1544.
Wu Y H, Luo Z C, Zhou B Y. 2016. Regional gravity modeling based on heterogeneous data sets by using Poisson wavelets radial basis functions. Chinese J. Geophys.(in Chinese), 59(3): 852-864.
Liang X, Zhi W Z, Balasubramaniam Shanker, et al. 2004. Element-free galerkin method forstatic and quasi-static electromagnetic field computation. IEEE Trans, on Mag, 40(1): 12-20. DOI:10.1109/TMAG.2003.821131
Xu S Z. Finite element method in geophysics.Beijing: Beijing Science Press, 1994.
Yan J B, Li J J. 2014. Magnetotelluric forward calculation by meshless method. Journal of Central South University (Science and Technology), 45(10): 3513-3520.
LiuG R, GuY T. 无网格法理论及程序设计.济南: 山东大学出版社, 2007.
冯德山, 王洪华, 戴前伟. 2013. 基于无单元Galerkin法探地雷达正演模拟. 地球物理学学报, 56(1): 298–307.
贾晓峰, 胡天跃, 王润秋. 2006. 无单元法用于地震波波动方程模拟与成像. 地球物理学进展, 21(1): 11–17.
李俊杰, 严家斌. 2104. 无网格法进展及在地球物理学中的应用. 地球物理学进展, 29(1): 452–461.
刘素贞, 杨庆新. 1999. 二维电场的无单元数值解法. 河北工业大学学报, 28(2): 10–15.
麻昌英, 柳建新, 刘海飞, 等. 2014. 复杂地形下高密度激电法2. 5维有限单元法数值模拟.物化探计算技术, 36(4): 405–409.
阮百尧, 熊彬, 徐世浙. 2001. 三维地电断面电阻率测深有限元数值模拟. 地球科学-中国地质大学学报, 26(1): 73–77.
王月英. 2007. 地震波正演模拟中无单元Galerkin法初探. 地球物理学进展, 22(5): 1539–1544.
吴怿昊, 罗志才, 周波阳. 2016. 基于泊松小波径向基函数融合多源数据的局部重力场建模. 地球物理学报, 59(3): 852–864.
徐世浙. 地球物理中的有限单元法.北京: 北京科学出版社, 1994.
严家斌, 李俊杰. 2014. 无网格法在大地电磁正演计算中的应用. 中南大学学报(自然科学版), 45(10): 3513–3520.