以多道面波分析技术(MASW)为代表的各种主、被动源模式波勘探方法近些年来逐渐成为近地表勘探的有力工具,尤其在环境和工程地球物理领域扮演着越来越重要的作用(Park et al., 1999;Socco et al., 2010;夏江海等,2015),它们主要利用瑞雷波(P-SV型模式波)和勒夫波(SH型模式波).无论主动源法还是被动源法,核心思想都是分析模式波观测数据获取可靠的频散信息,通过对其反演得到地层的横波速度.完全弹性介质中的瑞雷波频散曲线正演理论目前已较为成熟(Chen,1993;张碧星等,2002;何耀锋等,2006;刘雪峰和凡友华,2011;Liu and Fan, 2012).但是,实际的近地表介质由于压实度低、土层疏松,表现出很强的黏弹特性.因此,研究黏弹介质中的模式波频散曲线正演方法,探讨模式波复相速度变化规律,将进一步深化对模式波勘探方法的理解与应用.
早期实验表明,描述地层吸收衰减效应的重要参数-品质因子Q在地震勘探频带范围内一般近似为常数(McDonal et al., 1958;Johnston et al., 1979),称为常Q模型,该模型很快在勘探地震领域得到了广泛应用,成为描述地震波吸收衰减效应的主流模型.Xia等(2013)基于常Q地层假设,利用勒夫波衰减系数反演了地层横波品质因子Qs,但他们采用的是弱衰减条件下勒夫波衰减系数的近似公式(Anderson et al., 1965),避开了勒夫波频散特征复数方程的求解问题.Schwab和Knopoff (1971)率先讨论了常Q黏弹层状介质中的勒夫波频散特征复数方程求解问题,以弹性情况下面波的相速度作为初始值,通过Müller法迭代求解获得黏弹情况下的近似解.Cao和Dong (2010)进一步提出了一种Müller法与牛顿迭代法相结合的策略进行求解.张凯等(2016)同样基于Müller法求解了两层常Q黏弹层状介质中的瑞雷波频散特征方程,并对频散曲线交叉现象进行了分析.上述Müller法迭代类的计算策略需要给定合理的初始值,否则会收敛到错误的计算结果,所以Lai和Rix (2002)基于围道积分与留数定理,提出了计算常Q黏弹层状介质中Rayleigh波频散特征方程的策略.
一方面,由于近地表地质条件的复杂性,常Q的假设一直存在着争议.一些研究也表明浅层介质的Q值是频变的(Jongmans and Campillo, 1993;Malagnini,1996;Jeng et al., 1999).所以,开展Q值频变黏弹介质中的面波频散特征研究很有必要,而Kelvin-Voigt黏弹介质模型(以下简称KV模型)正是Q值频变衰减介质的典型代表.另一方面,Michaels (1998)的研究表明,当浅地表介质属于高渗透性水饱和土层时,采用KV模型进行刻画更为合理,他们首先开展了KV层状介质中的勒夫波频散特征研究(Michaels and Gottumukkula, 2010),由于对每个频率的复相速度都需进行粗略估计和精确迭代两步求解,所以计算效率很低.Morrison (2014)基于幅角定理进一步研究了多层KV黏弹介质中勒夫波频散特征值求解问题,采用有限差分近似处理频散函数对复相速度的偏导,为了求解一次偏导需要进行多次频散函数的计算,计算效率较低,还可能导致计算不稳定.
基于解析函数零点求解技术(Delves and Lyness, 1967;Davies,1986;Lai and Rix, 2002),本文将完全弹性、常Q黏弹和KV黏弹三种层状介质中的勒夫波频散特征方程求解问题归结到统一的计算框架下.只需要给定地层的实(复)横波速度表达式,即可实现这三类介质中勒夫波相速度频散曲线的正演计算.文中还给出了复频散函数对复相速度的偏导函数的解析递推式,提高了求根过程的计算效率与精度.此外,我们总结了发生频散曲线交叉现象时,复相速度平面上勒夫波频散特征根的相对运动规律.
本文首先介绍两类黏弹介质中勒夫波频散特征方程的差异及求解方法,然后对完全弹性与两类黏弹介质假设下的典型地层模型进行计算,探讨由于衰减效应的引入,代表勒夫波模式的频散特征方程的根如何在复相速度平面上随频率变化,这有助于加深对勒夫波频散特征的认识,对利用勒夫波进行近地表Q值反演研究有重要的参考价值.
2 方法原理 2.1 勒夫波频散特征复数方程的构建黏弹水平层状介质中的勒夫波频散特征方程构建过程与完全弹性层状介质类似.Buchen和Ben-Hador (1996)研究总结了完全弹性介质中多种瑞雷波频散特征方程构建技术,这些方法也同样适用于勒夫波.本文采用传递矩阵算法,其频散特征方程可表示为
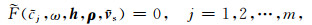
|
(1) |
具体过程见附录A.其中ω为角频率,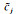
对于常Q黏弹性层状介质,其地层复横波速度可以表示为(Lai and Rix, 2002;张凯等,2016):
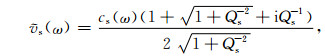
|
(2) |
复横波速度实部与虚部必须满足Kramers-Krönig频散关系(Aki and Richards, 2002),所以其中横波相速度cs(ω)为
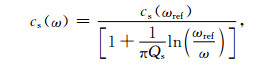
|
(3) |
其中,ωref为参考角频率.由(3)式可知,当Qs趋于无穷大时,代表完全弹性介质,cs(ω)=cs(ωref),横波无频散.当Qs为其他有限值时,代表黏弹性介质,当ω≤ωref时,cs(ω)≤cs(ωref);当ω>ωref时,cs(ω)>cs(ωref).张凯等(2016)选择了2π作为参考角频率,即1 Hz作为参考频率,但没有给出如何给定cs(ωref).如果将完全弹性时无频散横波速度设为cs(ωref),根据上面的讨论可知,会导致大部分频率成分(>1 Hz的部分)的相速度都大于cs(ωref).这从波形上来看,表现为黏弹性时地震波传播速度明显快于完全弹性时,而且随着传播距离的增加,这一时差还将继续扩大.为了避免这种情况的发生,我们采用了Zhang (2008)的方法给定参考频率,即以高频端作为参考频率,比如当拟合常Q的频率范围为1~100 Hz,则选择100 Hz作为参考频率,同时令对应的cs(ωref)为完全弹性时横波速度.
对于KV层状介质,一般用黏性系数η表示地层衰减程度,η值越大,地层衰减程度越高.地层复横波速度可以表示为(Carcione et al., 2004;Morrison,2014):
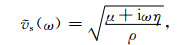
|
(4) |
其中,μ代表完全弹性时剪切模量.此类介质的Qs值是随频率变化的,它与黏性系数的关系为
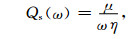
|
(5) |
所以,高频成分对应的Qs值更小,从而衰减更快.
无论哪种黏弹性介质,复波数
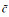
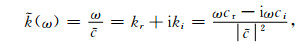
|
(6) |
其中,下标r与i表示相应物理量的实部与虚部.由(1)式求出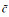
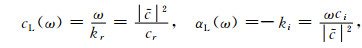
|
(7) |
其中,cL(ω)刻画了每个勒夫波模式的相速度变化特征,αL(ω)则刻画了每个勒夫波模式的振幅衰减特征.
2.2 勒夫波频散特征复数方程的求解 2.2.1 连带多项式的构建式(1)代表的勒夫波频散特征函数是一个高度非线性的隐式函数(张凯等,2016).严格来讲,该函数并非在整个复相速度平面上处处解析(Lai and Rix, 2002),在数值算例部分将会看到,底层半空间复横波速度点就是平面上的一个奇点,但是在我们主要关心的计算区域该函数依然是解析的.我们采用Delves和Lyness (1967)提出的解析函数零点计算技术来求解方程(1).其核心思想在于将解析函数零点求解问题转化为一个与该解析函数具有相同零点的多项式的求根问题.
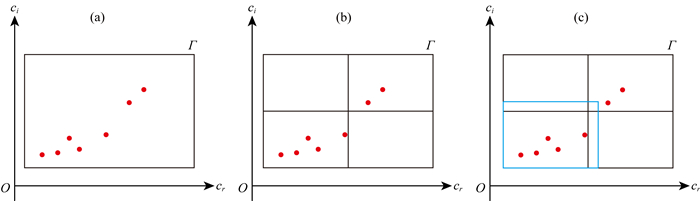
设Γ是复平面上的一条矩形闭围道(图 1a),复函数f(z)在Γ上及其内部解析,并且Γ不穿过f(z)的零点,由幅角定理与留数定理(Delves and Lyness, 1967;钟玉泉,2003)可知:
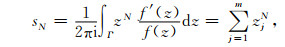
|
(8) |
|
图 1 围道细分与调整示意图 Fig. 1 Schematic diagram of contour subdivision and adjustment |
其中,zj(j=1, 2, …, m)代表Γ内部的零点,f′(z)为f(z)关于z的导函数.就本文而言,z相当于复相速度,f(z)则相当于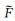

|
(9) |
其中,1, σ1, σ2, …, σm为多项式的系数.如果进一步由(8)式计算出s1, s2, …, sm,则可以利用牛顿恒等式(Antia,1995;Davies,1986;Delves and Lyness, 1967)的递推解出这组多项式系数,从而构建出连带多项式.牛顿恒等式的形式为(推导过程见附录B):
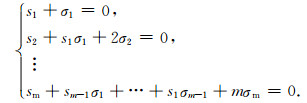
|
(10) |
由此可见,s0的作用在于估计f(z)在Γ内部的零点个数,而s1, s2, …, sm的作用在于转化问题-将f(z)的零点求解问题转化为更容易解决的多项式求根问题.
2.2.2 矩形围道的细分与调整
上述过程可能存在的问题是,如果s0较大,则由(10)式获得多项式系数的过程是一个病态问题,得到的是一个高阶多项式.要使这个高阶多项式的零点和f(z)的零点足够吻合,需要高精度地计算sm和多项式的零点.为了避免这种困难,Delves和Lyness (1967)采用了矩形围道细分策略:假设允许最大零点数为M(比如5),如果计算得到的s0大于M,则将Γ均分为4个小矩形,然后分别计算4个小矩形的s0.如果某个小矩形内的零点数依然大于M,则进一步将该小矩形继续细分,直至每个小矩形内的零点数都不大于M为止,至此就可以对每个矩形构建连带多项式求解.在细分过程中要避免出现零点过于靠近围线的情况(此时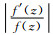
由(8)式被积函数可知,还需要获得解析函数的导函数f′(z),也就是勒夫波复频散特征函数相对于复相速度的导函数.Morrison (2014)采用了普通的有限差分近似进行处理,我们采用类似Cercato (2007)处理瑞雷波的手段,基于隐函数存在定理,推导了导函数递推解析形式.采用导函数解析形式有助于提高数值积分的计算精度与效率.
这里以KV层状介质为例给出推导过程,常Q黏弹性介质可作类似处理.根据附录A,虽然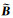
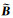
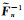
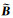
令:
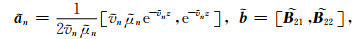
|
(11) |
所以有
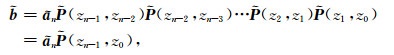
|
(12) |
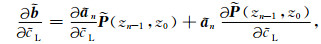
|
(13) |
其中:

|
(14) |
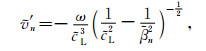
|
(15) |

|
(16) |
按照(16)式迭代计算,直到计算出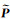
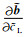

前人对于完全弹性介质中瑞雷波频散曲线交叉现象进行了较深入地研究(刘雪峰等,2009),他们对一个夹低速三层模型的分析表明,基阶模式频散曲线与其他高阶模式频散曲线之间存在两种情况:(1)两者靠得非常近,看似交叉,实际没有;(2)确实发生了交叉.张凯等(2016)对常Q黏弹两层模型的研究表明,当地层速度不变,只减小地层Q值时,两条瑞雷波频散曲线会逐渐靠近并最终发生交叉.我们在这里以勒夫波为例进一步从复相速度平面上来考察频散曲线交叉现象,并指出当频散特征根如何运动时将发生频散曲线交叉现象.
完全弹性时,简正模式勒夫波的相速度一般为实数,即其频散特征方程的根始终在复相速度平面的实轴上运动.但是考虑黏弹地层时,其特征根的运动不再局限于实轴,而是在复相速度平面上移动.设某个较低频率时刻,复相速度平面上存在两个特征根A和B (图 2),代表存在两个勒夫波模式,他们的坐标分别为(xA, yA)和(xB, yB).由(7)式可知,此时A模式的相速度为
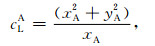
|
(17) |
|
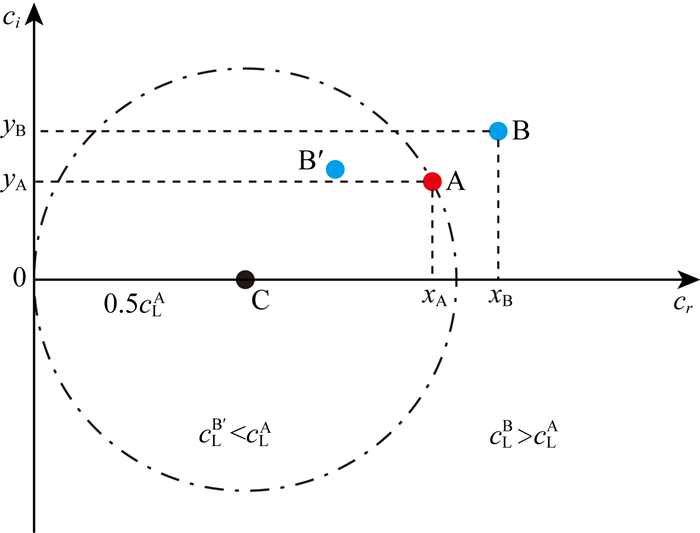
图 2 圆方程判别法示意图 Fig. 2 Schematic diagram of the circle equation discriminating method |
设另一个较高频率时刻,B模式特征根移动到了B′处.为方便讨论,设A模式特征根没有移动(这不影响结论的有效性,因为我们关心的是两者的相对位置).如果在这两个频率之间存在着A模式频散曲线与B模式频散曲线发生交叉,则意味着:
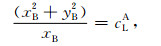
|
(18) |
进一步整理得到
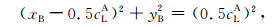
|
(19) |
这正好是一个以坐标(0.5cLA, 0)为圆心,以0.5cLA为半径的圆,A模式特征根位于圆的边界.所以,当B模式特征根位于该圆的外部时,cLB>cLA;当B模式特征根运动到该圆内部时,cLB' < cLA;无论它以哪种轨迹运动到B′处,都必然要跨过圆边界.当它恰好位于圆边界上时,就意味着cLB=cLA,发生频散曲线交叉现象.对于复相速度平面上的任意两个频散特征根,都可以利用该圆方程来判断这两个根所对应的相速度大小关系.只要在复相速度平面上移动的任意两个特征根之间存在如图 2所示的情况,就可以说这两条频散曲线必然发生交叉.显然,这个圆方程判别法既适用于勒夫波也适用于瑞雷波或其他模式波,具有一般性.
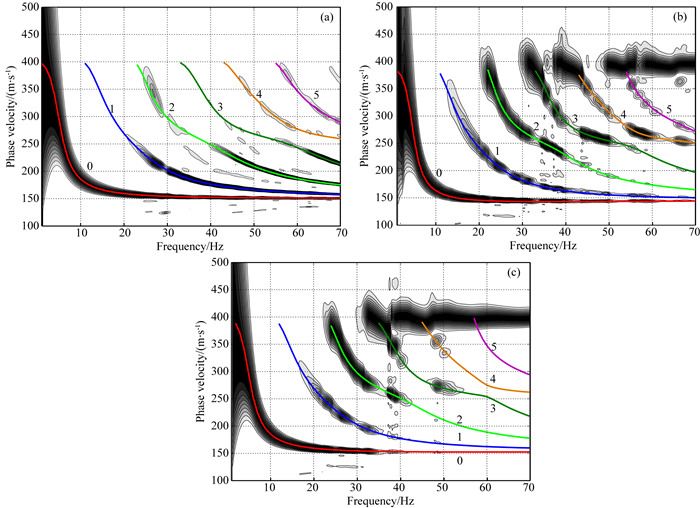
3 数值算例 3.1 三层速度递增模型首先建立一个三层速度递增模型来验证本文方法(参数见表 1).采用时间2阶、空间10阶精度标准交错网格有限差分数值模拟方法得到了完全弹性、常Q黏弹和KV黏弹情况下的勒夫波地震记录(图 3).震源函数为主频40 Hz的高斯函数.对常Q黏弹介质,表中横波速度为高频极限时的速度.对于KV黏弹介质,Q值为震源主频(即40 Hz频率分量)的Q值.利用互相关相移法得到三个勒夫波记录的相速度频散图像(图 4),彩色实线为本文方法计算得到的理论频散曲线,实线旁的数字表示对应的勒夫波阶数,0表示基阶模式,1表示第一高阶模式,以此类推.由图 4可见,理论频散曲线与相速度频散图像中的能量团十分吻合,表明了计算结果的正确性.
|
|
表 1 三层速度递增模型参数 Table 1 Parameters of a 3-layered model with layer velocity increasing with depth |

|
图 3 完全弹性(a)、常Q黏弹(b)和KV黏弹(c)三层速度递增模型中勒夫波地震记录 Fig. 3 Seismic records of Love waves in elastic (a), constant Q (b) and KV (c) viscoelastic 3-layered models with layer velocity increasing with depth |
|
图 4 完全弹性(a)、常Q黏弹(b)和KV黏弹(c)三层速度递增模型中勒夫波频散图像与理论频散曲线对比 Fig. 4 Comparison of Love wave dispersion images and theoretic dispersion curves in elastic (a), constant Q (b) and KV (c) viscoelastic 3-layered models with layer velocity increasing with depth |
从理论频散曲线来看,常Q黏弹介质中的6个模式相速度总体要低于完全弹性与KV黏弹的情况.这是因为在常Q黏弹介质中,衰减引起固有频散,地层横波相速度随频率增加,直至高频极限时趋于未松弛剪切模量对应的完全弹性横波速度,即表 1中给定的地层横波速度,所以1~70 Hz的频率成分是以低于表 1中所列横波速度传播的,这就造成计算出的理论勒夫波相速度总体低于完全弹性时勒夫波相速度.比较图 4b与图 4c中的理论频散曲线可知,两种黏弹介质中的理论频散曲线差异主要体现在第3~5高阶模式,其中KV黏弹时,第3、4高阶模式在60 Hz左右比较靠近,而常Q黏弹时两者相距较远,并且曲线弯曲度更低.
从频散图像的能量强度来看,完全弹性时基阶模式能量最强,并且1~70 Hz都清晰可辨.其他高阶模式的能量主要集中在高频部分,并且随着模式的增加,能够识别的频率范围越窄.而在常Q黏弹介质中,由于衰减对高频成分的吸收更强,所以对于同一个模式而言,高频部分被吸收,使得低频端得以凸显.比如图 4b中的第2、3高阶模式表现得尤为明显,此时高频部分几乎不可见,低频部分反而表现出很强的能量.对比图 4b与图 4c可以发现,KV黏弹介质的衰减程度更高,比如基阶模式在大于40 Hz之后已经十分微弱,并且第4、5高阶模式也基本被吸收,而在常Q黏弹介质中,这些部分都是十分清晰的.这是因为KV黏弹介质的Q值是随频率变化的,由(5)式可知,当地层黏性系数给定后,该地层对高频成分的吸收程度更强(对应的Q值更小),而表 1中给的Q值是对应震源主频40 Hz的,因此其他更高频率成分对应的Q值必然小于表中Q值,经历更强程度吸收衰减.
两种黏弹介质中勒夫波所经历的衰减程度差异也可以从理论衰减系数曲线得到体现(图 5).第一个明显差异在于,常Q黏弹介质中基阶模式衰减系数在大于10 Hz后基本呈线性递增趋势,第1高阶模式在大于30 Hz后同样如此,而KV黏弹介质中的相应模式则基本呈指数递增趋势.第二个明显差异在于,KV黏弹介质中的衰减系数总体要大于常Q黏弹时的情况,比如70 Hz时,基阶模式衰减系数约为0.25,而常Q黏弹时只有约0.15,KV黏弹介质中的第4、5高阶模式衰减系数也明显大于常Q黏弹中的情况,这就较好解释了两类黏弹介质中的相速度频散图像中能量分布的差异.
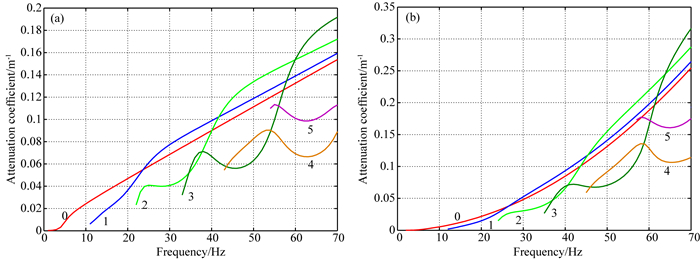
|
图 5 常Q黏弹(a)与KV黏弹(b)三层速度递增模型中勒夫波理论衰减系数曲线 Fig. 5 Attenuation coefficient curves of Love waves in constant Q(a) and KV (b) viscoelastic 3-layered models with layer velocity increasing with depth |
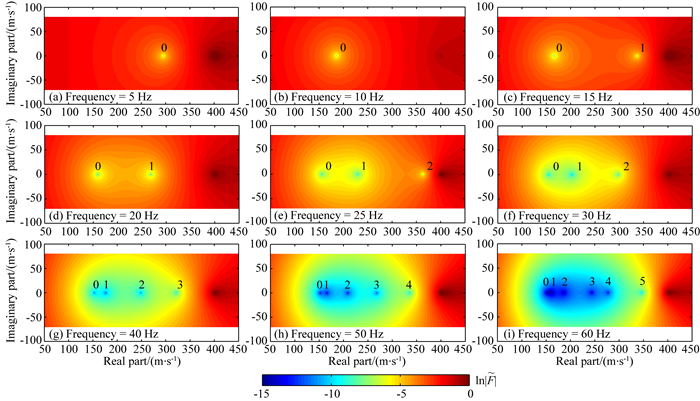
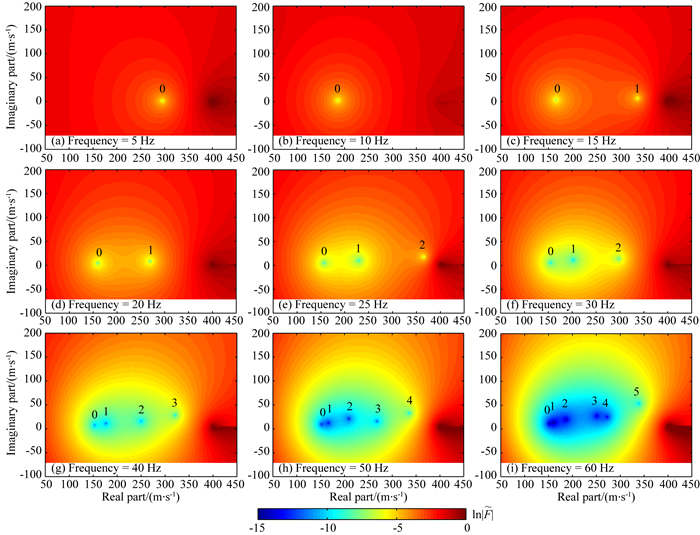
最后,我们考察三种介质中勒夫波频散特征根在复相速度平面上随频率的移动规律(图 6-图 8).由于面波频散函数值数量级变化很大,为了便于显示,仿照Morrison (2014)的办法,以频散函数的绝对值并取自然对数进行成图,即ln|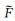
|
图 6 完全弹性三层速度递增模型中勒夫波频散特征根动态分布等值线图 Fig. 6 Dynamic distribution of Love waves dispersion eigenroots in elastic 3-layer model with layer velocity increasing with depth |

|
图 7 常Q黏弹三层速度递增模型中勒夫波频散特征根动态分布等值线图 Fig. 7 Dynamic distribution of Love waves dispersion eigenroots in constant Q 3-layer model with layer velocity increasing with depth |
|
图 8 KV黏弹三层速度递增模型中勒夫波频散特征根动态分布等值线图 Fig. 8 Contours showing dynamic distribution of Love waves dispersion eigenroots in KV viscoelastic 3-layer model with layer velocity increasing with depth |
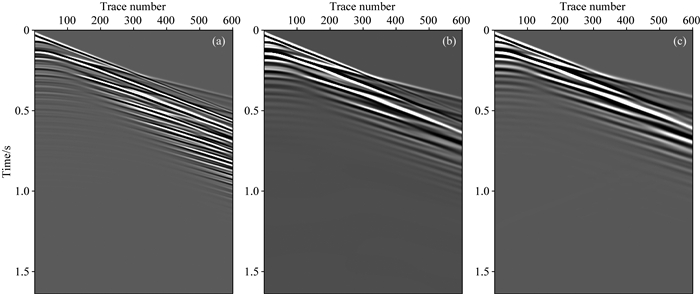
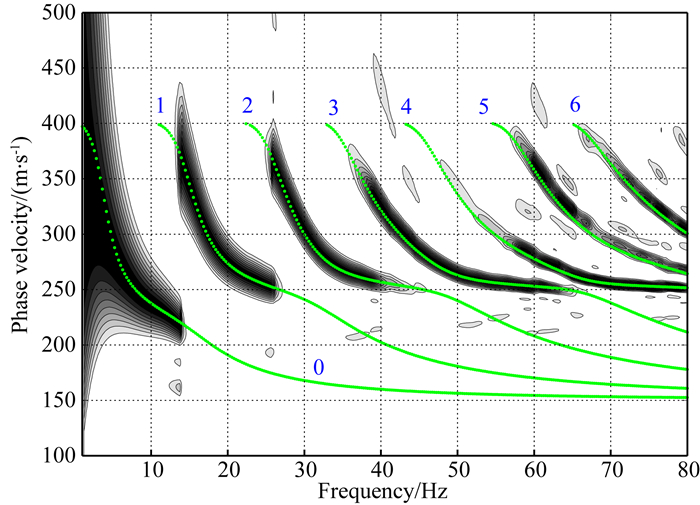
我们将表 1中的前两层介质进行交换,构建了一个夹低速三层模型(表 2).首先采用和速度递增情况下相同的正演方法和参数得到了勒夫波地震记录(图 9).图 10给出了互相关相移法得到的完全弹性时勒夫波相速度频散图像,绿色点线为理论频散曲线,两者吻合程度较好.比较图 10和图 4a可以发现,含低速层时面波能量不再由基阶模式主导,而存在模式跳跃现象,即不同频率段由不同模式主导.从图 10中能清晰分辨出7个勒夫波模式,并且能量分布比较均匀.值得注意的是,虽然第3、4阶模式在65 Hz左右比较靠近,但可以很好区分,没有发生频散曲线交叉现象.
|
图 9 完全弹性(a)、常Q黏弹(b)和KV黏弹(c)夹低速三层模型中勒夫波地震记录 Fig. 9 Seismic records of Love waves in elastic (a), constant Q (b) and KV (c) viscoelastic 3-layer models with a low velocity layer embedded |
|
图 10 完全弹性夹低速三层模型中勒夫波频散图像与理论频散曲线对比 Fig. 10 Comparison of Love wave dispersion images and theoretic dispersion curves in elastic 3-layer model with a low velocity layer embedded |
|
|
表 2 夹低速三层模型参数 Table 2 Parameters of 3-layer model with a low velocity layer embedded |
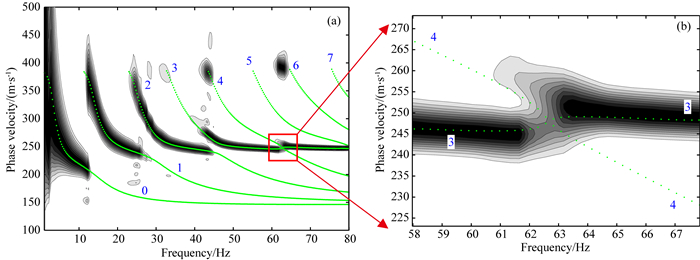
引入常Q衰减之后,情况发生了很大变化.图 11为常Q黏弹时勒夫波频散图像与本文方法得到的理论频散曲线.首先,由于吸收衰减作用,第4~第7阶模式的频散图像无法看到,并且第3阶模式也只能观察到大于40 Hz的部分.另一个更主要的差异是,在利用勒夫波频散进行地层横波速度反演时,首先需要从频散图像上进行模式识别,如果仅仅只有图 11a的频散图像,很可能将大于63 Hz部分的频散图像能量团识别为第4阶模式,并认为63 Hz附近频散能量团的不连续是因为两个模式靠的太近的缘故,这就造成了模式误判.该频率范围能量团依然属于第3阶模式,63 Hz左右频散能量团的不连续性是由于第3阶模式理论频散曲线在62~64 Hz之间相速度突然增加造成的.将图 11a的理论频散曲线交叉点附近区域进行放大显示,可以更清晰地展示两条理论频散曲线的变化(图 11b).可见,在小于62 Hz的部分,第3阶模式频散曲线近乎于水平直线,但是在62~64 Hz之间,相速度逐渐增加,随后又趋于水平直线.图 12为相应的理论衰减系数曲线,为了便于识别衰减系数曲线的交叉点,同样用数字标明了所属的模式号.
|
图 11 常Q黏弹夹低速三层模型中勒夫波频散图像与理论频散曲线对比 (a)整体图;(b)交叉点附近局部放大. Fig. 11 Comparison of Love wave dispersion images and theoretic dispersion curves in constant Q 3-layer model with a low velocity layer embedded (a) Whole diagram; (b) Magnification around cross point. |

|
图 12 常Q黏弹夹低速三层模型中勒夫波理论衰减系数曲线 Fig. 12 Attenuation coefficient curves of Love waves in constant Q viscoelastic 3-layer model with a low velocity layer embedded |
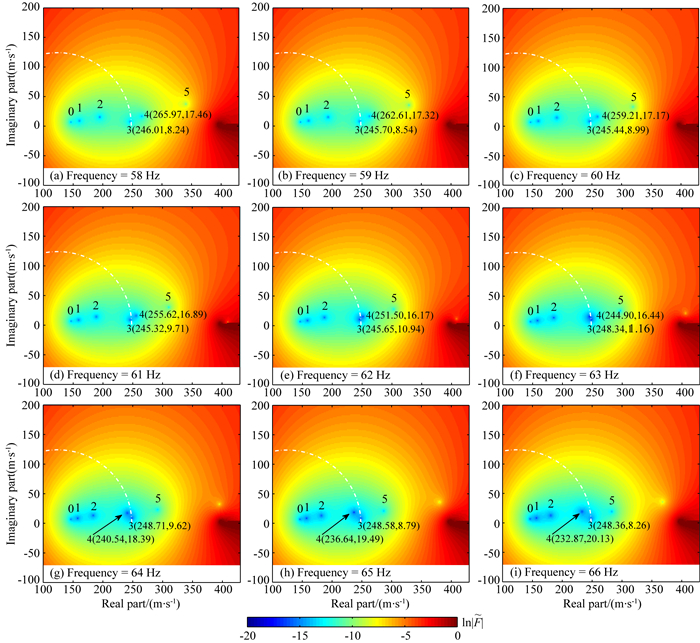
前面已经证明,如果出现频散曲线交叉现象,那么在复相速度平面上必然存在着一个模式特征根在随频率增加的移动过程中跨越了另一个模式特征根所在的圆边界,并给出了该圆的位置.接下来通过考察复相速度平面上频散特征根的分布等值线图来验证这一结论的正确性.由于频散曲线交叉位置发生在63 Hz附近,所以只给出了58~66 Hz之间的频散特征根分布结果(图 13),并将第3、4阶模式对应的特征根位置标注在极值点旁边以便于比较,其中白色点划线圆弧为根据66 Hz时第3阶模式特征根坐标按(19)式找到的参考圆.由图 13可知,从58~61 Hz,第3阶模式特征根的移动距离非常小.由所标坐标可知,它一直在向复平面的左上方微弱移动,第4阶模式特征根在这个频率范围内一直在向其逼近.但是从61~62 Hz,它转向复平面右上方移动,到63 Hz时,这一改变非常明显,并且此时第4阶模式频散特征根也跨过了圆弧,这与理论频散曲线中的两者的交叉点频率十分相符.随着频率的增加,第4阶模式特征根继续向圆内部移动,而第3阶模式特征根则基本趋于静止.
|
图 13 常Q黏弹夹低速三层模型中勒夫波频散特征根动态分布等值线图 Fig. 13 Contours showing dynamic distribution of Love wave dispersion eigenroots in constant Q viscoelastic 3-layer model with a low velocity layer embedded |
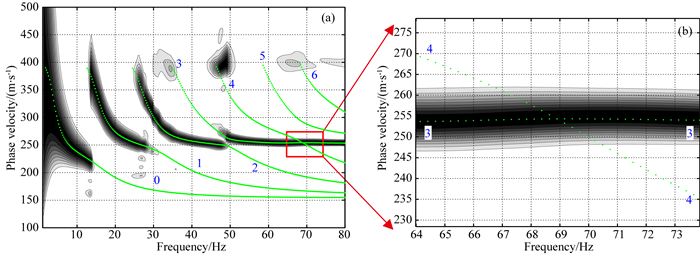
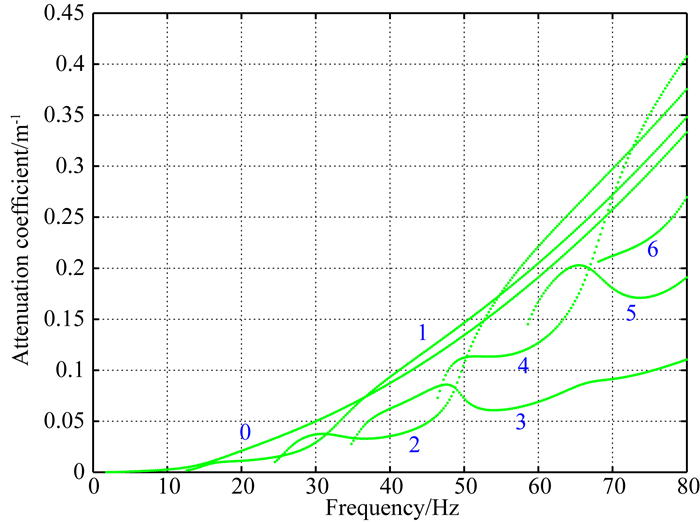
最后,考察KV黏弹介质中的情况.由图 14可知,此时的第3、4阶频散曲线之间同样发生了交叉,不过交叉点对应的频率提高到了约70 Hz左右.另外,50 Hz之后的第3阶模式频散图像能量团十分连续,不会引起模式误判.比较图 14与图 11中的两个局部放大图也可以发现,KV黏弹时的第3阶模式理论频散曲线在交叉点附近没有出现类似常Q黏弹时那种相速度突然增加.这可以从频散特征根随频率分布等值线图上进一步得到确认(图 15).图 15中的白色点划线通过第3阶模式特征根,用以帮助识别该根在60 Hz之后基本处于静止状态.随着频率的增加,第4阶模式特征根不断向左移动,在69 Hz后跨越了第3阶模式特征根所定义的圆边界.通过对常Q黏弹情况的讨论,我们对这一现象已经比较熟悉,所以图 15中没再给出这个圆的位置.图 16为相应的理论衰减系数曲线.显然它和速度递增情况下类似,即基阶模式的振幅衰减程度随频率增加呈指数增长趋势,各模式总体衰减程度也都高于常Q黏弹时.
|
图 14 KV黏弹夹低速三层模型中勒夫波频散图像与理论频散曲线对比 (a)整体图;(b)交叉点附近局部放大. Fig. 14 Comparison of Love wave dispersion images and theoretic dispersion curves in KV viscoelastic 3-layer model with a low velocity layer embedded (a) Whole diagram; (b) Enlarged around cross point. |

|
图 15 KV黏弹夹低速三层模型中勒夫波频散特征根动态分布等值线图 Fig. 15 Contours showing dynamic distribution of Love wave dispersion eigenroots in KV viscoelastic 3-layer model with a low velocity layer embedded |
|
图 16 KV黏弹夹低速三层模型中勒夫波理论衰减系数曲线 Fig. 16 Attenuation coefficient curves of Love waves in 3-layer KV model with a low velocity layer embedded |
本文采用解析函数零点求解技术,给出了完全弹性、常Q黏弹和KV黏弹层状介质中勒夫波频散特征方程的统一求解方法.特别是,考察了三种介质中勒夫波多模式相速度特征根在复相速度平面上随频率运动的变化规律,研究表明:
(1)这三种介质中的勒夫波简正模式频散特征根在复相速度平面上都产生于对应底层半空间地层横波速度值的位置.介质完全弹性时该位置严格位于复相速度平面的实轴上.随着介质Q值的减小,该位置逐渐偏离实轴.
(2)底层半空间横波速度对应复相速度平面上的一个奇点,所有勒夫波简正模式特征根都产生于该点附近.介质完全弹性时,各阶简正模式特征根沿复相速度平面的实轴从高速区向低速区移动;当介质为黏弹时,这些特征根在复相速度平面的第一象限从高速区向低速区沿弧线轨迹移动.
(3)当含有低速夹层时,黏弹介质中勒夫波理论频散曲线可能产生交叉现象.在复相速度平面上表现为随频率增加,某个模式特征根的移动轨迹跨越了另一个模式特征根所在的圆.本文给出了这个圆的解析表达式.这一结论具有一般性,也可推广到瑞雷波或其他模式波的情况.
(4)常Q黏弹时,基阶勒夫波模式衰减程度一般在大于某个低频之后呈线性增强趋势;而KV黏弹时,基阶勒夫波模式衰减程度随频率增加呈指数增加趋势.由于KV黏弹的Q值频变本质,其各阶模式的衰减程度总体上稍大于常Q黏弹介质的情形.
附录A
根据弹性-黏弹性对应法则(Carcione,2015),将完全弹性介质中的勒夫波频散特征方程(Aki and Richards, 2002)推广到黏弹性情况只需要将完全弹性时横波速度替换成复横波速度即可.这里以KV介质为例,对于常Q黏弹性介质,可作类似处理.建立如图 17所示水平层状介质模型,z轴正方向垂直向下指向地层深部,ρi,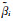

|
图 17 水平层状地层模型 Fig. 17 Horizontally layered stratum model |
因为勒夫波是由SH波干涉叠加形成,所以设其位移解形式为
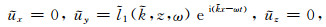
|
(A1) |
将(A1)代入KV介质中的SH波运动方程,整理得到如下常微分方程组:
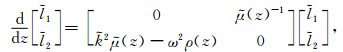
|
(A2) |
其中波浪线表示该物理量为复数,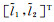
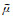

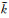
采用传递矩阵法(Aki and Richards, 2002)求解(A2),其解可以写为
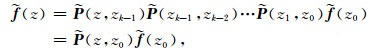
|
(A3) |
这里的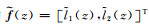
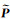

|
(A4) |
其中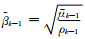
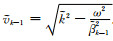
进一步引入半空间辐射边界条件与自由表面边界条件,得到方程组:
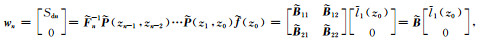
|
(A5) |
其中w n为半空间地层中上下行波向量,Sdn为下行波分量,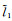
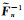
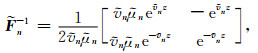
|
(A6) |
显然,要使(A5)有非零解,必须满足
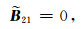
|
(A7) |
这就是任意多层KV介质中的勒夫波频散特征复数方程.
附录B由于zj(j=1, 2, …, m)是连带多项式Pm(z)的m个零点,所以由(9)式可得:
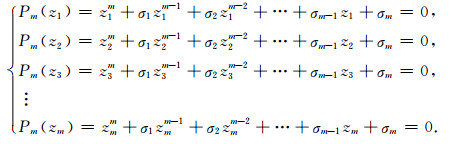
|
(B1) |
将(B1)各式对应相加可得:
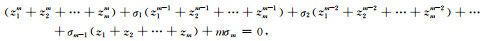
|
(B2) |
将(B2)式中括号内各项由(8)式代替,即可得:
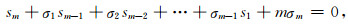
|
(B3) |
此即(10)式.
| Aki K, Richards P G. Quantitative Seismology.(2nd ed).California: University Science Books, 2002. | |
| Anderson D L, Ben-Menahem A, Archambeau C B. 1965. Attenuation of seismic energy in the upper mantle. J. Geophys. Res., 70(6): 1441-1448. DOI:10.1029/JZ070i006p01441 | |
| Antia H M. Numerical Methods for Scientists and Engineers.New Delhi: Tata McGraw-Hill Publishing Company Limited, 1995. | |
| Buchen P W, Ben-Hador R. 1996. Free-mode surface-wave computations. Geophys. J. Int., 124(3): 869-887. DOI:10.1111/gji.1996.124.issue-3 | |
| Cao Z L, Dong H F. 2010. Attenuation dispersion of Love waves in a viscoelastic multilayered half-space.//80th Annual Meeting of the Society of Exploration Geophysicists. Denver, Colorado:SEG, 2998-3002. | |
| Carcione J M. Wave Fields in Real Media.(3rd ed).Amsterdam: Elsevier Ltd, 2015. | |
| Carcione J M, Poletto F, Gei D. 2004. 3-D wave simulation in anelastic media using the Kelvin-Voigt constitutive equation. Journal of Computational Physics, 196(1): 282-297. DOI:10.1016/j.jcp.2003.10.024 | |
| Cercato M. 2007. Computation of partial derivatives of Rayleigh-wave phase velocity using second-order subdeterminants. Geophys. J. Int., 170(1): 217-238. DOI:10.1111/gji.2007.170.issue-1 | |
| Chen X F. 1993. A systematic and efficient method of computing normal modes for multilayered half-space. Geophys. J. Int., 115(2): 391-409. DOI:10.1111/gji.1993.115.issue-2 | |
| Davies B. 1986. Locating the zeros of an analytic function. Journal of Computational Physics, 66(1): 36-49. DOI:10.1016/0021-9991(86)90052-5 | |
| Delves L M, Lyness J N. 1967. A numerical method for locating the zeros of an analytic function. Math. Comp., 21(100): 543-560. DOI:10.1090/S0025-5718-1967-0228165-4 | |
| Feng K, et al. Numerical Computation Method (in Chinese).Beijing: National Defense Industry Press, 1978. | |
| He Y F, Chen W T, Chen X F. 2006. Normal mode computation by the generalized reflection-transmission coefficient method in planar layered half space. Chinese J. Geophys.(in Chinese), 49(4): 1074-1081. | |
| Jeng Y, Tsai J Y, Chen S H. 1999. An improved method of determining near-surface Q. Geophysics, 64(5): 1608-1617. DOI:10.1190/1.1444665 | |
| Johnston D H, Toksöz M N, Timur A. 1979. Attenuation of seismic waves in dry and saturated rocks:Ⅱ. Mechanisms. Geophysics, 44(4): 691-711. DOI:10.1190/1.1440970 | |
| Jongmans D, Campillo M. 1993. The determination of soil attenuation by geophysical prospecting and the validity of measured Q values for numerical simulations. Soil Dyn. Earthq. Eng., 12(3): 149-157. DOI:10.1016/0267-7261(93)90042-P | |
| Lai C G, Rix G J. 2002. Solution of the Rayleigh eigenproblem in viscoelastic media. Bulletin of the Seismological Society of America, 92(6): 2297-2309. DOI:10.1785/0120010165 | |
| Liu X F, Fan Y H. 2011. A study on 'jump point' frequencies of zigzag dispersion curves in Rayleigh wave exploration. Chinese J. Geophys.(in Chinese), 54(8): 2124-2135. DOI:10.3969/j.issn.0001-5733.2011.08.020 | |
| Liu X F, Fan Y H. 2012. On the characteristics of high-frequency Rayleigh waves in stratified half-space. Geophys. J. Int., 190(2): 1041-1057. DOI:10.1111/gji.2012.190.issue-2 | |
| Liu X F, Fan Y H, Chen X F. 2009. Research on the cross of the dispersion curves of Rayleigh waves and multi-modes coupling phenomenon. Chinese J. Geophys.(in Chinese), 52(9): 2302-2309. DOI:10.3969/j.issn.0001-5733.2009.09.014 | |
| Malagnini L. 1996. Velocity and attenuation structure of very shallow soils:evidence for a frequency-dependency Q. Bulletin of the Seismological Society of America, 86(5): 1471-1486. | |
| McDonal F J, Angona F A, Mills R L, et al. 1958. Attenuation of shear and compressional waves in Pierre shale. Geophysics, 23(3): 421-439. DOI:10.1190/1.1438489 | |
| Michaels P. 1998. In situ determination of soil stiffness and damping. J. Geotech. Geoenviron. Eng., 124(8): 709-719. DOI:10.1061/(ASCE)1090-0241(1998)124:8(709) | |
| Michaels P, Gottumukkula V. 2010. Theory of viscoelastic Love waves and their potential application to near-surface sensing of permeability.//Miller R D, Bradford J H, Holliger K. Advances in Near-Surface Seismology and Ground-Penetrating Radar. Tulsa:SEG, 263-278. | |
| Morrison M W. 2014. In-situ viscoelastic soil parameter estimation using Love wave inversion[Doctoral Dissertation]. Boise:Boise State University. | |
| Novotny O. 1970. Partial derivatives of dispersion curves of Love waves in a layered medium. Studia Geophysica et Geodaetica, 14(1): 36-50. DOI:10.1007/BF02585549 | |
| Park C B, Miller R D, Xia J H. 1999. Multichannel analysis of surface waves. Geophysics, 64(3): 800-808. DOI:10.1190/1.1444590 | |
| Press W H, Teukolsky S A, Vetterling W T, et al. Numerical Recipes in C.(2nd ed).Cambridge: Cambridge University Press, 1992. | |
| Schwab F, Knopoff L. 1971. Surface waves on multilayered anelastic media. Bulletin of the Seismological Society of America, 61(4): 893-912. | |
| Socco L V, Foti S, Boiero D. 2010. Surface-wave analysis for building near-surface velocity models-Established approaches and new perspectives. Geophysics, 75(5): 75A83-75A102. DOI:10.1190/1.3479491 | |
| Xia J H, Yin X F, Xu Y X. 2013. Feasibility of determining Q of near-surface materials from Love waves. Journal of Applied Geophysics, 95: 47-52. DOI:10.1016/j.jappgeo.2013.05.007 | |
| Xia J H, Gao L L, Pan Y D, et al. 2015. New findings in high-frequency surface wave method. Chinese J. Geophys.(in Chinese), 58(8): 2591-2605. DOI:10.6038/cjg20150801 | |
| Zhang B X, Lu L Y, Bao G S. 2002. A study on zigzag dispersion curves in Rayleigh wave exploration. Chinese J. Geophys.(in Chinese), 45(2): 263-274. | |
| Zhang C J. 2008. Seismic absorption estimation and compensation[Doctoral Dissertation]. Vancouver:The University of British Columbia. | |
| Zhang K, Zhang B W, Liu J X, et al. 2016. Analysis on the cross of Rayleigh-wave dispersion curves in viscoelastic layered media. Chinese J. Geophys.(in Chinese), 59(3): 972-980. DOI:10.6038/cjg20160319 | |
| Zhong Y Q. Complex Function Theory.(2nd ed (in Chinese)).Beijing: Higher Education Press, 2003. | |
| 冯康, 等. 数值计算方法.北京: 国防工业出版社, 1978. | |
| 何耀锋, 陈蔚天, 陈晓非. 2006. 利用广义反射-透射系数方法求解含低速层水平层状介质模型中面波频散曲线问题. 地球物理学报, 49(4): 1074–1081. | |
| 刘雪峰, 凡友华. 2011. Rayleigh波勘探中"之"字形频散曲线"起跳点"频率研究. 地球物理学报, 54(8): 2124–2135. DOI:10.3969/j.issn.0001-5733.2011.08.020 | |
| 刘雪峰, 凡友华, 陈晓非. 2009. Rayleigh波频散曲线交叉及多模式耦合作用研究. 地球物理学报, 52(9): 2302–2309. DOI:10.3969/j.issn.0001-5733.2009.09.014 | |
| 夏江海, 高玲利, 潘雨迪, 等. 2015. 高频面波方法的若干新进展. 地球物理学报, 58(8): 2591–2605. DOI:10.6038/cjg20150801 | |
| 张碧星, 鲁来玉, 鲍光淑. 2002. 瑞利波勘探中"之"字形频散曲线研究. 地球物理学报, 45(2): 263–274. | |
| 张凯, 张保卫, 刘建勋, 等. 2016. 层状黏弹性介质中Rayleigh波频散曲线"交叉"现象分析. 地球物理学报, 59(3): 972–980. DOI:10.6038/cjg20160319 | |
| 钟玉泉. 复变函数论(第2版).北京: 高等教育出版社, 2003. | |
 2017, Vol. 60
2017, Vol. 60


