2. 中国科学院油气资源研究重点实验室, 北京 100029
2. Key Laboratory of Petroleum Resources Research, Beijing 100029, China
随着勘探程度不断深入,所面临的地质问题日趋复杂,需要更高精度的成像,但良好的成像结果依赖于高精度速度模型,全波形反演作为一种高精度速度建模方法受到普遍关注.
20世纪80年代Tarantola (1984)等基于广义最小二乘的反演理论提出了时间域全波形反演,对地震反演理论产生了深远影响.该方法利用正传波场对时间二次导数与反传的残差波场互相关构造梯度方向,避免计算雅可比矩阵转而直接求取梯度方向,显著减少计算量.Mora (1988)利用共轭梯度法反演出纵波速度、横波速度和介质密度;Pratt等(1998)将梯度法、高斯牛顿法和全牛顿法应用到频率域波形反演中,Shin等(2001)基于虚震源构造了拟Hessian矩阵用于均衡梯度场的能量分布,改善了反演质量.Sirgue等(2008)通过离散傅里叶变换将时间域FWI和频率域FWI相结合,将正演放在时间域,反演放在频率域,从而提出了混合域FWI.
全波形反演方法具有精确刻画模型细节的潜力,这是未来地震勘探的发展的必然趋势(王华忠, 2015).然而,由于全波形反演容易陷于局部极小值以及巨大的存储量和计算量限制,该方法目前还无法广泛运用到实际地震资料中.因此,在全波形反演应用中发展高性能计算是十分必要的,一旦克服了计算方面的困难,解决局部极小值问题,全波形反演能够取得令人满意的结果.由于GPU多线程模式,相对CPU具有巨大计算优势,但相对CPU来说显存较小,一定程度上限制了其发展.前人通过研究,近年来在将GPU广泛而成功的应用到地球物理领域.如Micikevicius (2009)基于GPU的有限差分问题,实现有限差分快速算法,李博等(2009, 2010)实现了CPU/GPU协同并行加速逆时偏移;Kim等(2013)在GPU上实现了三维声波时间-拉普拉斯-傅里叶混合域FW;刘璐等(2013)在GPU上实现了基于修正拟牛顿公式的全波形反演;张猛等(2014)分析了CPU/GPU平台上的全波形反演的实用化;Liu等(2015)实现了单GPU的三维混合域全波形反演,但模型过小,不具有应用能力,因此发展出具有实际意义三维全波形反演,需要克服大模型的存储和计算问题,本文通过对模型数据进行分割,同时在数个小模型内进行梯度搜索,然后对比各个局域的梯度,最终找出合适的全局梯度,同时这样能更充分使用GPU硬件特性,使得算法具有良好的可扩展性.
2 全波形反演理论基础全波形反演的基础是正演,它描述了地震波在地下介质中的传播过程,可将其表示为
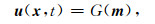
|
(1) |
x是空间向量,表示空间位置,t是时间,u表示的是波场,G是传播算子,描述地震波的传播机制,m是模型参数.
定义全波形反演的目标泛函数学方式众多,L2范数,两类L1范数,对数范数(Shin and Cha, 2008),振幅和相位目标函数(Shin et al., 2006),Huber范数(Brossier et al., 2010),幂指数函数,积分目标函数(Shin and Ha, 2008),互相关函数(Luo and Schuster, 1991).本文L2范数定义了以下目标函数:
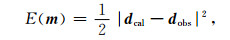
|
(2) |
式中, d cal表示为通过正演模拟得到的地震记录,d cal=Ru,R是一个限定算子,表示特定位置的波场,d obs表示野外观察的地震记录.
为使得函数最优化,在m 0处附近寻找目标函数E(m)的极小值.本质上来讲FWI是局部最优化.根据波恩近似理论,模型m可以看作是初始模型m0加上一个扰动模型Δ m构成的,m=m 0+Δ m.
将目标函数在m 0处进行泰勒展开:
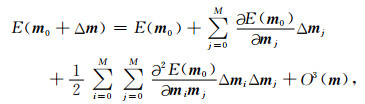
|
(3) |
因此,E(m)对m进行求导,可得:

|
(4) |
为了使目标函数在m处取得极小值,要求目标函数的导数为0,因此公式(4)等于0,由此可得:

|
(5) |
可以看出扰动模型是沿着目标函数在m 0处梯度的负方向进行搜索.
通过以上推导,可以得出以下迭代式:
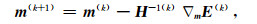
|
(6) |
H是误差函数在m 0处对模型的二阶导数:
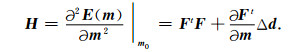
|
(7) |
H又称为Hessian矩阵,它有两部分构成.其中,Δ d ə F t/ə m为其非线性项目,它定义了目标函数在m 0处的曲度,其中Δ d是实际数据和模拟数据的残差.为了得到扰动模型,需要求出H -1(k)和Δ m E (k),然而实际运算中Hessian矩阵计算量巨大,可以用一个迭代步长α替换,(7)式变为
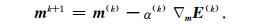
|
(8) |
α为迭代步长,k为迭代次数.迭代的方向即是目标函数梯度的反方向.因此为求取第k次的模型形,需求取梯度和迭代步长,这就是梯度法全波形反演的核心思想.
2.1 梯度的求取本文采用三维声波频率域反演,三维频率域声波方程最终梯度公式为
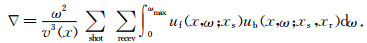
|
(9) |
uf和ub分别代表正传波场和残差反传波场.
2.2 步长求取梯度场求取以后,就需选择一个合理的步长来更新模型参量.多种步长求取的方法中,本文采用直接法,Pica等(1990)给出的公式如下:
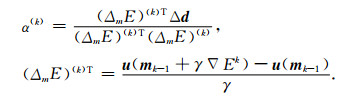
|
(10) |
其中,T表示转置,γ是系数且γ满足max (γ Δ mE(k))≤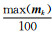
第2节,通过推导得出频率域FWI的梯度公式为

|
(11) |
类似的,可以得出时间域FWI的梯度公式为
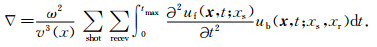
|
(12) |
式(11)(12)可以看出:
(1)时间域FWI首先进行正演,之后反传残差,重建残差波场和正传波场,正传波场对时间求二次导,之后做零延迟互相关.而频率域FWI先对系数矩阵进行分解,重建正传波场和反传残差波场只需要用分解结果乘以波场向量即可.频率域FWI比时间域FWI少做了一次正演,需要存储的波场更少.
(2)对比时间域和频率域正演计算复杂度,如表 1所示.现代计算机完全能够满足二维频率域正演的内存消耗.比如:一个3000×2000的模型,网格间距为10 m,模型矩阵分解大致需要1~2 G的内存.但是对于三维频率域正演,现代计算机无法满足其计算需求,Operto等(2007)做了一个测试,其结果显示,对于一个网格大小210×210×210三维速度模型,最小速度为2000 m·s-1,其一次矩阵分解需要320 GB的内存,通用计算机难以满足.所以,三维情况要选用时间域正演,二维情况要选用频率域正演.
|
|
表 1 时间域与频率域FWI对比 Table 1 Comparison of time domain and frequency domain FWI |
(3)相对时间域反演,频率域反演采用一部分频率参与反演就可以得到可靠的结果(Sirgue and Pratt, 2004),而且低频到高频的反演策略可以更好地解决全频段反演遇到的局部极小值问题.
频率域FWI是一种天然多尺度反演方法.而且采用Sirgue的频率优选策略(Sirgue and Pratt, 2004),2D频率域相对比时间域全波形反演更加高效.然而,对于三维频率域全波形反演,矩阵分解法内存需求极大和计算量庞大,这使得三维大模型频率域全波形反演变得异常困难.虽然可以利用迭代法来解决这个问题,但耗时较大,失去了频率域算法多炮高效正演的优势;并且随着频率的升高和模型复杂度的增加,这种方法的收敛性也会变差(Nihei and Li, 2007).而时间域全波形反演,在求解梯度时需要求取正传波场的对时间的二次导数,计算量巨大且需要存储更多的波场,当遇到三维大模型时,求解时间域梯度变得无比困难.
考虑到这些问题,Sirgue等(2010)提出了混合域的全波形反演,这种方法将波传播放到时间域,利用DFT去抽取相应波场的频率成分,在频率域求取梯度场.这种方法可以用最小的耗时来获得任意频率成分,而且在混合域时间窗函数相对频率域更好添加,从而得到某些特定的波至,比如早至波,反射波等等,这些波经常被用来减小反演的非线性(刘璐, 2014),整个流程如(图 1):
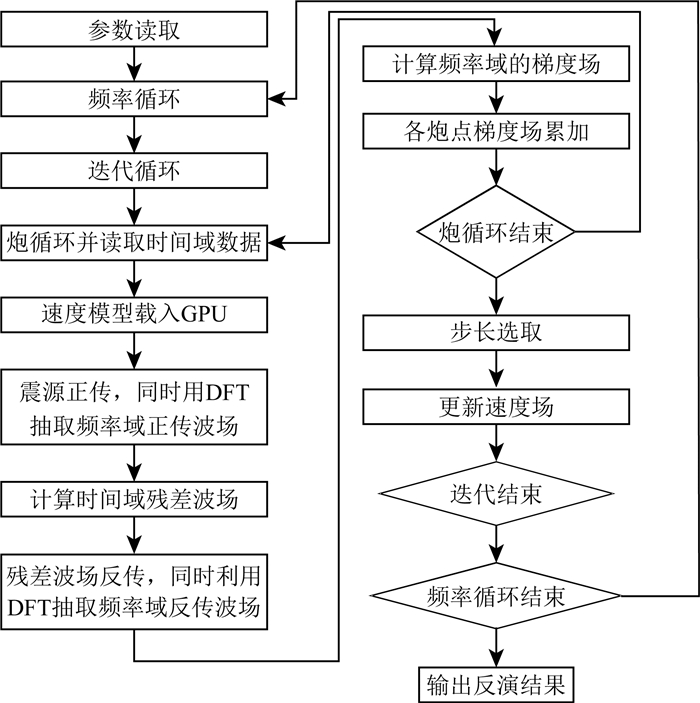
|
图 1 Sirgue混合域方法流程图 Fig. 1 Flow chart of Sirgue′s hybrid domain method |
在Sirgue混合域方法的基础上,针对三维大模型全波形反演,对Sirgue混合域方法的进行简化,并利用多GPU进行加速,提高计算效率.
3.2.1 简化混合域全波形反演Sirgue的混合域思想是用时间域传播算子和DFT来计算所有波场变量.下面我们对此流程进行简化.简化的混合域全波形反演流程如图 2.图中蓝色方块表示模块在GPU中执行.混合域全波形反演的详细流程可参考Sirgue的专利(Sirgue et al., 2010).本文方法的实现流程如图 2,其中流程图蓝色部分在GPU上进行.
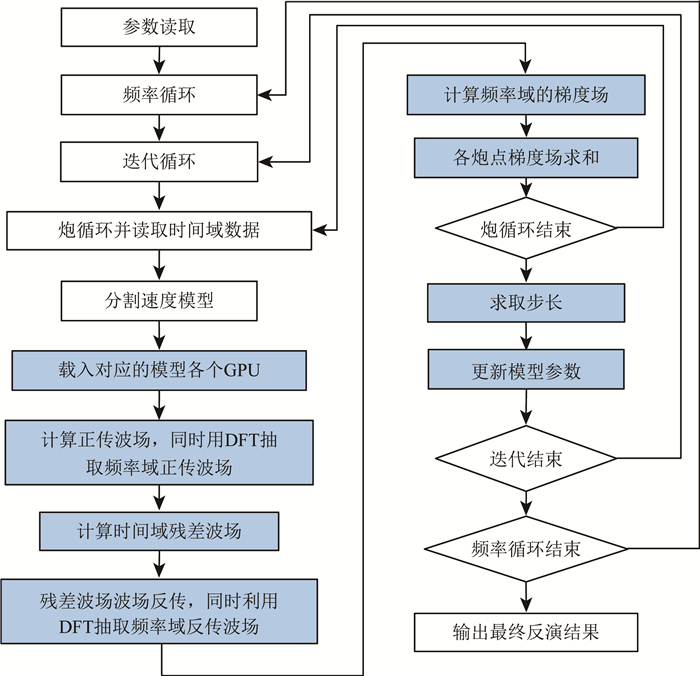
|
图 2 简化混合域全波形反演流程图 Fig. 2 Flow chart of simplified hybrid domain full waveform inversion |
两种方法都利用了两次DFT来得到频率域的震源正传波场和残差反传波场.两者的不同之处,简化的混合域全波形反演残差是在时间域求取的,而混合域全波形反演是在频率域求取残差,简化的混合域全波形反演不需要讲数据进行DFT求取频率域残差,再将频率域残差IDFT到时间域反传,意味着简化的混合域全波形反演比混合域全波形反演每次迭代少了一次DFT和一次IDFT.
3.2.2 多GPU并行策略由于硬件限制,GPU虽然具有强大的计算能力,但是相对于CPU来说,单个GPU显存过小极大限制了其应用范围,因此,需要一种新的并行策略来克服单个GPU显存过小,随之提出多GPU并行策略.将数据进行分割,使得单GPU上存储数据量减小,克服单GPU显存小的限制,相当于利用多个GPU联合,使得可用显存在总量上增大.
对于多GPU,有两种并行策略:
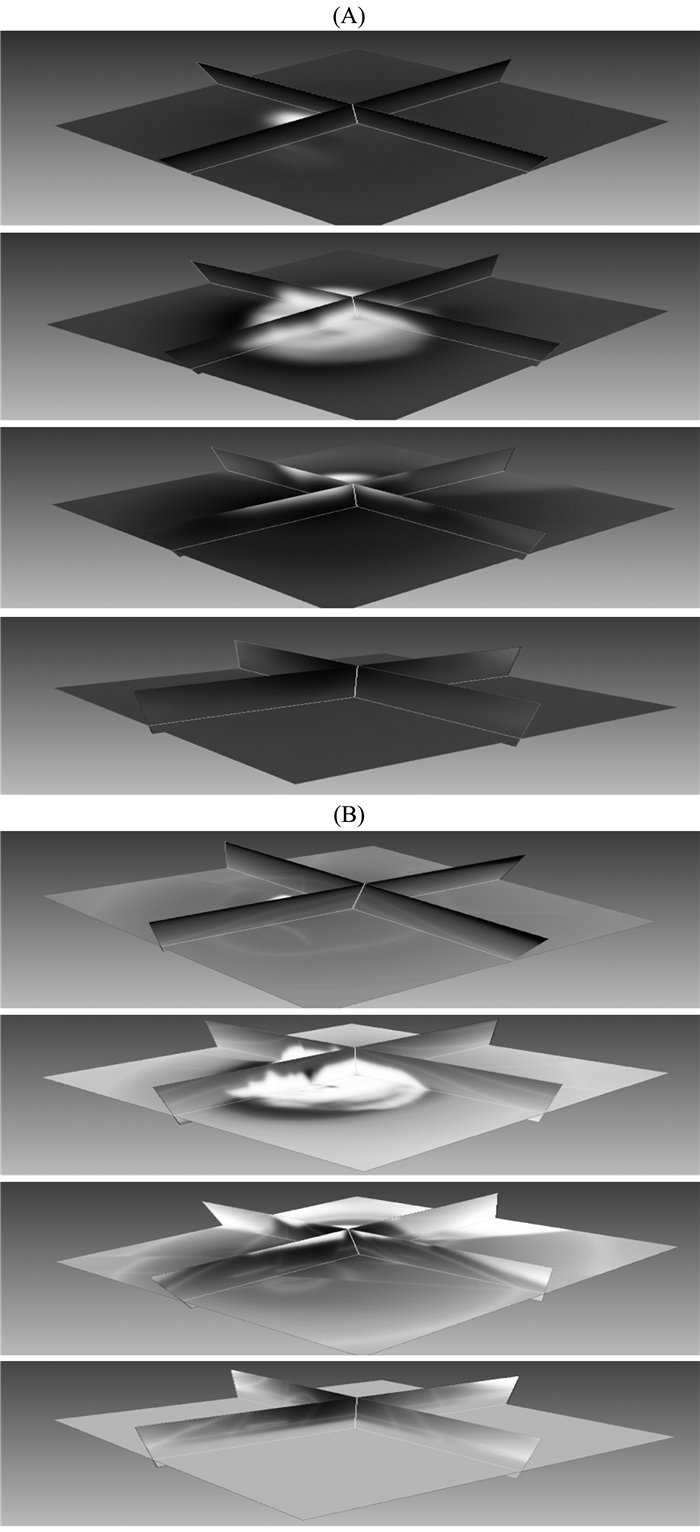
并行策略一:当模型不大时,一块GPU有足够的显存对模型进行计算时,采用单块GPU进行一炮的计算,当有N块GPU卡时,对N炮道集同时进行计算,这样相当于加速了N倍,但受到数据传输的影响,实际上是达不到N倍加速,在全波形反演正传以及残差反传阶段采用这种并行策略,示意图如图 3.
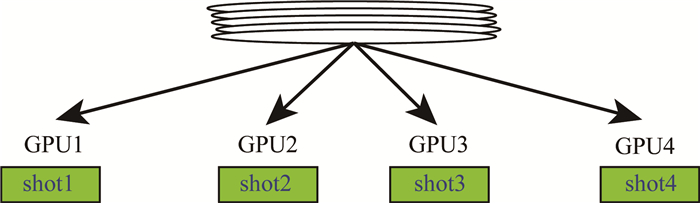
|
图 3 多GPU并行策略一示意图 Fig. 3 Schematic diagram of thefirst strategyof multi GPU parallel |
并行策略二:当模型太大时,由于GPU显存的限制,单块GPU无法对整个模型进行计算,必须对模型数据进行区域分解.沿着z方向对模型进行区域分解,是因为这样可以用时间来控制每块区域的搜索区间,减少这个模型的非线性,降低局部陷入极小的概率.每块GPU计算一部分模型数据,这样多个GPU并行就能完成整个模型的计算,需要注意的是区域分解后的模型数据大小,为了使得数据具有连续性,必须给每个分割的小模型数据顶和底各加一个交换的区域,分割后的模型数据在边界区需要进行数据交换.示意图如图 4.
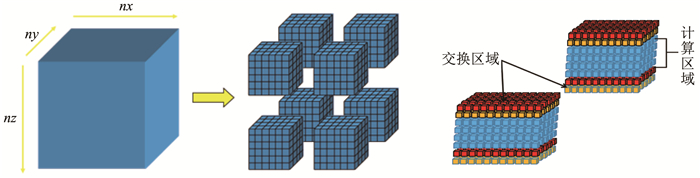
|
图 4 多GPU并行策略二示意图 Fig. 4 Schematic diagram of the second strategy of multi GPU parallel |
下面将使用多GPU简化混合域方法计算三维模型数据.本文分别对两种多GPU加速策略来进行测试.
模型1是SEG的salt模型,速度网格大小676×676×210,网格间距均为10 m.地表放炮,共放100炮,炮间距40 m,x方向和y方向各10炮,第一炮位置位于x=31800 m,y=3180 m处.使用主频为35 Hz的零相位雷克子波,采集系统是地表全接受.时间采样率,采样点数为2000.总共正演204 GB数据,一炮相当于2.1 GB数据,另外在计算时还需要存储模型数据、正传波场、残差波场以及反传残差波场,即使使用比较先进K20显卡,其显存为5 GB,也只能勉强满足计算需求.因此对此模型,本文分别使用上述两种并行加速策略进行测试,其反演频率从1.5 Hz开始,每次增加1.5 Hz,两个频率组成一个频率组,最大频率60 Hz,对比计算效率.
从图 6可知采用并行策略一时,并未对模型进行区域分解,再来对比图 5和图 7,反演结果和真实模型基本上一致;图 8,反演结果能过有效识别的出盐丘的顶部.图 9、图 11以及图 13是采用并行策略二时,程序根据使用的GPU个数不同对计算区域进行分解,然后每个GPU对一部分区域进行反演;图 10、图 12以及图 14是区域分解后初始模型以及反演结果的切片图,可以看出,反演结果很好恢复盐丘,能有有效地识别出盐丘的顶部.
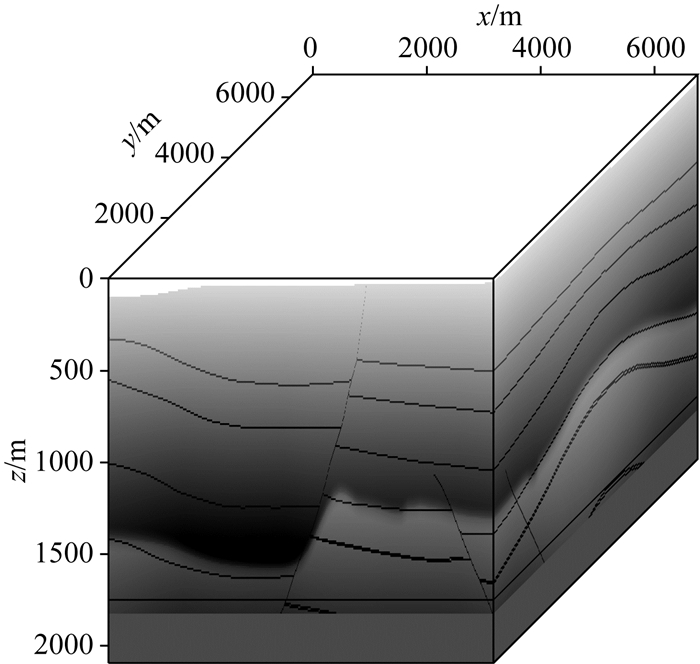
|
图 5 盐丘模型 Fig. 5 Salt dome model |
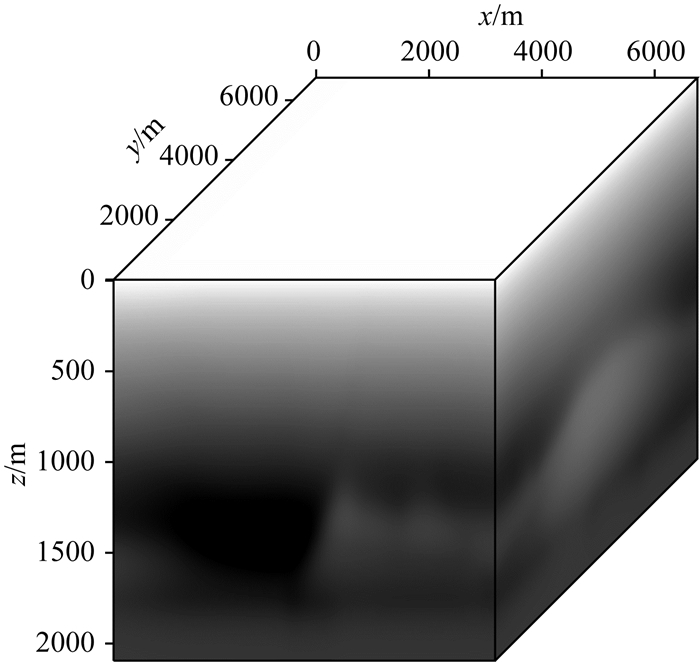
|
图 6 初始模型 Fig. 6 Initial model |
|
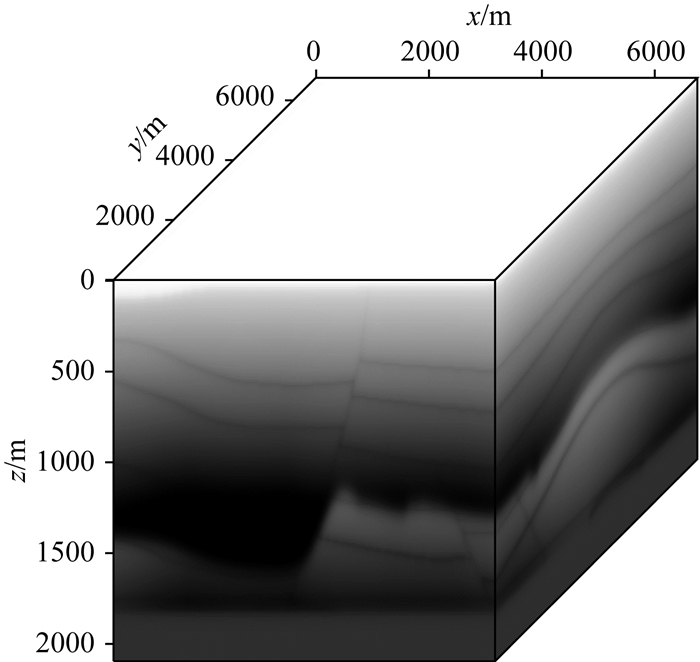
图 7 使用单GPU计算时最终结果 Fig. 7 The final results when using a single GPU calculation |

|
图 8 使用单GPU时切片图对比 (a)真实模型; (b)初始模型; (c)最终结果. Fig. 8 Slice graph comparison when using single GPU (a) Real model; (b) Initial model; (c) Final result. |
|
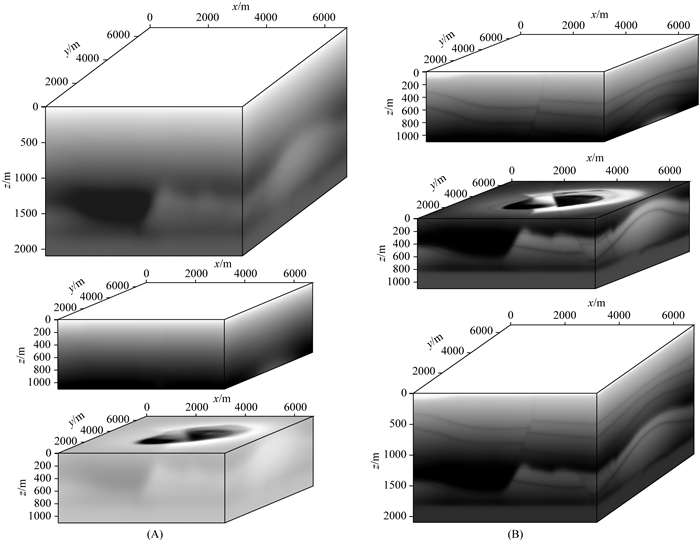
图 9 使用两块GPU时初始模型以及最终结果 (A)初始模型和分解区域; (B)分解区域反演结果和最终结果. Fig. 9 The initial model and the final results when using two GPUs (A) Sub region of domain decomposition; (B) Inversion results of sub region. |

|
图 10 使用两块GPU时模型切片对比 (A)分解区域初始模型切片;(B)分解区域反演结果切片. Fig. 10 Slice graph comparison when using two GPUs (A) Slice of the sub region of the initial model Bottom; (B) Slice of inversion results of sub region. |
|
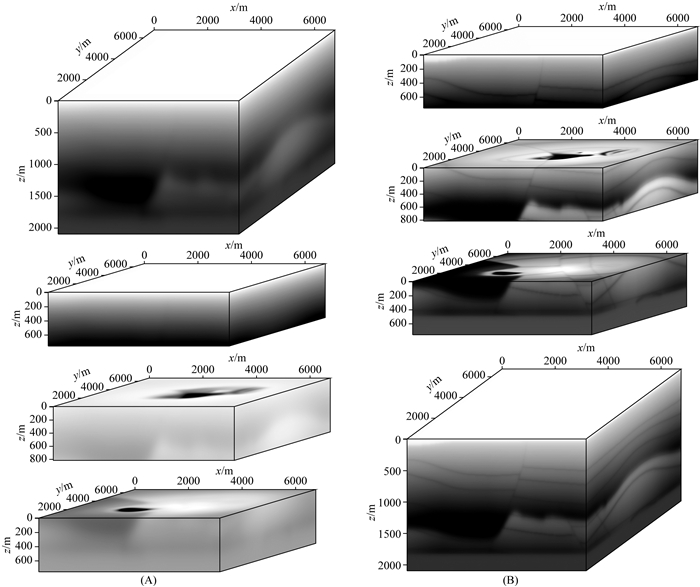
图 11 使用三块GPU计算时初始模型(A)以及最终结果(B) Fig. 11 The initial model and the final results when using three GPUs |
|
图 12 使用三块GPU时模型切片对比 (A)分解区域初始模型切片; (B)分解区域反演结果切片. Fig. 12 Slice graph comparison when using three GPUs (A) Slice of the sub region of the initial model; (B) Slice of inversion results of sub region. |
|
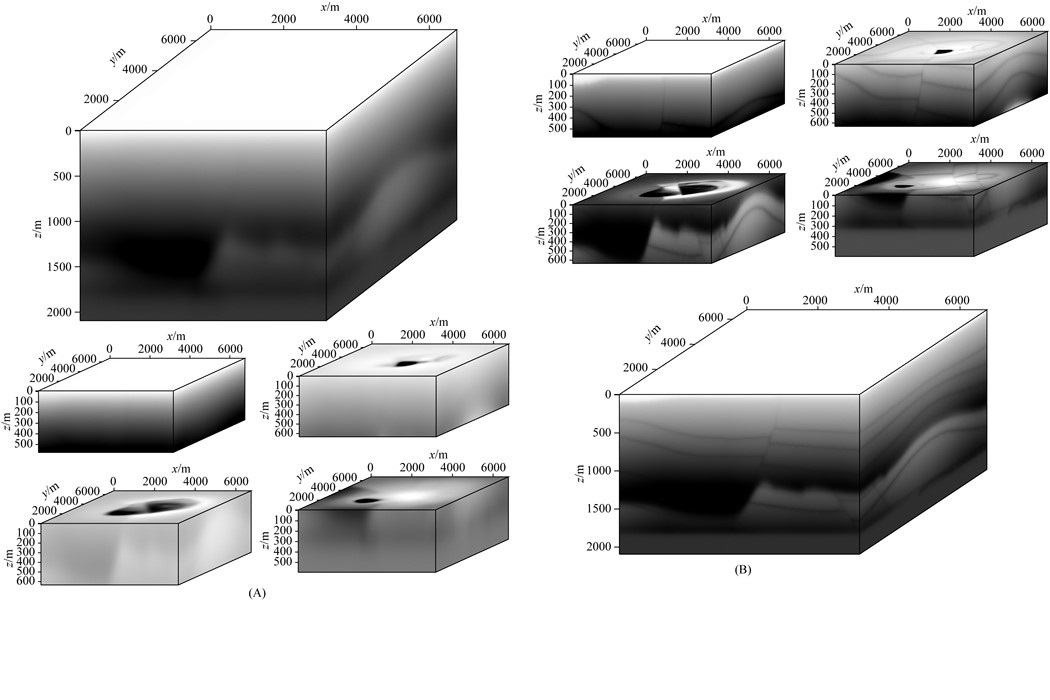
图 13 使用四块GPU计算时初始模型以及最终结果 (A)初始模型和分解区域;(B)分解区域反演结果和最终结果 Fig. 13 The initial model and the final results are calculated using the four GPUs (A) sub region of domain decomposition; (B) Inversion results of sub region. |
|
图 14 使用四块GPU时模型切片对比 (A)分解区域初始模型切片; (B)分解区域反演结果切片. Fig. 14 Slice graph comparison when using four GPUs (A) Slice of the sub region of the initial model; (B) Slice of inversion results of sub region. |
表 2中两种并行策略采用同样的初始模型,并行策略一是直接计算整个模型数据并进行迭代更新,并行策略二先将初始模型进行区域分解,对分区域分解后的模型数据进行计算并迭代更新,最后将各个GPU得到结果进行合成,输出最终结果.可以看出两种并行策略都能得到良好的反演结果,并且两种并行策略都具有较好的可扩展性,随着GPU数量增加,计算耗时成线性减少.无论是并行策略一还是并行策略二都比单GPU耗时少,通过对比发现并行策略一比并行策略二计算耗时更少,这是因为,一是由于交换区域的存在,区域分解后的各个小模型的总和要比完整模型大,导致计算量增大;二是并行策略二需要不断交换数据,数据传输占据一部分时间,导致整体耗时较大.
|
|
表 2 盐丘模型迭代一次耗时对比(单位:s) Table 2 Comparison of the time consuming of an iteration of the salt dome model (unit: s) |
模型2是SEG的overthrust模型,网格大小801×801×187,网格间距均为10 m.地表放炮,共放100炮,炮间距40 m,x方向和y方向各10炮,第一炮位置位于x=3800 m,y=380 m处.使用主频为35 Hz的零相位雷克子波,采集系统是地表全接受.时间采样率,采样点数为2000.总共正演478 GB数据,一炮相当于4.8 GB数据,外加存储的正演波场和反传波场,大约需要8 GB内存,单GPU的显存无法满足计算需求.使用并行策略二进行数值测试,同时对比同样节点数的CPU计算耗时.其反演频率从1.5 Hz开始,每次增加1.5 Hz,两个频率组成一个频率组,最大频率60 Hz.
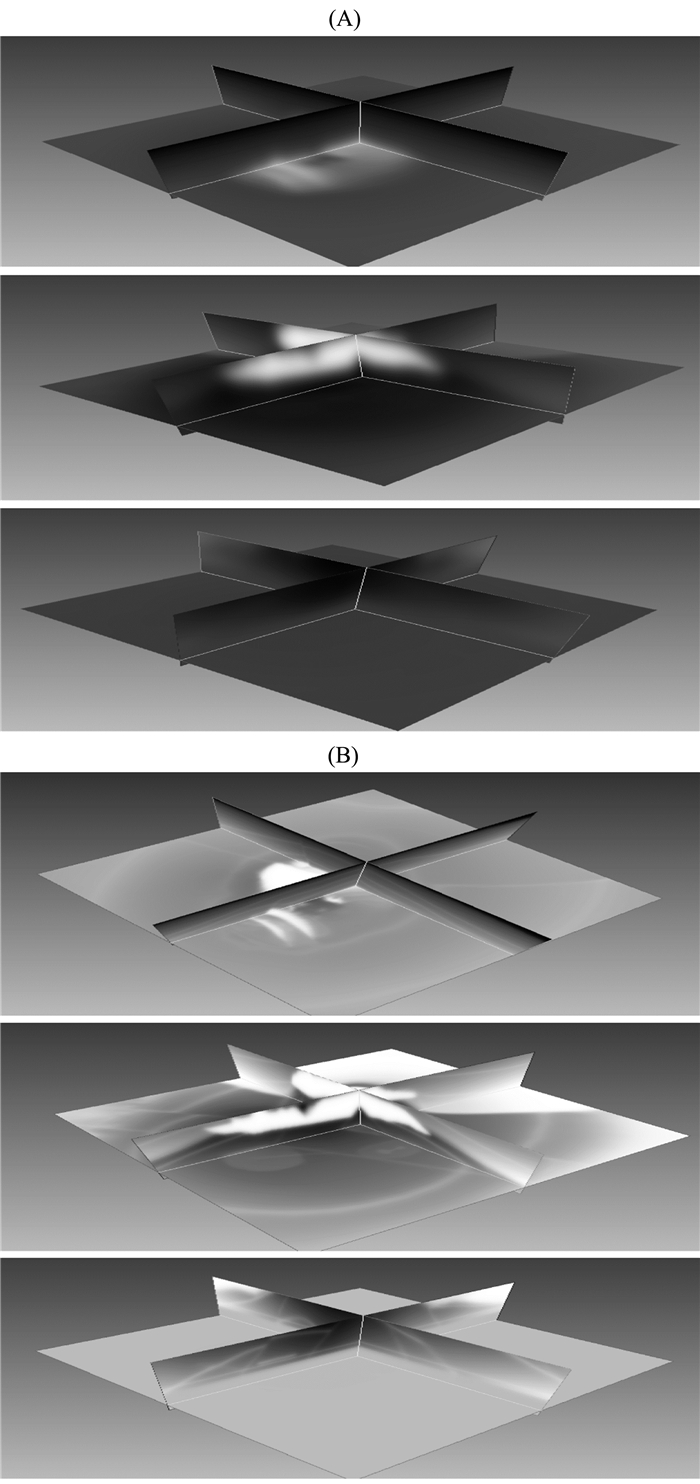
并行策略二首先根据GPU个数,先将初始模型数据进行了数据分解,每个GPU进行计算一个小数据体.图 16A组是对初始模型进行区域分解;图 16B组,每个GPU反演一部分区域的结果,最后合成最终反演结果;在反演结果中能清楚的识别逆掩断层断层之间褶皱成因的背斜,其最终结果与真实模型(图 15)能相互对应.图 17可以看出初始模型切片中的河道信息比较模糊,无法识别,反演结果很好地恢复出了河道信息,能有效恢复其识别出逆断层的原貌.可以看出,虽然局部信息有差别,但大体都恢复的得很好.
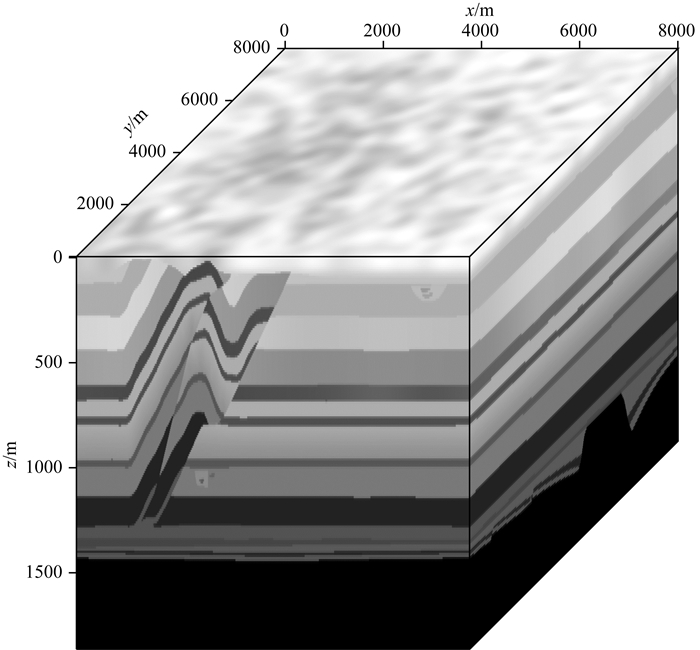
|
图 15 逆掩断层模型 Fig. 15 Overthrust Model |

|
图 16 使用四块GPU时初始模型以及最终结果 (A)初始模型和分解区域;(B)分解区域反演结果和最终结果 Fig. 16 The initial model and the final results when using the four GPUs (A) sub region of domain decomposition; (B) Inversion results of sub region. |

|
图 17 使用四块GPU时模型切片对比 (A)分解区域初始模型切片; (B)分解区域反演结果切片. Fig. 17 Slice graph comparison when using tfour GPUs (A) Slice of the sub region of the initial model; (B) Slice of inversion results of sub region. |
通过表 3对比看出来针对大模型时,并行策略二依然能得出良好的结果,且相比相同数量的CPU时,具有更小的耗时,其加速比能达到14.5倍.
|
|
表 3 逆掩断层迭代一次耗时对比 Table 3 Comparison of the time consuming of an iteration of the overthrust model |
通过对全波形反演理论推导,并对比了时间域和频率域FWI优缺点,最后结合两者的优点,sigure提出了混合域全波形反演,本文在此基础上进一步简化了混合域全波形反演,简化混合域方法直接利用时间域数据来实现多尺度反演,与以前的混合域方法相比,流程每次迭代少了一次DFT和IDFT,并且可以实现一样的反演效果,可以作为以前混合域FWI的替代方法.
针对三维全波形反演容易陷入局部极小值以及计算量巨大的问题,将模型进行分割,并采用GPU加速,每个GPU计算一小部分模型,对比各个GPU所得梯度,最后选择比较合理的全局极小值;就计算能力对比,相对于单GPU,本文提出的多GPU并行策略耗时更少,具有良好的可扩展性,随着GPU增加计算耗时不断减少,更能适应叠前大规模数据的计算,为全波形反演迈向实际应用提供可行性的计算方案.
| Brossier R, Operto S, Virieux J. 2010. Which data residual norm for robust elastic frequency-domain full waveform inversion?. Geophysics, 75(3): R37-R46. DOI:10.1190/1.3379323 | |
| Kim Y, Shin C, Calandra H. 2013.3D Hybrid Waveform Inversion With GPU Devices, edited, Society of Exploration Geophysicists. | |
| Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys.(in Chinese), 53(12): 2938-2943. DOI:10.3969/j.issn.0001-5733.2010.12.017 | |
| Li B, Liu G F, Liu H. 2009. A method of using GPU to accelerate seismic pre-stack time migration. Chinese J. Geophys.(in Chinese), 52(1): 245-252. | |
| Liu L, Liu H, Zhang H, et al. 2013. Full waveform inversion based on modified quasi-Newton equation. Chinese J. Geophys.(in Chinese), 56(7): 2447-2451. DOI:10.6038/cjg20130730 | |
| Liu L. Research on theory of multi-scale full waveform inversion and GPU accelerating technology(in Chinese).Beijing: University of Chinese Academy of Sciences, 2014. | |
| Liu L, Ding R W, Liu H W, et al. 2015. 3D hybrid-domain full waveform inversion on GPU. Computers & Geosciences, 83: 27-36. | |
| Luo Y, Schuster G. 1990. Parsimonious staggered grid finite-differencing of the wave equation. Geophysical Research Letters, 17(2): 155-158. DOI:10.1029/GL017i002p00155 | |
| Micikevicius P. 2009. 3D finite difference computation on GPUs using CUDA.//Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units. Washington, D.C., USA:ACM, 79-84. | |
| Mora P. 1988. Elastic wave-field inversion of reflection and transmission data. Geophysics, 53(6): 750-759. DOI:10.1190/1.1442510 | |
| Nihei K T, Li X. 2007. Frequency response modelling of seismic waves using finite difference time domain with phase sensitive detection (TD-PSD). Geophysical Journal International, 169(3): 1069-1078. DOI:10.1111/gji.2007.169.issue-3 | |
| Operto S, Virieux J, Amestoy P, et al. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver:A feasibility study. Geophysics, 72(5): SM195-SM211. DOI:10.1190/1.2759835 | |
| Pica A, Diet J P, Tarantola A. 1990. Nonlinear inversion of seismic reflection data in a laterally invariant medium. Geophysics, 55(3): 284-292. DOI:10.1190/1.1442836 | |
| Pratt R G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x | |
| Shin C, Jang S, Min D J. 2001. Improved amplitude preservation for prestack depth migration by inverse scattering theory. Geophysical Prospecting, 49(5): 592-606. DOI:10.1046/j.1365-2478.2001.00279.x | |
| Shin C, Ha W. 2008. A comparison between the behavior of objective functions for waveform inversion in the frequency and Laplace domains. Geophysics, 73(5): VE119-VE133. DOI:10.1190/1.2953978 | |
| Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain. Geophysical Journal International, 173(3): 922-931. | |
| Sirgue L, Etgen J, Albertin U. 2008. 3D frequency domain waveform inversion using time domain finite difference methods.//70th EAGE Conference and Exhibition. SPE, EAGE. | |
| Sirgue L, Etgen J T, Albertin U, et al. 2010. System and method for 3D frequency domain waveform inversion based on 3D time-domain forward modeling:U. S. Patent 7, 725, 266, B2. | |
| Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies. Geophysics, 69(1): 231-248. DOI:10.1190/1.1649391 | |
| Tarantola A, Nercessian A, Gauthier O. 1984. Nonlinear inversion of seismic reflection data.//SEG Technical Program Expanded Abstracts. SEG, 645-649. | |
| Wang H Z, Feng B, Wang X W, et al. 2015. Analysis of seismic inversion imaging and its technical core issues. Geophysical Prospecting for Petroleum(in Chinese), 54(2): 115-125. | |
| Zhang M, Wang H Z, Ren H R, et al. 2014. Full waveform inversion on the CPU/GPU heterogeneous platform and its application analysis. Geophysical Prospecting for Petroleum(in Chinese), 53(4): 461-467. | |
| 李博, 刘红伟, 刘国峰, 等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报, 53(12): 2938–2943. DOI:10.3969/j.issn.0001-5733.2010.12.017 | |
| 李博, 刘国峰, 刘洪. 2009. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报, 52(1): 245–252. | |
| 刘璐, 刘洪, 张衡, 等. 2013. 基于修正拟牛顿公式的全波形反演. 地球物理学报, 56(7): 2447–2451. DOI:10.6038/cjg20130730 | |
| 刘璐. 2014.多尺度全波形反演理论及GPU加速技术研究[博士论文].北京:中国科学院大学. | |
| 王华忠, 冯波, 王雄文, 等. 2015. 地震波反演成像方法与技术核心问题分析. 石油物探, 54(2): 115–125. | |
| 张猛, 王华忠, 任浩然, 等. 2014. 基于CPU/GPU异构平台的全波形反演及其实用化分析. 石油物探, 53(4): 461–467. | |
 2017, Vol. 60
2017, Vol. 60


