地球物理学报  2017, Vol. 60 Issue (12): 4887-4900   PDF    
引用本文
李刚, 李予国, 韩波, 等. 2017. 基于改进的接收点插值算法的频率域海洋可控源电磁法2.5维正演. 地球物理学报, 60(12): 4887-4900, doi: 10.6038/cjg20171228.  
Li G, Li Y G, Han B, et al. 2017. 2.5D marine CSEM modeling in the frequency-domain based on an improved interpolation scheme at receiver positions. Chinese J. Geophys. (in Chinese), 60(12): 4887-4900, doi: 10.6038/cjg20171228.  
基于改进的接收点插值算法的频率域海洋可控源电磁法2.5维正演
李刚1,4, 李予国2,3 , 韩波1,2, 段双敏1     
1. 中国海洋大学海洋地球科学学院, 青岛 266100;
2. 中国海洋大学海底科学与探测技术教育部重点实验室, 青岛 266100;
3. 海洋科学与技术国家实验室, 海洋矿产资源评价与探测技术功能实验室, 青岛 266071;
4. 德国GEOMAR亥姆霍兹基尔海洋研究中心, 基尔 24148
收稿日期 2016-11-13, 2016-12-02 收修定稿
基金项目: 国家自然科学基金项目（41704075，41604063）和山东省自然科学基金项目（ZR2016DQ15，ZR2016DB31）联合资助
第一作者简介: 李刚, 男, 1986年生, 博士, 主要从事海洋电磁场正反演及电磁与地震资料联合反演研究.E-mail:gli@geomar.de
通讯作者: 李予国, 1965年生, 教授, 主要从事电磁场数值模拟和反演方法以及海洋电磁法的研究工作.E-mail:yuguo@ouc.edu.cn
摘要：在海洋可控源电磁法勘探中，接收站常置于海底.在进行海洋电磁场模拟时，由于海水和海底介质存在显著电性差异，这给海底接收点处场值的求取带来困难.本文提出一种新的接收点插值算法，该算法考虑到海底电场法向分量不连续性问题，用法向电流分量进行插值以准确求取海底任意接收点处电磁场值.本文利用交错网格有限差分法实现了二维介质中频率域海洋可控源法（CSEM）正演.对构造走向做傅里叶变换，将三维电磁模拟问题转换为波数域2.5维问题，即三维场源激励下针对二维地电模型的电磁模拟问题.使用交错网格有限差分法，基于一次场/二次场分离方法导出波数域二次电场离散形式，并进一步求得波数域电磁场.采用本文提出的改进的插值算法可求得海底任意接收点处波数域电磁场，采用傅里叶逆变换对波数域电磁场进行积分可得到接收点处空间域电磁场.模型算例表明，与常规的线性插值和严格插值算法相比，本文提出的改进的插值算法具有更高的精度.
关键词: 海洋可控源电磁法      2.5维      数值模拟      接收点插值     
2.5D marine CSEM modeling in the frequency-domain based on an improved interpolation scheme at receiver positions
LI Gang1,4, LI Yu-Guo2,3, HAN Bo1,2, DUAN Shuang-Min1     
1. College of Marine Geosciences, Ocean University of China, Qingdao 266100, China;
2. Key Lab of Submarine Geosciences and Prospecting Techniques of Ministry of Education, Ocean University of China, Qingdao 266100, China;
3. Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
4. GEOMAR Helmholtz Centre for Ocean Research Kiel, Kiel 24148, Germany
Abstract: In the marine controlled-source electromagnetic (CSEM) survey, the receivers are usually placed at the seafloor. The resistivity contrast between the seawater and seafloor sediments is large, which can cause difficulties in numerical modeling of CSEM fields at receiver locations. In this paper, we present an improved interpolating method for calculating electric and magnetic fields at the seafloor with a resistivity contrast. This method is applied to the 2.5-dimensional (2.5D) frequency-domain CSEM modeling with towed transmitters and receivers located at the seafloor. Considering the discontinuity of the normal electric fields, we use the normal current electric density for interpolation. We simulate the 2.5D marine CSEM responses by the staggered finite-difference (SFD) method with Fourier transform to the strike direction. The final SFD equations are solved by the direct solver MUMPS (MUltifrontal Massively Parallel Sparse direct Solver). To avoid the source singularities, the secondary-field approach is used and the primary fields excited by the electric dipole source can be calculated quasi-analytically for the one-dimensional (1D) layered background model. We focus on interpolating of electric and magnetic fields in the wavenumber domain to the receiver locations at the seafloor interface between the conductive seawater and resistive seafloor formation. The secondary electric and magnetic fields are used for interpolation instead of the total fields for high numerical accuracy. After performing the inverse Fourier transform to the wavenumbers, the electric and magnetic fields in the space domain are obtained.To check the accuracy of our 2.5D marine CSEM SFD modeling algorithm with the improved receiver interpolating technique, we compare our results with both the 1D analytical results and the adaptive finite element results. The SFD numerical results are approved to be accurate.We also compare the numerical accuracy between our improved interpolation scheme and others, i.e., the conventional linear interpolation and the rigorous interpolation. The proposed interpolation only utilizes the nodes below/above the seafloor interface, and is proved to be much more accurate than the other two interpolating methods used.
Key words: Marine CSEM    2.5D    Numerical modeling    Interpolation scheme for receiver positions    
1 引言

海洋可控源电磁法(Controlled-Source ElectroMagnetic method, CSEM)作为一种新兴海洋地球物理勘探方法，已经成功应用于海底油气资源勘探中(Constable，2010).频率域CSEM方法使用位于海底上方的电偶源发射低频电磁信号(0.1~10 Hz)，而位于海底的接收站可采集来自海底地层的电磁感应信号(Weitemeyer et al., 2010).当前海洋CSEM一维反演(Key，2009；Crepaldi et al., 2011；Weitemeyer and Constable, 2014)和二维反演(Abubakar et al., 2008；Weitemeyer et al., 2010；Constable et al., 2015；Myer et al., 2015)发展较为成熟，三维反演算法正在不断发展中(Constable，2010；Zhdanov，2010).海洋CSEM三维反演由于内存需求高、计算量大，在实际资料解释中应用不多(Commer and Newman, 2008).在进行海洋CSEM实际资料解释时，仍以二维反演算法为主(Constable，2010).正演是反演的基础，高精度的稳定的正演算法是实现反演的关键(Avdeev，2005).本文工作主要围绕二维介质中海洋CSEM正演模拟展开.

2.5维电磁模拟是指三维场源激励下针对二维地电模型的电磁场正演问题(Mitsuhata，2000；Li and Key, 2007；李建慧等，2016).开展2.5维电磁场正演时，首先对地质构造走向做傅里叶变换，将电磁场分量转换至波数域，避免了对模型进行三维离散化；再使用有限元法或有限差分法等数值模拟方法求得波数域电磁响应，最后利用傅里叶逆变换将波数域电磁响应转换为空间域电磁响应.目前2.5维电磁场正演模拟算法发展较为成熟，可分为基于伪δ函数的总场方法(Mitsuhata，2000；Kong et al., 2008；Abubakar et al., 2008；沈金松和孙文博，2008；戴世坤等，2013)和基于一次场/二次场分离的二次场方法(Stoyer and Greenfield, 1976；Everett and Edwards, 1993；Unsworth et al., 1993；Torres-Verdín and Habashy, 1994；底青云等，2004；Li and Key, 2007；Streich et al., 2012；殷长春等，2015).总场方法使用伪δ函数来近似场源项，由于奇异性影响在源点附近数值精度不高；而使用二次场方法可有效克服场源的奇异性问题，数值解精度较高.2.5维电磁模拟数值方法以有限单元法和有限差分法为主.相对于有限单元法，有限差分法理论简单，容易实现，且精度也较高(Streich et al., 2012).本文基于二次场方法，使用交错网格有限差分技术实现海洋CSEM 2.5维正演.

关于2.5维电磁正演模拟，前人研究工作主要集中在地形影响分析(Li and Key, 2007；殷长春等，2015)、发射源姿态影响分析(Streich et al., 2012)和线性方程组的求解(Abubakar et al., 2008；Streich et al., 2012)等方面，而对于求取接收点处场值的讨论较少.在海洋CSEM正演模拟时，由于接收点一般置于海底任意位置，需要将网格节点场值插值到接收点位置(Abubakar et al., 2008).由于海水和海底地层存在显著电性差异，导致海底界面处电场法向分量不连续，这会给接收点插值带来较大的数值误差(Wirianto et al., 2011).目前关于接收点插值算法的讨论不多.最直接的处理方法为利用海底上下两侧单元节点场值，使用常规线性插值求得接收点处场值，此方法会带来较大的误差(Shantsev and Maaø，2015).de Groot-Hedlin(2006)认为，与简单线性插值相比，采用指数插值可获得更高的精度.Wirianto等(2011)提出基于自适用插值算子的高阶多项式插值方法来求取接收点处场值，该方法克服了高阶插值振荡性问题，但是插值方法复杂且计算量较大.Shantsev和Maaø(2015)提出一种严格插值方法，该方法使用海底界面两侧单元进行插值，不仅考虑到海底界面处法向电场分量的不连续性问题，还考虑到界面处电场分量和磁场分量一阶法向导数的不连续性问题，因此可获得较高的精度.Mackie等(1994)和Smith(1996)在处理陆地大地电磁三维交错网格有限差分正演问题时，提出一种仅使用地表下方单元进行插值的接收点插值算法.由于接收点置于地面，需要先采用线性插值方法将单元侧面中心处离散采样点上的电磁场值插值到地表，然后再使用线性插值方法插值到地面接收点处，该方法被证明具有较高的数值精度(Smith，1996).

本文改进了Mackie等(1994)和Smith(1996)提出的总场接收点插值方法并将其推广到海洋CSEM 2.5维二次场正演模拟算法中.使用交错网格有限差分法，基于一次场/二次场分离方法导出波数域二次电场离散形式，并进一步求得波数域电磁场.考虑到法向二次电场不连续性问题，在使用插值方法求取海底任意接收点处波数域电磁场时，采用电流分量代替二次电场分量进行插值，进一步采用傅里叶逆变换对波数域电磁场进行积分可得到接收点处空间域电磁场.数值模拟结果表明，与常规线性插值和严格插值相比，本文提出的改进的插值算法具有更高的精度.

2 2.5维正演理论 2.1 控制方程

在准静态条件下，设时谐因子为e-iωt，电场E和磁场H满足Maxwell方程(Ward and Hohmann, 1988)：

(1)

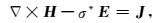
(2)

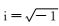
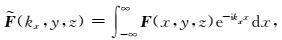
其中为虚数单位，ω=2πf为角频率，f为频率.μ0为真空中磁导率，σ*=σ－iωε0为复电导率，σ为地电模型电导率，ε0为真空中介电常数.M和J分别为磁流源和电流源强度.为克服源奇异性影响，将电磁场分解为一次场(即背景场，标记为P)和二次场(即异常场，标记为S)两部分(Newman and Alumbaugh, 1995；Li and Key, 2007).二维地电模型条件下，设x轴为构造走向方向，对走向方向做傅里叶变换，即

(3)

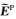
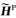
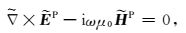
其中F可为电场分量E或磁场分量H.由式(1)和式(2)可得，电偶源激励下一次场(和)满足：

(4)

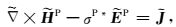
(5)

其中，场源项包含在式(5)中.式(4)和式(5)中背景场(和)可由解析算法求出(Li Y G and Li G，2016)，该一维解析算法可计算任意方位电偶极子或有限长度源激励下一次场.而二次场(和)满足如下方程：

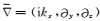
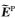
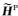
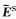
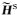
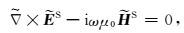
(6)

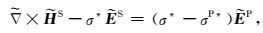
(7)

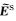
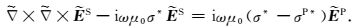
由式(6)和式(7)可得关于二次电场的Helmholtz方程：

(8)

2.2 交错网格离散

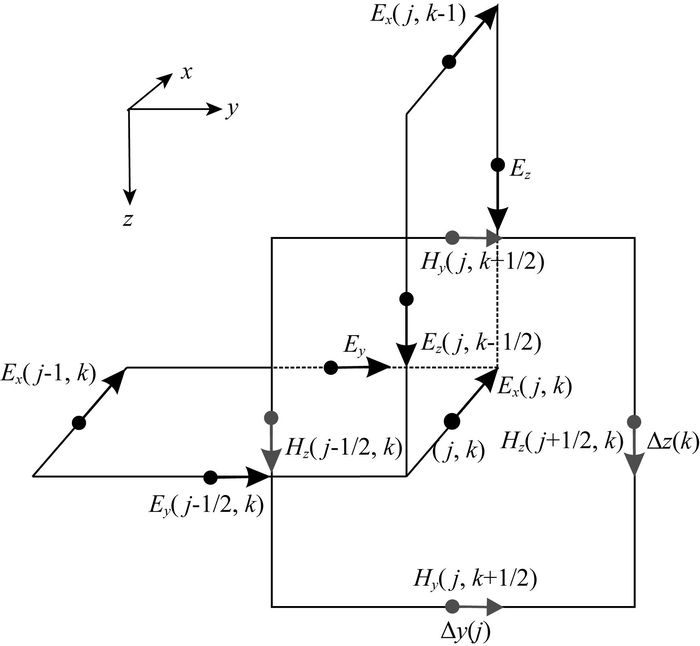
采用交错网格有限差分技术实现海洋CSEM 2.5维正演模拟(Newman and Alumbaugh, 1995；Streich，2009).首先对模拟区域进行离散化，设Ny和Nz分别为模拟区域y轴和z轴方向网格单元个数.如图 1所示，对于网格单元(j, k)，电场分量位于网格面中心，磁场分量位于网格边中点，其中Δy(j)和Δz(k)分别为y轴和z轴方向网格长度，网格单元内电导率σj, k为常量.对控制方程(8)进行离散后(离散形式见附录A)，可得关于二次电场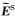的大型线性方程组：

图 1 二维网格单元中电磁场交错采样示意图 Fig. 1 Sketch showing 2D staggered-grid sampling

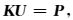
(9)

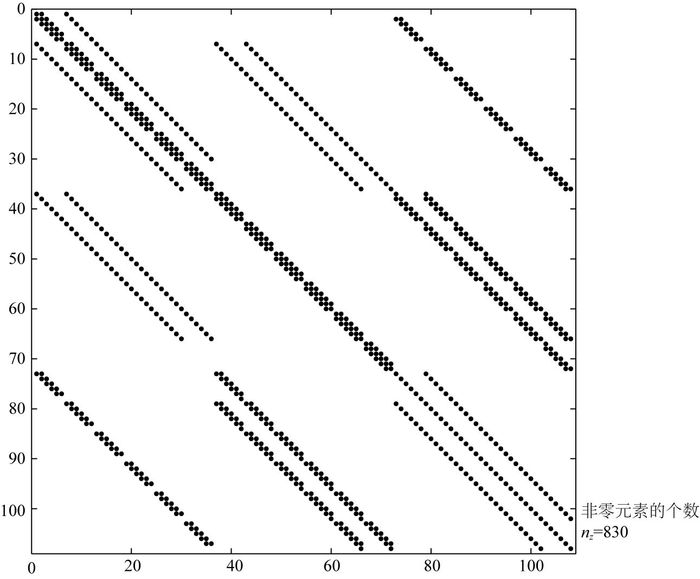
其中K为(3NyNz)×(3NyNz)的复稀疏系数矩阵，仅在主对角位置矩阵元素值为复数，矩阵中每行最多有9个非零元素，非零元素值与发射频率、单元尺寸及电导率有关；U为待求的二次电场向量，长度为3NyNz；P为与一次电场有关的右端源项，长度为3NyNz.图 2给出系数矩阵K中非零元素位置分布图.

图 2 6×6网格剖分情况下系数矩阵K非零元素位置分布 Fig. 2 Illustration of the symmetric structure of the stiffness matrix for a 6×6 staggered grid. Only the locations of nonzero entries are shown

加入边界条件后，即可对线性方程组(9)进行求解.本文采用Dirichlet边界条件，即令无穷远边界上切向电场分量为零：

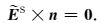
(10)

采用Dirichlet边界不会改变系数矩阵K的对称结构，为线性方程组的求解带来方便(Streich，2009).

2.3 线性方程组求解

与迭代法相比，直接法具有精度高、稳定性好等特点(Streich，2009；韩波等，2015；李建慧等，2016)；相对于2.5维电磁模拟问题，直接法内存需求不大、求解效率较高.本文使用直接法开源软件MUMPS(MUltifrontal Massively Parallel Sparse direct Solver)求解线性方程组(9)，由于系数矩阵K具有对称性，仅需要存储上三角矩阵或下三角矩阵(Amestoy et al., 2001)，可有效节省内存并提高计算效率.求得离散单元上二次电场分量后，通过(11)式可进一步求得波数域离散单元上二次磁场分量：

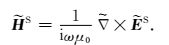
(11)

求得离散单元上二次电场和二次磁场分量后，还需要将其插值到任意接收点位置.将接收点处二次电磁场分量加上一次电磁场分量(可通过一维解析方法求得)，最终得到接收点处波数域电磁场总场值.进一步采用傅里叶逆变换对波数域电磁场进行积分可得到接收点处空间域电磁场.傅里叶逆变换形式为：

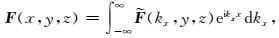
(12)

其中F可为电场分量E或磁场分量H.进行傅里叶逆变换时，本文采用Anderson(1983)给出的787点离散正/余弦变换算法.数值计算过程中，选取有限个波数kx计算波数域电磁场值，并通过对离散波数域电磁场进行三次样条插值来近似积分计算(Li and Key, 2007).沈金松和孙文博(2008)认为，在给定的波数kx范围内，在对数域等间隔选取若干波数，这样kx低值段要适当加密取值，高值段可以抽稀，以保证数值解精度.罗延钟和孟永良(1986)、Xu等(2000)、沈金松和孙文博(2008)认为，波数kx也可通过最优化方法选取(不在本文的讨论范围).本文模型计算时波数kx选取在1－6~1 m－1之间，且在对数域等间隔取61个.

3 接收点插值算法

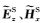
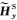
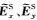
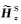
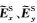
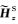
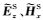
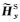
在假设网格单元剖分合理情况下，接收点处电磁场值精度取决于插值算法精度(Shantsev and Maaø，2015).接收点插值算法是本文的讨论重点.由于海底接收点处一次电磁场分量可通过一维解析方法求得，本文仅讨论接收点处二次电磁场分量的插值问题.假设海底面深度为zk0－1/2，如图 1所示，二次离散电磁场分量和的采样点位于海底，而和的采样点位于海底面上下(深度zk0或zk0－1处).需要采用插值方法将和垂向插值到相应海底面深度为zk0－1/2处.在得到海底面上所有二次电磁场分量后，可采用线性插值方法将其插值到任意接收点位置.本文所讨论的插值算法是指对二次离散电磁场分量和的垂向插值.

考虑到海底界面法向电场分量不连续性，在对电场分量进行插值时，使用电流分量代替电场分量进行插值(Smith，1996；Haber et al., 2000；Streich，2009).在海底界面处电流分量连续，即

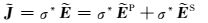
(13)

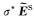
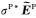
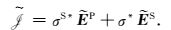
连续.式(13)中是不连续的，而一次电流分量连续(Streich，2009)，结合式σ*=σP*+σS*，可得如下电流分量是连续的：

(14)

需要指出的是，二次电流分量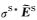是不连续的，不能直接用于插值.本文使用式(14)给出的连续电流分量进行插值.

本文改进了Mackie等(1994)和Smith(1996)提出的总场接收点线性插值方法并将其应用到海洋CSEM 2.5维二次场正演模拟中.为对比不同插值算法效果，本文还给出了两种常用的接收点插值算法：常规线性插值和严格插值(Shantsev and Maaø，2015).下面对这三种插值算法作简要介绍.

3.1 改进的插值

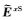
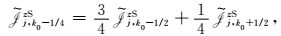
该改进插值算法使用海底一侧单元上离散电磁场分量进行插值.参考Mackie等(1994)和Smith(1996)，首先求取海底面上x方向二次电场分量的离散格式.由式(14)可得：

(15)

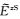
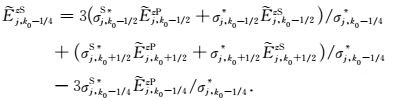
距离海底面1/4单元纵向长度处(zk0－1/4深度处)二次电场分量的离散形式为：

(16)

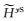
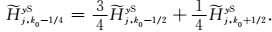
距离海底面1/4单元纵向长度处(zk0－1/4深度处)二次磁场分量的离散形式为：

(17)

由式(11)可得：

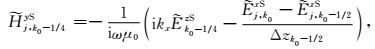
(18)

即

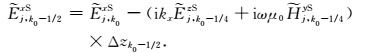
(19)

由式(16)、(17)和(19)可得海底面上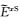的离散格式.

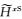
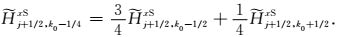
下面求取海底面上y方向二次电场分量的离散格式.由线性插值可得距离海底面1/4单元纵向长度处(zk0－1/4深度处)二次磁场分量的离散形式为：

(20)

由式(11)可得：

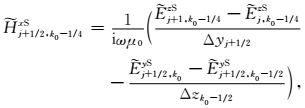
(21)

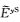
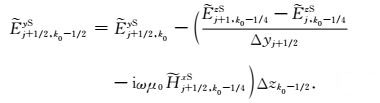
由式(21)得海底面上的离散格式：

(22)

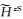
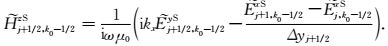
最后，由式(11)可得海底面上z方向二次磁场分量的离散形式为：

(23)

3.2 常规线性插值

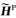
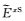
常规线性插值使用海底两侧单元上离散电磁场分量进行插值.由于x方向二次电场分量连续，故海底面上的离散形式为：

(24)

其中zr=zk0－1/2为接收点深度.

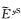
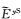
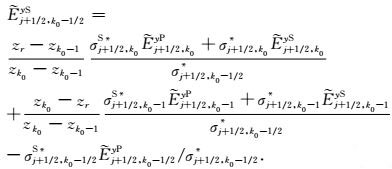
类似地，由于y方向二次电场分量可能不连续，故使用式(14)进行插值，可得海底面上的离散形式为：

(25)

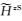
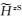
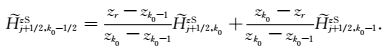
由于z方向二次磁场分量加连续，故海底面上的离散形式为：

(26)

3.3 严格插值

严格插值使用海底两侧单元上离散电磁场分量进行插值.该插值方法不仅考虑到海底界面处法向电场分量的不连续性问题，还考虑到界面处电场分量和磁场分量一阶法向导数的不连续性问题，因此相比于常规线性插值，可获得更高的精度，尤其适用于三维倾斜界面情况(Shantsev and Maaø，2015).

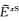
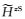
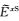
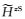
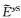
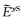
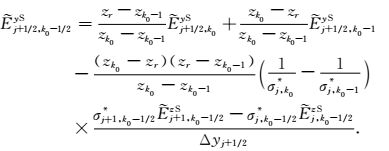
由于和分量及其一阶法向导数连续，故和分量插值格式与常规线性插值格式相同(式(24)和式(26)).在电导率分界面处，分量及其一阶法向导数不连续，故插值时需要考虑不连续性影响.海底面上y方向二次电场分量的离散形式可表示为：

(27)

4 结果验证 4.1 一维模型

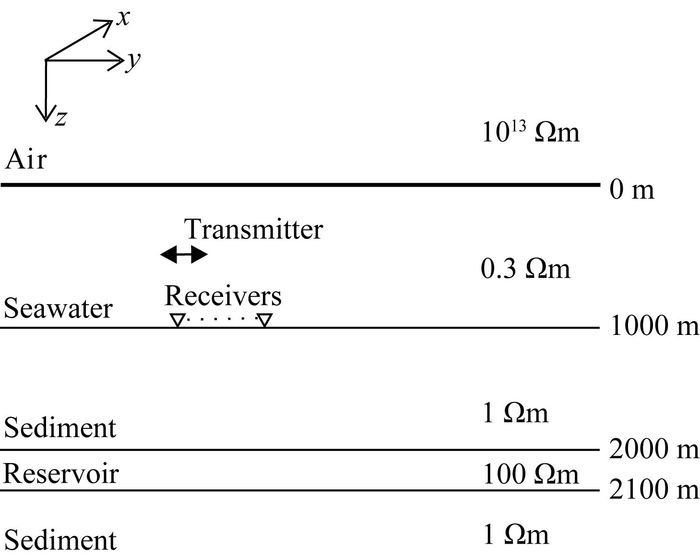
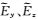
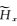
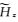
采用一维储层模型(图 3)来验证2.5维正演程序并对比三种不同的接收点插值算法(Li Y G and Li G，2016).如图 3所示，海水层厚度为1000 m，其电阻率为0.3 Ωm.厚度为100 m的高阻薄层埋深为2000~2100 m，其电阻率为100 Ωm.基岩电阻率为1 Ωm.设测线方向为y=0 m，沿测线方向的水平单位电偶极源位于海底上方50 m处，坐标为(0 m，0 m，950 m)，61个海底接收点等间距分布于y=－6 km至y=6 km范围内.电偶源发射频率为0.25 Hz.所有计算在Dell Precision T5500工作站上完成，该工作站配置2个CPU，型号为Intel Xeon E5630，主频为2.53 GHz.采用两种观测模式，即在轴向观测模式下(y方向电偶源激励)计算和分量；而在赤道观测模式下(x方向电偶源激励)计算和分量.

图 3 海洋一维储层模型 Fig. 3 1D canonical reservoir model

本节对比四种不同网格剖分情况下三种插值算法的精度(表 1).从网格1到网格2，网格3到网格4，y方向网格不变，z方向网格抽稀；从网格1到网格3，网格2到网格4，z方向网格不变，y方向网格抽稀；从网格1到网格4，y方向和z方向网格均抽稀.

表 1 一维模型情况下四种网格剖分对比 Table 1 Four cases of staggered-gridding of the 1D canonical reservoir model

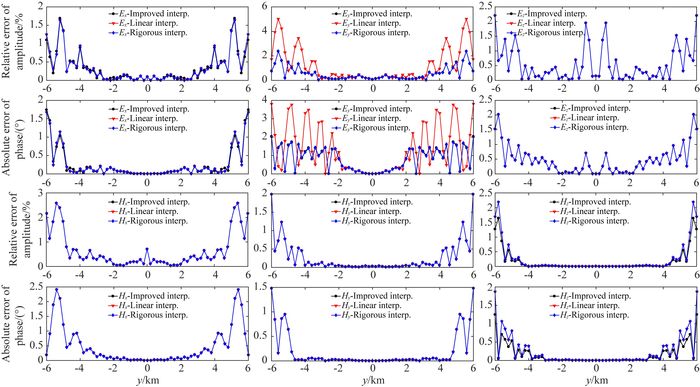
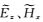
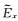
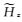
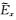
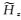
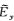
如图 4所示，在网格剖分较密情况下(网格剖分总数168×88)，本文提出的改进的插值和严格插值均具有较高的精度.和分量不需要垂向插值，三种插值算法的结果相同.对或分量，由于严格插值与常规线性插值公式相同，其插值结果相同.与解析解相比，和分量的振幅相对误差不超过2.5%左右，相位绝对误差不超过2°.对于分量，在海底电导率分界面处，插值时需要考虑不连续性影响.与改进的插值和严格插值结果相比，常规线性插值误差较大，在远收发距情况可达5%左右.

图 4 网格剖分为168×88情况下插值结果对比 Fig. 4 Comparison of interpolating results for the 168×88 staggered-gridding

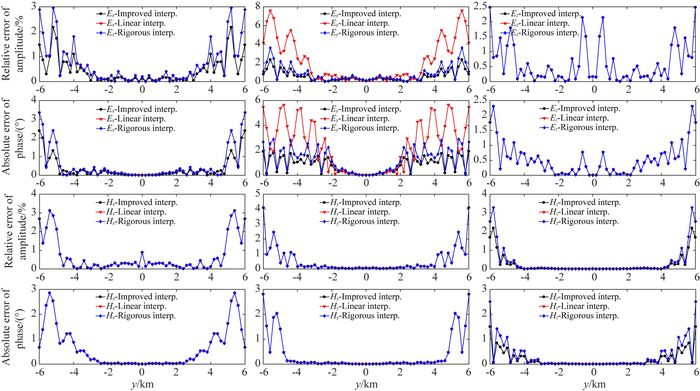
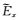
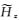
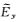
如图 5所示，在z方向网格抽稀情况下(网格剖分总数168×64)，与改进的插值结果相比，严格插值和常规线性插值情况下和分量的误差较大，这是因为插值公式使用海底面两侧单元进行距离平均，误差会随着z方向网格尺寸变大而变大.对于分量，严格插值和改进的插值的精度均较高，而线性插值误差仍较大.

图 5 网格剖分为168×64情况下插值结果对比 Fig. 5 Comparison of interpolating results for the 168×64 staggered-gridding

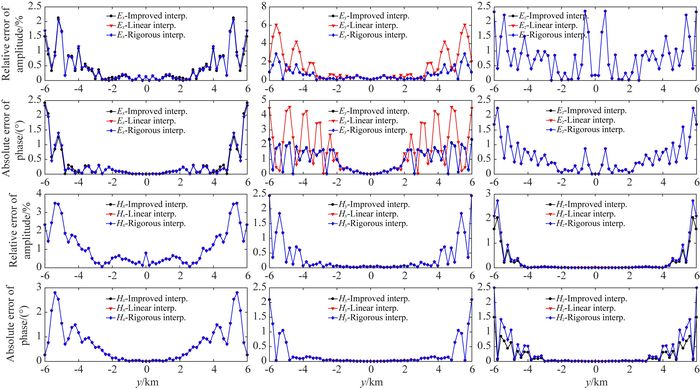
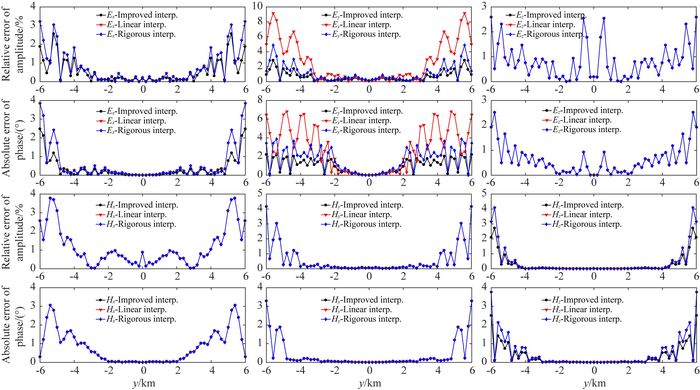
如图 6所示，在z方向网格抽稀情况下(网格总数112×88)，插值精度与网格较密情况(网格剖分总数168×88)近似.这说明，在水平网格剖分合理情况下，适当抽稀横向网格，对接收点插值精度影响不大.如图 7所示，网格y方向和z方向均抽稀情况下(网格剖分总数112×64)，插值精度与网格z方向抽稀情况(网格剖分总数168×64)近似.这进一步说明，网格剖分合理情况下，y方向网格尺寸变化对插值结果影响不大，插值精度主要取决于z方向网格尺寸.

图 6 网格剖分为112×88情况下插值结果对比 Fig. 6 Comparison of interpolating results for the 112×88 staggered-gridding
图 7 网格剖分为112×64情况下插值结果对比 Fig. 7 Comparison of interpolating results for the 112×64 staggered-gridding
4.2 二维模型

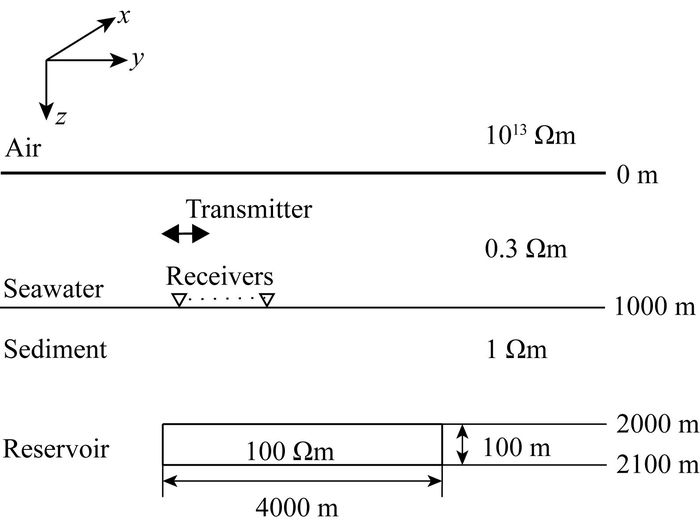
进一步采用如图 8所示的二维储层模型来验证2.5维正演程序并对比三种不同的接收点插值算法.其中海水层厚度为1000 m，其电阻率为0.3 Ωm.厚度为100 m的高阻储层埋深为2000~2100 m，水平方向延伸长度为4000 m，其电阻率为100 Ωm.基岩电阻率为1 Ωm.发射源与接收站布设与图 3一致，电偶源发射频率为0.25 Hz.

图 8 海洋二维储层模型 Fig. 8 2D canonical reservoir model

并对比四种不同网格剖分情况下三种插值算法的精度(表 2).从网格1到网格2，网格3到网格4，y方向网格不变，z方向网格抽稀；从网格1到网格3，网格2到网格4，z方向网格不变，y方向网格抽稀；从网格1到网格4，y方向和z方向网格均抽稀.

表 2 二维模型情况下四种网格剖分对比 Table 2 Four cases of staggered-gridding of the 2D canonical reservoir model

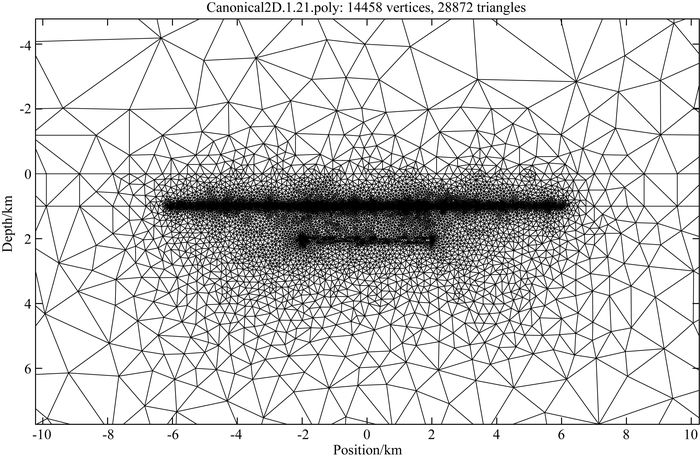
我们使用Li和Key(2007)提出的海洋可控源二维自适应有限元正演程序来验证本文提出的2.5维正演程序.如图 9给出了二维模型情况下三角网格剖分示意图，经过21次细化后网格总数为28872个.

图 9 海洋二维储层模型情况下三角网格剖分示意图 Fig. 9 Triangular gridding for 2D canonical reservoir model

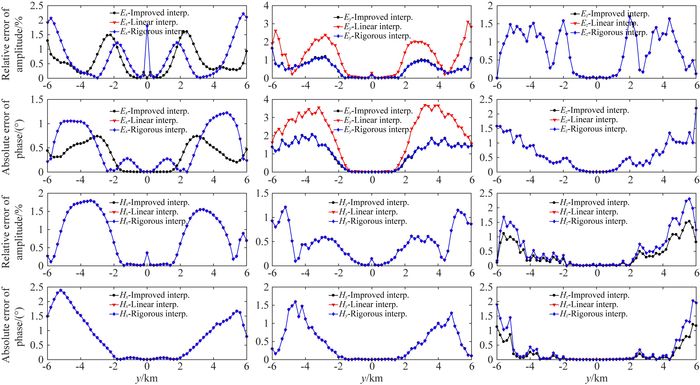
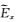
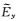
如图 10所示，在网格剖分较密情况下(网格剖分总数168×90)，本文提出的改进的插值和严格插值均具有较高的精度.如图 5所示，在z方向网格抽稀情况下(网格剖分总数168×66)，与改进的插值结果相比，严格插值和常规线性插值情况下和分量的误差较大，这是因为插值公式使用海底面两侧单元进行距离平均，误差会随着z方向网格尺寸变大而变大.对于分量，严格插值和改进的插值的精度均较高，而线性插值误差仍较大.如图 6所示，在z方向网格抽稀情况下(网格剖分总数112×90)，插值精度与网格较密情况(网格剖分总数168×90)近似.这说明，在水平网格剖分合理情况下，适当抽稀横向网格，对接收点插值精度影响不大.如图 7所示，网格y方向和z方向均抽稀情况下(网格剖分总数112×66)，插值精度与网格z方向抽稀情况(网格剖分总数168×64)近似.这进一步说明，网格剖分合理情况下，y方向网格尺寸变化对插值结果影响不大，插值精度主要取决于z方向网格尺寸.对于常规线性插值，由于使用海底面两侧单元，故其插值精度会随z方向网格尺寸变大而变大；严格插值亦使用海底两侧单元进行距离平均，但由于考虑到电磁场分量一阶法向导数的不连续性，其插值精度有较大改善；本文提出的改进的插值仅使用海底一侧单元，其插值精度比较高.

图 10 网格剖分为168×90情况下插值结果对比 Fig. 10 Comparison of interpolating results for the 168×90 staggered-gridding
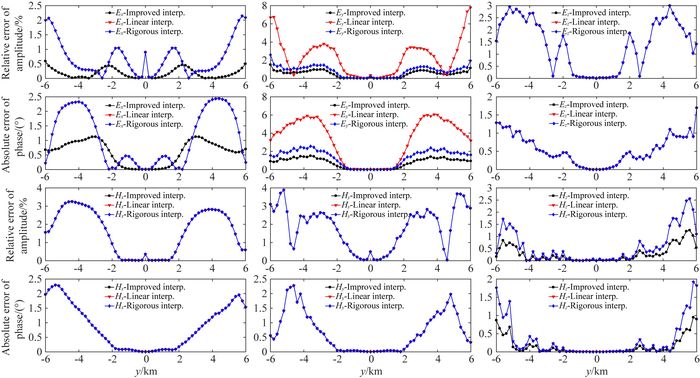
图 11 网格剖分为168×66情况下插值结果对比 Fig. 11 Comparison of interpolating results for the 168×66 staggered-gridding
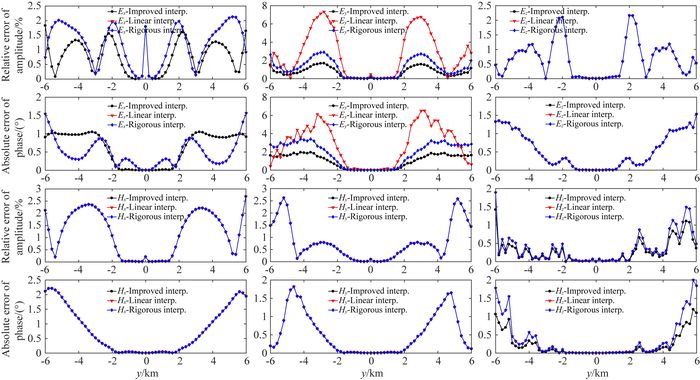
图 12 网格剖分为112×90情况下插值结果对比 Fig. 12 Comparison of interpolating results for the 112×90 staggered-gridding
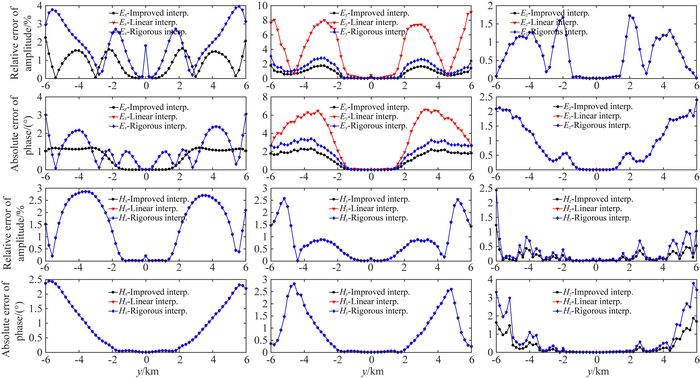
图 13 网格剖分为112×66情况下插值结果对比 Fig. 13 Comparison of interpolating results for the 112×66 staggered-gridding
5 结论

本文提出了一种改进的海底接收点插值算法，该算法考虑到海水和海底介质的电性差异和海底电场法向分量不连续性问题，用法向电流分量进行插值以准确求取海底任意接收点处电磁场值.对于常规线性插值，由于使用海底面两侧单元，故其插值精度会随垂直网格尺寸变大而变大.严格插值亦使用海底两侧单元进行距离平均，但由于考虑到电磁场分量一阶法向导数的不连续性，其插值精度有较大改善.本文提出的改进的插值算法仅使用海底一侧单元，与严格插值和常规线性插值算法相比，避免使用海底两侧单元带来的平均效应的影响，其精度较高.

本文将改进的接收点线性插值算法用于海洋CSEM二维交错网格正演，取得较好应用效果.该改进的线性插值算法可进一步推广到海洋CSEM三维正演，以及陆地CSEM二维/三维正演中.

附录A控制方程的离散形式

控制方程(8)可分解为三个坐标轴方向上的标量方程：

(A1)

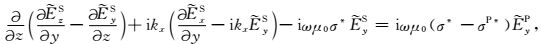
(A2)

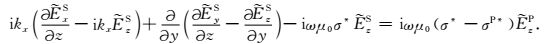
(A3)

如图 1所示，使用交错网格有限差分法对方程(A1)—(A3)进行离散可得：

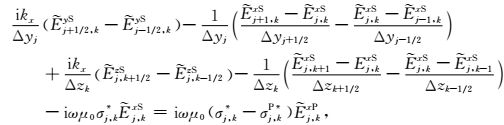
(A4)

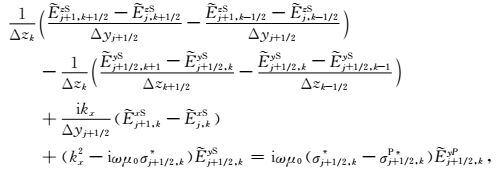
(A5)

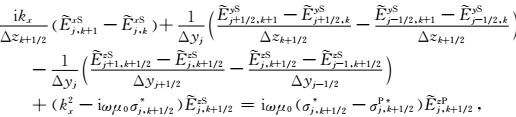
(A6)

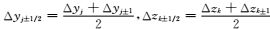
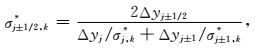
其中.由于电场分量在单元边界上可能不连续，本文采用电导率调和平均方法来求取单元界面上电导率值(Haber et al., 2000)，即

(A7)

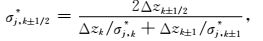
(A8)

这样可保证单元边界上电流的连续性，即

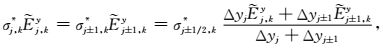
(A9)

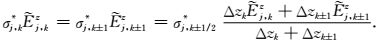
(A10)

致谢

感谢开源线性运算库MUMPS的开发者们的无私贡献.匿名审稿人对本文提出了宝贵修改意见，在此表示衷心感谢.作者李刚感谢2016中德(CSC-DAAD)博士后奖学金项目(57251553，201600110021)的支持和资助.

参考文献
Abubakar A, Habashy T M, Druskin V L, et al. 2008. 2.5 D forward and inverse modeling for interpreting low-frequency electromagnetic measurements. Geophysics, 73(4): F165-F177. DOI:10.1190/1.2937466
Amestoy P R, Duff I S, L'Excellent J Y, et al. 2001. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM Journal on Matrix Analysis and Applications, 23(1): 15-41. DOI:10.1137/S0895479899358194
Anderson W L. 1983. Fourier cosine and sine transforms using lagged convolutions in double-precision (subprograms DLAGF0/DLAGF1). Technical report, U. S. Department of the Interior, Geological Survey (Open-File Report 83-320).
Avdeev D B. 2005. Three-dimensional electromagnetic modelling and inversion from theory to application. Surveys in Geophysics, 26(6): 767-799. DOI:10.1007/s10712-005-1836-x
Commer M, Newman G A. 2008. New advances in three-dimensional controlled-source electromagnetic inversion. Geophysical Journal International, 172(2): 513-535. DOI:10.1111/gji.2008.172.issue-2
Constable S. 2010. Ten years of marine CSEM for hydrocarbon exploration. Geophysics, 75(5): 75A67-75A81. DOI:10.1190/1.3483451
Constable S, Orange A, Key K. 2015. And the geophysicist replied:"Which model do you want?". Geophysics, 80(3): E197-E212. DOI:10.1190/geo2014-0381.1
Crepaldi J L S, Buonora M P P, Figueiredo I. 2011. Fast marine CSEM inversion in the CMP domain using analytical derivatives. Geophysics, 76(5): F303-F313. DOI:10.1190/geo2010-0237.1
Dai S K, Wang S G, Zhang Q J, et al. 2013. 2. 5D forward and inversion of CSEM in frequency domain. The Chinese Journal of Nonferrous Metals, 23(9): 2513-2523.
de Groot-Hedlin C. 2006. Finite-difference modeling of magnetotelluric fields:Error estimates for uniform and nonuniform grids. Geophysics, 71(3): G97--G106. DOI:10.1190/1.2195991
Di Q Y, Unsworth M, Wang M Y. 2004. 2.5-D CSAMT modeling with the finite element method over 2-D complex earth media. Chinese Journal of Geophysics, 47(4): 723-730.
Everett M E, Edwards R N. 1993. Transient marine electromagnetics:the 2.5-D forward problem. Geophysical Journal International, 113(3): 545-561. DOI:10.1111/gji.1993.113.issue-3
Haber E, Ascher U M, Aruliah D A, et al. 2000. Fast simulation of 3D electromagnetic problems using potentials. Journal of Computational Physics, 163(1): 150-171. DOI:10.1006/jcph.2000.6545
Han B, Hu X Y, Huang Y F, et al. 2015. 3-D frequency-domain CSEM modeling using a parallel direct solver. Chinese Journal of Geophysics, 58(8): 2812-2826. DOI:10.6038/cjg20150816
Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. DOI:10.1190/1.3058434
Kong F N, Johnstad S E, Røsten T, et al. 2008. A 2.5D finite-element-modeling difference method for marine CSEM modeling in stratified anisotropic media. Geophysics, 73(1): F9-F19. DOI:10.1190/1.2819691
Li J H, Farquharson C G, Hu X Y, et al. 2016. A vector finite element solver of three-dimensional modelling for a long grounded wire source based on total electric field. Chinese Journal of Geophysics, 59(4): 1521-1534. DOI:10.6038/cjg20160432
Li Y G, Key K. 2007. 2D marine controlled-source electromagnetic modeling:Part 1-An adaptive finite-element algorithm. Geophysics, 72(2): WA51-WA62. DOI:10.1190/1.2432262
Li Y G, Li G. 2016. Electromagnetic field expressions in the wavenumber domain from both the horizontal and vertical electric dipoles. Journal of Geophysics and Engineering, 13(4): 505-515. DOI:10.1088/1742-2132/13/4/505
Luo Y Z, Meng Y L. 1986. Some problems on resistivity modeling for two-dimensional structures by the finite element method. Chinese Journal of Geophysics (Acta Geophysica Sinica), 29(6): 613-621.
Mackie R L, Torquil S J, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite difference equations:The magnetotelluric example. Radio Science, 29(4): 923-935. DOI:10.1029/94RS00326
Mitsuhata Y. 2000. 2-D electromagnetic modeling by finite-element method with a dipole source and topography. Geophysics, 65(2): 465-475. DOI:10.1190/1.1444740
Myer D, Key K, Constable S. 2015. Marine CSEM of the Scarborough gas field, Part 2:2D inversion. Geophysics, 80(3): E187--E196. DOI:10.1190/geo2014-0438.1
Newman G A, Alumbaugh D L. 1995. Frequency domain modeling of airborne electromagnetic responses using staggered finite differences. Geophysical Prospecting, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8
Shantsev D V, Maaø F A. 2015. Rigorous interpolation near tilted interfaces in 3-D finite-difference EM modelling. Geophysical Journal International, 200(2): 743-755.
Shen J S, Sun W B. 2008. A study on the 2. 5-D electromagnetic modeling by the finite element method and the wave number selection. Computing Techniques for Geophysical and Geochemical Exploration, 30(2): 135-144.
Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part Ⅰ:Properties and error analysis. Geophysics, 61(5): 1308-1318. DOI:10.1190/1.1444054
Stoyer C H, Greenfield R J. 1976. Numerical solutions of the response of a two-dimensional earth to an oscillating magnetic dipole source. Geophysics, 41(3): 519-530. DOI:10.1190/1.1440630
Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy. Geophysics, 74(5): F95-F105. DOI:10.1190/1.3196241
Streich R, Becken M, Ritter O. 2012. 2.5D controlled-source EM modeling with general 3D source geometries. Geophysics, 76(6): F387-F393.
Torres-Verdín T, Habashy T M. 1994. Rapid 2.5-dimensional forward modeling and inversion via a new nonlinear scattering approximation. Radio Science, 29(4): 1051-1079. DOI:10.1029/94RS00974
Unsworth M J, Travis B J, Chave A D. 1993. Electromagnetic induction by a finite electric dipole source over a 2-D earth. Geophysics, 58(2): 198-214. DOI:10.1190/1.1443406
Ward S H, Hohmann G W. 1988. Electromagnetic theory for geophysical applications.//Nabighian M N. Electromagnetic Methods in Applied Geophysics. Society of Exploration Geophysics, 131-311.
Weitemeyer K, Gao G Z, Constable S, et al. 2010. The practical application of 2D inversion to marine controlled-source electromagnetic data. Geophysics, 75(6): F199-F211. DOI:10.1190/1.3506004
Weitemeyer K, Constable S. 2014. Navigating marine electromagnetic transmitters using dipole field geometry. Geophysical Prospecting, 62(3): 573-596. DOI:10.1111/gpr.2014.62.issue-3
Wirianto M, Mulder W A, Slob E C. 2011. Applying essentially non-oscillatory interpolation to controlled-source electromagnetic modelling. Geophysical Prospecting, 59(1): 161-175. DOI:10.1111/gpr.2010.59.issue-1
Xu S Z, Duan B C, Zhang D H. 2000. Selection of the wavenumbers k using an optimization method for the inverse Fourier transform in 2.5D electrical modelling. Geophysical Prospecting, 48(5): 789-796. DOI:10.1046/j.1365-2478.2000.00210.x
Yin C C, Zhang B, Liu Y H, et al. 2015. 2.5-D forward modeling of the time-domain airborne EM system in areas with topographic relief. Chinese Journal of Geophysics, 58(4): 1411-1424. DOI:10.6038/cjg20150427
Zhdanov M S. 2010. Electromagnetic geophysics:Notes from the past and the road ahead. Geophysics, 75(5): 75A.
戴世坤, 王顺国, 张钱江, 等. 2013. 频率域可控源电磁法2.5D正反演. 中国有色金属学报, 23(9): 2513–2523.
底青云, UnsworthM, 王妙月. 2004. 复杂介质有限元法2.5维可控源音频大地电磁法数值模拟. 地球物理学报, 47(4): 723–730.
韩波, 胡祥云, 黄一凡, 等. 2015. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报, 58(8): 2812–2826. DOI:10.6038/cjg20150816
李建慧, FarquharsonC G, 胡祥云, 等. 2016. 基于电场总场矢量有限元法的接地长导线源三维正演. 地球物理学报, 59(4): 1521–1534. DOI:10.6038/cjg20160432
罗延钟, 孟永良. 1986. 关于用有限单元法对二维构造作电阻率法模拟的几个问题. 地球物理学报, 29(6): 613–621.
沈金松, 孙文博. 2008. 2.5维电磁响应的有限元模拟与波数取值研究. 物探化探计算技术, 30(2): 135–144.
殷长春, 张博, 刘云鹤, 等. 2015. 2.5维起伏地表条件下时间域航空电磁正演模拟. 地球物理学报, 58(4): 1411–1424. DOI:10.6038/cjg20150427