在地面电磁法勘探中,可控源音频大地电磁法(CSAMT)在普查和勘探石油、地热、金属矿产、水文、环境等各个方面发挥了重要的作用(底青云等,2013).海洋可控源电磁法(CSEM)是一种新的海洋地球物理勘探方法,它可以帮助地震方法识别有效储层,提高钻井成功率.海洋CSEM技术在海洋油气资源勘探中已经得到广泛应用,并取得显著的效果(Constable, 2010).可控源电磁法中,源、场、观测系统本质上都是三维的,解决三维问题是提高数据的可靠性和分辨率的最重要的途径(付长民等,2009).
近年来,可控源电磁场三维正演方法研究取得了很大进展,提出了众多基于积分方程法(Avdeev and Knizhnik, 2009; 陈桂波等,2009)、有限差分法/有限体积法(Streich, 2009; 殷长春等,2014;Weiss and Constable, 2006; 杨波等,2012;韩波等,2015)和规则网格有限单元法的数值模拟方法(阎述和陈明生, 2000; 张继锋等,2009; 徐志锋和吴小平,2010; Da Silva et al., 2012; 李勇等, 2015).这些算法大都是在结构网格上实现的,但结构网格不能精确地模拟地形起伏和倾斜界面等复杂地质构造,而非结构网格有限元法更适于模拟这些复杂地电模型.完全非结构网格能够真实地模拟地形起伏、倾斜界面等复杂地质构造,特别是非结构网格非常适合于模拟多尺度构造,如嵌入大规模区域构造中的许多小的不均匀体(Li and Key, 2007; Li and Constable, 2007).基于非结构网格有限元法的二维和三维可控源电磁场数值模拟方法研究取得了一些很好的结果(Ren et al., 2013, 2014; Puzyrev et al., 2013; Koldan et al., 2014; Ansari and Farquharson, 2014; Börner et al., 2015; 杨军等, 2015; 等等).
数值模拟结果的精度在很大程度上取决于模型的离散化网格,合理可靠的离散化网格设计是获得高精度数值模拟结果的关键.理论上讲,网格越精细模拟结果越准确,但过于精细的网格会导致计算量过大,以致根本无法计算.因此,需要找到能在计算精度与计算效率之间达到平衡的最优网格.显然,对于不同的模型和不同的观测系统最优网格亦不同,因而基于经验很难设计出最优网格.新近发展起来的自适应有限元技术是解决这个问题的一种有效手段,其基本思路是:首先,对模型求解区域进行剖分,得到一个粗糙的初始网格,基于该初始网格进行正演计算;并计算每个单元的局部误差,选取一定比例具有较大局部误差的单元进行网格细化,产生一个新网格;然后在细化后的新网格上再进行正演计算;重复以上过程,直至解满足收敛条件或达到最大网格细化次数为止.非结构网格自适应有限元法在二维电磁场数值模拟中已经取得了很好的应用效果(Li and Key, 2007; Li and Pek, 2008;Li and Dai, 2011;Key and Ovall, 2011).而对于三维电磁场正演问题,目前仅有少数几个学者进行了这方面的尝试(刘长生,2009;Ren et al., 2013, 2014; Grayver and Burg, 2014; Grayver and Kolev, 2015),且大都是针对大地电磁场三维正演问题的.
可控源电磁场正演模拟可以采用自适应有限元法求解关于总场的边值问题,但由于源点的奇异性可能会造成数值求解困难,在源点附近难以得到较好的结果,即使采用伪delta函数对源点进行离散,也难以完全消除其影响(刘颖,2014).为了消除源点附近电磁场的奇异性,可以采用将电磁场分解为一次场和二次场的二次场方法(Li and Key, 2007),即一维层状背景模型的一次场由拟解析法求得,二次场由自适应矢量有限元方法得到.但背景模型的选择是需要进一步讨论的问题,在背景模型难以确定或起伏地面情况下,往往难以计算或数值精度难以保证,且需要计算一次场,计算量增加许多.但在平坦地面或海洋环境中,二次场方法具有较高的数值精度,尤其在海洋可控源电磁法中,发射源附近的电磁场响应包含有发射场源姿态、位置和海底浅层介质的丰富信息,在发射源附近获得高精度的数值解对反演至关重要.
本文基于非结构四面体网格矢量有限元法和自适应网格细化技术实现了可控源电磁场三维正演计算.首先,介绍本文算法及一些实现细节,包括三维非结构矢量有限元法和基于后验误差估计的自适应网格细化算法;接着给出一维和三维理论模型计算结果,并分别与解析解和三维有限体积法数值解进行了对比分析.最后,使用本文算法模拟了一个含三维倾斜板状异常体的可控源电磁响应,表明了本文算法模拟复杂地电结构电磁场的能力和有效性.
2 非结构网格矢量有限元法 2.1 控制方程假定时间因子为e-iωt,在似稳态情形下,电场(E)和磁场(H)满足的控制方程为
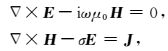
|
(1) |
这里μ0为真空中的磁导率,ω为角频率,J为电流源,σ为电导率.为了消除源点附近电磁场的奇异性,把电磁场分解为由源在电导率为σp的一维层状背景模型中产生的一次场(Ep和Hp)和电导率为σs=σ-σp的异常体产生的二次场(Es和Hs).一次场可以由拟解析法求得(Li Y G and Li G, 2016).二次电磁场满足如下方程:
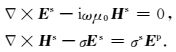
|
(2) |
由(2)式可以推导出关于二次电场Es的偏微分方程

|
(3) |
我们采用有限元法求解方程(3).当求得二次电场Es后,二次磁场可以采用(4)式计算得到:
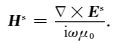
|
(4) |
利用加权余量法,可以导出偏微分方程(3)对应的积分方程.将方程(3)左右两边乘以电场的任意变分δEs,并对模拟区域Ω积分,结合散度公式及格林定理(Zienkiewicz,1977),可以得到:
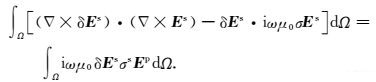
|
(5) |
假定二次电场在模拟区域外边界上满足齐次边界条件:

|
(6) |
有限元方程式(5)可以采用常规节点有限元方法和矢量有限元方法求解,但采用节点有限元方法求解时,电场法向分量连续的边界条件和电磁场散度为零的条件得不到保证,从而有可能出现伪解,且旋度算子的处理和边界条件的施加较为麻烦(Jin, 2002; Schwarzbach et al., 2011).方程(5)可以通过一定的变换得到在库仑规范或洛伦兹规范下的电磁势方程,求解电磁势避免了地球介质中电场的法向不连续问题,可以直接利用节点有限元方法进行求解,但由于节点有限元的插值函数不满足散度为零的条件,会产生伪解,且先求解电磁势再通过差分格式求解电磁场时显然也会降低数值模拟的精度(Badea et al., 2001).而采用矢量有限元方法则可以克服上述问题.
我们用非结构四面体单元对模拟区域进行离散.图 1所示为一个四面体单元,它有4个节点和6条棱边.假定棱边上的电场切向分量为Ei(i=1, …, 6),且棱边中点处电场切向分量方向与棱边的方向一致.单元内任意点处的电场可以通过单元中6条棱边上电场线性插值得到,

|
图 1 四面体单元节点及矢量边示意图 Fig. 1 Sketch of nodes and vector edges of a tetrahedron element |
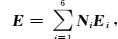
|
(7) |
式中,Ni为线性插值基函数.我们选用Nédélec型矢量基函数(Nédélec, 1980)

|
(8) |
这里li为第i条边的长度,Li1、Li2分别为第i条边起点(i1)和终点(i2)的节点基函数(Jin, 2002).对Ni取散度,得▽·Ni=0,即Nédélec型矢量基函数满足散度为零的条件.
将式(7)代入积分方程(5),并计算单元积分,可得:

|
(9) |
其中,ne为四面体单元的个数,

|
(10) |

|
(11) |

|
(12) |
考虑到变分δEs的任意性,由方程(9)可以得到有限元线性方程组,用直接法解该线性方程组可以得到二次场,再与一次场矢量相加可得到总电磁场.
3 基于后验误差估计的自适应网格细化算法方程式(5)可以用算子B表示成
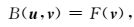
|
(13) |
其中

|
(14) |
式中,k2=iωμσ.
假设函数G为电磁场精确解u与有限元数值解uh的误差u-uh的泛函,式(13)的对偶方程为
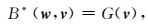
|
(15) |
其中,B*是对偶算子或者伴随算子.假定B*(w, v)=B(v, w),则有
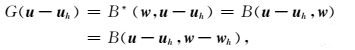
|
(16) |
其中,w和wh分别是对偶问题的精确解和有限元数值解.
根据式(14)可知,对偶方程(15)的右端项为:

|
(17) |
其中,Ω为包含接收点的连续区域,∂Ω为连续区域的边界,v为任意向量.求解方程(15)可得到对偶问题的有限元解wh.
定义基于残差和对偶加权的后验误差估计(Zhong et al., 2012):
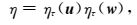
|
(18) |
其中
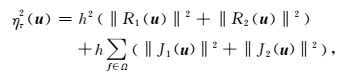
|
(19) |
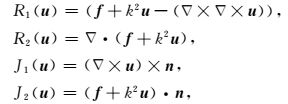
|
(20) |
式中,h为四面体外接圆的直径.ητ(w)的计算式与ητ(u)类似.
自适应有限元算法的步骤如下:(1)给定一个初始粗糙网格,并利用有限元法求解式(13)得到其有限元解;(2)求解对偶问题有限元方程(15),得到对偶问题有限元解;(3)根据式(18)计算每个单元的后验误差,对一定比例(本文算例均设定为总单元数的5%)误差较大的单元进行细化,得到一个新的网格;(4)重复步骤(1)—(3),直到网格细化前后有限元解的均方根误差满足精度要求或者达到设定的最大网格细化次数为止.具体流程如图 2.

|
图 2 自适应有限元算法的计算流程 Fig. 2 Flow chart of adaptive finite element algorithm |
为了验证算法和程序的正确性,设计如图 3所示的1D模型.假定海水电阻率为0.3 Ωm,海水深度为1000 m;海底下方为1000 m厚的覆盖层,电阻率为1 Ωm;覆盖层下方为500 m厚的高阻油气薄层,电阻率为100 Ωm;油气薄层下方是电阻率为1 Ωm的地层;电偶源布置于海底上方50 m处,其中心点位置为(0 m,0 m,950 m),长度为1 m,发射电流为1 A,发射频率为0.25 Hz;假定总共20个接收点沿测线方向(X=0),在Y=500~10000 m范围内等间隔均匀布置于海底.

|
图 3 1D油气模型 Fig. 3 1D canonical model |
图 4为自适应有限元解与1D解析解(Li, 2016)对比.图中Ex, Hy, Hz对应的曲线为源沿X方向布置的结果,Ey, Ez, Hx对应的曲线为源沿Y方向布置的结果.可以看出,水平电磁场分量的振幅相对误差均小于1%,相位差在1°以内.对于垂直电磁场分量,当收发距较小时(小于5 km),振幅相对误差小于1%,相位差在1°以内,而当收发距大于5 km时,振幅相对误差较大,Ez分量的最大相位差为1.4°.
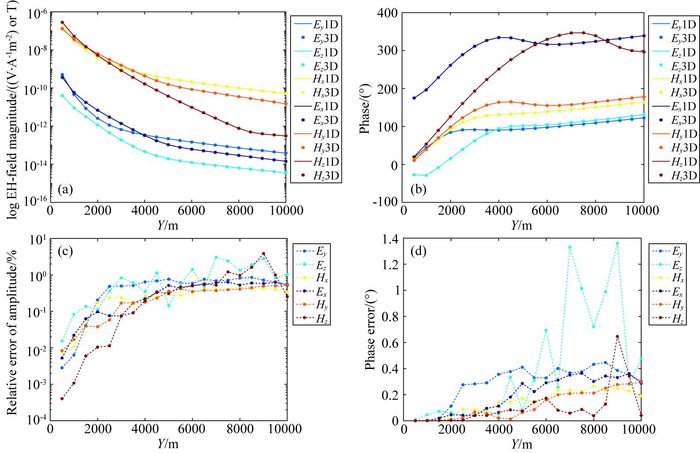
|
图 4 自适应有限元解与解析解对比(1D油气模型) (a)振幅; (b)相位; (c)振幅相对误差; (d)相位差. Fig. 4 Comparison of solution from adaptive finite element method and analytical solution (1D canonical model) (a) Amplitude; (b) Phase; (c) Relative error of amplitude; (d) Phase error. |
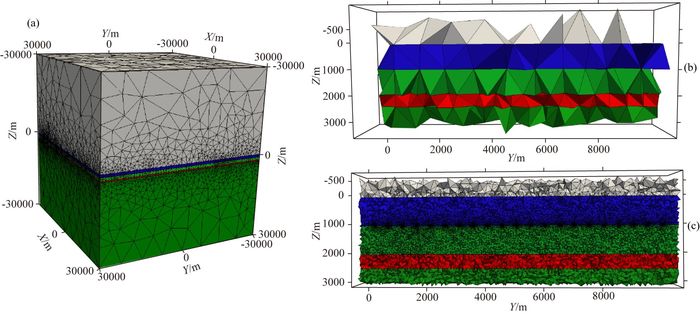
有限元模拟区域为60 km×60 km×60 km,初始网格如图 5a所示,提取网格中感兴趣的部分区域网格(图 5b)(0 km<X < 1 km, -0.5 km<Y < 10.5 km,-0.5 km<Z < 3 km),可以看出初始网格非常粗糙,而且发射源和接收点区域网格没有细化.经过10次网格细化后,得到的最终网格如图 5c所示.由图可见,在接收点附近区域,网格得到很好的加密,且接收点下方的网格也有一定程度的细化,从而确保了数值解的精度.
|
图 5 网格示意图(1D油气模型) (a)初始网格; (b)部分区域初始网格; (c)部分区域最终网格. Fig. 5 Sketch of mesh of 1D canonical model (a) Initial mesh; (b) A part of initial mesh; (c) A part of final mesh. |
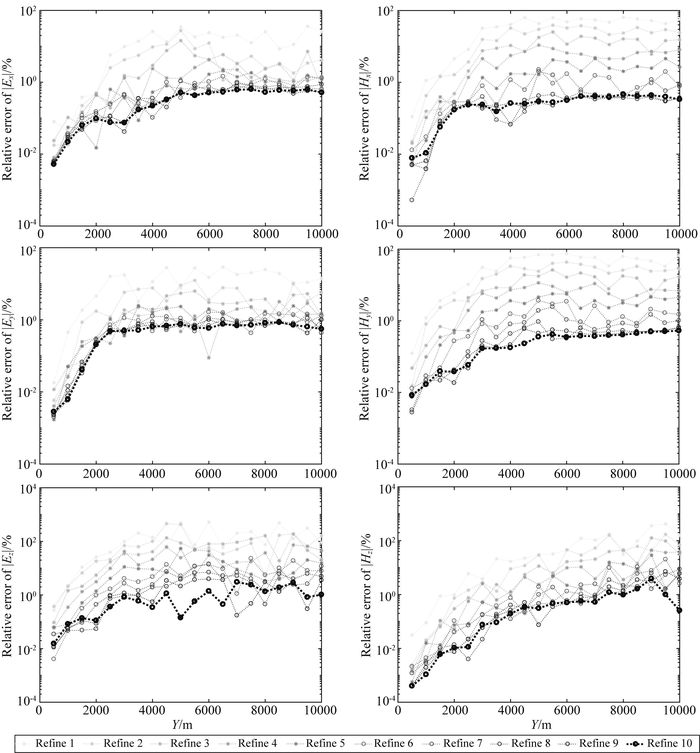
在有限元数值模拟中,若想得到高精度数值解,就需要将有限元网格离散得足够细.自适应网格细化算法采用后验误差估计方法对有限元数值解精度进行估算,对误差较大的网格逐步细化,从而保证了网格细化的合理性.每次参与细化的网格数量不能太少,过少则需要较多的细化次数;但也不能太多,过多则将会对误差并不大的网格也进行细化,从而增加计算量.经过多次模拟测试,对部分误差较大的单元(总单元数5%)进行细化,效果最好.图 6所示为自适应网格细化过程中电磁场振幅相对误差的变化情况.从图中可知,初始网格上(部分区域如图 5b)得到的数值解振幅相对误差基本都在10%以上,然而随着细化次数的增加,电磁场振幅相对误差逐渐减小,经过10次网格细化后(部分区域如图 5c),振幅相对误差基本收敛于1%左右.
|
图 6 自适应网格细化过程中电磁场振幅相对误差变化 Fig. 6 Change of relative error of electromagnetic field during mesh refinement |
在上述算例的网格细化过程中,理论上要求每次只对总单元数的5%进行细化.但是由于网格剖分软件基于Delaunay剖分算法(Delaunay, 1934),可能会导致每次被细化的网格单元数大于5%.表 1详细列出了在网格细化过程中网格的单元数、棱边数、CPU时间、求解器耗时、内存消耗、一次场耗时和RMS等.其中RMS为每次迭代的计算结果与上次迭代计算结果的均方根误差.从表中可见,在网格数较小时,一次场计算时间占主要部分,但当网格数越来越大时,求解线性方程组所需的计算时间越来越长,经过10次迭代后RMS收敛于1.0.
|
|
表 1 网格细化参数 Table 1 Parameters of grid refinement |
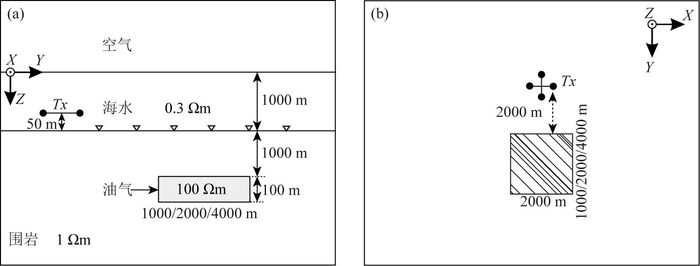
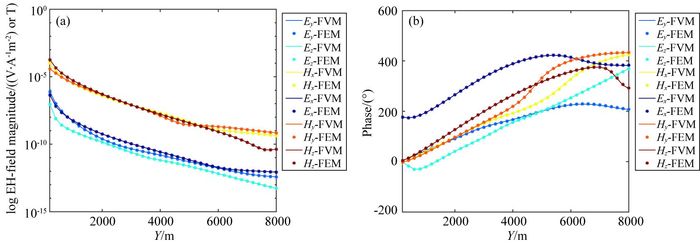
建立如图 7所示的三维海洋油气储层模型.假定海水电阻率为0.3 Ωm,海水深度为1000 m;海底下方1000 m深处存在100 m厚的高阻油气薄层,其电阻率为100 Ωm,在X方向长度为2000 m, 分布范围为[-1000,1000]m;在Y方向上设计三个不同长度,分布范围分别为[2000,3000]m、[2000,4000]m和[2000,6000]m;油气薄层周围是电阻率为1 Ωm的围岩;电偶源布置于海底上方50 m处,其中心点位置为(0 m,0 m,950 m),长度为100 m,发射电流为1 A,频率为0.25 Hz;共有41个接收点沿测线方向(X=0),在收发距为0 m和8 km范围内等间隔均匀布置于海底.为了进一步验证算法的正确性,采用本文自适应矢量有限元算法和基于交错网格有限体积(FVM)法的海洋可控源电磁三维正演算法(韩波等,2015)分别模拟图 7所示三维模型的电磁场响应.图 8所示为两种算法的模拟结果.图中Ex, Hy, Hz曲线为源沿X方向布置的结果,Ey, Ez, Hx曲线为源沿Y方向布置的结果.由图可见,振幅曲线和相位曲线都重合得非常好.
|
图 7 三维海洋油气储层模型 Fig. 7 3D model of marine reservoir |
|
图 8 自适应有限元解与有限体积法(韩波,2015)对比图(三维油气模型) (a)振幅曲线; (b)相位曲线. Fig. 8 Comparison of adaptive finite element method and finite volume method (Han, 2015) (3D reservoir model) (a) Amplitude curves; (b) Phase curves. |
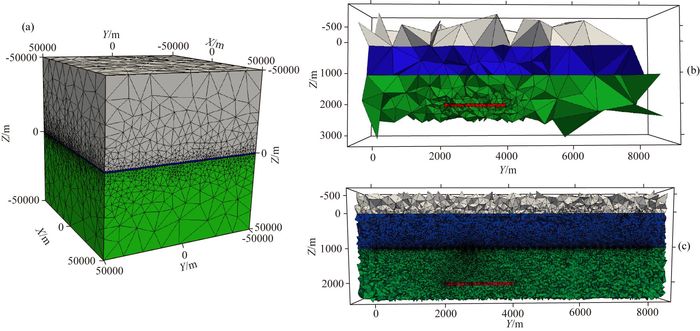
整个模拟区域为100 km×100 km×100 km(以2 km×2 km大小的油气储层模型为例),初始网格如图 9a所示,网格区域虽然非常大,但是在外边界附近的单元非常大;提取网格中感兴趣的区域部分进行单独显示如图 9b(0 km<X < 1 km, -0.5 km<Y < 8.5 km,-0.5 km<Z < 2.5 km),可以看出初始的网格非常粗糙,而且发射源、接收点及油气储层区域网格没有任何细化;经过15次网格细化后收敛,部分区域的网格细化情况如图 9c,在接收点附近和油气储层区域都有很好的加密,保证了数值解的精度.
|
图 9 网格示意图(三维油气模型) (a)初始网格; (b)部分区域初始网格; (c)部分区域最终网格. Fig. 9 Sketch showing grid of 3D reservoir model (a) Initial grid; (b) Part of initial grid; (c) Part of final grid. |
对水平薄板状高阻体油气储层模型的电场曲线进行分析发现,只有当其水平尺寸至少为埋深的2倍时,才可以利用CSEM将其分辨出来(Constable and Weiss, 2006).目前常用的海洋CSEM资料定性解释方法是计算含有油气储层的电磁场振幅与不含油气储层背景模型的电磁场振幅的比值,称为归一化场.Brown等(2012)把观测误差和噪声等干扰因素考虑在内,计算目标模型与背景模型电磁场振幅差与背景噪声比值,来衡量异常的大小,称为有效异常(裴建新等,2015),计算公式为:

|
(21) |
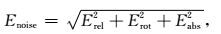
|
(22) |
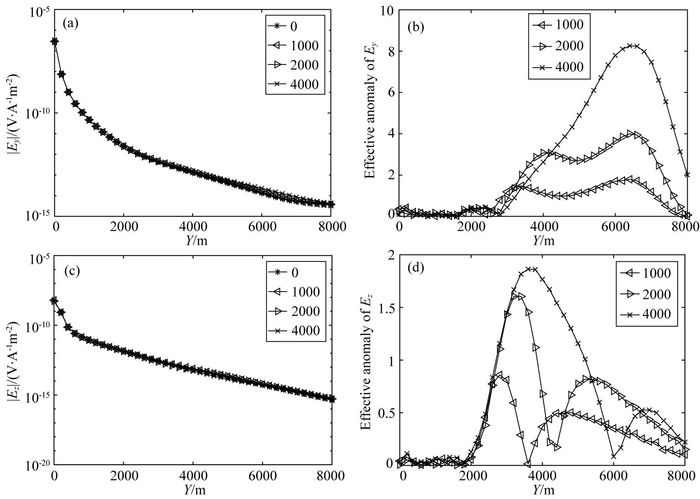
其中,|EM|是含有油气储层模型的电场振幅;|Eo|是不含油气储层背景模型的电场振幅;|Enoise|是电场噪声;Erel为振幅的相对误差,包括仪器系统产生的误差和观测误差;Eabs是绝对误差,是发射-接收系统的本底噪声,通常取Eabs=10-16 V·A-1m-2;Erot为接收站旋转角度引起的误差,这里取旋转角度误差为5°.图 10a和10b分别为海洋油气储层模型(图 7)中不同长度(Y方向长度分别为0 m(即不含油气储层),1 km,2 km,4 km)的水平电场Ey的振幅曲线和有效异常曲线,图 10c和10d分别对应为垂直电场Ez的振幅曲线和有效异常曲线.可以看出,如果仅从振幅曲线来看,很难分辨油气储层长度为1 km,2 km的水平电场异常,但是有效异常曲线(图 10b,10d)中异常比较明显,尤其是垂直电场计算的有效异常,在油气储层的两端都有高异常反映,而且有效异常考虑到了数据观测误差及发射源姿态误差对电磁场响应的影响,异常分辨更为清楚有效,油气储层长度越长,有效异常越大.
|
图 10 不同油气储层的水平电场振幅(a, c)和有效异常(b, d) Fig. 10 Amplitudes (a, c) and effective anomalies (b, d) of horizontal electromagnetic fields in different reservoirs |
断层破碎带、接触带和金属矿脉往往可由倾斜板状体予以近似(李建慧等,2016).建立如图 11所示的三维陆地模型:空气电阻率108 Ωm,在电阻率为100 Ωm的均匀半空间模型内存在一个角度为45°的倾斜板状体,顶部出露于地表,电阻率为30 Ωm.板状体三维尺度为200 m×3000 m×1500 m,沿X方向分布范围:宽度为200 m,其顶部为[750,950]m,底部为[-950,-750]m;沿Y方向分布范围为[5500,8500]m,长度为3000 m.在地表(Z=0 m)分别布置了Y=5 km、6 km、7 km、8 km、9 km的5条测线、共205个测点,其中每条测线长度为2 km、含41个测点,间隔为50 m.接地长导线源长度为1 km,中心置于(0,0,0),沿X方向放置,发射电流为1 A,发射频率在-1~1000 Hz之间对数等间隔采样,共11个采样点.

|
图 11 倾斜板状体陆地模型 Fig. 11 Land model including an inclined plate |
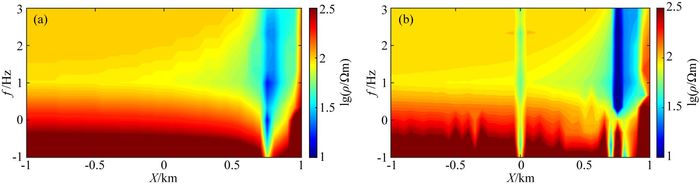
本算例计算区域为60 km×60 km×60 km,提取网格中感兴趣的区域部分进行单独显示如图 12(0 km<X < 2 km, 4.5 km<Y < 9.5 km,0 km<Z < 2 km),初始网格剖分断面图 12a,经过10次迭代后收敛(以10 Hz为例),此时网格对结果的变化影响较小,最终网格剖分如图 12b,在接收点和倾斜板状体处都有较好的加密.图 13所示为卡尼亚视电阻率切片图,在5 km和9 km测线上看不到倾斜板状体异常,6 km、7 km和8 km测线上能够清楚地看到低阻异常,三个切片视电阻率剖面基本一致,在出露地表的区域750~950 m处,由于静态效应的影响(黄兆辉等,2006),视电阻率存在挂面条现象,需进一步做反演才能更好地确定倾斜板状体的倾斜情况,而在-750~750 m之间仍然能够看到一条较为清晰的电阻率分界面,此部分异常即倾斜板状体的影响.为了验证结果的正确性,尤其是高频情况下的结果,我们对比了与2D自适应有限元算法(Li and Key, 2007)在7 km测线处的剖面图,结果基本一致,见图 14.在高频段(100~1000 Hz),[-1 km,0]范围内的视电阻率均为100 Ωm,从而验证了高频结果的正确性.在视电阻率切片上,我们能够看到较为明显的倾斜板状体异常,且在750~950 m处,均存在挂面条现象,但2D切片反映的是在Y方向无限延伸的倾斜板状体,视电阻率低阻异常值更低,且在源附近由于算法的影响,存在较大的计算误差.

|
图 12 部分网格示意图(陆地模型) (a)初始网格;(b)最终网格. Fig. 12 Part of grid for the land model including an inclined plate (a) Initial grid; (b) Final grid. |

|
图 13 卡尼亚视电阻率3D切片 Fig. 13 3D slices of Cagniard apparent resistivity |
|
图 14 Y=7 km测线的视电阻率切片图 (a) 3D数值解;(b) 2D数值解. Fig. 14 Apparent resistivity slice of line Y=7 km (a) 3D numerical solution; (b) 2D numerical solution. |
(1) 采用自适应矢量有限元算法实现了CSEM 3D正演模拟,采用一次场和二次场分离的算法计算电磁场响应,并运用基于后验误差估计的自适应网格细化算法细化网格,降低源点奇异性,提高场源附近及接收点的电磁场数值精度.有限元求解过程中采用非结构化四面体单元网格对地电模型进行离散化,利用后验误差估计方法指导网格加密细化,能够得到高质量的有限元解.本算法能够计算任意姿态有限长度的电偶源的电磁场,且源和接收点可以放置于任意位置,具有良好的通用性.
(2) 建立层状油气模型,通过与解析解对比,水平电磁场分量的振幅相对误差均小于1%,相位差在1°以内.对于垂直电磁场分量,当收发距较小时(小于5 km),振幅相对误差小于1%,相位差在1°以内,而当收发距大于5 km时,振幅相对误差较大,Ez分量的最大相位差为1.4°,从而验证了算法的正确性和精度.
(3) 建立水平薄板状高阻体油气储层模型,采用本文的自适应矢量有限元算法与基于交错网格有限体积离散的海洋可控源电磁三维正演算法对比,振幅和相位重合得非常好,进一步验证了算法的正确性.设计不同的板状体延伸长度,计算了水平电场分量的有效异常并分析发现,相对于振幅曲线,有效异常能够对高阻油气有更好的反映.
(4) 建立倾斜板状体陆地模型并计算5条测线的视电阻率,横跨板状体上方的3条测线存在明显的低阻异常,能够根据视电阻率剖面判断倾斜板状体的倾斜方向.在地表露头处存在明显的静态效应,需进一步做反演才能更好地确定倾斜板状体的位置和倾斜角度等信息.
Ansari S, Farquharson C G.
2014. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids. Geophysics, 79(4): E149-E165.
DOI:10.1190/geo2013-0172.1 |
|
Avdeev D, Knizhnik S.
2009. 3D integral equation modeling with a linear dependence on dimensions. Geophysics, 74(5): F89-F94.
DOI:10.1190/1.3190132 |
|
Badea E A, Everett M E, Newman G A, et al.
2001. Finite element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials. Geophysics, 66(3): 786-799.
DOI:10.1190/1.1444968 |
|
Börner R U, Ernst O G, Güttel S.
2015. Three-dimensional transient electromagnetic modelling using Rational Krylov methods. Geophys. J. Int., 202(3): 2025-2043.
DOI:10.1093/gji/ggv224 |
|
Brown V, Hoversten M, Key K, et al.
2012. Resolution of reservoir scale electrical anisotropy from marine CSEM data. Geophysics, 77: E147-E158.
DOI:10.1190/geo2011-0159.1 |
|
Chen G B, Wang H N, Yao J J, et al.
2009. Three-dimensional numerical modeling of marine controlled-source electromagnetic responses in a layered anisotropic seabed using integral equation method. Acta Physica Sinica, 58(6): 3848-3857.
|
|
Constable S C, Weiss C J.
2006. Mapping thin resistors and hydrocarbons with marine EM methods:insights from 1D modeling. Geophysics, 71(2): G43.
DOI:10.1190/1.2187748 |
|
Constable S C.
2010. Ten years of marine CSEM for hydrocarbon exploration. Geophysics, 75(5): 75A67-75A81.
DOI:10.1190/1.3483451 |
|
Da Silva N V, Morgan J V, MacGregor L, et al.
2012. A finite element multifrontal method for 3D CSEM modeling in the frequency domain. Geophysics, 77(2): E101-E115.
DOI:10.1190/geo2010-0398.1 |
|
Delaunay B N.
1934. Sur 1a Sphère Vide. Bulletin of Academy of Sciences of the USSSR(6): 793-800.
|
|
Di Q Y, Fang G Y, Zhang Y M.
2013. Research of the Surface Electromagnetic Prospecting (SEP) system. Chinese J. Geophys. , 56(11): 3629-3639.
DOI:10.6038/cjg20131104 |
|
Fu C M, Di Q Y, Wang M Y.
2009. 3D numeric simulation of marine controlled source electromagnetics (MCSEM). OGP , 44(3): 358-363.
|
|
Grayver A V, Burg M.
2014. Robust and scalable 3-D geo-electromagnetic modelling approach using the finite element method. Geophys. J. Int., 198(1): 110-125.
DOI:10.1093/gji/ggu119 |
|
Grayver A V, Kolev T V.
2015. Large-scale 3D geoelectromagnetic modeling using parallel adaptive high-order finite element method. Geophysics, 80(6): E277-E291.
DOI:10.1190/geo2015-0013.1 |
|
Han B, Hu X Y, Huang Y F, et al.
2015. 3-D frequency-domain CSEM modeling using a parallel direct solver. Chinese J. Geophys. , 58(8): 2812-2826.
DOI:10.6038/cjg20150816 |
|
Huang Z H, Di Q Y, Hou S L.
2006. CSAMT static correction and its application. Progress in Geophysics , 21(4): 1290-1295.
|
|
Jin J M. 2002.
The Finite Element Method in Electromagnetics. (2nd ed). New York: Wiley-IEEE Press.
|
|
Key K, Ovall J.
2011. A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling. Geophys. J. Int., 186(1): 137-154.
DOI:10.1111/gji.2011.186.issue-1 |
|
Koldan J, Puzyrev V, de la Puente J, et al.
2014. Algebraic multigrid preconditioning within parallel finite-element solvers for 3-D electromagnetic modelling problems in geophysics. Geophys. J. Int., 197(3): 1442-1458.
DOI:10.1093/gji/ggu086 |
|
Li J H, Farquharson C G, Hu X Y, et al.
2016. A vector finite element solver of three-dimensional modelling for a long grounded wire source based on total electric field. Chinese J. Geophys. , 59(4): 1521-1534.
DOI:10.6038/cjg20160432 |
|
Li Y, Pek J.
2008. Adaptive finite element modeling of two-dimensional magnetotelluric fields in general anisotropic media. Geophys. J. Int., 175(3): 942-954.
DOI:10.1111/gji.2008.175.issue-3 |
|
Li Y, Dai S.
2011. Finite element modeling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures. Geophys. J. Int., 185(2): 622-636.
DOI:10.1111/gji.2011.185.issue-2 |
|
Li Y G, Key K.
2007. 2D marine controlled-source electromagnetic modeling:Part 1-An adaptive finite-element algorithm. Geophysics, 72(2): WA51-WA62.
DOI:10.1190/1.2432262 |
|
Li Y G, Constable S C.
2007. 2D marine controlled-source electromagnetic modeling:Part 2-The effect of bathymetry. Geophysics, 72(2): WA63-WA71.
DOI:10.1190/1.2430647 |
|
Li Y, Wu X P, Lin P R.
2015. Three-dimensional controlled source electromagnetic finite element simulation using the secondary field for continuous variation of electrical conductivity within each block. Chinese J. Geophys. , 58(3): 1072-1087.
DOI:10.6038/cjg20150331 |
|
Li Y G, Li G.
2016. Electromagnetic field expressions in the wavenumber domain from both the horizontal and vertical electric dipoles. Journal of Geophysics and Engineering, 13(4): 505-515.
DOI:10.1088/1742-2132/13/4/505 |
|
Liu C S. 2009. Three-dimensional magnetotellurics adaptive edge finite-element numerical simulation based on unstructured meshes[Ph. D. thesis] (in Chinese). Changsha:Central South University.
|
|
Liu Y. 2014. 2D finite element modelling and inversion for marine controlled-source electromagnetic fields[Ph. D. thesis] (in Chinese). Qingdao:Ocean University of China.
|
|
Nedelec J C.
1980. Mixed finite elements in R3. Numerische Mathematik, 35(3): 315-341.
DOI:10.1007/BF01396415 |
|
Pei J X, Wang Q, Zhang X L.
2015. Effective anomaly for gas hydrate detection with marine CSEM method. OGP , 50(1): 177-183.
|
|
Puzyrev V, Koldan J, de la Puente J, et al.
2013. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling. Geophys. J. Int., 193(2): 678-693.
DOI:10.1093/gji/ggt027 |
|
Ren Z, Kalscheuer T, Greenhalgh S, et al.
2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophys. J. Int., 194(2): 700-718.
DOI:10.1093/gji/ggt154 |
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al.
2014. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling. Geophysics, 79(6): E255-E268.
DOI:10.1190/geo2013-0376.1 |
|
Schwarzbach C, Börner R U, Spitzer K.
2011. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics-a marine CSEM example. Geophys. J. Int., 187(1): 63-74.
DOI:10.1111/gji.2011.187.issue-1 |
|
Streich R.
2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy. Geophysics, 74(5): F95-F105.
DOI:10.1190/1.3196241 |
|
Weiss C J, Constable S C.
2006. Mapping thin resistors and hydrocarbons with marine EM methods, Part Ⅱ-Modeling and analysis in 3D. Geophysics, 71(6): G321-G332.
DOI:10.1190/1.2356908 |
|
Xu Z F, Wu X P.
2010. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method. Chinese J. Geophys. , 53(8): 1931-1939.
DOI:10.3969/j.issn.0001-5733.2010.08.019 |
|
Yan S, Chen M S.
2000. Finite element solution of three dimensional geoelectric models in frequency electromagnetic sounding excited by a horizontal electric dipole. Coal Geology & Exploration , 28(3): 50-56.
|
|
Yang B, Xu Y X, He Z X, et al.
2012. 3D frequency-domain modeling of marine controlled source electromagnetic responses with topography using finite volume method. Chinese J. Geophys. , 55(4): 1390-1399.
DOI:10.6038/j.issn.0001-5733.2012.04.035 |
|
Yang J, Liu Y, Wu X P.
2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids. Chinese J. Geophys. , 58(8): 2827-2838.
DOI:10.6038/cjg20150817 |
|
Yin C C, Ben F, Liu Y H, et al.
2014. MCSEM 3D modeling for arbitrarily anisotropic media. Chinese J. Geophys. , 57(12): 4110-4122.
DOI:10.6038/cjg20141222 |
|
Zhang J F, Tang J T, Yu Y, et al.
2009. Three dimensional controlled source electromagnetic numerical simulation based on electric field vector wave equation using finite element method. Chinese J. Geophys. , 52(12): 3132-3141.
DOI:10.3969/j.issn.0001-5733.2009.12.023 |
|
Zhong L, Chen L, Shu S, et al.
2012. Convergence and optimality of adaptive edge finite element methods for time-harmonic Maxwell equations. Mathematics of Computation, 81(278): 623-642.
|
|
Zienkiewicz O C. 1977.
The Finite Element Method. (Third Edition). London: McGraw-Hill Book Company (UK) Limited.
|
|
陈桂波, 汪宏年, 姚敬金, 等.
2009. 各向异性海底地层海洋可控源电磁响应三维积分方程法数值模拟. 物理学报, 58(6): 3848–3857.
DOI:10.7498/aps.58.3848 |
|
底青云, 方广有, 张一鸣.
2013. 地面电磁探测系统(SEP)研究. 地球物理学报, 56(11): 3629–3639.
DOI:10.6038/cjg20131104 |
|
付长民, 底青云, 王妙月.
2009. 海洋可控源电磁法三维数值模拟. 石油地球物理勘探, 44(5): 358–363.
|
|
韩波, 胡祥云, 黄一凡, 等.
2015. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报, 58(8): 2812–2826.
DOI:10.6038/cjg20150816 |
|
黄兆辉, 底青云, 侯胜利.
2006. CSAMT的静态效应校正及应用. 地球物理学进展, 21(4): 1290–1295.
|
|
李建慧, FarquharsonC G, 胡祥云, 等.
2016. 基于电场总场矢量有限元法的接地长导线源三维正演. 地球物理学报, 59(4): 1521–1534.
|
|
李勇, 吴小平, 林品荣.
2015. 基于二次场电导率分块连续变化的三维可控源电磁有限元数值模拟. 地球物理学报, 58(3): 1072–1087.
DOI:10.6038/cjg20150331 |
|
刘长生. 2009. 基于非结构化网格的三维大地电磁自适应矢量有限元数值模拟[博士论文]. 长沙: 中南大学.
|
|
刘颖. 2014. 海洋可控源电磁法二维有限元正演及反演[博士论文]. 青岛: 中国海洋大学.
|
|
裴建新, 王启, 张秀丽.
2015. 海洋CSEM探测海底天然气水合物的有效异常研究. 石油地球物理勘探, 50(1): 177–183.
|
|
徐志锋, 吴小平.
2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931–1939.
DOI:10.3969/j.issn.0001-5733.2010.08.019 |
|
阎述, 陈明生.
2000. 电偶源频率电磁测深三维地电模型有限元正演. 煤田地质与勘探, 28(3): 50–56.
|
|
杨波, 徐义贤, 何展翔, 等.
2012. 考虑海底地形的三维频率域可控源电磁响应有限体积法模拟. 地球物理学报, 55(4): 1390–1399.
DOI:10.6038/j.issn.0001-5733.2012.04.035 |
|
杨军, 刘颖, 吴小平.
2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827–2838.
DOI:10.6038/cjg20150817 |
|
殷长春, 贲放, 刘云鹤, 等.
2014. 三维任意各向异性介质中海洋可控源电磁法正演研究. 地球物理学报, 57(12): 4110–4122.
DOI:10.6038/cjg20141222 |
|
张继锋, 汤井田, 喻言, 等.
2009. 基于电场矢量波动方程的三维可控源电磁法有限单元法数值模拟. 地球物理学报, 52(12): 3132–3141.
DOI:10.3969/j.issn.0001-5733.2009.12.023 |
|
 2017, Vol. 60
2017, Vol. 60


