2. 中国科学院地球科学研究院, 北京 100029;
3. 中国科学院大学, 北京 100049;
4. 中国石油东方地球物理公司物探技术研究中心, 河北涿州 072751
2. Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. R & D Center BGP CNPC, Zhuozhou Hebei 072751, China
弹性多分量数据的波动方程偏移通常包括两个步骤.第一步是从由地表记录的数据重建地下波场,第二步是应用成像从重构波场中提取反射率信息.多分量数据的弹性波动方程偏移通常用两种方式实现.第一种方法是先在地表对多分量资料分离为纵波、横波资料,然后使用标量方程进行纵、横波偏移、成像.但是通常是基于P和S资料可以成功在地表分离的假设,这在很多情况下是不准确的(Etgen, 1988; Zhe and Greenhalgh, 1997; Yan and Sava, 2008).该方法的缺点是不能很好地进行波场分离而且忽略了转换波效应.第二种方法是使用弹性波方程对多分量资料进行波场分离,然后分别互相关成像,这种方法可以得到有明确物理意义的成像结果,本文采用这种方法.
地球中广泛存在地震各向异性,而且各向异性的效应不容忽视,用各向同性算法对各向异性介质进行偏移成像,并不能保证同相轴很好地归位并且会引入人为的噪音.有关各向异性的理论研究、数值模拟和实际资料处理方法发展了很多,并成功应用于提高成像质量、鉴别岩性、裂隙检测等众多方面.如何对各向异性地区进行精细成像,将成为研究的重点.逆时偏移作为全波场成像有着诸如对高陡构造成像较好、适应横向速度剧烈变化且能对回转波及棱柱波进行成像等优势,将其应用到各向异性介质的精细偏移成像是必然的趋势.
逆时偏移的核心是全波动方程正演,地震波的传播效应得以考虑,所以有利于真振幅成像,且无成像倾角限制.弹性逆时偏移较声波逆时偏移,增加的计算量主要因为弹性模拟代替声波模拟,而采用基于非规则非结构化网格的格子法可以获得计算效率的显著改进.格子法综合了有限元法和有限差分法的优点,既可以对目标区域用非规则非结构化网格进行离散,又有和有限差分相当的计算量,这一方法的核心是积分平衡的微分方程弱形式.此外,我们还可以灵活设定吸收边界,减少计算区域,进一步节省计算开销.传统各向异性成像方法主要是对波动方程进行近似(Alkhalifah, 1998),并推导出拟声波方程进行纵波成像,但是这样很难以完全消除横波对纵波的影响,同时由于其对波动方程进行了近似,在损失一部分能量的同时也可能会加入某些不必要的噪声,导致最终成像结果不理想.基于双程波方程的各向异性弹性波逆时偏移弥补了这方面的不足,但是波场分离对其来说是一个难点.在各向同性介质中,如果不考虑振幅、相位的改变,根据亥姆霍茨理论(Aki and Richards, 2002)纵、横波可以通过散度、旋度的求取得以分离.但是对于各向异性介质,只能通过在波数域求解Christoffel方程,然后将其变换回空间域,得到拟散度、拟旋度算子(Dellonger and Etgen, 1990),进而实现波场分离,该方法对于均匀介质有效;在非均匀介质中,Yan和Sava(2009)通过将局部极化方向向量定义为非稳态空间滤波器,得到拟散度、拟旋度算子.但是,该方法分离纵横波需要大量使用傅里叶变换,这十分耗时且运算量巨大;此后为改进效率,Zhang和McMechan(2010)以及Yan和Sava(2011)在此基础上使用了一些相关近似,使其减小了计算量,得到效率上的显著提升.随后,程玖兵等(程玖兵等, 2013, Cheng et al., 2014)提出low-rank approximating方法,虽然在一定程度上减少了计算量,但是依赖于模型的大小和复杂程度.尤其是到三维的情况,计算和存储将是无比巨大.Zhou and Wang(2017)将波场的波数向量旋转到极化向量通过构建两者之间的偏差角,以此来完成各向异性介质中的波场分离.但是他们的方法需要相位和振幅校正,而且和传统的方法一样都是基于规则网格,不适用于非规则网格的方法.
弹性逆时偏移另外一个关键是成像条件,传统逆时偏移多用互相关成像条件.但是,互相关成像条件有一个缺点,因时间域互相关相当于频率域相乘,最终成像的结果受震源函数振幅谱形状影响很大.而且,震源波场正传过程中存在半积分效应,这一效应也应给与考虑并消除.我们在偏移前对这些因素进行考虑,对数据进行预处理,以避免震源波场互相关引起的冗余效应,在这里使用去冗余的震源效应和半积分效应互相关成像条件(Liu et al., 2017).在二维情况下本文解耦获得的是标量场.近年关于弹性波解耦成像的研究是一个热点,波场模式可以通过解耦得到qP和qS波的矢量场(Zhang and McMechan, 2010; Cheng and Fomel, 2014)或者通过某种解耦传播算子获得矢量场(Wang and McMechan, 2015),再施加成像条件,施加所谓的矢量成像条件(Wang et al., 2016),矢量解耦和矢量成像条件结合,可以自动回避PS波成像的极性反转问题(Wang et al., 2016).本文需要PS成像极性校正,我们采用Du等(2012)提出的利用坡印廷矢量的叉乘进行极性判定.
本文首先简单回顾了格子法(Zhang and Liu, 1999,2002;徐义等,2008)在弹性波模拟中的应用.然后在前人的基础上提出了一种在非均匀TI介质中进行波场分离的方法,这是一种角度域的波场分离方法.该方法的核心是先利用坡印廷矢量(能流密度)求取群角,通过Christoffel方程得到相角和极化角的关系,再由相速度和群速度的关系得到相角和群角的关系,由相角作为中间桥梁得到群角和极化角的关系,由极化角分离各向异性波场,最后运用成像条件得到偏移剖面.首先,在均匀模型中验证了该方法的有效性.最后,即使Hess这种复杂的各向异性模型,我们的方法依旧适用.数值算例证明了本文方法的有效性.
2 基本理论 2.1 控制方程在没有外力的情况下,非均匀介质中的各向异性弹性波方程,可以写成如下形式:

|
(1) |
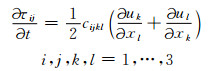
|
(2) |
这里ρ表示密度,ui是位移,τij分别表示应力张量,cijkl表示四阶弹性张量,cijkl满足cijkl=cjikl=cklij对称性质.
介质的各向异性是由刚度矩阵来决定的,它确定了应力和应变的关系,但是弹性常数并没有确切的物理意义,不是很直观,导致了在研究地震波传播的时候,决定其传播的相速度隐含在波动方程的系数中.1986年Thomsen(1986)引入五个各向异性参数来描述弹性介质的各向异性,并且有明确的物理意义:
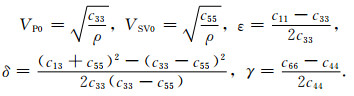
|
(3) |
其中VP0和VSV0分别表示为P波和S波垂直TI介质各向同性面的相速度;ε是P波各向异性参数的度量;Δ是纵横波速度比的相关参数;γ是横波各向异性和横波分裂强度的参数.
TI介质的Thomsen参数表示,明确了弹性参数的物理意义.另一方面,TI介质的弹性参数也可以利用Thomsen参数来得到.例如,二维VTI介质的弹性矩阵参数可以用如下的Thomsen参数来表征:
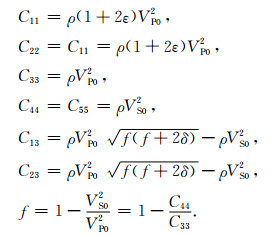
|
(4) |
二维情况下方程(1)的一阶速度—应力弹性波方程可表达为
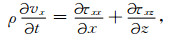
|
(5) |
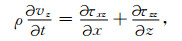
|
(6) |
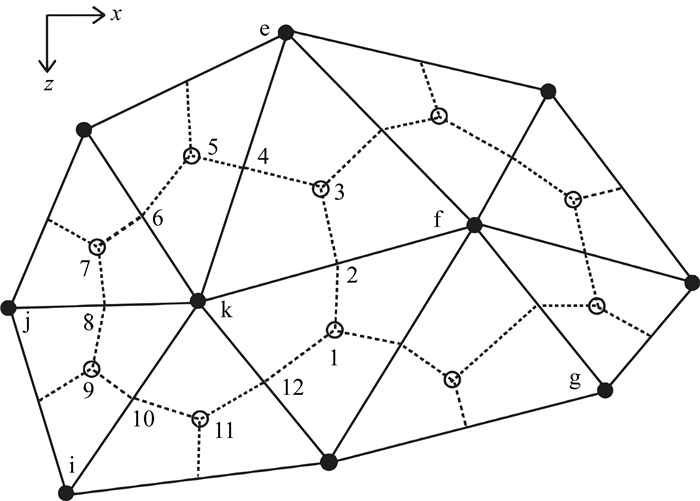
其中,vx和vz分别为质点振动速度的水平分量和垂直分量;τxx和τzz分别为水平和垂直方向的正应力;τxz为切向应力;ρ为介质密度;λ和μ为介质的拉梅常数.我们进行格子法正演模拟的局部离散网格如图 1所示,其中实线三角形网格是基本离散单元,虚线连接三角形的重心和相应边的中点.两个速度分量vx和vz分别定义在单元结点处,如图 1中黑色实心点所示;三个应力分量τxx,τxz和τzz分别定义在单元重心,如图 1中空心点所示.
|
图 1 格子法局部网格示意图 实线所示非规则三角形是格子法的基本离散单元.两个速度分量定义在网格节点处,如实心黑点所示;三个应力分量定义在单元重心处,如空心黑点所示.图中虚线连接起单元重心与单元边界中点. Fig. 1 Local mesh The triangles drawn by solid lines are basic cells in the grid method. The two velocity components are defined at the grid nodes, represented by black dot; The three stress components are defined at the cell barycenters, represented by empty dot. The dash lines link the centers of the grids and the edges. |
以图 1中节点k周围虚线1-2-3-4-5-6-7-8-9-10-11-12-1围成区域Ω为例,对方程(5)(6)做面积分,并对其右端应用格林定理,可得
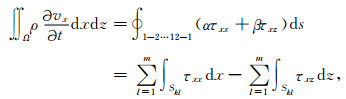
|
(7) |

|
(8) |
在方程(7)和(8)中,m是围绕节点k的三角形单元个数,α和β是虚线外包络法线方向余弦,Skl表示节点k周围第l个三角形单元的虚线段.对方程(7)和(8)左端利用动力学计算中的集中质量模型,假设沿面分布的ρ都被集中到各节点.那么左端的面积分可以近似为Mk(∂ux/∂t)k和Mk(∂uz/∂t)k,其中Mk表示k点邻域各三角形单元中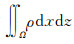
对于一个典型三角形单元ijk,在数值计算中用对三角单元用线性插值函数,然后进行空间一阶导数可得
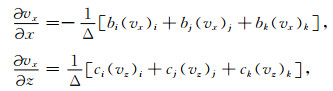
|
(9) |
其中Δ表示单元ijk的面积,bi=(zk-zj)/2,ci=(xk-xj)/2,同理可按照i-j-k-i方向计算bj和cj等.这里(xi(jk), zi(jk))是对应节点i(jk)的空间坐标.同理,方程(9)可用于vz空间导数的计算.这样,我们就可以对方程(2)进行计算.对于每一个小离散三角单元,其中应力τxx、τxz和τzz可视为常数.那么方程(7)和(8)的右端可表示为
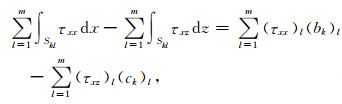
|
(10) |

|
(11) |
式中(bk)l和(ck)l表示节点k周围第l个三角形中相应的几何参数,(τxx)l,(τxz)l和(τzz)l表示节点k周围第l个三角形中的应力值.
在数值计算过程中,给定t时刻的vx和vz,可以借助式(2),由t-0.5Δt时刻的τxx,τxz和τzz求得t+0.5Δt时刻的应力值.然后借助公式(5)和(6),求得t+1时刻的vx和vz,进而完成波场更新.
3 弹性各向异性波场分离及逆时偏移 3.1 波场分离理论在各向同性介质中,通过散度和旋度算子来分离弹性波场(Aki and Richards, 2002):
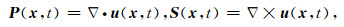
|
(12) |
式中P和S表征纵波、横波;x=(x, y, z)表征空间坐标;t表示时刻;

|
(13) |
这里i为虚数单位,k=(kx, ky, kz)为波数向量,ik可写作

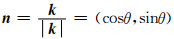
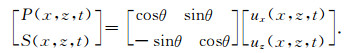
|
(14) |
角度域波场分离的好处是能够保持u的振幅、相位特征.
Dellinger和Etgen (1990)通过把qP波的极化向量替代波矢量k将这种思想应用到各向异性介质中:
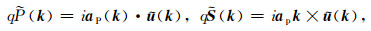
|
(15) |
同样的思路可以得到角度域的各向异性波场分离公式:

|
(16) |
这里的角度υ为极化角,各向异性介质中相角和极化角不相同.
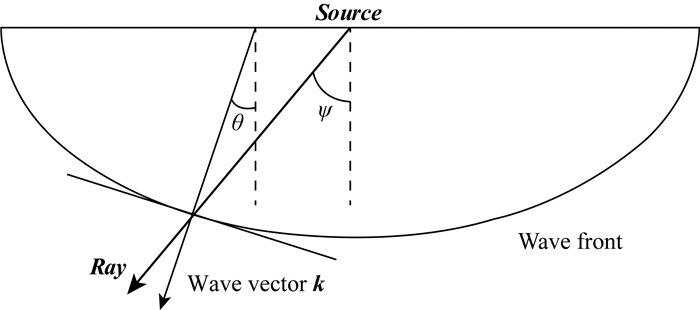
3.2 群角、相角和极化角的计算以及关系我们研究是以群速度方向为基础的,在这里先展开群速度和相速度之间关系的讨论.在各向同性介质中,群速度与相速度方向相同,所以在前文中,我们可以直接使用群速度方向代替相速度方向进行各向同性波场分离;在各向异性介质均匀介质中,群速度的方向就是该点与炮点连线的径向方向,而波前面法线方向即相速度方向,两者并不相同.例如在VTI介质中,如图 2所示,相速度方向如wave vector所示,而群速度方向如ray所示.因为各向异性的存在,均匀介质中波前面的形状不再是球状而是发生波前面形变,相速度与群速度的方向不再相同.
|
图 2 相速度角度与群速度角度的区别示意图 Fig. 2 Schematic diagram of phase velocity and group velocity |
在二维情况下,根据Berryman (1979),相速度和群速度之间的关系可以表示为:
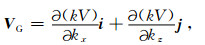
|
(17) |
其中的两项可以分别展开为

|
(18) |
ψ表示群速度的角度,θ表示相速度的角度.借助于(17)式和(18)式,我们可以得到ψ和θ的关系为
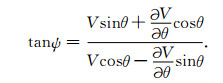
|
(19) |
我们可以通过求解Christoffel方程获得极化向量U(k)(Aki and Richards, 2002; Tsvankin, 2005):
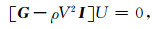
|
(20) |
这里G是Christoffel矩阵Gij=cijklnjnk,cijkl表示四阶弹性张量,nj和nl表示归一化的波矢量,参数V对应着矩阵G的特征值, 也表示不同波(纵横波)的相速度.
在VTI介质中,令ky为0有Christoffel方程:
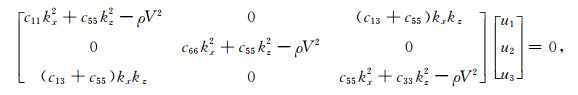
|
(21) |
其中,因
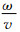
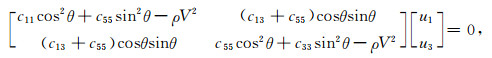
|
(22) |
令

|
(23) |
求得
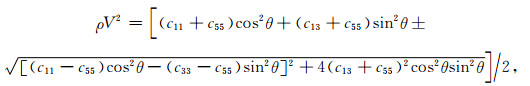
|
(24) |
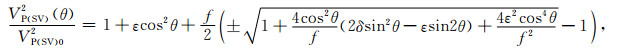
|
(25) |
即

|
(26) |
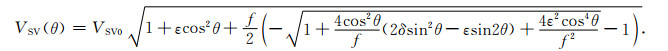
|
(27) |
由此我们就可以得到前面所述的VP(θ), 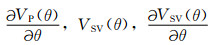
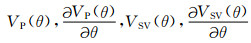
将相速度代入(22)式,我们可以得到相角和极化角的关系(Tsvankin, 1995):

|
(28) |
公式(28)只适合于二维情形,三维TI介质中的模式解耦和成像问题要复杂得多(Wang et al., 2015, 2016), 三维问题是我们以后研究的一个方向.这样我们通过(19)和(28)两式的相角作为桥梁建立起群角和极化角的关系, 完成各向异性介质中波场分离,两者关系可以简单的记作
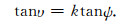
|
(29) |
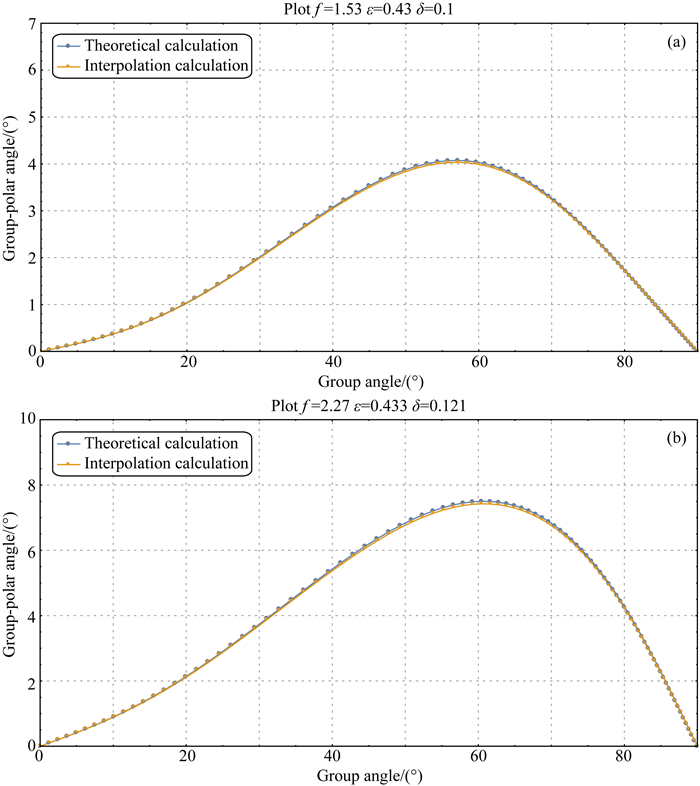
这样在波场延拓过程中求出群角,由公式(29)得到极化角,代入公式(16)可以完成各向异性的波场分离.算法的核心是建立一个群角和极化角的数值表,从公式(4)、(19)和(28)我们可以分析出影响群角和极化角两者关系的是参数:VP/VS, ε, δ.通过计算可以判断出三个影响最大的是VP/VS,其次是ε,最后是Δ.例如我们得到某个模型的参数范围为VP/VS∈[1.5, 2.5],ε∈[0, 0.5], δ∈[0, 0.3],然后我们可以采样:VP/VS间隔为0.1, ε和Δ可以取同样的间隔0.05, 群角ψ按1°来取样.图 4显示了精确计算和插值计算的对比,为了便于分析,我们把群角减去极化角的差做为因变量.浅黄色线条表示精确计算,浅红色线条表示按以上间隔取值,然后插值得到的结果.分析可以看出,插值计算的误差几乎不影响结果.另外需要注意一个问题,坡印廷矢量求取角度在P和S波交叉混叠的地方存在不准确(Zhou and Wang, 2017).在混叠的地方不能准确的分离,图 5中箭头显示了这种情况.这跟传统的拟散度、旋度算子相比是一个不足的地方,优势的地方在于高效的计算和相对较小的存储量,但是对最后的叠加剖面的影响可以忽略.对于TTI介质,我们可以通过VTI介质对应关系经过角度旋转得到.给定TTI介质的Tilt,假定为α,我们的思路是首先经过α的旋转,将角度关系调整到VTI介质所在的平面内或者基准线上,在得到对应关系后,再经过-α的旋转,得到TTI介质的对应关系.

|
图 3 (a) 和(b)分别对应着坡应廷矢量的x和z分量 Fig. 3 (a) and (b) is Poyting vector x-and z-component, respectively |
|
图 4 (a)、(b)分别为二种情况下精确求解和插值求解得到的群角和极化角的差.可以看到即使参数的各项异性程度很高,精确解和插值求解依然吻合的很好.这里的f为VP/VS Fig. 4 (a) and (b) are the difference between the group angle and the polarization angle obtained by solving the exact solution and interpolation in three cases. Note that the exact solutions and interpolation are well matched even if the degree of anisotropic is strong. Here f=VP/VS |

|
图 5 (a) 双层VTI介质波场快照; (b)分离的qP和qS波场快照;(c)极化角(弧度) Fig. 5 (a) Snapshots of the elastic wavefield in the x-and z-direction for a two-layer VTI model; (b) Separated qP-and qS-waves using the separation method proposed in this paper; (c) Polarization angle (radian) |
坡印廷矢量s也称作能流密度,是由坡印廷在1884年提出,用以测量单位时间内穿过单位面积垂直方向的电磁场能量,可用以描述能量传播的方向.Yoon和Marfurt(2006)给出声波波动方程坡印廷矢量计算表达式, 坡应廷矢量也可以用来计算角道集(Dickens and Winbow, 2011; Yoon et al., 2011; Vyas et al., 2011).在弹性波延拓过程中,坡印廷矢量非常容易获得:

|
(30) |
这里j和k表示坡应廷矢量s的x和z分量,式中τjk为应力张量,vk为质点速度矢量.具体来说,从公式(30)可以看到,弹性波坡印廷矢量的表达极其简洁,τjk和vk都是在弹性波延拓过程中天然存在,并不需要刻意进行时间、空间求导处理.在二维情况下,坡印廷矢量的水平分量、垂直分量如图 3所示.我们可以看出,坡印廷矢量表现出很好的方向指示特性.利用群角的定义可以得到:

|
(31) |
在各向同性介质中我们可以用单位化之后的坡印廷矢量
为提高算法的稳定性,我们从局部最小二乘准则出发,得到新的能流密度单位向量为

|
(32) |
式中∑Ω表示在以成像点为中心的邻域Ω中相加求和.本文中值得注意的是,一切与角度有关的运算都以单位向量间运算完成.原因是求取角度需要反三角函数,该运算占用较多时钟周期,且只能取到0到π,另外的0到-π需借助其他的判断准则.单位向量的运算则不存在这些问题,相对方便和快捷.
3.4 各向异性波矢量逆时偏移图 6展示了各项异性弹性逆时偏移的流程,在进行成像之前我们已经根据模型各向异性参数的范围提前计算出群角和极化角的关系,可以看出我们的运算复杂程度和流程的复杂程度大大减少,成像的过程也较为清晰明了.
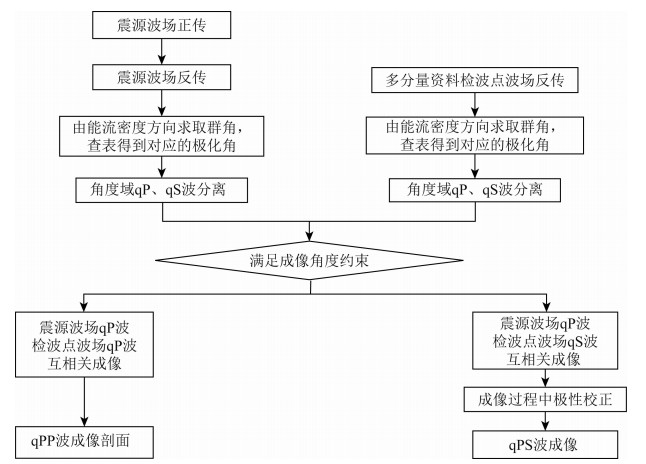
|
图 6 各向异性弹性逆时偏移流程图 Fig. 6 Flowchart of anisotropic elastic reverse time migration |
我们对TI介质进行测试.HTI介质或者TTI介质,都可视为最简单的VTI介质经过角度旋转而成.这里讨论两组介质,它们有着同样的纵波速度、横波速度和密度,均为VP=3000 m·s-1,VS=2000 m·s-1,ρ=2400 kg·cm-3.区别是两者在各向异性参数方面不同:
第一组介质的各向异性参数为ε=0.3,δ=0.1,Tilt=0度, Tilt=45度,其中Tilt为对称轴的倾角;在该组介质中,对于特定时刻波场快照;波场的水平分量和垂直分量如图 7a和7b;分离后的VTI和TTI介质中的qP波和qS波如图 7c、图 7d.
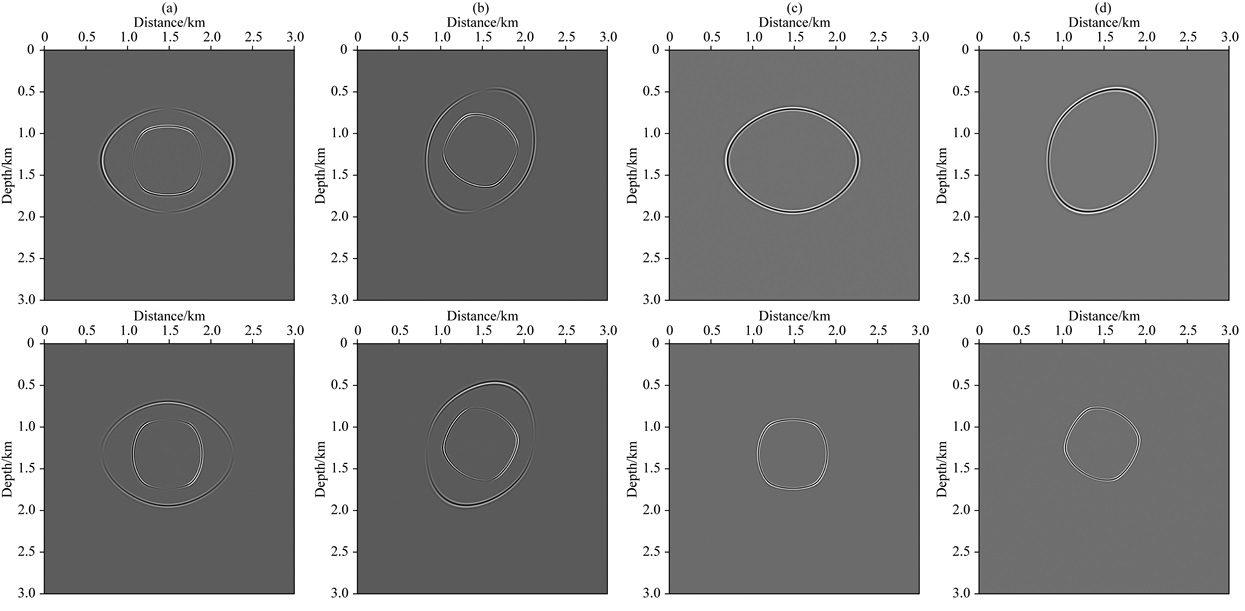
|
图 7 各向异性参数ε=0.3, δ=0.1 (a)波场的水平分量和垂直分罱,tilt=0°; (b)波场的水平分量和垂直分量,tiit=45°; (c)分离后的qP波和qS, tilt=0°: (d)分离后的qP波和qS,tilt=45°. Fig. 7 Anisotropic parameters ε=0.3, δ=0.1 (a) Horizontal and vertical components of the wavefields, tilt=0°; (b) Horizontal and vertical components of the wavefields, tilt=45°; (c) Separated qP-and qS-waves, tilt=0°; (d) Separated qP-and qS-waves, tilt=45°. |
第二组介质的各向异性参数为ε=0.3,δ=-0.1,Tilt=0度, Tilt=45度,其中Tilt为对称轴的倾角;在该组介质中,对于特定时刻波场快照;波场的水平分量和垂直分量如图 8a和8b;分离后的VTI和TTI介质中的qP波和qS波如图 8c、图 8d.

|
图 8 向异性参数ε=0.3, δ=-0.1 (a)波场的水平分短和垂直分童,tilt=45°: (b)波场的水平分虽和垂直分:tilt=45°: (c)分离后的qP波和qS, tilt=0°: (d)分离后的qP波和qS, tilt=45°. Fig. 8 Anisotropic parameters ε=0.3, δ=-0.1 (a) Horizontal and vertical components of the wavefields, tilt=0°; (b) Horizontal and vertical components of the wavefields, tilt=45°; (c) Separated qP-and qS-waves, tilt=0°; (d) Separated qP-and qS-waves, tilt=45° |
再将本方法应用于SEG的Hess模型,得到较好效果.正演算法是逆时偏移的核心,我们这里使用格子法.图 9展示了Hess模型的P波速度、S波速度和各向异性参数,模型大小为横向21702 m,深度为9000 m.包含360炮,炮间距50 m;地面上全偏移距接收,检波点间距10 m;炮集记录长度为6 s,时间采样间隔为0.4 ms.我们用基于非规则网格的格子法进行逆时偏移.在单炮逆时偏移成像完成后,我们将成像剖面投影到规则网格进行展示.图 10a、10b分别展示弹性逆时偏移成像qPP、qPS剖面,图 10c、10d分别展示没有用各向异性的弹性逆时偏移成像qPP、qPS剖面,可以看到各向异性的重要性.图 11是局部对比图.即使对于Hess这种复杂的各向异性模型,构造也得到较好刻画,证实了我们方法的有效性.
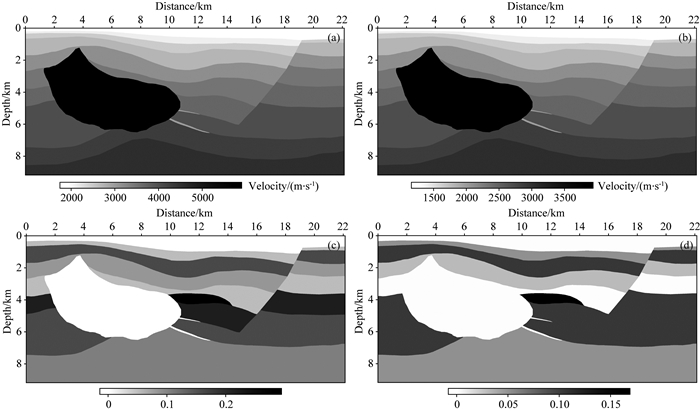
|
图 9 SEG Hess模型参数 (a) P波速度模型; (b) S波速度模型; (c) ε模型; (d) δ模型. Fig. 9 SEG Hess model (a) P-wave velocity model; (b) S-wave velocity model; (c) ε model; (d) δ model. |
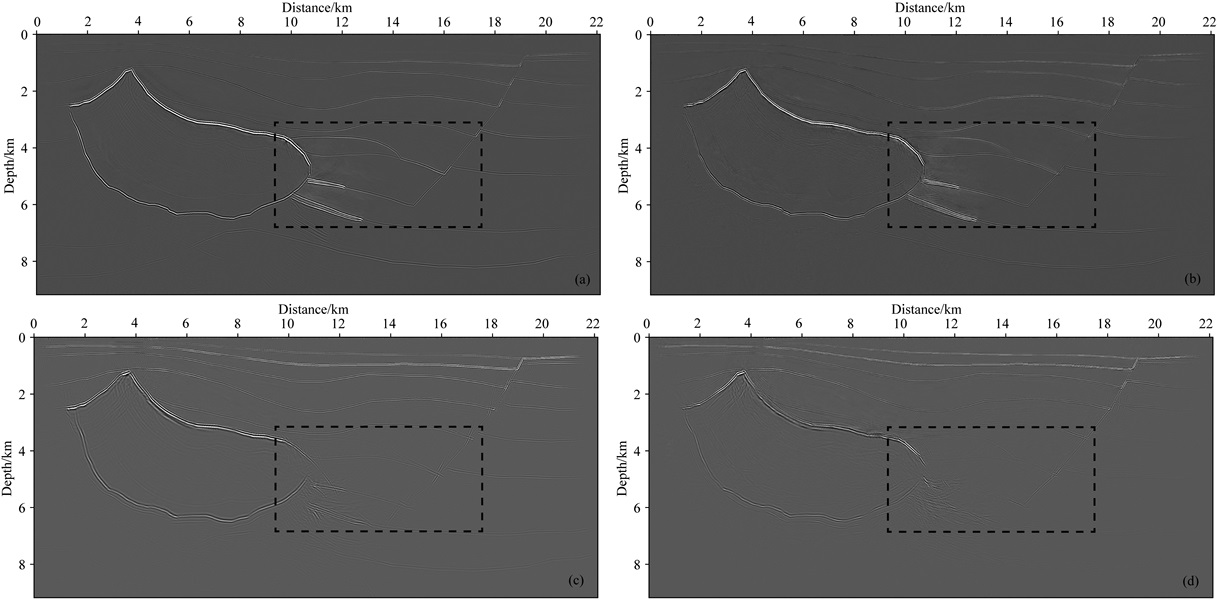
|
图 10 Hess模型叠加成像剖面 (a)各向异性PP波成像剖面; 各向异性PS波成像剖面; (c)各向同性PP波成像剖面; (d)各向同性PS波成像剖面. Fig. 10 Stacked images for Hess model (a) Anisotropic reverse time migration PP images; (b) Anisotropic reverse time migration PS images; (c) Isotropic reverse time migration PP images; (d) Isotropic reverse time migration PS images. |

|
图 11 图 10的局部对比图 (a) PP波成像剖面的局部对比图; (b) PS波成像剖面的局部对比图. Fig. 11 Zoomed in views of Fig.10 (a) Local comparison of PP images; (b) Local comparison of PS images. |
本文在非规则非结构化格子法的基础上,提出了一套弹性各向异性矢量逆时偏移方法.此方法能较好实现各向异性波场分离和成像.根据能流密度的方向特性,在局部最小二乘准则下求取能量传播角度,即群速度角度.各向异性介质中,因为群速度角度和相速度角度不相同,通过相角作为中间桥梁得到极化角,我们可在成像过程中在角度域完成了拟纵横波场分离、大角度低频噪音压制、以及极性反转校正.本方法的优点是一种在角度域快速实施分离的算法,而且存储量很小,适用于规则网格和非规则网格.同时避免在波场延拓过程中多次求导,保持了相位和振幅的特征.虽然在波场复杂情况下存在角度不准确的情况,但是对于叠加成像的影响甚小.以上的数值算例证实了我们方法的有效性.
致谢感谢东方物探提供的数据及模型,本研究受中国石油集团《弹性波地震成像技术合作研发项目》资助.十分感谢两位审稿人耐心与细致的评审,提出建议使我们的工作能够更加的完善.
Aki K, Richards P G. 2002. Quantitative Seismology, Theory and Methods. 2nd ed. San Francisco:W. H. Freeman and Co.
|
|
Alkhalifah T.
1998. Acoustic approximations for processing in transversely isotropic media. Geophysics, 63(2): 623-631.
DOI:10.1190/1.1444361 |
|
Berryman J G.
1979. Long-wave elastic anisotropy in transversely isotropic media. Geophysics, 44(5): 896-917.
DOI:10.1190/1.1440984 |
|
Cheng J B, Kang W, Wang T F.
2013. Description of qP-wave propagation in anisotropic media, Part Ⅰ:Pseudo-pure-mode wave equations. Chinese Journal of Geophysics (in chinese), 56(10): 3474-3486.
DOI:10.6038/cjg20131022 |
|
Cheng J B, Wu Z D, Alkhalifah T. 2014. Simulating propagation of decomposed elastic waves using low-rank approximate mixed-domain integral operators for heterogeneous transversely isotropic media.//SEG Technical Program. Expanded Abstracts, 3393-3399.
|
|
Cheng J B, Fomel S.
2014. Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media. Geophysics, 79(4): C97-C110.
DOI:10.1190/geo2014-0032.1 |
|
Dellinger J, Etgen J.
1990. Wave-field separation in two-dimensional anisotropic media. Geophysics, 55(7): 914-919.
DOI:10.1190/1.1442906 |
|
Dickens T A, Winbow G A. 2011. RTM angle gathers using Poynting vectors.//81th Annual International Meeting, SEG. Expanded Abstracts, 3109-3113.
|
|
Du Q Z, Zhu Y T, Ba J.
2012. Polarity reversal correction for elastic reverse time migration. Geophysics, 77(2): S31-S41.
DOI:10.1190/geo2011-0348.1 |
|
Etgen J T. 1988. Prestacked migration of P and SV-waves.//58th Annual International Meeting, SEG. Expanded Abstracts, 972-975.
|
|
Thomsen L.
1986. Weak elastic anisotropy. Geophysics, 51(10): 1954-1966.
DOI:10.1190/1.1442051 |
|
Liu Q C, Zhang J F, Gao H W.
2017. Reverse-time migration from rugged topography using irregular, unstructured mesh. Geophysical Prospecting, 65(2): 453-466.
DOI:10.1111/gpr.2017.65.issue-2 |
|
Tsvankin I.
1995. Normal moveout from dipping reflectors in anisotropic media. Geophysics, 60(1): 268-284.
DOI:10.1190/1.1443755 |
|
Tsvankin I. 2005. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media, 2nd ed. Amsterdam:Elsevier.
|
|
Vyas M, Nichols D, Mobley E. 2011. Efficient RTM angle gathers using source directions.//81st Annual International Meeting, SEG. Expanded Abstracts, 3136-3140.
|
|
Wang W L, McMechan G A.
2015. Vector-based elastic reverse time migration. Geophysics, 80(6): S245-S258.
DOI:10.1190/geo2014-0620.1 |
|
Wang C L, Cheng J B, Arntsen B. 2015, Imaging condition for converted waves based on decoupled elastic wave modes.//85th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 4385-4390.
|
|
Wang C L, Cheng J B, Arntsen B.
2016. Scalar and vector imaging based on wave mode decoupling for elastic reverse time migration in isotropic and transversely isotropic media. Geophysics, 81(5): S383-S398.
DOI:10.1190/geo2015-0704.1 |
|
Xu Y, Zhang J F.
2008. An irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling. Chinese Journal of Geophysics (in Chinese), 51(5): 1520-1526.
DOI:10.3321/j.issn:0001-5733.2008.05.026 |
|
Yan J, Sava P.
2008. Isotropic angle-domain elastic reverse-time migration. Geophysics, 73(6): S229-S239.
DOI:10.1190/1.2981241 |
|
Yan J, Sava P.
2009b. Elastic wave-mode separation for VTI media. Geophysics, 74(5): WB19-WB32.
DOI:10.1190/1.3184014 |
|
Yan J, Sava P.
2011. Improving the efficiency of elastic wave-mode separation for heterogeneous tilted transverse isotropic media. Geophysics, 76(4): T65-T78.
DOI:10.1190/1.3581360 |
|
Yoon K, Marfurt K J.
2006. Reverse-time migration using the Poynting vector. Exploration Geophysics, 37(1): 102-107.
DOI:10.1071/EG06102 |
|
Yoon K, Guo M H, Cai J, et al. 2011. 3D RTM angle gathers from source wave propagation direction and dip of reflector.//81th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 3136-3140.
|
|
Zhang J F, Liu T L.
1999. P-SV-wave propagation in heterogeneous media:grid method. Geophysical Journal International, 136(2): 431-438.
DOI:10.1111/j.1365-246X.1999.tb07129.x |
|
Zhang J F, Liu T L.
2002. Elastic wave modeling in 3-D heterogeneous media:3-D grid method. Journal International, 150: 780-799.
|
|
Zhang Q S, McMechan G A.
2010. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media. Geophysics, 75(3): D13-D26.
DOI:10.1190/1.3431045 |
|
Zhe J P, Greenhalgh S A.
1997. Prestack multicomponent migration. Geophysics, 62(2): 598-613.
DOI:10.1190/1.1444169 |
|
Zhou Y, Wang H Z.
2017. Efficient wave-mode separation in vertical transversely isotropic media. Geophysics, 82(2): C35-C47.
DOI:10.1190/geo2016-0191.1 |
|
程玖兵, 康玮, 王腾飞.
2013. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程. 地球物理学报, 56(10): 3474–3486.
DOI:10.6038/cjg20131022 |
|
徐义, 张剑锋.
2008. 地震波数值模拟的非规则网格PML吸收边界. 地球物理学报, 51(5): 1520–1526.
DOI:10.3321/j.issn:0001-5733.2008.05.026 |
|
 2017, Vol. 60
2017, Vol. 60

